Identification of the Physical and Mechanical Properties of Moroccan Sisal Yarns Used as Reinforcements for Composite Materials
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Characterization of Sisal Fibers
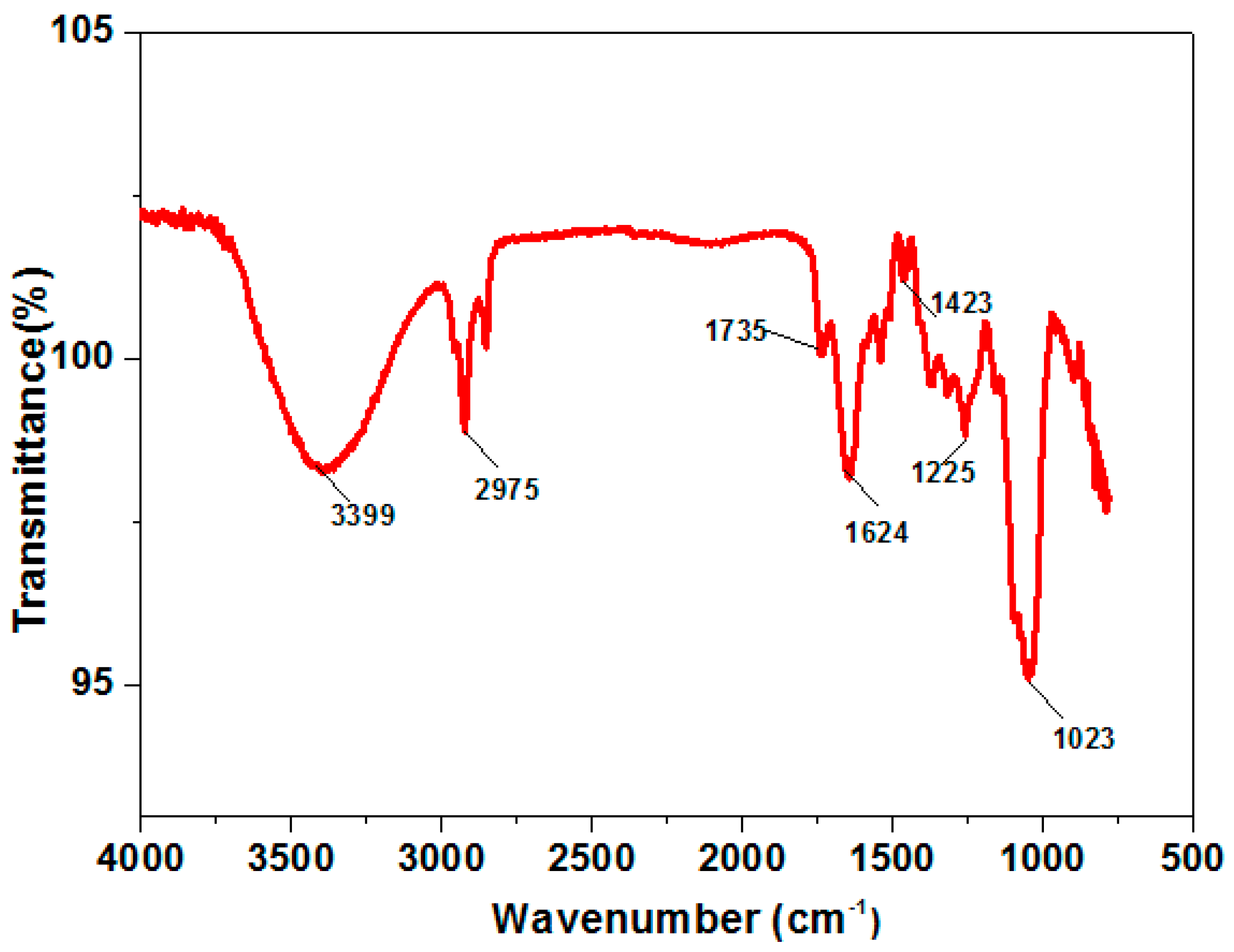
2.2.1. FTIR Analysis
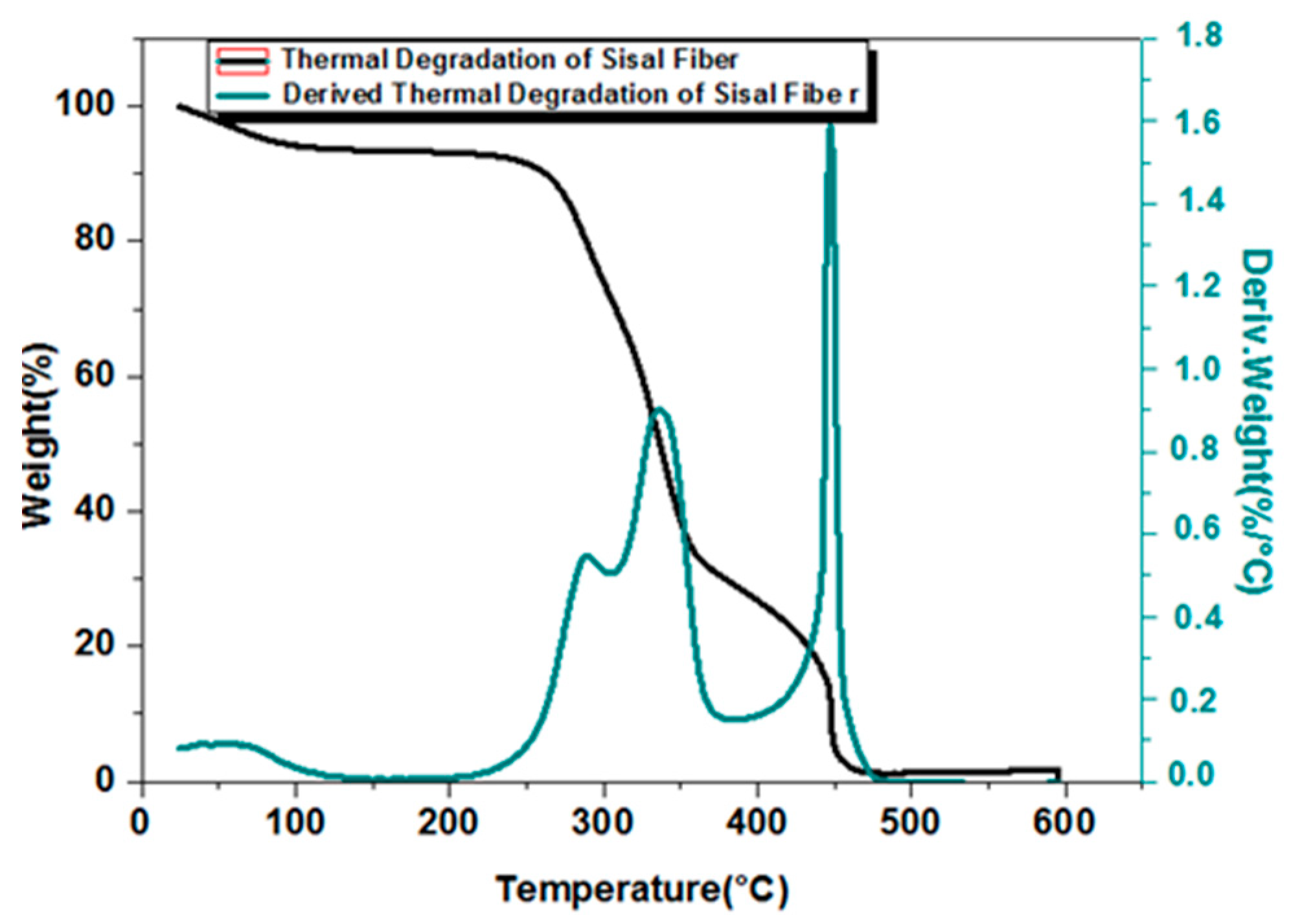
2.2.2. Thermogravimetric Analysis (TGA)
2.2.3. Contact Angle Measurement
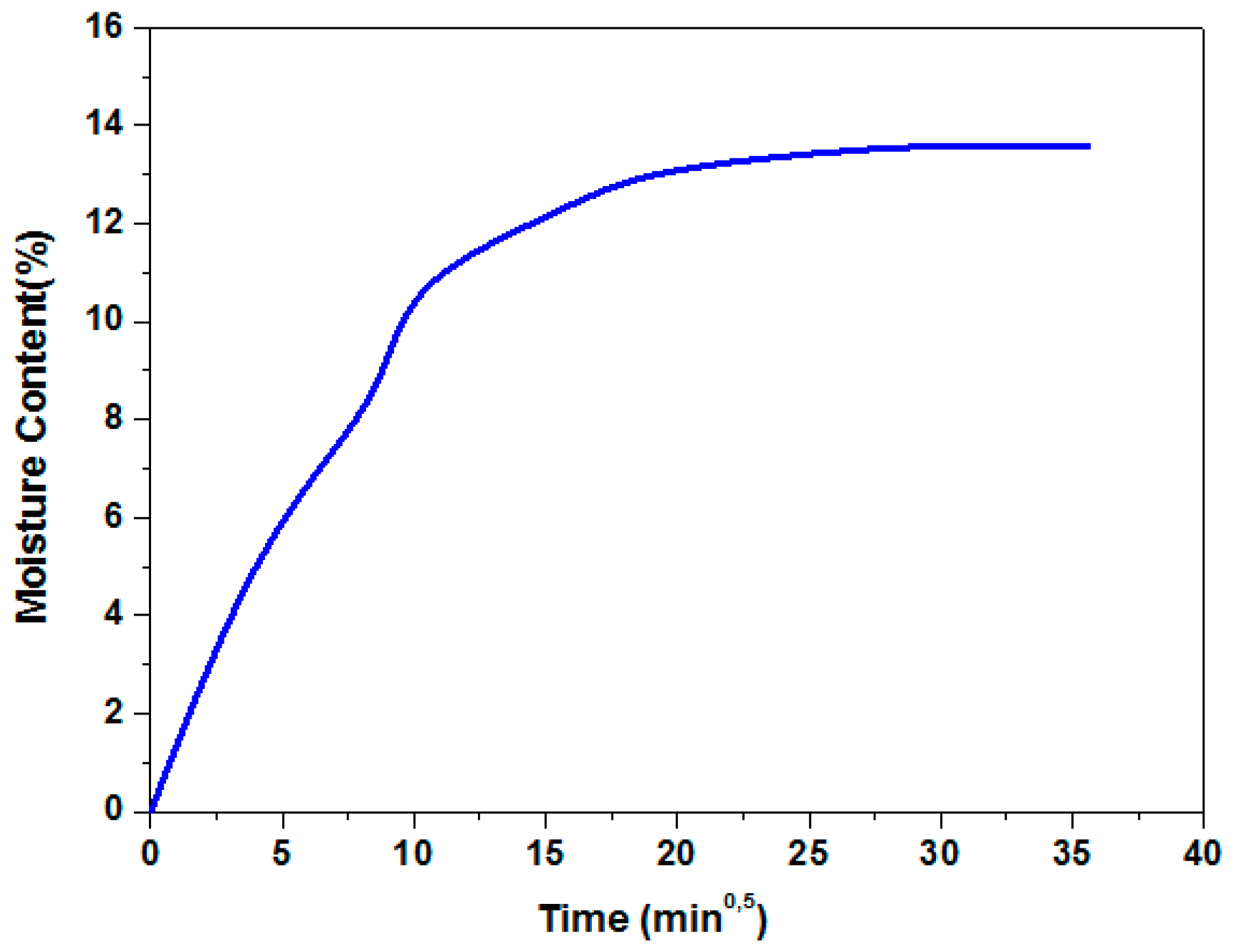
2.2.4. Moisture Absorption Analysis
2.2.5. Fiber Geometry
2.2.6. Impregnated Fiber Bundle Test
- Ef, Ec and Em are the stiffness of fibers, composites and the matrix, respectively.
- Vf, Vm and Vp are the volume fraction of fibers, the matrix and porosity, respectively.
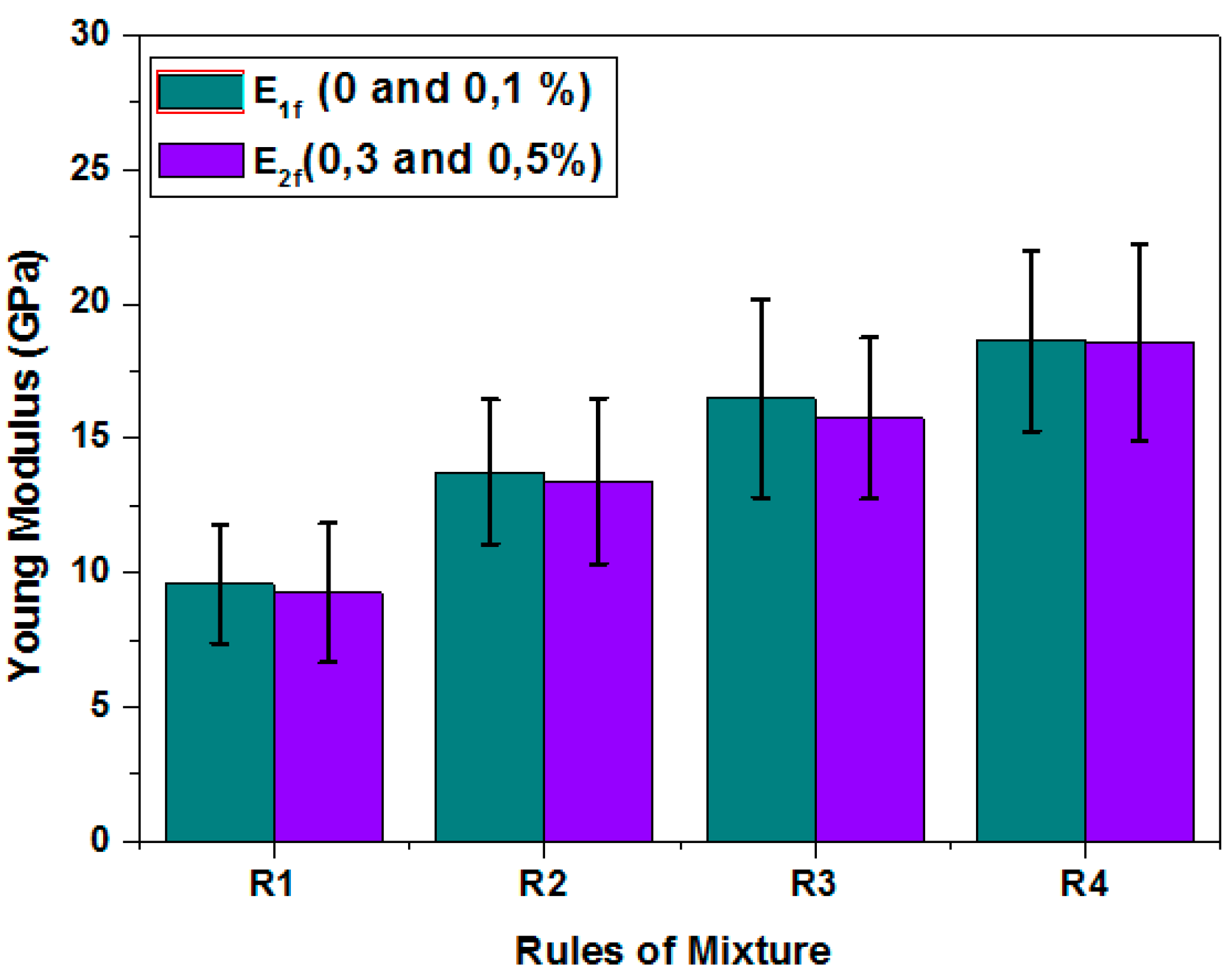
- n is the porosity efficiency exponent. If n = 0, Equation (4) does not consider the level of porosity and will be denoted here as rule of mixtures R1. n = 2 corresponds to the general value of the composites based on natural fibers (denoted here, rule of mixtures R2).
- ƞ0 is the fiber orientation efficiency factor.
- ρ is the density of Moroccan sisal fibers (1.45 kg/m3);
- L is the linear density of sisal yarns (3300 Tex);
- T is the twist level in tpm (turns per meters);
2.3. Characterization of Sisal Yarns
2.3.1. Diameter and Linear Density Measurement
2.3.2. Tensile Analysis
3. Results and Discussion
3.1. FTIR spectroscopy of Sisal Fibers
3.2. Thermal Behavior of Sisal Fibers
3.3. Contact Angle of Sisal Fibers
3.4. Moisture Absorption
3.5. Structural Fiber Geometry
3.6. Tensile Properties of Sisal Fibers
3.7. Diameter and Linear Density of Sisal Yarns
- ρ is the density of Moroccan sisal fibers (1.45 kg/m3).
- T is the twist level in tpm (turns per meters).
- KTex is the linear density of yarns (Ktex).
- ρ is the density of Moroccan sisal fibers (1.45 kg/m3).
- KTex is the linear density of yarns (Ktex).
- Afil is the yarn cross-sectional area (m2).
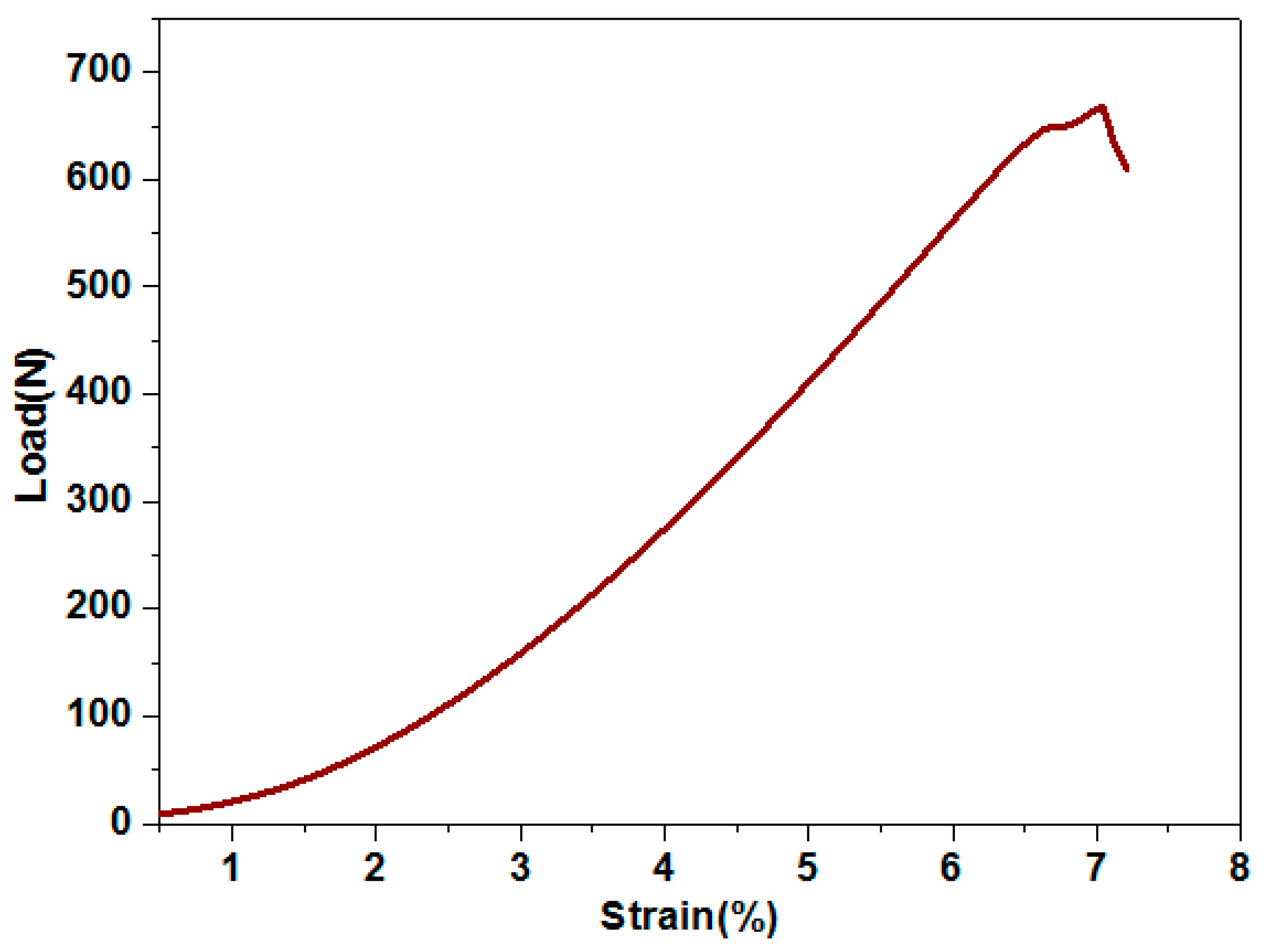
3.8. Tensile Behavior of Sisal Yarns
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- La Mantia, F.P.; Morreale, M. Green composites: A brief review. Compos. Part A Appl. Sci. Manuf. 2011, 42, 579–588. [Google Scholar] [CrossRef]
- Zini, E.; Scandola, M. Green composites: An overview. Polym. Compos. 2011, 32, 1905–1915. [Google Scholar] [CrossRef]
- Dicker, M.P.; Duckworth, P.F.; Baker, A.B.; François, G.; Hazzard, M.K.; Weaver, P.M. Green composites: A review of material attributes and complementary applications. Compos. Part A Appl. Sci. Manuf. 2014, 56, 280–289. [Google Scholar] [CrossRef]
- Fowler, P.A.; hughes, J.M.; Elias, R.M. Biocomposites: Technology, environmental credentials and market forces. J. Sci. Food Agric. 2006, 86, 1781–1789. [Google Scholar] [CrossRef]
- Gurunathan, T.; Mohanty, S.; Nayak, S.K. A review of the recent developments in biocomposites based on natural fibers and their application perspectives. Compos. Part A Appl. Sci. Manuf. 2015, 77, 1–25. [Google Scholar] [CrossRef]
- Satyanarayana, K.G.; Arizaga, G.G.C.; Wypych, F. Biodegradable composites based on lignocellulosic fibers—An overview. Prog. Polym. Sci. 2009, 34, 982–1021. [Google Scholar] [CrossRef]
- Ravi, M.; Dubey, R.R.; Shome, A.; Guha, S.; Kumar, C.A. Effect of surface treatment on Natural fibers composite. IOP Publ. 2018, 376. [Google Scholar] [CrossRef]
- Joshi, S.V.; Drzal, L.T.; Mohanty, A.K.; Arora, S. Are natural fiber composites environmentally superior to glass fiber reinforced composites? Compos. Part A Appl. Sci. Manuf. 2004, 35, 371–376. [Google Scholar] [CrossRef]
- Wu, Y.; Xia, C.; Cai, L.; Garcia, A.C.; Shi, S.Q. Development of natural fiber-reinforced composite with comparable mechanical properties and reduced energy consumption and environmental impacts for replacing automotive glass-fiber sheet molding compound. J. Clean. Prod. 2018, 184, 92–100. [Google Scholar] [CrossRef]
- Biswas, S.; Satapathy, A. A comparative study on erosion characteristics of red mud filled bamboo-epoxy and glass-epoxy composites. Mater. Des. 2010, 31, 1752–1767. [Google Scholar] [CrossRef]
- Mohammed, L.; Ansari, M.N.; Pua, G.; Jawaid, M.; Islam, M.S. A review on natural fiber reinforced polymer composite and its applications. Int. J. Polym. Sci. 2015, 2015. [Google Scholar] [CrossRef]
- Gallo, E.; Schartel, B.; Acierno, D.; Cimino, F.; Russo, P. Tailoring the flame retardant and mechanical performances of natural fiber-reinforced biopolymer by multi-component laminate. Compos. Part B Eng. 2013, 44, 112–119. [Google Scholar] [CrossRef]
- Sanjay, M.R.; Siengchin, S.; Parameswaranpillai, J.; Jawaid, M.; Pruncu, C.I.; Khan, A. A comprehensive review of techniques for natural fibers as reinforcement in composites: Preparation, processing and characterization. Carbohydr. Polym. 2019, 207, 108–121. [Google Scholar]
- Kim, H.S.; Lee, B.H.; Kim, H.J.; Yang, H.S. Mechanical-thermal properties and VOC emissions of natural-flour-filled biodegradable polymer hybrid bio-composites. J. Polym. Environ. 2011, 19, 628–636. [Google Scholar] [CrossRef]
- Lansiaux, H.; Soulat, D.; Boussu, F.; Labanieh, A.R. Manufacture and Characterization of 3D Warp Interlock Fabric Made of Flax Roving. In Proceedings of the 13th International Conference on Textile Composites (TEXCOMP-13), Milan, Italy, 17–19 September 2018. [Google Scholar]
- Mounika, M.; Ramaniah, K.; Prasad, A.R.; Rao, K.M.; Reddy, K.H.C. Thermal conductivity characterization of bamboo fiber reinforced polyester composite. J. Mater. Environ. Sci. 2012, 3, 1109–1116. [Google Scholar]
- Cai, M.; Takagi, H.; Nakagaito, A.N.; Li, Y.; Waterhouse, G.I. Effect of alkali treatment on interfacial bonding in abaca fiber-reinforced composites. Compos. Part A Appl. Sci. Manuf. 2016, 90, 589–597. [Google Scholar] [CrossRef]
- Zihlif, A.M.; Ragosta, G. A study on the physical properties of rock wool fiber—Polystyrene composite. J. Thermoplast. Compos. Mater. 2003, 16, 273–283. [Google Scholar] [CrossRef]
- Yuan, Q.; Yao, J.; Chen, X.; Huang, L.; Shao, Z. The preparation of high performance silk fiber/fibroin composite. Polymer 2010, 51, 4843–4849. [Google Scholar] [CrossRef]
- Pothan, L.A.; Oommen, Z.; Thomas, S. Dynamic mechanical analysis of banana fiber reinforced polyester composites. Compos. Sci. Technol. 2003, 63, 283–293. [Google Scholar] [CrossRef]
- Devi, L.U.; Bhagawan, S.S.; Thomas, S. Mechanical properties of pineapple leaf fiber-reinforced polyester composites. J. Appl. Polym. Sci. 1997, 64, 1739–1748. [Google Scholar] [CrossRef]
- Akil, H.; Omar, M.F.; Mazuki, A.A.M.; Safiee, S.Z.A.M.; Ishak, Z.M.; Bakar, A.A. Kenaf fiber reinforced composites: A review. Mater. Des. 2011, 32, 4107–4121. [Google Scholar] [CrossRef]
- Yu, T.; Ren, J.; Li, S.; Yuan, H.; Li, Y. Effect of fiber surface-treatments on the properties of poly (lactic acid)/ramie composites. Compos. Part A Appl. Sci. Manuf. 2010, 41, 499–505. [Google Scholar] [CrossRef]
- Kim, S.J.; Moon, J.B.; Kim, G.H.; Ha, C.S. Mechanical properties of polypropylene/natural fiber composites: Comparison of wood fiber and cotton fiber. Polym. Test. 2008, 27, 801–806. [Google Scholar] [CrossRef]
- Rao, K.M.M.; Rao, K.M. Extraction and tensile properties of natural fibers: Vakka, date and bamboo. Compos. Struct. 2007, 77, 288–295. [Google Scholar] [CrossRef]
- Komuraiah, A.; Kumar, N.S.; Prasad, B.D. Chemical composition of natural fibers and its influence on their mechanical properties. Mech. Compos. Mater. 2014, 50, 359–376. [Google Scholar] [CrossRef]
- Singh, B.; Gupta, M.; Tarannum, H.; Randhawa, A. Natural Fiber-Based Composite Building Materials. In Cellulose Fibers: Bio-and Nano-Polymer Composites; Kalia, S., Kaith, B.S., Kaur, I., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 154–196. [Google Scholar]
- Corbin, A.C.; Boussu, F.; Ferreira, M.; Soulat, D. Influence of 3D warp interlock fabrics parameters made with flax rovings on their final mechanical Behavior. J. Ind. Text. 2020, 49, 1123–1144. [Google Scholar] [CrossRef]
- Kim, J.T.; Netravali, A.N. Development of aligned-hemp yarn-reinforced green composites with soy protein resin: Effect of pH on mechanical and interfacial properties. Compos. Sci. Technol. 2011, 71, 541–547. [Google Scholar] [CrossRef]
- Prapavesis, A.; Tojaga, V.; Östlund, S.; van Vuure, A.W. Back calculated compressive properties of flax fibers utilizing the Impregnated Fiber Bundle Test (IFBT). Compos. Part A Appl. Sci. Manuf. 2020, 135, 105930. [Google Scholar] [CrossRef]
- Bensadoun, F.; Verpoest, I.; Baets, J.; Müssig, J.; Graupner, N.; Davies, P.; Gomina, M.; Kervoelen, A.; Baley, C. Impregnated fiber bundle test for natural fibers used in composites. J. Reinf. Plast. Compos. 2017, 36, 942–957. [Google Scholar] [CrossRef]
- Lansiaux, H.; Soulat, D.; Boussu, F.; Labanieh, A.R. Development and Multiscale Characterization of 3D Warp Interlock Flax Fabrics with Different Woven Architectures for Composite Applications. Fibers 2020, 8, 15. [Google Scholar] [CrossRef]
- Mukherjee, P.S.; Satyanarayana, K.G. Structure and properties of some vegetable fibers. J. Mater. Sci. 1984, 19, 3925–3934. [Google Scholar] [CrossRef]
- Mishra, S.; Mohanty, A.K.; Drzal, L.T.; Misra, M.; Hinrichsen, G. A review on pineapple leaf fibers, sisal fibers and their biocomposites. Macromol. Mater. Eng. 2004, 289, 955–974. [Google Scholar] [CrossRef]
- Mwaikambo, L.A.; Ansell, M.P. Mechanical properties of alkali treated plant fibers and their potential as reinforcement materials. I. Hemp fibers. J. Mater. Sci. 2006, 41, 2483–2496. [Google Scholar] [CrossRef]
- Jayabal, S.; Gurusideswar, S. Comparison of Mathematical Model and ANN Model for the prediction of Thrust and Torque forces in drilling of NFRC. In Proceedings of the 2nd National Conference on “Advances in Mechanical Sciences”, Coimbatore, India, 27–28 March 2008. [Google Scholar]
- Malkapuram, R.; Kumar, V.; Negi, Y.S. Recent development in natural fiber reinforced polypropylene composites. J. Reinf. Plast. Compos. 2009, 28, 1169–1189. [Google Scholar] [CrossRef]
- Chand, N.; Tiwary, R.K.; Rohatgi, P.K. Bibliography resource structure properties of natural cellulosic fibers—An annotated bibliography. J. Mater. Sci. 1988, 23, 381–387. [Google Scholar] [CrossRef]
- Belaadi, A.; Bezazi, A.; Bourchak, M.; Scarpa, F. Tensile static and fatique Behavior of sisal fibers. Mater. Des. 2013, 46, 76–83. [Google Scholar] [CrossRef]
- Belaadi, A.; Bezazi, A.; Bourchak, M.; Scarpa, F.; Zhu, C. Thermochemical and statistical mechanical properties of natural sisal fibers. Compos. Part B Eng. 2014, 67, 481–489. [Google Scholar] [CrossRef]
- Samouh, Z.; Molnar, K.; Boussu, F.; Cherkaoui, O.; El Moznine, R. Mechanical and thermal characterization of sisal fiber reinforced polylactic acid composites. Polym. Adv. Technol. 2019, 30, 529–537. [Google Scholar] [CrossRef]
- de Andrade Silva, F.; Chawla, N.; de Toledo Filho, R.D. Tensile Behavior of high performance natural (sisal) fibers. Compos. Sci. Technol. 2008, 68, 3438–3443. [Google Scholar] [CrossRef]
- Pappu, A.; Pickering, K.L.; Thakur, V.K. Manufacturing and characterization of sustainable hybrid composites using sisal and hemp fibers as reinforcement of poly (lactic acid) via injection moulding. Ind. Crop. Prod. 2019, 137, 260–269. [Google Scholar] [CrossRef]
- Okeola, A.A.; Abuodha, S.O.; Mwero, J. Experimental investigation of the physical and mechanical properties of Sisal fiber-reinforced concrete. Fibers 2018, 6, 53. [Google Scholar] [CrossRef]
- Moghaddam, M.S.; Claesson, P.M.; Wålinder, M.E.; Swerin, A. Wettability and liquid sorption of wood investigated by Wilhelmy plate method. Wood Sci. Technol. 2014, 48, 161–176. [Google Scholar] [CrossRef]
- Célino, A.; Fréour, S.; Jacquemin, F.; Casari, P. Characterization and modeling of the moisture diffusion Behavior of natural fibers. J. Appl. Polym. Sci. 2013, 130, 297–306. [Google Scholar] [CrossRef]
- Ho Thi, T.N. Étude de L’influence de la Température et de L’humidité sur les Propriétés Mécaniques en Traction des Fibers de Chanvre et de Coco. Ph.D. Thesis, École de Technologie Supérieure, Montreal, QC, Canada, 28 April 2008. [Google Scholar]
- Gudayu, A.D.; Steuernagel, L.; Meiners, D.; Gideon, R. Effect of surface treatment on moisture absorption, thermal, and mechanical properties of sisal fiber. J. Ind. Text. 2020. [Google Scholar] [CrossRef]
- Shah, D.U.; Schubel, P.J.; Clifford, M.J. Modelling the effect of yarn twist on the tensile strength of unidirectional plant fiber yarn composites. J. Compos. Mater. 2013, 47, 425–436. [Google Scholar] [CrossRef]
- Madsen, B.; Thygesen, A.; Lilholt, H. Plant fiber composites-porosity and stiffness. Compos. Sci. Technol. 2009, 69, 1057–1069. [Google Scholar] [CrossRef]
- Fan, M.; Dai, D.; Huang, B. Fourier Spectroscopy for Natural Fibers Transform Infrared. In Fourier Transform Materials Analysis; Salih, S., Ed.; Intech: Rijeka, Croatia, 2012; pp. 45–68. [Google Scholar]
- Hinterstoisser, B.; Salmén, L. Application of dynamic 2D FTIR to cellulose. Vib. Spectrosc. 2000, 22, 111–118. [Google Scholar] [CrossRef]
- Srivastava, H.C.; Adams, G.A. Uronic Acid Components of Jute Fiber Hemicellulose. J. Am. Chem. Soc. 1959, 81, 2409–2412. [Google Scholar] [CrossRef]
- Célino, A.; Gonçalves, O.; Jacquemin, F.; Fréour, S. Utilisation de la spectrométrie infrarouge pour une quantification rapide du taux d’humidité dans des fibres végétales. Rev. Compos. Matériaux Av. 2014, 24, 81–95. [Google Scholar] [CrossRef]
- Orfão, J.J.; Antunes, F.J.; Figueiredo, J.L. Pyrolysis kinetics of lignocellulosic materials—Three independent reactions model. Fuel 1999, 78, 349–358. [Google Scholar] [CrossRef]
- Poletto, M.; Júnior, H.L.O.; Zattera, A.J. Thermal Decomposition of Natural Fibers: Kinetics and Degradation Mechanisms. In Reactions and Mechanisms in Thermal Analysis of Advanced Materials; Tiwari, A., Raj, B., Eds.; Wiley & Sons: Hoboken, NJ, USA, 2015; pp. 515–545. [Google Scholar]
- Antal, M.J.; Varhegyi, G.; Jakab, E. Cellulose pyrolysis kinetics: Revisited. Ind. Eng. Chem. Res. 1998, 37, 1267–1275. [Google Scholar] [CrossRef]
- Grønli, M.G.; Várhegyi, G.; Di Blasi, C. Thermogravimetric analysis and devolatilization kinetics of wood. Ind. Eng. Chem. Res. 2002, 41, 4201–4208. [Google Scholar] [CrossRef]
- Lau, K.T.; Hung, P.Y.; Zhu, M.H.; Hui, D. Properties of natural fiber composites for structural engineering applications. Compos. Part B Eng. 2018, 136, 222–233. [Google Scholar] [CrossRef]
- John, M.J.; Anandjiwala, R.D. Recent developments in chemical modification and characterization of natural fiber-reinforced composites. Polym. Compos. 2008, 29, 187–207. [Google Scholar] [CrossRef]
- Pucci, M.F.; Liotier, P.J.; Drapier, S. Caractérisation de la Mouillabilité de Fibers—Application aux Fibers Naturelles. Characterization of Fiber Wettability—Application to Natural Fibers. In Proceedings of the Comptes Rendus des JNC 20—École des Ponts ParisTech, Paris, France, 28–30 June 2017. [Google Scholar]
- Roy, A.; Chakrborty, S.; Kundu, S.P.; Basak, R.K.; Majumder, S.B.; Adhikari, B. Improvement in mechanical properties of jute fibers through mild alkali treatment as demonstrated by utilisation of the Weibull distribution model. Bioresour. Technol. 2012, 107, 222–228. [Google Scholar] [CrossRef] [PubMed]
- Morton, W.E.; Hearle, J.W.S. Equilibrium Absorption of Water. In Physical Properties of Textile Fibers, 4th ed.; Morton, W.E., Hearle, J.W.S., Eds.; CRC Press: Cambridge, UK, 2008; pp. 178–194. [Google Scholar]
- Baley, C.; Le Duigou, A.; Bourmaud, A.; Davies, P. Influence of drying on the mechanical behaviour of flax fibres and their unidirectional composites. Compos. Part A Appl. Sci. Manuf. 2012, 43, 1226–1233. [Google Scholar] [CrossRef]
- Nam, S.; Netravali, A.N. Green composites. I. Physical properties of ramie fibers for environment-friendly green composites. Fibers Polym. 2006, 7, 372–379. [Google Scholar] [CrossRef]
- Sgriccia, N.; Hawley, M.C.; Misra, M. Characterization of natural fiber surfaces and natural fiber composites. Compos. Part A Appl. Sci. Manuf. 2008, 39, 1632–1637. [Google Scholar] [CrossRef]
- Joseph, P.V.; Joseph, K.; Thomas, S. Short sisal fiber reinforced polypropylene composites: The role of interface modification on ultimate properties. Compos. Interfaces 2002, 9, 171–205. [Google Scholar] [CrossRef]
- Taj, S.; Munawar, M.A.; Khan, S. Natural fiber-reinforced polymer composites. Proc. Pak. Acad. Sci. 2007, 44, 129. [Google Scholar]
- Alias, A.H.; Tahir, P.M.; Abdan, K.; Sapuan, M.S.; Wahab, M.S.; Saiman, M.P. Evaluation of kenaf yarn properties as affected by different linear densities for woven fabric laminated composite production. Sains Malays. 2018, 47, 1853–1860. [Google Scholar] [CrossRef]
- Belaadi, A.; Bourchak, M.; Aouici, H. Mechanical properties of vegetal yarn: Statistical approach. Compos. Part B Eng. 2016, 106, 139–153. [Google Scholar] [CrossRef]
- Xue, D.; Hu, H. Mechanical properties of biaxial weft-knitted flax composites. Mater. Des. 2013, 46, 264–269. [Google Scholar] [CrossRef]
- Shukla, A.; Basak, S.; Ali, S.W.; Chattopadhyay, R. Development of fire retardant sisal yarn. Cellulose 2017, 24, 423–434. [Google Scholar] [CrossRef]





| Fibers | Tensile Strength (Mpa) | Young Modulus (Gpa) | Failure Strain (%) | References |
|---|---|---|---|---|
| hemp | 40 | 37.5 | 2.5 | [35] |
| Coir | 131–220 | 4–6 | 15–40 | [36] |
| Sisal | 468–700 | 9.4–38 | 2.0–7.0 | [36] |
| Jute | 400–800 | 10–30 | 1.16–1.8 | [36] |
| Flax | 345–1100 | 27.6 | 2.7–3.2 | [37] |
| E-glass | 1800–3500 | 70–73 | 2.5–3.0 | [36] |
| Fiber | Tensile Strength (Mpa) | Young Modulus (GPa) | Fiber Origin | References |
|---|---|---|---|---|
| Sisal Fiber | 391.00 ± 89 | 10.7 ± 4.0 | Brazil | [42] |
| 462.00 ± 71 | 7.47 ± 1.37 | Algeria | [39] | |
| 294.00 ± 113 | 9.8 ± 0.9 | India | [43] | |
| 340.02 ± 70.4 | 12.5 ± 7.8 | Morocco | [41] | |
| 371 ± 28 MPa | 12.43 ± 2.23 | Kenya | [44] |
| Fibers | Contact Angle (°) | References | |
|---|---|---|---|
| Sisal Fiber | 73.13 | 53.06 | Current Study |
| Flax Fiber | 73.13 | 41.5 | [61] |
| Jute Fiber | 73.13 | 63.9 | [62] |
| Fiber | Diffusion Coefficient (mm2/s) | Permeability Coefficient (mm2/s) | Moisture Content at t∞ (%) | References |
|---|---|---|---|---|
| Sisal Fiber | 1.77 × 10−4 | 2.00 × 10−4 | 13.6 | Current Study |
| Flax Fiber | 2.00 × 10−4 | - | 12.0 | [46] |
| Jut Fiber | 4.02 × 10−4 | - | 12.3 | [46] |
| Length Interval (mm) | Average Length (mm) | Diameter Interval (µm) | Average Diameter (µm) |
|---|---|---|---|
| 50–110 | 74.5 ± 30.23 | 121.6–411.0 | 239.0 ± 80.18 |
| Fiber | Origin | Elastic Modulus (Gpa) | Method of Testing | References |
|---|---|---|---|---|
| Sisal Fiber | Brazil | 10.7 ± 4.0 | Tensile Test of elementary Fiber | [42] |
| Algeria | 7.47 ± 1.37 | Tensile Test of elementary Fiber | [39] | |
| India | 9.8 ± 0.9 | Tensile Test of elementary Fiber | [43] | |
| Morocco | 12.5 ± 7.8 | Tensile Test of elementary Fiber | [41] | |
| Morocco | 17.02 ± 3.74 | IFBT Method | Current Study |
| Yarn | Average Diameter (mm) | Average Linear Density (Ktex) | Twist Level (Tpm) |
|---|---|---|---|
| Sisal Yarn | 2.01 ± 0.9 | 3.3 ± 0.7 | 80 |
| Sisal Yarns | Method 1 (Theoretical Method with Packing Factor) | Method 2 (Theoretical Method without Packing Factor) | Verification Method Based on the IFBT Samples | Experimental Method |
|---|---|---|---|---|
| Twist Angle | 26.92° | 23.16° | 24.16 ± 3.65° | 23.14 ± 2.75° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samouh, Z.; Cherkaoui, O.; Soulat, D.; Labanieh, A.R.; Boussu, F.; moznine, R.E. Identification of the Physical and Mechanical Properties of Moroccan Sisal Yarns Used as Reinforcements for Composite Materials. Fibers 2021, 9, 13. https://doi.org/10.3390/fib9020013
Samouh Z, Cherkaoui O, Soulat D, Labanieh AR, Boussu F, moznine RE. Identification of the Physical and Mechanical Properties of Moroccan Sisal Yarns Used as Reinforcements for Composite Materials. Fibers. 2021; 9(2):13. https://doi.org/10.3390/fib9020013
Chicago/Turabian StyleSamouh, Zineb, Omar Cherkaoui, Damien Soulat, Ahmad Rashed Labanieh, François Boussu, and Reddad El moznine. 2021. "Identification of the Physical and Mechanical Properties of Moroccan Sisal Yarns Used as Reinforcements for Composite Materials" Fibers 9, no. 2: 13. https://doi.org/10.3390/fib9020013
APA StyleSamouh, Z., Cherkaoui, O., Soulat, D., Labanieh, A. R., Boussu, F., & moznine, R. E. (2021). Identification of the Physical and Mechanical Properties of Moroccan Sisal Yarns Used as Reinforcements for Composite Materials. Fibers, 9(2), 13. https://doi.org/10.3390/fib9020013









