Continuous Fiber Angle Topology Optimization for Polymer Composite Deposition Additive Manufacturing Applications
Abstract
1. Introduction
1.1. Polymer Composite Deposition Additive Manufacturing
1.2. Topology Optimization and Additive Manufacturing
1.3. Simultaneous Topology and Fiber Orientation Optimization
2. Methodology
2.1. CFAO Topology Optimization Formulation
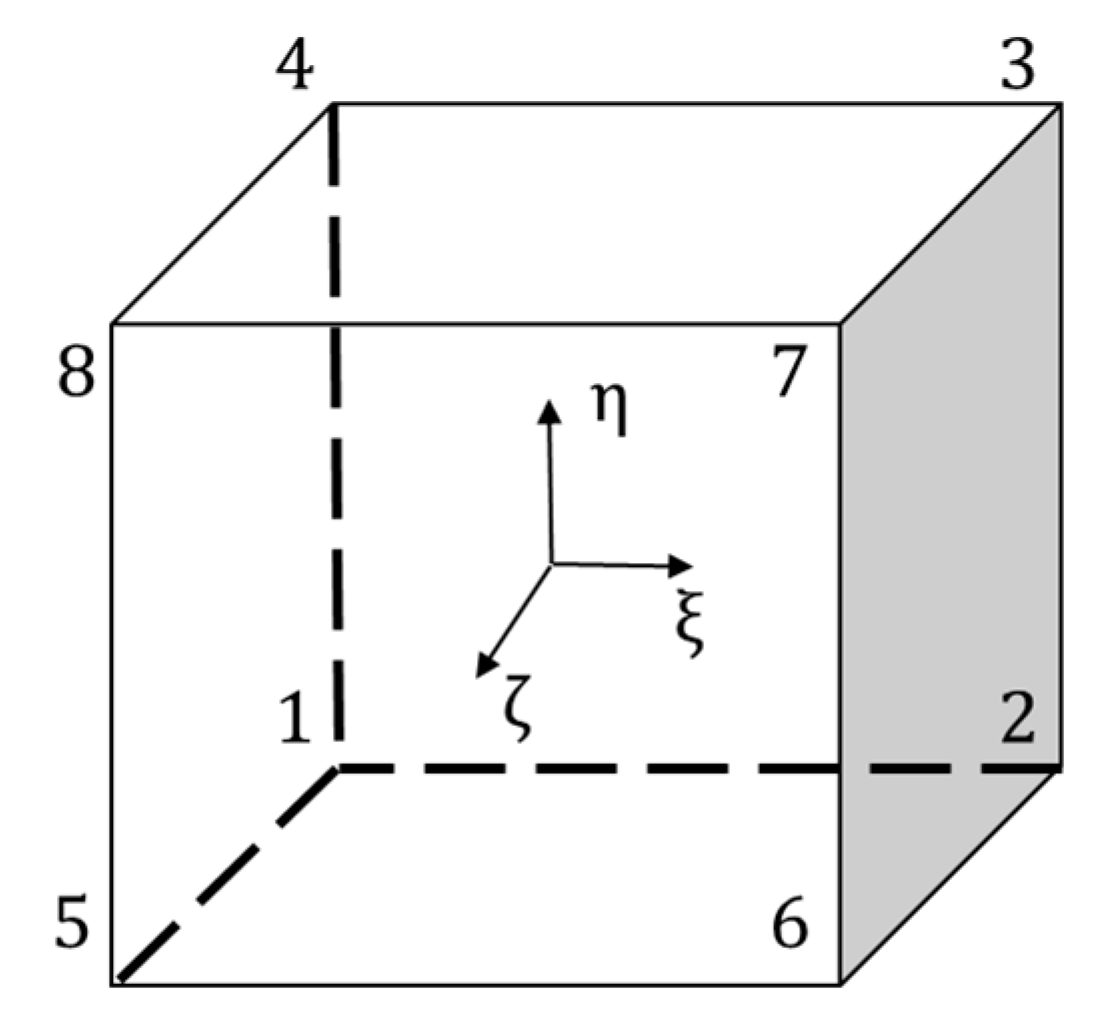
2.2. Isoparametric Hexagonal Element
2.3. Design Sensitivities
2.4. Optimization Process
3. CFAO Design Examples
3.1. One-Dimensional (1D) CFAO Topology Optimization Example
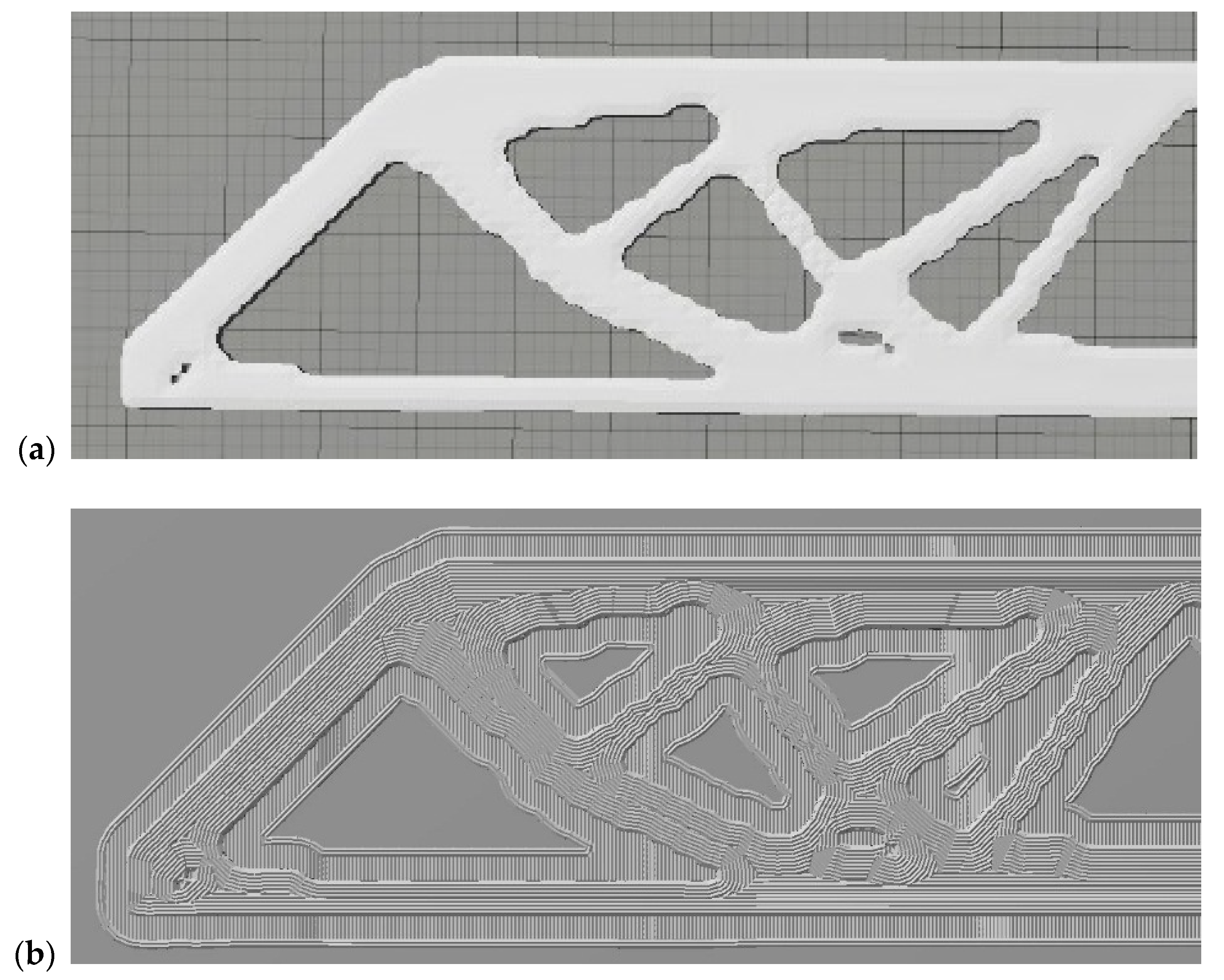
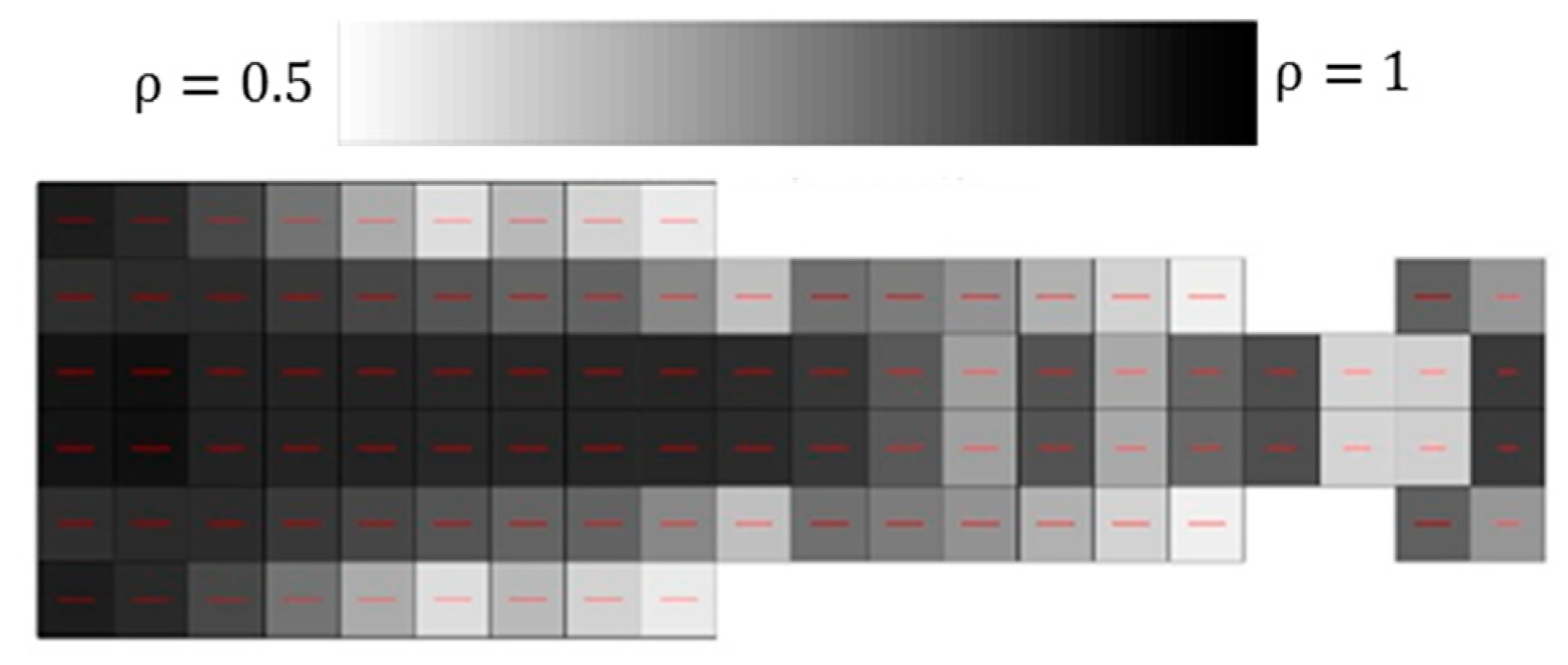
3.2. 2D CFAO Beam Experimental Verification of Computed Results
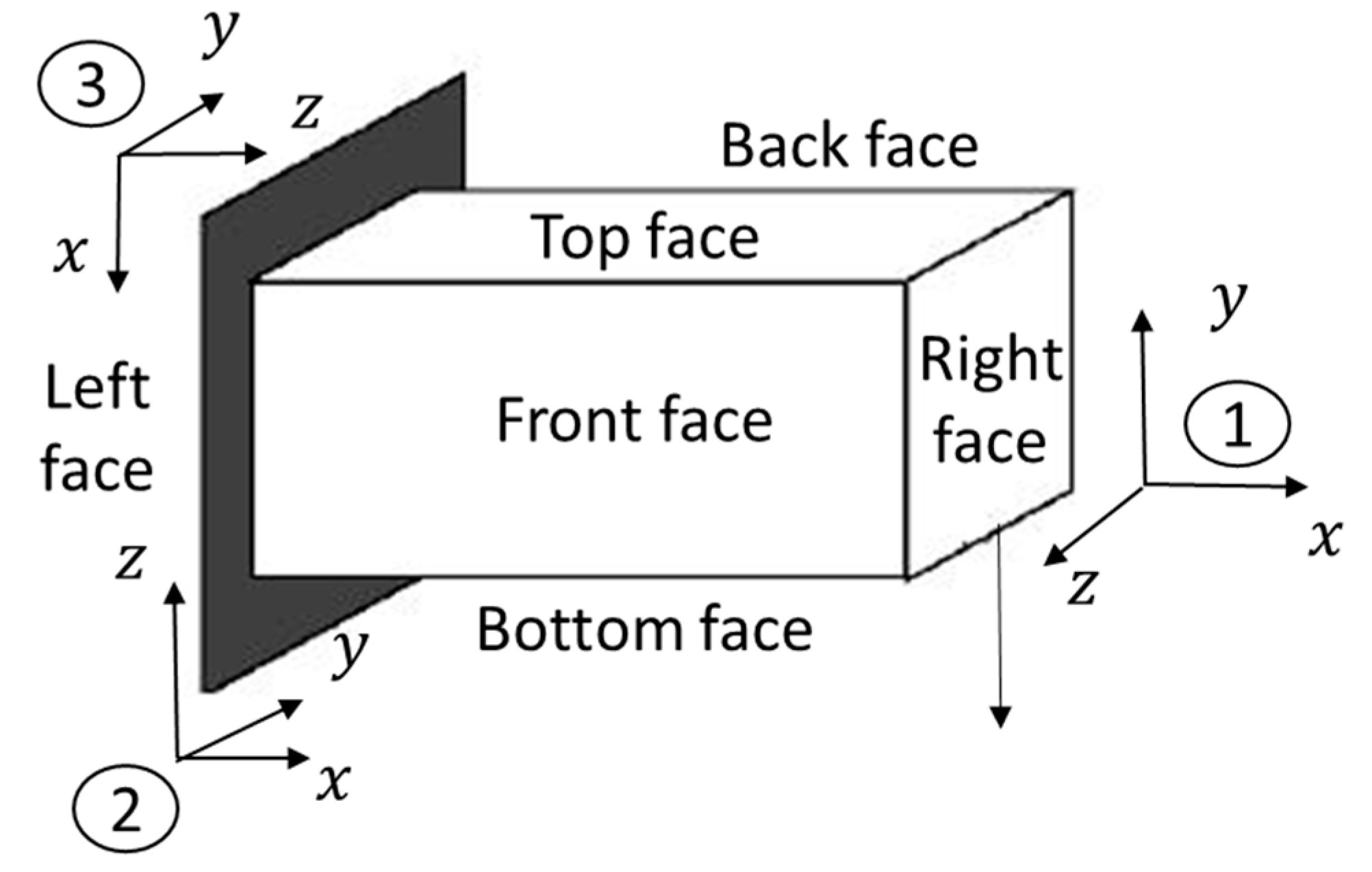
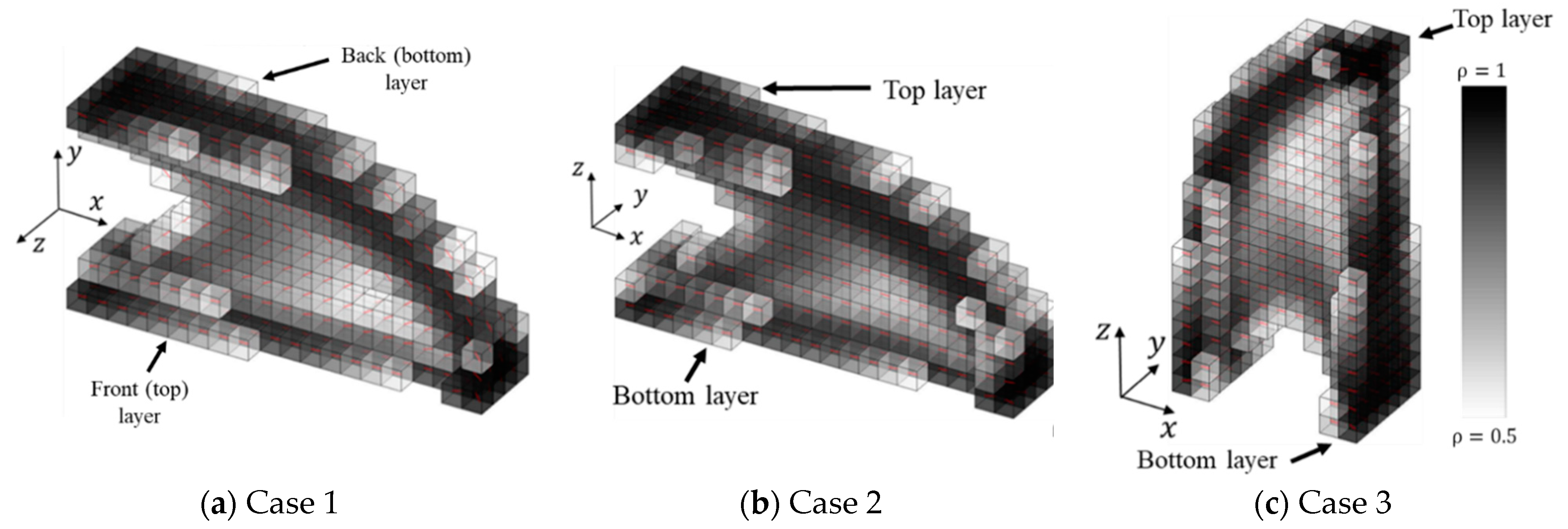
3.3. 3D CFAO Topology Optimization Example
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ahn, S.H.; Montero, M.; Odell, D.; Roundy, S.; Wright, P.K. Anisotropic Material Properties of Fused Deposition Modeling ABS. Rapid Prototyp. J. 2002, 8, 248–257. [Google Scholar] [CrossRef]
- Bagsik, A.; Schöppner, V. Mechanical Properties of Fused Deposition Modeling Parts Manufactured with ULTEM* 9085. In Proceedings of the ANTEC 2011, Boston, MA, USA, 1–5 May 2011. [Google Scholar]
- Ziemian, C.; Sharma, M.; Ziemi, S. Anisotropic Mechanical Properties of ABS Parts Fabricated by Fused Deposition Modelling. In Mechanical Engineering; Gokcek, M., Ed.; InTech Open: London, UK, 2012. [Google Scholar]
- Bendsøe, M.P.; Sigmund, O. Topology Optimization; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Sundararajan, V.G. Topology Optimization for Additive Manufacturing of Customized Meso-Structures Using Homogenization and Parametric Smoothing Functions. Ph.D .Thesis, University of Texas at Austin, Austin, TX, USA, 2010. [Google Scholar]
- Gaynor, A.T.; Meisel, N.A.; Williams, C.B.; Guest, J.K. Multiple-Material Topology Optimization of Compliant Mechanisms Created Via PolyJet Three-Dimensional Printing. J. Manuf. Sci. Eng. 2014, 136, 061015. [Google Scholar] [CrossRef]
- Wang, X.; Xu, S.; Zhou, S.; Xu, W.; Leary, M.; Choong, P.; Qian, M.; Brandt, M.; Xie, Y.M. Topological Design and Additive Manufacturing of Porous Metals for Bone Scaffolds and Orthopaedic Implants: A Review. Biomaterials 2016, 83, 127–141. [Google Scholar] [CrossRef] [PubMed]
- Langelaar, M. Topology Optimization of 3D Self-Supporting Structures for Additive Manufacturing. Addit. Manuf. 2016, 12, 60–70. [Google Scholar] [CrossRef]
- Mass, Y.; Amir, O. Topology Optimization for Additive Manufacturing: Accounting for Overhang Limitations Using a Virtual Skeleton. Addit. Manuf. 2017, 18, 58–73. [Google Scholar] [CrossRef]
- Zhang, P.; Toman, J.; Yu, Y.; Biyikli, E.; Kirca, M.; Chmielus, M.; To, A.C. Efficient Design-Optimization of Variable-Density Hexagonal Cellular Structure by Additive Manufacturing: Theory and Validation. J. Manuf. Sci. Eng. 2015, 137, 021004. [Google Scholar] [CrossRef]
- Wohlers, T. Wohlers Report 2016; Wohlers Associates, Inc.: Fort Collins, CO, USA, 2016. [Google Scholar]
- Perez, A.R.T.; Roberson, D.A.; Wicker, R.B. Fracture Surface Analysis of 3D-Printed Tensile Specimens of Novel ABS-Based Materials. J. Fail. Anal. Prev. 2014, 14, 343–353. [Google Scholar] [CrossRef]
- Zhong, W.; Li, F.; Zhang, Z.; Song, L.; Li, Z. Short Fiber Reinforced Composites for Fused Deposition Modeling. Mater. Sci. Eng. A 2001, 301, 125–130. [Google Scholar] [CrossRef]
- Gray, R.W.; Baird, D.G.; Bøhn, J.H. Thermoplastic Composites Reinforced with Long Fiber Thermotropic Liquid Crystalline Polymers for Fused Deposition Modeling. Polym. Compos. 1998, 19, 383–394. [Google Scholar] [CrossRef]
- Shofner, M.L.; Lozano, K.; Rodríguez-Macías, F.J.; Barrera, E.V. Nanofiber-Reinforced Polymers Prepared by Fused Deposition Modeling. J. Appl. Polym. Sci. 2003, 89, 3081–3090. [Google Scholar] [CrossRef]
- Hwang, S.; Reyes, E.I.; Moon, K.; Rumpf, R.C.; Kim, N.S. Thermo-Mechanical Characterization of Metal/Polymer Composite Filaments and Printing Parameter Study for Fused Deposition Modeling in the 3D Printing Process. J. Electron. Mater. 2014, 44, 771–777. [Google Scholar] [CrossRef]
- Dul, S.; Fambri, L.; Pegoretti, A. Fused Deposition Modelling with ABS–Graphene Nanocomposites. Compos. Part Appl. Sci. Manuf. 2016, 85, 181–191. [Google Scholar] [CrossRef]
- Tekinalp, H.L.; Kunc, V.; Velez-Garcia, G.M.; Duty, C.E.; Love, L.J.; Naskar, A.K.; Blue, C.A.; Ozcan, S. Highly Oriented Carbon Fiber–Polymer Composites via Additive Manufacturing. Compos. Sci. Technol. 2014, 105, 144–150. [Google Scholar] [CrossRef]
- Jiang, D.; Smith, D.E. Anisotropic Mechanical Properties of Oriented Carbon Fiber Filled Polymer Composites Produced with Fused Filament Fabrication. Addit. Manuf. 2017, 18, 84–94. [Google Scholar] [CrossRef]
- Ning, F.; Cong, W.; Qiu, J.; Wei, J.; Wang, S. Additive Manufacturing of Carbon Fiber Reinforced Thermoplastic Composites Using Fused Deposition Modeling. Compos. Part B Eng. 2015, 80, 369–378. [Google Scholar] [CrossRef]
- Love, L.J.; Kunc, V.; Rios, O.; Duty, C.E.; Elliott, A.M.; Post, B.K.; Smith, R.J.; Blue, C.A. The Importance of Carbon Fiber to Polymer Additive Manufacturing. J. Mater. Res. 2014, 29, 1893–1898. [Google Scholar] [CrossRef]
- Love, L.J. Utility of Big Area Additive Manufacturing (BAAM) for the Rapid Manufacture of Customized Electric Vehicles; ORNL/TM-2014/607; Oak Ridge National Lab. (ORNL): Oak Ridge, TN, USA, 2015. [Google Scholar]
- Post, B.; Lloyd, P.D.; Lindahl, J.; Lind, R.F.; Love, L.J.; Kunc, V. The Economics of Big Area Addtiive Manufacturing. In Proceedings of the 27th Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 8–10 August 2016. [Google Scholar]
- Spinnie, N.K. Large Scale Fused Deposition Modeling: The Effect of Process Parameters on Bead Geometry. Master’s Thesis, Baylor University, Waco, TX, USA, 2016. [Google Scholar]
- Heller, B.P.; Smith, D.E.; Jack, D.A. Effects of Extrudate Swell and Nozzle Geometry on Fiber Orientation in Fused Filament Fabrication Nozzle Flow. Addit. Manuf. 2016, 12, 252–264. [Google Scholar] [CrossRef]
- Wang, Z.; Smith, D.E. Rheology Effects on Predicted Fiber Orientation and Elastic Properties in Large Scale Polymer Composite Additive Manufacturing. J. Compos. Sci. 2018, 2, 10. [Google Scholar] [CrossRef]
- Suzuki, K.; Kikuchi, N. A Homogenization Method for Shape and Topology Optimization. Comput. Methods Appl. Mech. Eng. 1991, 93, 291–318. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Kikuchi, N. Generating Optimal Topologies in Structural Design Using a Homogenization Method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Bendsøe, M.P. Optimal Shape Design as a Material Distribution Problem. Struct. Optim. 1989, 1, 193–202. [Google Scholar] [CrossRef]
- Mlejnek, H.P. Some Aspects of the Genesis of Structures. Struct. Optim. 1992, 5, 64–69. [Google Scholar] [CrossRef]
- Zhou, M.; Rozvany, G.I.N. The COC Algorithm, Part II: Topological, Geometrical and Generalized Shape Optimization. Comput. Methods Appl. Mech. Eng. 1991, 89, 309–336. [Google Scholar] [CrossRef]
- Sigmund, O. A 99 Line Topology Optimization Code Written in Matlab. Struct. Multidiscip. Optim. 2001, 21, 120–127. [Google Scholar] [CrossRef]
- Andreassen, E.; Clausen, A.; Schevenels, M.; Lazarov, B.S.; Sigmund, O. Efficient Topology Optimization in MATLAB Using 88 Lines of Code. Struct. Multidiscip. Optim. 2011, 43, 1–16. [Google Scholar] [CrossRef]
- Liu, K.; Tovar, A. An Efficient 3D Topology Optimization Code Written in Matlab. Struct. Multidiscip. Optim. 2014, 50, 1175–1196. [Google Scholar] [CrossRef]
- Xie, Y.M.; Steven, G.P. A Simple Evolutionary Procedure for Structural Optimization. Comput. Struct. 1993, 49, 885–896. [Google Scholar] [CrossRef]
- Tang, Y.; Kurtz, A.; Zhao, Y.F. Bidirectional Evolutionary Structural Optimization (BESO) Based Design Method for Lattice Structure to Be Fabricated by Additive Manufacturing. Comput.-Aided Des. 2015, 69, 91–101. [Google Scholar] [CrossRef]
- Yang, R.J.; Chuang, C.H. Optimal Topology Design Using Linear Programming. Comput. Struct. 1994, 52, 265–275. [Google Scholar] [CrossRef]
- Jia, H.P.; Jiang, C.D.; Li, G.P.; Mu, R.Q.; Liu, B.; Jiang, C.B. Topology Optimization of Orthotropic Material Structure. Mater. Sci. Forum. 2008, 575–578, 978–989. [Google Scholar] [CrossRef]
- Bruyneel, M.; Fleury, C. Composite Structures Optimization Using Sequential Convex Programming. Adv. Eng. Softw. 2002, 33, 697–711. [Google Scholar] [CrossRef]
- Lindgaard, E.; Lund, E. Optimization Formulations for the Maximum Nonlinear Buckling Load of Composite Structures. Struct. Multidiscip. Optim. 2011, 43, 631–646. [Google Scholar] [CrossRef]
- Sigmund, O.; Petersson, J. Numerical Instabilities in Topology Optimization: A Survey on Procedures Dealing with Checkerboards, Mesh-Dependencies and Local Minima. Struct. Optim. 1998, 16, 68–75. [Google Scholar] [CrossRef]
- Sigmund, O. Morphology-Based Black and White Filters for Topology Optimization. Struct. Multidiscip. Optim. 2007, 33, 401–424. [Google Scholar] [CrossRef]
- Setoodeh, S.; Abdalla, M.M.; Gürdal, Z. Combined Topology and Fiber Path Design of Composite Layers Using Cellular Automata. Struct. Multidiscip. Optim. 2005, 30, 413–421. [Google Scholar] [CrossRef]
- Nomura, T.; Dede, E.M.; Lee, J.; Yamasaki, S.; Matsumori, T.; Kawamoto, A.; Kikuchi, N. General Topology Optimization Method with Continuous and Discrete Orientation Design Using Isoparametric Projection. Int. J. Numer. Methods Eng. 2015, 101, 571–605. [Google Scholar] [CrossRef]
- Hoglund, R.; Smith, D.E. Non-Isotropic Material Distribution Topology Optimization for Fused Deposition Modeling Products. In Proceedings of the 26th Annual Solid Freeform Fabrication Symposium, Austin, TX, USA, 12–14 August 2015. [Google Scholar]
- Hoglund, R.; Smith, D.E. Continuous Fiber Angle Topology Optimization for Polymer Fused Filament Fabrication. In Proceedings of the 27th Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 8–10 August 2016. [Google Scholar]
- Jiang, D.; Smith, D.E. Topology Optimization for 3D Material Distribution and Orientation in Additive Manufaturing. In Proceedings of the 28th Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 7–9 August 2017. [Google Scholar]
- Xia, Q.; Shi, T. Optimization of Composite Structures with Continuous Spatial Variation of Fiber Angle through Shepard Interpolation. Compos. Struct. 2017, 182, 273–282. [Google Scholar] [CrossRef]
- Huebner, K.H.; Dewhirst, D.L.; Byrom, T.G.; Smith, D.E. The Finite Element Method for Engineers; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Barbero, E.J. Introduction to Composite Materials Design, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Kollár, L.P.; Springer, G.S. Mechanics of Composite Structures; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Tortorelli, D.A.; Michaleris, P. Design Sensitivity Analysis: Overview and Review. Inverse Probl. Eng. 1994, 1, 71–105. [Google Scholar] [CrossRef]
- Find Minimum of Constrained Nonlinear Multivariable Function—MATLAB Fmincon. Available online: https://www.mathworks.com/help/optim/ug/fmincon.html (accessed on 17 December 2016).
- Soto, C.A.; Yang, R. Optimum Topology of Embossed Ribs in Stamped Plates. In Proceedings of the ASME Design Engineering Technical Conference Proceedings, Atlanta, GA, USA, 13–16 September 1998. [Google Scholar]
- Soto, C.; Yang, R.-J. Optimum Layout of Embossed Ribs to Maximize Natural Frequencies in Plates. Des. Optim. Int. J. Prod. Process Improv. 1999, 1, 44–54. [Google Scholar]
- Hoglund, R. An Anisotropic Topology Optimization Method for Carbon Fiber-Reinforced Fused Filament Fabrication. Master’s Thesis, Baylor University, Waco, TX, USA, 2016. [Google Scholar]
- Jiang, D. Three Dimensional Topology Optimization with Orthotropic Material Orientation Design for Additive Manufacturing Structures. Master’s Thesis, Baylor University, Waco, TX, USA, 2017. [Google Scholar]
- Stegmann, J.; Lund, E. Discrete Material Optimization of General Composite Shell Structures. Int. J. Numer. Methods Eng. 2005, 62, 2009–2027. [Google Scholar] [CrossRef]
- Flow-INDUCED Alignment in Composite Materials, 1st ed. Available online: https://www.elsevier.com/books/flow-induced-alignment-in-composite-materials/papthanasiou/978-1-85573-254-4 (accessed on 20 December 2018).
- Liu, K. Top3dSTL_v3, Top3d: An Efficient 3D Topology Optimization Program. Top3d. Available online: https://top3dapp.com/download-archive/ (accessed on 20 December 2018).











| Mesh Size | Number of Design Variables | Number of Iterations | CPU Time (s) | Minimum Compliance |
|---|---|---|---|---|
| 60 × 10 | 1200 | 78 | 188 | 13.6 |
| 90 × 15 | 2700 | 151 | 847 | 11.8 |
| 120 × 20 | 4800 | 169 | 2094 | 12.1 |
| 150 × 25 | 7500 | 241 | 6415 | 12.6 |
| 180 × 30 | 10,800 | 341 | 17,681 | 13.2 |
| MBB Sample | Average Stiffness (N/m) | Standard Deviation (N/m) | Coefficient of Variation |
|---|---|---|---|
| Horizontal bead [45] | 2.90 × 105 | 0.12 × 105 | 0.042 |
| Vertical bead [45] | 2.51 × 105 | 0.052 × 105 | 0.021 |
| CFAO | 3.26 × 105 | 0.015 × 105 | 0.0047 |
| 7.34 | 3.43 | 1.39 | 0.42 | 0.47 |
| Case Study | Initial Compliance (Nm) | CPU Time (s) | Iterations | Optimized Compliance (Nm) |
|---|---|---|---|---|
| Case 1 | 30.27 | 246.3 | 78 | 3.48 |
| Case 2 | 30.27 | 165.5 | 54 | 4.28 |
| Case 3 | 37.86 | 144.2 | 47 | 5.66 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, D.; Hoglund, R.; Smith, D.E. Continuous Fiber Angle Topology Optimization for Polymer Composite Deposition Additive Manufacturing Applications. Fibers 2019, 7, 14. https://doi.org/10.3390/fib7020014
Jiang D, Hoglund R, Smith DE. Continuous Fiber Angle Topology Optimization for Polymer Composite Deposition Additive Manufacturing Applications. Fibers. 2019; 7(2):14. https://doi.org/10.3390/fib7020014
Chicago/Turabian StyleJiang, Delin, Robert Hoglund, and Douglas E. Smith. 2019. "Continuous Fiber Angle Topology Optimization for Polymer Composite Deposition Additive Manufacturing Applications" Fibers 7, no. 2: 14. https://doi.org/10.3390/fib7020014
APA StyleJiang, D., Hoglund, R., & Smith, D. E. (2019). Continuous Fiber Angle Topology Optimization for Polymer Composite Deposition Additive Manufacturing Applications. Fibers, 7(2), 14. https://doi.org/10.3390/fib7020014





