In this section, we summarize the currently available models for determining the shear and flexural capacity of SFRC. We used these expressions to prepare the experiments presented in this article, for the interpretation and analysis of the experimental results, and to derive recommendations for the use of a certain fiber volume fraction.
2.1. Ultimate Shear Capacity
There are several theories that describe the shear behavior of reinforced concrete such as the Modified Compression Field Theory (MCFT) [
15] based on equilibrium conditions, compatibility requirements, and stress-strain relationships, or the Critical Shear Crack Displacement Theory (CSDT) proposed by Yang [
16], which takes into account the different shear-carrying mechanisms after cracking (aggregate interlock, dowel action, and concrete in the compression zone). The original version of the CSDT does not take into account the contribution of fibers. However, Filian et al. [
17] extended the CSDT to take into account the capacity of steel fibers to carry tension across the crack as an additional shear-resisting mechanism.
Different expressions to determine the shear capacity of SFRC beams are provided in
Table 1. Research conducted by Lee et al. [
18] extends the concept of the Dual Potential Capacity Model (DPCM), proposed in previous studies [
19,
20,
21] by the authors, to SFRC. To calculate the shear demand in reinforced concrete, the DPCM considers aggregate interlock in the cracked tension zone and in the compression zone, as well as crack widths in the tension zone. However, when applied to SFRC, the model only considers the capacity in the tension zone based on the crack width. The contribution of fibers is taken into account based on the Direct Tension Force Transfer Model (DTFTM), proposed by the authors in their previous research [
22,
23,
24,
25,
26,
27,
28], the random distribution of the steel fibers, and the pull-out strength of the steel fibers. The ultimate shear strength of the SFRC beam is calculated by summing the minimum shear contribution of the concrete (i.e., intersection between demand and capacity at compression and tension zone) and the contribution of fiber as determined in Equation (3).
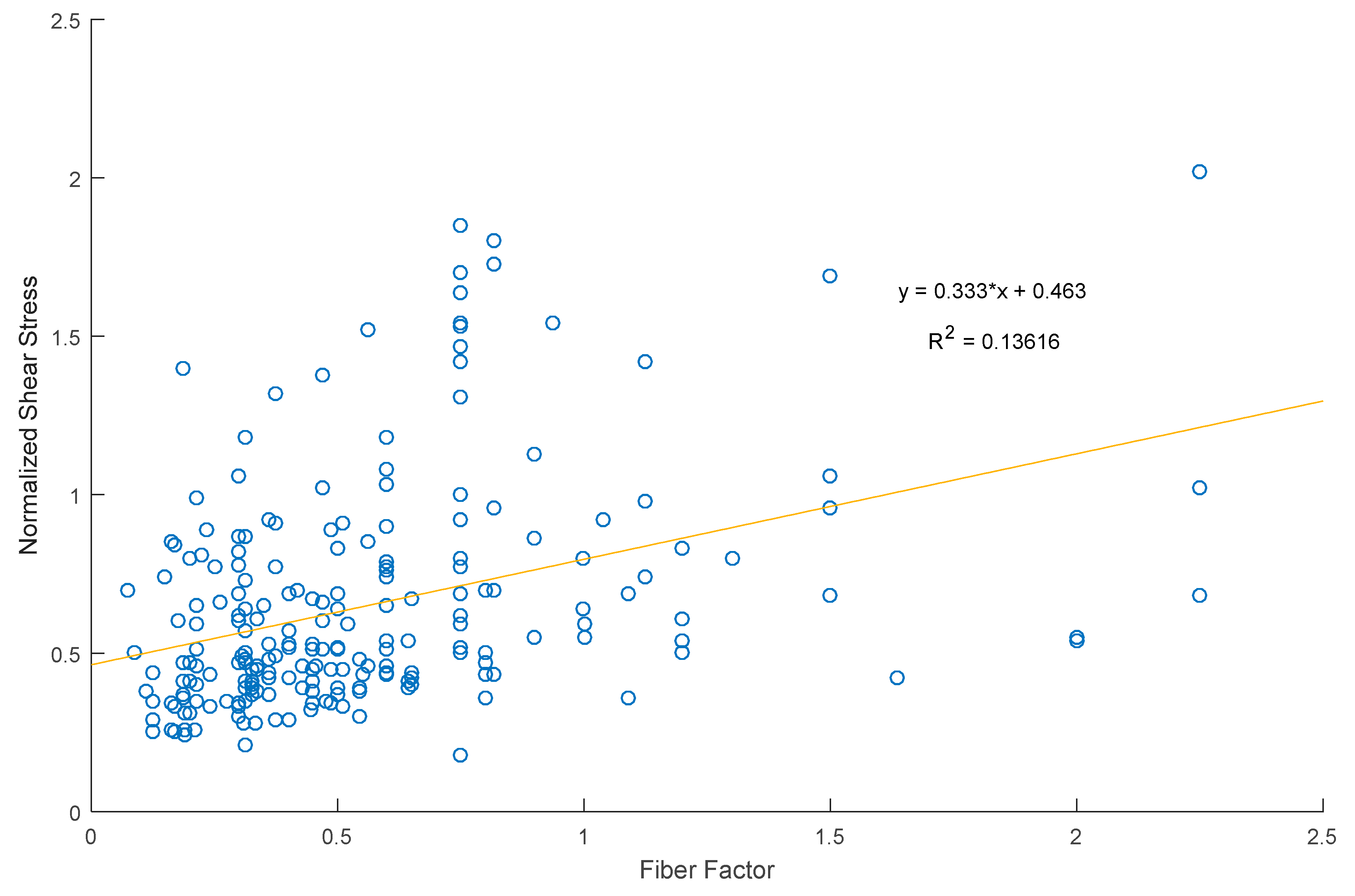
To calculate the shear capacity of SFRC, mostly (semi)-empirical expressions are used. Most expressions take into account the properties and geometry of the fibers, often in the form of the fiber factor
F, a concept proposed by Narayanan and Palanjian [
29]. The fiber factor
F is calculated as follows:
where
L = length of the fiber.
D = diameter of the fiber.
Vf = fiber volume fraction.
Df = fiber bond factor.
The fiber bond factor (
Df) accounts for the geometry and bond characteristics of the fibers. For steel fibers, it has a value of 1.00 for hooked fibers, 0.75 for crimped fibers and 0.50 for straight fibers as recommended by Narayanan and Darwish [
30]; another method to calculate the fiber bond factor is suggested by [
31,
32] and it is equal to the ratio between the mean fiber–matrix shear stress and the strength in direct tension of the material. This approach is useful when fibers of materials different than steel are used.
Different parameters are considered in the equations summarized in
Table 1, for instance the aggregate size factor, which considers the maximum aggregate size, is considered in Equations (7), (12) and (13). Imam et al. [
33] studied the effect of adding fibers in simply reinforced high-strength concrete beams without stirrups and its influence on flexure/shear interaction. The authors proposed an equation to predict the ultimate strength of SFRC based on the simultaneous occurrence of arching action and shear-resisting mechanisms, considering the equilibrium of forces in the shear span at the ultimate state. The expression is a function of the fiber factor (
F) and the longitudinal steel ratio (
ρ) considered in one term (
ω), the effect of relative beam size to the maximum aggregate size (
d/da), and the aggregate size (
da), which is considered in the size effect term (
ψ). Yakoub [
34] provides two different equations to predict the shear capacity of slender SFRC beams (
a/d > 2.5). The first equation (Equation (12)) is a modification to include the effect of steel fibers of the shear capacity proposed by Bažant and Kim [
35] for normal-strength reinforced concrete. The expression takes into account the size of aggregates (
da), the concrete compressive strength (
fc), shear span to depth ratio (
a/d), and longitudinal reinforcement ratio (
ρ). The second equation by Yakoub [
34], Equation (13) is an extension of the expression for the shear capacity of the Canadian Code CSA A23.3-04 [
36] to include the contribution of the steel fibers. This expression is a function of the strain at mid-depth of the beam (
εx) and crack spacing (
sx) as a function of the aggregate size (
da). Equation (13) does not consider arching action.
Combining the concrete contribution and the fiber contribution to find the shear resistance is an approach followed by a number of authors. Dinh et al. [
37] conducted an experimental program which resulted in an expression to estimate the shear strength provided by the fibers in SFRC beams without stirrups based on the tensile strength of plain fiber-reinforced concrete prisms and the measured crack widths according to the standard ASTM C-1609 [
38]. The model proposed by Dinh et al. [
37] combines the contribution of the fibers, evaluated as the vertical component of the tensile strength from the fibers bridging the crack, which depends on the crack width, with the concrete contribution, determined as the shear contribution of the concrete in the compression zone. The fiber contribution is a function of the crack width (
w). An equivalent uniform tensile stress (
ff) is used to find the force resultant of the fiber contribution. The result of these procedures is that the ultimate shear strength is calculated by the summation of Equations (9) and (10). Similarly, Mansur et al. [
39] conducted an experimental program to provide an expression to predict the shear capacity of SFRC by adding the contribution of fibers (
Vsf) to the concrete contribution (
Vc) as calculated in Equation (15). Both Dinh et al. [
37] and Mansur et al. [
39] use similar expressions for
Vsf and include similar parameters such as the tensile strength of concrete (
ft), the geometry of the beam, and the diagonal crack angle (taken as 30 degrees by [
37] and 45 degrees by [
39]). On the other hand, the expressions for the concrete contribution are based on different assumptions. Dinh et al. [
37] consider a uniform shear stress over the depth of the compression zone, whereas Mansur et al. [
39] consider the ratio of external shear to moment according to the recommendation of the ACI-ASCE Committee 426 [
40].
Empirical equations have been developed and validated through experimental programs. Narayanan and Darwish [
30] developed Equation (17) for the ultimate shear strength by testing SFRC beams with different crimped fiber contents and fiber aspect ratios of 100 and 133, with variable
a/d ratio and concrete compressive strengths from 36 to 75 MPa. A similar experimental program [
13] with two different compressive strengths (31 and 65 MPa) and hooked-end steel fibers with an aspect ratio of 62.5 was used to develop Equation (19). Moreover, Shin et al. [
41] developed Equation (20) by testing 22 reinforced concrete beams with and without steel fibers and with a concrete compressive strength of 80 MPa. The main variables in this program were the fiber content,
a/d ratio, amount of longitudinal reinforcement, and amount of shear reinforcement. All of the proposed equations consider three shear-resisting mechanisms: (1) the fiber contribution represented by the splitting cylinder strength
fsp, (2) dowel action provided by the longitudinal reinforcement and taking into account the influence of the shear span to depth ratio, and (3) the fiber pullout stresses along the inclined cracks,
vb. Arching action is taken into account by using the factor
e, but small differences exist between Equations (17) and (19), and the effect of arching action is not considered in Equation (20).
A second set of empirical expressions takes into account the concrete compressive strength (
fc), fiber factor (
F), longitudinal reinforcement ratio (
ρ), and shear span to depth ratio (
a/d). Based on testing high strength (
fc about 93 MPa) SFRC beams with variable hooked-end steel fiber (aspect ratio of 75) content, longitudinal reinforcement ratio, and shear span to depth ratio (
a/d), Ashour et al. [
42] developed two expressions: (1) Equation (21), an extension of Zsuty’s equation [
43] to include the contribution of the fibers through the fiber factor
F, and (2) Equation (22), an extension of the ACI 318-89 [
44] shear equation to include the contribution of the fibers, as well as the effect of the shear span to depth ratio and the longitudinal reinforcement ratio. The factor 0.7 accounts for the action of high strength concrete. Khuntia et al. [
45] developed Equation (23) based on 10 different experimental programs in which the main variables were concrete compressive strength (
fc), shear span to depth ratio (
a/d), fiber factor (
F), fiber content (
Vf), and longitudinal reinforcement ratio (
ρ). The expression sums the concrete contribution from ACI 318-95 [
46] and the contribution of the fibers, assuming a diagonal crack of 45 degrees. The arching action that is developed when
a/d is less than 2.5 is taken into account in the factor α.
A different approach is followed by Kara [
47], who used gene expression programming (GEP) to predict the ultimate shear strength of SFRC beams without stirrups. A database of 101 tests was used to build the GEP model with five main variables: concrete compressive strength (
fc), effective depth (
d), shear span to depth ratio (
a/d), longitudinal reinforcement ratio (
ρ), and fiber factor (
F). The model resulted in Equation (24) were the coefficients
c0,
c1,
c2, and
c3 are constants provided by the formulation of the GEP model.