Abstract
The application of externally bonded fiber-reinforced polymer (EB-FRP) as shear transverse reinforcement applied in vulnerable reinforced concrete (RC) beams has been proved to be a promising strengthening technique. However, past studies revealed that the effectiveness of this method depends on how well the reinforcement is bonded to the concrete surface. Thus, although the application of EB-FRP wrapping around the perimeter of rectangular cross-sections leads to outstanding results, U-jacketing in shear-critical T-beams seems to undergo premature debonding failures resulting in significant reductions of the predictable strength. In this work, five shear-critical RC beams with T-shaped cross-section were constructed, strengthened and tested in four-point bending. Epoxy bonded carbon FRP (C-FRP) sheets were applied on the three sides and along the entire length of the shear-strengthened T-beams as external transverse reinforcement. Furthermore, the potential enhancement of the C-FRP sheets anchorage using bolted steel laminates has been examined. Test results indicated that although the C-FRP strengthened beams exhibited increased shear capacity, the brittle failure mode was not prevented due to the debonding of the FRP from the concrete surface. Nevertheless, the applied mechanical anchor of the C-FRP sheets delayed the debonding. Moreover, the design provisions of three different code standards (Greek Code of Interventions, Eurocode 8 and ACI Committee 440) concerning the shear capacity of T-shaped RC beams retrofitted with EB-FRP jackets or strips in U-jacketing configuration are investigated. The ability of these code standards to predict safe design estimations is checked against 165 test data from the current experimental project and data available in the literature.
1. Introduction
Shear failure of reinforced concrete (RC) structural members is characterized by the brittle nature and the formation of crucial diagonal cracking. It has been experimentally verified that the ratio of the transverse reinforcement combined with the amount of the tension reinforcing bars and the span-to-depth ratio controls the inclined shear cracking and the overall behavior. It is also well known that the initial shear cracking capacity of a RC member is governed by the tensile strength of concrete and, for this reason, any enhancement of the deficient concrete behavior under tension would improve the shear performance of the member. Thus, the effectiveness of non-traditional shear reinforcement such as steel fibers and spirals instead of common steel stirrups has been indicated as a potential alternative technique which provides noticeable improvement of the shear response [1,2,3,4,5].
Strengthening of existing low-capacity RC structures using externally bonded fiber-reinforced polymers (EB-FRP) has become very popular because of the advantages of these materials such as their superior strength-to-weight ratio, their easy-to-apply character, their durability and their chemical and corrosion resistance [6,7,8]. For shear-critical RC elements with rectangular cross-sections in particular, full jacketing application of EB-FRP sheets wrapping around the cross-section and along their entire length provides increased strength and enhanced structural performance since it alters the shear brittle response to a ductile one [9,10,11,12]. However, common constructional limitations, such as the existence of a slab, usually prevent the wrapping of EB-FRP sheets around the cross-section. Thus, most RC beams with a T-shaped cross-section are shear strengthened using EB-FRP sheets (jackets or strips) on the three sides of the web of the beam (U-shaped retrofitting). A significant deficiency of this technique is the premature failure of the strengthened member due to the debonding of the EB-FRP at the adhesive composite and concrete interface [13,14,15,16,17,18,19,20].
Several experimental studies have demonstrated the effectiveness of the use of EB-FRP sheets in strengthening procedures of shear-deficient RC members. Chaallal et al. [21] proposed one of the first models for predicting the shear contribution of the EB-FRP based on the assumption that the composite fibers contribute to the shear capacity similar to internal transverse reinforcement. It further assumes that the limiting EB-FRP tensile strength is reached when the composite is intersected by the shear failure crack if the bond length is sufficient. Triantafillou [22] used the truss theory to estimate the effective strain on FRPs, which developed from a regression of experimental data. This model disregards the different strengthening schemes and failure modes. Triantafillou and Antonopoulos [23] proposed an extension of Triantafillou’s model, in which different effective strain expressions and coefficients were adopted for carbon FRP wrapping and other schemes, based on regression of a larger database (75 tests).
Khalifa et al. [24] and Khalifa and Nanni [25] amended the previous models by introducing coefficients to consider the reduced strain developed due to an increase of shear crack width and loss of aggregate interlock. Deniaud and Cheng [26,27] proposed a model assuming a uniform strain distribution among the composite fibers crossing the concrete shear crack. Pellegrino and Modena [28], assuming the EB-FRP strains were equal to those of internal stirrups, introduced a reduction factor for Khalifa’s model [24] considering the interaction between the EB-FRP and the internal shear steel reinforcement according to experimental results. Chen and Teng [29,30] analyzed shear failure in RC beams strengthened with EB-FRP and concluded that the stress distribution of the fibers along the crack is non-uniform. They proposed an analytical model for failure by EB-FRP rupture [29] and another for failure by EB-FRP debonding [30], in which the limiting stresses are determined by the effective bond length and the width coefficients of the applied EB-FRP. Carolin and Täljsten [31] presented an expression to predict the contribution of the EB-FRP based on a refinement of the truss model theory. Strain limitations are prescribed for the principal strain in the concrete instead of the fiber strain. Monti and Liotta [32] proposed a debonding model for EB-FRP shear-strengthened RC beams. This model has three core components: a generalized constitutive mode for the EB-FRP concrete bond, boundary limitation and shear crack opening provision. It also introduced a generalized criterion for EB-FRP failure. The design proposal described in this model and relative aspects of some of the aforementioned models have been incorporated into the Italian design Code CNR-DT 200 R1/2013 and the guidelines of fib Bulletin 90 [33,34].
Lavorato et al. [35] tested two “real” RC beams which have been properly extracted during retrofitting works from an old existing RC building and then strengthened against shear using inclined U-shaped carbon EB-FRP strips. EB-FRP sheets have also been applied in RC beams and beam-column joints that suffer shear stresses. Constructional difficulties and limitations in RC beam-column joints and frames also caused undesirable shear failure in the joint specimens retrofitted with EB-FRPs [36,37,38,39,40].
This paper investigates the shear strengthening of T-shaped RC beams using EB-FRP U-jackets and its aim is twofold: firstly, to present new test results of an experimental project concerning the shear behavior, the cracking performance and the failure mode of RC T-beams retrofitted with U-shaped carbon FRP (C-FRP) sheets. The effectiveness of a mechanical anchor of the EB-FRP sheets using bolted laminates on the debonding and overall response is also examined; secondly, to evaluate the results of the design provisions of three different code standards; Greek Code of Interventions [41], Eurocode 8 part 3 [42] and ACI Committee 440 [43] for the design of shear strengthened RC T-beams with EB-FRP materials using 165 test data available in the literature.
2. Experimental Program
The experimental program consisted of 5 beams with a common T-shaped cross-section, total length and shear span equal to 1.40 m and 0.5 m, respectively. The cross-section dimensions of the specimens were bw/h/bf/hf = 150/200/300/50 mm, as shown in Figure 1, whereas the effective depth was equal to d = 175 mm. The steel longitudinal reinforcement of the web of the tested beams comprised 2 bars Ø16 up and 4 bars Ø16 down in order to avoid bending failure. The reinforcement of the flange of the specimens was 2 steel longitudinal bars Ø8 and transversal horizontal steel bars Ø4 at a uniform spacing of 150 mm (Figure 1).
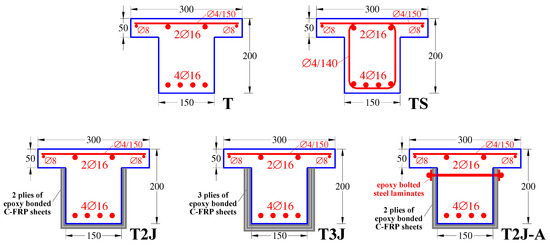
Figure 1.
Cross-section dimensions and reinforcement details of the tested beams.
All specimens, except beam TS, had no stirrups or other steel shear reinforcement. Specimen T was used as the control specimen whereas three specimens (T2J, T3J and T2J-A) have been strengthened using EB-FRP sheets with carbon fibers that have been bonded continuously along the entire length of the beams. In these specimens C-FRP sheets wrapped the vertical sides and the bottom width of the beams (U-wrapped beams). The fiber direction of the C-FRP sheets oriented perpendicular to the longitudinal axis of the beam, as external shear transversal reinforcement. Specimens T2J and T3J comprised 2 and 3 plies of C-FRP sheets, respectively, whereas specimen T2J-A comprised 2 plies of C-FRP sheets that were additionally anchored using two bolted steel laminates (Figure 1). Two 40 mm wide and 10 mm thick mild steel S275 laminates have been epoxy bonded at each vertical side of the web of the beam and bolted with 10 mm diameter bolts spaced longitudinally at 400 mm. All retrofitted beams and the control specimen had no stirrups in order for the contribution of the C-FRP sheets as the only transverse reinforcement on the shear capacity of the tested beams to be investigated. For comparison reasons, the experimental program also includes one specimen (beam TS) with mild steel shear reinforcement. The steel transversal reinforcement of beam TS was 4 mm diameter closed plain stirrups at a uniform spacing of 140 mm, as shown in Figure 1.
2.1. Materials
In order to determine the compressive and the tensile strength of the concrete used, supplementary compression and splitting tests of six 150 × 300 mm cylinders for each test were also carried out. The mean values of the compressive and the tensile strength of the concrete were fcm = 35.15 MPa and fctm = 3.01 MPa, respectively. The values of standard deviation and coefficient of variation for the compressive strength were 2.96 and 0.08, respectively, whereas for the tensile strength were 0.28 and 0.09, respectively.
The shear non-metallic reinforcement of the strengthened beams T2J, T3J and T2J-A was unidirectional carbon fiber sheets with thickness 0.13 mm per ply (Sikawrap Hex 230 C). According to data provided by the FRP supplier, the elastic modulus, the ultimate tensile strength and the elongation at failure of the sheets were Ef = 230 GPa, ffu = 3500 MPa and εfu = 1.5% mm/mm, respectively. A two-component rubber-toughened cold-curing-construction epoxy adhesive with density 1310 kg/m3 and tensile strength 30 MPa was used for bonding the FRP sheets to concrete (Sikadur-330).
2.2. Test Setup and Instrumentation
The beams were simply supported on two roller supports 1.20 m apart and tested in monotonic load, as shown in Figure 2. The load applied in a steel distribution beam in order to generate two concentrated loads 200 mm apart in the midspan of the beam as a four-point loading. This way, the ratio of the shear span to the effective depth ratio was equal to a/d = 2.86. The load was imposed consistently in a low rate and was measured by a load cell with accuracy equal to 0.05 kN. Midspan deflection of the tested beams was measured by a linear variable differential transducer with accuracy equal to 0.01 mm. Measurements for load and deflection were read and recorded continuously.

Figure 2.
Test setup (control specimen T).
3. Test Results and Commentary
All tested beams exhibited diagonal cracks and eventually failed in a brittle manner due to shear as shown in Figure 3. Figure 3a,b illustrate, in particular, the typical shear cracking of the control beams without transverse reinforcement (specimen T) and with inadequate steel stirrups (specimen TS), respectively. Both beams exhibited typical inclined cracking through the shear span. Figure 3c,d show the failure of the FRP-strengthened beams T2J and T3J, respectively. These beams demonstrated severe brittle diagonal failure right after the debonding of the epoxy bonded C-FRP sheets. The failure of the FRP-strengthened specimen T2J-A with bolted steel laminates is depicted in Figure 3e. Although in this case the concrete diagonal cracking is not visible since it has occurred behind the C-FRP sheets, there is no doubt about the shear failure of the beam obtained. This is based on the fact that the loading bearing capacity of the beam has been abruptly decreasing along with the debonding failure of the C-FRP sheets and the concrete interface. Nevertheless, the installed mechanical anchor delayed the debonding failure and prevented the peeling-off of the C-FRP sheets in specimen T2J-A (Figure 3e), whereas the debonding and the peeling-off of the C-FRP sheets are apparent in specimens T2J and T3J (Figure 3c,d). It is noted that in the study of Bae and Belarbi [44] the application of a sandwich discontinuous mechanical anchorage system succeeded in altering the failure mode of EB-FRP strengthened RC T-beams from debonding to fiber rupture under certain circumstances.

Figure 3.
Cracking and shear failure of the tested beams: (a) T; (b) TS; (c) T2J; (d) T3J; (e) T2J-A.
The total applied load at shear cracking (Pcr) and the corresponding midspan deflection (δPcr), as well as the ultimate applied load (Pu) and the corresponding midspan deflection (δPu) as measured from the tests, are reported in Table 1. It is noted that values at cracking and at ultimate load are equal in the cases of beams T3J and TS. Further, Figure 4 shows the entire shear response of the tested beams in terms of the total applied load versus midspan deflection experimental curves. The first graph of Figure 4 presents and compares the behavior of the control beam T with the behavior of the strengthened beams T2J and T3J with 2 and 3 plies of C-FRP sheets, respectively. The effect of the special anchorage of the C-FRP sheets on the shear performance of the beams is shown in the second graph of Figure 4 that compares the experimental curves of the beam T2J-A with bolted steel laminates and the beam T2J without laminates.

Table 1.
Test results.
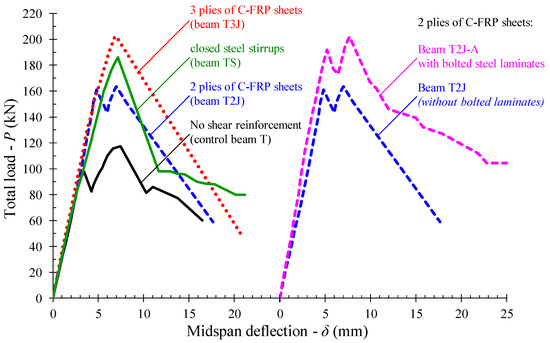
Figure 4.
Total applied load versus midspan deflection experimental curves.
Based on the experimental results reported in Table 1 and presented in Figure 4 it can be deduced that all the U-jacketed specimens using EB-FRP sheets exhibited increased shear capacity. Values of the ultimate shear load of the strengthened beams T2J, T3J and T2J-A were 1.39, 1.72 and 1.72 times higher than the ultimate shear load of the beam without shear reinforcement (control specimen T), respectively. It is noted that the conventionally shear-reinforced beam TS with rather inadequate amount of closed steel stirrups exhibited 1.58 times higher shear capacity.
Furthermore, the comparison of the load versus deflection behavioral curves of the tested beams (see also Figure 4) reveals that the failure load of the conventionally reinforced beam TS is close to the ultimate load of the retrofitted beams, although the ratio of the steel stirrups provided in beam TS is about 3 and 4 times lower than the shear reinforcement ratio of the C-FRP sheets applied in beams T2J and T3J, respectively (see also Table 2). Nevertheless, the experimentally obtained increase of the shear strength due to the external application of EB-FRP U-jacketing is noticeable since the C-FRP sheets form the only transverse reinforcement.

Table 2.
Effect of FRP sheets on the shear strength.
In order to evaluate the effect of the epoxy-bonded U-shaped C-FRP sheets on the shear strength of the tested beams, Table 2 and Figure 5 have been drawn. Table 2 presents the volume of the shear reinforcement, the ultimate shear strength, the contribution of the shear reinforcement (C-FRP sheets or stirrups) to the shear strength and the percentage increase of the shear strength due to the shear reinforcement, for each tested beam.
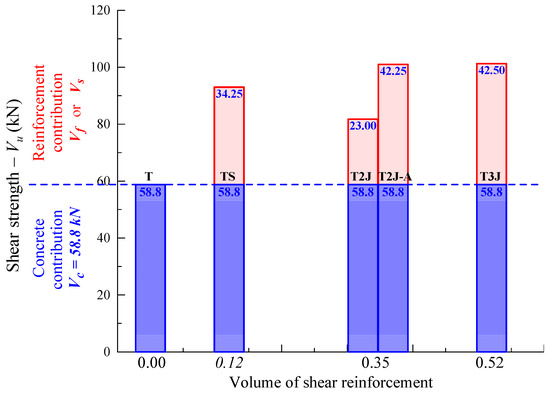
Figure 5.
Concrete and fiber-reinforced polymer (FRP) contribution in shear strength.
Moreover, the volume of each beam’s shear reinforcement and the corresponding values of the concrete contribution (Vc) and the shear reinforcement contribution (Vf for the beams with C-FRP or Vs for the beam TS with stirrups) to the total shear strength (Vu) are plotted in Figure 5. It is noted that the contribution of FRP sheets to the shear capacity (Vf) is obtained by subtracting the total shear strength (Vu) of the strengthened beams with C-FRP from the shear capacity of the control beam without shear reinforcement (specimen T). The total shear strength of the control beam T represents the concrete contribution (Vc).
Based on the shear strength values of Table 2 and Figure 5 it can be observed that the presence of U-wrapped C-FRP sheets as transversal reinforcement increases the shear load carrying capacity of the tested T-beams. Beams T2J and T3J with volume of C-FRP reinforcement equal to 0.347% and 0.520%, respectively, exhibited 39% and 72% increased shear strength with reference to the non-strengthened beam T (control beam), respectively. It is noted that the steel-reinforced beam TS with volume of steel stirrups equal to 0.120% showed 58% higher shear strength than the control beam.
Furthermore, from the comparison of the experimental curves and the shear strength values of beams T2J and T2J-A (Figure 4 and Figure 5, Table 2) it is observed that a significant increase in the shear capacity was achieved due to the use of the special anchorage of the C-FRP sheets using bolted steel laminates. Beam T2J-A with 2 plies of C-FRP sheets and bolted steel laminates exhibited 23% higher shear strength than the beam T2J without laminates and 72% than the control beam T. Besides, the entire shear performance of the beam T2J-A was more improved and ameliorated even than the response of beam T3J with 3 plies of C-FRP sheets.
4. Design Provision
Several guidelines and design provisions for the shear strengthening of RC beams using EB-FRP materials have been proposed. Based on them, the nominal shear strength of an EB-FRP retrofitted RC beam, Vn, is calculated by adding the contribution of the EB-FRP to the shear resistance, Vf, with the corresponding resistance of the concrete, Vc, and the steel shear reinforcement (stirrups or/and bent-up bars), Vs:
The strength components of Vc and Vs are usually calculated according to the provisions of the existing design codes for a non-strengthened RC member. The contribution of the EB-FRP materials to the shear resistance is usually obtained by multiplying the ultimate vertical stress developed in the EB-FRP by the area of the fibers that cross a potential shear crack. Thus, the EB-FRPs that are intersected by this diagonal shear crack are assumed to contribute the same effective strain. Most of the design guidelines and models use a similar design relationship with different definitions or estimations of the EB-FRP effective design strain or/and the corresponding stress.
4.1. Greek Code of Interventions (KAN.EPE.)
The Greek Code of Interventions, also known as KAN.EPE. [41], adopts the model proposed by Chen and Teng [29,30] and estimates the EB-FRP contribution using the following expression:
where ρj is the reinforcement ratio of the EB-FRPs; bw is the width of the web of the RC beam; hj,ef is the effective depth of EB-FRP that can be assumed to be equal to hj,ef = 2/3d; d is the effective depth of the beam; θ is the strut inclination angle that can be taken as θ = 45°; α is the angle between the fiber direction and the longitudinal axis of the member; σjd is the EB-FRP effective design stress at failure:
where fjk = Ej εj,crit is the design tensional strength of the EB-FRP; Ej is the modulus of elasticity of EB-FRP; εj,crit = kv εj,max is the design (critical) strain of the EB-FRP; kv = 0.5; εj,max = εju ψ ≤ 1.5% is the ultimate strain of the EB-FRP; ψ = k −1/4 if k ≥ 4 and ψ = 1 if k < 4 is a degrease coefficient of multiple EB-FRP plies; k is the number of the EB-FRP plies; γm = 1.2 is the partial safety factor.
where σj,crit = kv σj,max is the design (critical) stress of the EB-FRP; γRd = 1.2 is the safety factor for modeling uncertainty; kv = 0.4 + 0.25λ ≤ 0.65; σj,max is the ultimate stress of the EB-FRP as calculated by the following expression; λ = Lav/Le ≤ 1; Lav = hj,ef is the available bond length of the EB-FRP; Le is the effective bond length of the EB-FRP that can be calculated by the following empirical expression:
where fctm is the mean compressive strength of concrete; tj = ψ k tj1 is the thickness of the EB-FRP; tj1 is the thickness of one EB-FRP ply.
where wj and sj are the width and the spacing of the EB-FRP strips, respectively, that in the case of jackets sj = wj.
Concerning the parameter βL, it can be calculated according to Neubauer and Rostasy [45] equation for the case of C-FRP plates as: βL = λ(2 − λ), which has been modified as follows [46,47]:
where λ is the ratio between the bonded length, Lav, and the effective bond length, Le, as mentioned above.
It is noted that the ratio of the applied EB-FRP is calculated based on the following expression:
Thus, Equation (2) can be written in the form of:
4.2. Eurocode 8 Part 3
Eurocode 8 part 3 [42] adopts the model proposed by Monti and Liotta [32] and estimates the EB-FRP contribution by the following expression:
where d is the effective depth of the beam; tf is the total thickness of the EB-FRP; wf is the width of the EB-FRP strips that in the case of EB-FRP jackets it is equal to wf = min(0.9d, hw) sin(θ + β)/sinθ; sf is the axial spacing of the EB-FRP strips that in the case of jackets sf = wf, hw is the height of the web of the beam; θ is the strut inclination angle; β is the angle between the fiber direction and the longitudinal axis of the member; ffdd,e is the effective design stress of the EB-FRP that depends on the type of the retrofitting scheme (fully wrapped, U-shaped and side bonded) and in the examined case of U-shaped retrofitting it is calculated by:
where ffdd is the design debonding strength of the case of U-shaped EB-FRP that equals:
where γfd = 1.5 is the partial safety factor for EB-FRP debonding; fctm is the mean compressive strength of concrete; Ef is the modulus of elasticity of EB-FRP; k = (1 − 2/π); z = 0.9d; kb is the covering coefficient; Le is the effective bond length of the EB-FRP as calculated by the following expressions:
τmax = 1.8fctm kb is the maximum bond strength.
4.3. ACI Committee 440
ACI Committee 440 [43] is based on the design equations derived by Khalifa et al. [24] and estimates the EB-FRP contribution by the following expression:
where Afv = 2ntfwf is the area of the EB-FRP; df is the effective depth of the EB-FRP; n is the number of the EB-FRP plies; tf is the thickness of one EB-FRP ply; wf and sf are the width and the spacing of the EB-FRP strips, respectively, in the case of continuous jackets sf = wf; a is the angle between the fiber direction and the longitudinal axis of the member; ffe = Ef εfe is the effective design stress of the EB-FRP; Ef is the modulus of elasticity of the EB-FRP; εfe = kv εfu ≤ 0.4% is the EB-FRP effective strain; εfu is the ultimate rupture strain of the EB-FRP; kv is a bond-reduction coefficient that depends on the specified concrete compressive strength, fc, the type of the retrofitting scheme and the stiffness of the EB-FRP:
where k1 = (fc/27)2/3; k2 = (df-Le)/df (for U-wraps) and Le = 23,000/(ntfEf)0.58 (fc and Ef given in MPa, df, Le and tf given in mm). Thus, Equation (13) can be written in the form of:
and the design value of the EB-FRP contribution to shear is ϕψfVf (reduction factors: ϕ = ψf = 0.85).
5. Database Results and Discussion
The database used consists of 165 shear-critical RC beams with T-shaped cross-section that have been externally strengthened with U-shaped EB-FRP continuous and discontinuous sheets (jackets and strips, respectively). Test results are used to compare the analytical predictions of the design provisions concerning the EB-FRP contribution to the shear capacity with the experimentally obtained values. The 165 tested beams were collected from the current experimental study and the following 26 existing works around the world [25,26,27,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70].
The beams of the database are sorted into two groups; “jackets” and “strips”. The first group consists of 92 RC beams strengthened with EB-FRP jackets, in which 27 have an anchorage system. The second consists of 73 RC beams strengthened with EB-FRP strips, in which 27 have an anchorage system.
Externally EB-FRP sheets with fibers from Carbon, Glass and Aramid are examined. The EB-FRP thickness varies from 0.063 mm to 2.10 mm. The minimum values of the concrete compressive and the tensile strength are 20.6 MPa and 1.64 MPa, respectively.
In the first group (jackets), 44 beams have also steel transverse reinforcement (stirrups) from which 39 have EB-FRP from carbon fibers and 5 from glass fibers. Further, 48 beams have no steel shear reinforcement (without stirrups) from which 38 have EB-FRP from carbon fibers, 6 from glass fibers and 4 from aramid fibers. In the second group (strips), 49 beams have also steel transverse reinforcement (stirrups) from which 48 have EB-FRP from carbon fibers and 1 from glass fibers. Furthermore, 24 beams have no steel shear reinforcement (without stirrups) from which 22 have EB-FRP from carbon fibers and 2 from glass fibers.
In Figure 6, Figure 7 and Figure 8, the analytical predictions derived from the provisions of the Greek Code of Interventions [41], the Eurocode 8 part 3 [42] and the ACI Committee 440 [43], respectively (denoted as Vjd in “KAN.EPE.”, VRd,f in “EC8” and ϕψfVf in “ACI”) are compared with the test results (Vf,exp) of the EB-FRP contribution to the shear resistance of the examined RC T-beams retrofitted with U-shaped EB-FRP jackets and strips. The diagonal lines signify the design datum (test results are equal to the analytical ones). The design values have been calculated with the safety factors and the area above these lines denotes the safe side.
Figure 6.
Results obtained based on the provisions of the Greek Code of Interventions (KAN.EPE.): (a) U-shaped retrofitted T-beams with EB-FRP jackets; (b) U-shaped retrofitted T-beams with EB-FRP strips.
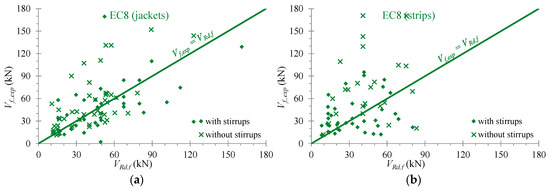
Figure 7.
Results obtained based on the provisions of the Eurocode 8 part 3: (a) U-shaped retrofitted T-beams with EB-FRP jackets; (b) U-shaped retrofitted T-beams with EB-FRP strips.
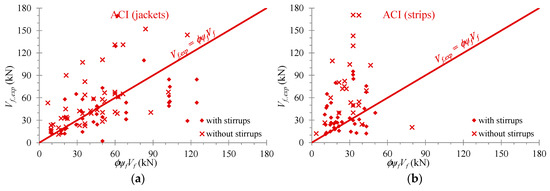
Figure 8.
Results obtained based on the provisions of the ACI Committee 440: (a) U-shaped retrofitted T-beams with EB-FRP jackets; (b) U-shaped retrofitted T-beams with EB-FRP strips.
Table 3 summarizes the minimum and maximum values of the main features of the shear-critical T-shaped RC beams of the database such as the cross-sectional dimensions bs/bw/h/hs (slab width/web width/height/slab depth), the mean concrete compressive strength fcm, the ratio of the steel tensional longitudinal reinforcement ρsl, the ratio of the steel transverse web reinforcement (stirrups) ρsw, the modulus of elasticity of the EB-FRP Ef, the ratio of the EB-FRP ρf and the contribution of the EB-FRP to the shear resistance Vf,exp. Furthermore, 4 full detailed Tables (Table A1, Table A2, Table A3 and Table A4) presenting the properties of all the 165 collected beams of the experimental database are included in the Appendix A of this paper.

Table 3.
Summary of the experimental database characteristics.
The comparisons between the test results and the design predictions of the examined code provisions in Figure 6, Figure 7 and Figure 8 indicate a rather large scatter between the predicted values and the experimental results. Furthermore, unsafe estimations (points below the diagonal line of the design datum) of all three codes can be observed for certain specimens. The unsafe predictions are less in the case of beams with EB-FRP strips than in the case of beams with jackets. Nevertheless, for the majority of the collected beams the code provisions provide safe estimations and satisfactory correlation (see also Table 4).

Table 4.
Code provisions predictions.
The observed discrepancies could be justified by the following facts. The analysis and the prediction of the shear resistance of shear-critical RC beams is a difficult task due to the influence of the complex interacting phenomena involved [1,11,12]. This complexity is augmented by the application of EB-FRP to increase the shear capacity of RC beams. Code provisions are based on analytical models for the prediction of the EB-FRP contribution to the shear resistance of RC beams, which, in general, were calibrated from (a) a reduced amount of experimental results, (b) rather unrealistic geometric conditions (laboratory beams) and (c) test programs of only rectangular cross-section beams [71,72]. Furthermore, most theoretical approaches for the case of T-shaped beams are treated as a special case of the rectangular beams with bonded fibers over a fraction of the cross section and in some cases, they have been validated with experimental data obtained from rectangular cross sections [73].
The evaluation of the effective strain in fibers is an important parameter that, in most analytical models, determines the contribution of the EB-FRP to the shear resistance of the RC beams. Furthermore, the ratio of the strains εfe/εfu (effective strain to the ultimate strain of the EB-FRP) indicates the effectiveness of the EB-FRP on the basis that cases of premature debonding failures exhibit low ratio values whereas cases of fiber rupture failures exhibit high ratio values. It is known that the majority of the strengthened T-shaped RC beams with U-wraps of EB-FRP materials fail due to debonding. Figure 9, Figure 10 and Figure 11 display the diagrams of the ratio εfe/εfu versus the amount of the applied EB-FRP in terms of the ratio Ef ρf/fctm. It is noted that the values of the effective strain have been calculated based on the provisions of the Greek Code of Interventions (KAN.EPE.) [41], the Eurocode 8 part 3 [42] and the ACI Committee 440 [43], respectively. The values of the mean compressive strength of concrete, the ultimate strain, the modulus of elasticity and the reinforcement ratio of the EB-FRPs have been taken from the experimental data of the beams examined.
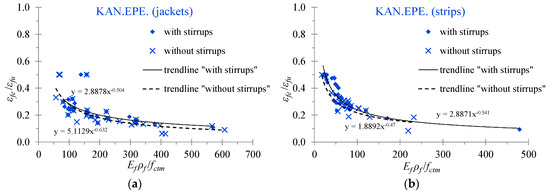
Figure 9.
Effectiveness of the EB-FRP U-jacketing based on the provisions of the Greek Code of Interventions (KAN.EPE.): (a) U-shaped retrofitted T-beams with EB-FRP jackets; (b) U-shaped retrofitted T-beams with EB-FRP strips.
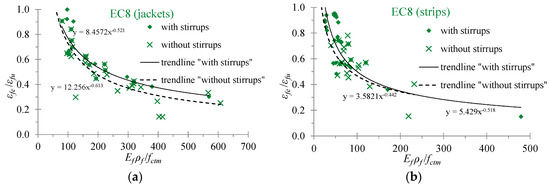
Figure 10.
Effectiveness of the EB-FRP U-jacketing based on the provisions of the Eurocode 8 part 3: (a) U-shaped retrofitted T-beams with EB-FRP jackets; (b) U-shaped retrofitted T-beams with EB-FRP strips.
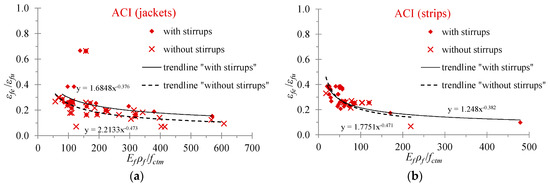
Figure 11.
Effectiveness of the EB-FRP U-jacketing based on the provisions of the ACI Committee 440: (a) U-shaped retrofitted T-beams with EB-FRP jackets; (b) U-shaped retrofitted T-beams with EB-FRP strips.
6. Conclusions
The effectiveness of U-jacketing in shear-critical T-beams using EB-FRP sheets is investigated. The following conclusions can be drawn within the scope of this study:
- U-jacketing is an open-form strengthening technique with inadequate anchorage at the edges of the externally applied EB-FRP sheet. The lack of any special anchorage system at these edges significantly affects the shear capacity and the overall behavior of the U-shaped retrofitted RC T-beams. Substantial low potential shear strength and low values of the effective strain of the applied EB-FRP materials are reported due to the occurrence of premature debonding failures.
- U-jacketed beams failed due to brittle shear exhibiting severe diagonal cracking of concrete along with the debonding and the peeling-off of the C-FRP sheets from the concrete surface of the beam. However, the examined FRP-strengthened beams demonstrated higher shear strength values than the corresponding non-strengthened beams (control specimens). More specifically, the U-jacketed beams with 2 and 3 plies of C-FRP sheets exhibited 39% and 72% increased shear capacity with respect to the control specimen without transverse reinforcement.
- The failure of the strengthened beam with 2 plies of C-FRP sheets and an additional mechanical anchor of the sheets is also governed by brittle shear although the applied anchorage system prevented the peeling-off of the EB-FRP sheets and the concrete diagonal cracking was not visible since it was hidden behind the C-FRP sheets. Nevertheless, the applied mechanical anchor of the U-shaped C-FRP sheets delayed the debonding resulting in a 72% increase of the shear capacity with respect to the control specimen without transverse reinforcement.
- The provisions and consequently the predictions of the Greek Code of Interventions (KAN.EPE.), Eurocode 8 part 3 and the ACI Committee 440 for shear strengthened RC T-beams using U-shaped EB-FRP jackets or strips vary. Different expressions for the estimation of the effective design strain or/and the corresponding stress are used. Comparisons between 165 test data of T-beams from existing studies and analytical design predictions derived from these provisions indicate that for the majority of the examined beams the Codes provide safe estimations. However, unsafe estimations of all three Codes are observed for certain specimens.
- The present and recent relative studies reveal that although a lot of analytical and experimental investigations on the shear strength of EB-FRP-retrofitted RC beams with rectangular cross-section have been conducted, there is a lack of research concerning the performance of T-beams. Furthermore, ongoing research aims to reduce the scatter in the predictions of the design models. However, additional questions concerning the effectiveness of these estimations also arise from the existing variety of the examined code provisions concerning the shear capacity of EB-FRP strengthened RC T-beams presented herein. The observed discrepancies between test results and analytical predictions and between the existing models are justified, up to a point, by the fact that the shear problem involves the influence of complex interacting phenomena and a number of parameters, such as the properties and the efficiency of the applied EB-FRP materials, the existence of the internal steel reinforcement, the effect of the slab on the shear performance and on the anchorage of the composite sheets among others. Thus, further research efforts are required to understand better the aforementioned issues, to obtain more and reliable experimental results, and to interpret them in order to refine the existing models and code standard provisions.
Author Contributions
All authors contributed extensively to this study, discussed the results and reviews, prepared the manuscript, and agreed to the amendments at all stages of the paper. C.G.K. and C.E.C. performed the tests and designed the experiments. C.E.C. and A.G.Z. analyzed the test results, developed the aspects of the analytical investigation and prepared the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
Author Adamantis G. Zapris gratefully acknowledges the financial support received from Eugenides Foundation towards doctoral studies. The contribution of C.A. Argiriou to the collection of the test database is greatly appreciated.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Properties of the retrofitted T-beams with EB-FRP continuous U-jackets and stirrups of the database.
Table A1.
Properties of the retrofitted T-beams with EB-FRP continuous U-jackets and stirrups of the database.
| Ref. | Name | bs/bw/h/hs (mm) | fcm (MPa) | ρsl (%) | ρsw (%) | Ef (GPa) | εfu (%) | ffu (MPa) | FRP 1 | wf/sf | a (deg) | ρf (%) | Vn,exp (kN) | Vf,exp (kN) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [26] | T6S4-G90 | 400/140/600/150 | 44.1 | 2.8 | 0.10 | 17.7 | 0.60 | 106 | G | 1 | 90 | 2.57 | 297.5 | 109.9 |
| [26] | T6S4-Tri | 400/140/600/150 | 44.1 | 2.8 | 0.10 | 8.1 | 1.53 | 124 | G | 1 | 60 | 3.46 | 316.7 | 129.1 |
| [27] | T4S4-G90 | 400/140/400/150 | 38.0 | 2.1 | 0.10 | 17.7 | 0.60 | 106 | G | 1 | 90 | 2.57 | 205.6 | 48.6 |
| [27] | T4S2-G90 | 400/140/400/150 | 38.3 | 2.1 | 0.20 | 17.7 | 0.60 | 106 | G | 1 | 90 | 2.57 | 225.6 | 24.3 |
| [27] | T4S2-Tri | 400/140/400/150 | 38.4 | 2.1 | 0.20 | 8.1 | 1.53 | 124 | G | 1 | 60 | 3.46 | 242.7 | 41.4 |
| [49] | No.2 | 400/150/300/100 | 44.3 | 5.5 | 0.67 | 230 | 1.51 | 3480 | C | 1 | 90 | 0.15 | 264.0 | 65.0 |
| [49] | No.3 | 400/150/300/100 | 43.8 | 5.5 | 0.67 | 230 | 1.51 | 3480 | C | 1 | 90 | 0.15 | 223.0 | 24.0 |
| [52] | 5 | 300/100/300/50 | 33.4 | 3.6 | 0.75 | 240 | 1.42 | 3400 | C | 1 | 90 | 0.32 | 120.1 | 38.1 |
| [53] | G5.5-1L | 584/122/444.5/89 | 37.9 | 2.7 | 0.83 | 231 | 1.58 | 3650 | C-a | 1 | 90 | 0.24 | 320.3 | 31.2 |
| [53] | G5.5-2L | 584/122/444.5/89 | 37.9 | 2.7 | 0.83 | 231 | 1.58 | 3650 | C-a | 1 | 90 | 0.47 | 342.5 | 53.4 |
| [53] | G8.0-1L | 584/122/444.5/89 | 37.9 | 2.7 | 0.57 | 231 | 1.58 | 3650 | C-a | 1 | 90 | 0.24 | 298.0 | 31.1 |
| [53] | G8.0-2L | 584/122/444.5/89 | 37.9 | 2.7 | 0.57 | 231 | 1.58 | 3650 | C-a | 1 | 90 | 0.47 | 329.2 | 62.3 |
| [53] | G8.0-3L | 584/122/444.5/89 | 37.9 | 2.7 | 0.57 | 231 | 1.58 | 3650 | C-a | 1 | 90 | 0.71 | 351.4 | 84.5 |
| [53] | G16-1L | 584/122/444.5/89 | 37.9 | 2.7 | 0.29 | 231 | 1.58 | 3650 | C-a | 1 | 90 | 0.24 | 275.8 | 40.0 |
| [53] | G16-2L | 584/122/444.5/89 | 37.9 | 2.7 | 0.29 | 231 | 1.58 | 3650 | C-a | 1 | 90 | 0.47 | 320.3 | 84.5 |
| [53] | G24-1L | 584/122/444.5/89 | 37.9 | 2.7 | 0.19 | 231 | 1.58 | 3650 | C-a | 1 | 90 | 0.24 | 258.0 | 53.4 |
| [53] | G24-2L | 584/122/444.5/89 | 37.9 | 2.7 | 0.19 | 231 | 1.58 | 3650 | C-a | 1 | 90 | 0.47 | 253.5 | 48.9 |
| [53] | G24-3L | 584/122/444.5/89 | 37.9 | 2.7 | 0.19 | 231 | 1.58 | 3650 | C-a | 1 | 90 | 0.71 | 258.0 | 53.4 |
| [55] | DB-S1-1L | 270/95/220/55 | 25.5 | 3.6 | 0.38 | 231 | 1.58 | 3650 | C-a | 1 | 90 | 0.14 | 162.5 | 12.7 |
| [55] | DB-S1-2L | 270/95/220/55 | 25.5 | 3.6 | 0.38 | 231 | 1.58 | 3650 | C-a | 1 | 90 | 0.28 | 166.8 | 17.0 |
| [55] | SB-S1-1L | 270/95/220/55 | 25.5 | 3.6 | 0.38 | 231 | 1.58 | 3650 | C-a | 1 | 90 | 0.14 | 95.7 | 2.8 |
| [55] | SB-S1-2L | 270/95/220/55 | 25.5 | 3.6 | 0.38 | 231 | 1.58 | 3650 | C-a | 1 | 90 | 0.28 | 105.1 | 12.2 |
| [56] | DB_S1_1L | 508/152/406/102 | 25.0 | 3.8 | 0.38 | 231 | 1.40 | 3650 | C | 1 | 90 | 0.14 | 355.5 | 32.0 |
| [56] | DB_S1_2L | 508/152/406/102 | 25.0 | 3.8 | 0.38 | 231 | 1.40 | 3650 | C | 1 | 90 | 0.28 | 357.7 | 34.2 |
| [56] | DB_S2_1L | 508/152/406/102 | 25.0 | 3.8 | 0.75 | 231 | 1.40 | 3650 | C | 1 | 90 | 0.14 | 389.7 | 58.0 |
| [56] | DB_S2_2L | 508/152/406/102 | 25.0 | 3.8 | 0.75 | 231 | 1.40 | 3650 | C | 1 | 90 | 0.28 | 404.8 | 73.1 |
| [56] | SB_S1_05L | 508/152/406/102 | 25.0 | 3.8 | 0.38 | 231 | 1.40 | 3650 | C | 1 | 90 | 0.07 | 282.0 | 19.2 |
| [56] | SB_S1_1L | 508/152/406/102 | 25.0 | 3.8 | 0.38 | 231 | 1.40 | 3650 | C | 1 | 90 | 0.14 | 255.0 | 0.0 |
| [56] | SB_S1_2L | 508/152/406/102 | 25.0 | 3.8 | 0.38 | 231 | 1.40 | 3650 | C | 1 | 90 | 0.28 | 267.2 | 4.4 |
| [56] | SB_S2_1L | 508/152/406/102 | 25.0 | 3.8 | 0.75 | 231 | 1.40 | 3650 | C | 1 | 90 | 0.14 | 309.4 | 14.3 |
| [56] | SB_S2_2L | 508/152/406/102 | 25.0 | 3.8 | 0.75 | 231 | 1.40 | 3650 | C | 1 | 90 | 0.28 | 297.2 | 2.1 |
| [60] | S1-0.33R | 508/150/406/102 | 31.0 | 3.8 | 0.38 | 230 | 1.50 | 3450 | C | 1 | 90 | 0.15 | 378.3 | 27.7 |
| [63] | WT-SH-100 | 508/152/406/102 | 37.0 | 3.8 | 0.38 | 230 | 1.50 | 3450 | C | 1 | 90 | 0.21 | 250.6 | 169.4 |
| [65] | TB2 | 300/130/275/75 | 34.0 | 4.4 | 0.17 | 119 | 1.60 | 1400 | C | 1 | 90 | 0.23 | 140.0 | 18.0 |
| [65] | TB3 | 300/130/275/75 | 34.0 | 4.4 | 0.17 | 119 | 1.60 | 1400 | C-a | 1 | 90 | 0.23 | 180.0 | 58.0 |
| [65] | TB4 | 300/130/275/75 | 34.0 | 4.4 | 0.17 | 119 | 1.60 | 1400 | C-a | 1 | 90 | 0.23 | 156.0 | 34.0 |
| [67] | S.S1.1L | 270/95/220/55 | 30.0 | 3.6 | 0.37 | 231 | 1.40 | 3650 | C | 1 | 90 | 0.14 | 98.0 | 3.0 |
| [67] | M.S1.1L | 508/152/406/102 | 30.0 | 3.8 | 0.38 | 231 | 1.40 | 3650 | C | 1 | 90 | 0.14 | 260.0 | 0.0 |
| [67] | L.S1.1L | 745/275/605/150 | 30.0 | 3.6 | 0.41 | 231 | 1.40 | 3650 | C | 1 | 90 | 0.12 | 590.0 | 0.0 |
| [67] | S.S1.2L | 270/95/220/55 | 30.0 | 3.6 | 0.37 | 231 | 1.40 | 3650 | C | 1 | 90 | 0.28 | 107.0 | 12.0 |
| [67] | M.S1.2L | 508/152/406/102 | 30.0 | 3.8 | 0.38 | 231 | 1.40 | 3650 | C | 1 | 90 | 0.28 | 272.0 | 4.0 |
| [67] | L.S1.2L | 745/275/605/150 | 30.0 | 3.6 | 0.41 | 231 | 1.40 | 3650 | C | 1 | 90 | 0.24 | 629.0 | 29.0 |
| [70] | H3A | 600/200/550/150 | 44.7 | 2.1 | 0.12 | 263 | 1.04 | 2739 | C-a | 1 | 90 | 0.17 | 382.2 | 55.1 |
| [70] | H3B | 600/200/550/150 | 49.6 | 2.1 | 0.12 | 263 | 1.04 | 2739 | C-a | 1 | 90 | 0.17 | 408.6 | 74.6 |
1 C: Carbon; G: Glass; A: Aramid; -a: with additional anchorage.

Table A2.
Properties of the retrofitted T-beams with EB-FRP continuous U-jackets without stirrups of the database.
Table A2.
Properties of the retrofitted T-beams with EB-FRP continuous U-jackets without stirrups of the database.
| Ref. | Name | bs/bw/h/hs (mm) | fcm (MPa) | ρsl (%) | ρsw (%) | Ef (GPa) | εfu (%) | ffu (MPa) | FRP 1 | wf/sf | a (deg) | ρf (%) | Vn,exp (kN) | Vf,exp (kN) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p.s. | T2J | 300/150/200/50 | 35.2 | 3.1 | 0.00 | 230 | 1.50 | 3500 | C | 1 | 90 | 0.35 | 81.9 | 23.1 |
| p.s. | T3J | 300/150/200/50 | 35.2 | 3.1 | 0.00 | 230 | 1.50 | 3500 | C | 1 | 90 | 0.52 | 101.3 | 42.5 |
| p.s. | T2J-A | 300/150/200/50 | 35.2 | 3.1 | 0.00 | 230 | 1.50 | 3500 | C-a | 1 | 90 | 0.35 | 101.0 | 42.2 |
| [25] | BT2 | 380/150/405/100 | 35.0 | 2.3 | 0.00 | 228 | 1.66 | 3790 | C | 1 | 90 | 0.22 | 155.0 | 65.0 |
| [25] | BT3 | 380/150/405/100 | 35.0 | 2.3 | 0.00 | 228 | 1.66 | 3790 | C-a | 1 | 90 | 0.22 | 157.5 | 67.5 |
| [25] | BT6 | 380/150/405/100 | 35.0 | 2.3 | 0.00 | 228 | 1.66 | 3790 | C-a | 1 | 90 | 0.22 | 221.0 | 131.0 |
| [27] | T4NS-G90 | 400/140/400/150 | 38.2 | 2.1 | 0.00 | 17.7 | 0.60 | 106 | G | 1 | 90 | 2.57 | 159.0 | 43.6 |
| [48] | A1 | 140/64/191/64 | 59.6 | 2.1 | 0.00 | 13.2 | 2.25 | 296 | A | 1 | 90 | 3.28 | 38.7 | 19.7 |
| [48] | A2 | 140/64/191/64 | 55.0 | 2.1 | 0.00 | 13.2 | 2.25 | 296 | A | 1 | 90 | 3.28 | 30.0 | 11.0 |
| [48] | E1 | 140/64/191/64 | 56.8 | 2.1 | 0.00 | 12.8 | 1.34 | 172 | G | 1 | 90 | 2.08 | 36.7 | 17.7 |
| [48] | E2 | 140/64/191/64 | 53.3 | 2.1 | 0.00 | 12.8 | 1.34 | 172 | G | 1 | 90 | 2.08 | 34.0 | 15.0 |
| [50] | C-BT2 | 380/150/405/100 | 43.3 | 2.3 | 0.00 | 228 | 1.54 | 3790 | C | 1 | 90 | 0.22 | 155.0 | 65.0 |
| [50] | C-BT3 | 380/150/405/100 | 43.3 | 2.3 | 0.00 | 228 | 1.54 | 3790 | C | 1 | 90 | 0.44 | 157.5 | 67.5 |
| [50] | C-BT6 | 380/150/405/100 | 43.3 | 2.3 | 0.00 | 228 | 1.54 | 3790 | C | 1 | 90 | 0.22 | 221.0 | 131.0 |
| [51] | JS2A | 660/152/381/76 | 20.6 | 0.5 | 0.00 | 228 | 1.66 | 3790 | C | 1 | 90 | 0.22 | 237.1 | 25.2 |
| [51] | JS2B | 660/152/381/76 | 20.6 | 0.5 | 0.00 | 228 | 1.66 | 3790 | C | 1 | 90 | 0.22 | 234.2 | 22.3 |
| [51] | JS3A | 660/152/381/76 | 20.6 | 0.5 | 0.00 | 228 | 1.66 | 3790 | C | 1 | 90 | 0.22 | 293.4 | 81.5 |
| [51] | JS3B | 660/152/381/76 | 20.6 | 0.5 | 0.00 | 228 | 1.66 | 3790 | C | 1 | 90 | 0.22 | 275.7 | 63.8 |
| [51] | JS4A | 660/152/381/76 | 20.6 | 0.5 | 0.00 | 228 | 1.66 | 3790 | C | 1 | 90 | 0.43 | 243.1 | 31.2 |
| [51] | JS4B | 660/152/381/76 | 20.6 | 0.5 | 0.00 | 228 | 1.66 | 3790 | C | 1 | 90 | 0.43 | 207.5 | 0.0 |
| [51] | JS5A | 660/152/381/76 | 20.6 | 0.5 | 0.00 | 228 | 1.66 | 3790 | C | 1 | 90 | 0.43 | 278.6 | 66.7 |
| [51] | JS5B | 660/152/381/76 | 20.6 | 0.5 | 0.00 | 228 | 1.66 | 3790 | C | 1 | 90 | 0.43 | 266.8 | 54.9 |
| [51] | JS6A | 660/152/381/76 | 20.6 | 0.5 | 0.00 | 117 | 1.30 | 1517 | A | 1 | 90 | 0.79 | 269.7 | 57.8 |
| [51] | JS6B | 660/152/381/76 | 20.6 | 0.5 | 0.00 | 117 | 1.30 | 1517 | A | 1 | 90 | 0.79 | 240.1 | 28.2 |
| [55] | DB-S0-1L | 270/95/220/55 | 25.5 | 3.6 | 0.00 | 231 | 1.58 | 3650 | C-a | 1 | 90 | 0.14 | 162.2 | 15.4 |
| [55] | DB-S0-2L | 270/95/220/55 | 25.5 | 3.6 | 0.00 | 231 | 1.58 | 3650 | C-a | 1 | 90 | 0.28 | 160.6 | 13.8 |
| [55] | SB-S0-1L | 270/95/220/55 | 25.5 | 3.6 | 0.00 | 231 | 1.58 | 3650 | C-a | 1 | 90 | 0.14 | 59.3 | 23.2 |
| [55] | SB-S0-2L | 270/95/220/55 | 25.5 | 3.6 | 0.00 | 231 | 1.58 | 3650 | C-a | 1 | 90 | 0.28 | 68.5 | 32.4 |
| [56] | DB_S0_05L | 508/152/406/102 | 25.0 | 3.8 | 0.00 | 231 | 1.40 | 3650 | C | 1 | 90 | 0.07 | 268.2 | 90.0 |
| [56] | DB_S0_1L | 508/152/406/102 | 25.0 | 3.8 | 0.00 | 231 | 1.40 | 3650 | C | 1 | 90 | 0.14 | 285.5 | 107.3 |
| [56] | DB_S0_2L | 508/152/406/102 | 25.0 | 3.8 | 0.00 | 231 | 1.40 | 3650 | C | 1 | 90 | 0.28 | 289.0 | 110.8 |
| [56] | SB_S0_05L | 508/152/406/102 | 25.0 | 3.8 | 0.00 | 231 | 1.40 | 3650 | C | 1 | 90 | 0.07 | 102.4 | 21.2 |
| [56] | SB_S0_1L | 508/152/406/102 | 25.0 | 3.8 | 0.00 | 231 | 1.40 | 3650 | C | 1 | 90 | 0.14 | 120.0 | 38.8 |
| [56] | SB_S0_2L | 508/152/406/102 | 25.0 | 3.8 | 0.00 | 231 | 1.40 | 3650 | C | 1 | 90 | 0.28 | 121.7 | 40.5 |
| [60] | S0-0.17R2 | 508/150/406/102 | 31.0 | 3.8 | 0.00 | 230 | 1.50 | 3450 | C | 1 | 90 | 0.07 | 154.7 | 32.0 |
| [60] | S0-0.33R | 508/150/406/102 | 31.0 | 3.8 | 0.00 | 230 | 1.50 | 3450 | C | 1 | 90 | 0.15 | 181.2 | 58.5 |
| [60] | S0-0.66R | 508/150/406/102 | 31.0 | 3.8 | 0.00 | 230 | 1.50 | 3450 | C | 1 | 90 | 0.29 | 183.8 | 61.1 |
| [62] | SB1 | 350/150/175/50 | 27.9 | 3.4 | 0.00 | 68.3 | 2.53 | 172.79 | G | 1 | 90 | 1.30 | 115.0 | 34.0 |
| [62] | SB8 | 350/150/175/50 | 27.1 | 3.4 | 0.00 | 68.3 | 2.53 | 172.79 | G-a | 1 | 90 | 1.30 | 126.0 | 45.0 |
| [62] | SB9 | 350/150/175/50 | 26.1 | 3.4 | 0.00 | 77.9 | 2.68 | 209.09 | G-a | 1 | 90 | 0.33 | 134.0 | 53.0 |
| [63] | NT-SH-100 | 508/152/406/102 | 37.0 | 3.8 | 0.00 | 230 | 1.50 | 3450 | C | 1 | 90 | 0.21 | 120.0 | 38.8 |
| [63] | NT-SH-200 | 508/152/406/102 | 37.0 | 3.8 | 0.00 | 230 | 1.50 | 3450 | C | 1 | 90 | 0.42 | 121.7 | 40.5 |
| [67] | S.S0.1L | 270/95/220/55 | 30.0 | 3.6 | 0.00 | 231 | 1.40 | 3650 | C | 1 | 90 | 0.14 | 62.0 | 24.0 |
| [67] | M.S0.1L | 508/152/406/102 | 30.0 | 3.8 | 0.00 | 231 | 1.40 | 3650 | C | 1 | 90 | 0.14 | 125.0 | 39.0 |
| [67] | L.S0.1L | 745/275/605/150 | 30.0 | 3.6 | 0.00 | 231 | 1.40 | 3650 | C | 1 | 90 | 0.12 | 334.0 | 152.0 |
| [67] | S.S0.2L | 270/95/220/55 | 30.0 | 3.6 | 0.00 | 231 | 1.40 | 3650 | C | 1 | 90 | 0.28 | 71.0 | 33.0 |
| [67] | M.S0.2L | 508/152/406/102 | 30.0 | 3.8 | 0.00 | 231 | 1.40 | 3650 | C | 1 | 90 | 0.28 | 127.0 | 41.0 |
| [67] | L.S0.2L | 745/275/605/150 | 30.0 | 3.6 | 0.00 | 231 | 1.40 | 3650 | C | 1 | 90 | 0.24 | 326.0 | 144.0 |
1 C: Carbon; G: Glass; A: Aramid; -a: with additional anchorage.

Table A3.
Properties of the retrofitted T-beams with EB-FRP U-strips and stirrups of the database.
Table A3.
Properties of the retrofitted T-beams with EB-FRP U-strips and stirrups of the database.
| Ref. | Name | bs/bw/h/hs (mm) | fcm (MPa) | ρsl (%) | ρsw (%) | Ef (GPa) | εfu (%) | ffu (MPa) | FRP 1 | wf/sf | a (deg) | ρf (%) | Vn,exp (kN) | Vf,exp (kN) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [26] | T6S4-C90 | 400/140/600/150 | 44.1 | 2.8 | 0.10 | 230 | 1.48 | 3400 | C | 0.50 | 90 | 0.08 | 272.8 | 85.2 |
| [26] | T6S2-C90 | 400/140/600/150 | 44.1 | 2.8 | 0.20 | 230 | 1.48 | 3400 | C | 0.50 | 90 | 0.08 | 309.8 | 0.0 |
| [27] | T4S2-C45 | 400/140/400/150 | 37.4 | 2.2 | 0.20 | 230 | 1.48 | 3400 | C | 0.35 | 45 | 0.08 | 219.1 | 17.8 |
| [52] | 6 | 300/100/300/50 | 33.4 | 3.6 | 0.75 | 155 | 1.55 | 2400 | G | 0.33 | 90 | 0.80 | 107.2 | 25.1 |
| [54] | 2S_4M(1) | 450/180/400/100 | 38.1 | 2.8 | 0.11 | 240 | 1.50 | 3600 | C | 0.33 | 90 | 0.07 | 186.7 | 4.4 |
| [54] | 2S_7M(1) | 450/180/400/100 | 38.1 | 2.8 | 0.11 | 240 | 1.50 | 3600 | C | 0.53 | 90 | 0.10 | 195.1 | 12.8 |
| [54] | 2S_7M(2) | 450/180/400/100 | 38.1 | 2.8 | 0.11 | 240 | 1.50 | 3600 | C | 0.53 | 90 | 0.21 | 222.1 | 39.8 |
| [54] | 4S_4M(1) | 450/180/400/100 | 41.0 | 2.8 | 0.18 | 240 | 1.50 | 3600 | C | 0.33 | 90 | 0.07 | 250.4 | 27.6 |
| [54] | 4S_7M(1) | 450/180/400/100 | 41.0 | 2.8 | 0.18 | 240 | 1.50 | 3600 | C | 0.53 | 90 | 0.10 | 253.8 | 31.0 |
| [57] | TT1-1 | 400/120/340/100 | 38.0 | 1.7 | 0.79 | 230 | 1.65 | 3800 | C | 0.53 | 90 | 0.08 | 120.6 | 33.3 |
| [57] | TT1-1I | 400/120/340/100 | 38.0 | 1.7 | 0.79 | 230 | 1.65 | 3800 | C | 0.53 | 90 | 0.08 | 140.5 | 53.2 |
| [57] | TT1-2 | 400/120/340/100 | 38.0 | 1.7 | 0.79 | 230 | 1.65 | 3800 | C | 0.40 | 90 | 0.06 | 133.9 | 46.6 |
| [57] | TS1-1 | 400/120/340/100 | 38.0 | 1.7 | 0.40 | 230 | 1.65 | 3800 | C | 0.53 | 90 | 0.08 | 94.0 | 26.6 |
| [57] | TS1-1I | 400/120/340/100 | 38.0 | 1.7 | 0.40 | 230 | 1.65 | 3800 | C | 0.53 | 90 | 0.08 | 60.7 | 0.0 |
| [57] | TS1-2 | 400/120/340/100 | 38.0 | 1.7 | 0.40 | 230 | 1.65 | 3800 | C | 0.40 | 90 | 0.06 | 80.7 | 13.3 |
| [58] | 2 | 360/120/360/75 | 33.2 | 2.4 | 0.16 | 231 | 1.70 | 4100 | C | 0.40 | 90 | 0.08 | 50.7 | 19.7 |
| [58] | 3 | 360/120/360/75 | 32.9 | 2.4 | 0.16 | 231 | 1.70 | 4100 | C | 0.33 | 90 | 0.07 | 45.8 | 14.8 |
| [58] | 4 | 360/120/360/75 | 32.8 | 2.4 | 0.16 | 231 | 1.70 | 4100 | C | 0.25 | 90 | 0.05 | 42.3 | 11.3 |
| [58] | 5 | 360/120/360/75 | 32.8 | 2.4 | 0.16 | 231 | 1.70 | 4100 | C | 0.40 | 90 | 0.08 | 56.3 | 25.3 |
| [58] | 6 | 360/120/360/75 | 33.0 | 2.4 | 0.16 | 231 | 1.70 | 4100 | C | 0.33 | 90 | 0.07 | 54.9 | 23.9 |
| [58] | 7 | 360/120/360/75 | 32.9 | 2.4 | 0.16 | 231 | 1.70 | 4100 | C | 0.25 | 90 | 0.05 | 54.9 | 23.9 |
| [59] | VTC1 | 400/120/300/80 | 68.0 | 2.0 | 0.11 | 221 | 1.24 | 2728 | C | 0.33 | 90 | 0.06 | 110.0 | 37.5 |
| [59] | VTC3 | 400/120/300/80 | 68.5 | 2.0 | 0.11 | 219 | 1.24 | 2730 | C | 0.40 | 90 | 0.11 | 100.0 | 27.5 |
| [59] | VTC4 | 400/120/300/80 | 67.6 | 2.0 | 0.11 | 219 | 1.24 | 2730 | C | 0.40 | 90 | 0.11 | 152.5 | 80.0 |
| [59] | VTC5 | 400/120/300/80 | 68.0 | 2.0 | 0.11 | 221 | 1.50 | 2915 | C | 0.29 | 90 | 0.07 | 121.5 | 49.0 |
| [59] | VTC6 | 400/120/300/80 | 65.6 | 2.0 | 0.11 | 221 | 1.35 | 2915 | C | 0.29 | 90 | 0.07 | 137.5 | 65.0 |
| [60] | S1-0.17R1 | 508/150/406/102 | 31.0 | 3.8 | 0.38 | 230 | 1.50 | 3450 | C | 0.50 | 90 | 0.07 | 365.9 | 15.3 |
| [60] | S1-0.17R2 | 508/150/406/102 | 31.0 | 3.8 | 0.38 | 230 | 1.50 | 3450 | C | 0.50 | 90 | 0.07 | 372.5 | 21.9 |
| [60] | S1-0.23R | 508/150/406/102 | 31.0 | 3.8 | 0.38 | 230 | 1.50 | 3450 | C | 0.70 | 90 | 0.10 | 383.4 | 32.8 |
| [63] | WT-ST-50 | 508/152/406/102 | 37.0 | 3.8 | 0.38 | 230 | 1.50 | 3450 | C | 0.50 | 90 | 0.11 | 246.7 | 14.5 |
| [63] | WT-ST-70 | 508/152/406/102 | 37.0 | 3.8 | 0.38 | 230 | 1.50 | 3450 | C | 0.70 | 90 | 0.15 | 253.9 | 21.7 |
| [64] | S8-U | 500/200/400/100 | 46.1 | 3.8 | 0.25 | 226 | 1.93 | 4361 | C | 0.50 | 90 | 0.08 | 300.8 | 29.7 |
| [64] | S8-UFA1 | 500/200/400/100 | 46.1 | 3.8 | 0.25 | 226 | 1.93 | 4361 | C-a | 0.50 | 90 | 0.08 | 321.0 | 49.9 |
| [64] | S8-UFA2 | 500/200/400/100 | 46.1 | 3.8 | 0.25 | 226 | 1.93 | 4361 | C-a | 0.50 | 90 | 0.08 | 366.3 | 95.1 |
| [64] | S8-UEA1 | 500/200/400/100 | 46.1 | 3.8 | 0.25 | 226 | 1.93 | 4361 | C-a | 0.50 | 90 | 0.08 | 361.9 | 90.8 |
| [70] | M1-a | 600/200/550/150 | 42.8 | 1.6 | 0.12 | 263 | 1.04 | 2739 | C | 0.21 | 90 | 0.04 | 349.4 | 40.0 |
| [70] | M1-b | 600/200/550/150 | 42.8 | 1.6 | 0.12 | 263 | 1.04 | 2739 | C | 0.21 | 90 | 0.04 | 324.7 | 15.7 |
| [70] | M2-a | 600/200/550/150 | 39.8 | 1.6 | 0.12 | 263 | 1.04 | 2739 | C | 0.42 | 90 | 0.07 | 284.9 | 0.0 |
| [70] | M2-b | 600/200/550/150 | 39.8 | 1.6 | 0.12 | 263 | 1.04 | 2739 | C | 0.42 | 90 | 0.07 | 259.1 | 0.0 |
| [70] | M1A | 600/200/550/150 | 39.0 | 1.6 | 0.12 | 263 | 1.04 | 2739 | C-a | 0.21 | 90 | 0.04 | 335.8 | 33.5 |
| [70] | M1B | 600/200/550/150 | 38.5 | 1.6 | 0.12 | 263 | 1.04 | 2739 | C-a | 0.21 | 90 | 0.04 | 328.1 | 26.5 |
| [70] | M2A | 600/200/550/150 | 39.0 | 1.6 | 0.12 | 263 | 1.04 | 2739 | C-a | 0.42 | 90 | 0.07 | 348.0 | 45.4 |
| [70] | M2B | 600/200/550/150 | 38.5 | 1.6 | 0.12 | 263 | 1.04 | 2739 | C-a | 0.42 | 90 | 0.07 | 325.0 | 23.6 |
| [70] | H1-a | 600/200/550/150 | 44.4 | 2.1 | 0.12 | 263 | 1.04 | 2739 | C | 0.21 | 90 | 0.04 | 333.8 | 8.1 |
| [70] | H1-b | 600/200/550/150 | 49.7 | 2.1 | 0.12 | 263 | 1.04 | 2739 | C | 0.21 | 90 | 0.04 | 335.8 | 1.1 |
| [70] | H2-a | 600/200/550/150 | 44.4 | 2.1 | 0.12 | 263 | 1.04 | 2739 | C | 0.42 | 90 | 0.07 | 338.1 | 12.2 |
| [70] | H2-b | 600/200/550/150 | 49.7 | 2.1 | 0.12 | 263 | 1.04 | 2739 | C | 0.42 | 90 | 0.07 | 340.4 | 6.9 |
| [70] | H2A | 600/200/550/150 | 44.7 | 2.1 | 0.12 | 263 | 1.04 | 2739 | C-a | 0.42 | 90 | 0.07 | 402.9 | 75.8 |
| [70] | H2B | 600/200/550/150 | 49.6 | 2.1 | 0.12 | 263 | 1.04 | 2739 | C-a | 0.42 | 90 | 0.07 | 401.6 | 67.6 |
1 C: Carbon; G: Glass; A: Aramid; -a: with additional anchorage.

Table A4.
Properties of the retrofitted T-beams with EB-FRP U-strips without stirrups of the database.
Table A4.
Properties of the retrofitted T-beams with EB-FRP U-strips without stirrups of the database.
| Ref. | Name | bs/bw/h/hs (mm) | fcm (MPa) | ρsl (%) | ρsw (%) | Ef (GPa) | εfu (%) | ffu (MPa) | FRP 1 | wf/sf | a (deg) | ρf (%) | Vn,exp (kN) | Vf,exp (kN) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [25] | BT4 | 380/150/405/100 | 35.0 | 2.3 | 0.00 | 228 | 1.66 | 3790 | C | 0.40 | 90 | 0.09 | 162.0 | 72.0 |
| [26] | T6NS-C45 | 400/140/600/150 | 44.1 | 2.8 | 0.00 | 230 | 1.48 | 3400 | C | 0.50 | 45 | 0.11 | 213.6 | 103.5 |
| [50] | C-BT4 | 380/150/405/100 | 43.3 | 2.3 | 0.00 | 228 | 1.54 | 3790 | C | 0.40 | 90 | 0.09 | 162.0 | 72.0 |
| [60] | S0-0.12R | 508/150/406/102 | 31.0 | 3.8 | 0.00 | 230 | 1.50 | 3450 | C | 0.35 | 90 | 0.05 | 182.6 | 59.9 |
| [60] | S0-0.17R1 | 508/150/406/102 | 31.0 | 3.8 | 0.00 | 230 | 1.50 | 3450 | C | 0.50 | 90 | 0.07 | 203.1 | 80.4 |
| [60] | S0-0.17R2 | 508/150/406/102 | 31.0 | 3.8 | 0.00 | 230 | 1.50 | 3450 | C | 0.61 | 90 | 0.09 | 204.9 | 82.2 |
| [60] | S0-0.20R1 | 508/150/406/102 | 31.0 | 3.8 | 0.00 | 230 | 1.50 | 3450 | C | 0.60 | 90 | 0.09 | 197.9 | 75.2 |
| [60] | S0-0.20R2 | 508/150/406/102 | 31.0 | 3.8 | 0.00 | 230 | 1.50 | 3450 | C | 0.70 | 90 | 0.10 | 227.3 | 104.6 |
| [61] | S0-1L-ST-U-90 | 250/100/260/60 | 40.0 | 2.8 | 0.00 | 13.2 | 1.21 | 160 | G | 0.50 | 90 | 0.36 | 62.0 | 12.0 |
| [62] | SB3 | 350/150/175/50 | 26.3 | 3.4 | 0.00 | 68.3 | 2.53 | 172.79 | G | 0.50 | 90 | 0.67 | 107.5 | 26.5 |
| [63] | NT-ST-35 | 508/152/406/102 | 37.0 | 3.8 | 0.00 | 230 | 1.50 | 3450 | C | 0.35 | 90 | 0.07 | 120.9 | 39.7 |
| [63] | NT-ST-50 | 508/152/406/102 | 37.0 | 3.8 | 0.00 | 230 | 1.50 | 3450 | C | 0.50 | 90 | 0.11 | 134.5 | 53.3 |
| [63] | NT-ST-60 | 508/152/406/102 | 37.0 | 3.8 | 0.00 | 230 | 1.50 | 3450 | C | 0.60 | 90 | 0.13 | 131.1 | 49.9 |
| [63] | NT-ST-61 | 508/152/406/102 | 37.0 | 3.8 | 0.00 | 230 | 1.50 | 3450 | C | 0.61 | 90 | 0.13 | 135.7 | 54.5 |
| [63] | NT-ST-70 | 508/152/406/102 | 37.0 | 3.8 | 0.00 | 230 | 1.50 | 3450 | C | 0.70 | 90 | 0.15 | 150.6 | 69.4 |
| [64] | S0-U | 500/200/400/100 | 43.0 | 3.8 | 0.00 | 226 | 1.93 | 4361 | C | 0.50 | 90 | 0.08 | 223.7 | 39.7 |
| [64] | S0-UFA1 | 500/200/400/100 | 43.0 | 3.8 | 0.00 | 226 | 1.93 | 4361 | C-a | 0.50 | 90 | 0.08 | 233.9 | 49.9 |
| [64] | S0-UFA2 | 500/200/400/100 | 43.0 | 3.8 | 0.00 | 226 | 1.93 | 4361 | C-a | 0.50 | 90 | 0.08 | 313.5 | 129.5 |
| [64] | S0-UEA1 | 500/200/400/100 | 43.0 | 3.8 | 0.00 | 226 | 1.93 | 4361 | C-a | 0.50 | 90 | 0.08 | 326.7 | 142.7 |
| [64] | S0-UEA12 | 500/200/400/100 | 43.0 | 3.8 | 0.00 | 226 | 1.93 | 4361 | C-a | 0.50 | 90 | 0.08 | 354.5 | 170.5 |
| [66] | 1 | 360/120/360/80 | 23.0 | 2.4 | 0.00 | 236 | 1.50 | 3450 | C | 0.50 | 90 | 0.11 | 166.8 | 109.4 |
| [68] | Single Layer | 450/150/420/100 | 70.0 | 3.8 | 0.00 | 230 | 1.80 | 4800 | C | 0.56 | 90 | 0.12 | 221.0 | 24.4 |
| [68] | Double Layers | 450/150/420/100 | 70.0 | 3.8 | 0.00 | 230 | 1.80 | 4800 | C | 0.56 | 90 | 0.25 | 217.0 | 20.4 |
| [69] | BSU | 450/180/350/100 | 45.9 | 1.4 | 0.00 | 228 | 2.10 | 4830 | C | 0.67 | 90 | 0.13 | 318.6 | 170.3 |
1 C: Carbon; G: Glass; A: Aramid; -a: with additional anchorage.
References
- Karayannis, C.G.; Chalioris, C.E. Shear tests of reinforced concrete beams with continuous rectangular spiral reinforcement. Constr. Build. Mater. 2013, 46, 86–97. [Google Scholar] [CrossRef]
- Chalioris, C.E.; Sfiri, E.F. Shear performance of steel fibrous concrete beams. Procedia Eng. 2011, 14, 2064–2068. [Google Scholar] [CrossRef]
- Lantsoght, E.O.L. Database of Shear Experiments on Steel Fiber Reinforced Concrete Beams without Stirrups. Materials 2019, 12, 917. [Google Scholar] [CrossRef] [PubMed]
- Torres, J.A.; Lantsoght, E.O.L. Influence of Fiber Content on Shear Capacity of Steel Fiber-Reinforced Concrete Beams. Fibers 2019, 7, 102. [Google Scholar] [CrossRef]
- Lantsoght, E.O.L. How do steel fibers improve the shear capacity of reinforced concrete beams without stirrups? Compos. Part B Eng. 2019, 175, 107079. [Google Scholar] [CrossRef]
- Gribniak, V.; Tamulenas, V.; Ng, P.-L.; Arnautov, A.K.; Gudonis, E.; Misiunaite, I. Mechanical behavior of steel fiber-reinforced concrete beams bonded with external carbon fiber sheets. Materials 2017, 10, 666. [Google Scholar] [CrossRef]
- Taha, M.R. FRP for Infrastructure Applications: Research Advances. Fibers 2018, 6, 1. [Google Scholar] [CrossRef]
- Naser, M.Z.; Hawileh, R.A.; Abdalla, J.A. Fiber-reinforced polymer composites in strengthening reinforced concrete structures: A critical review. Eng. Struct. 2019, 198, 109542. [Google Scholar] [CrossRef]
- Chalioris, C.E. Shear Performance of RC Beams Using FRP Sheets Covering Part of the Shear Span. In Proceedings of the 1st International Conference on Concrete Repair, St–Malo, Brittany, France, 15–17 July 2003; pp. 809–816. [Google Scholar]
- Chalioris, C.E. Analytical model for the torsional behaviour of reinforced concrete beams retrofitted with FRP materials. Eng. Struct. 2007, 29, 3263–3276. [Google Scholar] [CrossRef]
- Ferreira, D.; Oller, E.; Marí, A.; Bairán, J. Numerical Analysis of Shear Critical RC Beams Strengthened in Shear with FRP Sheets. J. Compos. Constr. 2013, 17, 04013016. [Google Scholar] [CrossRef]
- Manos, G.C.; Theofanous, M.; Katakalos, K. Numerical simulation of the shear behaviour of reinforced concrete rectangular beam specimens with or without FRP-strip shear reinforcement. Adv. Eng. Softw. 2014, 67, 47–56. [Google Scholar] [CrossRef]
- Karayannis, C.G.; Chalioris, C.E. Strengthening of Shear T–Beams Using Carbon FRP. In Proceedings of the 1st International Conference on Concrete Repair, St–Malo, Brittany, France, 15–17 July 2003; pp. 775–782. [Google Scholar]
- Karayannis, C.G.; Chalioris, C.E. Experimental Investigation of the Contribution of Bonded C–FRP Jackets to Shear Capacity of RC Beams. In Proceedings of the International Symposia Celebrating Concrete: People and Practice, Vol. Role of Concrete in Sustainable Development, University of Dundee, Scotland, UK, 3–4 September 2003; pp. 689–696. [Google Scholar]
- Chalioris, C.E. Torsional strengthening of rectangular and flanged beams using carbon fibre–reinforced–polymers—Experimental study. Constr. Build. Mater. 2008, 22, 21–29. [Google Scholar] [CrossRef]
- Belarbi, A.; Bae, S.-W.; Brancaccio, A. Behavior of full-scale RC T-beams strengthened in shear with externally bonded FRP sheets. Constr. Build. Mater. 2012, 32, 27–40. [Google Scholar] [CrossRef]
- Afefy, H.M.E.D.; Mahmoud, M.H.; Fawzy, T.M. Rehabilitation of defected RC stepped beams using CFRP. Eng. Struct. 2013, 49, 295–305. [Google Scholar] [CrossRef]
- Panigrahi, S.K.; Deb, A.; Bhattacharyya, S.K. Modes of Failure in Shear Deficient RC T–Beams Strengthened with FRP. J. Compos. Constr. 2016, 20, 04015029. [Google Scholar] [CrossRef]
- Ferreira, D.; Oller, E.; Marí, A.; Bairán, J. Analysis of FRP Shear Strengthening Solutions for Reinforced Concrete Beams Considering Debonding Failure. J. Compos. Constr. 2016, 20, 04016018. [Google Scholar] [CrossRef]
- Chalioris, C.E.; Kosmidou, P.M.; Papadopoulos, N.A. Investigation of a new strengthening technique for RC deep beams using carbon FRP ropes as transverse reinforcements. Fibers 2018, 6, 52. [Google Scholar] [CrossRef]
- Chaallal, O.; Nollet, M.-J.; Perraton, D. Shear Strengthening of RC Beams by Externally Bonded Side CFRP Strips. J. Compos. Constr. 1998, 2, 111–113. [Google Scholar] [CrossRef]
- Triantafillou, T.C. Shear Strengthening of Reinforced Concrete Beams Using Epoxy–Bonded FRP Composites. Aci. Sj 1998, 95, 107–115. [Google Scholar]
- Triantafillou, T.C.; Antonopoulos, C.P. Design of Concrete Flexural Members Strengthened in Shear with FRP. J. Compos. Constr. 2000, 4, 198–205. [Google Scholar] [CrossRef]
- Khalifa, A.; Gold, W.J.; Nanni, A.; Abdel Aziz, M.I. Contribution of Externally Bonded FRP to Shear Capacity of RC Flexural Members. J. Compos. Constr. 1998, 2, 195–202. [Google Scholar] [CrossRef]
- Khalifa, A.; Nanni, A. Improving shear capacity of existing RC T–section beams using CFRP composites. Cem. Concr. Compos. 2000, 22, 165–174. [Google Scholar] [CrossRef]
- Deniaud, C.; Cheng, J.J.R. Shear behavior of reinforced concrete T-beams with externally bonded fiber-reinforced polymer sheets. Aci. Sj 2001, 98, 386–394. [Google Scholar]
- Deniaud, C.; Cheng, J.J.R. Reinforced Concrete T–Beams Strengthened in Shear with Fiber Reinforced Polymer Sheets. J. Compos. Constr. 2003, 7, 302–310. [Google Scholar] [CrossRef]
- Pellegrino, C.; Modena, C. Fiber Reinforced Polymer Shear Strengthening of Reinforced Concrete Beams with Transverse Steel Reinforcement. J. Compos. Constr. 2002, 6, 104–111. [Google Scholar] [CrossRef]
- Chen, J.F.; Teng, J.G. Shear Capacity of Fiber–Reinforced Polymer–Strengthened Reinforced Concrete Beams: Fiber Reinforced Polymer Rupture. J. Struct. Eng. 2003, 129, 615–625. [Google Scholar] [CrossRef]
- Chen, J.F.; Teng, J.G. Shear capacity of FRP–strengthened RC beams: FRP debonding. Constr. Build. Mater. 2003, 17, 27–41. [Google Scholar] [CrossRef]
- Carolin, A.; Täljsten, B. Theoretical Study of Strengthening for Increased Shear Bearing Capacity. J. Compos. Constr. 2005, 9, 497–506. [Google Scholar] [CrossRef]
- Monti, G.; Liotta, M. Tests and design equations for FRP-strengthening in shear. Constr. Build. Mater. 2007, 21, 799–809. [Google Scholar] [CrossRef]
- National Research Council. Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Existing Structures; CNR-DT 200 R1/2013; National Research Council: Roma, Italy, 2014. [Google Scholar]
- Fédération Internationale du Béton (Fib). Externally Applied FRP Reinforcement for Concrete Structures; Fib Bulletin 90; International Federation for Structural Concrete: Lausanne, Switzerland, 2019. [Google Scholar]
- Lavorato, D.; Nuti, C.; Santini, S. Experimental Investigation of the Shear Strength of RC Beams Extracted from an Old Structure and Strengthened by Carbon FRP U-Strips. Appl. Sci. 2018, 8, 1182. [Google Scholar] [CrossRef]
- Tsonos, A.G. Effectiveness of CFRP–jackets in post–earthquake and pre–earthquake retrofitting of beam–column subassemblages. Struct. Eng. Mech. 2007, 27, 393–408. [Google Scholar] [CrossRef]
- Karayannis, C.G.; Sirkelis, G.M. Strengthening and rehabilitation of RC beam–column joints using carbon–FRP jacketing and epoxy resin injection. Earthq. Eng. Struct. Dyn. 2008, 37, 769–790. [Google Scholar] [CrossRef]
- Kakaletsis, D.J.; David, K.N.; Karayannis, C.G. Effectiveness of some conventional seismic retrofitting techniques for bare and infilled R/C frames. Struct. Eng. Mech. 2011, 39, 499–520. [Google Scholar] [CrossRef]
- Kabir, M.R.; Alam, M.S.; Said, A.M.; Ayad, A. Performance of Hybrid Reinforced Concrete Beam Column Joint: A Critical Review. Fibers 2016, 4, 13. [Google Scholar] [CrossRef]
- Ercan, E.; Arisoy, B.; Ertem, O.B. Experimental Assessment of RC Beam-Column Connections with Internal and External Strengthening Techniques. Adv. Civ. Eng. 2019, 2019, 12. [Google Scholar]
- KAN.EPE. 2017 Greek Code of Interventions; Team for development of code of interventions on reinforced concrete buildings, Harmonization team of code of interventions to Eurocodes: Council of Europe, European Centre on Prevention and Forecasting of Earthquakes (E.C.P.F.E.), Earthquake Planning and Protection Organization (E.P.P.O.): Athens, Greece, 2017. [Google Scholar]
- European Committee for Standardization. Eurocode 8: Design of Structures for Earthquake Resistance—Part 3: Assessment and Retrofitting of Buildings (EN 1998-3); CEN: Brussels, Belgium, 2005. [Google Scholar]
- ACI Committee 440. Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures; American Concrete Institute: Hong Hua, MI, USA, 2017; ISBN 978–1–945487–59–0. [Google Scholar]
- Bae, S.-W.; Belarbi, A. Behavior of Various Anchorage Systems Used for Shear Strengthening of Concrete Structures with Externally Bonded FRP Sheets. J. Bridge Eng. 2013, 18, 837–847. [Google Scholar] [CrossRef]
- Neubauer, U.; Rostasy, F.S. Design Aspects of Concrete Structures Strengthened with Externally Bonded CFRP-Plates. In Proceedings of the 7th International Conference on Structural Faults and Repair, Edinburgh, UK, 8 July 1997; Volume 2, pp. 109–118. [Google Scholar]
- Chen, J.F.; Teng, J.G. Anchorage Strength Models for FRP and Steel Plates Bonded to Concrete. ASCE J. Struct. Eng. 2001, 127, 784–791. [Google Scholar] [CrossRef]
- Biscaia, H.C.; Chastre, C.; Silva, M.A.G. Nonlinear Numerical Analysis of the Debonding Failure Process of FRP-to-Concrete Interfaces. Compos. Part B Eng. 2013, 50, 210–223. [Google Scholar] [CrossRef]
- Chajes, M.J.; Januszka, T.F.; Mertz, D.R.; Thomson, T.A.; Finch, W.W. Shear strengthening of reinforced concrete beams using externally applied composite fabrics. Aci. Sj 1995, 92, 295–303. [Google Scholar]
- Sato, Y.; Ueda, T.; Kakuta, Y.; Ono, S. Ultimate Shear Force Capacity of Reinforced Concrete Beams with Carbon Fibre Sheet. In Proceedings of the 3rd International Symposium on Non–Metallic (FRP) Reinforcement for Concrete Structures, Sapporo, Japan, 14–16 October 1997; pp. 499–505. [Google Scholar]
- Khalifa, A.; Tumialan, G.; Nanni, A.; Belarbi, A. Shear Strengthening of Continuous RC Beams Using Externally Bonded CFRP Sheets. SP–188, American Concrete Institute. In Proceedings of the 4th International Symposium on FRP for Reinforcement of Concrete Structures (FRPRCS4), Baltimore, MD, USA, 31 October–5 November 1999; pp. 995–1008. [Google Scholar]
- Annaiah, R.H.; Myers, J.J.; Nanni, A. Shear Performances of RC Beams Strengthened In Situ with FRP Composites; Report for CIES 99-11; University of Missouri: Rolla, MO, USA, 2001. [Google Scholar]
- Park, S.Y.; Namaan, A.E.; Lopez, M.M.; Till, R.D. Shear Strengthening Effect of RC Beams Using Glued CFRP Sheets. In Proceedings of the International Conference on FRP Composites in Civil Engineering, Hong Kong, China, 12–15 December 2001; pp. 669–676. [Google Scholar]
- Chaallal, O.; Shahawy, M.; Hassan, M. Performance of Reinforced Concrete T–Girders Strengthened in Shear with Carbon Fiber–Reinforced Polymer Fabric. Aci. Sj 2002, 99, 335–343. [Google Scholar]
- Dias, S.J.E.; Barros, J.A.O. Influência da Percentagem e Orientação de Laminados de CFRP no Reforço ao Corte de Vigas de Betão Armado. In Proceedings of the Anais do VIº Simpósio EPUSP Sobre Estruturas de Concreto, São Paulo, Brazil, 8–11 April 2006. [Google Scholar]
- Bousselham, A.; Chaallal, O. Effect of transverse steel and shear span on the performance of RC beams strengthened in shear with CFRP. Compos. Part B Eng. 2006, 37, 37–46. [Google Scholar] [CrossRef]
- Bousselham, A.; Chaallal, O. Behavior of Reinforced Concrete T–Beams Strengthened in Shear with Carbon Fiber–Reinforced Polymer—An Experimental Study. Aci. Sj 2006, 103, 339–347. [Google Scholar]
- Jayaprakash, J.; Samad, A.A.A.; Abbasovich, A.A.; Ali, A.A.A. Repair of precracked RC rectangular shear beams using CFRP strip technique. Struct. Eng. Mech. 2007, 26, 427–439. [Google Scholar] [CrossRef]
- Altin, S.; Anil, Ö.; Kopraman, Y.; Mertoğlu, Ç.; Kara, M.E. Improving Shear Capacity and Ductility of Shear–deficient RC Beams Using CFRP Strips. J. Reinf. Plast. Compos. 2010, 29, 2975–2991. [Google Scholar] [CrossRef]
- Gamino, A.L.; Sousa, J.L.A.O.; Manzoli, O.L.; Bittencourt, T.N. Estruturas de concreto reforçadas com PRFC Parte II: Análise dos modelos de cisalhamento. Rev. Ibracon Estrut. Mater. 2010, 3, 24–49. [Google Scholar] [CrossRef]
- Mofidi, A.; Chaallal, O. Shear Strengthening of RC Beams with Externally Bonded FRP Composites: Effect of Strip–Width–to–Strip–Spacing Ratio. J. Compos. Constr. 2011, 15, 732–742. [Google Scholar] [CrossRef]
- Panda, K.C.; Bhattacharyya, S.K.; Barai, S.V. Strengthening of RC T–beams with shear deficiencies using GFRP strips. J. Civ. Eng. Archit. 2011, 5, 56–67. [Google Scholar]
- Panigrahi, A.K.; Biswal, K.C.; Barik, M.R. Strengthening of shear deficient RC T–beams with externally bonded GFRP sheets. Constr. Build. Mater. 2014, 57, 81–91. [Google Scholar] [CrossRef]
- Mofidi, A.; Chaallal, O. Tests and Design Provisions for Reinforced–Concrete Beams Strengthened in Shear Using FRP Sheets and Strips. Int. J. Concr. Struct. Mater. 2014, 8, 117–128. [Google Scholar] [CrossRef]
- Chen, G.M.; Zhang, Z.; Li, Y.L.; Li, X.Q.; Zhou, C.Y. T–section RC beams shear–strengthened with anchored CFRP U–strips. Compos. Struct. 2016, 144, 57–79. [Google Scholar] [CrossRef]
- Frederick, F.F.R.; Sharma, U.K.; Gupta, V.K. Influence of End Anchorage on Shear Strengthening of Reinforced Concrete Beams Using CFRP Composites. Curr. Sci. 2017, 112, 973–981. [Google Scholar] [CrossRef]
- Manos, G.; Katakalos, K.; Mpalaskas, G. Experimental Measurements and Numerical Simuation of Novel Anchoring Devices for Open Hoop Fiber Reinforcing Polymer Strips Used in the Shear Upgrade Of R/C T–Beams. In Proceedings of the 6th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN 2015), Rhodes Island, Greece, 15–17 June 2017; pp. 120–141. [Google Scholar]
- Benzeguir, Z.E.A.; El–Saikaly, G.; Chaallal, O. Size Effect in RC T–Beams Strengthened in Shear with Externally Bonded CFRP Sheets: Experimental Study. J. Compos. Constr. 2019, 23, 04019048. [Google Scholar] [CrossRef]
- Ibrahim, B.; Leblouba, M.; Al–Toubat, S.; Barakat, S. Shear strength of FRP–Externally strengthened High Strength RC T–Beams. IOP Conf. Ser. Mater. Sci. Eng. 2019, 601, 012018. [Google Scholar] [CrossRef]
- Mhanna, H.H.; Hawileh, R.A.; Abdalla, J.A. Shear Strengthening of Reinforced Concrete Beams Using CFRP Wraps. Procedia Struct. Integr. 2019, 17, 214–221. [Google Scholar] [CrossRef]
- Oller, E.; Pujol, M.; Marí, A. Contribution of externally bonded FRP shear reinforcement to the shear strength of RC beams. Compos. Part B Eng. 2019, 164, 235–248. [Google Scholar] [CrossRef]
- Chalioris, C.E.; Argiriou, C.A. Shear Strengthening of Reinforced Concrete T-beams with EB-FRP Sheets. In Proceedings of the 6th International Conference on Concrete Repair, Thessaloniki, Greece, 20–23 June 2016; pp. 479–486. [Google Scholar]
- Pellegrino, C.; Vasic, M. Assessment of design procedures for the use of externally bonded FRP composites in shear strengthening of reinforced concrete beams. Compos. Part B Eng. 2013, 45, 727–741. [Google Scholar] [CrossRef]
- Sas, G.; Täljsten, B.; Barros, J.; Lima, J.; Carolin, A. Are Available Models Reliable for Predicting the FRP Contribution to the Shear Resistance of RC Beams? J. Compos. Constr. 2009, 13, 514–534. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).