A Method to Process Hollow-Core Anti-Resonant Fibers into Fiber Filters
Abstract
:1. Introduction
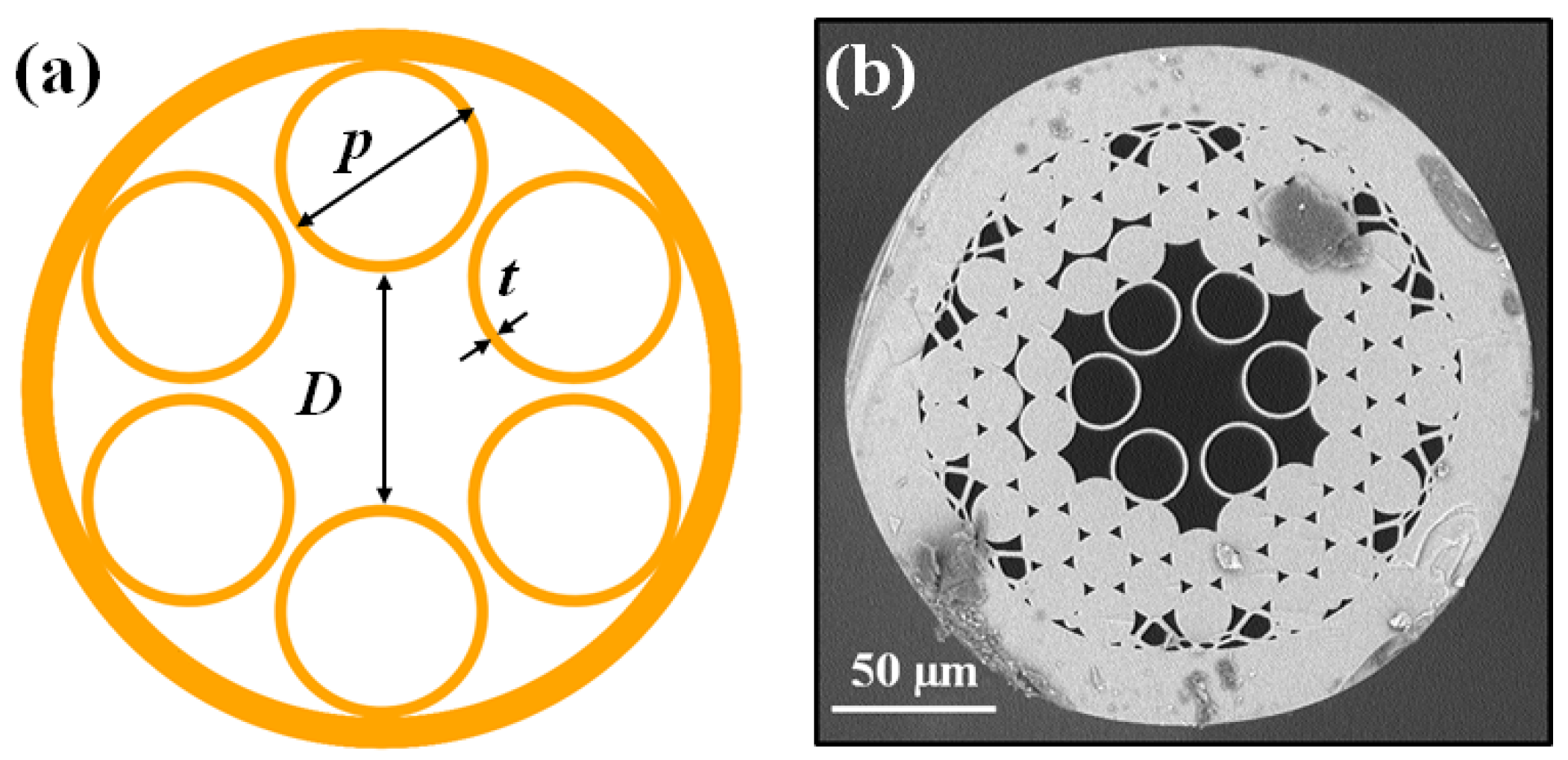
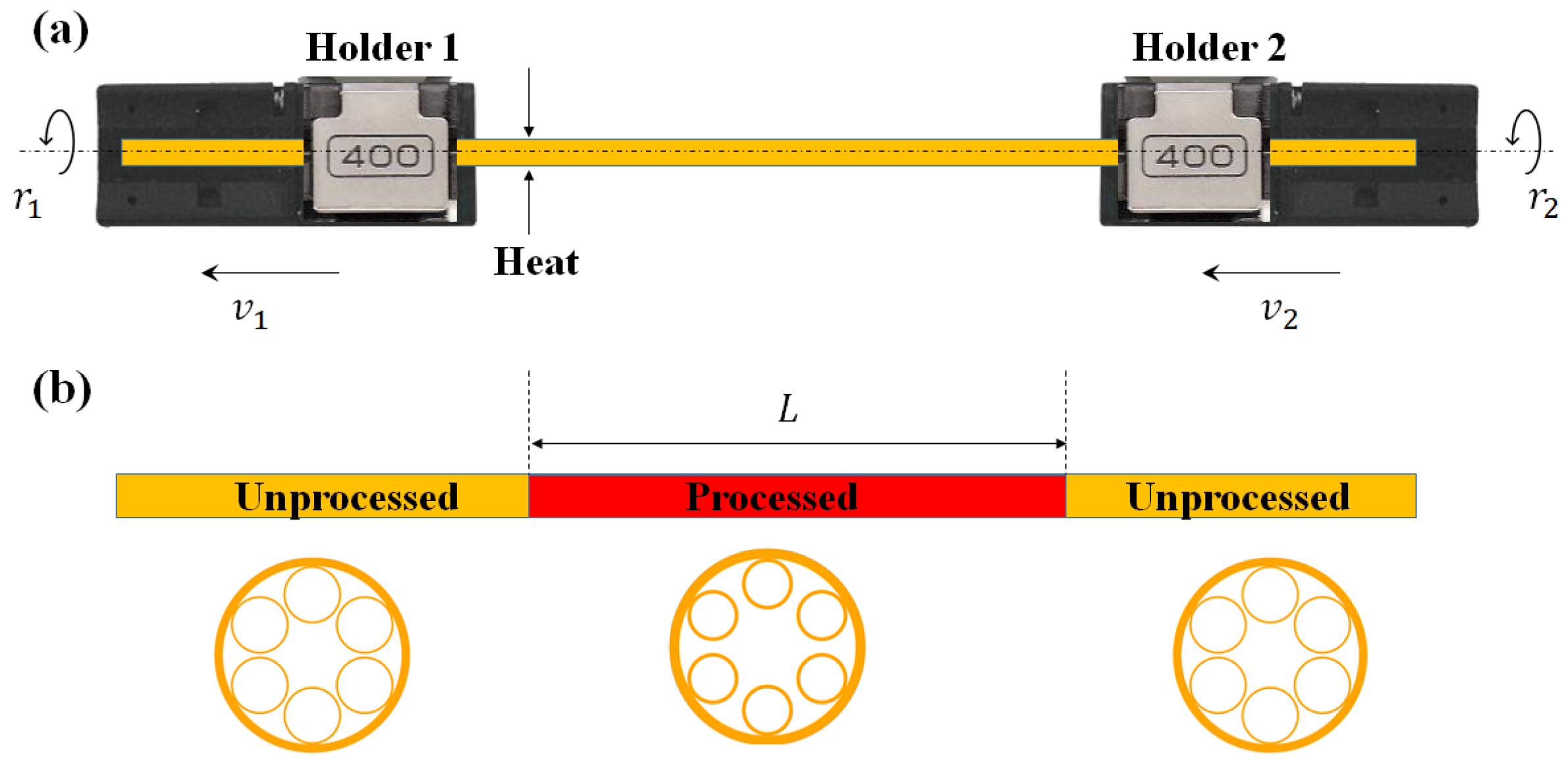
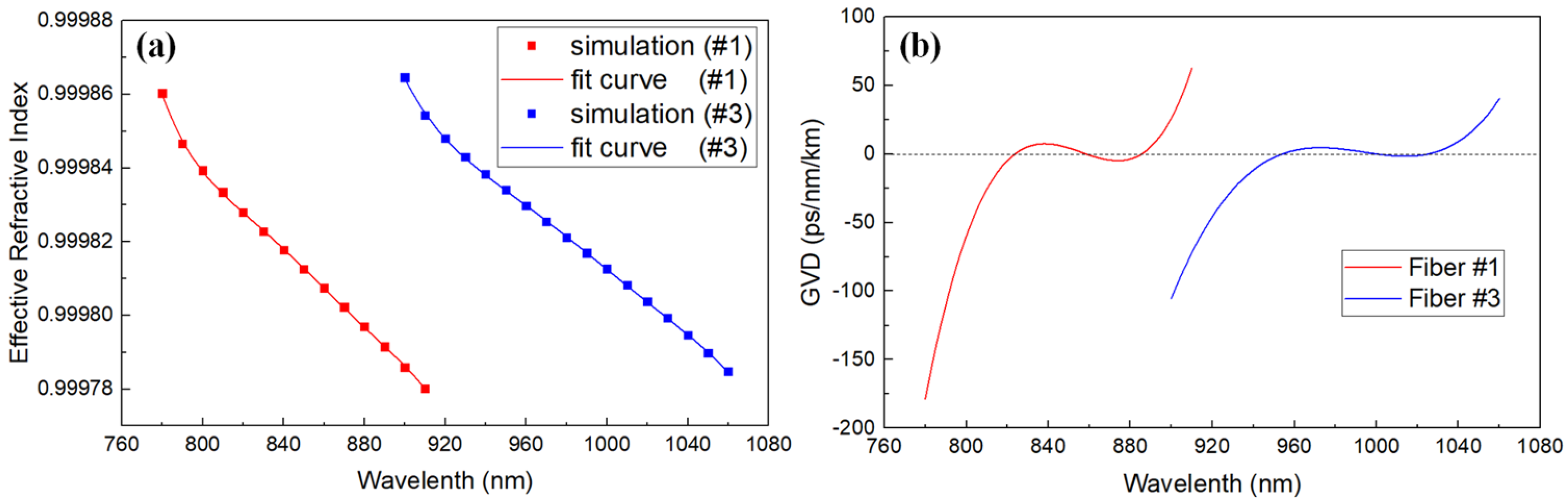
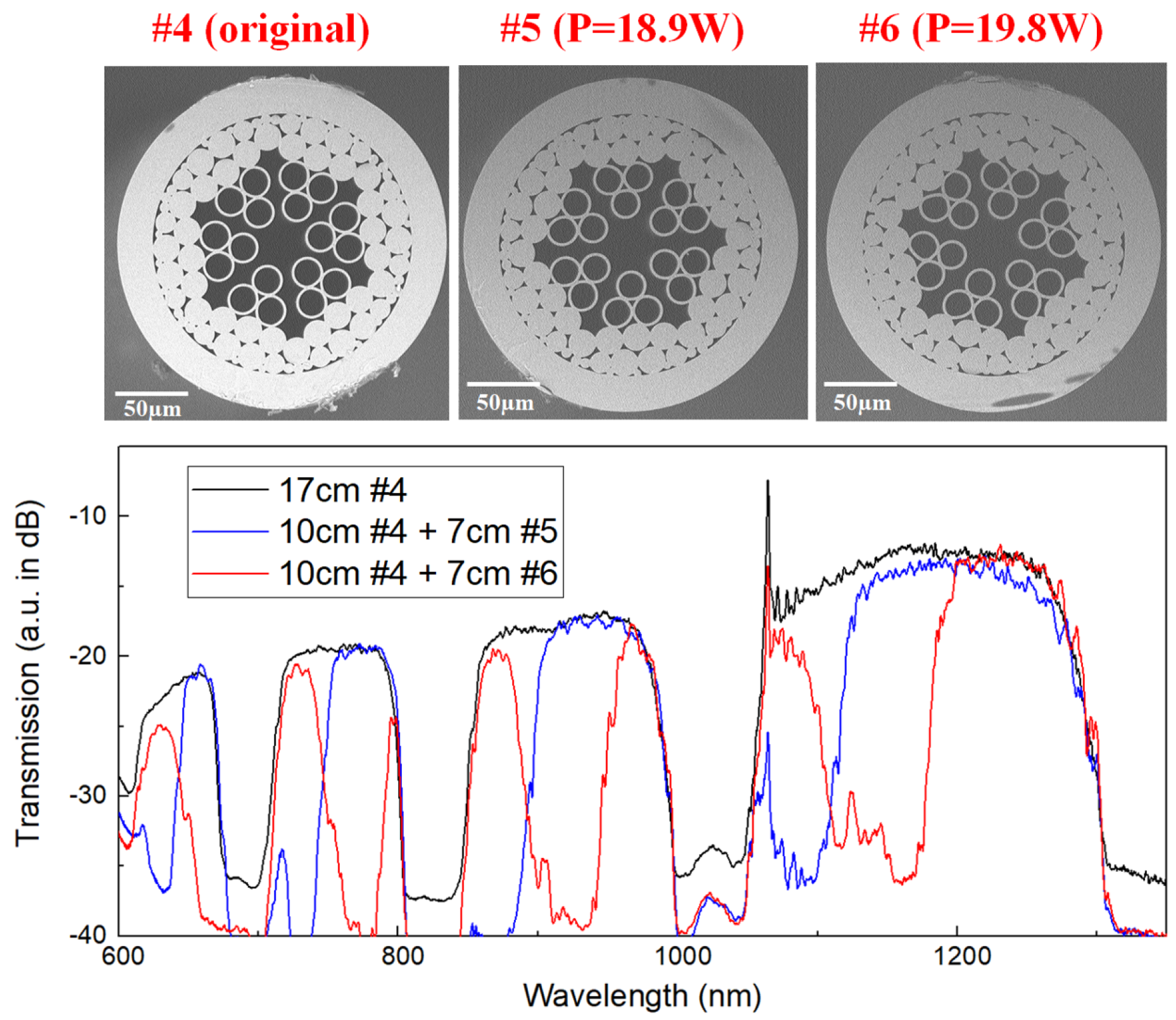
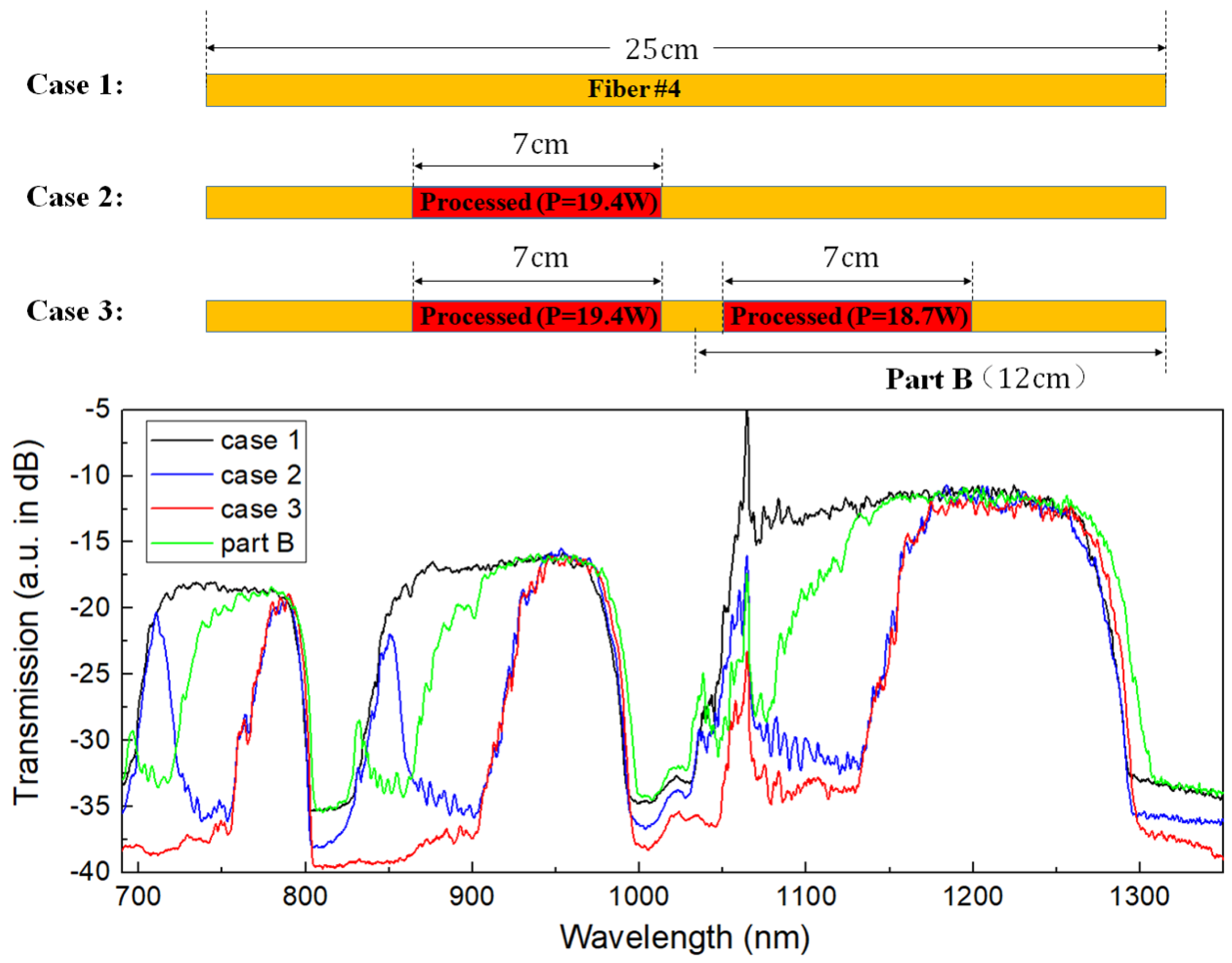
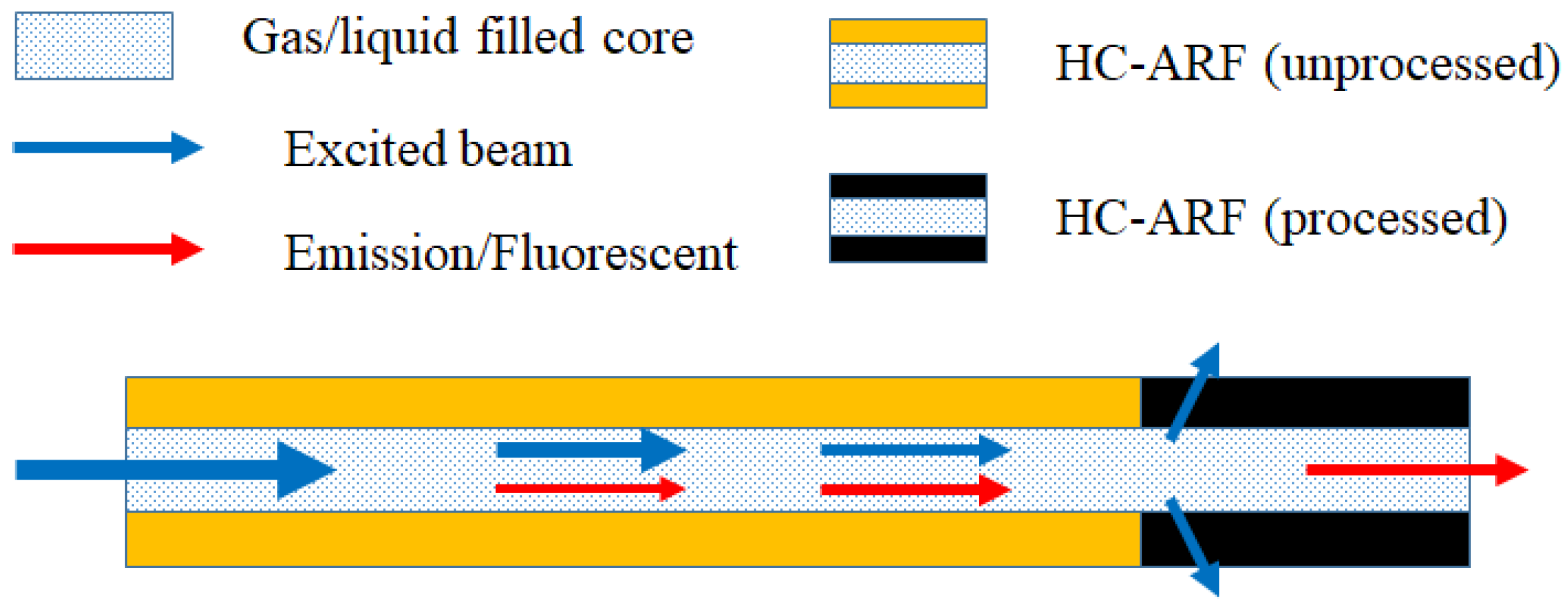
2. Methods
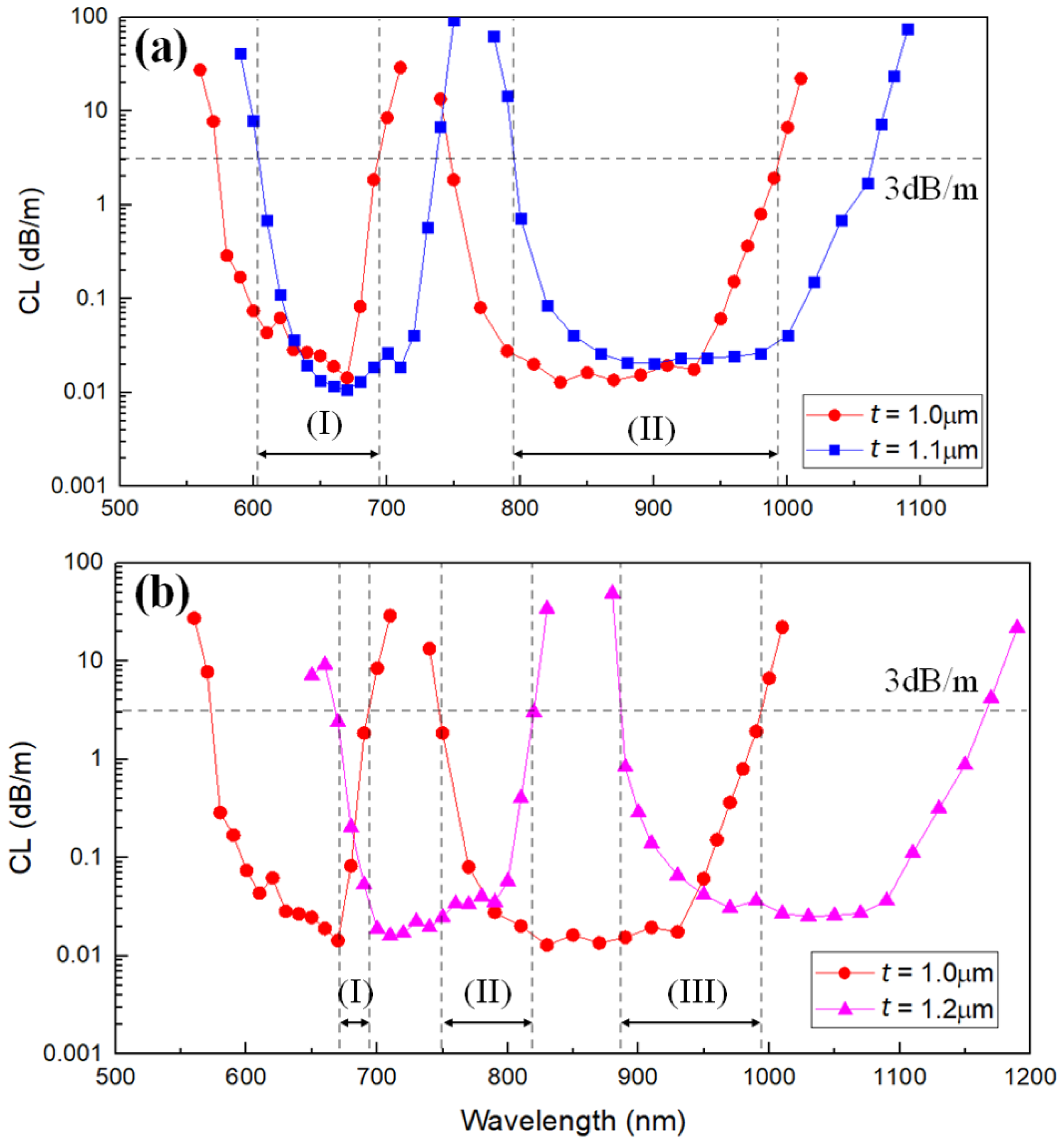
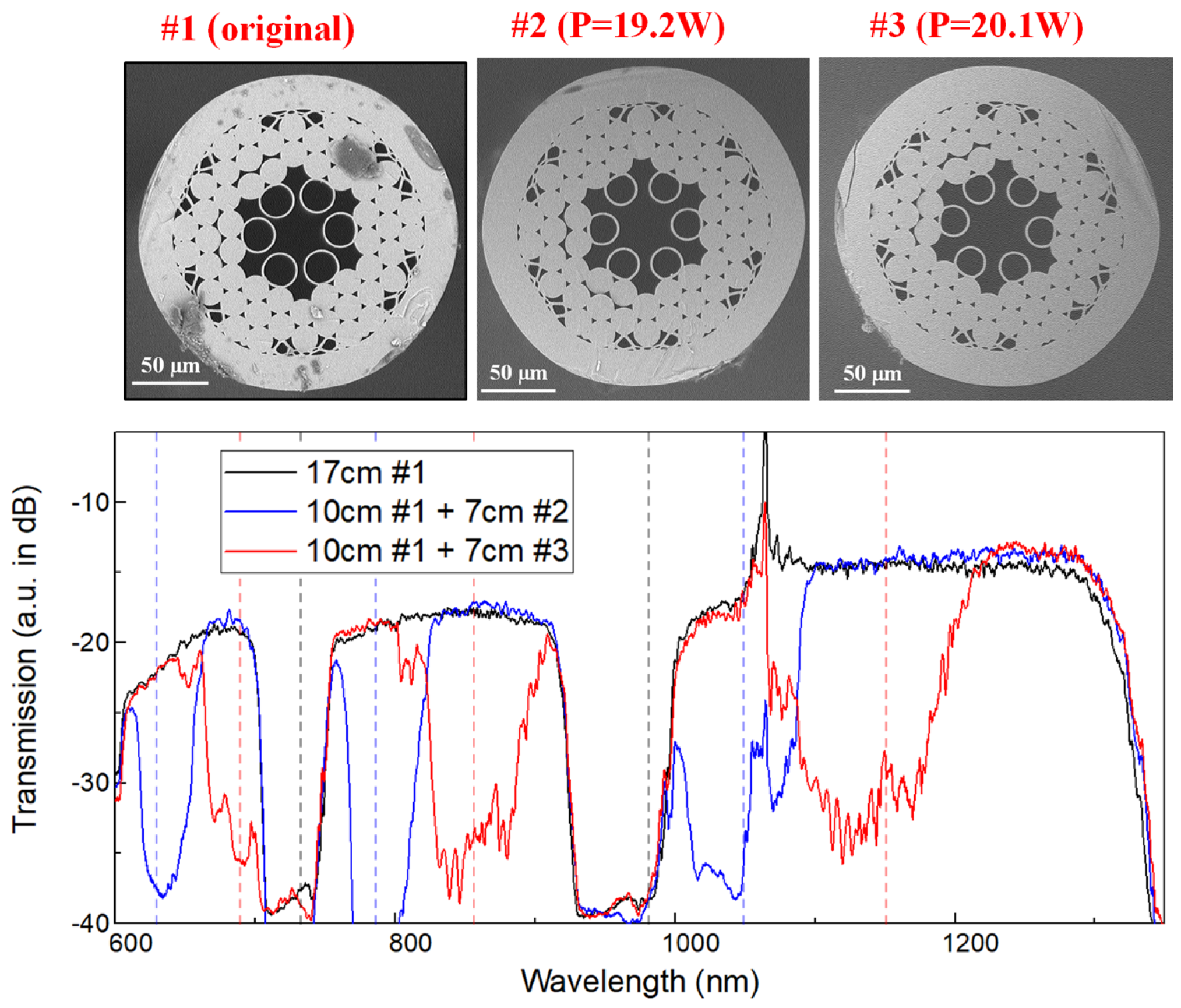
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| HC-PCF | Hollow-Core Photonic Crystal Fiber |
| HC-PBGF | Hollow-Core Photonic Bandgap Fiber |
| HC-ARF | Hollow-Core Anti-Resonant Fiber |
| ERI | Effective Refractive Index |
| GVD | Group Velocity Dispersion |
References
- Birks, T.A.; Roberts, P.J.; Russell, P.S.J.; Atkin, D.M.; Shepherd, T.J. Full 2-D photonic bandgaps in silica/air structures. Electron. Lett. 1995, 31, 1941–1943. [Google Scholar] [CrossRef]
- Smith, C.M.; Venkataraman, N.; Gallagher, M.T.; Müller, D.; West, J.A.; Borrelli, N.F.; Allan, D.C.; Koch, K.W. Low-loss hollow-core silica/air photonic bandgap fibre. Nature 2003, 424, 657–659. [Google Scholar] [CrossRef] [PubMed]
- Jaworski, P.; Yu, F.; Carter, R.M.; Knight, J.C.; Shephard, J.D.; Hand, D.P. High energy green nanosecond and picosecond pulse delivery through a negative curvature fiber for precision micro-machining. Opt. Express 2015, 23, 8498–8506. [Google Scholar] [CrossRef] [PubMed]
- Gérôme, F.; Cook, K.; George, A.K.; Wadsworth, W.J.; Knight, J.C. Delivery of sub-100fs pulses through 8 m of hollow-core fiber using soliton compression. Opt. Express 2007, 15, 7126–7131. [Google Scholar] [CrossRef] [PubMed]
- Poletti, F.; Wheeler, N.V.; Petrovich, M.N.; Baddela, N.; Fokoua, E.N.; Hayes, J.R.; Gray, D.R.; Li, Z.; Slavík, R.; Richardson, D.J. Towards high-capacity fibre-optic communications at the speed of light in vacuum. Nat. Photonics 2013, 7, 279–284. [Google Scholar] [CrossRef]
- Roberts, P.J.; Couny, F.; Sabert, H.; Mangan, B.J.; Williams, D.P.; Farr, L.; Mason, M.W.; Tomlinson, A.; Birks, T.A.; Knight, J.C.; et al. Ultimate low loss of hollow-core photonic crystal fibres. Opt. Express 2005, 13, 236–244. [Google Scholar] [CrossRef] [PubMed]
- Couny, F.; Benabid, F.; Roberts, P.J.; Light, P.S.; Raymer, M.G. Generation and photonic guidance of multi-octave opticalfrequency combs. Science 2007, 318, 1118–1121. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.F.; Wang, Y.Y.; Ding, W.; Jiang, D.L.; Gu, S.; Zhang, X.; Wang, P. Hollow-core conjoined-tube negative-curvature fibre with ultralow loss. Nat. Common. 2018, 9, 2828. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Yoo, S.; Yong, K. Function of second cladding layer in hollow core tube lattice fibers. Sci. Rep. 2017, 7, 1618. [Google Scholar] [CrossRef] [PubMed]
- Poletti, F. Nested anti-resonant nodeless hollow core fiber. Opt. Express 2014, 22, 23807–23828. [Google Scholar] [CrossRef] [PubMed]
- Yu, F.; Knight, J.C. Negative curvature hollow core optical fiber. IEEE J. Sel. Top. Quantum Electron. 2016, 22, 4400610. [Google Scholar] [CrossRef]
- Huang, X.; Qi, W.; Ho, D.; Yong, K.T.; Luan, F.; Yoo, S. Hollow core anti-resonant fiber with split cladding. Opt. Express 2016, 24, 7670–7678. [Google Scholar] [CrossRef] [PubMed]
- Belardi, W.; Knight, J.C. Effect of core boundary curvature on the confinement losses of hollow anti-resonant fibers. Opt. Express 2013, 21, 21912–21917. [Google Scholar] [CrossRef] [PubMed]
- Hayes, J.R.; Sandoghchi, S.R.; Bradley, T.D.; Liu, Z.; Slavík, R.; Gouveia, M.A.; Wheeler, N.V.; Jasion, G.; Chen, Y.; Fokoua, E.N.; et al. Antiresonant hollow core fiber with an octave spanning bandwidth for short haul data communications. J. Lightwave Technol. 2017, 35, 437–442. [Google Scholar] [CrossRef]
- Debord, B.; Amsanpally, A.; Chafer, M.; Baz, A.; Maurel, M.; Blondy, J.; Hugonnot, E.; Scol, F.; Vincetti, L.; Gérôme, F.; et al. Ultralow transmission loss in inhibited-coupling guiding hollow fibers. Optica 2017, 4, 209–217. [Google Scholar] [CrossRef]
- Belardi, W.; Knight, J.C. Hollow anti-resonant fibers with reduced attenuation. Opt. Lett. 2014, 39, 1853–1856. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.F.; Wang, Y.Y.; Ding, W.; Wang, P. Hollow-core negative-curvature fiber for UV guidance. Opt. Lett. 2018, 43, 1347–1350. [Google Scholar] [CrossRef] [PubMed]
- Yu, F.; Wadsworth, W.J.; Knight, J.C. Low loss silica hollow core fibers for 3–4 µm spectral region. Opt. Express 2012, 20, 11153–11158. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.L.; Ding, W.; Wang, Y.Y.; Gao, S.F.; Cao, L.; Feng, X.; Wang, P. Characterization of a liquid-filled nodeless anti-resonant fiber for biochemical sensing. Opt. Lett. 2012, 42, 863–866. [Google Scholar] [CrossRef] [PubMed]
- Williams, G.O.; Euser, T.G.; Arlt, J.; Russell, P.S.J.; Jones, A.C. Hollow anti-resonant fibers with reduced attenuation. ACS Photonics 2014, 1, 790–793. [Google Scholar] [CrossRef]
- Russell, P.S.J.; Hölzer, P.; Chang, W.; Abdolvand, A.; Travers, J.C. Hollow-core photonic crystal fibres for gas-based nonlinear optics. Nat. Photonics 2014, 8, 278–286. [Google Scholar] [CrossRef]
- Huang, X.; Ma, J.; Tang, D.; Yoo, S. Hollow-core air-gap anti-resonant fiber couplers. Opt. Express 2017, 25, 29296–29306. [Google Scholar] [CrossRef]
- Liu, X.; Fan, Z.; Shi, Z.; Ma, Y.; Yu, J.; Zhang, J. Dual-core anti-resonant hollow core fibers. Opt. Express 2016, 24, 17453–17458. [Google Scholar] [CrossRef] [PubMed]
- Argyros, A.; Leon-Saval, S.G.; van Eijkelenborg, M.A. Twin-hollow-core optical fibres. Opt. Commun. 2009, 282, 1785–1788. [Google Scholar] [CrossRef]
- Ouellette, F. All-fiber filter for efficient dispersion compensation. Opt. Lett. 1991, 16, 303–305. [Google Scholar] [CrossRef] [PubMed]
- Antonio-Lopez, J.E.; Castillo-Guzman, A.; May-Arrioja, D.A.; Selvas-Aguilar, R.; LiKamWa, P. Tunable multimode-interference bandpass fiber filter. Opt. Lett. 2010, 35, 324–326. [Google Scholar] [CrossRef] [PubMed]
- Pryamikov, A.D.; Biriukov, A.S.; Kosolapov, A.F.; Plotnichenko, V.G.; Semjonov, S.L.; Dianov, E.M. Demonstration of a waveguide regime for a silica hollow-core microstructured optical fiber with a negative curvature of the core boundary in the spectral region >3.5 µm. Opt. Express 2011, 19, 1441–1448. [Google Scholar] [CrossRef] [PubMed]
- Kolyadin, A.N.; Kosolapov, A.F.; Pryamikov, A.D.; Biriukov, A.S.; Plotnichenko, V.G.; Dianov, E.M. Light transmission in negative curvature hollow core fiber in extremely high material loss region. Opt. Express 2013, 21, 9514–9519. [Google Scholar] [CrossRef] [PubMed]
- KolBrilland, L.; Smektala, F.; Renversez, G.; Chartier, T.; Troles, J.; Nguyen, T.N.; Traynor, N.; Monteville, A. Fabrication of complex structures of Holey Fibers in Chalcogenide glass. Opt. Express 2006, 14, 1280–1285. [Google Scholar] [CrossRef]
- Litchinitser, N.M.; Dunn, S.C.; Usner, B.; Eggleton, B.J.; White, T.P.; McPhedran, R.C.; de Sterke, C.M. Resonances in microstructured optical waveguides. Opt. Express 2003, 11, 1243–1251. [Google Scholar] [CrossRef] [PubMed]
- Issa, N.A.; Poladian, L. Vector wave expansion method for leaky modes of microstructured optical fibers. J. Lightwave Technol. 2003, 21, 1005–1012. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Yong, K.-T.; Yoo, S. A Method to Process Hollow-Core Anti-Resonant Fibers into Fiber Filters. Fibers 2018, 6, 89. https://doi.org/10.3390/fib6040089
Huang X, Yong K-T, Yoo S. A Method to Process Hollow-Core Anti-Resonant Fibers into Fiber Filters. Fibers. 2018; 6(4):89. https://doi.org/10.3390/fib6040089
Chicago/Turabian StyleHuang, Xiaosheng, Ken-Tye Yong, and Seongwoo Yoo. 2018. "A Method to Process Hollow-Core Anti-Resonant Fibers into Fiber Filters" Fibers 6, no. 4: 89. https://doi.org/10.3390/fib6040089
APA StyleHuang, X., Yong, K.-T., & Yoo, S. (2018). A Method to Process Hollow-Core Anti-Resonant Fibers into Fiber Filters. Fibers, 6(4), 89. https://doi.org/10.3390/fib6040089



