Self-Folding Textiles through Manipulation of Knit Stitch Architecture

Abstract

This research presents a preliminary study on finding predictable methods of controlling the self-folding behaviors of weft knit textiles for use in the development of smart textiles and garment devices, such as those with shape memory, auxetic behavior or transformation abilities. In this work, Shima Seiki SDS-One Apex computer-aided knitting technology, Shima Seiki industrial knitting machines, and the study of paper origami tessellation patterns were used as tools to understand and predict the self-folding abilities of weft knit textiles. A wide range of self-folding weft knit structures was produced, and relationships between the angles and ratios of the knit and purl stitch types were determined. Mechanical testing was used as a means to characterize differences produced by stitch patterns, and to further understand the relationships between angles and folding abilities. By defining a formulaic method for predicting the nature of the folds that occur due to stitch architecture patterns, we can better design self-folding fabrics for smart textile applications.

1. Introduction

Knitting is the interlacing of yarns into loops resulting in fabrics that have inherent self-folding abilities. A greater understanding of these knit structures could facilitate the design of technical textiles for engineering applications and smart garments requiring compression and expansion properties. Study of origami paper folding techniques has gained popularity over the last decade as a means of designing these transformable structures in many types materials for a wide variety of applications. The unique characteristics of tessellated structures, which allow them to expand, compress and transform, have been used to develop nanoscale to macro scale products [1] from medical stents [2] to origami robots [3,4,5] and tunable antennas [6]. Recent interest in the use of self-folding–inspired structures for extraterrestrial applications has also grown, including research conducted through the National Aeronautics and Space Administration on folded solar arrays [7], where benefits lie in the ability of the structures to remain small while in transit, and then grow exponentially for use in outer space.

Origami structures have been explored in a variety of materials including paper, cardboard, plastic and metal sheeting, and textiles. Structures have also been created through the use of three-dimensional (3D) printing technology, where engineered mechanical instabilities produce folding behaviors as the object is compressed [8]. Using origami-like patterns and the self-folding behavior of knits, textiles exhibiting auxetic behavior have been developed [9,10,11,12,13]. However, this area of research would benefit from a deeper understanding of how and why the self-folding mechanisms are created. Discovering methods of controlling and understanding the self-folding mechanisms that occur with knit fabric relaxation would help expand the field of smart textiles, and benefit designs such as drug release [14] or compression bandages by affording smart textiles the ability to transform shape [9,15,16]. Additionally, creating these structures in fabric could capitalize on preexisting production methods with computer-programmed knitting machines that have successfully been used in the garment industry for decades [17].

The first step for successfully converting these paper-folding techniques into fabric form is to understand the mechanism through which folds in fabrics may be formed. While the paper-style folds may be mimicked through the use of processing techniques such as steaming, ironing and chemical processing (such as permanent press), utilization of the self-folding abilities of knit textile structures would allow for economical and repeatable production of a material without the need for additional manipulation [17]. Our research began through the study of knit stitch geometry arrangements, and the observation of paper-folding mechanisms in origami tessellation patterns. These remained an integral part of the pattern development throughout, as research was conducted to find a recognizable relationship to convert from one medium to another and to understand the effect of specific stitch architecture on folding behavior.

2. Materials and Methods

2.1. Materials

Yarns used in this study included Supra-merino (7500 ypp, Silk City Fibers, Paterson, NJ, USA) Jaguar (85% Modal/15% Nylon, 8750 ypp, Silk City Fibers, Paterson, NJ, USA), high bulk polyester (150 denier) and spandex (0.12 mm diameter). Mechanical testing was carried out on samples made from the high bulk polyester yarn.

2.2. Computer-Aided Knitting

Industrial knitting technology is an important tool for the development of smart textiles and garment devices [17]. It provides advantages over other textile productions methods such as weaving by facilitating rapid prototyping without the need for large quantities of a material. Using industrial knitting machines, a wide variety of shapes and textures can be developed from various stitches, such as knit, purl, miss and tuck, as well as shaping through widening and narrowing of the fabric. All textiles produced in this body of work utilize only knit and purl stitches. While it should be noted that the purl stitch is actually the technical back of the knit stitch, here we designate each stitch as it is seen from one side of the fabric, the designated technical front. Knit stitches are those seen as small “V” shapes, and purl stitches are those appearing as small loops (Figure 1). All knit samples were produced on Shima Seiki Industrial knitting machinery, including the Shima Seiki SWG041N and the Shima Seiki SV122SG. Before prototypes of each textile were created, the Shima Seiki SDS-Apex Design System was used to program each textile, and examine computer-simulated images of the knit architecture.

Figure 1. Self-folding in knits: (A) knit and purl stitches; (B) transition line; (C) textile sample of rib structure; (D) stitch diagram of rib structure with directions of folding forces.

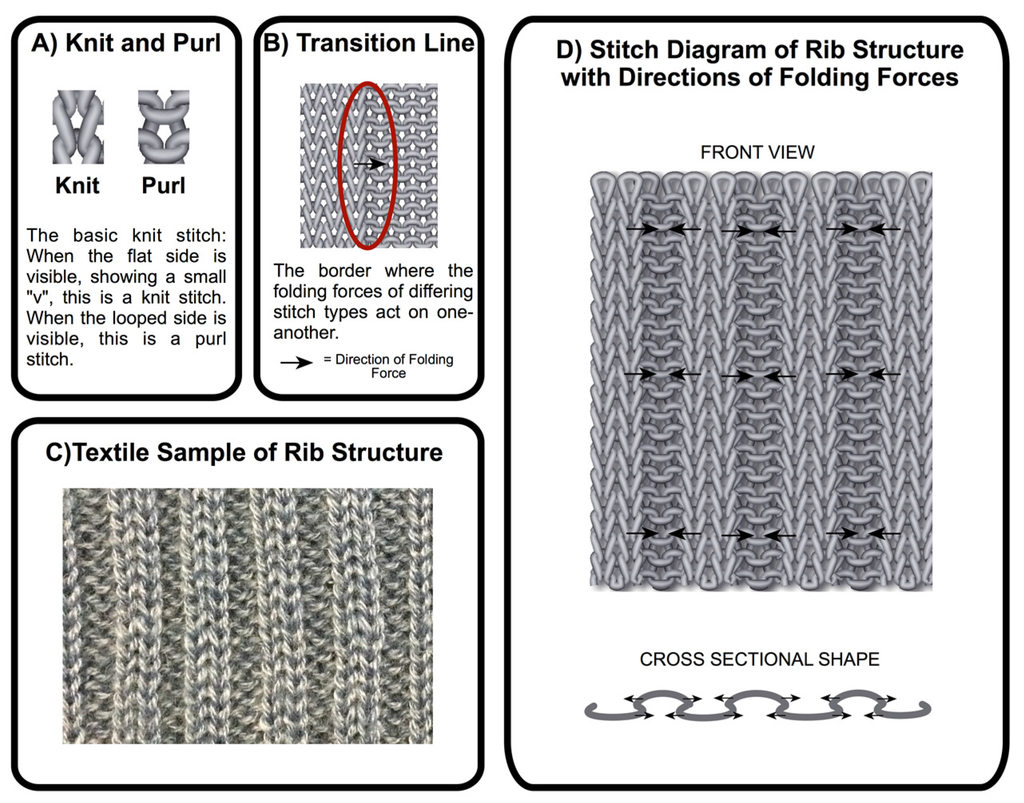
Figure 1. Self-folding in knits: (A) knit and purl stitches; (B) transition line; (C) textile sample of rib structure; (D) stitch diagram of rib structure with directions of folding forces.

While the computer simulations provided by this software accurately show a detailed image of the stitch architecture, they do nothing to predict the physical outcome of the textile that may be influenced by a number of factors such as yarn material, stretch and fabric relaxation [18]. Therefore, it is important to develop a better understanding of the movements and folds created by specific stitch arrangements in order to develop a predicative model for the design of self-folding textiles.

From traditional knit structures such as the 2 × 2 rib knit, we know that changes in the stitch pattern can produce self-folding in knitted textiles. In Figure 1A we see the basic two components of the knit textiles, the knit and purl stitch. When placed side by side, forming vertical stripes, this produces a knit structure commonly referred to as ribbing. Between each section there is a transition line (Figure 1B) where the folding forces of the two different stitches act upon each other, forcing one section of the fabric up while the other is pushed down. Figure 1C depicts a sample of an actual fabric that is created due to the directional folding forces (Figure 1D) of the rib structure. If these forces are unbalanced either in number or strength it can cause the fabric to fold on itself vertically. From this understanding, we predicted that we could manipulate these folding forces to create folds at predetermined angles and locations by changing the geometry of the stitch pattern.

2.3. Study of Origami Tessellation

Study of the folding mechanisms in knitted textiles began by recreating several distorting knit patterns described in the thesis work The Design of 3D Shape Knitted Preforms by Jennifer Underwood [19] in order to better understand and validate the folding and stretching movements afforded by their knit structures. Though this provided insight to the range of structures that could be created, the examples in the thesis did not explain the mechanics of the folding behavior. Further research led us to the work of Liu et al. [12] and Hu et al. [13], who developed weft-knitted negative Poisson’s ratio fabrics. Upon observing these textiles in physical form, it was noted that they shared a number of similarities with origami tessellation patterns [20] (Figure 2). Tessellations are repeated geometric tiling patterns. Using these geometrical patterns, traditional paper folding techniques may be used to create paper structures with auxetic characteristics due to the folding mechanisms of these repeated patterns. Applied forces cause the folded structures to tessellate outwards, creating multidirectional expansion. Therefore, origami tessellations were studied as a means of understanding how to create self-folding structures through geometric principles, and to discover a relationship between paper folds, and self-folding fabrics.

Using this repeated zig-zag pattern, a fabric structure may be engineered that is similar to a common origami structure, featuring repeated zig-zag valleys and peaks [12]. What is different between these two mediums, however, is how and where these features are created. In the paper model, folds occur along the boundary lines of the geometric shapes. In a textile model, we see that strong points in the shape of the geometry, indicated by the grey circles in the diagram in Figure 2, cause the fabric to buckle. This creates a linear fold, running through the geometrical shapes instead of along the perimeters. Though the fold lines in the knit structure are shifted when compared to the paper folds, the resulting structures are similar.

Figure 2. (A) Diagram of paper folding lines, represented by dotted lines; (B) paper sample; (C) diagram of textile folding lines, represented by dotted lines; (D) merino wool textile sample.

Figure 2. (A) Diagram of paper folding lines, represented by dotted lines; (B) paper sample; (C) diagram of textile folding lines, represented by dotted lines; (D) merino wool textile sample.

2.4. Mapping of Folding Patterns

After designing and knitting a wide variety of prototypes based on many different origami tessellation patterns, computer-simulated images were used to map the locations of folds on the physical models. Since the software is unable to show the folds that are present in the textiles, lines were drawn to map the self-folding actions occurring in each sample, and to indicate directionality of the fold. For each stitch architecture design, two knit samples were produced. The first sample was knit in a high bulk polyester yarn, while the second sample was knit with a combination of high bulk polyester and spandex (Figure 3). In some samples, folding mechanisms occurred along lines of stitch change. In others, it was an entire geometric segment of the sample that folded up or down.

Figure 3. Mapping of folding patterns. (A) Computer simulation of original pattern; (B) original pattern knit with polyester yarn; (C) original pattern knit with polyester and spandex yarns; (D) computer simulation of readjusted pattern; (E) readjusted pattern knit with polyester and spandex yarns produces the same self-folding structure as the original sample. Shima Seiki SDS-One Apex Software.

Figure 3. Mapping of folding patterns. (A) Computer simulation of original pattern; (B) original pattern knit with polyester yarn; (C) original pattern knit with polyester and spandex yarns; (D) computer simulation of readjusted pattern; (E) readjusted pattern knit with polyester and spandex yarns produces the same self-folding structure as the original sample. Shima Seiki SDS-One Apex Software.

2.5. Ratios in Knit Patterns

The design used in Figure 3 shows a key example of the importance of ratios in controlling self-folding behavior. This pattern was instrumental in determining methods of correcting and re-adjusting ratios in order to recreate effects using different materials. Figure 3A shows a simulation of the pattern, and Figure 3B shows the sample knit in a high bulk yarn. Strong self-folding abilities are clearly seen. The photograph in Figure 3C shows the first attempt at recreating this same pattern, with the addition of a fine spandex yarn. As seen, there is a clear discrepancy between the two fabrics. With the addition of spandex, the magnitude of the folding forces changed. Folding occurred normally between the squares of the checkerboard pattern (at the line along which the knit and purl stitch forces meet); however, the strong linear folds running down the length of the whole fabric became far less dominant. By calculating the ratio of shrinkage that occurred in the first spandex attempt, the pattern was scaled up proportionally to produce a fabric with the same size patterning dimensions as the original sample. This was achieved by measuring the dimensions of the two samples knit using the original computer program (Figure 3B,C). These dimensions were then used to calculate the proportional change necessary to produce the new program. It is important to note that due to yarn relaxation, stitch size change occurs differently in the horizontal and vertical directions, and must be accounted for separately. Therefore, proportional changes in the height and width must be accounted for separately.

The two computer simulations in Figure 3 are to scale, and show the difference between the size of the original pattern (Figure 3A) and the readjusted pattern (Figure 3D). While the computer program for the spandex sample is considerably larger, the fabric produced is to the same scale as the plain polyester version. While denser than the original, the fabric produced replicated the same folding effects as the plain polyester sample (Figure 3E).

2.6. Horizontal vs. Vertical Stitch Arrangements

In order to determine a formulaic method of designing self-folding textiles, it was important to observe and understand the effect of stitch arrangements. On the simplest level, we may note the difference between horizontal and vertical arrangements of knit and purl stitches. As explained earlier, when knit and purl stitches are arranged in a repeating pattern of vertical columns, a self-folding effect is exhibited where the knit stitches naturally overtake the purl and rise to the surface of the fabric. When knit and purl stitches are arranged in a repeating pattern of horizontal rows, an opposite effect is achieved and the purl stitches become dominant.

From the understanding of the behaviors of both vertical and horizontal rib knits and the effects of stitch height/width ratios, it was determined that a critical angle should exist that marks the change between a knit-dominant fold, and a purl-dominant fold. A study was conducted observing the effect of changing the angle of transition between the knit and purl fields of a textile. Knit swatches were created by dividing a square between knit and purl, with the line of transition placed at varying angles between 0 and 90 degrees, three of which are depicted in Figure 4. It is important to note that the angle range of 57–59 degrees is used, rather than one single angle. This is due to the nature of the grid-based programming. Only a limited number of angles are available that consist of a regular repeating pattern of stitches. While at 45 degrees our slope steps up one stitch at a time, and at 75 degrees our slope steps up four stitches and over one, the pattern repeats of angles in between become increasingly more complex. Since the pattern repeat around 58 degrees is quite long (occurring over a width of 21 stitches) depending on the size of the sample, different amounts of partial repeats may occur. This can change the degree of the angle slightly, but still produces a flat fabric.

Additionally, it should be noted that while each stitch is represented as a perfect square in the program, this is not the case in the actual fabric, and these dimensions will change depending on the material used as well as other parameters such as tension and takedown. Regardless of these changes, similar folding behavior is observed when knitting the same knit programs in a variety of materials, as well as on different types of knitting machines.

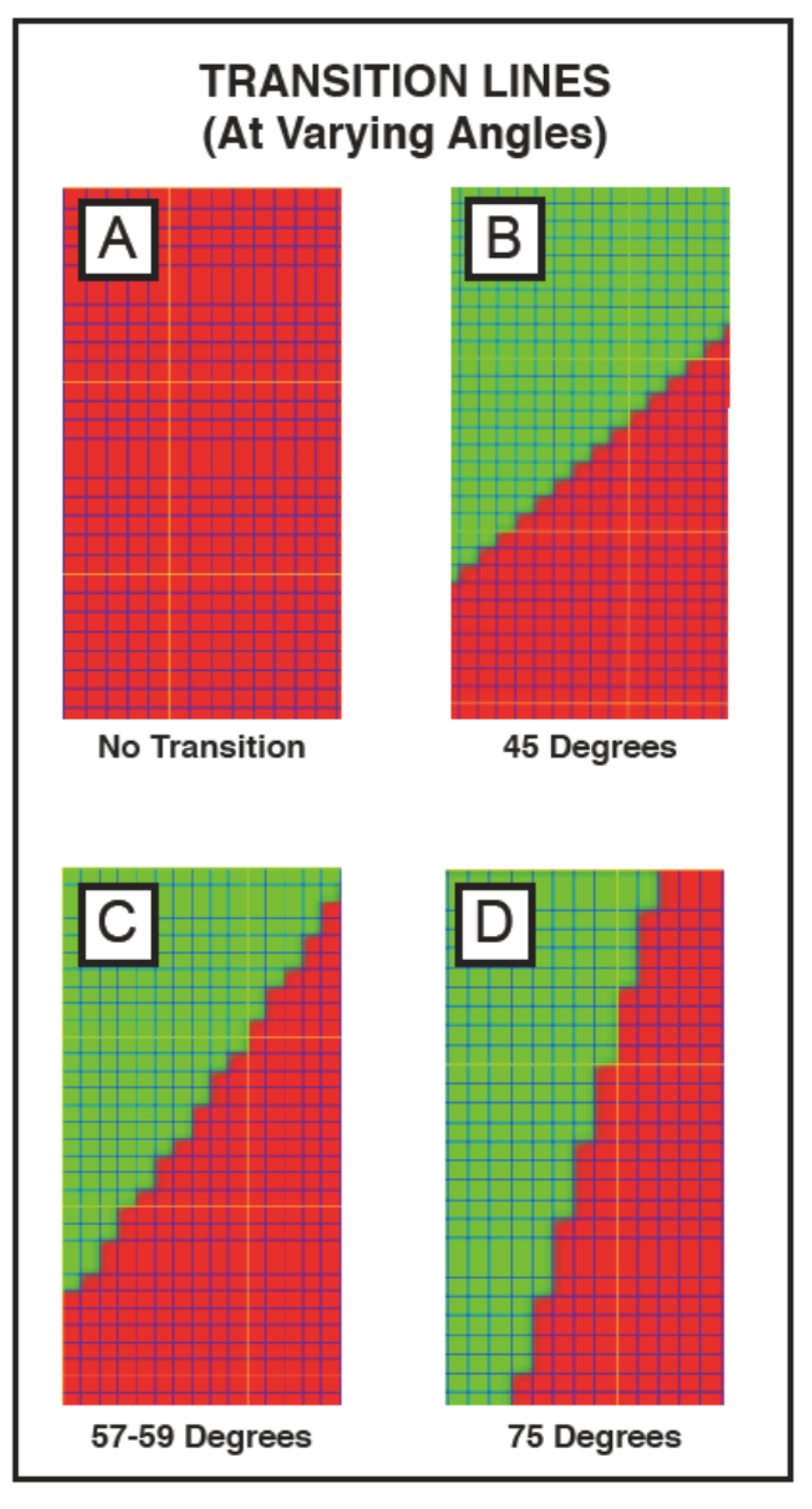
Figure 4. Transition line angles of knit samples: (A) No transition; (B) 45 degrees; (C) 57–59 degrees; (D) 75 degrees. Shima Seiki SDS-One Apex Software.

Figure 4. Transition line angles of knit samples: (A) No transition; (B) 45 degrees; (C) 57–59 degrees; (D) 75 degrees. Shima Seiki SDS-One Apex Software.

2.7. Sample Preparation and Mechanical Testing

Samples sets (N = 3) were knit on the Shima Seiki SWG041N industrial knitting machine for all possible transition angles between 0 and 90 degrees. While the angle of transition varied between sample sets, all other variables including stitch length, yarn tension and knitting speed remained constant.

Mechanical testing of sample segments was carried out on the two angles that we observed to have the strongest folding behavior, as well as the angle at which a flat fabric was produced. This was used to observe the effect of changes in the transition angle on the mechanical properties of the textile [21,22,23]. Each sample tested was 20 stitches in the course direction and 44 stitches in the wale direction. Each was secured on a sample card to facilitate improved grip into a Bose Electro Force 3200 Series III Axial Configuration tensile testing machine (Figure 5). After placement, the side of the sample card was cut before testing began.

Figure 5. Sample placed in grips of the Bose Electro Force 3200 Series Axial Configuration tensile tester.

Figure 5. Sample placed in grips of the Bose Electro Force 3200 Series Axial Configuration tensile tester.

During testing, the temperature of the room was 22.9 °C, with a 21% humidity level. Once tightened between two clamps, a load was applied and samples were extended to a maximum displacement of 6.5 centimeters. Data for time, displacement and loading were recorded. Using MATLAB and Excel software, graphs were created showing stress vs. strain curves (Figure 6) and Young’s modulus comparisons (Figure 7) for the range of samples. Samples are designated first by the angle of the transition line, and then by the percentage of purl stitches in the sample, which dictates the length of the transition line (45p23 indicates a 45 degree angle transition, in a sample that consists of 23% purl stitches and 77% knit stitches).

Figure 6. Stress vs. strain graph of samples with a 75-degree transition line, MATLAB.

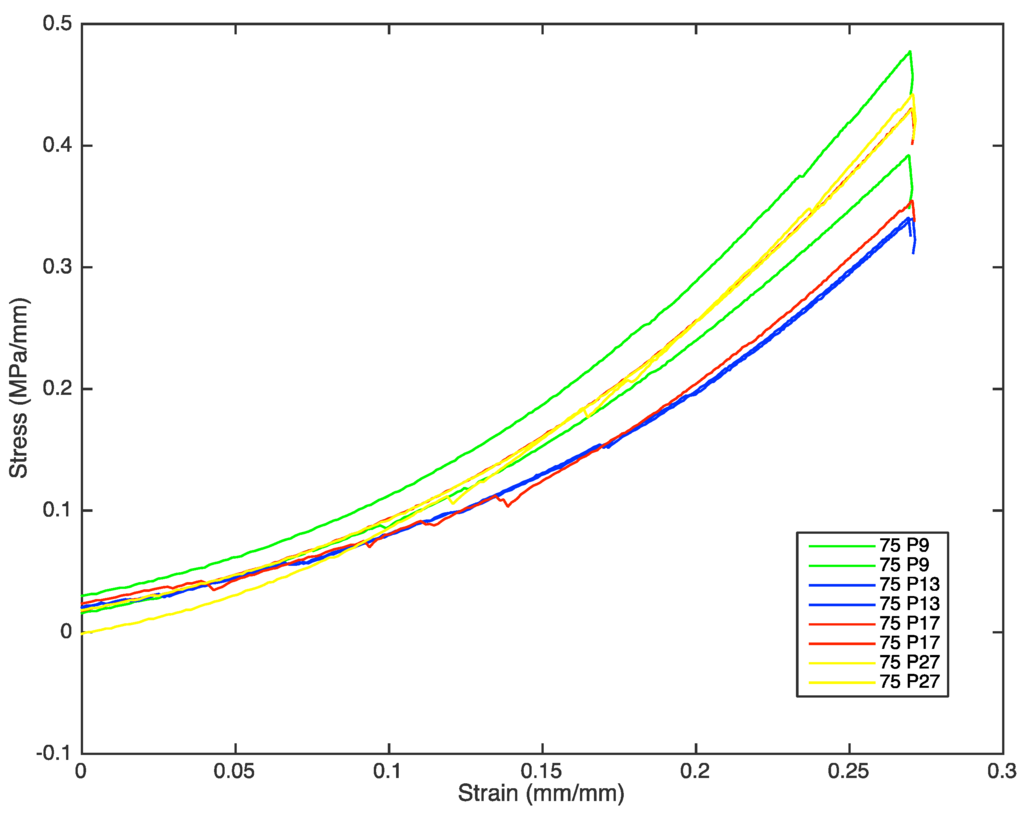
Figure 6. Stress vs. strain graph of samples with a 75-degree transition line, MATLAB.

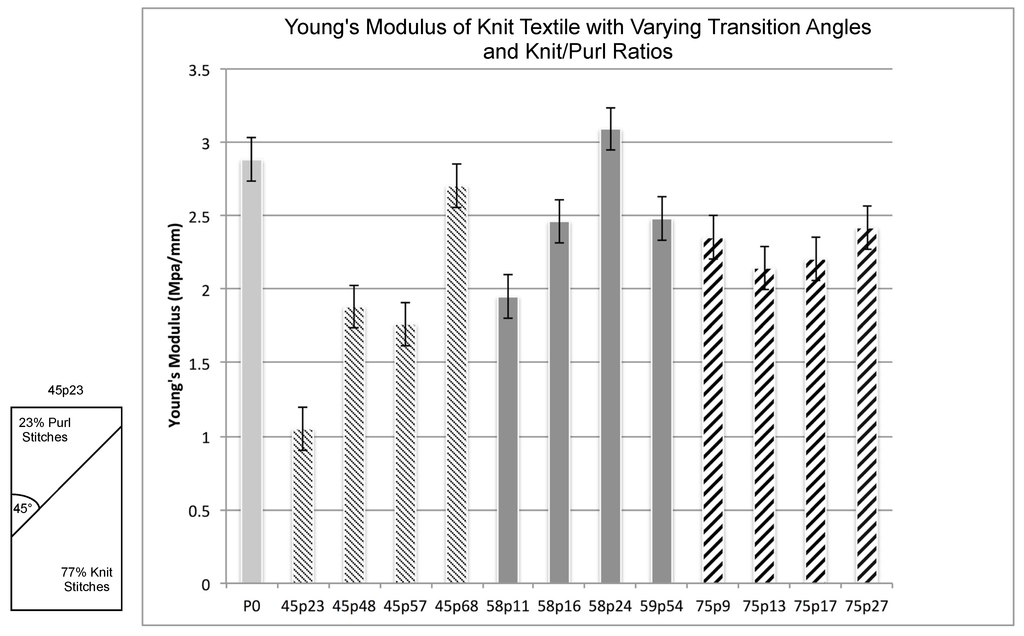
Figure 7. Young’s modulus comparisons between transition angles and lengths, Excel.

Figure 7. Young’s modulus comparisons between transition angles and lengths, Excel.

3. Results

3.1. Self-Folding Angle Behaviors

From these knit samples, it was observed that that:

• With transition lines between 0 and 45 degrees, purl stitches are dominant; the self-folding mechanisms create a strong fold that pushes the knit stitches down below.
• With transition lines between 75 and 90 degrees, knit stitches are dominant; the self-folding mechanisms create a strong fold that pushes the purl stitches down below.
• With transition lines at angles greater than 45 but less than 57 degrees, the strength of the purl-dominant folds diminishes as the angle approaches 57 degrees.
• With transition lines at angles less than 75 but greater than 59 degrees, the strength of the knit-dominant fold diminishes as the angle approaches 59 degrees.
• With transition lines at the angle of 57–59 degrees, neither the knit nor the purl stitches are dominant: the self-folding mechanisms are in equilibrium and a flat fabric is produced.

3.2. Mechanical Testing Data

By looking at the results of the tensile test, we can see several trends. At transition angles of 45 and 58 degrees, we can see a possible positive correlation between the Young’s modulus and an increase in the length of the transition line (which occurs with an increase in the percentage of purl stitches) however, this will require further validation through statistical analysis. For transition angles of 75 degrees, however, we see less change in the Young’s modulus occurring with an increase in the length of the transition line.

This result of the tensile tests helps to support the hypothesis that the demonstrated self-folding angle effects are a result of the folding forces along the line of transition, which will vary with an increase or decrease in the length of the line. By the time the knit-dominant force in the folding line is strong enough to overtake the purl (at angles greater than 75 degrees), the ratio of purl stitches is so low that the horizontal folding forces are finally overcome, allowing a more vertical folding action to occur (Figure 4). Once the horizontal effect of the purl stitches is this low, there is no longer an observable trend in the effect on the Young’s modulus of the fabric.

4. Discussion

Through understanding the self-folding mechanisms created by knit and purl stitches, and the angles at which these are most effective, it was observed that the angle of stitch geometries may be used to consistently control the self-folding behavior of knit textiles. Though material characteristics of the yarn may result in variance of properties in the fabricated textiles, mechanical properties demonstrate consistent effects created by these angles. Ideally, using this formula, a wide range of textiles may be designed for smart textile applications, including those with auxetic characteristics, buckling mechanisms, cell-like structuring, high levels of articulation, and transforming mechanisms. Future designs will be explored in terms of scalability and performance under stress and continued fatigue. Using the defined parameters for angular folds, we may use the results of this study to develop stitch architecture designs that will give auxetic characteristics to smart textile garments and devices.

5. Future Work

While a polyester yarn was primarily used in this research, we found that similar structures could be produced using the same structure patterns paired with a variety of yarn materials. Moving forward we will work on developing a statistical model that can be used to validate our observations and help us further predict folding behavior, as well as characterize the specific effects of yarn type on the self-folding behavior and on the material and mechanical properties of the textile.