Abstract
In current compression practice for the treatment of chronic venous disorders, there has always been a challenge of controlled compression by a bandage to achieve a particular pressure range in the affected region of the limb. The challenges in compression in the products could be solved if there were the possibility of stress control in fabric. Herein, we are exploiting the newly discovered phenomena, i.e., stress memory, in a memory polymer (MP) for the design and investigation of a smart bandage for functional compression benefits. A memory bandage is developed using a blend yarn consisting of MP filaments (segmented polyurethane) and nylon filaments. Results showed the possibility to control or manage the internal stress developed in the bandage in wrapped position by simple heating, and thus allowing pressure readjustment externally. Extra pressure generated by the bandage increases with increasing the level of temperature and strain (p < 0.05). The pressure variations also depend on the number of layers and limb circumference (p < 0.05). The memory bandage could have a great potential over existing conventional compression products, as they could give more freedom to govern pressure level whenever needed during the course of compression therapy as a novel wound care management system.
1. Introduction
Compression therapy provides a means to treat venous leg ulceration, edema, venous hypertension, and other chronic venous disorders [1]. The objectives of compression therapy are to reduce the venous hypertension in the affected area, reduce the swollen limb to minimize the size and maintain a uniform pressure gradient in the leg from toe to knee to improve the venous return to the heart [2]. External compression is given to the affected leg portion during compression therapy using compression materials like bandage, stockings, pressure garments, etc. [3]. The pressure is generated in the interface between bandage and skin because of compression by the bandage during its application over the limb by the application of external force. This pressure is called interface pressure [4,5]. The success of this treatment depends to a great degree on the level of pressure applied by the bandage at the affected portion on the limb, and sustenance of this pressure during the course of the treatment. This interface pressure has to be quite accurate within certain limits and should not be below or above the prescribed level, otherwise it can lead to certain complications during treatment.
Several researchers have used Laplace's law to find the relationship among several factors affecting the interface pressure [6]. In the context of compression therapy by a bandage, the relevant equation derived from the above law is expressed as:
where P is the pressure, F is fabric tension per unit width, N is number of bandage layers and C is the limb circumference. The interface pressure produced by a bandage depends on the complex interaction of many factors—the tension in the fabric, the physical structure and elastomeric properties of the fibers from which it is manufactured, the size and shape of the limb to which it is applied, the application technique (number of layers wrapped) and the nature of any physical activity undertaken by the patient [7]. Achieving desired compression range is difficult as the pressure applied by the bandage is governed by leg attributes (shape or size) and the elasticity or stiffness of the fabric [8]. Moreover, pressure drop over time is a cause of concern. Experimental studies showed that the pressure decreases over time due to reduction in swelling of leg, and also decrease in the internal stress in the fibrous structure of the bandage [9,10]. Replacement of the bandage is needed once the pressure fall below a target level. Clearly, pressure management and its sustenance is a huge challenge to provide effective treatment.
Currently, no external means exists to govern pressure exerted by the bandage at wrapped position on the leg. Controlling or readjusting pressure on the leg would provide many advantages to health practitioners, and would make treatment more effective. The challenges in compression products could be solved if there were the possibility of stress control in fabric materials. In this regard, smart polymer fibers could offer choices with internal stress responsive to an external stimulus. Among stimulus-responsive polymers, shape memory polymers (SMPs) have high relevance to the present needs and have been solving many real life problems in the areas of aerospace, biomedicine, transport, construction, electronic, textile and consumer products [11,12]. SMPs can sense the environment and/or their own state, make a judgment and then change their functions according to predetermined purpose. They can memorize the original shape and allow the materials to recover the original shape from a temporarily deformed shape under appropriate stimuli, such as heat, light, magnetic field, water, etc. The shape memory effect (SME) of a SMP involves two aspects: fixability and recoverability. Fixability refers to the capability of the SMP to change from the original un-deformed shape to a temporary deformed shape through a suitable programming process, i.e., shape fixing, while the recoverability indicates its ability to recover the original shape. In the programming process, SMPs are mechanically deformed above a particular temperature (also known as transition temperature, Tg) and the deformed shape is temporarily fixed by cooling the SMP below Tg. The most important characteristic of SME is the stability of this temporarily deformed shape in which the internal stress is frozen and does not change in the absence of suitable stimuli. The deformed shape is actively triggered to recover the original permanent shape by exposure to an appropriate stimulus. Owing to this unique property, SMPs have found increasing applications in engineering and medical fields where the potential of shape fixity or recovery is primarily exploited for desired functions [13,14,15,16]. Recently, however, several other memory behaviors, including stress memory [17], temperature memory [18], chrome memory [19] and electric memory [20], have also been reported in such polymers, and it seems more appropriate therefore to call them memory polymers (MPs) in general.
Similar to shape memory, a new phenomenon, i.e. stress memory, has been discovered recently in MPs [17]. In stress memory, the stress in a polymer can be programmed, stored and retrieved reversibly with an external stimulus (e.g., heat), similar to the shape memory effect. Herein, the stress is stored upon inducing certain strain level beyond the Tg and cooling below this point. The stress is further released under constraint upon triggering by an external stimulus such as heat. This stress memory might be mistaken as recovery stress, which has been studied quite extensively [21], but investigation has confirmed that they are quite different phenomena. Although stress freezing can be obtained via a normal shape fixing process of the MP, where the internal stress is also frozen or stored at lower temperature (<Tg) in a deformed MP, but upon triggering the MP under constraint, the recovered stress does not remain stable but decreases over time. This is primarily because of the viscous stress that causes stress relaxation. This adds limitations to the use MP for some applications where the stress level has to be maintained, or a stable cyclic stress variation is required, such as pressure bandage, massage devices, etc. It has been confirmed that the recovery stress contains multi-components including elastic, thermal and viscoelastic forces in addition to possible memory stress [17,22]. In order to obtain stress memory phenomenon, the recovery stress should be pure so that it can be repeated, analyzed, and a meaningful signal for different applications. If only the memory stress is properly identified and exploited in a MP using suitable programming methods, then this could serve the special functions in stress control [17]. This opens several new research domains for MPs where stimuli-responsive forces are required/involved, including in sensors, sportswear, compression garments, massage devices, nerve conduits, bone tissue engineering, artificial muscles and dynamic mattress. Herein, this novel stress memory phenomenon has been used for smart and functional compression benefits by a memory bandage fabric.
2. Experimental Section
2.1. Preparation of SMP filaments
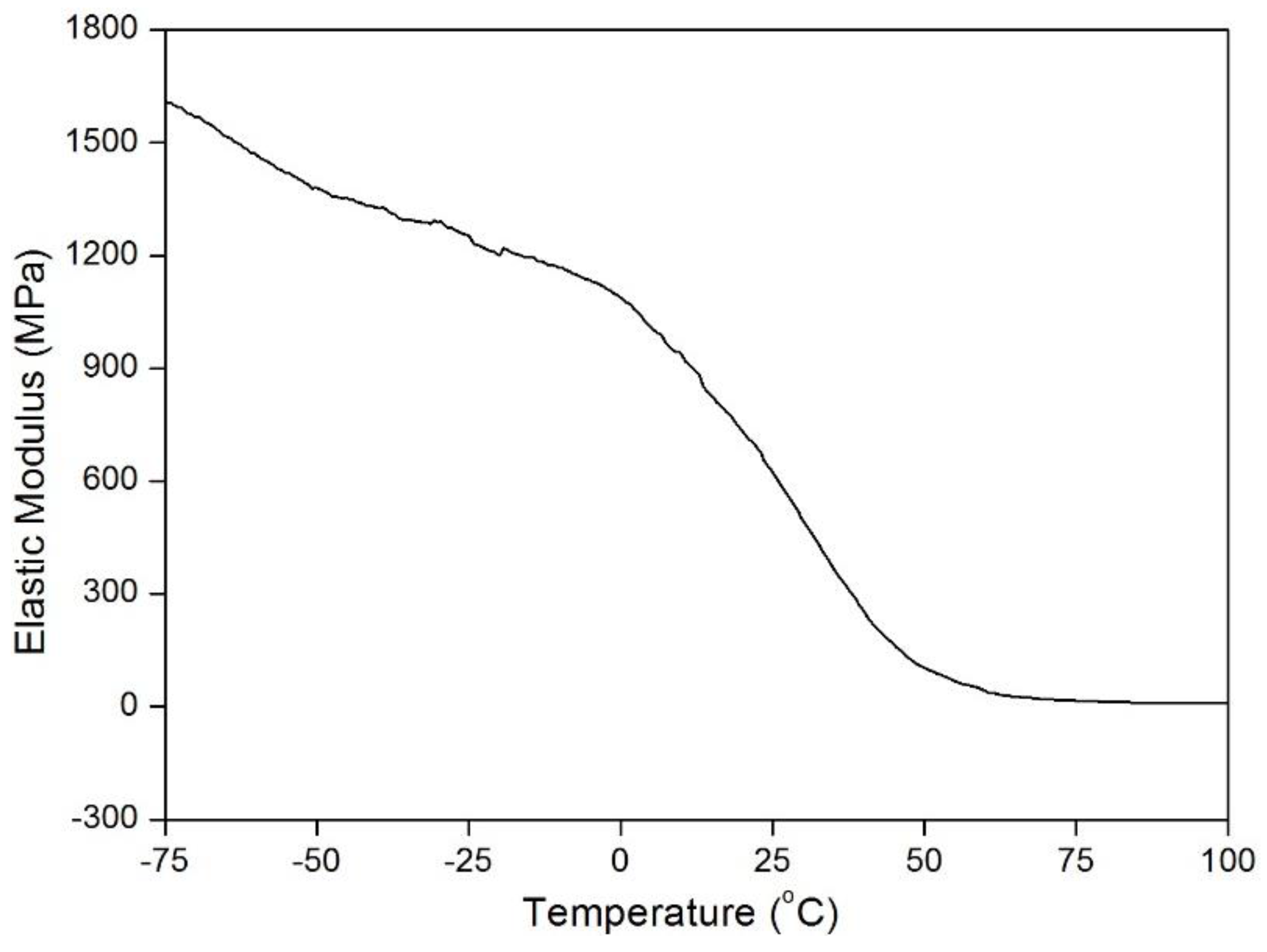
The MP filament was prepared using segmented polyurethane (PU) via melt spinning process. For filament spinning, the MP polymer chips were initially prepared using bulk polymerization method. The MP was synthesized using polytetramethylene ether glycol (PTMEG; Aldrich Chemical Company, Atlanta, GA, USA; Mn = 650) as soft segment, and 4,4′-methylene diphenyl diisocyanate (MDI; Aldrich Chemical Company, Atlanta, GA, USA) and 1,4-butanediol (BDO; Acros Organics, Geel, Belgium) as hard segment. First, the PTMEG and MDI was mixed and stirred for 2 h to form a pre-polymer at 80 °C. Thereafter, the BDO was added for cross-linking to complete the reaction. The ratio (weight) of hard to soft segments was 13:12. The MP chips was obtained after curing the mixture for 24 h at 100 °C. These chips were used for melt spinning to spin the filaments. The filaments were spun in pure nitrogen environment using single screw extruder with a temperature range from 175 to 202 °C [23]. The winding speed was set at 500 m/min, and the obtained linear density of the filaments was 18.6 tex. The glass transition temperature of the MP filaments chosen in the study was around 30 °C, as can be observed in Figure 1. The shape fixity and shape recovery of the filaments were 23.7% and 95%, respectively. More information on thermo-mechanical characterization of the MP can be found in the [23].
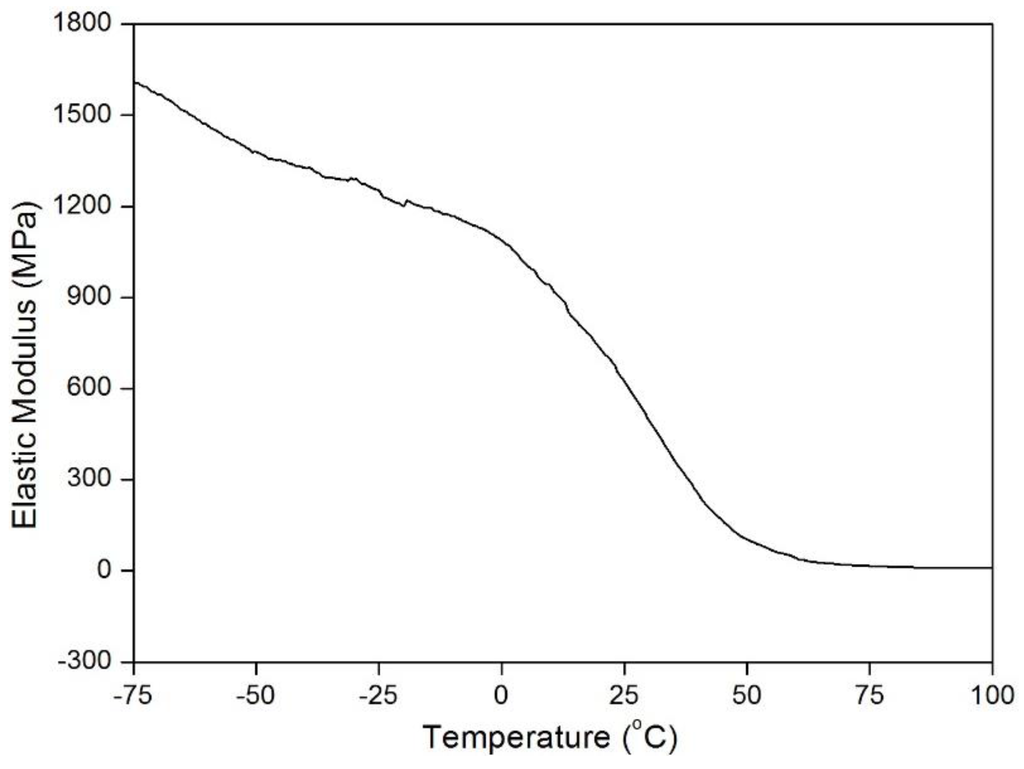
Figure 1.
Variation of elastic modulus vs. temperature of the MP using DMA.
2.2. Development of Memory Bandage
The memory bandage was prepared from a yarn blend consisting of the MP and Nylon filaments using V-bed double jersey flat weft knitting machine. The fabric characteristics are given in Table 1. As an example to demonstrate the pressure control using memory bandage, the measurement was conducted using a Kikuhime™ pressure sensor (Figure 2). After the application of the bandage on the cylindrical tube, the entire set-up was placed in a heated chamber for the MP activation, and the variation in the interface pressure was obtained. Different cylindrical tubes were used to stimulate different circumferences of a human leg. Extra pressure generated by the bandage was obtained at different levels each for the factors—temperature (T), number of layers (N), cylinder circumference (C) and applied strain (ε).

Table 1.
Characteristics of the memory bandage.

Figure 2.
Set-up for interface pressure measurement.
3. Results and Discussion
As the recovery in a MP is largely governed by entropy elasticity, the change in material stress σ could be expressed by temperature T as [24,25]:
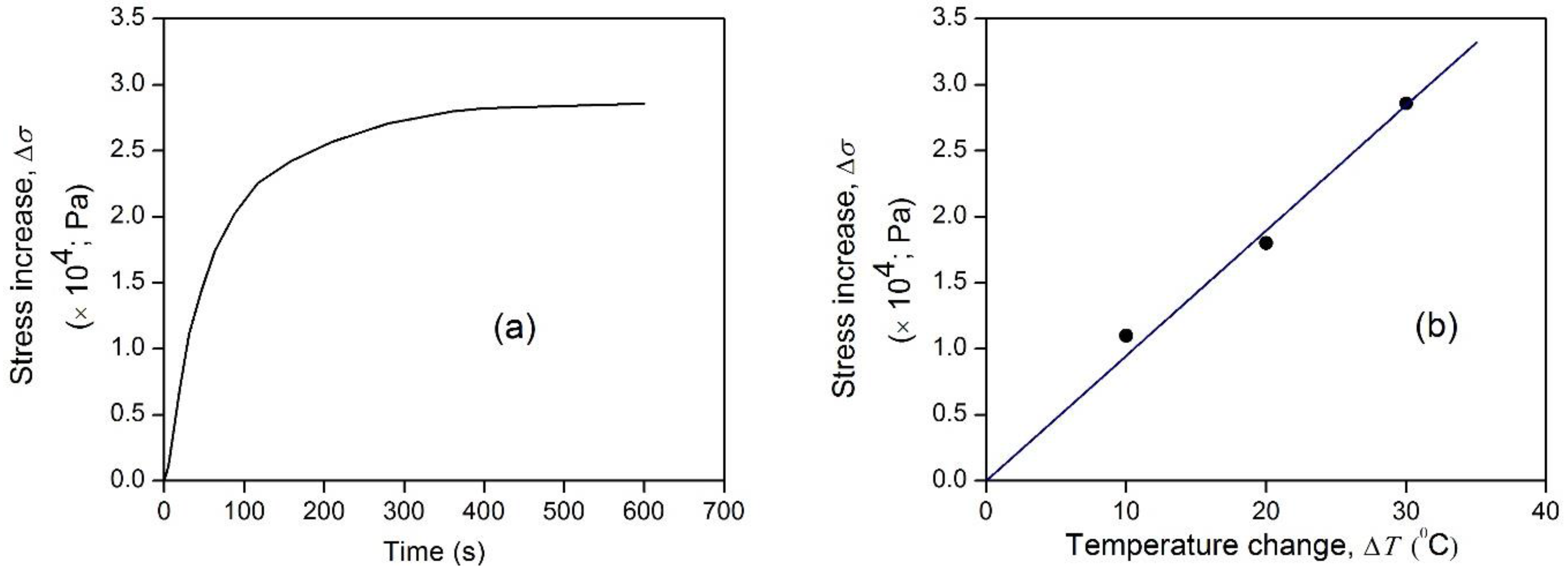
where the sample length l and volume V are kept constant. The equation indicates the possibility of controlling the stress in the MP by external temperature control. The stress in the bandage fabric could be changed if MP filaments in its structure exist. To confirm this, thermo-mechanical tensile testing was employed to examine the stress variation in a deformed memory bandage specimen upon activating under constraint. The measurement was done using a tensile tester (Instron 5566) for loading and unloading, anchored with temperature chamber for heating and cooling. Figure 3 shows the result of stress increase (Δσ) in the specimen under a fixed tensile strain. It can be inferred that the stress increase (Δσ) in the fabric is due to presence of MP filaments. The Δσ increased rapidly for the initial time and finally saturated to a fixed value for the given temperature. Figure 3b shows the results of stress variation with temperature. The increase in stress varies linearly with the temperature, as shown in Equation (4).
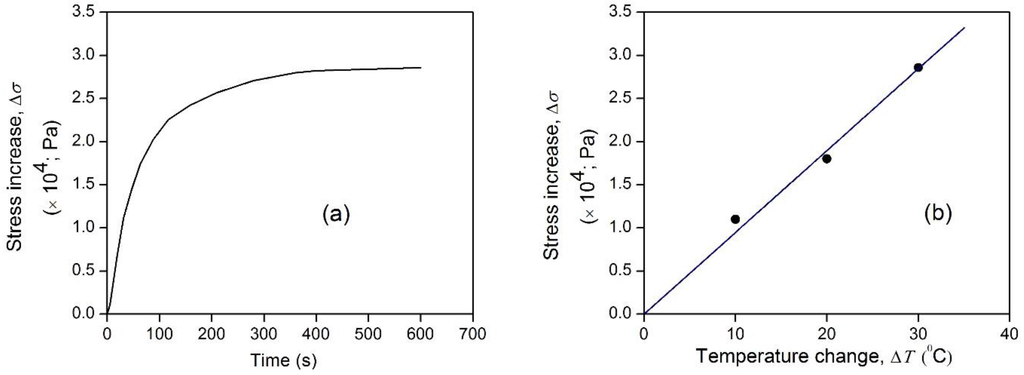
Figure 3.
(a) Stress increase Δσ in the bandage upon activation under constraint deformation (ɛ = 30%; T = 50 °C). (b) Results of stress increase Δσ with increase in temperature ΔT (Equation (4)).
If such MP bandage is applied over a limb surface (here it is applied to a cylindrical tube), there is an external constraint imposed to the bandage by the interface surface. As the interface pressure depends on the stress in the bandage as expressed by Laplace's law (Equation (1)), the bandage could allow pressure change directly over the limb by simple temperature modulation. Figure 4 shows the pressure variation by the bandage once the temperature is increased. Increasing the temperature (>Tg) allows the activation of memory stress in MP filaments (similar to Figure 3), and the overall stress is increased, which allows the pressure to change. At lower temperatures (T < Tg = 30 °C), the memory stress in the MP filaments is not activated, and a constant pressure is maintained, which is present only due to elastic stress present in the structure of bandage while wrapping on the cylindrical surface.
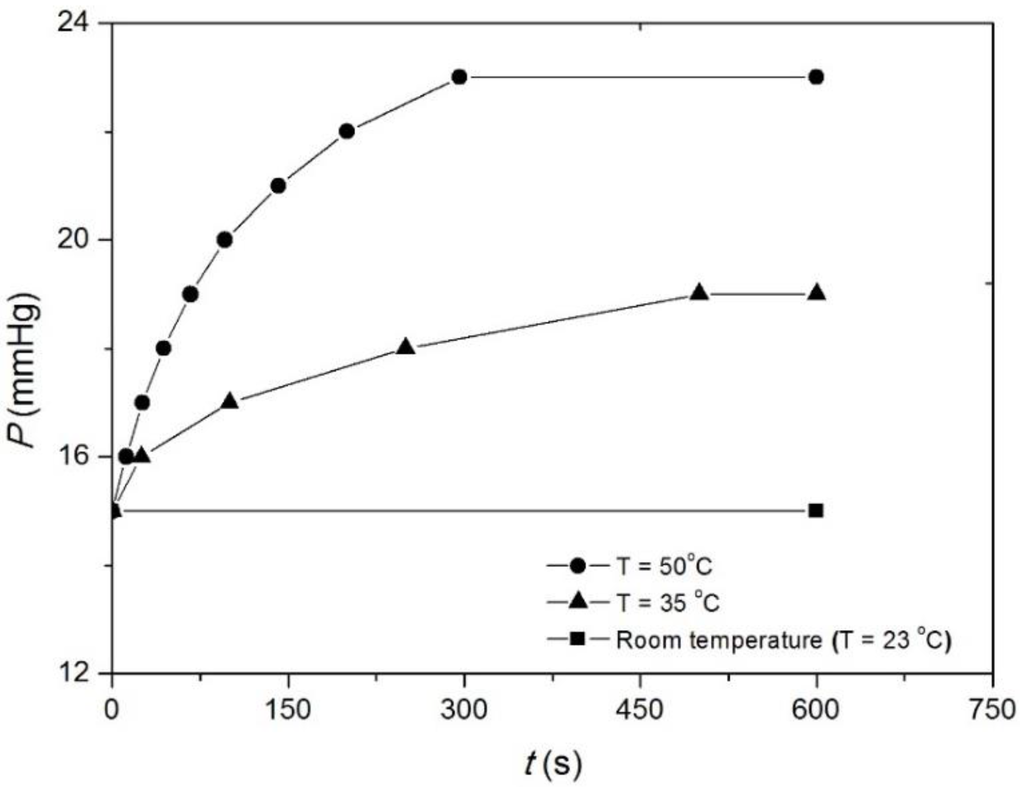
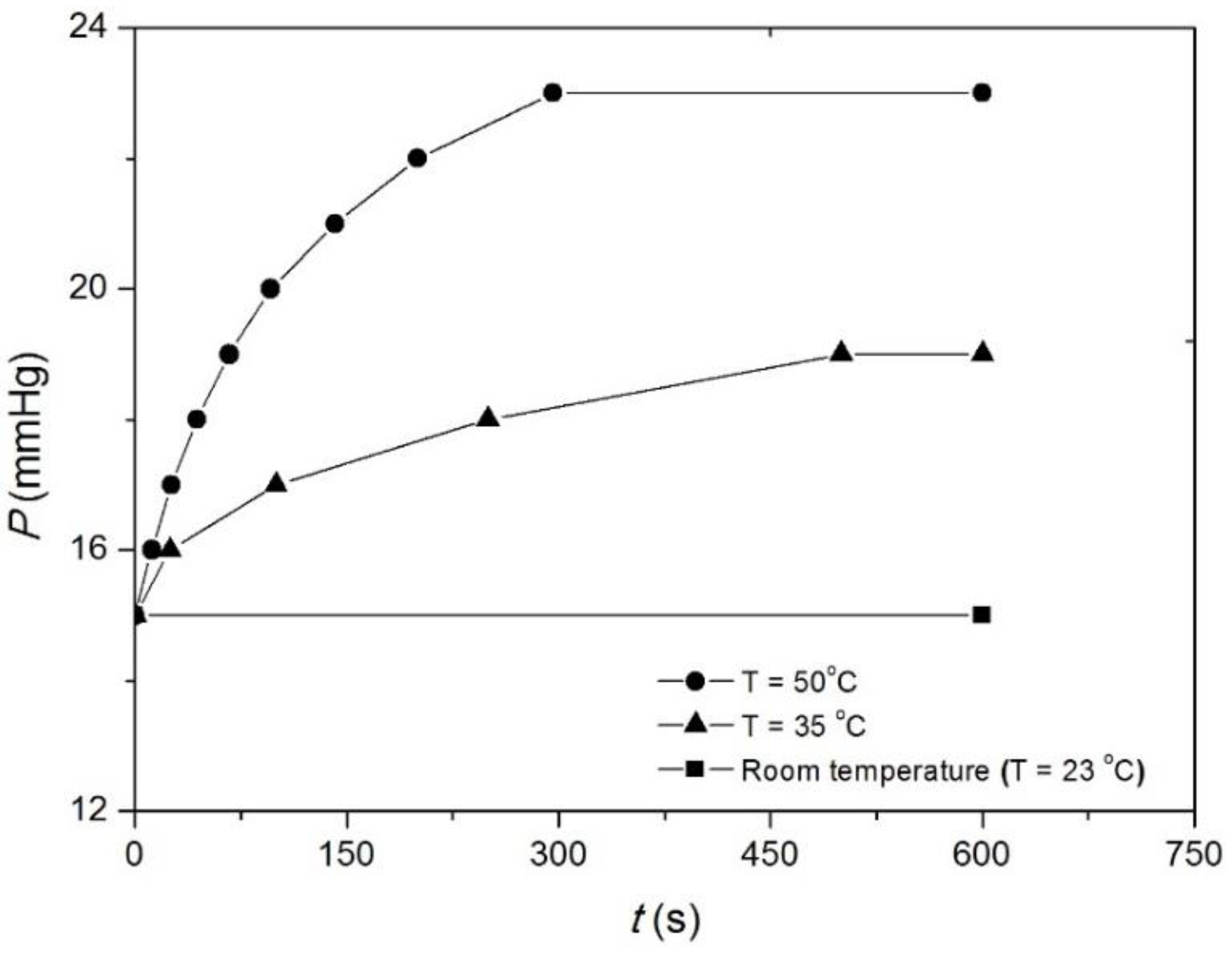
Figure 4.
Pressure variation at different levels of temperatures (ε = 30%; C = 23.6 cm; N = 1).
For a given T (>Tg), the P increases rapidly for the initially period (600 s) and then finally reaches saturation. The rate and amount of extra pressure generated during activation is greater at higher temperatures (p < 0.01). The extra pressure increases (ΔP) are 8 mmHg and 4 mmHg, respectively, at 50 °C and 35 °C. The MP filaments used in the fabric has a transition range (~20–50 °C; Figure 1), because of which, it is highly unlikely that all switching segments would activate together with increasing temperature to a fixed level. It is expected that more switching segments are activated at higher T (~50 °C) as compared to lower T (~35 °C). Therefore, more memory stress is generated in the MP filaments at higher temperatures, which therefore results in greater pressure increases. No significant pressure changes were observed beyond 50 °C. This is due to activation of all switching segments in the MP network around 50 °C.
For practical application, the temperature should not be increased too much above body temperature, as this could cause patient discomfort. This is why the transition range of MP actuation needs to carefully optimized to obtain the desired pressure variation in the achievable and allowable temperature conditions. The Tg could be optimized to a particular range by the proper choice of different components (type and molecular weight of switching segment and hard segment content) involved in the formation of the MP [23,26,27]. Herein, we developed MP filament using segmented polyurethane with low Tg (~30 °C) and the activation domain was 20–50 °C.
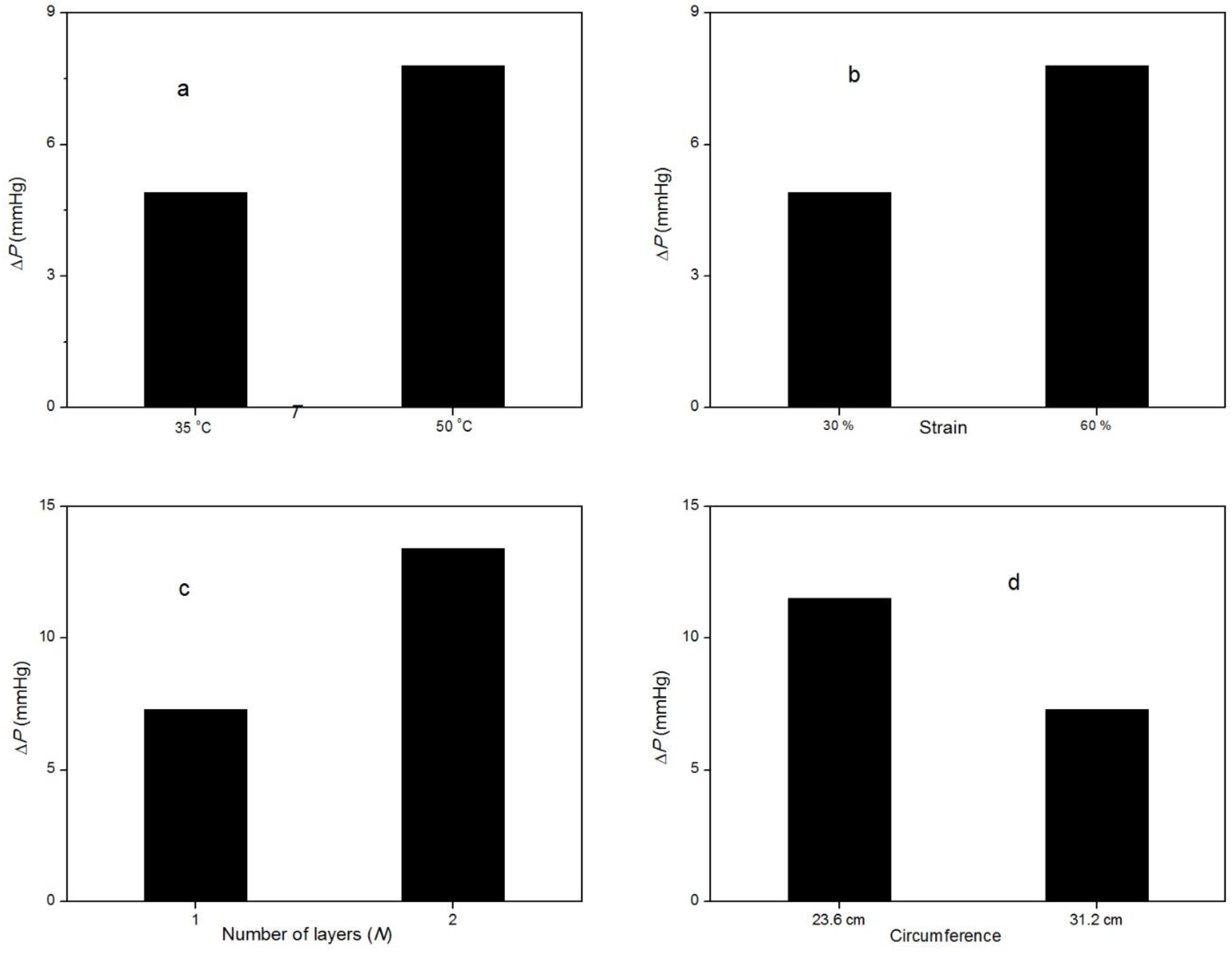
Before recommending the SMP and suggesting it as a credible compression product, there are many aspects that need to be thoroughly examined, such as how much extra pressure could be achieved, the temperature range, other external factors that could decide pressure variation, the repeatability, etc. Apart from temperature change, several other variables that could affect the pressure results exist. Figure 5 summarizes the effect of important variables on the amount of ΔP generated by the bandage upon activation. Similar to temperature, strain has the same effect on the MP bandage (Figure 5b). More ΔP is observed at high strain level. This is due to differences in the extent of recovery of memory polymer at different levels of strain. Inducing more strain in the MP results in significant entropy reduction because of orientation of polymer chains, and upon heating the stretched MP, the shrinkage is more favorable to increase the entropy by coiling of polymer chains, as explained by rubber elasticity. Therefore, high strain in the MP is expected to have more stress upon heating. The effect of number of layers and circumference can be derived from the equation of Laplace’s law. The pressure is inversely related to the limb circumference due to which ΔP observed at higher circumference (31.2 cm) is lower than pressure observed at 23.6 cm circumference (Figure 5d). Increasing the number of wrapping layers will also have an additive effect (Figure 5c), although the ΔP is not doubled if the number of layers (N) is increased from one to two. Primarily, the compression provided by the top layer is absorbed by the inner layers; thus, the total pressure exerted by multiple layers is less than the sum of pressure exerted by individual layers. The relation of P and N, as described by Laplace’s law (Equation (1)), overestimates the pressure values. This relation is valid for thin-wall cylinder vessel and for continuum materials. Assuming fabric as a continuum and neglecting its thickness may also cause this discrepancy. Table 2 shows all the ΔP results of different levels of influencing factors.
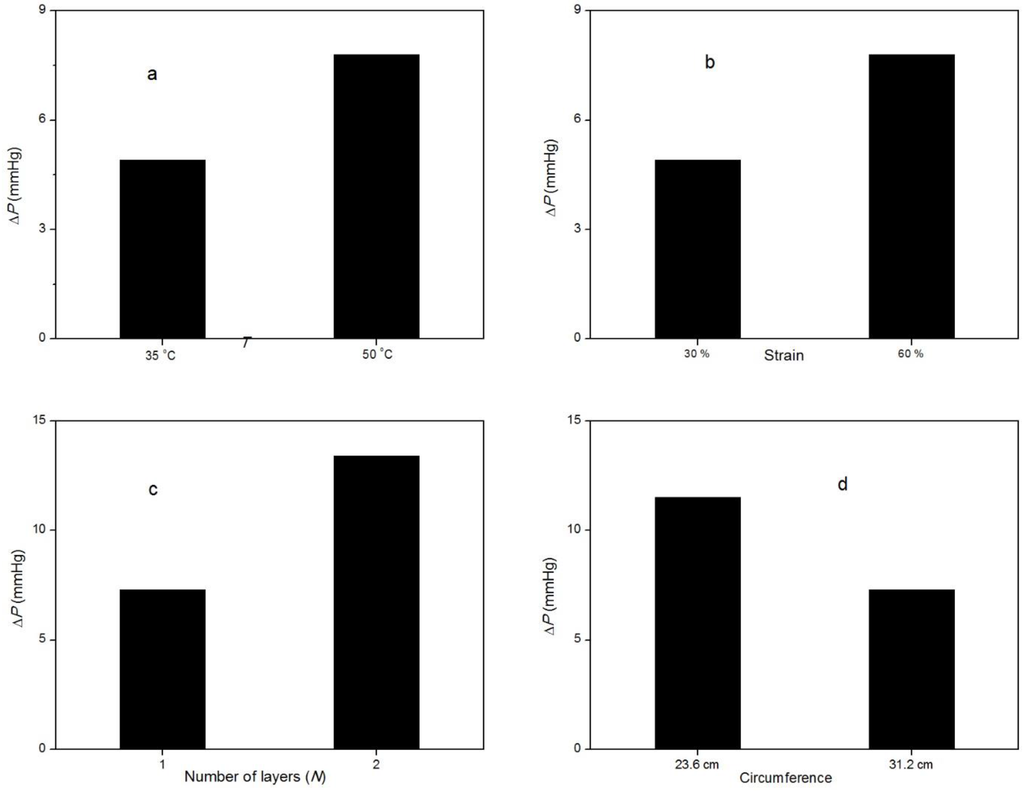
Figure 5.
Result of extra pressure ΔP: (a) by changing temperature; (b) by changing strain; (c) by changing number of wrapping layers; and (d) by changing cylinder circumference.

Table 2.
Results of extra pressure (ΔP, in mmHg) by the MP bandage at different levels of factors.
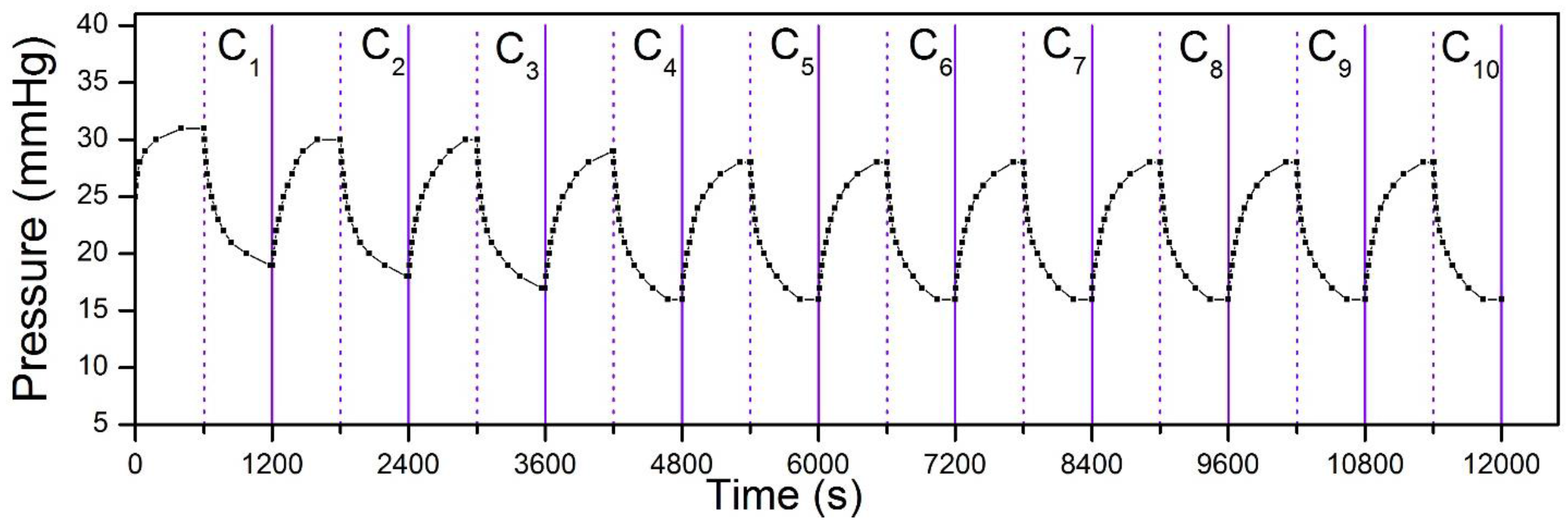
Finally, we also tested the repeatability of pressure change by the bandage under continuous heating and cooling cycles. The result is summarized in Figure 6. After an initial adjustment for the first four cycles, the pressure variation show similar results. This indicates that the bandage has the potential to reproduce the same pressure results, even after multiple uses, and thus allow readjusting pressure levels whenever needed.
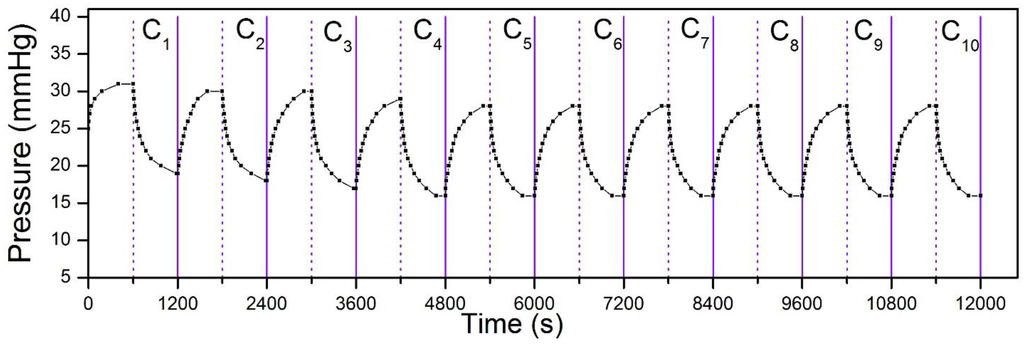
Figure 6.
Cyclic pressure variation by the bandage upon continuous heating and cooling cycles. Each cycle (C1 to C10) includes heating of the bandage for 10 min in heated chamber (T = 50 °C), and then cooling down for another 10 min at room temperature (T = 23 °C).
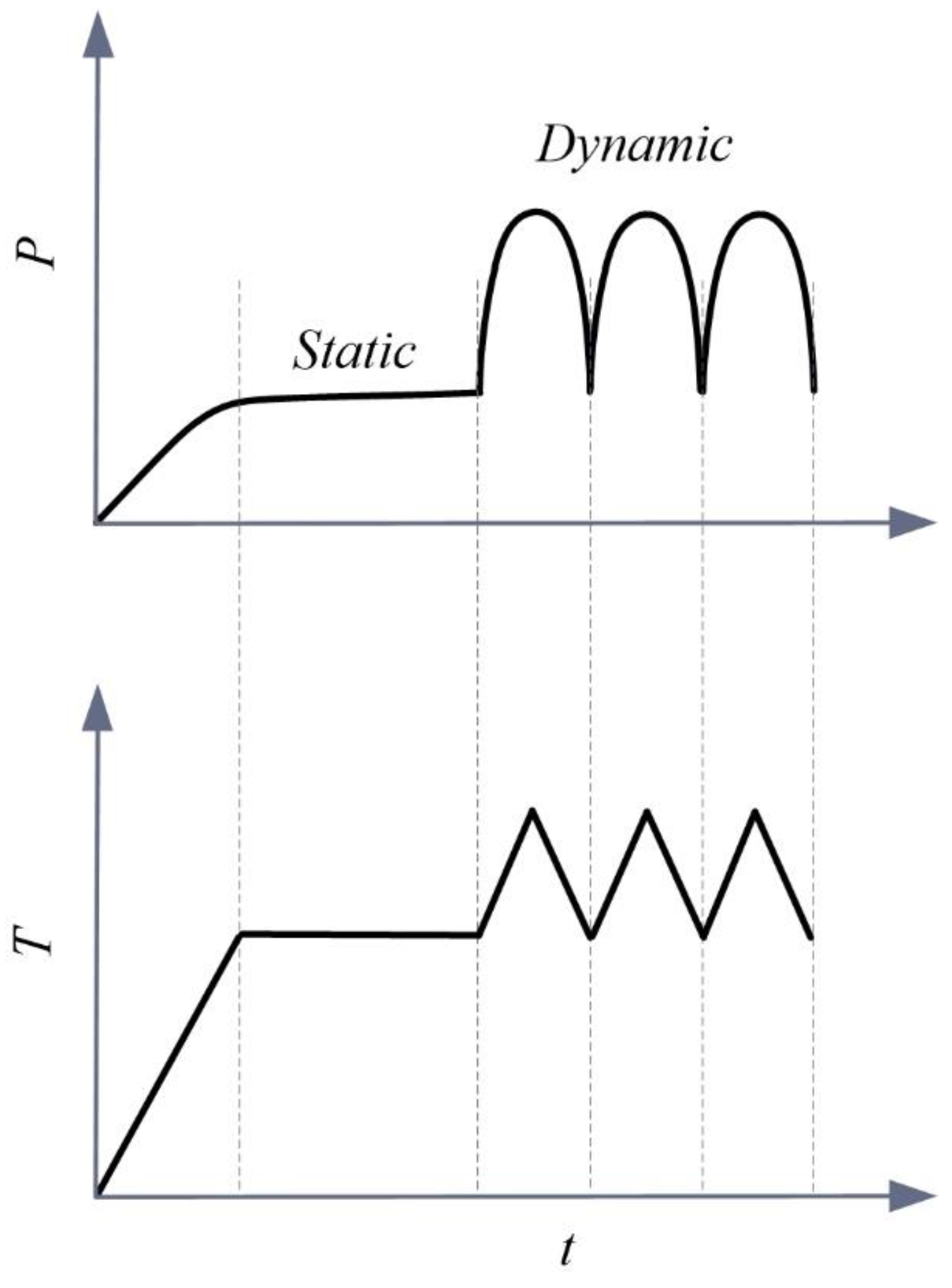
The memory bandage could offer several advantages in compression management. First, this could give more freedom to nurses to control or readjust pressure at wrapped position, and to achieve an appropriate level of pressure. Second, it would be possible to counter the effect of pressure drop during the course of compression treatment. Earlier studies suggested that the pressure drop is inevitable for most of the compression bandages due to fiber’s stress relaxation or due to limb reduction [9,28]. However, the advantage of memory bandage over the existing conventional product would be that, when the pressure drops below a targeted level, it would be possible to readjust pressure level even without replacing the bandage, and therefore could provide sustained compression. Third, it would be possible to extract multi-functionalities of static and dynamic compression benefits from the memory bandage. Most of the current means for compression are passive, meaning that they only provide a fixed level of initial pressure, incapable of having massage effect. For dynamic treatment (massaging of leg), the equipment like intermittent pneumatic compression (IPC) is recommended, which is too costly, noisy, bulky, and, once attached, requires immobile patients [29]. This novel bandage could be used for multiple compression benefits (static and dynamic) via a programmed heating stimulus (Figure 7).
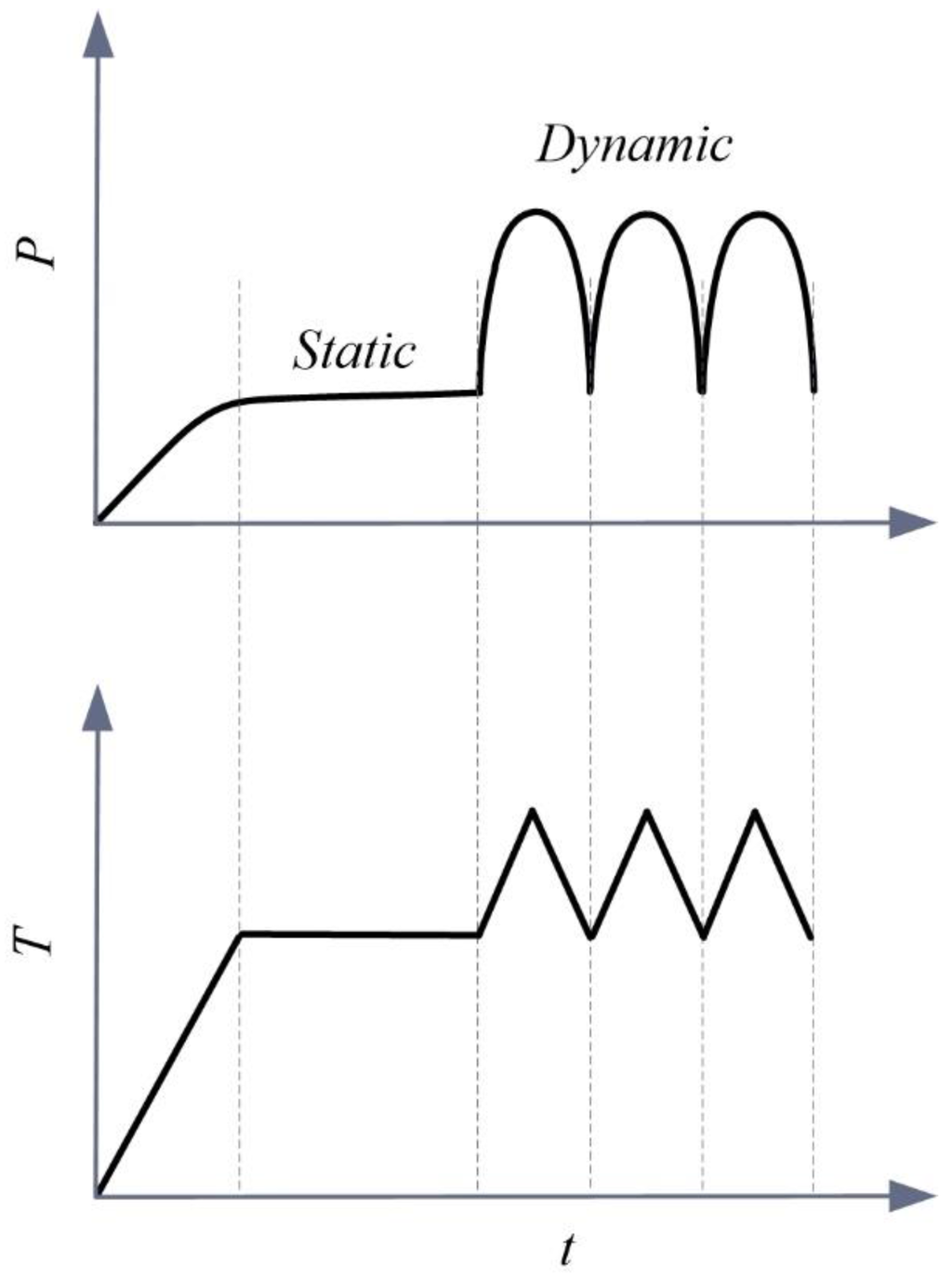
Figure 7.
Exploiting controlled static and dynamic compression benefits from a memory bandage using a programmed heating stimulus.
4. Conclusions
The present work introduces a novel application of MP filaments in medical bandage for the functional compression management for the treatment of chronic venous disorders. A memory bandage was developed using MP filaments in the structure. The bandage was able to change the internal stress in its structure by external means, i.e., using heating stimulus. It was possible to control or manage the pressure exerted by the bandage in wrapped position, and extra pressure (ΔP) was generated by simple heating. Increasing the temperature and strain stimulated more ΔP. Other factors, i.e., circumference and number of layers, also affect the magnitude of ΔP. The bandage could offer the advantage of controlled compression to meet the desired needs for a given patient.
It is envisioned that the memory bandage could revolutionize compression treatment, and this goal could be achieved with more scientific effort, sharp vision, tremendous creativity and huge investment. There are many studies that are still needed to ensure the memory bandage is a credible compression product. In real practice, heating of MP on the leg to a particular temperature is a challenge, and simple and efficient heating arrangements need to be assured to have precise control on the pressure. The use of flexible heating systems (conductive fabrics) could be a good alternative. Another method is to develop body-temperature activated memory filament, where the activation could be performed by body heat. All this could be a part of future study where an integrated system (heating device and memory bandage) will be designed and examined. The other work is to conduct the pressure study on a soft surface. Naturally, the pressure on a soft surface (such as a real body) may vary compared to the hard surface presented in this study. The soft tissue compressibility could lead to changes in circumference C, and the parameters in Equation (1) will have to be adjusted accordingly for accurate pressure predictions. Future work should also focus on the effect of several other factors, e.g., different MPs, hard segment content, proportion of MP, fabric structure, time dependent study, etc.
Acknowledgments
The authors acknowledge the support of team members who helped directly or indirectly during the preparation of the work, including Han Jianping and Lv Jing who helped in polymer synthesis and filament preparation. We also thank Harishkumar Narayana and Wu You for initial discussions.
Author Contributions
The main author, Bipin Kumar, initiated the project, contributed in design of experiments, observed the key results of the paper and wrote up the manuscript. Jinlian Hu participated in experimental design, paper discussion and revision. Ning Pan helped in proof-reading and final editing of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Partsch, H. Compression therapy in leg ulcers. Rev. Vasc. Med. 2013, 1, 9–14. [Google Scholar] [CrossRef]
- Ramelet, A.A. Compression therapy. Dermatol. Surg. 2002, 28, 6–10. [Google Scholar] [PubMed]
- Partsch, H. Compression for the management of venous leg ulcers: Which material do we have? Phlebology 2014, 29, 140–145. [Google Scholar] [CrossRef] [PubMed]
- Kumar, B.; Das, A.; Alagirusamy, R. Study on interface pressure generated by a bandage using in vitro pressure measurement system. J. Text. Inst. 2013, 104, 1374–1383. [Google Scholar] [CrossRef]
- Kumar, B.; Singh, J.; Das, A.; Alagirusamy, R. Comfort and compressio nal characteristics of padding bandages. Mater. Sci. Eng. C 2015, 57, 215–221. [Google Scholar] [CrossRef] [PubMed]
- Basford, J.R. The Law of Laplace and its relevance to contemporary medicine and rehabilitation. Arch. Phys. Med. Rehabil. 2002, 83, 1165–1170. [Google Scholar] [CrossRef] [PubMed]
- Farah, R.S.; Davis, M.D.P. Venous Leg Ulcerations:A Treatment Update. Curr. Treat. Options Cardiovasc. Med. 2010, 12, 101–116. [Google Scholar] [CrossRef] [PubMed]
- Kumar, B.; Das, A.; Alagirusamy, R. Analysis of sub-bandage pressure of compression bandages during exercise. J. Tissue Viability 2012, 21, 115–124. [Google Scholar] [CrossRef] [PubMed]
- Kumar, B.; Das, A.; Alagirusamy, R. Effect of material and structure of compression bandage on interface pressure variation over time. Phlebology 2013, 29, 376–385. [Google Scholar] [CrossRef] [PubMed]
- Kumar, B.; Das, A.; Alagirusamy, R. Study of the effect of composition and construction of material on sub-bandage pressure during dynamic loading of a limb in vitro. Biorheology 2013, 50, 83–94. [Google Scholar] [PubMed]
- Zhao, Q.; Qi, H.J.; Xie, T. Recent progress in shape memory polymer: New behavior, enabling materials, and mechanistic understanding. Prog. Polym. Sci. 2015, 49–50, 79–120. [Google Scholar] [CrossRef]
- Hu, J.L.; Zhu, Y.; Huang, H.H.; Lu, J. Recent advances in shape-memory polymers: Structure, mechanism, functionality, modeling and applications. Prog. Polym. Sci. 2012, 37, 1720–1763. [Google Scholar] [CrossRef]
- Lendlein, A.; Behl, M.; Hiebl, B.; Wischke, C. Shape-memory polymers as a technology platform for biomedical applications. Expert Rev. Med. Devices 2010, 7, 357–379. [Google Scholar] [CrossRef] [PubMed]
- Mather, P.T.; Luo, X.F.; Rousseau, I.A. Shape Memory Polymer Research. Annu. Rev. Mater. Res. 2009, 39, 445–471. [Google Scholar] [CrossRef]
- Leng, J.S.; Lan, X.; Liu, Y.; Du, S. Shape-memory polymers and their composites: Stimulus methods and applications. Prog. Mater. Sci. 2011, 56, 1077–1135. [Google Scholar] [CrossRef]
- Zhang, D.W.; George, O.J.; Petersen, K.M.; Jimenez-Vergara, A.C.; Hahn, M.S.; Grunlan, M.A. A bioactive “self-fitting”shape memory polymer scaffold with potential to treat cranio-maxillo facial bone defects. Acta Biomater. 2014, 10, 4597–4605. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.L.; Kumar, B.; Narayan, H.K. Stress Memory Polymers. J. Polym. Sci. Part B Polym. Phys. 2015, 53, 893–898. [Google Scholar] [CrossRef]
- Kratz, K.; Madbouly, S.; Wagermaier, W. Temperature-Memory Polymer Networks with Crystallizable Controlling Units. Adv. Mater. 2011, 23, 4058–4062. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Hu, J.; Huang, H.; Li, J.; Zhu, Y.; Tang, B.; Han, J.; Li, L. Memory Chromic Polyurethane with Tetraphenylethylene. J. Polym. Sci. Part B Polym. Phys. 2014, 52, 104–110. [Google Scholar] [CrossRef]
- Yuan, J.K.; Zakri, C.; Grillard, F.; Neri, W.; Poulin, P. Temperature and Electrical Memory of Polymer Fibers. In Proceedings of the 7th International Conference on Times of Polymers (TOP) and Composites, Melville, NY, USA, 22–26 June 2014.
- Liu, Y.P.; Gall, K.; Dunn, M.L.; Greenberg, A.R.; Diani, J. Thermomechanics of shape memory polymers: Uniaxial experiments and constitutive modeling. Int. J. Plast. 2006, 22, 279–313. [Google Scholar] [CrossRef]
- Narayana, H.; Hu, J.; Kumar, B.; Shang, S. Constituent Analysis of Stress Memory in Semicrystalline Polyurethane. J. Polym. Sci. Part B Polym. Phys. 2016. [Google Scholar] [CrossRef]
- Hu, J.; Meng, Q.H.; Zhu, Y.; Lu, J.; Zhuo, H.T. Shape Memory Fibers Prepared via Wet, Reaction, Dry, Melt, and Electro Spinning. US20090093606 A1, 9 October 2007. [Google Scholar]
- Rosen, S. Rubber Elasticity. In Fundamental Principles of Polymeric Materials; Wiley-Interscience Publications: Hoboken, NJ, USA, 1982; pp. 189–198. [Google Scholar]
- Kumar, B.; Hu, J.L.; Pan, N. Smart medical stocking using memory polymer for chronic venous disorders. Biomaterials 2016, 75, 174–181. [Google Scholar] [CrossRef] [PubMed]
- Meng, Q.H.; Hu, J.; Yeung, L.Y.; Hu, Y. The Influence of Heat Treatment on the Properties of Shape Memory Fibers. II. Tensile Properties, Dimensional Stability, Recovery Force Relaxation, and Thermomechanical Cyclic Properties. J. Appl. Polym. Sci. 2009, 111, 1156–1164. [Google Scholar] [CrossRef]
- Zhu, Y.; Hu, J.; Yeung, L.-Y.; Liu, Y.; Ji, F.; Yeung, K. Development of shape memory polyurethane fiber with complete shape recoverability. Smart Mater. Struct. 2006, 15, 1385–1394. [Google Scholar] [CrossRef]
- Kumar, B.; Das, A.; Alagirusamy, R. An Approach to Determine Pressure Profile Generated by Compression Bandage Using Quasi-Linear Viscoelastic Model. J. Biomech. Eng. Trans. Asme 2012, 134. [Google Scholar] [CrossRef] [PubMed]
- Feldman, J.L.; Stout, N.L.; Wanchai, A.; Stewart, B.R.; Cormier, J.N.; Armer, J.M. Intermittent Pneumatic Compression Therapy: A Systematic Review. Lymphology 2012, 45, 13–25. [Google Scholar] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).