Concrete-Filled-Large Deformable FRP Tubular Columns under Axial Compressive Loading

Abstract

The behavior of concrete-filled fiber tubes (CFFT) polymers under axial compressive loading was investigated. Unlike the traditional fiber reinforced polymers (FRP) such as carbon, glass, aramid, etc., the FRP tubes in this study were designed using large rupture strains FRP which are made of recycled materials such as plastic bottles; hence, large rupture strain (LRS) FRP composites are environmentally friendly and can be used in the context of green construction. This study performed finite element (FE) analysis using LS-DYNA software to conduct an extensive parametric study on CFFT. The effects of the FRP confinement ratio, the unconfined concrete compressive strength ($f_c^{\prime }$), column size, and column aspect ratio on the behavior of the CFFT under axial compressive loading were investigated during this study. A comparison between the behavior of the CFFTs with LRS-FRP and those with traditional FRP (carbon and glass) with a high range of confinement ratios was conducted as well. A new hybrid FRP system combined with traditional and LRS-FRP is proposed. Generally, the CFFTs with LRS-FRP showed remarkable behavior under axial loading in strength and ultimate strain. Equations to estimate the concrete dilation parameter and dilation angle of the CFFTs with LRS-FRP tubes and hybrid FRP tubes are suggested.

1. Introduction

Green buildings are environmentally sound buildings. The ideal green project preserves and restores the habitat that is vital for sustaining life by acting as a net producer and exporter of resources, materials, energy, and water rather than being a net consumer. The Environmental Protection Agency (EPA) suggests using recycled industrial goods such as demolition debris in construction projects for green buildings. Energy efficient building materials and appliances are promoted in the United States through energy rebate programs. However, using green materials in construction is usually costly. Recently, new fiber reinforced polymer (FRP) composites have been manufactured from recycled plastic bottles. They were introduced as alternatives to traditional FRPs such as glass, aramid, and carbon FRP. The new FRP composites are much cheaper than the traditional FRPs. These new FRP composites are made of polyethylene terephthalate (PET) and polyethylene naphthalate (PEN) fibers. The traditional FRP composites have linear elastic stress-strain relationships with a rupture failure strain ranged around 1.0% to 2.5%. However, the new FRP composites have bilinear stress-strain relationships with elastic modulus and tangent modulus. This bilinear stress-strain relation is because of the effect of amorphous phase motion and macromolecular chains sliding between LRS fibers and matrix [1]. However, the elastic modulus of the new FRP composites is, in general, lower than that of the traditional FRPs. They have much larger rupture strains, usually larger than 6.0%. Therefore, the new FRP composites were called large rupture strain FRPs (LRS-FRPs). PET polymers keep their mechanical strengths up to a temperature of 150–175 °C [2].

Use of the FRP in new structures has grown rapidly in the past two decades. The main purpose of using FRP is to enhance the strength and ductility of a structural member. Concrete-filled FRP tubes (CFFTs) have many benefits such as light weight-to-strength ratio, high confinement, and corrosion resistance. The FRP tube acts as a stay-in-place formwork, confines the concrete structural element, and increase its compressive strength. Several researchers investigated the behavior of CFFT columns using the traditional FRP tubes under different loadings [3,4,5,6,7,8,9,10]. Recently, some experimental works have been conducted to investigate the performance of the LRS-FRPs in jacketing concrete members to examine their behavior under different loading such as axial, flexural, shear loadings [1,11,12,13,14,15]. This research has shown that LRS-FRP jacketed concrete members had superior behavior compared to members retrofitted using conventional FRP. However, no studies were conducted to determine the benefits of combining both traditional and LRS-FRPs in a hybrid system.

The FRP confinement pressure (f_l) and the concrete dilation angle (ψ) are essential parameters in characterizing the performance of concrete under compression stress in the CFFTs. Confinement pressure is the lateral pressure from the FRP tube that confines the concrete core when the concrete material starts to expand. The confinement pressure and the confinement ratio can be calculated using Equations (1) and (2). The dilation angle is defined as the inclination of the failure surface towards the hydrostatic axis. Physically, the dilation angle is interpreted as a concrete internal friction. The dilation angle varies depending on the axial stress level and the FRP jacketing stiffness [16,17]. However, previous studies used the dilation angle to vary with the FRP jacketing stiffness and to be a constant value under varied axial load levels in the finite element analysis [18,19,20]. The finite element results of these studies agreed with the experimental results with reasonable accuracy. For unconfined concrete material, the dilation angle is usually taken between 36° to 40° with an average value of 38° [21,22,23].

$$\left(f_l\right)=\frac{2 E_f {\mathrm{\epsilon }}_f t_f}{D}$$

(1)

$$Confinement ratio \left(CR\right)=\frac{f_l}{f_c^{\prime }}$$

(2)

where $E_f$ is the elastic modulus of the FRP tube in the confinement direction, ${\mathrm{\epsilon }}_f$ is the ultimate tensile strain of the FRP in the confinement direction, $t_f$ is the FRP tube thickness, D is the column’s diameter, and $f_c^{\prime }$ the characterized concrete cylindrical strength at 28 days.

An extensive finite element (FE) study is presented to investigate the behavior of the CFFTs using LRS-FRP under axial compressive loading. LS-DYNA software [24] was used during this study. A high range of confinement ratios was investigated for the traditional FRP and LRS-FRP. New state-of-the-art CFFT columns using hybrid FRP tubes combined with traditional FRP and LRS-FRP are introduced. In addition, the effect of the concrete strength ($f_c^{\prime }$), column size, and column aspect ratio on the behavior of the CFFT were studied. This study introduces recommendations for using of the most effective FRP type in CFFT tubes. A new equation to estimate the dilation angle for the CFFT column with LRS-FRP tubes is suggested.

2. Finite Element Model Validation

FE modeling was used to analyze the behavior of CFFT with LRS-FRP under axial loading. The LS-DYNA 971 R3 software was used to design and validate the models against the experimental results that were gathered from 12 CFFT columns with LRS-FRP by Dai et al. [13]. Each column had a circular cross-section with an outer diameter of 150 mm and a height of 300 mm. These columns had a concrete compressive strength ($f_c^{\prime }$) that was between 32.5 and 39.2 MPa. Either PET-FRP or PEN-FRP was used to manufacture the FRP tubes (Table 1). These models were next used to conduct a parametric study investigating the differences between LRS-FRP, tradition FRP, and hybrid system of a combination of both by analyzing the effects of the confinement ratio, column’s size, and the column’s aspect ratio on the CFFT behavior under axial loading.

Table 1. Summary of cylinders variables (Modified from Dai et al. [13], copyright 2011 ASCE).

Cylinder Label	Diameter (mm) X Height (mm)	${\mathit{f}}_{\mathit{c}}^{\mathbf{\prime }}$ (MPa)	FRP Type	No. of Layers	Total Thickness (mm)
PEN-600-I	150 × 300	39.2	PEN-600	One	0.85
PEN-600-II				Two	1.70
PEN-600-III				Three	2.54
PET-600-I		32.5	PET-600	One	0.84
PET-600-II				Two	1.68
PET-600-III				Three	2.52
PET-900-I		39.2	PET-900	One	1.26
PET-900-II				Two	2.52
PET-900-III				Three	3.79

Table 1. Summary of cylinders variables (Modified from Dai et al. [13], copyright 2011 ASCE).

Cylinder Label	Diameter (mm) X Height (mm)	${\mathit{f}}_{\mathit{c}}^{\mathbf{\prime }}$ (MPa)	FRP Type	No. of Layers	Total Thickness (mm)
PEN-600-I	150 × 300	39.2	PEN-600	One	0.85
PEN-600-II				Two	1.70
PEN-600-III				Three	2.54
PET-600-I		32.5	PET-600	One	0.84
PET-600-II				Two	1.68
PET-600-III				Three	2.52
PET-900-I		39.2	PET-900	One	1.26
PET-900-II				Two	2.52
PET-900-III				Three	3.79

2.1. Geometry

The concrete cylinder and steel plates were modeled using solid elements (Figure 1). The outer FRP tube was simulated using shell elements. All solid elements were modeled with constant-stress and a one-point quadrature to reduce the computational time. Hourglass control was used to avoid spurious singular modes (i.e., hourglass modes) for solid elements. The hourglass value for all models was taken as the default value of 0.10. Surface-to-surface contact elements were used to simulate the interface between the concrete cylinder and the outer FRP tube. Node-to-surface contact elements were used between the rigid plates and the cylinder. The coefficient of friction for all of the contact elements was taken as 0.6 [25].

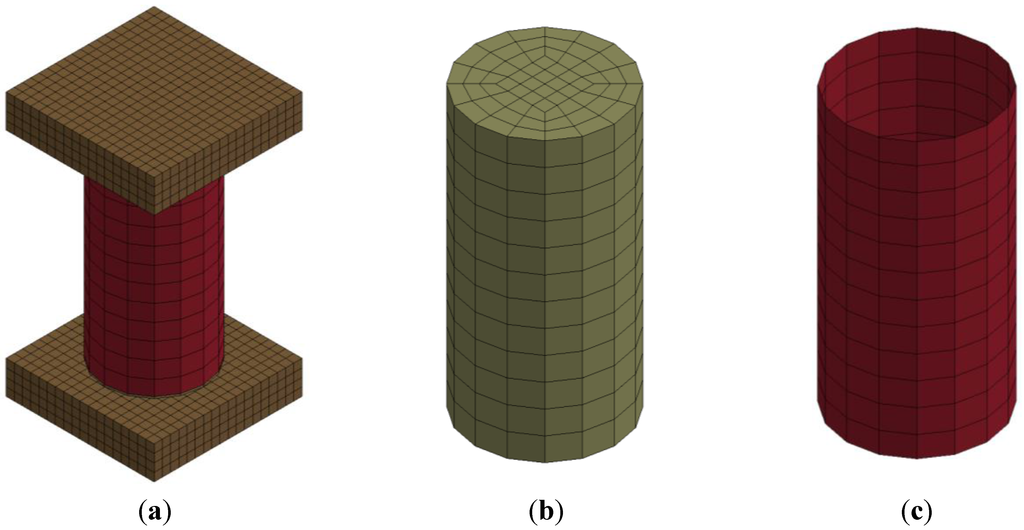
Figure 1. Finite element model components: (a) 3-D view; (b) concrete cylinder; and (c) FRP tube.

Figure 1. Finite element model components: (a) 3-D view; (b) concrete cylinder; and (c) FRP tube.

2.2. Concrete Material Model

Different material models are available in LS-DYNA to simulate concrete materials. Because the Karagozian and Case Concrete Damage Model Release 3 (K & C model) exhibited good agreement with the experimental results collected in previous studies, it was chosen for this study (e.g., [25]). The model was developed based on the theory of plasticity. The model has three shear failure surfaces: yield, maximum, and residual [26]. This material model has eighty parameters that can be either user defined or automatically generated. This study used the automatic generation option for the failure surface where $f_c^{\prime }$ was the main input to the model. Another input to the model, the fractional dilation parameter ($\omega$), considers any volumetric change in concrete. The fractional dilation parameter is related to the dilation angle by Equation (3). Youssf et al. [20] suggested an Equation (4) to calculate the dilation parameter to the CFFT with traditional FRP. Youssef et al.’s equation was modified to propose a new Equation (5) to calculate the dilation parameter of the CFFT with LRS-FRP based on the validation of the experimental results. In the case of a conventional concrete column without FRP confinement, the equation yields a dilation parameter of a constant value of 0.8, which is approximately equal to Tan 38°. This result agreed with the common value of the dilation angle of the concrete material without FRP confinement. The dilation parameter for the hybrid system of a combination of the LRS-FRP and the traditional FRP was equal to the summation of the two dilation parameters (Equation (6)).

$$\mathrm{Dilation} \mathrm{parameter} (\mathrm{\omega }) =\tan \mathrm{\psi }$$

(3)

$$\mathrm{Dilation} \mathrm{parameter} \mathrm{in} \mathrm{case} \mathrm{of} \mathrm{traditional} \mathrm{FRP} ({\mathrm{\omega }}_1)=-0.195\ln \frac{E_{f1}}{f_c^{\prime }}+0.6115$$

(4)

$$\mathrm{Dilation} \mathrm{parameter} \mathrm{in} \mathrm{case} \mathrm{of} \text{LRS-FRP}\hspace{0.17em}{(\mathrm{\omega }}_2)=\frac{0.8-0.015 E_1/f_c^{\prime }}{1+0.075 E_1/f_c^{\prime }}$$

(5)

$$\begin{gathered} \mathrm{Dilation} \mathrm{parameter} \mathrm{in} \mathrm{case} \mathrm{of} \mathrm{combination} \mathrm{of} \mathrm{traditional} \mathrm{and} \\ \text{LRS-FRP}\hspace{0.17em}({\mathrm{\omega }}_3)=(-0.195\ln \frac{E_{f1}}{f_c^{\prime }}+0.6115)+ \frac{0.8-0.015 E_1/f_c^{\prime }}{1+0.075 E_1/f_c^{\prime }}) \end{gathered}$$

(6)

$$E_1=\frac{2 E_{f2} t_f}{D }$$

(7)

where $E_1$ is the confinement modulus ratio, $E_{f1}$ is the elastic modulus of the traditional FRP, $E_{f2}$ is the tangent modulus of the LRS-FRP, $t_f$ is the thickness of the FRP, D is the column’s diameter, and $f_c^{\prime }$ is the characteristic cylindrical concrete strength at 28 days.

2.3. FRP Material Model

The material properties of PET-FRP and PEN-FRP composites have been studied by Dai et al. [13]. Such types of FRP have approximate bilinear stress-strain relationships that can be described in terms of two moduli of elasticity: the initial elastic modulus (E_f1) and the tangent modulus (E_f2). The material properties of PET-FRP and PEN-FRP are summarized in Table 2. The material properties of the glass and carbon FRP referenced in the manufacturer data sheet of Tyfo^® SEH-51 and Tyfo^® SCH-41 are summarized as well in Table 2. FRP composites were modeled as orthotropic materials using “108-ortho_elastic_plastic” material for LRS-FRP to simulate the bilinear behavior. Material model “002-orthotropic-elastic” was used for the traditional FRP to simulate the linear behavior. The “108-ortho_elastic_plastic” material model combines orthotropic, elastic, and plastic behaviors for shells only. This material is defined by the engineering constants: elastic modulus (E_f1), tangent modulus (E_f2), shear modulus (G), and Poisson’s ratio (PR) in the two principle axes (a and b). Additionally, the fiber orientation is defined by a vector. However, the tangent modulus does not exist in the material model of “002-orthotropic-elastic”. Failure criterion for FRP composites was defined using “000-add_erosion,” to assign the ultimate strain of FRP in the “EFFEPS” card.

Table 2. Material properties of FRP composites (part of this reproduced after Dai et al. [13], copyright 2011 ASCE).

FRP Type	Ef1 (GPa)	Ef2 (GPa)	Tensile Strength (MPa)	Rupture Strain (%)
PET-FRP	17.9	8.3	750	8.7
PEN-FRP	27.0	12.0	760	6.3
Glass-FRP	26.1	–	575	2.2
Carbon-FRP	95.8	–	986	1.0

Table 2. Material properties of FRP composites (part of this reproduced after Dai et al. [13], copyright 2011 ASCE).

FRP Type	Ef1 (GPa)	Ef2 (GPa)	Tensile Strength (MPa)	Rupture Strain (%)
PET-FRP	17.9	8.3	750	8.7
PEN-FRP	27.0	12.0	760	6.3
Glass-FRP	26.1	–	575	2.2
Carbon-FRP	95.8	–	986	1.0

2.4. Loading and Boundary Conditions

Displacements and rotations in all directions were prevented at the bottom of the bottom plate. Displacements in X and Y directions were prevented for all of the nodes of the top plate. Monotonic downward (negative Z direction) displacement loading was applied on the top plate for axial compressive loading until failure occurred. Failure was defined as the rupture of the FRP or the crushing of the concrete cylinder.

2.5. Validation Results

Figure 2 illustrates the axial strain-axial stress relationships for all of the cylinders gathered from the FE and the experimental results. The axial strain of each cylinder was obtained by dividing the axial displacement of the loading plate by the cylinder’s height of 300 mm. The axial stress of each cylinder was obtained by dividing the axial reactions at the bottom of the bottom plate by the cross-sectional area of the cylinder. All simulated columns behaved in a manner similar to the tested cylinders until failure. All of the cylinders failed by FRP rupture whether in the experimental or FE category (Figure 3). The FE’s average error rates in predicting the ultimate axial stress and ultimate axial strain were 9% and 10%, respectively. The error was calculated as the absolute value of the difference between the experimental results and the FE results divided by the experimental results.

Figure 2. FE results versus experimental results by Dai et al. [13] of the CFFT with: (a) PEN-FRP-600; (b) PET-FRP-600; and (c) PET-FRP-900.

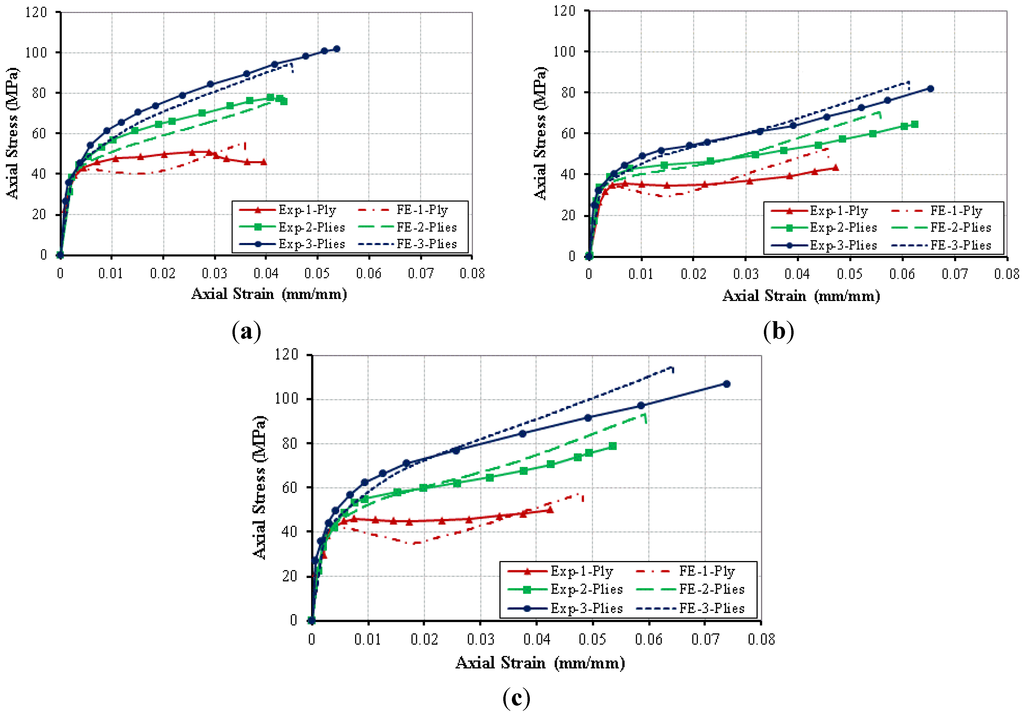
Figure 2. FE results versus experimental results by Dai et al. [13] of the CFFT with: (a) PEN-FRP-600; (b) PET-FRP-600; and (c) PET-FRP-900.

Figure 3. FRP rupture in FE analysis and experimental work by Dai et al. [13] (reprinted with permission from [13]. Copyright 2011 ASCE) of the PEN-600-I: (a) Experimental and (b) FE.

Figure 3. FRP rupture in FE analysis and experimental work by Dai et al. [13] (reprinted with permission from [13]. Copyright 2011 ASCE) of the PEN-600-I: (a) Experimental and (b) FE.

The FE predicted accurately the initial stiffness and stiffness degradation of all of the cylinders until the axial stress reached the unconfined concrete cylindrical strength $(f_c^{\prime }$). After this stress, the FE differentiated a little in values with the experimental results until failure. This difference in values was because the dilation angle was taken as a constant value in the FE. However, it would change with the axial stress level. However, the effect of the dilation did not significantly affect the overall behavior as the accuracy in predicting the ultimate strain was 91%, and the accuracy in predicting the ultimate stress was 90%.

3. Parametric Study

The LRS-FRP is a new composite that has only recently been investigated. Once the finite element model was validated, a comprehensive parametric study was conducted to numerically investigate the behavior of the CFFTs with LRS-FRP. The behavior of the CFFT using different FRP types, including traditional FRP and LRS-FRP, was investigated. A new hybrid system of FRP composites was investigated by combining traditional FRP with LRS-FRP to confine the concrete. The influence of fiber stacking sequences was investigated by placing the PET-FRP layers in the inner surface of the FRP tube and placing the traditional FRP in the outer tube for some columns and vice versa for others. In addition, the effects of the confinement ratio, the unconfined concrete nominal compressive strength ($f_c^{\prime }$), the column’s size, and the column’s aspect ratio were investigated.

All of the investigated columns had a diameter of 150 mm, a height of 300 mm, and an aspect ratio of 2 except columns C44 to C48. Four different column sizes with aspect ratios of 2 were investigated during this study. The diameters × heights ranged from 150 mm × 300 mm to 1500 mm × 3000 mm. Three different column aspect ratios ranging from 2 to 10 were investigated. Seven different confinement ratios ranging from 0.3 to 1.2 were investigated for PET-FRP, PEN-FRP, Glass-FRP, and Carbon-FRP. Five concrete cylindrical compressive strengths ($f_c^{\prime }$) ranging from 27.6 MPa to 82.8 MPa were examined. Each parameter was studied independently, resulting in an analysis of 49 columns. Table 3 summarizes the investigated columns’ variables.

Table 3. Parametric study columns’ variables.

Parameter	Col. Label	Diameter (mm)	Height (mm)	Aspect Ratio	LRS-FRP Thickness (mm)	Traditional FRP Thickness (mm)	${\mathit{f}}_{\mathit{c}}^{\prime }$ (MPa)	Conf. Ratio	Dilation Parameter
PET-FRP	C0	150	300	2	3.4	0	27.6	1.20	0.29
	C1	150	300	2	2.97	0	27.6	1.05	0.33
	C2	150	300	2	2.55	0	27.6	0.90	0.37
	C3	150	300	2	2.13	0	27.6	0.75	0.41
	C4	150	300	2	1.7	0	27.6	0.60	0.46
	C5	150	300	2	1.28	0	27.6	0.45	0.52
	C6	150	300	2	0.85	0	27.6	0.30	0.60
PEN-FRP	C7	150	300	2	3.1	0	27.6	1.20	0.23
	C8	150	300	2	2.7	0	27.6	1.05	0.26
	C9	150	300	2	2.32	0	27.6	0.90	0.30
	C10	150	300	2	1.92	0	27.6	0.75	0.34
	C11	150	300	2	1.54	0	27.6	0.60	0.40
	C12	150	300	2	1.15	0	27.6	0.45	0.47
	C13	150	300	2	0.78	0	27.6	0.30	0.55
GLASS-FRP	C14	150	300	2	0	4.33	27.6	1.20	−0.17
	C15	150	300	2	0	3.8	27.6	1.05	−0.14
	C16	150	300	2	0	3.25	27.6	0.90	−0.11
	C17	150	300	2	0	2.7	27.6	0.75	−0.08
	C18	150	300	2	0	2.15	27.6	0.60	−0.03
	C19	150	300	2	0	1.62	27.6	0.45	0.02
	C20	150	300	2	0	1.07	27.6	0.30	0.10
CARBON-FRP	C21	150	300	2	0	2.6	27.6	1.20	−0.32
	C22	150	300	2	0	2.27	27.6	1.05	−0.30
	C23	150	300	2	0	1.94	27.6	0.90	−0.27
	C24	150	300	2	0	1.62	27.6	0.75	−0.23
	C25	150	300	2	0	1.3	27.6	0.60	−0.19
	C26	150	300	2	0	0.98	27.6	0.45	−0.13
	C27	150	300	2	0	0.65	27.6	0.30	−0.05
PET/Glass (inside/outside)	C28	150	300	2	2.55	1.07	27.6	1.20	0.47
	C29	150	300	2	1.7	2.15	27.6	1.20	0.43
	C30	150	300	2	0.85	3.25	27.6	1.20	0.48
Glass/PET (inside/outside)	C31	150	300	2	2.55	1.07	27.6	1.20	0.47
	C32	150	300	2	1.7	2.15	27.6	1.20	0.43
	C33	150	300	2	0.85	3.25	27.6	1.20	0.48
PET/Carbon (inside/outside)	C34	150	300	2	2.55	0.65	27.6	1.20	0.31
	C35	150	300	2	1.7	1.3	27.6	1.20	0.27
	C36	150	300	2	0.85	1.95	27.6	1.20	0.33
Carbon/PET (inside/outside)	C37	150	300	2	2.55	0.65	27.6	1.20	0.31
	C38	150	300	2	1.7	1.3	27.6	1.20	0.27
	C39	150	300	2	0.85	1.95	27.6	1.20	0.33
Concrete Strength ($f_c^{\prime }$)	C40	150	300	2	5.1	0	41.4	1.20	0.29
	C41	150	300	2	6.8	0	55.2	1.20	0.29
	C42	150	300	2	8.5	0	69	1.20	0.29
	C43	150	300	2	10.2	0	82.8	1.20	0.29
Column size	C44	200	400	2	4.55	0	27.6	1.20	0.29
	C45	300	600	2	6.8	0	27.6	1.20	0.29
	C46	1500	3000	2	34	0	27.6	1.20	0.29
Column aspect ratio	C47	300	1500	5	6.8	0	27.6	1.20	0.29
	C48	300	3000	10	6.8	0	27.6	1.20	0.29

Table 3. Parametric study columns’ variables.

Parameter	Col. Label	Diameter (mm)	Height (mm)	Aspect Ratio	LRS-FRP Thickness (mm)	Traditional FRP Thickness (mm)	${\mathit{f}}_{\mathit{c}}^{\prime }$ (MPa)	Conf. Ratio	Dilation Parameter
PET-FRP	C0	150	300	2	3.4	0	27.6	1.20	0.29
	C1	150	300	2	2.97	0	27.6	1.05	0.33
	C2	150	300	2	2.55	0	27.6	0.90	0.37
	C3	150	300	2	2.13	0	27.6	0.75	0.41
	C4	150	300	2	1.7	0	27.6	0.60	0.46
	C5	150	300	2	1.28	0	27.6	0.45	0.52
	C6	150	300	2	0.85	0	27.6	0.30	0.60
PEN-FRP	C7	150	300	2	3.1	0	27.6	1.20	0.23
	C8	150	300	2	2.7	0	27.6	1.05	0.26
	C9	150	300	2	2.32	0	27.6	0.90	0.30
	C10	150	300	2	1.92	0	27.6	0.75	0.34
	C11	150	300	2	1.54	0	27.6	0.60	0.40
	C12	150	300	2	1.15	0	27.6	0.45	0.47
	C13	150	300	2	0.78	0	27.6	0.30	0.55
GLASS-FRP	C14	150	300	2	0	4.33	27.6	1.20	−0.17
	C15	150	300	2	0	3.8	27.6	1.05	−0.14
	C16	150	300	2	0	3.25	27.6	0.90	−0.11
	C17	150	300	2	0	2.7	27.6	0.75	−0.08
	C18	150	300	2	0	2.15	27.6	0.60	−0.03
	C19	150	300	2	0	1.62	27.6	0.45	0.02
	C20	150	300	2	0	1.07	27.6	0.30	0.10
CARBON-FRP	C21	150	300	2	0	2.6	27.6	1.20	−0.32
	C22	150	300	2	0	2.27	27.6	1.05	−0.30
	C23	150	300	2	0	1.94	27.6	0.90	−0.27
	C24	150	300	2	0	1.62	27.6	0.75	−0.23
	C25	150	300	2	0	1.3	27.6	0.60	−0.19
	C26	150	300	2	0	0.98	27.6	0.45	−0.13
	C27	150	300	2	0	0.65	27.6	0.30	−0.05
PET/Glass (inside/outside)	C28	150	300	2	2.55	1.07	27.6	1.20	0.47
	C29	150	300	2	1.7	2.15	27.6	1.20	0.43
	C30	150	300	2	0.85	3.25	27.6	1.20	0.48
Glass/PET (inside/outside)	C31	150	300	2	2.55	1.07	27.6	1.20	0.47
	C32	150	300	2	1.7	2.15	27.6	1.20	0.43
	C33	150	300	2	0.85	3.25	27.6	1.20	0.48
PET/Carbon (inside/outside)	C34	150	300	2	2.55	0.65	27.6	1.20	0.31
	C35	150	300	2	1.7	1.3	27.6	1.20	0.27
	C36	150	300	2	0.85	1.95	27.6	1.20	0.33
Carbon/PET (inside/outside)	C37	150	300	2	2.55	0.65	27.6	1.20	0.31
	C38	150	300	2	1.7	1.3	27.6	1.20	0.27
	C39	150	300	2	0.85	1.95	27.6	1.20	0.33
Concrete Strength ($f_c^{\prime }$)	C40	150	300	2	5.1	0	41.4	1.20	0.29
	C41	150	300	2	6.8	0	55.2	1.20	0.29
	C42	150	300	2	8.5	0	69	1.20	0.29
	C43	150	300	2	10.2	0	82.8	1.20	0.29
Column size	C44	200	400	2	4.55	0	27.6	1.20	0.29
	C45	300	600	2	6.8	0	27.6	1.20	0.29
	C46	1500	3000	2	34	0	27.6	1.20	0.29
Column aspect ratio	C47	300	1500	5	6.8	0	27.6	1.20	0.29
	C48	300	3000	10	6.8	0	27.6	1.20	0.29

3.1. LRS-FRP versus Traditional FRP

The CFFTs with LRS-FRP and with traditional FRP were investigated with different confinement ratios ranging from 0.3 to 1.2. Figure 4 illustrates the typical axial strain-normalized strength behavior of the CFFTs with LRS-FRP and with traditional FRP. The normalized strength was calculated as the axial stress divided by the $f_c^{\prime }$. All of the columns failed by FRP rupture. However, the CFFTs with traditional FRP behaved, as expected, with bilinear strain-stress relationships. The CFFTs with LRS-FRP behaved with trilinear behavior. This behavior of CFFTs with LRS-FRP was because of the effect of the bilinear behavior on the LRS-FRP instead of the linear behavior in the traditional FRP. All of the columns had the same initial stiffness. The reason was that the effect of the FRP confinement did not appear until the axial stress reached to almost the $f_c^{\prime }$ when the concrete volume change started to become positive (expansion; reference). The CFFTs with traditional FRP continued with the secant modulus until failure occurred. The CFFTs with LRS-FRP showed a stiffness degradation after axial strain of approximately 0.016 and 0.013 for PEN-FRP and PET-FRP, respectively. The CFFTs with LRS-FRP showed higher ultimate strain and lower secant stiffness than those with traditional FRP. As expected, the CFFTs with carbon FRP tubes showed higher secant stiffness and lower ultimate strain. The CFFTs with PET-FRP showed higher ultimate strain and lower secant stiffness. The CFFTs with LRS-FRP showed a higher strength than those with traditional FRP. The reason was the high hoop rupture strain of the LRS-FRP reached 8.7 times that of the carbon FRP and 2.9 times that of the glass FRP. The axial strength of the CFFTs with PEN-FRP and PET-FRP was almost the same. However, the axial strength of the CFFT with PET-FRP was approximately 1.25 times that of the CFFT with PEN-FRP.

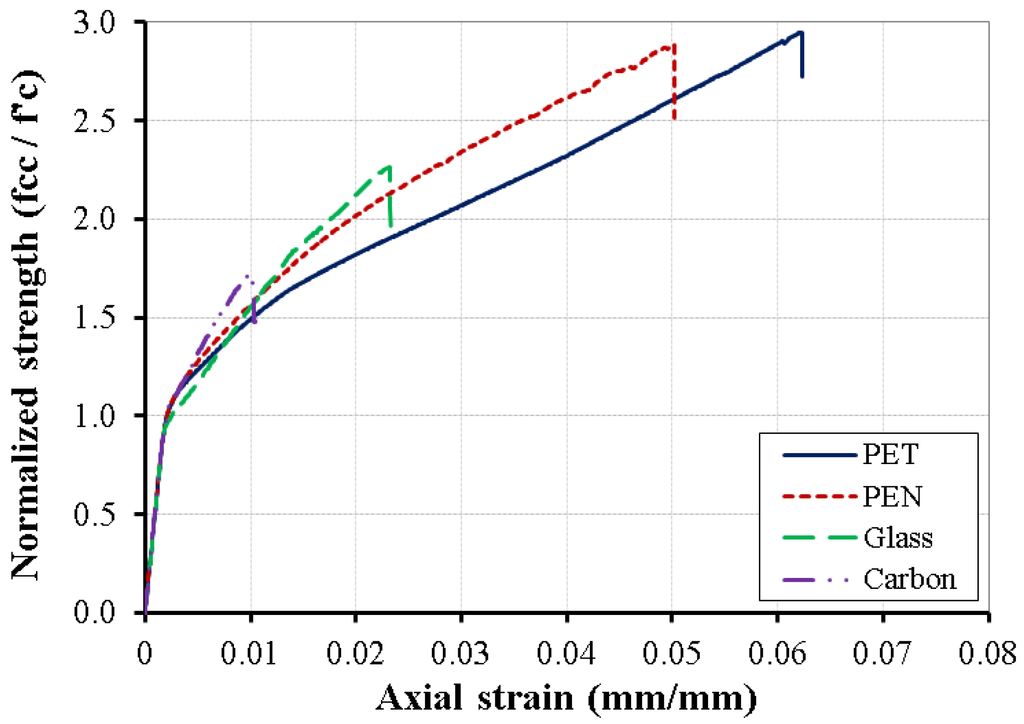
Figure 4. Axial strain-normalized strength ($f_{cc}/f_c^{\prime })$ relationship for PET, PEN, Glass, and Carbon FRP with same confinement ratio of 0.9.

Figure 4. Axial strain-normalized strength ($f_{cc}/f_c^{\prime })$ relationship for PET, PEN, Glass, and Carbon FRP with same confinement ratio of 0.9.

Figure 5 illustrates the relation between the confinement ratio and the normalized strength and between the confinement ratio and the ultimate axial strain for all of the FRP composites. This figure illustrates the efficiency of the different types of FRP in normalized strength and ultimate axial strain at the same confinement ratio. It is very clear in the figure that the CFFTs with LRS-FRP were more efficient than those with traditional FRP. This clearly indicated the great effect high rupture strain had on the confinement.

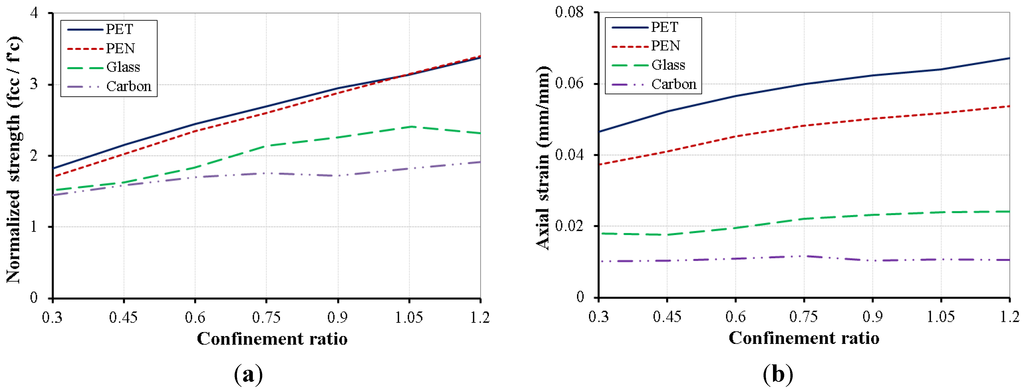
Figure 5. Efficiency of the traditional versus LRS-FRP composites in: (a) normalized axial strength; (b) axial strain.

Figure 5. Efficiency of the traditional versus LRS-FRP composites in: (a) normalized axial strength; (b) axial strain.

Figure 6 illustrates the axial strain-normalized strength for the CFFTs with traditional FRP, LRS-FRP, and hybrid FRP with the same confinement ratio of 1.2. Fiber stacking sequences were investigated by placing PET-FRP in the inner surface of the FRP tube and placing glass or carbon FRPs in the outer surface and vice versa. Figure 6a illustrates the PET, glass, and hybrid PET/glass where the PET was in the inner surface. In general, placing the LRS-FRP in the inner surface and the traditional FRP in the outer surface revealed a better performance than placing the traditional FRP in the inner surface. The reason for this behavior was that the rupture strain of the traditional FRP is much lower than that of the LRS-FRP. Therefore, the traditional FRP ruptured earlier than the LRS-FRP. Hence, when the traditional FRP was placed in the inner surface, the LRS-FRP was controlled by the traditional FRP rupture strain, and it ruptured directly after the rupture of the traditional FRP. However, when the traditional FRP was placed in the outer surface, the LRS-FRP was controlled by it, and it continued until ruptured with high hoop strains. Therefore, the hybrid FRP of PET/traditional FRP reached higher hoop strains than the traditional FRP. However, the hybrid FRP ruptured at a lower strain than that of the LRS-FRP alone because of the synergistic effect from hybridization.

Figure 6. Axial strain-normalized strength relationship of the traditional, LRS, and hybrid FRP: (a) PET/Glass-FRP; (b) Glass/PET; (c) PET/Carbon-FRP; and (d) Carbon/PET-FRP. Note: PET/Glass-FRP is the stacking sequence of inside/outside FRP and vice versa.

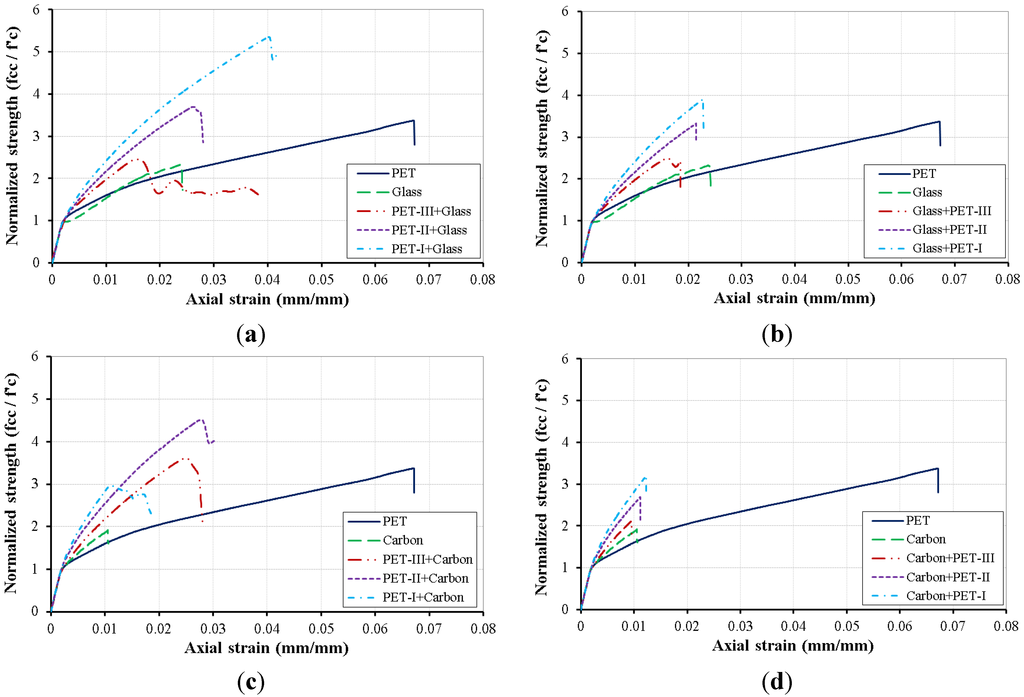
Figure 6. Axial strain-normalized strength relationship of the traditional, LRS, and hybrid FRP: (a) PET/Glass-FRP; (b) Glass/PET; (c) PET/Carbon-FRP; and (d) Carbon/PET-FRP. Note: PET/Glass-FRP is the stacking sequence of inside/outside FRP and vice versa.

In general, the hybrid of PET/glass performed better than PET/carbon. The reason for that was the large difference in rupture strains between the PET and carbon. In general, the axial strain-normalized strength relation of the CFFTs with hybrid FRP was nonlinear instead of bilinear in the case of LRS-FRP alone. The relation was linear in the case of traditional FRP alone. The strength and ultimate axial strain of the CFFTs with hybrid FRP increased when the traditional FRP was increased. This indicated that using few layers of LRS-FRP with the traditional FRP would improve the CFFT’s performance a lot. However, the difference in the confinement ratio contribution of the LRS-FRP has to be considerable in order to avoid sudden failure as in the case of (PET-I + Carbon) in Figure 5c. When the carbon FRP reached its ultimate strain (1% only), it failed and one layer of PET-FRP was not enough to continue to confine the concrete core, which led to rupture of the PET layer as well.

3.2. Unconfined Concrete Compressive Strength ($f_c^{\prime }$)

Five columns were studied with different concrete unconfined compressive strengths ($f_c^{\prime })$ ranging from 27.6 MPa to 82.8 MPa. Figure 7 illustrates the axial strain-normalized strength relation of the CFFTs with different $f_c^{\prime }$. In general, changing the $f_c^{\prime }$ did not affect the normalized strength or the ultimate axial strain because the columns had the same FRP confinement ratios. However, when the concrete core was high-strength ($f_c^{\prime }$ ≥ 55.2 MPa), the strength and ultimate axial strain were inversely proportional with the $f_c^{\prime }$. The lateral concrete expansion is dependent on the concrete mechanical properties. Therefore, the lateral expansion of high-strength concrete is significantly higher than that of the normal strength concrete, which reduces the effect of FRP confinement. The ultimate axial strain and the normalized strength decreased by 14.6% and 9.0%, respectively when the $f_c^{\prime }$ of the high-strength concrete increased by 25% (from 55.2 MPa to 69.0 MPa). The ultimate axial strain and the normalized strength decreased by 21.1% and 24.9%, respectively when the $f_c^{\prime }$ of the high-strength concrete increased by 50% (from 55.2 MPa to 82.8 MPa).

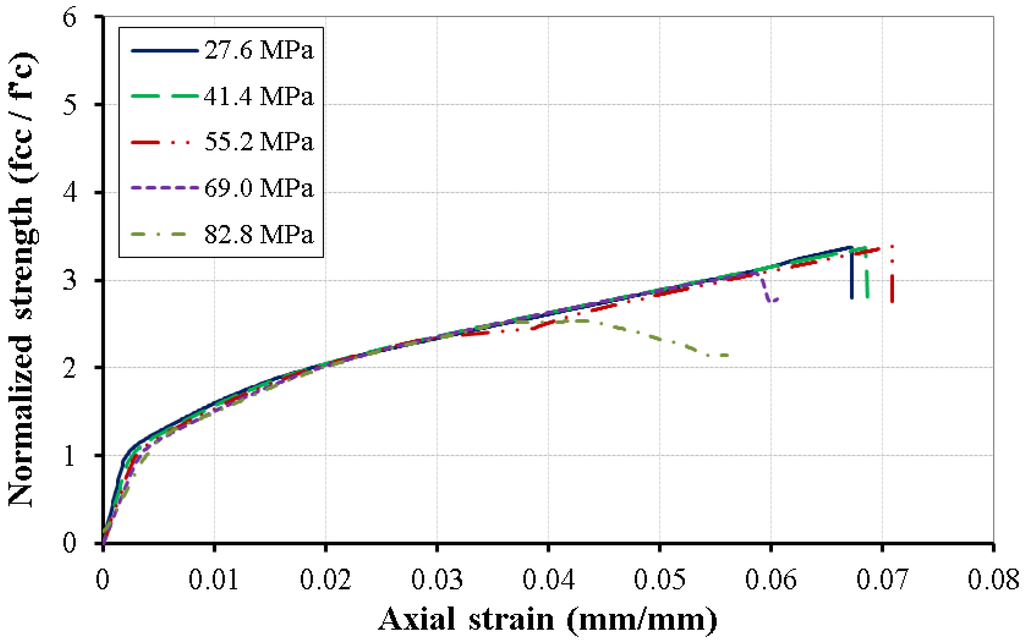
Figure 7. Axial strain-normalized strength relationship of CFFT with LRS-FRP with different concrete compressive strength ($f_c^{\prime }$).

Figure 7. Axial strain-normalized strength relationship of CFFT with LRS-FRP with different concrete compressive strength ($f_c^{\prime }$).

3.3. Column Size

Four columns with sizes ranging from 150 mm × 300 mm to 1500 mm × 3000 mm were studied. Figure 8 illustrates the axial strain-normalized strength relation of the CFFTs with different column sizes. In general, the strength was reduced when the column size was increased as the FRP confinement could not affect the whole cross-section. Figure 9 shows the axial stress distribution of all of the columns in the mid and top cross-sections. It is very clear that the FRP confinement affected a zone along the outer perimeter in the cross-section, and this zone decreased when the column diameter increased. However, the behavior of the columns with dimensions of 150 mm × 300 mm and 200 mm × 400 mm was almost the same in axial strain-normalized strength as the behavior in cross-section. This behavior was because both dimensions were considerably low for a confinement ratio of 1.2.

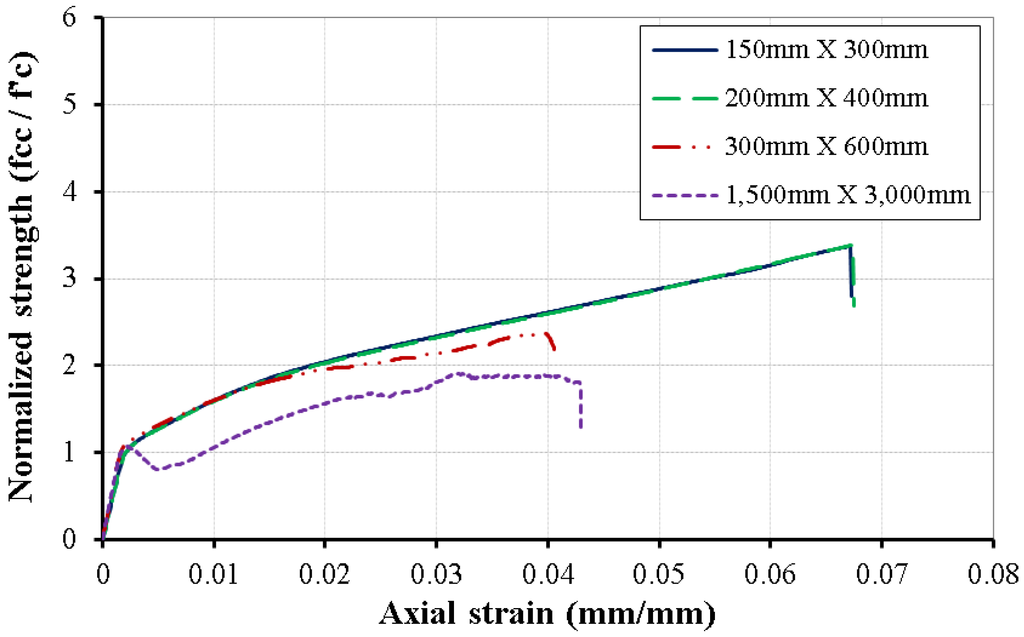
Figure 8. Axial strain-normalized strength relationship of CFFT with LRS-FRP with different column sizes.

Figure 8. Axial strain-normalized strength relationship of CFFT with LRS-FRP with different column sizes.

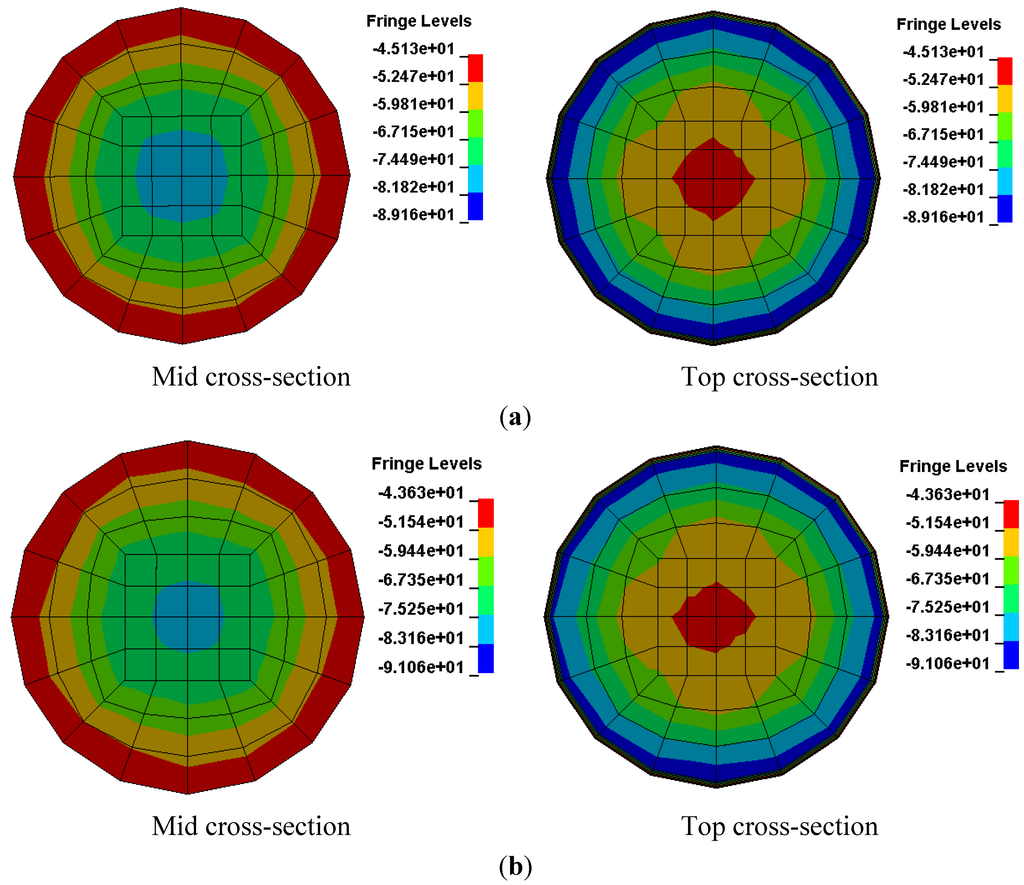
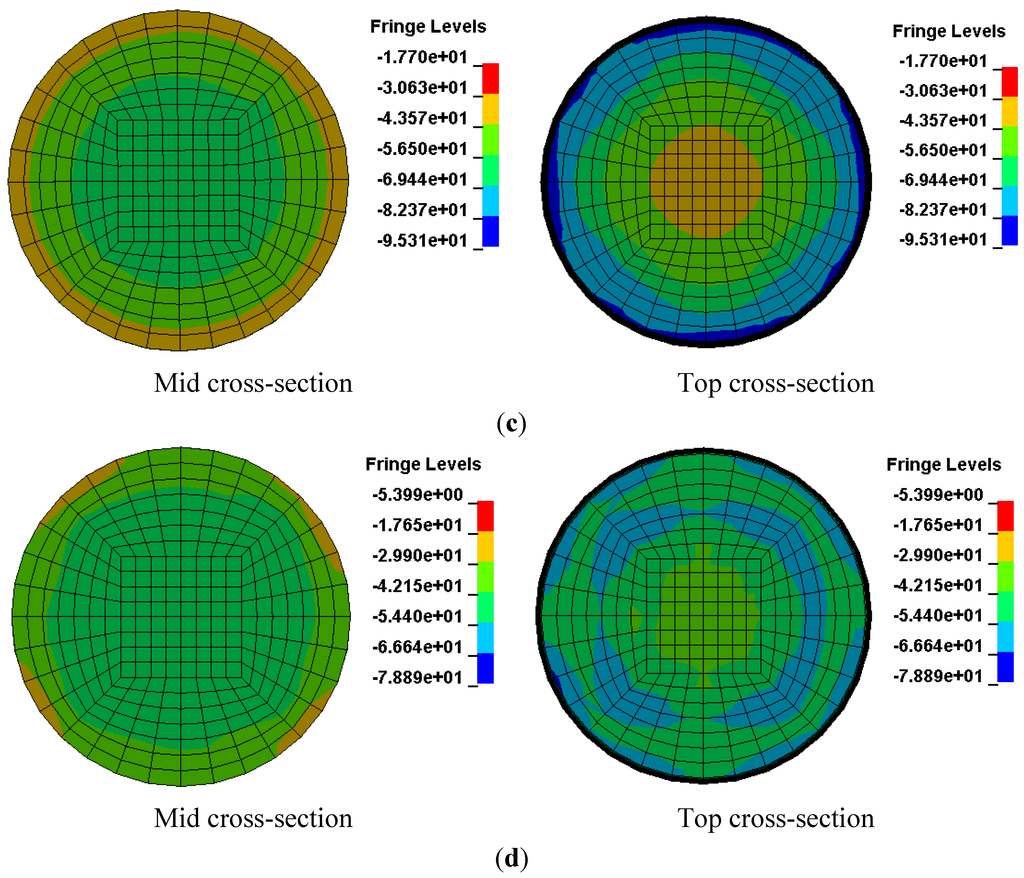
Figure 9. Axial stress in cross-section of the columns of sizes: (a) 150 mm × 300 mm; (b) 200 mm × 100 mm; (c) 300 mm × 600 mm; and (d) 1500 mm × 3000 mm. Note: Fringe levels shows the axial stresses legend in MPa.

Figure 9. Axial stress in cross-section of the columns of sizes: (a) 150 mm × 300 mm; (b) 200 mm × 100 mm; (c) 300 mm × 600 mm; and (d) 1500 mm × 3000 mm. Note: Fringe levels shows the axial stresses legend in MPa.

3.4. Column Aspect Ratio

Three columns with different column aspect (height-to-diameter) ratios ranging from 2 to 10 were studied. Figure 10 illustrates the axial strain-normalized strength relation of the CFFTs with different aspect ratios. The ultimate axial strain and axial strength decreased when the column’s aspect ratio increased. The column with an aspect ratio of 2 failed by FRP rupture. However, the columns with aspect ratios of 5 and 10 failed by compression failure. Figure 11 illustrates the column’s deformation for different aspect ratios. Figure 11a illustrates the global buckling that occurred in the column with an aspect ratio of 10, leading to compression failure. Figure 11b illustrates the deformation of the column, with an aspect ratio of 5, that bulged in the top and bottom thirds leading to compression failure. Figure 11c,d illustrate the common failure of the confined short column of FRP rupture at the middle part. The ultimate axial strain decreased by 26% and the axial strength of the CFFT with LRS-FRP decreased by 48% when the aspect ratio increased from 2 to 5. The ultimate axial strain decreased by 63% and the axial strength of the CFFT with LRS-FRP decreased by 58% when the aspect ratio increased from 2 to 10.

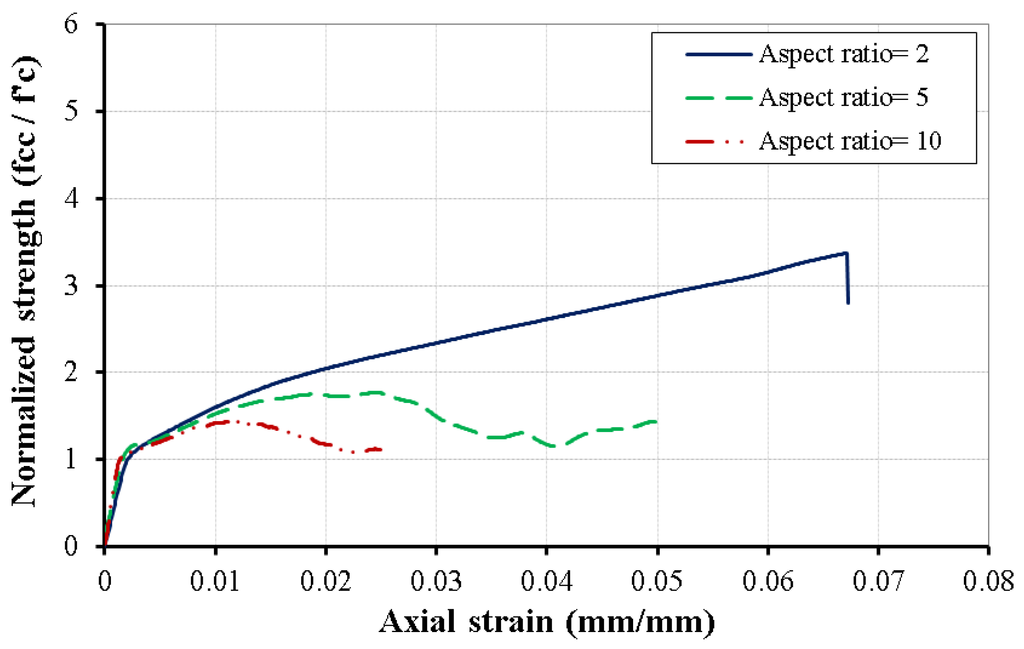
Figure 10. Axial strain-normalized strength relationship of CFFT with LRS-FRP with different column aspect ratios.

Figure 10. Axial strain-normalized strength relationship of CFFT with LRS-FRP with different column aspect ratios.

Figure 11. Column deformation with different aspect ratios: (a) aspect ratio of 10; (b) aspect ratio of 5; (c) aspect ratio of 2; and (d) FRP rupture of column with aspect ratio of 2.

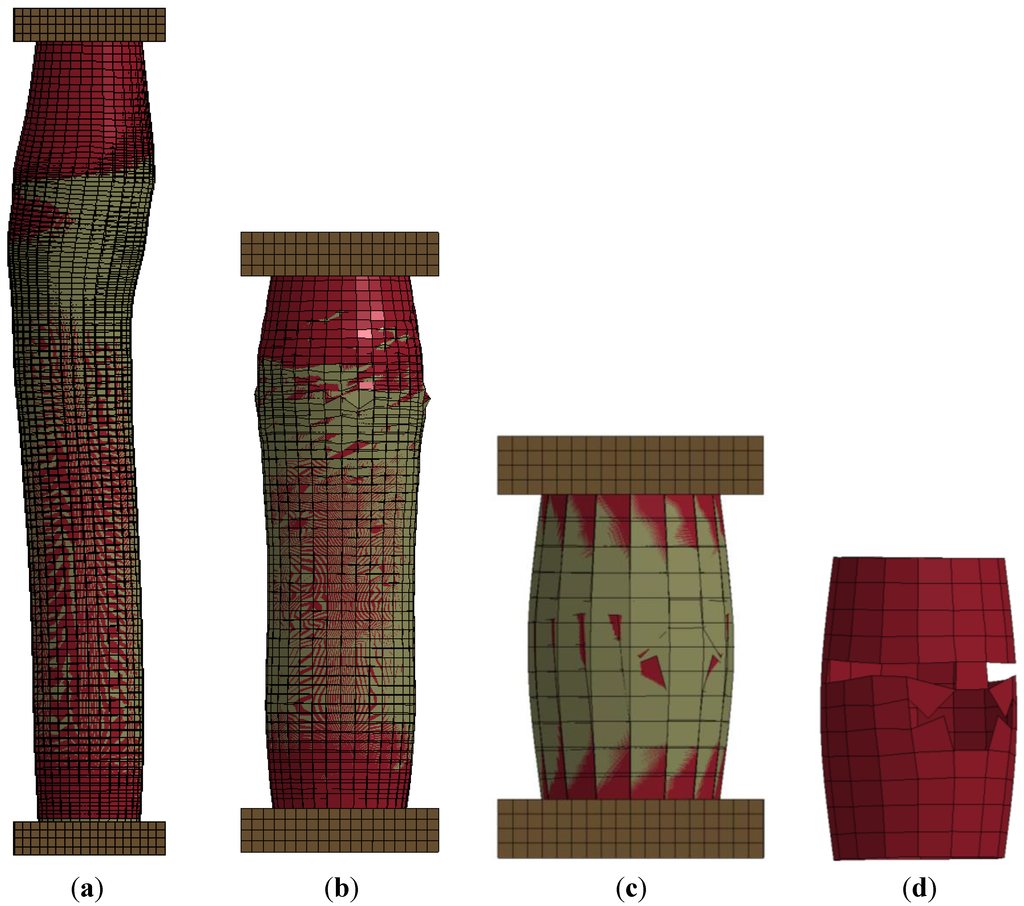
Figure 11. Column deformation with different aspect ratios: (a) aspect ratio of 10; (b) aspect ratio of 5; (c) aspect ratio of 2; and (d) FRP rupture of column with aspect ratio of 2.

4. Findings and Conclusions

The behavior of the concrete-filled fiber tubes (CFFT) with new high deformable fiber reinforced polymers under axial compressive loading was investigated. Unlike the traditional fiber reinforced polymers (FRP) like carbon, glass, aramid, etc., the new FRP composites have a large rupture strain and are made with cheap materials. The large rupture strain (LRS) FRP composites are made with polyethylene naphthalate (PEN) and polyethylene terephthalate (PET) fibers. The PEN and PET fibers can be used in green buildings. They are environmentally friendly as they are made from recycled materials (e.g., bottles). They have a high ultimate strain (>5.0%), however their elastic modulus is low. This study used finite element (FE) analysis using LS-DYNA software to conduct an extensive parametric study to investigate the behavior of the CFFTs with the LRS-FRP under axial compressive loading. Forty-nine columns were investigated to determine important factors may affect the behavior of the CFFTs under axial compressive loading. A high range of FRP confinement ratios was investigated. In addition, the effects of the unconfined concrete compressive strength ($f_c^{\prime }$), column size, and column aspect ratio on the behavior of the CFFT were studied. A comparison between the behavior of the CFFTs with LRS-FRP and the traditional FRP (carbon and glass) with a high range of confinement ratios was conducted as well. This paper introduced a new state-of-the-art hybrid FRP to be used for the CFFT columns by investigating different combinations of traditional FRP with LRS-FRP. Generally, the CFFTs with LRS-FRP showed a remarkable behavior under axial loading in strength and ultimate strain. The LRS-FRP composites were more efficient than the traditional FRP composites in strength and ultimate strain. The behavior of the hybrid FRP with a stacking sequence of LRS/glass (inner/outer of the tube) showed much better behavior in strength than the traditional FRP or the LRS-FRP. However, this hybrid FRP showed a higher ultimate axial strain than the traditional FRP. The LRS alone was better in the ultimate axial strain. A new equation to estimate the concrete dilation parameter and dilation angle of the CFFT columns with LRS-FRP tubes or hybrid FRP tubes was suggested.

In conclusion LRS-FRP is a promising family of new material; however, more research is still required to characterize their fire resistance and durability. Their behavior with different matrices and their bonding with concrete members should be investigated as well.