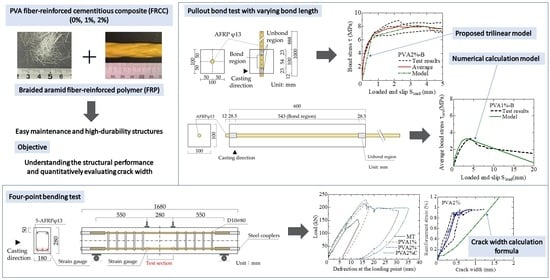
Bond and Cracking Characteristics of PVA-Fiber-Reinforced Cementitious Composite Reinforced with Braided AFRP Bars †
Abstract
1. Introduction
2. Pullout Bond Test
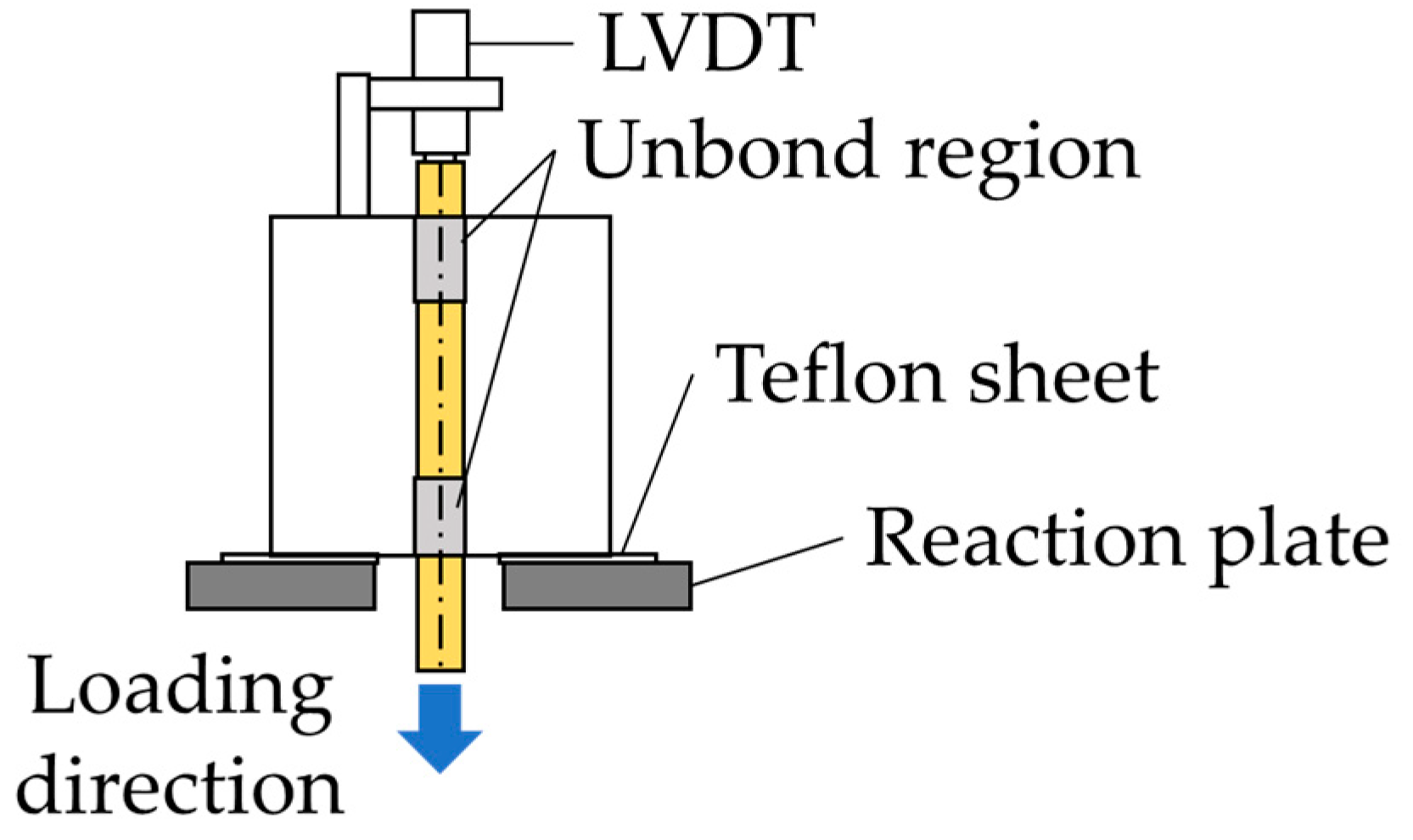
2.1. Outline of Pullout Bond Test [31]
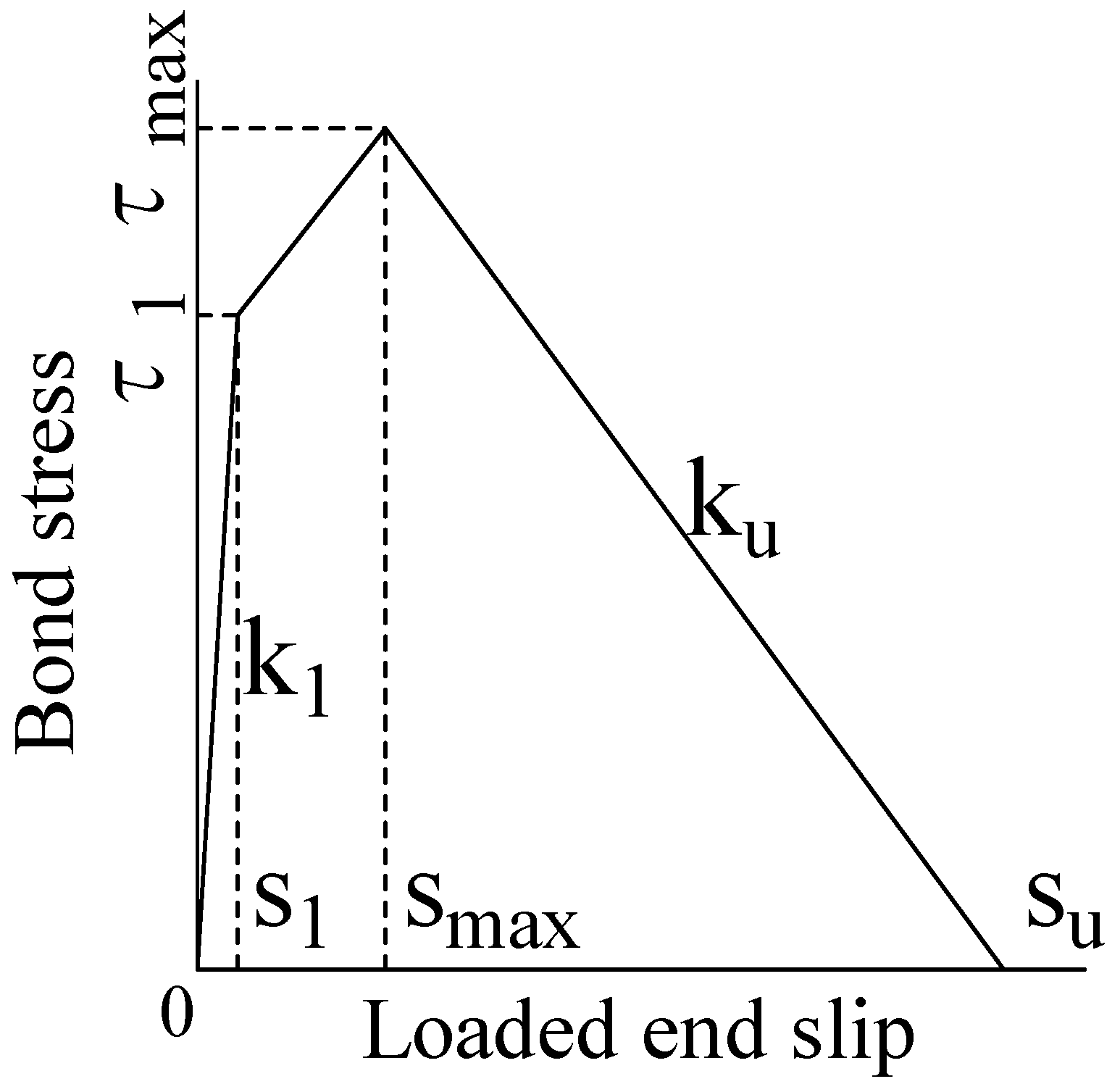
2.2. Modeling of Bond Constitutive Law
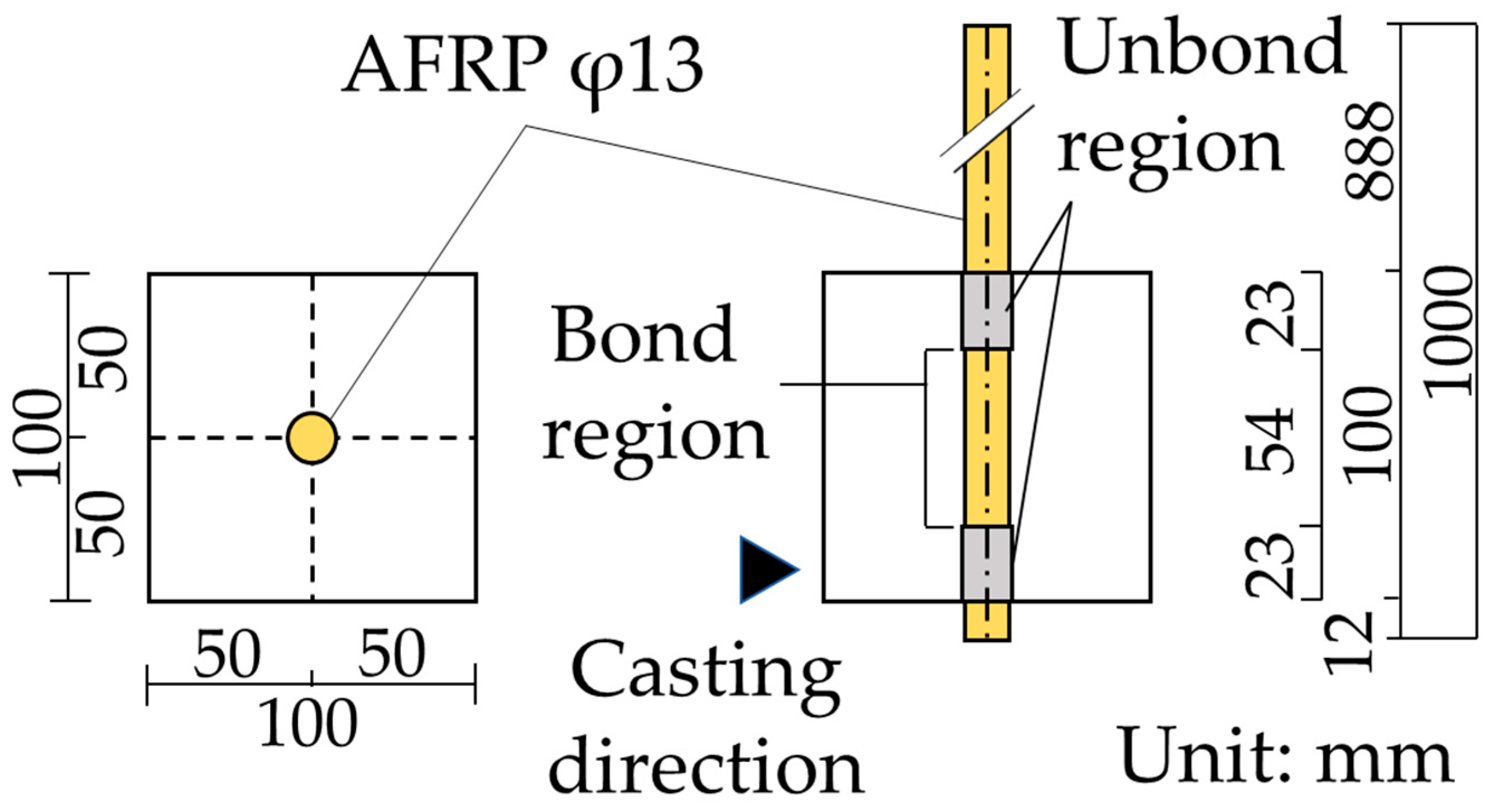
3. Pullout Bond Test with Long Bond Length
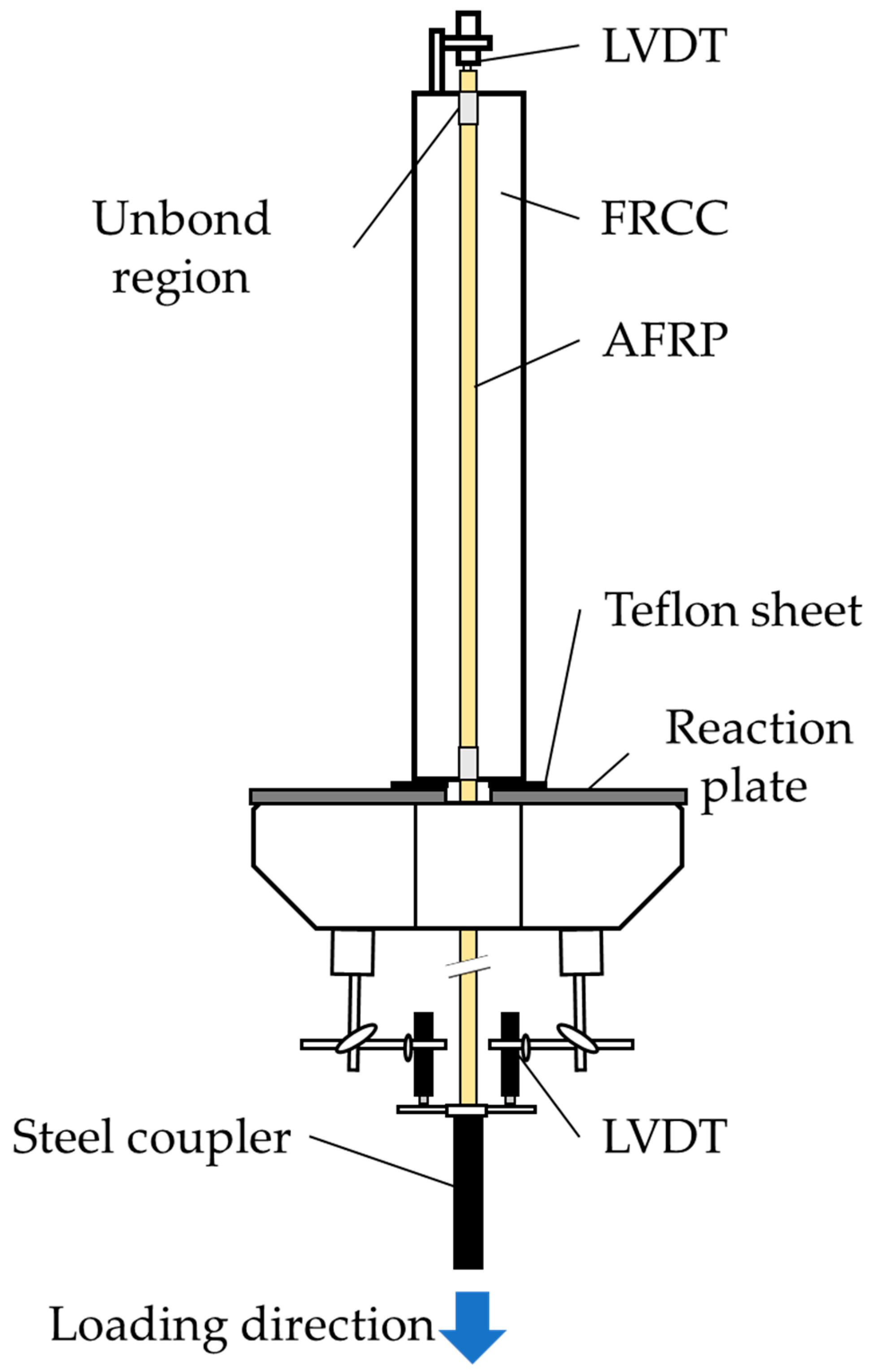
3.1. Outline of Pullout Bond Test
3.1.1. Specimens
3.1.2. Materials
3.1.3. Loading Method
3.2. Test Results
3.2.1. Specimens after Loading
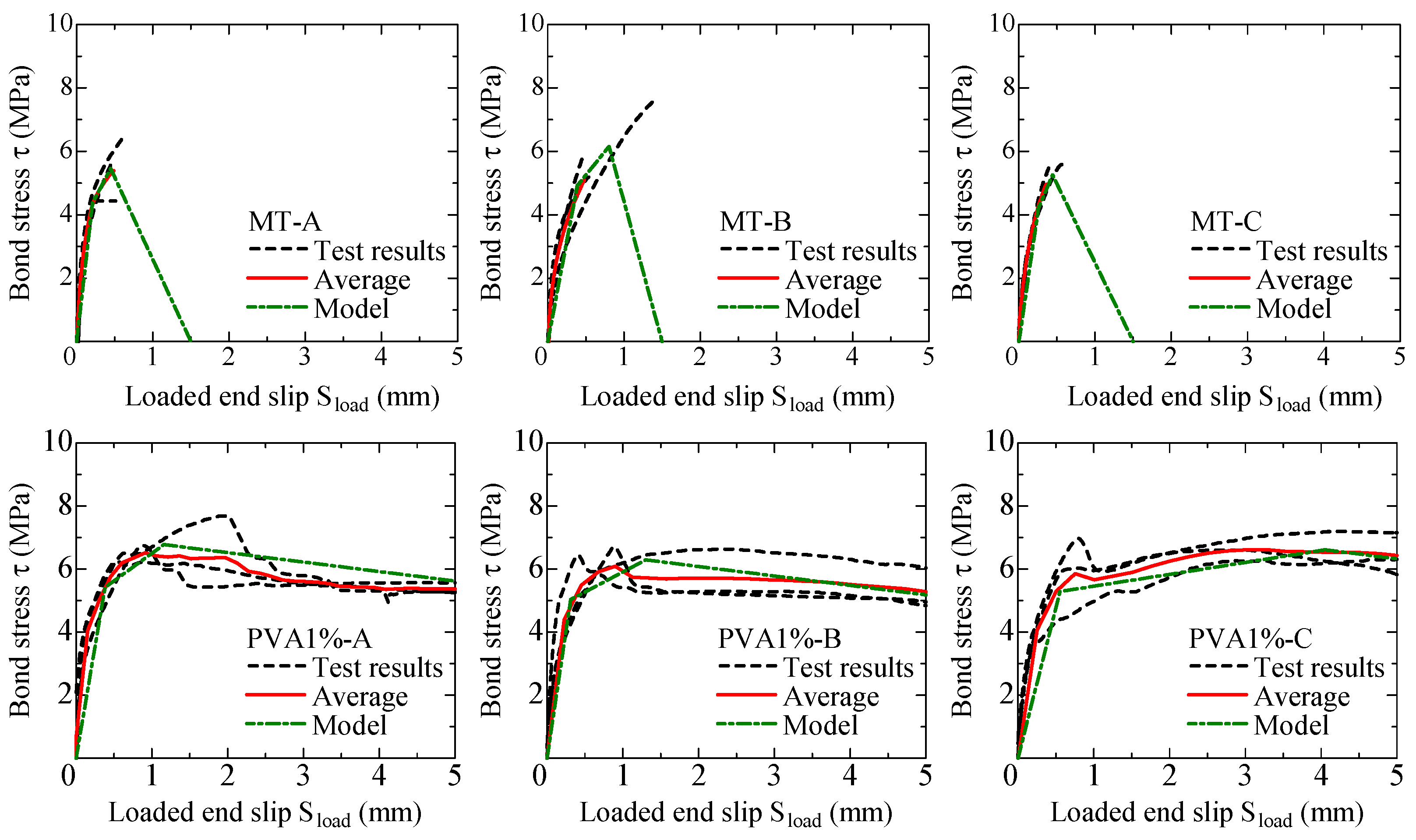
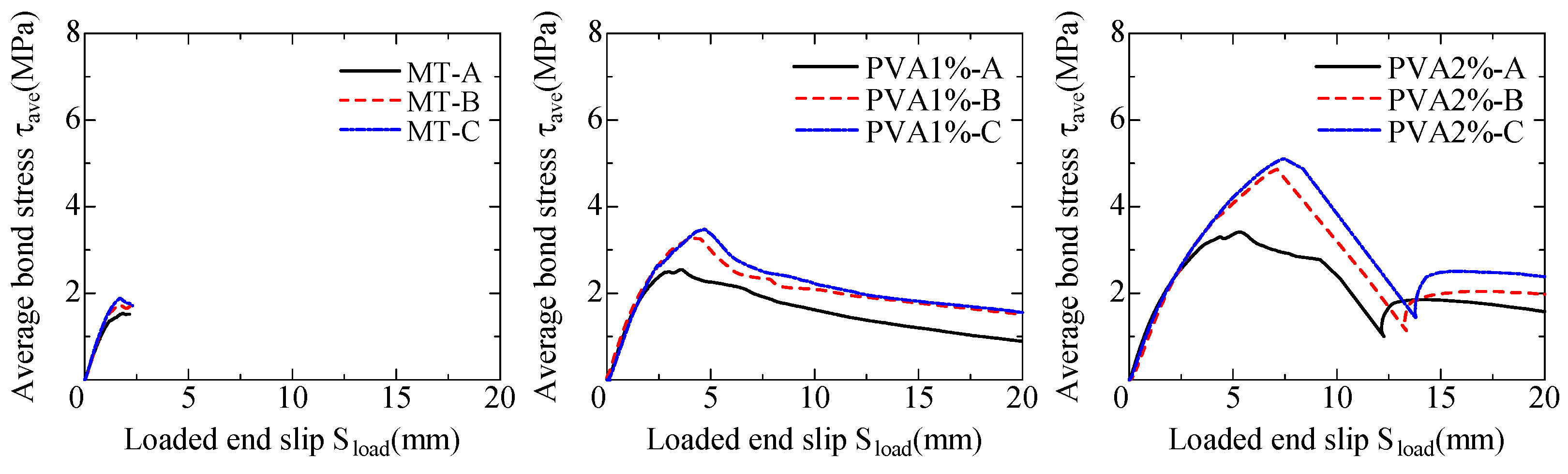
3.2.2. Average Bond Stress–Loaded-end Slip Relationship
3.3. Numerical Calculation of Bond Properties
3.3.1. Method of Numerical Calculation
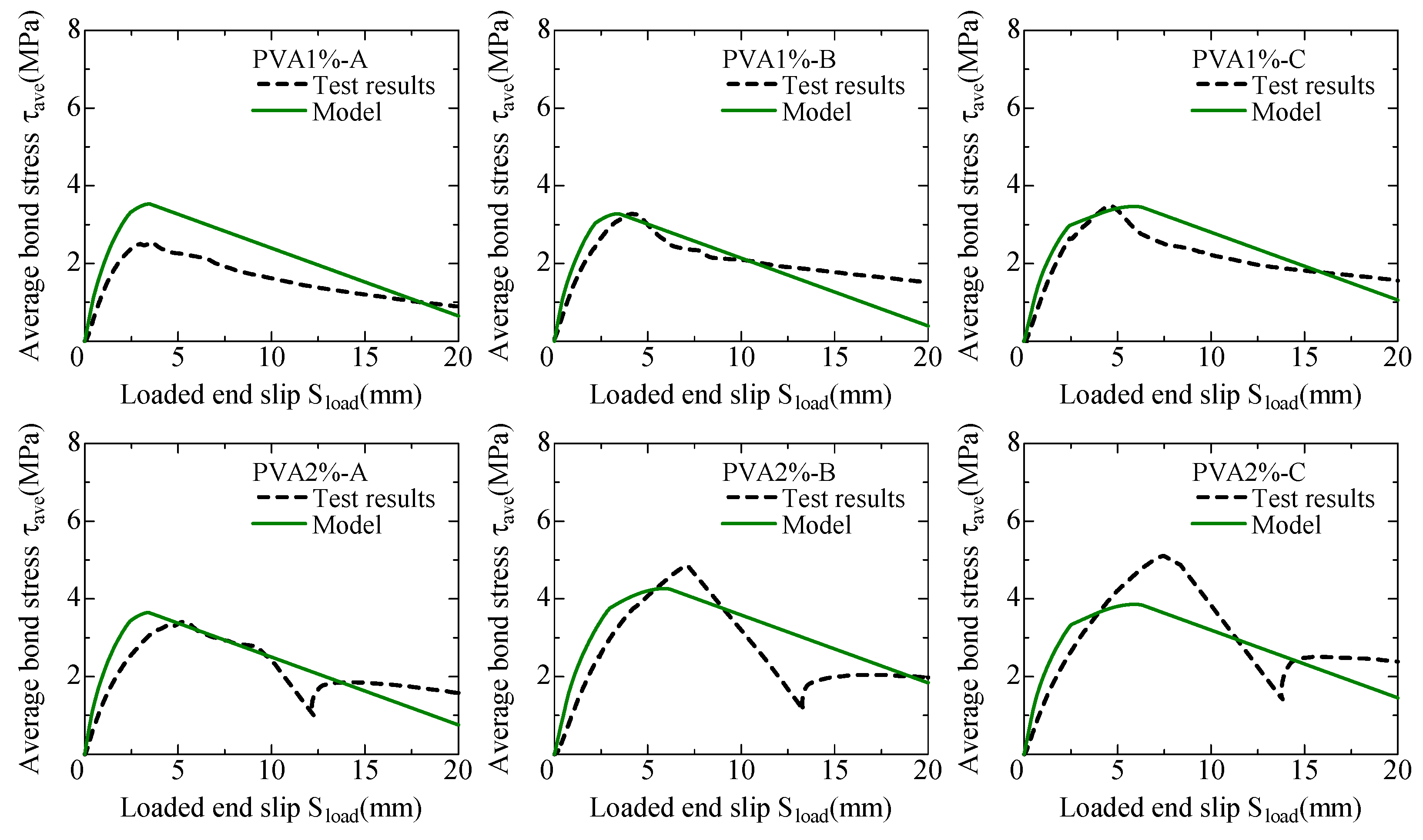
3.3.2. Comparison of Average Bond Stress–Loaded-end Slip Relationships
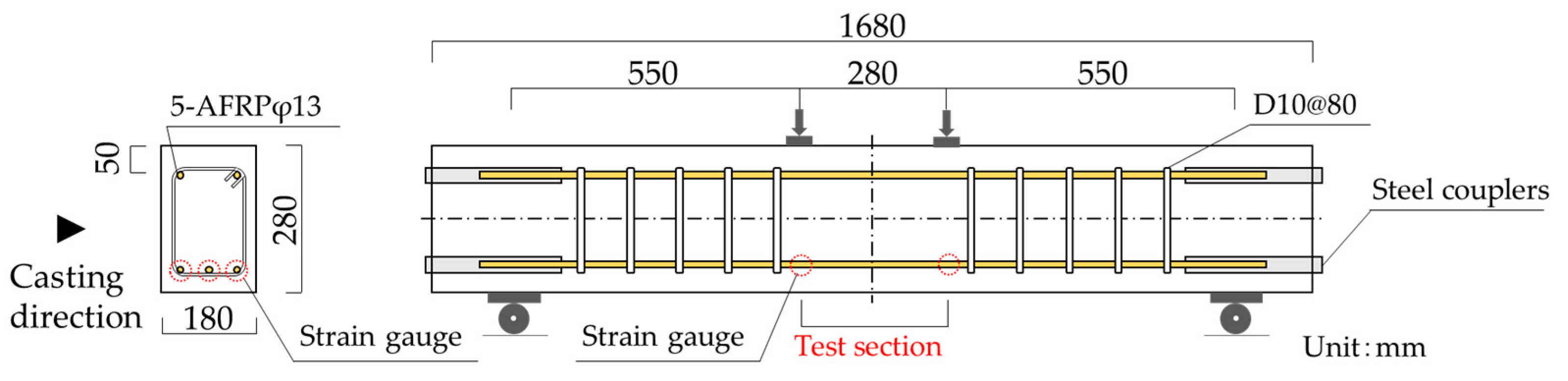
4. Bending Test of AFRP/PVA-FRCC Beams
4.1. Outline of Bending Test
4.1.1. Specimens
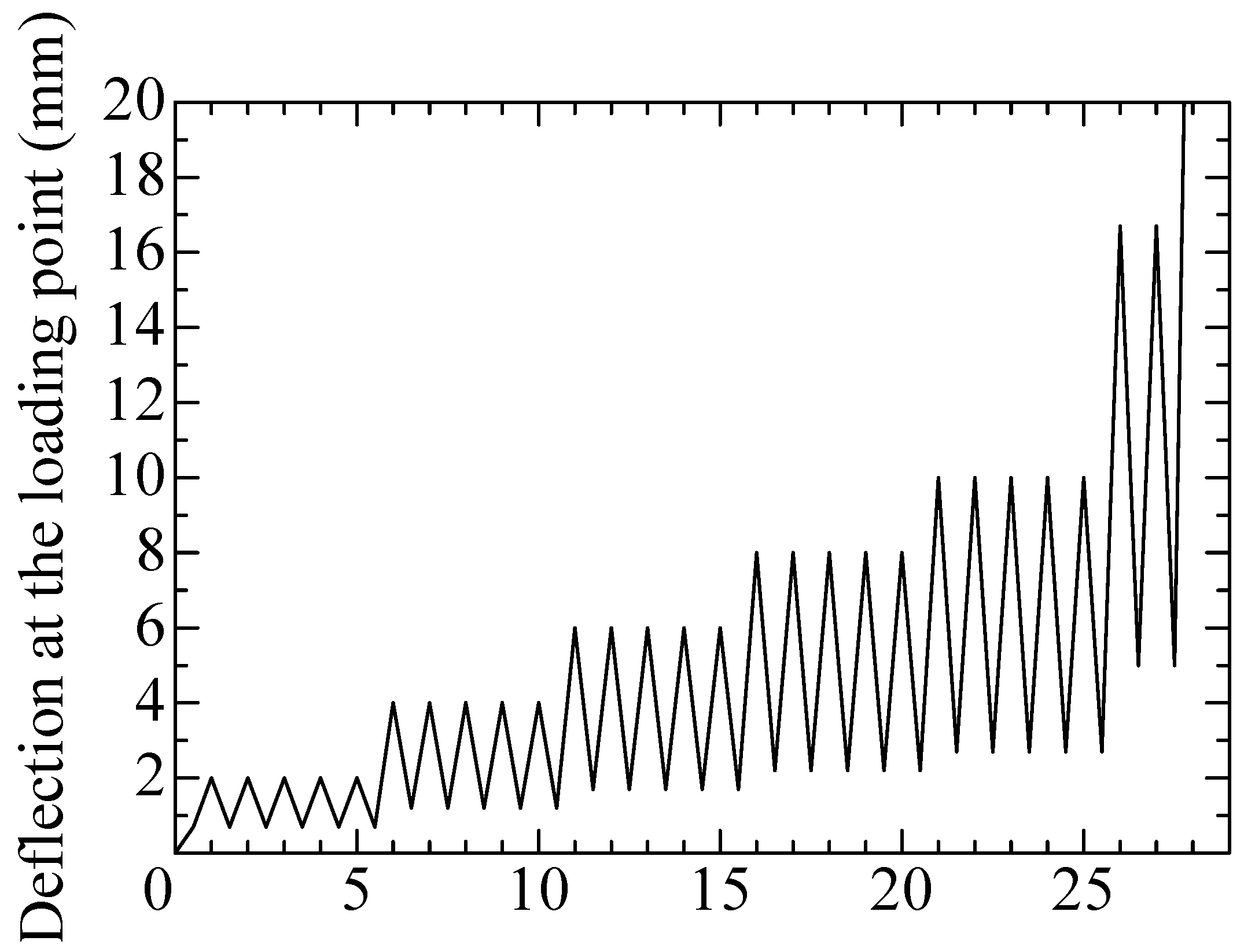
4.1.2. Loading Method
4.2. Test Results
4.2.1. Specimens after Loading
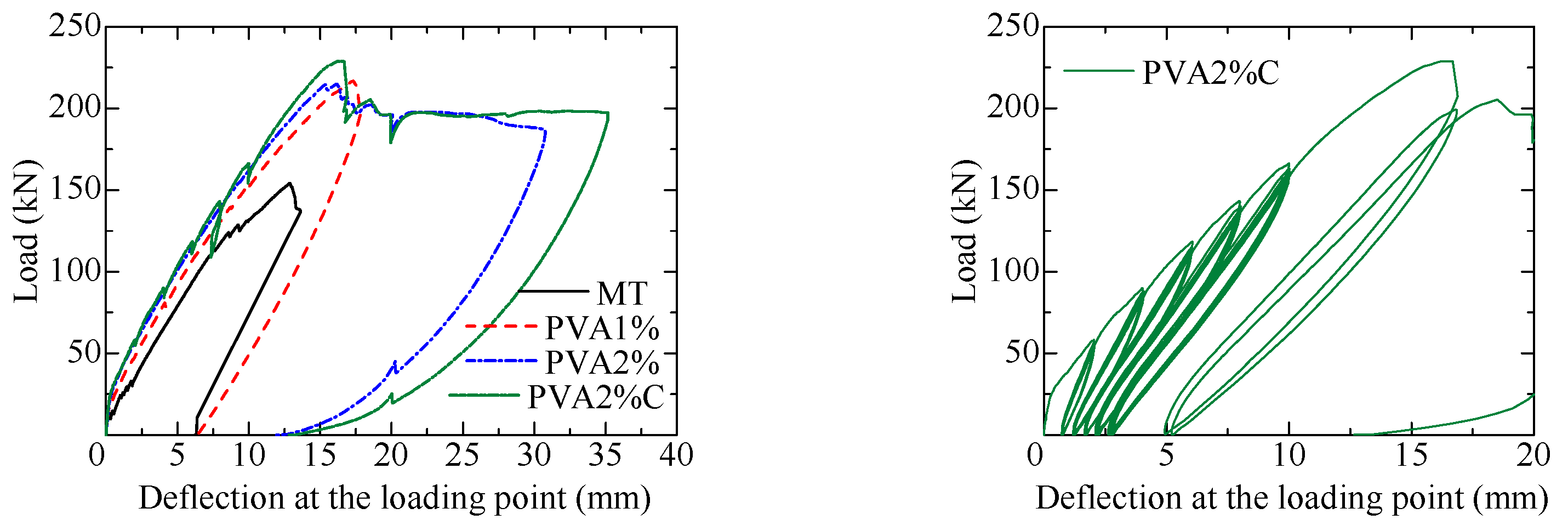
4.2.2. Load–Deflection Relationships
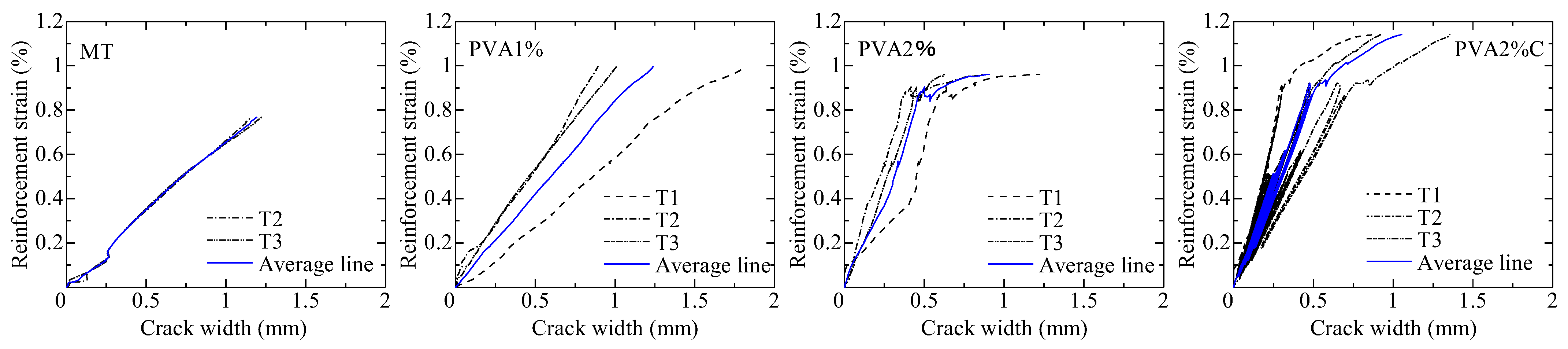
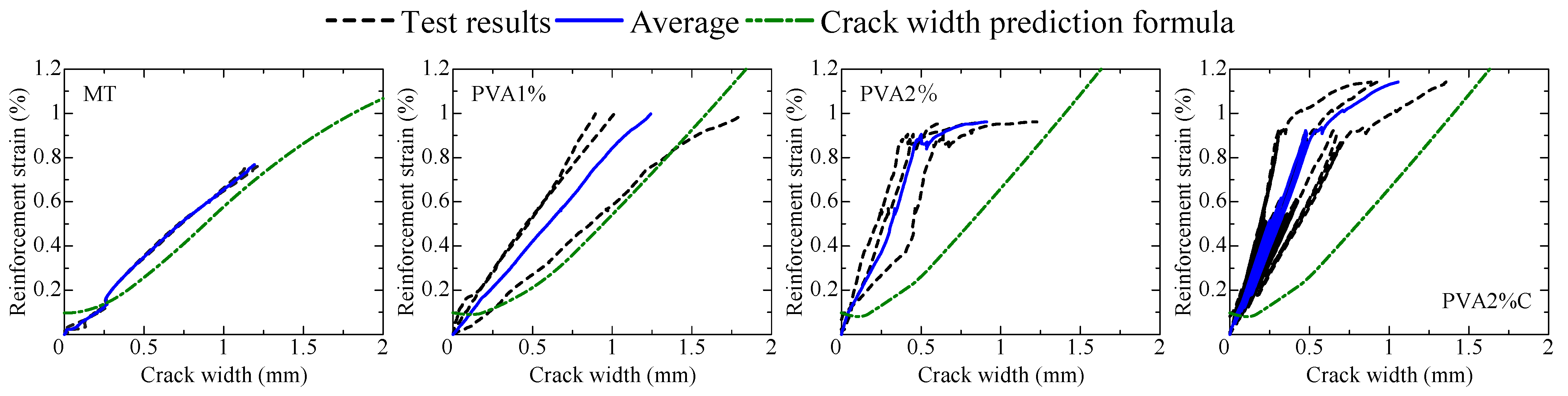
4.2.3. Cracking Characteristics
5. Conclusions
- In the pullout bond test, a trilinear model for the bond constitutive law (bond stress–loaded-end slip relationship) was proposed.
- According to the pullout bond test with specimens of long bond length, the bond strength increased with increases in both the fiber volume fraction and the cross-section of the specimens. These characteristics can be attributed to the fiber bridging effect, which results in control of crack width opening.
- Bond behavior with a long bond length was analyzed numerically using the proposed bond constitutive law. The calculated average bond stress–loaded-end slip relationships favorably fitted the test results.
- The bending test results for AFRP/PVA-FRCC beam specimens showed that the number of cracks increased with the increases in fiber volume fraction. The maximum loads recorded for each type of specimen were as follows: MT: 154 kN; PVA1%: 217 kN; PVA2%: 198 kN; and PVA2%C: 229 kN. In the case of specimens with a fiber volume fraction of 2%, the load reached its maximum value due to the compression fracture of the FRCC, and cyclic loading had no discernible effect.
- The adaptability of the crack width prediction formula, considering the bond constitutive law and the fiber bridging law with respect to PVA-FRCC, was discussed. The reinforcement strain–crack width relationship obtained from the bending test exhibited good compatibility with the crack width prediction formula.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- American Concrete Institute. Guide for the Design and Construction of Structural Concrete Reinforced with Fiber-Reinforced Polymer (FRP) Bars, ACI 440.1R-15; American Concrete Institute: Farmington Hills, MI, USA, 2015. [Google Scholar]
- Nanni, A. Flexural Behavior and Design of RC Members Using FRP Reinforcement. J. Struct. Eng. 1993, 119, 3344–3359. [Google Scholar] [CrossRef]
- Pecce, M.; Manfredi, G.; Cosenza, E. Experimental Response and Code Modelsof GFRP RC Beams in Bending. J. Compos. Constr. 2000, 4, 182. [Google Scholar] [CrossRef]
- Gravina, R.J.; Smith, S.T. Flexural Behaviour of Indeterminate Concrete Beams Reinforced with FRP Bars. Eng. Struct. 2008, 30, 2370–2380. [Google Scholar] [CrossRef]
- Burgoyne, C.J. Should FRP Be Bonded to Concrete? Special Publication Series; American Concrete Institute: Farmington Hills, MI, USA, 1993; SP-138; pp. 367–368. [Google Scholar]
- Kanakubo, T.; Yonemaru, K.; Fukuyama, H.; Fujisawa, M.; Sonobe, Y. Bond Performance of Concrete Members Reinforced with FRP Bars; Special Publication Series; American Concrete Institute: Farmington Hills, MI, USA, 1993; SP-138; pp. 767–788. [Google Scholar]
- Toutanji, H.; Deng, Y. Deflection and Crack-Width Prediction of Concrete Beams Reinforced with Glass FRP Rods. Constr. Build. Mater. 2003, 17, 69–74. [Google Scholar] [CrossRef]
- El-Nemr, A.; Ahmed, E.A.; El-Safty, A.; Benmokrane, B. Evaluation of the Flexural Strength and Serviceability of Concrete Beams Reinforced with Different Types of GFRP Bars. Eng. Struct. 2018, 173, 606–619. [Google Scholar] [CrossRef]
- Aydın, F.; Arslan, Ş. Investigation of The Durability Performance of FRP Bars in Different Environmental Conditions. Adv. Concr. Constr. 2021, 12, 295–302. [Google Scholar]
- Solyom, S.; Balázs, G.L. Analytical and Statistical Study of the Bond of FRP Bars with Different Surface Characteristics. Compos. Struct. 2021, 270, 113953. [Google Scholar] [CrossRef]
- Matsumoto, T.; Mihashi, H. JCI-DFRCC Summary Report on DFRCC Terminologies and Application Concepts. In Proceedings of the JCI International Workshop on Ductile Fiber Reinforced Cementitious Composites (DFRCC), Takayama, Japan, 21–22 October 2002; pp. 59–66. [Google Scholar]
- Rokugo, K.; Kanda, T. (Eds.) Strain Hardening Cement Composites: Structural Design and Performance RILEM State-of-the-Art Reports 6; Springer: Berlin/Heidelberg, Germany, 2013; p. 90. [Google Scholar]
- Lövgren, I. Fibre-Reinforced Concrete for Industrial Construction—A Fracture Mechanics Approach to Material Testing and Structural Analysis; Chalmers University of Technology: Gothenburg, Sweden, 2005. [Google Scholar]
- Balaguru, P.N.; Shah, S.P. Basic Concepts and Mechanical Properties: Tension, Fiber-Reinforced Cement Composites; McGraw-Hill: New York, NY, USA, 1992; pp. 37–84. [Google Scholar]
- Amin, A.; Foster, S.J.; Muttoni, A. Derivation of the σ- w Relationship for SFRC from Prism Bending Tests. Struct. Concr. 2015, 16, 93–105. [Google Scholar] [CrossRef]
- Pereira, E.B.; Fischer, G.; Barros, J.A.O. Direct Assessment of Tensile Stress-Crack Opening Behavior of Strain Hardening Cementitious Composites (SHCC). Cem. Concr. Res. 2012, 42, 834–846. [Google Scholar] [CrossRef]
- Yu, J.; Leung, C.K.Y. Novel Experimental Method to Determine Crack-Bridging Constitutive Relationship of SHCC Using Digital Image Processing. In Strain-Hardening Cement-Based Composites SHCC-4; Springer: Dresden, Germany, 2018; Volume 15, pp. 55–62. [Google Scholar]
- Li, V.C.; Stang, H.; Krenchel, H. Micromechanics of Crack Bridging in Fibre-Reinforced Concrete. Mater. Struct. 1993, 26, 486–494. [Google Scholar] [CrossRef]
- Laranjeira de Oliveira, F. Design-Oriented Constitutive Model for Steel Fiber Reinforced Concrete. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2010. [Google Scholar]
- Yang, E.-H.; Wang, S.; Yang, Y.; Li, V.C. Fiber-Bridging Constitutive Law of Engineered Cementitious Composites. J. Adv. Concr. Technol. 2008, 6, 181–193. [Google Scholar] [CrossRef]
- Kanakubo, T.; Miyaguchi, M.; Asano, K. Influence of fiber orientation on bridging performance of polyvinyl alcohol fiber-reinforced cementitious composite. ACI Mater. J. 2016, 113, 131–141. [Google Scholar] [CrossRef]
- Yuriko, O.; Masaru, M.; Toshiyuki, K. Modeling of Bridging Law for PVA Fiber-Reinforced Cementitious Composite Considering Fiber Orientation. J. Civ. Eng. Archit. 2018, 12, 651–661. [Google Scholar] [CrossRef]
- Kanakubo, T.; Echizen, S.; Wang, J.; Mu, Y. Pullout behavior of bundled aramid fiber in fiber-reinforced cementitious composite. Materials 2020, 13, 1746. [Google Scholar] [CrossRef]
- Fischer, G.; Li, V.C. FRP reinforced ECC structural members under reversed cyclic loading conditions, Advances in Building Technology. In Proceedings of the International Conference on Advances in Building Technology, Hong Kong, China, 4–6 December 2002; Volume I; pp. 781–788. [Google Scholar]
- Tolou Kian, M.J.; Ghazizadeh, S.; Cruz Noguez, C.A. An Experimental Investigation of FRCC Shear Walls Reinforced with Steel and GFRP Bars. J. Compos. Sci. 2018, 2, 55. [Google Scholar] [CrossRef]
- Hu, B.; Zhou, Y.; Xing, F.; Sui, L.; Luo, M. Experimental and Theoretical Investigation on the Hybrid CFRP-ECC Flexural Strengthening of RC Beams with Corroded Longitudinal Reinforcement. Eng. Struct. 2019, 200, 109717. [Google Scholar] [CrossRef]
- Hou, W.; Li, Z.-Q.; Gao, W.-Y.; Zheng, P.-D.; Guo, Z.-X. Flexural Behavior of RC Beams Strengthened with BFRP Bars-Reinforced ECC Matrix. Compos. Struct. 2020, 241, 112092. [Google Scholar] [CrossRef]
- Ge, W.; Song, W.; Ashour, A.F.; Lu, W.; Cao, D. Flexural Performance of FRP/Steel Hybrid Reinforced Engineered Cementitious Composite Beams. J. Build. Eng. 2020, 31, 101329. [Google Scholar] [CrossRef]
- Kanakubo, T.; Yamato, N. Crack Width Prediction Method for Steel and FRP Reinforcement Based on Bond Theory. J. Adv. Concr. Technol. 2014, 12, 310–319. [Google Scholar] [CrossRef][Green Version]
- Sunaga, D.; Namiki, K.; Kanakubo, T. Crack Width Evaluation of Fiber-Reinforced Cementitious Composite Considering Interaction between Deformed Steel Rebar. Constr. Build. Mater. 2020, 261, 119968. [Google Scholar] [CrossRef]
- Takasago, S.; Kanakubo, T.; Kobayashi, H. Crack Width Evaluation of DFRCC Members Reinforced with Braided AFRP Bar. In Strain Hardening Cementitious Composites. SHCC 2022; RILEM Bookseries; Kunieda, M., Kanakubo, T., Kanda, T., Kobayashi, K., Eds.; Springer: Cham, Switzerland, 2023; Volume 39, pp. 156–166. [Google Scholar]
- JIS A 1108; Method of Test for Compressive Strength of Concrete. Japanese Industrial Standard, Japanese Standards Association: Tokyo, Japan, 2018.
- JIS A 1192; Test Method for Tensile Properties of Fiber Reinforced Polymer (FRP) Bars and Grids for Reinforcement of Concrete. Japanese Industrial Standard, Japanese Standards Association: Tokyo, Japan, 2021.
- JIS A 6201; Fly Ash for Use in Concrete. Japanese Industrial Standard, Japanese Standards Association: Tokyo, Japan, 2015.
- Yasojima, A.; Kanakubo, T. Bond Splitting Strength of RC Members Based on Local Bond Stress and Slip Behavior. In Proceedings of the 11th International Conference on Fracture, Turin, Italy, 20–25 March 2005; pp. 1566–1571. [Google Scholar]
- Kanakubo, T.; Hosoya, H. Bond-Splitting Strength of Reinforced Strain-Hardening Cement Composite Elements with Small Bar Spacing. Struct. J. 2015, 112, 189–198. [Google Scholar] [CrossRef]








| Type | Common Factor | Cross-Section | Fiber Volume Fraction | Number of Specimens |
|---|---|---|---|---|
| MT-A | Height: 100 mm Bond length: 54 mm (=4d) Reinforcement: Braided AFRP bar (Diameter 13.58 mm) Fiber type of FRCC: PVA | 100 mm × 100 mm (A series) | - | 3 |
| PVA1%-A | 1.0% | 3 | ||
| PVA2%-A | 2.0% | 3 | ||
| MT-B | 120 mm × 120 mm (B series) | - | 3 | |
| PVA1%-B | 1.0% | 3 | ||
| PVA2%-B | 2.0% | 3 | ||
| MT-C | 140 mm × 140 mm (C series) | - | 3 | |
| PVA1%-C | 1.0% | 3 | ||
| PVA2%-C | 2.0% | 3 |
| Reinforcement | Diameter (mm) | Tensile Strength (MPa) | Elastic Modulus (GPa) |
|---|---|---|---|
| Braided AFRP bar | 13.58 | 1261 | 66.0 |
| Fiber | Length (mm) | Diameter (mm) | Tensile Strength (MPa) | Elastic Modulus (GPa) |
|---|---|---|---|---|
| PVA | 12 | 0.10 | 1200 | 28 |
| Type | Unit Weight (kg/m3) | PVA Fiber (kg) | Compressive Strength (MPa) | Elastic Modulus (GPa) | |||
|---|---|---|---|---|---|---|---|
| W | C | S | F | ||||
| MT | 380 | 678 | 484 | 291 | 0 | 48.8 | 17.5 |
| PVA 1% | 13 | 46.2 | 17.0 | ||||
| PVA 2% | 26 | 47.1 | 16.4 | ||||
| Specimens | (MPa) | (mm) | (N/mm3) | (MPa) | (mm) | (N/mm3) | (mm) |
|---|---|---|---|---|---|---|---|
| MT-A | 4.37 | 0.21 | 20.9 | 5.46 | 0.45 | −5.18 | 1.50 |
| MT-B | 4.92 | 0.39 | 12.7 | 6.15 | 0.80 | −8.83 | 1.50 |
| MT-C | 4.21 | 0.26 | 16.5 | 5.26 | 0.44 | −4.97 | 1.50 |
| PVA1%-A | 5.42 | 0.38 | 14.2 | 6.77 | 1.16 | −0.30 | 23.7 |
| PVA1%-B | 5.03 | 0.31 | 16.2 | 6.29 | 1.30 | 22.3 | |
| PVA1%-C | 5.29 | 0.55 | 9.55 | 6.61 | 4.05 | 26.1 | |
| PVA2%-A | 5.59 | 0.29 | 19.6 | 6.99 | 1.03 | 24.3 | |
| PVA2%-B | 6.52 | 0.61 | 10.7 | 8.15 | 3.39 | 30.5 | |
| PVA2%-C | 5.89 | 0.42 | 14.0 | 7.36 | 3.80 | 28.3 |
| Type | Common Factors | Cross-Section | Volume Fraction | Number of Specimens |
|---|---|---|---|---|
| MT-A | Height: 600 mm Bond length: 543 mm (=40d) Reinforcement: Braided AFRP bar (Diameter 13.52 mm) Fiber type of FRCC: PVA | 100 mm × 100 mm (A series) | - | 1 |
| PVA1%-A | 1.0% | 1 | ||
| PVA2%-A | 2.0% | 1 | ||
| MT-B | 120 mm × 120 mm (B series) | - | 1 | |
| PVA1%-B | 1.0% | 1 | ||
| PVA2%-B | 2.0% | 1 | ||
| MT-C | 140 mm × 140 mm (C series) | - | 1 | |
| PVA1%-C | 1.0% | 1 | ||
| PVA2%-C | 2.0% | 1 |
| Reinforcement | Diameter (mm) | Tensile Strength (MPa) | Elastic Modulus (GPa) |
|---|---|---|---|
| Braided AFRP bar | 13.52 | 1315 | 66.6 |
| Type | Compressive Strength (MPa) | Elastic Modulus (GPa) |
|---|---|---|
| MT | 61.5 | 20.2 |
| PVA1% | 58.7 | 19.0 |
| PVA2% | 60.1 | 19.1 |
| Specimens | (MPa) | (mm) | (N/mm3) | (MPa) | (mm) | (mm) |
|---|---|---|---|---|---|---|
| PVA1%-A | 2.93 | 0.38 | 7.68 | 3.66 | 1.16 | 23.7 |
| PVA1%-B | 2.72 | 0.31 | 8.75 | 3.40 | 1.30 | 22.3 |
| PVA1%-C | 2.85 | 0.55 | 5.16 | 3.57 | 4.05 | 26.1 |
| PVA2%-A | 3.02 | 0.29 | 10.6 | 3.78 | 1.03 | 24.3 |
| PVA2%-B | 3.52 | 0.61 | 5.76 | 4.40 | 3.39 | 30.5 |
| PVA2%-C | 3.18 | 0.42 | 7.58 | 3.97 | 3.80 | 28.3 |
| Type | Common Factor | Loading Method | Fiber Volume Fraction |
|---|---|---|---|
| MT | Reinforcement: Braided AFRP bar (Diameter 13.52 mm) pt = 1.04(%) Fiber type of FRCC: PVA | Monotonic loading | - |
| PVA1% | 1% | ||
| PVA2% | 2% | ||
| PVA2%-C | One-sided cyclic loading |
| Type | Compressive Strength (MPa) | Elastic Modulus (GPa) |
|---|---|---|
| MT | 42.4 | 17.4 |
| PVA1% | 47.5 | 16.6 |
| PVA2% | 41.2 | 15.9 |
| PVA2%-C | 47.0 | 16.4 |
| Parameters | MT | PVA1% | PVA2% | PVA2%C | |
|---|---|---|---|---|---|
| Braided AFRP bar | (mm2) | 143.6 | |||
| (mm) | 43 | ||||
| (GPa) | 66 | ||||
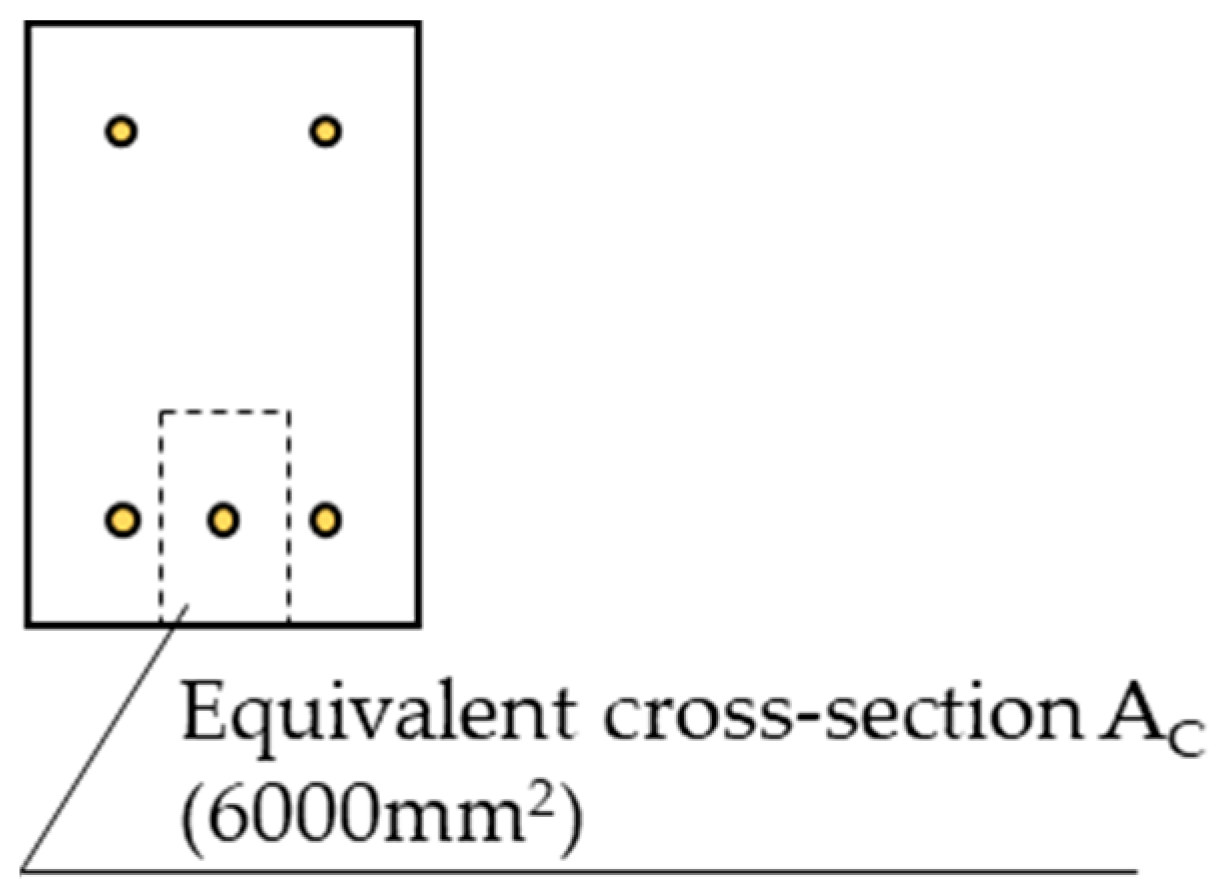
| FRCC | (mm2) | 6000 | |||
| (GPa) | 17.4 | 16.6 | 15.9 | 16.4 | |
| (MPa) | 2.82 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takasago, S.; Kanakubo, T.; Kobayashi, H.; Sasaki, H. Bond and Cracking Characteristics of PVA-Fiber-Reinforced Cementitious Composite Reinforced with Braided AFRP Bars. Fibers 2023, 11, 107. https://doi.org/10.3390/fib11120107
Takasago S, Kanakubo T, Kobayashi H, Sasaki H. Bond and Cracking Characteristics of PVA-Fiber-Reinforced Cementitious Composite Reinforced with Braided AFRP Bars. Fibers. 2023; 11(12):107. https://doi.org/10.3390/fib11120107
Chicago/Turabian StyleTakasago, Shugo, Toshiyuki Kanakubo, Hiroya Kobayashi, and Hideto Sasaki. 2023. "Bond and Cracking Characteristics of PVA-Fiber-Reinforced Cementitious Composite Reinforced with Braided AFRP Bars" Fibers 11, no. 12: 107. https://doi.org/10.3390/fib11120107
APA StyleTakasago, S., Kanakubo, T., Kobayashi, H., & Sasaki, H. (2023). Bond and Cracking Characteristics of PVA-Fiber-Reinforced Cementitious Composite Reinforced with Braided AFRP Bars. Fibers, 11(12), 107. https://doi.org/10.3390/fib11120107