Next Article in Journal
Modulating the Partitioning of Microparticles in a Polyethylene Glycol (PEG)-Dextran (DEX) Aqueous Biphasic System by Surface Modification
Next Article in Special Issue
Adhesion Performance of Electrodeposited Ni Films with Different Treating Methods
Previous Article in Journal
Improving the Tribological Properties of Spark-Anodized Titanium by Magnetron Sputtered Diamond-Like Carbon
Previous Article in Special Issue
Tuning the Friction of Silicon Surfaces Using Nanopatterns at the Nanoscale
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Coatings
Volume 8
Issue 2
10.3390/coatings8020084
coatings-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

X-ray Microanalysis of Precious Metal Thin Films: Thickness and Composition Determination

by
Walter Giurlani
1,*,
Massimo Innocenti
1,2 and
Alessandro Lavacchi
2,*
1
Dipartimento di Chimica, Università degli Studi di Firenze, via della Lastruccia 3, 50019 Sesto Fiorentino (FI), Italy
2
Consiglio Nazionale delle Ricerche—Istituto di Chimica dei Composti OrganoMetallici (CNR-ICCOM), via Madonna del Piano 10, 50019 Sesto Fiorentino (FI), Italy
*
Authors to whom correspondence should be addressed.
Coatings 2018, 8(2), 84; https://doi.org/10.3390/coatings8020084
Submission received: 4 December 2017 / Revised: 9 February 2018 / Accepted: 12 February 2018 / Published: 24 February 2018
(This article belongs to the Special Issue Development and Characterization of Nanostructured Functional Coatings/Films)
Browse Figures
Versions Notes

Abstract

:
Measuring the thickness and the composition of precious metal thin films is a challenging task. Currently, the available techniques for thickness measurements are either destructive or need heavy assumptions on the nature of the sample, relying on information that are not always available with sufficient accuracy. In this paper we propose a new methodology based on X-ray microanalysis that can complement, with better lateral resolution, the use of X-ray Fluorescence, the most widely employed technique for measuring the thickness of electrodeposited coatings. The proposed method employs a combination of energy dispersive microanalysis spectra acquisition and Monte Carlo simulation. The effectiveness of the technique has been demonstrated by the measure of the thickness and the composition of a thin 24 kt gold electroplated film that contained small amount of nickel. Results have been validated by comparing data with those obtained by X-ray fluorescence and the scanning electron microscopy of metallographic cross-sections.

1. Introduction

Electrodeposited films for decorative applications have a thickness that generally varies between 50 nm and more than 10 μm. In electroplating companies, the most used technique for analyzing such films is the energy dispersive X-ray Fluorescence spectroscopy (XRF), which is fast and non-destructive. Alternative destructive methods include. cross-sectional Scanning Electron Microscopy (SEM, wide range of thicknesses but destructive and slow) and wet chemical analysis (e.g., atomic absorption, require sample destruction). Other well-known methods are ellipsometry [1] and profilometry [2]. However, ellipsometry is not applicable to metallic coatings because for thicknesses over 50 nm works only for optically transparent coatings. On the other side, profilometry needs a sample preparation before the coating deposition (masking) which is not practical in industrial field, and, in this sense, it is a destructive analysis. Secondary Ions Mass Spectrometry (SIMS) have also been employed [3,4], but the technique is micro-destructive, generally difficult to quantify.
Despite its popularity, a reliable thickness determination with XRF is not straightforward and requires exact knowledge of the composition of the coating. Additionally, in practical applications coatings consist of multilayer of various materials. In such cases, the determination of the thickness of the topmost layer requires the accurate knowledge of the thickness and the composition of all the underlying layers. The cumulative error in the introduction of such parameters in the analysis software lead to significant error in thickness measurements.
XRF systems devoted to the analysis of coatings use only three points to generate a second order calibration curve (generally a zero point, a bulk material measurement for infinity and a third point of known thickness standard). This is required to keep the cost low; indeed, standards are expensive and the use of many of them would increase the time to set up the analysis. Errors exceeding 10% in the thickness determination of the top layer are typical. This is not always acceptable, especially when the coating consists of precious metals.
The situation gets even worse in the case of the determination of the composition. In fact, for mechanic and aesthetic reasons, single metal coatings are rare and even a 24 kt gold film contain a small percentage of other metals such as iron or nickel, being the karat a quite rough measure of purity. Through XRF it is very complex to extract an accurate quantification of these metals, particularly if the thickness of the layer is unknown.
The investigation of these films with microanalysis, also known as Electron Probe MicroAnalysis (EPMA) [5,6], could open a new way of making coating analysis, even in the industrial field. The EPMA can be conducted using two methods: wavelength dispersive X-ray spectroscopy (WDS) [6] or energy dispersive X-ray spectroscopy (EDX) [5,7,8,9,10]. WDS is generally considered an excellent method for microanalysis because is more sensitive and has a higher EDX resolution but needs a dedicated device. EDX, on the other hand, can be conducted by simply coupling a detector to SEM, a widespread instrument in the academic and industrial sphere (especially since the recent spread of inexpensive desktop instrument), which is still valid for the quantification thickness and composition of ordinary galvanic deposits. For this reason, in this work the latter setup was used.
Energy dispersive X-ray spectroscopy (EDX) is an attractive candidate because it enables fast, quantitative [11,12], non-destructive [13] and inexpensive analysis with the additional benefit of having lateral resolution in the micron range [14] than XRF. In addition to that, in comparison to XRF, as the probe (electrons) is not very penetrating, it is possible (by adjusting the beam energy) to analyze only the outer layer and to obtain its composition [15,16,17,18,19].
EPMA was first developed in 1951 by Casting [20]. EPMA analyzes the composition of homogeneous materials in a region of few microns from the surface. Although this is a technique that interprets every sample as homogeneous and do not give direct information on the thicknesses but, varying the acceleration voltage of the electrons, a different composition ratio is got. It is likewise possible to get the same behavior by using standards with different known thickness keeping fixed the acceleration voltage. In this way, a calibration curve is built to extrapolate the thickness of the investigated sample. However, the preparation of standards with known thickness is unpractical in many situations for the variability of the materials and the thickness range. An alternative can consist of designing semiquantitative approaches that are based on calibration curves obtained with a simulation software [21,22,23].
These features open the possibility of extending the technique for the investigation of the film thickness [24,25,26] (or mass thickness [27,28,29,30]). Indeed, there are many works in which the problem has been addressed by choosing different approaches: both in terms of obtaining the calibration curve, using standard [31,32], of known thickness or Monte Carlo simulations [33,34]; and for the quantification method, the K-ratio [35,36,37], the ratio of intensity [38], critical energy [39] or atomic ratio [31]. There are some commercial software like STRATAGEM [22,40], developed by Pouchou and Pichoir [41], and LayerProbe [42] (evolution of ThinFilmID [43]), developed by Oxford Instruments, which determine the composition and thickness of multi-layered and multi-element samples but the software are black boxes with undisclosed methods of calculation. GMRFILM [11] an open source software developed by General Motors also works. However, GMRFILM is an old platform that run only under MS-DOS.
The maximum thickness that can be analyzed with the EDX method is about some microns: this is determined by the different range of the electrons as a function of the acceleration potential together with average atomic number of the sample [44]. Figure 1 shows the maximum thickness that can be detected by EDX for some metals in relation to the electron beam energy, notice that both color deposit and thick deposit are theoretically measurable.
The lower detection limit is given by a combination of the X-ray energy characteristics of the elements in the sample and the properties of the detector and can be as low as a few monolayer [45].
The sources of errors in the results, using simulated standards, are due to the number of electron simulated, which affects the precision, and the knowledge of the sample (elemental composition and disposition) that we must model, besides to the goodness of the physical model used from the software, which affect the accuracy of the results.
The purpose of this work is to establish a method applicable to film thickness and composition measurements in industrial environment. For this purpose, simulation software has been used, since the preparation of known standards is a long, expensive and complex process. Different EDX simulation software operate with different algorithm and models, for this reason we have tested some of them to find the best one for our purpose. In the paper we have used this software to determine theoretically the K-ratios building calibration curves for thickness determination.

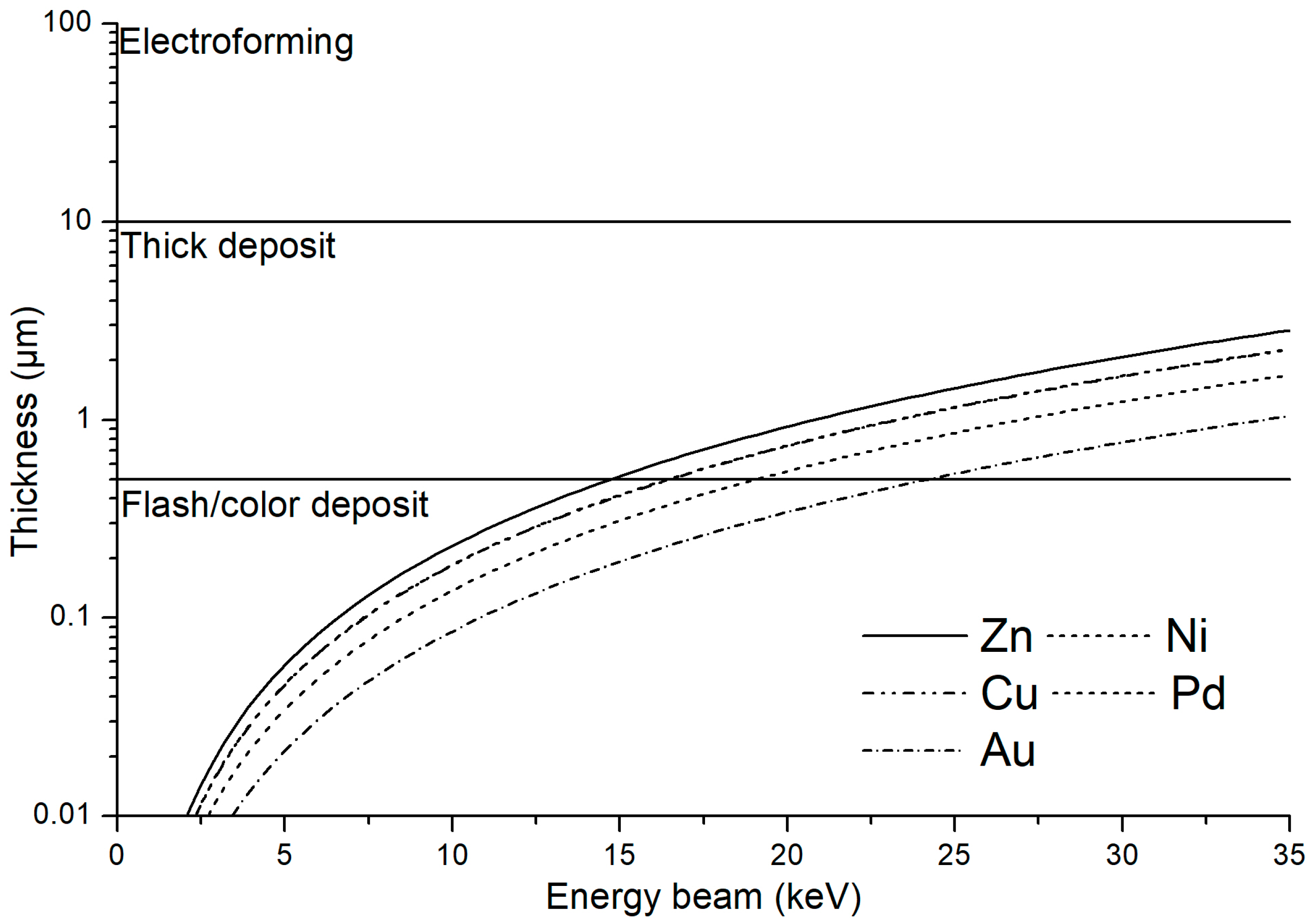
2. Materials and Methods

2.1. Samples Preparation

In this study, nine samples, with three different metal coatings, were prepared. Copper slabs (10 × 25 × 1.2 mm3), polished with brushes and cotton by a bijou producer, were chosen as substrate to have the same material to those used in the galvanic industry.
The plates were ultrasonically cleaned in acetone for 10 min, then rinsed several times in ethanol and finally dried in a stove at 65 °C for 40 min.
Keeping in mind the theoretical limits in detection showed in Figure 1 we deposit, by Physical Vapor Deposition (PVD) by the sputtering method, few hundred nanometers of metal; sputtering was chosen instead of electrodeposition from solution because this kind of deposit is more reproducible and homogeneous and therefore more suitable for the study of the technique but technically not different from a galvanic deposit. Furthermore, even PVD is used in industrial applications for film deposition. An Emithch K575X coater (Lewes, UK) was used equipped with a DC sputter. Au, Pd and Ni have been chosen for the deposit because they represent the most common metals used in the galvanic accessories and bijou. The argon pressure in the chamber was set to 1 × 10−2 mbar, and for each metal the following cycles were done: one to three cycles of 4 min in horizontal position at 50 mA for Au and 100 mA for Pd and Ni, and the targets have a diameter of 54 mm and are 40 mm away from the deposition stage. To achieve the maximum uniformity, the samples were placed on a rotating plate during the deposition, out of the rotation axe. Furthermore, we marked the center of the sample to take the spot measurements (EDX, XRF and SEM), approximately, in the same place.
The plates were weighed with a scale (Mettler AE240, Columbus, OH, USA, accuracy 0.01 mg) before and after deposition to obtain the amount of deposited metal and, by means of the surface area and the density of the deposited metal, the thickness. Standardless industrially-used XRF and, after EDX, cross section SEM measurements were also performed to obtain more data for the thickness of deposit. The XRF used is a Bowman (Schaumburg, IL, USA) P series and the measurement were performed with 50 kV acceleration voltage, at 12 mm focal distance with 0.3 mm window; the quantification were standardless and done with the commercial software of the instrument. The SEM and EDX measurement was performed with a FEI QUANTA (Hillsboro, OR, USA) 200 equipped with EDAX GmbH NEW XL-30 detector (Mahwah, NJ, USA) and analyzed with EDAX Genesis software [46] and a Hitachi S-2300 (Tokyo, Japan) equipped with a Thermo Scientific Noran System 7 detector (Waltham, MA, USA) and analyzed with Pathfinder software [47]. The SEM samples were prepared as follows: first the metal samples were galvanized with a layer of about 20 μm of copper to obtain a sandwich-like sample and a clear profile after the lapping process. The samples were then incorporated into resin, cut in the middle and lapped at first with gradually finer sandpaper and then with diamond suspension up to 0.3 microns. Finally, the SEM measurement were performed using backscattered electrons (Figure 2) and the images were analyzed with ImageJ [48].
To evaluate the applicability of the technique developed in this paper, and to give it a practical value, a sample was prepared also by a bijou producer using a common industrial galvanic process: a brass plate was coated galvanically with copper (5 min alkaline copper solution, 0.5 A/dm2 + 10 min acid copper solution, 2 A/dm2) and then with gold (10 min gold-nickel 24 karats, 1 A/dm2).

2.2. EDX Measurements

The EDX measurements of the samples and pure elements were performed at both 20 keV and 30 keV with a 300× magnification by analyzing an area of about 0.2 mm2, a low magnification was chosen to mediate the geometric and deposition heterogeneities. We used a Dead Time (the time after each event during which the system is not able to record another event) of about 30% and we varied the live time to obtain spectra with a total of 106 counts. The SEM-EDX system was calibrated before the measurements, obtaining a resolution (FWHM at Mn Kα) of 129.1 eV.

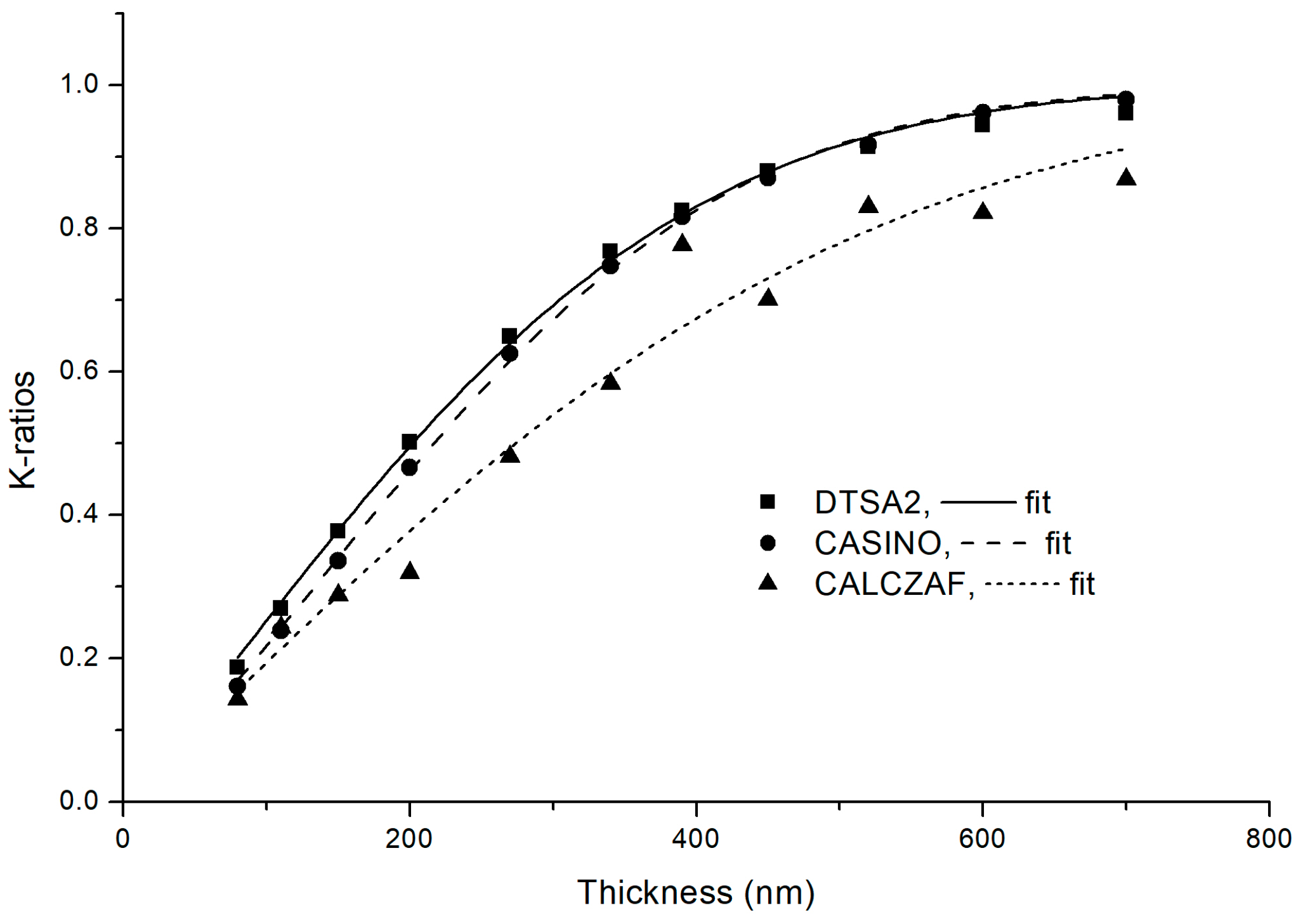
2.3. Simulations of the Standards

Monte Carlo simulations were performed at 20 keV and 30 keV with the following thickness parameters:
  • 80, 110, 150, 200, 270, 340, 390, 450, 520, 600, 700 nm of Au on Cu
  • 110, 140, 190, 260, 370, 500, 570, 660, 760, 890, 1090 nm of Pd on Cu
  • 45, 60, 80, 110, 150, 200, 250, 300, 350, 400, 460, 540 nm of Ni on Cu
  • Au, Pd, Ni, Cu bulk pure elements
The interaction of 16,000 electrons with the standards was simulated using the following software: NIST DTSA-II Jupiter 2017-07-05 [49] (from now indicated as DTSA2), CASINO 2.4.8.1 [50,51] and CalcZAF 11.7.4 [52]. The total number of simulations is 228.

2.4. Quantification

With the simulated spectra at known thickness, curves of calibration are built and, using the measured spectra, the thickness of samples has been extrapolated.
To build the calibration curves, K-ratio has been used. This information has been extracted from the spectra with different software and to find the best one, all the possible combinations have been tried, accounting for the software limitations. For the quantification, we used the L line of Au and Pd and K line of Ni and Cu. For the conversion of each spectrum into K-ratios we used the automatic mode of each software, interfering only if the baseline had not been taken properly. The K-ratios were extracted from measured spectra using three software: (1) the Built-In Commercial Software (BICS) of the instruments used in the measurement. This quantification is standardless (or semi-quantitative) and uses as reference the spectra collected by the manufacturer and stored in a file. With it, it is possible to extract both K-ratios; (2) DTSA2. In this case the analysis is quantitative and the K-ratio is obtained by dividing the background-corrected peak intensity of the sample by the same quantity measured on the pure bulk element. Also, with DTSA2, it is possible extract the K-ratios.
The K-ratios of simulated spectra (using the pure elements spectra simulated) were extracted with the built-in algorithm of DTSA2 and CalcZAF in the same way as the measured spectra. Casino doesn’t generate a spectrum but directly the emitted intensities, thus we manually calculate the K-ratios by dividing the intensities of the standards by the intensity of the pure element.
The K-ratios calibration curves, built with simulated spectra, were used with the K-ratios of measured spectra, combining different interpretations, for a total of 6 interpretations for the thickness of a single layer at one energy.
Measured spectra of pure elements were used to quantify the measured spectra of the samples and the simulated spectra of pure elements were used for simulated spectra of the standards, except for the quantification by BICS which is standardless.
We used the following notation to name the methods: M/C. Where M are the software used to quantify the measured spectra; C are the software used to build calibration curve.
For example, BICS/DTSA2 means that we extract the K-ratio with BICS, then the number obtained was converted in a thickness value with the calibration curve obtained from the K-ratios of the simulations of DTSA2.

2.5. Fitting

The calibration curve was fitted on simulated data with the Equation (1):
y = 1 − e − ( A x + B x 2 )
This simple analytical function permits the fitting in a wide thickness range [37]. The dependent variable x represents the thickness of the film and the independent variable y the resulting K-ratio. A and B are free parameters adjustable in the fitting process with values close to 10−3 and 10−6 respectively. A influences the linear term and could be interpreted as correlated to the attenuation (stopping power) of electrons and photons in the sample while the parameter next to the quadratic term, B, includes the electron backscattering and instrumental factors. According to that, the linear parameter tends to decrease increasing the atomic number in contrast to the quadratic term which increase with the atomic number.

3. Results

3.1. Sputtering Samples Thickness

Data have been fitted (examples in Figure 3) and the function used appears to be in good agreement with the experimental data.
Results have been compared against the XRF ones. This because XRF is currently the reference technique for non-destructive measurement of thickness for electrodeposited metal coatings. XRF well mediates any inhomogeneity (contrary to SEM) but considers a relatively small portion (contrary to weight scale measurement).
The best EDX results, relative to XRF, come from 30 keV measurements. This probably because the higher probe penetration is needed for the thickness investigated. Moreover, all the best results come from the use of the weight fraction, and all with the quantification of the instrument (BICS) and the calibration curve obtained from the simulation with DTSA2. The deviation of EDX from XRF are showed in Table 1.
The results tell us that BICS works better than DTSA2 in the analysis of measured spectra but for the simulated curves DTSA2 is the best software.
In Table 2 is shown a comparison between the thickness measurement obtained among the different instruments used; in Figure 4 these results are plotted overlapping the calibration curves (inverse function). The EDX results are quite comparable to XRF results, instead SEM and weight scale results doesn’t seem to be in such agreement.
In Table 2 it can be observed that the deviation between EDX and XRF increases with the thickness in the case of gold coatings, while there is an opposite trend in the case of nickel films. This is due to the complementarity of the two instruments and the probes they use: with EDX the electrons are not very penetrating, therefore thick films of heavy elements, such as gold, are measured with more difficulty, while thin films of lighter elements, such as nickel, generate a small signal in XRF measurements due to the strong penetration of X-rays.

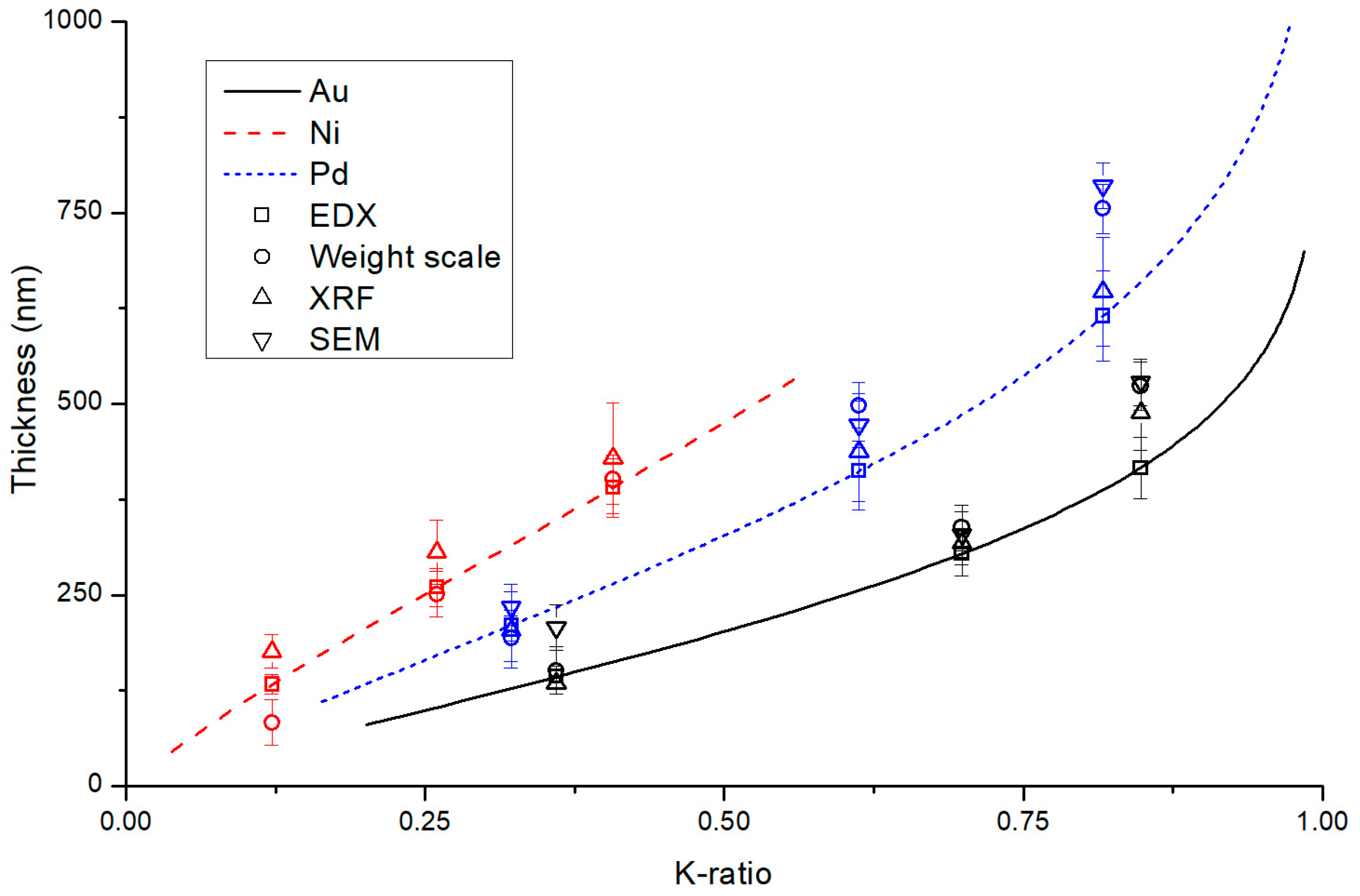
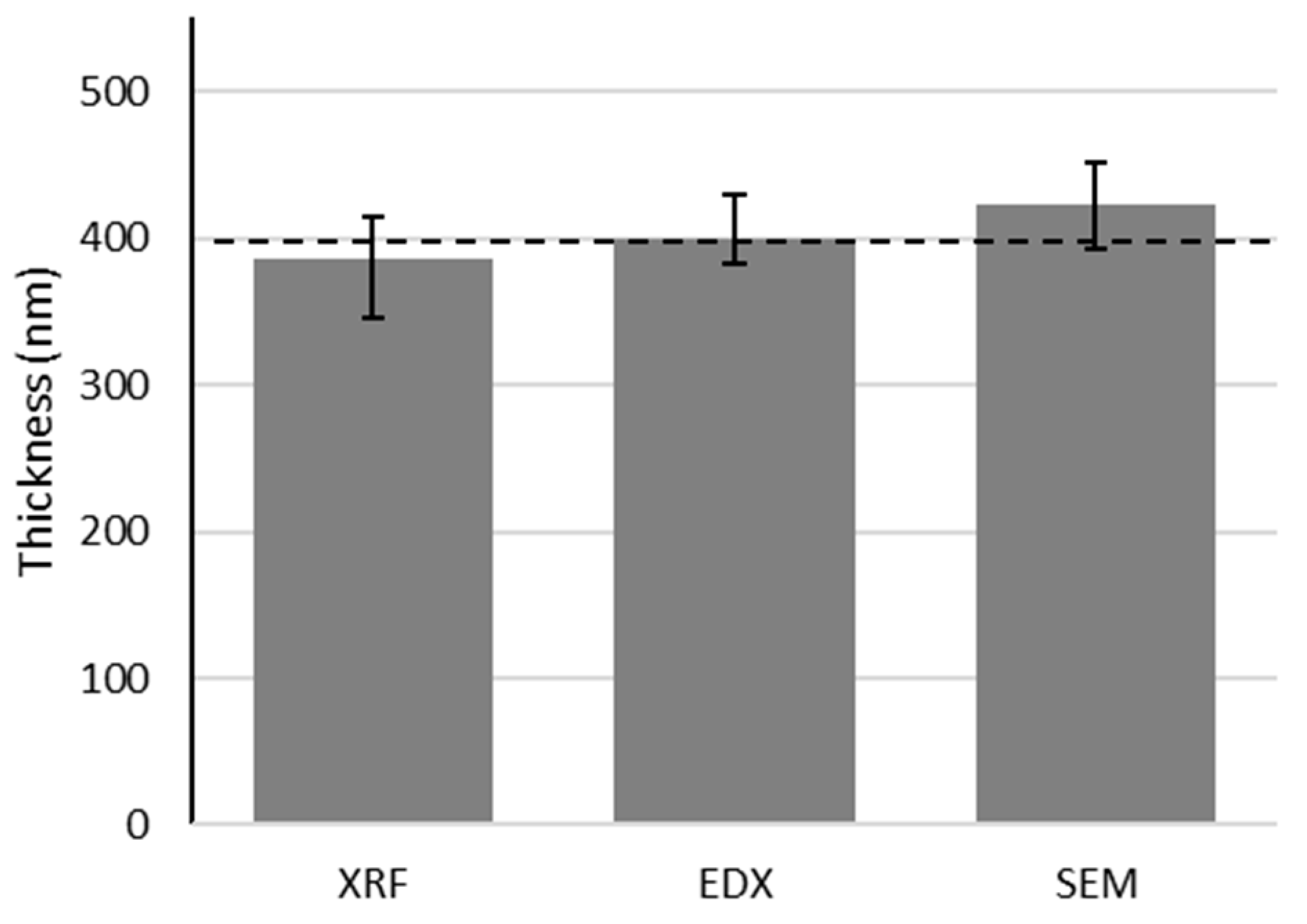
3.2. Galvanic Samples Thickness and Composition

The effectiveness of the method, studied on samples prepared with sputtering, has been now tested in the case of a non-ideal galvanic deposit.
With the electron beam energies used in this study, the X-rays come from a maximum depth on about 2 μm; for the deposition time used the copper deposit (under the thinner gold one) is between 6 and 10 μm, so it is reasonable to consider the copper layer as a massive substrate. On the sample was performed an XRF analysis, the EDX measurement, and then, after depositing a further layer of copper as a support, a SEM measure of the cross section.
The gold deposit, although marketed as 24 kt, has a minimum percentage of nickel. Through the EDX were obtained the actual gold karats of the deposit. Since film is not enough thick copper is visible in the spectrum, so it has been quantified by the K line. Applying ZAF correction, the percentage by weight of the three metals was obtained. Since copper is not present in the deposition solution, and consequently in the coating, the sum of the percentages by weight of gold and nickel has been normalized to 1, obtaining a Ni:Au fraction of 2.5% in average, with an actual gold rating of 23.4 kt. This data is already very important itself for the characterization of the coating and it is an information very difficult to obtain through XRF since the volume investigated is bigger, so small fractions of metals are hard to quantify. As mentioned in the introduction, the use of karat could hide the presence of small percentages of other metals, therefore the formalism in percentage by weight is more accurate. This type of data extraction has been validated by performing simulations of film thicknesses 200, 400, 600 nm and infinity (bulk) at 20 keV; calculating the fraction of nickel compared to gold, as described, it always gets a percentage of 2.5% on average, with small oscillations intrinsic in the simulation and which fall into the measurement error and the background assessment. We have performed also simulation keeping the same film thickness of 400 nm and varying the beam energy (15, 20 and 25 keV), obtaining similar results. This kind of test has been performed also on the sample, and the results are shown in Table 3.
For the thickness quantification of this sample it was chosen to use the combination of algorithms BICS/DTSA2.
From a preliminary XRF measurement the thickness of the coating results to be 400 nm. Therefore, we simulated 6 standards in a range of thicknesses from 300 nm to 550 nm, in this way our sample was within the calibration curve. For the film simulation, a 97.5% gold-nickel alloy, with density of 18.75 g/cm3 was used.
Figure 5 shows the results obtained from XRF, EDX and SEM measurement. The difference in the EDX measurement from XRF is 3.9%. The dash line represents the average of the three measurements.

4. Conclusions

We have presented a method for the determination of the thickness and the composition of electrodeposited precious metal thin films. This method, has better lateral resolution than the XRF technique currently used in the galvanic industry and allows reliable measurement on thin (<500 nm) precious metal films with the capability to determine metals in the 1% concentration range in metal thin films with thickness lower than 500 nm.
The calibration curve was built entirely using simulated spectra with low computational and instrumental cost. The time consuming to obtain a simulated standard it is much less than for a real standard, the material costs are zero and it does not degrade over time.
The approach was validated thereby the analysis of three common electroplated metals with known thickness using various approaches and software. The results were compared with other investigation techniques to evaluate its accuracy. Thickness results have an uncertainty of about 9% which is consistent with the data from literature obtained from calibration curves using real standards [38]. The three metals chosen for the coating had largely different characteristic X-ray emissions as they had different atomic numbers. This shows that the method has a good generality and can work properly for most of the coatings consisting of transition metals.
The method has been proved to be effective by the analysis of a coating architecture consisting of a 24 kt topmost layer of gold containing a tiny amount of nickel deposited on a copper interlayer on mass substrate. The thickness result was in excellent agreement with the control measurement methods, with a deviation of 2.3%. In addition we determined the concentration of Ni in the layer which was undetectable with the benchtop ED-XRF thickness analyzer. The final gold title was found to be 23.4 kt.

Acknowledgments

The authors acknowledge the financial support that has been given from Freschi & Vangelisti srl and Ente Cassa di Risparmio di Firenze and Centro di Microscopie Elettroniche “Laura Bonzi” (CeME) for the measuring instruments disposability. We also thanks Carlo Bartoli, technician at ICCOM, for the support in microscope maintenance and Ferdinando Capolupo of the Department of Chemistry of the University of Florence for the preparation of galvanic coatings cross-sections.

Author Contributions

Walter Giurlani is the first author since he performed all the experiments, the simulations and wrote the paper; Alessandro Lavacchi conceived and designed the experiments and gave a contribution to the paper writing; Massimo Innocenti gave theoretical support to experiment design and execution and contributed to the paper writing.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Malarde, D.; Powell, M.J.; Quesada-Cabrera, R.; Wilson, R.L.; Carmalt, C.J.; Sankar, G.; Parkin, I.P.; Palgrave, R.G. Optimized Atmospheric-Pressure Chemical Vapor Deposition Thermochromic VO2 Thin Films for Intelligent Window Applications. ACS Omega 2017, 2, 1040–1046. [Google Scholar] [CrossRef]
  2. Nash, C.R.; Fenton, J.C.; Constantino, N.G.N.; Warburton, P.A. Compact chromium oxide thin film resistors for use in nanoscale quantum circuits. J. Appl. Phys. 2014, 116. [Google Scholar] [CrossRef]
  3. Bardi, U.; Caporali, S.; Chenakin, S.P.; Lavacchi, A.; Miorin, E.; Pagura, C.; Tolstogouzov, A. Characterization of electrodeposited metal coatings by secondary ion mass spectrometry. Surf. Coat. Technol. 2006, 200, 2870–2874. [Google Scholar] [CrossRef]
  4. Bardi, U.; Chenakin, S.P.; Ghezzi, F.; Giolli, C.; Goruppa, A.; Lavacchi, A.; Miorin, E.; Pagura, C.; Tolstogouzov, A. High-temperature oxidation of CrN/AlN multilayer coatings. Appl. Surf. Sci. 2005, 252, 1339–1349. [Google Scholar] [CrossRef]
  5. Ortel, E.; Hertwig, A.; Berger, D.; Esposito, P.; Rossi, A.M.; Kraehnert, R.; Hodoroaba, V.-D. New Approach on Quantification of Porosity of Thin Films via Electron-Excited X-ray Spectra. Anal. Chem. 2016, 88, 7083–7097. [Google Scholar] [CrossRef] [PubMed]
  6. Richter, S.; Pinard, P.T. Combined EPMA, FIB and Monte Carlo simulation: A versatile tool for quantitative analysis of multilayered structures. IOP Conf. Ser. Mater. Sci. Eng. 2016, 109, 12014. [Google Scholar] [CrossRef]
  7. Eggert, F. EDX-spectra simulation in electron probe microanalysis. Optimization of excitation conditions and detection limits. Microchim. Acta 2006, 155, 129–136. [Google Scholar] [CrossRef]
  8. Armigliato, A. Thin film X-ray microanalysis with the analytical electron microscope. J. Anal. At. Spectrom. 1999, 14, 413–418. [Google Scholar] [CrossRef]
  9. Christien, F.; Pierson, J.F.; Hassini, A.; Capon, F.; Le Gall, R.; Brousse, T. EPMA-EDS surface measurements of interdiffusion coefficients between miscible metals in thin films. Appl. Surf. Sci. 2010, 256, 1855–1890. [Google Scholar] [CrossRef]
  10. Pascual, R.; Cruz, L.R.; Ferreira, C.L.; Gomes, D.T. Thin film thickness measurement using the energy-dispersive spectroscopy technique in a scanning electron microscope. Thin Solid Films 1990, 185, 279–286. [Google Scholar] [CrossRef]
  11. Waldo, R.A.; Militello, M.C.; Gaarenstroom, S.W. Quantitative thin-film analysis with an energy-dispersive X-ray detector. Surf. Interface Anal. 1993, 20, 111–114. [Google Scholar] [CrossRef]
  12. Gauvin, R. Quantitative X-ray microanalysis of heterogeneous materials using Monte Carlo simulations. Microchim. Acta 2006, 155, 75–81. [Google Scholar] [CrossRef]
  13. Sokolov, S.A.; Kelm, E.A.; Milovanov, R.A.; Abdullaev, D.A.; Sidorov, L.N. Non-destructive determination of thickness of the dielectric layers using EDX. Proc. SPIE Int. Soc. Opt. Eng. 2016, 10224. [Google Scholar] [CrossRef]
  14. Stenberg, G.; Boman, M. Thickness measurement of light elemental films. Diam. Relat. Mater. 1996, 5, 1444–1449. [Google Scholar] [CrossRef]
  15. Willich, P.; Obertop, D. Composition and thickness of submicron metal coatings and multilayers on Si determined by EPMA. Surf. Interface Anal. 1988, 13, 20–24. [Google Scholar] [CrossRef]
  16. Hunger, H.-J.; Baumann, W.; Schulze, S. A new method for determining the thickness and composition of thin layers by electron probe microanalysis. Cryst. Res. Technol. 1985, 20, 1427–1433. [Google Scholar] [CrossRef]
  17. Ares, J.R.; Pascual, A.; Ferrer, I.J.; Sánchez, C. A methodology to reduce error sources in the determination of thin film chemical composition by EDAX. Thin Solid Films 2004, 450, 207–210. [Google Scholar] [CrossRef]
  18. Sempf, K.; Herrmann, M.; Bauer, F. First results in thin film analysis based on a new EDS software to determine composition and/or thickness of thin layers on substrates. In Proceedings of the EMC 2008 14th European Microscopy Congress, Aachen, Germany, 1–5 September 2008; Springer: Aacher, Germany, 2008; pp. 751–752. [Google Scholar]
  19. Hodoroaba, V.-D.; Kim, K.J.; Unger, W.E.S. Energy dispersive electron probe microanalysis (ED-EPMA) of elemental composition and thickness of Fe-Ni alloy films. Surf. Interface Anal. 2012, 44, 1459–1461. [Google Scholar] [CrossRef]
  20. Raymond Casting Application of Electron Probes to Local Chemical and Crystallographic Analysis. 1951. Available online: http://www.microbeamanalysis.org/history/Castaing-Thesis-clearscan.pdf (accessed on 14 February 2018).
  21. Ritchie, N.W.M. Efficient Simulation of Secondary Fluorescence via NIST DTSA-II Monte Carlo. Microsc. Microanal. 2017, 23, 618–633. [Google Scholar] [CrossRef] [PubMed]
  22. Kühn, J.; Hodoroaba, V.-D.; Linke, S.; Moritz, W.; Unger, W.E.S. Characterization of Pd-Ni-Co alloy thin films by ED-EPMA with application of the STRATAGEM software. Surf. Interface Anal. 2012, 44, 1456–1458. [Google Scholar] [CrossRef]
  23. Ritchie, N.W.M. Spectrum simulation in DTSA-II. Microsc. Microanal. 2009, 15, 454–468. [Google Scholar] [CrossRef] [PubMed]
  24. Osada, Y. Electron probe microanalysis (EPMA) measurement of aluminum oxide film thickness in the nanometer range on aluminum sheets. X-ray Spectrom. 2005, 34, 92–95. [Google Scholar] [CrossRef]
  25. Bastin, G.F.; Heijligers, H.J.M. A systematic database of thin-film measurements by EPMA: Part I—Aluminum films. X-ray Spectrom. 2000, 29, 212–238. [Google Scholar] [CrossRef]
  26. Merlet, C. Thin film quantification by EPMA: Accuracy of analytical procedure. Microsc. Microanal. 2006, 12, 842. [Google Scholar] [CrossRef]
  27. August, H.; Wernisch, J. A Method for Determining the Mass Thickness of Thin Films Using Electron Probe Microanalysis. Scanning 1987, 9, 145–155. [Google Scholar] [CrossRef]
  28. Shang, Y.; Guo, Y.; Liu, Z.; Xu, L. An EPMA software for determination of thin metal film thickness and it’s application. Acta Metall. Sin. 1997, 33, 443–448. [Google Scholar]
  29. Watanabe, M.; Horita, Z.; Nemoto, M. Absorption correction and thickness determination using the zeta factor in quantitative X-ray microanalysis. Ultramicroscopy 1996, 65, 187–198. [Google Scholar] [CrossRef]
  30. Bishop, H.E.; Poole, D.M. A simple method of thin film analysis in the electron probe microanalyser. J. Phys. D Appl. Phys. 1973, 6, 1142–1158. [Google Scholar] [CrossRef]
  31. Canli, S. Thickness Analysis of Thin Films by Energy Dispersive X-ray Spectroscopy. 2010. Available online: https://etd.lib.metu.edu.tr/upload/12612822/index.pdf (accessed on 14 February 2018).
  32. Bastin, G.F.; Dijkstra, J.M.; Heijligers, H.J.M.; Klepper, D. In-depth profilingwith the electron probe microanalyser. In Proceedings of the EMAS’98 3rd Regional Workshop, Barcelona, Spain, 3–16 May 1998; pp. 25–55. [Google Scholar]
  33. Roming, A.D.; Plimpton, S.J.; Michael, J.R.; Myklebust, R.L. Newbury DE Microbeam Analysis; San Francisco Press: San Francisco, CA, USA, 1990. [Google Scholar]
  34. Kyser, D.F.; Murata, K. Quantitative Electron Microprobe Analysis of Thin Films on Substrates. IBM J. Res. Dev. 1974, 352–363. [Google Scholar] [CrossRef]
  35. Moller, A.; Weinbruch, S.; Stadermann, F.J.; Ortner, H.M.; Neubeck, K.; Balogh, A.G.; Hahn, H. Accuracy of film thickness determination in electron-probe microanalysis. Mikrochim. Acta 1995, 119, 41–47. [Google Scholar] [CrossRef]
  36. Procop, M.; Radtke, M.; Krumrey, M.; Hasche, K.; Schädlich, S.; Frank, W. Electron probe microanalysis (EPMA) measurement of thin-film thickness in the nanometre range. Anal. Bioanal. Chem. 2002, 374, 631–634. [Google Scholar] [CrossRef] [PubMed]
  37. Campos, C.S.; Coleoni, E.A.; Trincavelli, J.C.; Kaschny, J.; Hubbler, R.; Soares, M.R.F.; Vasconcellos, M.A.Z. Metallic thin film thickness determination using electron probe microanalysis. X-ray Spectrom. 2001, 30, 253–259. [Google Scholar] [CrossRef]
  38. Zhuang, L.; Bao, S.; Wang, R.; Li, S.; Ma, L.; Lv, D. Thin film thickness measurement using electron probe microanalyzer. In Proceedings of the International Conference on Applied Superconductivity and Electromagnetic Devices (ASEMD 2009), Chengdu, China, 25–27 September 2009; pp. 142–144. [Google Scholar] [CrossRef]
  39. Ng, F.L.; Wei, J.; Lai, F.K.; Goh, K.L. Thickness Measurement of Metallic Thin Film by X-ray Microanalysis; SIMTech Technical Reports; Singapore Institute of Manufacturing Technology: Singapore, 2010; Volume 11, pp. 21–25. [Google Scholar]
  40. Dumelié, N.; Benhayoune, H.; Balossier, G. TF_Quantif: A Quantification Procedure for Electron Probe Microanalysis of Thin Films on Heterogeneous Substrates. J. Phys. D 2007, 40, 2124. [Google Scholar] [CrossRef]
  41. Pouchou, J.L.; Pichoir, F. Surface film X-ray microanalysis. Scanning 1990, 12, 212–224. [Google Scholar] [CrossRef]
  42. Instruments, O. LayerProbe. Available online: https://www.oxford-instruments.com/products/microanalysis/solutions/layerprobe (accessed on 14 February 2018).
  43. Instruments, O. ThinFilmID. Available online: http://www.oxford-instruments.cn/OxfordInstruments/media/nanoanalysis/brochures and thumbs/ThinFilmID_Brochure.pdf (accessed on 14 February 2018).
  44. Katz, L.; Penfold, A.S. Range-energy relations for electrons and the determination of beta-ray end-point energies by absorption. Rev. Mod. Phys. 1952, 24, 28–44. [Google Scholar] [CrossRef]
  45. Cockett, G.H.; Davis, C.D. Coating thickness measurement by electron probe microanalysis. Br. J. Appl. Phys. 1963, 14, 813–816. [Google Scholar] [CrossRef]
  46. EDAX Genesis. Available online: http://www.edax.com/support/software-licensing (accessed on 14 February 2018).
  47. Pathfinder. Available online: https://www.thermofisher.com/order/catalog/product/IQLAADGABKFAQOMBJE (accessed on 14 February 2018).
  48. ImageJ. Available online: https://imagej.nih.gov/ij/ (accessed on 14 February 2018).
  49. DTSA-II. Available online: http://www.cstl.nist.gov/div837/837.02/epq/dtsa2/ (accessed on 14 February 2018).
  50. CASINO. Available online: http://www.gel.usherbrooke.ca/casino/ (accessed on 14 February 2018).
  51. Demers, H.; Poirier-Demers, N.; Couture, A.R.; Joly, D.; Guilmain, M.; De Jonge, N.; Drouin, D. Three-dimensional electron microscopy simulation with the CASINO Monte Carlo software. Scanning 2011, 33, 135–146. [Google Scholar] [CrossRef] [PubMed]
  52. CalcZAF. Available online: http://www.probesoftware.com/Technical.html (accessed on 14 February 2018).
Coatings 08 00084 g001 550
Figure 1. Maximum energy dispersive X-ray spectroscopy (EDX) mesurable thickness as function of energy beam, depending on the energy of the beam, for Zn, Ni, Cu, Pd and Au. The typical thickness range of electroplated coatings for decorative applications is also shown.
Figure 1. Maximum energy dispersive X-ray spectroscopy (EDX) mesurable thickness as function of energy beam, depending on the energy of the beam, for Zn, Ni, Cu, Pd and Au. The typical thickness range of electroplated coatings for decorative applications is also shown.
Coatings 08 00084 g001
Coatings 08 00084 g002 550
Figure 2. Cross section of gold sample: (a) 1200× magnification to show the external galvanic copper coating, the boxed area is magnified in (b); (b) film detail, used for the quantification, 24600× magnification.
Figure 2. Cross section of gold sample: (a) 1200× magnification to show the external galvanic copper coating, the boxed area is magnified in (b); (b) film detail, used for the quantification, 24600× magnification.
Coatings 08 00084 g002
Coatings 08 00084 g003 550
Figure 3. Examples of simulated data and fitted calibration curves. Curves of 30 keV Au K-ratios.
Figure 3. Examples of simulated data and fitted calibration curves. Curves of 30 keV Au K-ratios.
Coatings 08 00084 g003
Coatings 08 00084 g004 550
Figure 4. Metal thickness (nm) deposited on samples measured with weight scale, XRF, SEM cross section and EDX (BICS/DTSA2 simulations results) with error bars. The calibration curves (inverse function) are overlapped.
Figure 4. Metal thickness (nm) deposited on samples measured with weight scale, XRF, SEM cross section and EDX (BICS/DTSA2 simulations results) with error bars. The calibration curves (inverse function) are overlapped.
Coatings 08 00084 g004
Coatings 08 00084 g005 550
Figure 5. XRF, EDX and SEM thickness measurement of galvanized sample. The dotted line shows the average thickness of 399 nm.
Figure 5. XRF, EDX and SEM thickness measurement of galvanized sample. The dotted line shows the average thickness of 399 nm.
Coatings 08 00084 g005
Table
Table 1. List of the deviation from the X-ray fluorescence spectroscopy (XRF) results, in growing order.
Table 1. List of the deviation from the X-ray fluorescence spectroscopy (XRF) results, in growing order.
Extrapolation MethodEDX–XRF Deviation
BICS/DTSA29.6%
BICS/CASINO9.7%
BICS/CALCZAF20.4%
DTSA2/DTSA224.8%
DTSA2/CASINO27.0%
DTSA2/CALCZAF50.1%
Table
Table 2. Measured thickness values with all the different measurement methods. For EDX the result derived from the simulations of the combination BICS/DTSA2 is reported, which has the smallest deviation respect to XRF, considered as the reference value. We also reported the deviation between EXD and XRF for all individual measurements.
Table 2. Measured thickness values with all the different measurement methods. For EDX the result derived from the simulations of the combination BICS/DTSA2 is reported, which has the smallest deviation respect to XRF, considered as the reference value. We also reported the deviation between EXD and XRF for all individual measurements.
SampleWeight Scale (nm)XRF (nm)SEM Cross Section (nm)EDX (nm)EDX-XRF Deviation
Au1151 ± 31135 ± 8207 ± 30143 ± 145%
Au2338 ± 30318 ± 29329 ± 30304 ± 29−5%
Au3523 ± 32488 ± 49528 ± 30416 ± 40−15%
Pd4193 ± 30204 ± 50234 ± 30210 ± 203%
Pd5498 ± 30437 ± 76473 ± 30412 ± 40−6%
Pd6755 ± 32647 ± 71785 ± 30615 ± 59−5%
Ni783 ± 30176 ± 22n.a.133 ± 13−24%
Ni8251 ± 30306 ± 42n.a.260 ± 25−15%
Ni9401 ± 32429 ± 72n.a.390 ± 38−9%
Table
Table 3. Ni:Au fractions in simulation and measurements of gold–nickel alloy on copper varying thickness and energy.
Table 3. Ni:Au fractions in simulation and measurements of gold–nickel alloy on copper varying thickness and energy.
Thickness (nm)Energy Beam (keV)Ni (wt.%)Cu (wt.%)Au (wt.%)Ni:Au %
200201.7920.6077.612.25
400202.289.8987.832.53
600202.287.9489.792.48
Bulk202.600.0097.402.60
400152.167.6190.242.34
400251.9011.9386.172.16
Sample151.884.6193.501.97
Sample202.698.0889.232.92
Sample252.1514.4283.432.52

Share and Cite

MDPI and ACS Style

Giurlani, W.; Innocenti, M.; Lavacchi, A. X-ray Microanalysis of Precious Metal Thin Films: Thickness and Composition Determination. Coatings 2018, 8, 84. https://doi.org/10.3390/coatings8020084

AMA Style

Giurlani W, Innocenti M, Lavacchi A. X-ray Microanalysis of Precious Metal Thin Films: Thickness and Composition Determination. Coatings. 2018; 8(2):84. https://doi.org/10.3390/coatings8020084

Chicago/Turabian Style

Giurlani, Walter, Massimo Innocenti, and Alessandro Lavacchi. 2018. "X-ray Microanalysis of Precious Metal Thin Films: Thickness and Composition Determination" Coatings 8, no. 2: 84. https://doi.org/10.3390/coatings8020084

APA Style

Giurlani, W., Innocenti, M., & Lavacchi, A. (2018). X-ray Microanalysis of Precious Metal Thin Films: Thickness and Composition Determination. Coatings, 8(2), 84. https://doi.org/10.3390/coatings8020084

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop