Numerical Verification of Gallium Nitride Thin-Film Growth in a Large MOCVD Reactor
Abstract
:1. Introduction
2. Materials and Methods
2.1. Numerical Modeling
2.2. Two-Dimensional Analysis
2.2.1. Two-Dimensional Numerical Assumptions
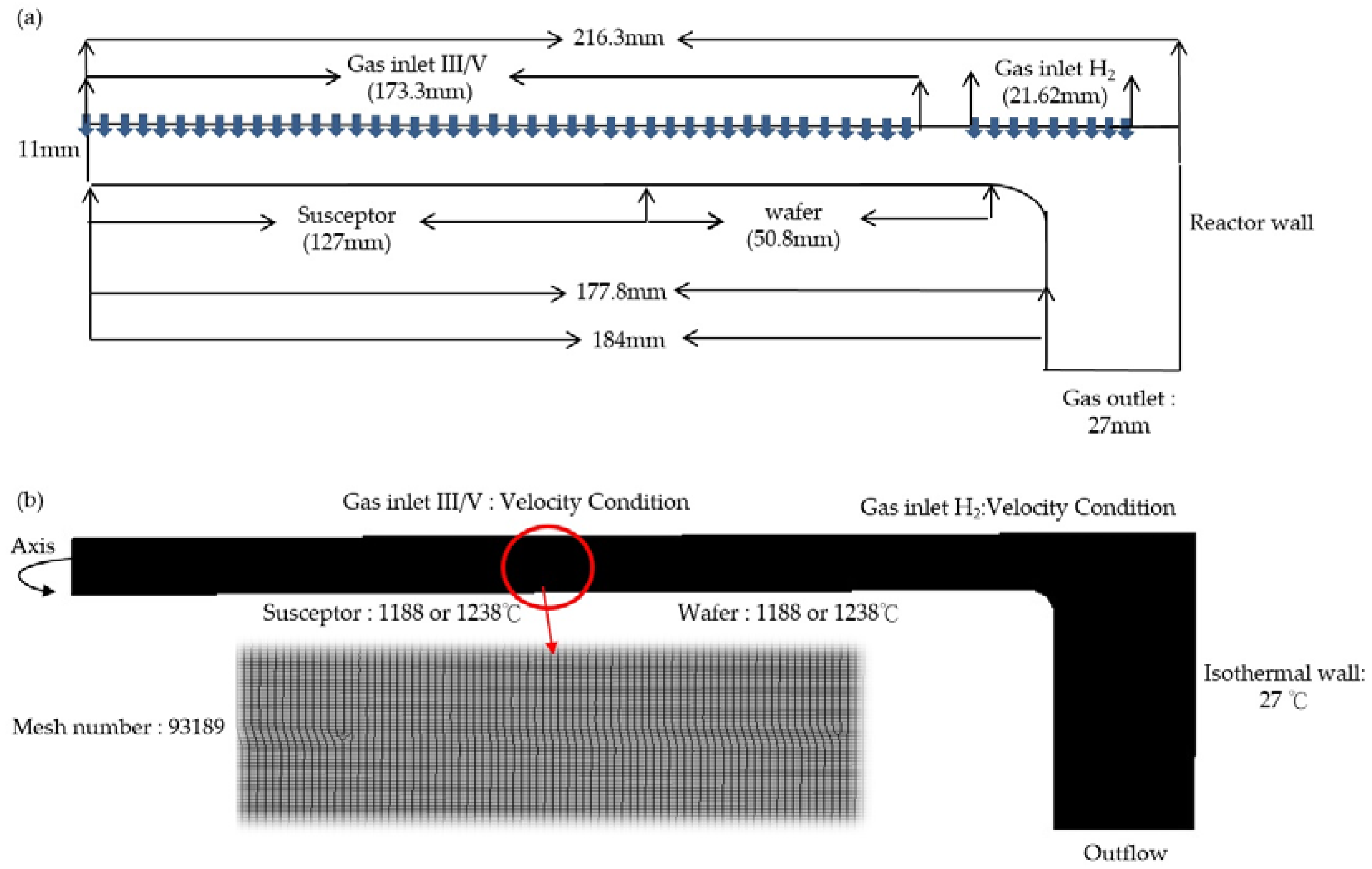
2.2.2. Boundary Conditions
2.3. Development of Numerical Modeling
2.3.1. Experiment Schematic
2.3.2. Schematic of the Numerical Modeling
3. Results and Discussion
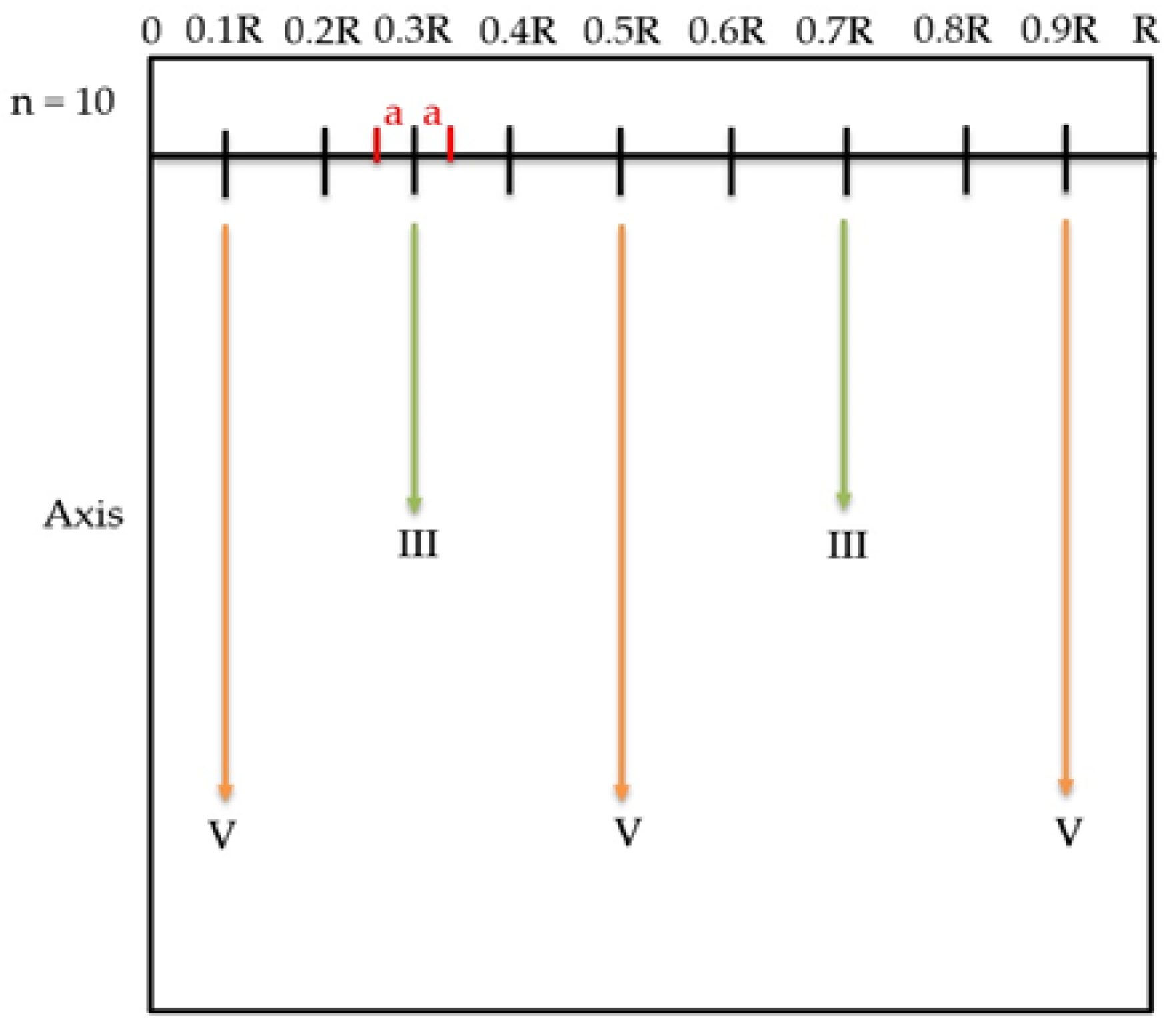
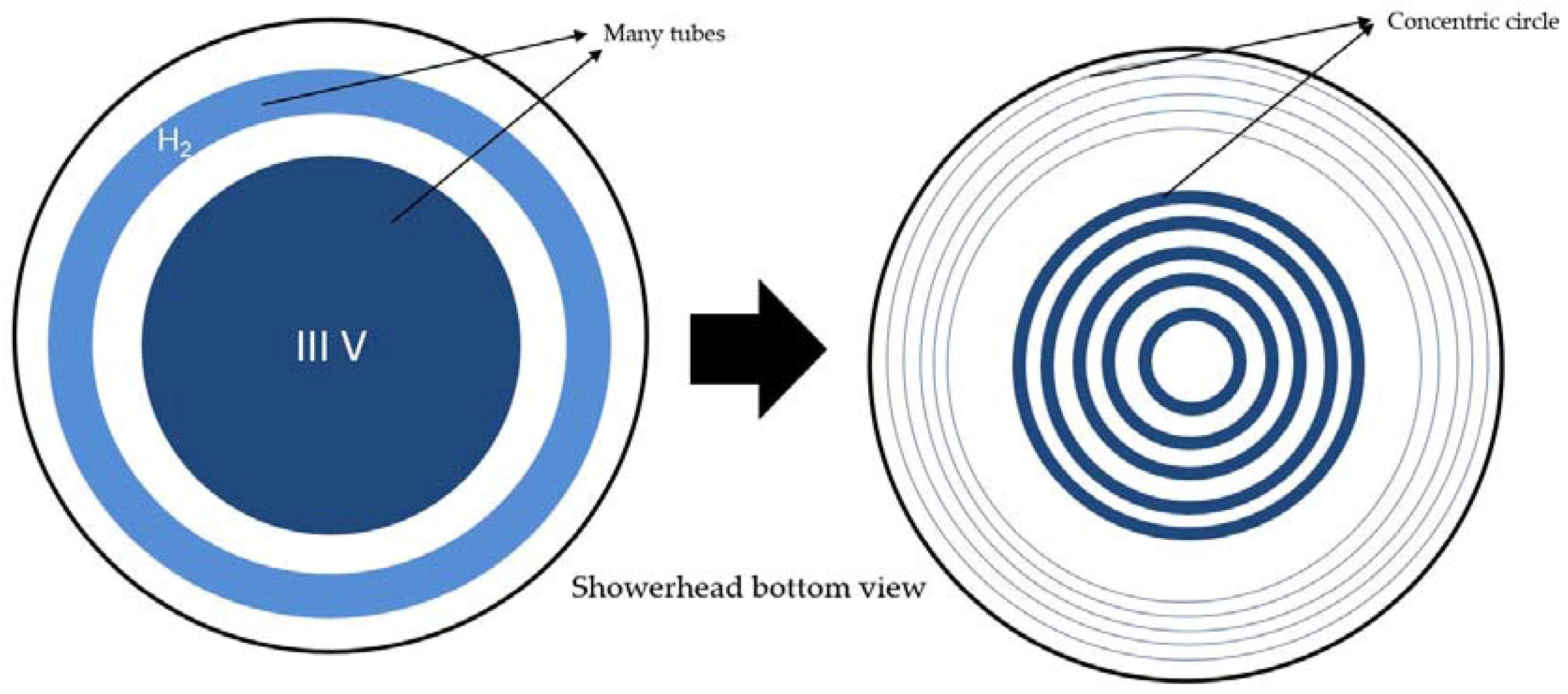
3.1. Approximate Approach of the Real Showerhead
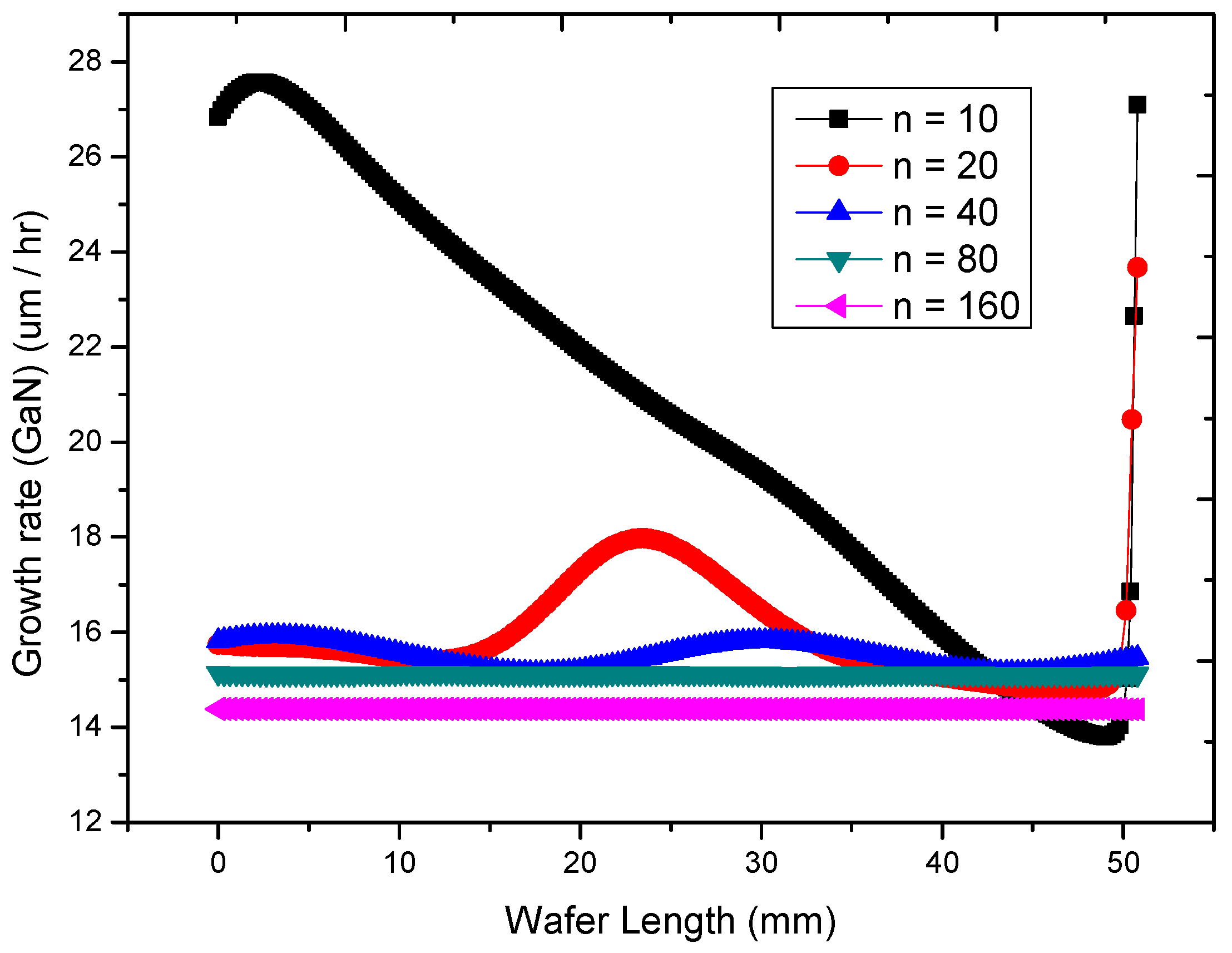
3.2. Verification of Two-Dimensional Numerical Modeling
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Evans, G.H.; Greif, R. A Numerical Model of the Flow and Heat Transfer in a Rotating Disk Chemical Vapor Deposition Reactor. J. Heat Transfer 1987, 109, 928–935. [Google Scholar] [CrossRef]
- Thompson, A.G.; Stall, R.A.; Zawadzki, P.; Evans, G.H. The scaling of CVD rotating disk reactors to large sizes and comparison with theory. J. Electron. Mater. 1996, 25, 1487–1494. [Google Scholar] [CrossRef]
- Fotiadis, D.I.; Kieda, S.; Jensen, J.F. Transport phenomena in vertical reactors for metalorganic vapor phase epitaxy. J. Cryst. Growth 1990, 102, 441–470. [Google Scholar] [CrossRef]
- Zuo, R.; Zhang, H.; Liu, X.L. Transport phenomena in radial flow MOCVD reactor with three concentric vertical inlets. J. Cryst. Growth 2006, 293, 498–508. [Google Scholar] [CrossRef]
- Soong, C.Y.; Chyuan, C.H.; Tzong, R.Y. Thermo-Flow Structure and Epitaxial Uniformity in Large-Scale Metalorganic Chemical Vapor Deposition Reactors with Rotating Susceptor and Inlet Flow Control. J. Appl. Phys. 1998, 37, 5823–5834. [Google Scholar] [CrossRef]
- Mitrovic, B.; Gurary, A.; Kadinski, L. On the flow stability in vertical rotating disc MOCVD reactos under a wide range of process parameters. J. Cryst. Growth 2006, 287, 656–663. [Google Scholar] [CrossRef]
- Mitrovic, B.; Gurary, A.; Quinn, W. Process conditions optimization for the maximum deposition rate and uniformity in vertical rotating disc MOCVD reactors based on CFD modeling. J. Cryst. Growth 2007, 303, 323–329. [Google Scholar] [CrossRef]
- Talalaev, R.A.; Yakovlev, E.V.; Karpov, S.Y.; Makarov, Y.N. On low temperature kinetic effects in metal–organic vapor phase epitaxy of III–V compounds. J. Cryst. Growth 2001, 230, 232–238. [Google Scholar] [CrossRef]
- Karpov, S.Y.; Prokofyev, V.G.; Yakovlev, E.V.; Talalaev, R.A.; Makarov, Y.N. Novel approach to simulation of group-III nitrides growth by MOVPE. MRS J. Nitride Semicond. Res. 1999, 4, e4. [Google Scholar] [CrossRef]
- Yakovlev, E.V.; Shpolyanskiy, Y.A.; Talalaev, R.A.; Karpov, S.Y.; Makarov, Y.N.; Bergunde, T.; Lowry, S.A. Detailed Modeling of Metal Origanic Vapor Phase Epitaxy of III-V Ternary Compounds in Production-Scale AIX 2400G3 Planetary Reactor. In Fundamental Gas-Phase and Surface Chemistry of Vapor Deposition II and Process Control, Diagnostics and Modeling in Semiconductor Manufacturing IV: Proceedings of the Internatioal Symposium; Swihart, M.T., Allendorf, M.D., Meyyappan, M., Eds.; The Electrochemical Society: Atlantic, NJ, USA, 2001; Volume 2001–2013, pp. 292–300. [Google Scholar]
- Crose, M.; Kwon, J.S.; Tran, A.; Christofides, P.D. Multiscale modeling and run-to-run control of PECVD of thin film solar cells. Renew. Energy 2017, 100, 129–140. [Google Scholar] [CrossRef]
- Crose, M.; Tran, A.; Christofides, P.D. Multiscale Computational Fluid Dynamics: Methodology and Application to PECVD of Thin Film Solar Cells. Coatings 2017, 7, 22. [Google Scholar] [CrossRef]
- Hu, C.K.; Chien, H.I.; Li, T.T. Numerical analysis for the growth of epitaxy layer in a large-size MOCVD reactor. Key Eng. Mater. 2015, 656, 515–519. [Google Scholar] [CrossRef]
- Hu, C.K.; Li, T.T.; Lin, Y. The optimization of thermal flow field in a large-size MOCVD reactor. ECS Trans. 2013, 52, 1021–1026. [Google Scholar] [CrossRef]
- Hu, C.K.; Chen, C.J.; Wei, T.C.; Li, T.T.; Wang, C.C.; Huang, C.Y. Investigation of a Simplified Mechanism Model for Prediction of Gallium Nitride Thin Film Growth through Numerical Analysis. Coatings 2017, 7, 43. [Google Scholar] [CrossRef]

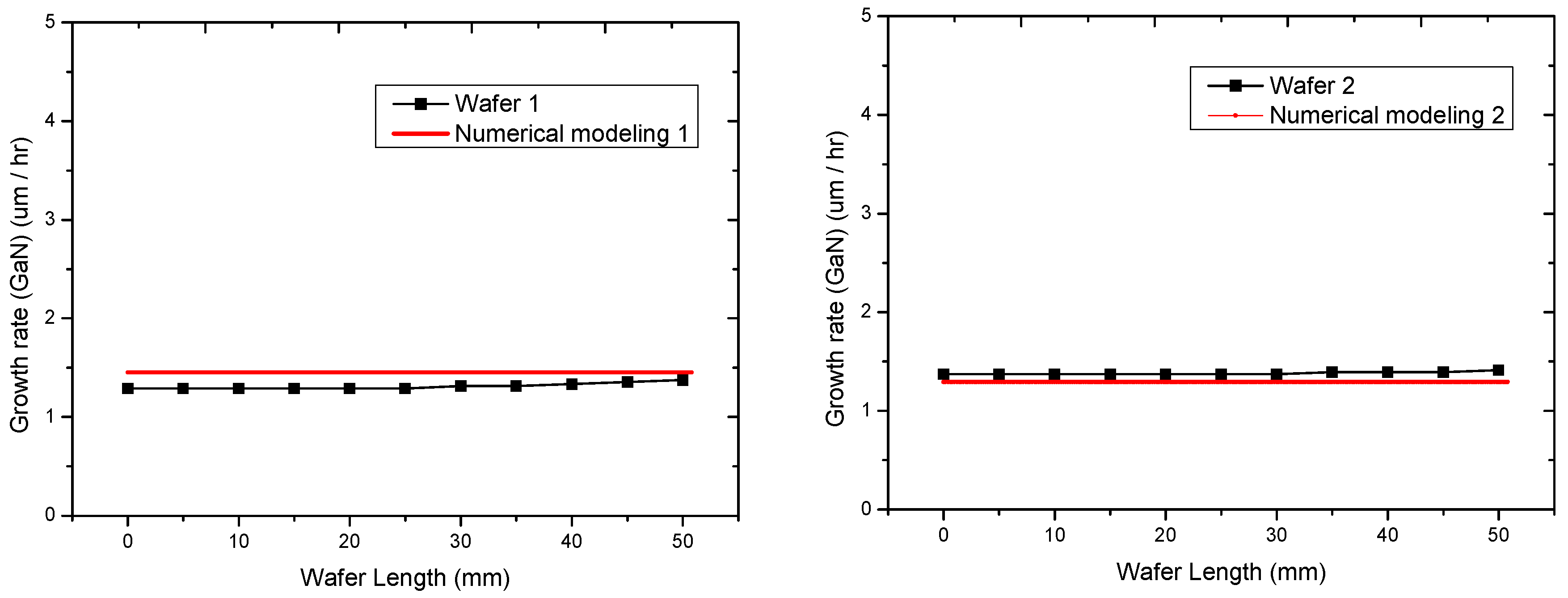
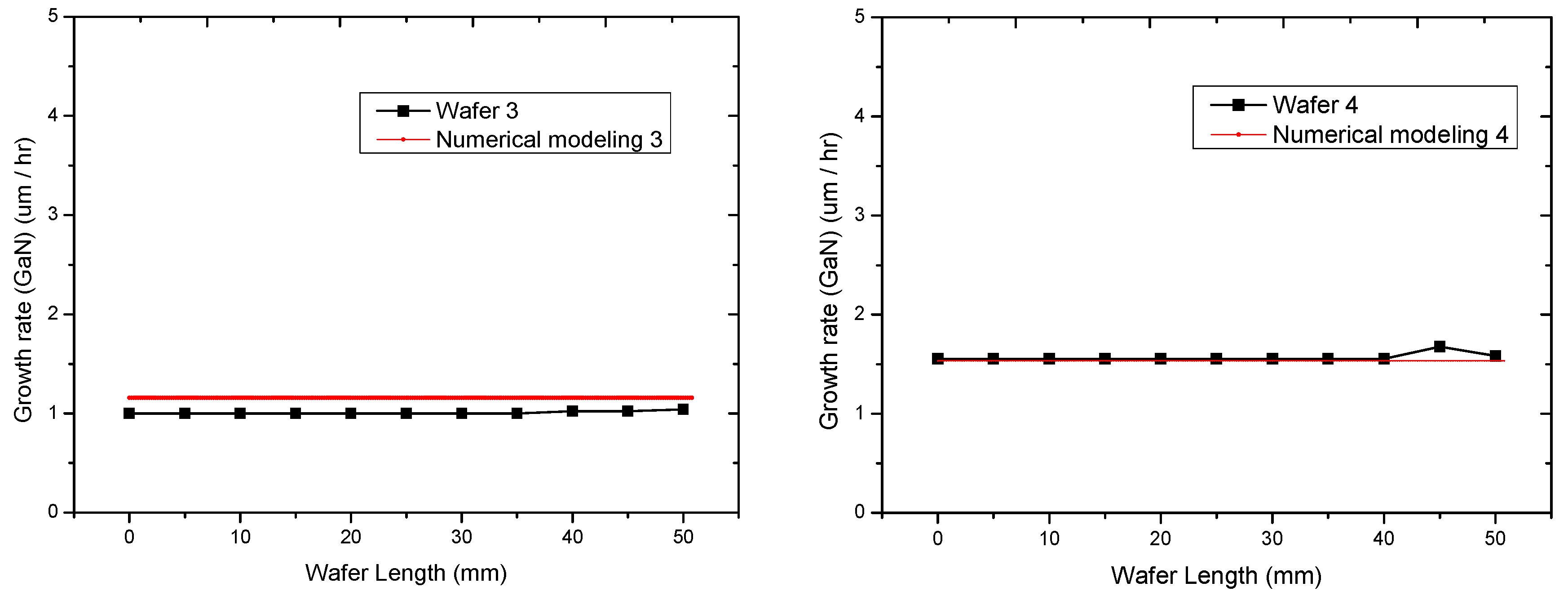
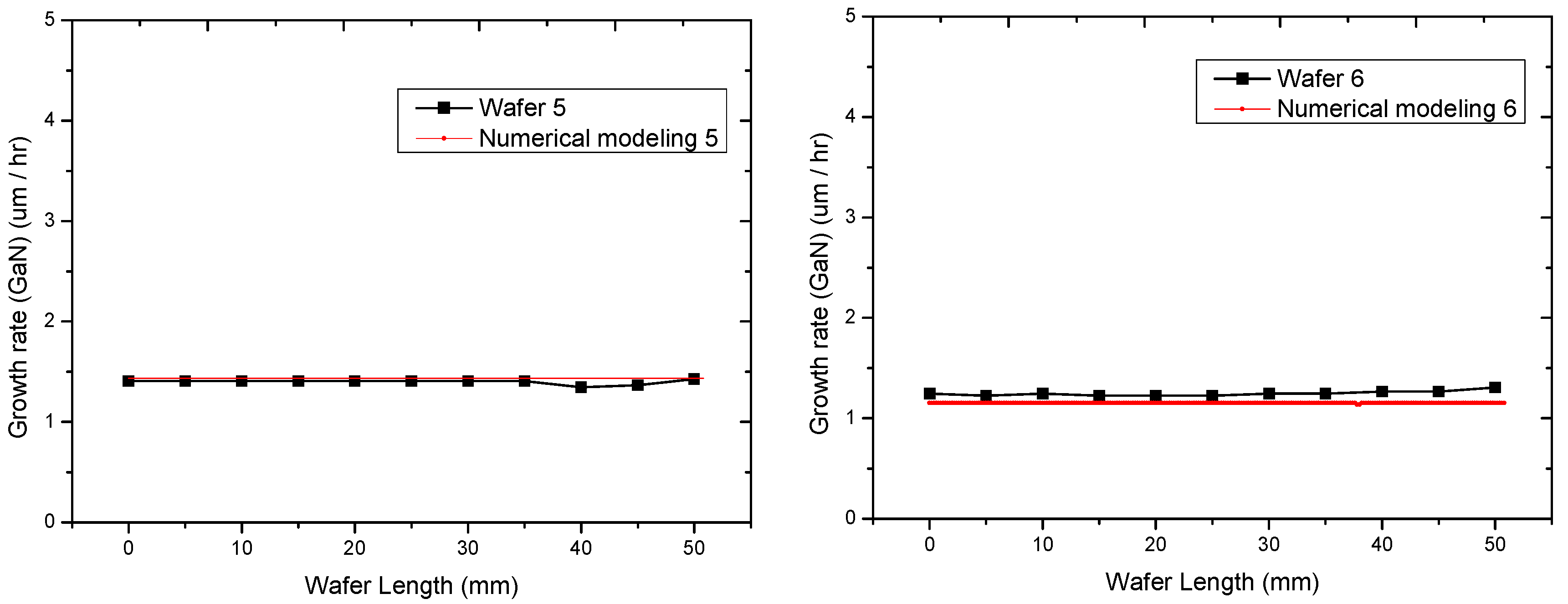
| Wafer Code | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Parameter | ||||||
| Temperature (°C): Susceptor | 1238 | 1188 | 1188 | 1188 | 1188 | 1188 |
| Temperature (°C): Wall | 27 | 27 | 27 | 27 | 27 | 27 |
| Pressure (mbar) | 267 | 267 | 400 | 133 | 133 | 133 |
| Pressure (torr) | 200 | 200 | 300 | 100 | 100 | 100 |
| TMGa (sccm) | 220 | 220 | 220 | 220 | 165 | 150 |
| NH3 (sccm) | 20,000 | 20,000 | 20,000 | 20,000 | 20,000 | 20,000 |
| H2 (sccm) | 2500 | 2500 | 2500 | 2500 | 2500 | 2500 |
| Rotation rate (rpm) | 60 | 60 | 60 | 60 | 60 | 60 |
| Process time (min) | 180 | 180 | 180 | 180 | 180 | 180 |
| Average Thickness (um) | 4 | 4.2 | 3.15 | 4.8 | 4.16 | 3.8 |
| Parameter | A | n |
|---|---|---|
| Origin K | 3.68 × 109 | 2.05 |
| Modified K | 3.68× 106 | 0.72 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, C.-K.; Chen, C.-J.; Wei, T.-C.; Li, T.T.; Huang, C.-Y.; Chao, C.-L.; Lin, Y.-J. Numerical Verification of Gallium Nitride Thin-Film Growth in a Large MOCVD Reactor. Coatings 2017, 7, 112. https://doi.org/10.3390/coatings7080112
Hu C-K, Chen C-J, Wei T-C, Li TT, Huang C-Y, Chao C-L, Lin Y-J. Numerical Verification of Gallium Nitride Thin-Film Growth in a Large MOCVD Reactor. Coatings. 2017; 7(8):112. https://doi.org/10.3390/coatings7080112
Chicago/Turabian StyleHu, Chih-Kai, Chun-Jung Chen, Ta-Chin Wei, Tomi T. Li, Chih-Yung Huang, Chu-Li Chao, and Yi-Jiun Lin. 2017. "Numerical Verification of Gallium Nitride Thin-Film Growth in a Large MOCVD Reactor" Coatings 7, no. 8: 112. https://doi.org/10.3390/coatings7080112
APA StyleHu, C.-K., Chen, C.-J., Wei, T.-C., Li, T. T., Huang, C.-Y., Chao, C.-L., & Lin, Y.-J. (2017). Numerical Verification of Gallium Nitride Thin-Film Growth in a Large MOCVD Reactor. Coatings, 7(8), 112. https://doi.org/10.3390/coatings7080112





