Performance Analysis of Stainless Steel Fiber Recycled Aggregate Concrete Under Dry and Wet Cycles Based on Response Surface Methodology

Abstract

Recycled aggregate concrete refers to concrete made by using recycled aggregates produced from construction waste to replace natural aggregates. The performance of recycled aggregate concrete is extremely unstable. Internal factors such as water–cement ratio, porosity, and the properties of recycled aggregates, as well as external factors like temperature, humidity, environmental erosion, and the addition of improvement materials, may all have an impact on its mechanical properties. The response surface analysis method was employed to investigate the impact of three key factors—the number of dry–wet cycles, the content of stainless steel fibers, and the concentration of Na₂SO₄—on the mechanical properties of stainless steel fiber recycled aggregate concrete (SSFRAC) under dry–wet cycling conditions in the study. By incorporating stainless steel fibers into the cementitious gel network, SSFRAC is conceptualized as a composite material where the metal fibers are integrated into the gel matrix, forming a hybrid system akin to metallogels. The response models for compressive strength durability coefficient S_c and flexural strength durability coefficient S_f are established using Design-Expert software to evaluate the significance of these factors and their interactions. The version of Design-Expert used in this study is Design Expert 13.0. The results demonstrated that both S_c and S_f models exhibit high fitting accuracy, effectively capturing the relationships among the factors. The number of dry–wet cycles exhibit the highest significance, followed by Na₂SO₄ concentration and stainless steel fiber content. The interaction between dry–wet cycle number and Na₂SO₄ concentration has a particularly significant impact on S_c. For S_f, stainless steel fiber content is the most significant factor, followed by dry–wet cycle number and Na₂SO₄ concentration, with the interaction between fiber content and Na₂SO₄ concentration exerting a notably strong influence. This study highlights the potential of cement-based gels as raw materials for synthesizing functional composite materials, where the incorporation of metal fibers enhances mechanical performance and durability under aggressive environmental conditions. The findings provide insights into the design and optimization of hybrid gel–metal systems for advanced construction applications.

1. Introduction

Currently, due to infrastructure updates, urban relocation, road and bridge construction, and natural disasters, etc., there is a continuous cycle of new building constructions and demolitions taking place. However, the construction of new buildings inevitably leads to substantial consumption of natural resources while the demolition process generates significant amounts of waste. According to statistics, billions of tons of natural aggregate are consumed in the global concrete industry annually and an immense volume of construction waste is simultaneously produced. In 2005 alone, China witnessed at least 210 million tons of total construction waste (including both from construction activities and demolition) along with a minimum estimate of 100 million tons of waste concrete (comprising both production process leftovers and demolished structures). It is projected that these figures are still on the rise [1]. Consequently, research focusing on recycling construction waste for reuse in new buildings has emerged as a crucial area for investigation. The proposition of recycled aggregate concrete (RAC) not only addressed concerns regarding excessive depletion of natural resources but also offered a solution to the challenge posed by limited disposal options for construction waste. Moreover, it aligns with China’s strategic objective towards sustainable development and environmental conservation [2].

The term RAC refers to the production of concrete through the mixing of crushed, screened, washed, and graded debris from demolished buildings and roads with a specific proportion and gradation of recycled aggregate obtained by crushing, screening, washing, and grading waste concrete. However, due to the presence of internal pores and cracks in most recycled aggregates which are primarily composed of pebbles and cement mortar blocks wrapped in sand, their high water absorption rate significantly impacts the mechanical properties of RAC. Li et al. [3] demonstrated that as the replacement ratio increases when using recycled aggregate instead of ordinary gravel, there is a corresponding decrease in concrete compressive strength. This reduction becomes more pronounced when the replacement ratio for recycled coarse aggregate exceeds 70%. Bravo et al. [4] revealed that incorporating recycled aggregate into concrete leads to a reduction in both tensile strength and modulus of elasticity.

To address these challenges, the incorporation of metal fibers into cementitious gel networks has emerged as a promising approach, drawing inspiration from the concept of metallogels—composite materials where metals are integrated into gel matrices to enhance mechanical and functional properties [5]. Ahmadi et al. [6] conducted a study that demonstrated that the addition of steel fibers resulted in increased tensile strength, flexural strength, and flexural toughness of RAC. The maximum strength of RAC was achieved when the steel fiber content reached 1%. Bayraktar et al. [7] revealed that incorporating steel fibers significantly improved both split tensile strength and flexural strength of RAC, and the enhancement effect was more pronounced as the aspect ratio of steel fibers increased.

However, steel fibers are susceptible to corrosion, particularly in the saline soil area of the Yellow River Basin in China where high sulfate levels lead to sulfate ion penetration and the formation of ettringite and gypsum, resulting in cracks. Corrosion-induced rust cracking is not uncommon and has caused significant concrete aggregate loss, leading to premature structural failure and a notable decline in concrete’s mechanical and durability performance [8]. Incorporating ordinary steel fibers into reinforced concrete components can shorten their service life due to fiber corrosion, thereby affecting long-term durability. Poorsaheli et al. [9] demonstrated that steel fibers may compromise concrete’s anti-corrosion performance and even weaken the positive impact of polyolefin fibers on corrosion resistance. Stainless steel fibers, as a novel industrial material with inherent non-rusting properties along with high tensile strength and modulus of elasticity, offer potential benefits when added to concrete. Their distributed presence can effectively inhibit internal microcrack expansion while their chromium (Cr) and nickel (Ni) elements enhance acid and alkali resistance, thus improving overall corrosion resistance [10]. The innovative addition of stainless steel fibers not only enhances the properties of recycled concrete but also avoids the decrease in the properties of recycled concrete due to the incorporation of ordinary steel fibers.

Wang et al. [11] utilized fractal dimension to characterize the self-similarity and structural complexity of the fracture network, elucidating the morphological disparities of fractures in dry–wet cycles. Zhang et al. [12] demonstrated that the compressive strength, local density, dynamic modulus of elasticity, etc., of RAC were more responsive than ordinary concrete in sulfate-rich environments, particularly during frequent or periodic humidity fluctuations. Simultaneously, they postulated that the interface transition zone (ITZ) between the new aggregate and the cement paste as well as the old mortar played a pivotal role in determining the durability of RAC. Sobhan et al. [13] investigated the deleterious effects of wet–dry cycles and repeated mechanical loading on a rolled concrete pavement composed of recycled concrete aggregate (RCA) and cement, uncovering that the absorption rate of the ITZ was primarily responsible for diminishing compressive and residual bending strength of RCA concrete under dry–wet exposure. Liu et al. [14] analyzed the load–deflection curve (F-δ curve) and characteristic parameters of steel fiber concrete subjected to dry–wet cycles and sulfate corrosion, revealing distinct morphological variations characterized by multi-crack structures and pore formations after successive dry–wet cycles and sulfate corrosion events within localized regions. Shahidzadeh-Bonn et al. [15] discovered through their research that sulfate can induce severe damage to porous materials following dry–wet cycles due to partial dissolution of anhydrous sodium sulfate crystals with concurrent formation of numerous hydrated crystals (Na₂SO₄ ·10H₂O) when relative humidity increases. However, most previous studies have focused on the influence of a single or two factors on the performance of concrete. In reality, the environment is often the result of multiple factors acting simultaneously. There are relatively few studies on the combined effect of the content of stainless steel fibers, the concentration of sulfate solution, and the number of dry–wet cycles.

In addition to recycled aggregate concrete, the durability of cement-based composites under aggressive environments has been widely studied in other material systems. For example, Verre [16] investigated the debonding behavior of fiber-reinforced cementitious matrix–concrete joints conditioned in alkaline and hot water environments, highlighting the significant influence of environmental exposure on bond capacity and failure mechanisms. Such findings demonstrate that the deterioration of cementitious composites in aggressive conditions is a broader concern across different structural applications, which further underpins the necessity of exploring the sulfate resistance of recycled aggregate concrete reinforced with stainless steel fibers.

The present study builds upon the existing research foundation to investigate the mechanical properties and corrosion resistance of SSFRAC under various sulfate dry–wet cycles. By incorporating stainless steel fibers into the cementitious gel network, SSFRAC is conceptualized as a hybrid material that combines the principles of metallogels and functional composites. Regenerated concrete samples with 1%, 1.5%, and 2% volume fractions of stainless steel fibers were subjected to 30, 60, and 90 cycles of dry–wet exposure in Na₂SO₄ solutions with concentrations ranging from 0% to 5%. Using response surface methodology (RSM), this study explores the significant effects of three key factors—dry–wet cycle number, stainless steel fiber volume fraction, and Na₂SO₄ concentration—on the compressive strength corrosion resistance coefficient S_c and flexural strength corrosion resistance coefficient S_f. The findings highlight the potential of cement-based gels as raw materials for synthesizing durable and high-performance composites, where the integration of metal fibers enhances both mechanical properties and environmental resistance. These results provide valuable theoretical support for the further development and practical application of SSFRAC in advanced construction materials, particularly in aggressive environments.

2. Test Materials and Methods

2.1. Raw Materials

The cement used is P.O.42.5 grade ordinary Portland cement provided by Zhongjian Commercial Concrete Co., Ltd. Jiangxia Factory in Wuhan, China; the standard consistency water content is 26.6%, the compressive strength is 49.8 MPa, the initial setting time is 196 min, and the final setting time is 265 min; the coarse aggregate consists of natural coarse aggregate and recycled coarse aggregate, both with a grain size of 5–20 mm and a continuous gradation aggregate; the fine aggregate is non-coastal common fine river sand, with a fineness modulus of 0.7–1.5, and the use of non-coastal river sand is to control and reduce the sulfate and chloride content in the sand. The particle size distribution curves of natural coarse aggregates, recycled coarse aggregates, and fine aggregates are shown in Figure 1. Fly ash and slag powder are double-added II grade fly ash and S95 grade slag powder; the parameters of fly ash and slag powder are shown in

Table 1. Parameters of fly ash and slag powder.

Types	Density (g/cm3)	Specific Surface Area (m2/kg)	Loss on Ignition (%)	28-Day Activity Index	Water Demand Ratio (%)	45-Nanometer Residue (%)
II grade fly ash	2.17	426	3.0	84	93.6
S95 grade slag powder	2.80	515		97	92.8	4

. Sodium sulfate is used as a sulfate admixture; the superplasticizer is a polycarboxylate high-efficiency superplasticizer, with a slump loss of no more than 25%; the fiber used is 304 straight stainless steel fiber. The chromium content of the fibers is 18%–20%, the nickel content is 8%–11%, the length is 50–60 mm, the diameter is 0.33–0.4 mm, the aspect ratio is 150, the longitudinal elastic modulus is 193 GPa, and the tensile strength is greater than or equal to 1200 MPa. The measurement of the strength of stainless steel fibers is based on Steel Fibers for Concrete (GB/T 39147-2020) [17]. Figure 2 shows the pictures of the main materials used in the experiment.

2.2. Test Mix Proportions and Specimen Preparation

The test procedure follows the Chinese industry standard Technical Specification for Application of Recycled Aggregate (JGJ/T 240-2011) [18], issued by the Ministry of Housing and Urban–Rural Development of the People’s Republic of China, applicable within the People’s Republic of China, and implemented on 1 December 2011. The SSFRAC mixture design was conducted using C30 as the reference strength, as detailed in

Table 2. Mix proportions (kg/m³).

Type	Cement	Fly Ash	Slag Powder	Recycled Aggregate	Natural Aggregate	Sand	Stainless Steel Fiber	Water	Superplasticizer
C	226	76	76	0	1147	673	0	174	7.6
RAC	226	76	76	229	918	673	0	174	7.6
1%SSFRAC	226	76	76	229	906	673	11.47	174	7.6
1.5%SSFRAC	226	76	76	229	901	673	17.21	174	7.6
2%SSFRAC	226	76	76	229	895	673	22.94	174	7.6

. The recycled aggregate replacement rate is 20%, and both fly ash and slag powder were added at a volume fraction of 20%. Additionally, the stainless steel fiber dosage ranges from 1% to 2%. Before adding fibers, the recycled aggregates should be pre-treated to reach the saturated surface dry state. Then, the aggregates, fibers, cement, and water should be added in sequence and stirred in a powerful mixer for a sufficient period of time to ensure that the fibers are as evenly distributed as possible in the concrete.

In this study, the replacement level of recycled coarse aggregate was fixed at 20%. This choice was made to balance two considerations. On the one hand, previous studies have shown that when the replacement ratio exceeds approximately 30%–40%, the mechanical properties of RAC decline significantly due to the high porosity and water absorption of recycled aggregates [3,4]. On the other hand, using a 20% replacement ratio allows the RAC specimens to retain sufficient baseline strength while still reflecting the performance modifications introduced by stainless steel fiber incorporation. Furthermore, since the objective of this work was to investigate the effects of stainless steel fiber dosage, Na₂SO₄ concentration, and dry–wet cycle number, fixing the recycled aggregate content helped to reduce the number of experimental variables and simplify the response surface design.

According to the Standard for Test Methods of Concrete Physical and Mechanical Properties (GB/T 50081-2019) [19], the standard cube specimen for compressive strength tests is 150 mm × 150 mm × 150 mm. In this study, 100 mm × 100 mm × 100 mm specimens were used due to preparation and equipment limitations. This size has been widely adopted in related research, and the standard also provides testing procedures for such non-standard specimens. The molds were demolded from the concrete specimens after 48 h of casting. Subsequently, the specimens underwent standard curing conditions (20 ± 2 °C, with relative humidity exceeding 95%) for a duration of 26 days.

2.3. Test Methods

We removed the specimens that had been maintained for 26 days, wiped off any surface moisture, and then dried them in an oven at 80 °C for 48 h. Once the drying process was completed, we allowed the specimens to cool in a dry environment to room temperature before placing them into the LSY-18 sulfate dry–wet cycling test equipment, which is from Jinan Yongce Industrial Equipment Co., Ltd. in Jinan, China. We ensured a spacing of 20 mm between adjacent specimens and maintained a distance of over 20 mm between the specimens and the inner wall of the equipment. An appropriate concentration of Na₂SO₄ solution was poured into the upper water tank through the filling port for each dry–wet cycle. Each cycle consisted of 24 h, with immersion lasting for 15 h followed by a drainage and air-drying period of 0.5 h. The subsequent drying time was set at 6 h with an additional cooling time of one hour, resulting in a total cycling time of 24 h, maintaining drying temperature at 80 °C and cooling temperature at 28 °C while controlling solution temperature within the range of 20–25 °C. pH levels were monitored every ten cycles in both upper and lower water tanks to ensure they remained between pH values of six and eight. After completing thirty cycles, we assessed the compressive strength using a DYE-2000S microcomputer servo-hydraulic pressure testing machine from Dongguan Senming Equipment Co., Ltd in Dongguan, Guangdong as well as an MTS microcomputer-controlled electronic pressure testing machine from Jinan Wenteng Testing Instrument Co., Ltd. in Jinan, Shandong. The test procedure follows the Standard for Test Methods of Concrete Physical and Mechanical Properties (GB/T 50081-2019) and the Standard for Test Methods of Long-Term Performance and Durability of Ordinary Concrete (GB/T 50082-2019) [20].

3. Compressive Strength

3.1. Compressive Strength Test Results

Table 3. Cube compressive strength test results.

Type of Concrete	Fiber Content/(%)	Cube Compressive Strength/(MPa)
		Sample 1	Sample 2	Sample 3	Average
C	-	49.9	49.7	49.8	49.80
RAC	-	44.0	43.6	43.3	43.63
1%SSFRAC	1%fiber	49.8	49.7	49.4	49.63
1.5%SSFRAC	1.5%fiber	53.1	53.6	53.2	53.30
2%SSFRAC	2%fiber	54.8	54.7	54.7	54.73

shows the cube compressive strengths of ordinary concrete, RAC, and SSFRAC. Three parallel tests were conducted for each group of specimens to reduce test errors. It can be seen that the compressive strength of SSFRAC is lower than that of ordinary concrete. This is because RAC contains pores and cracks within its structure, resulting in a compressive strength significantly lower than that of natural aggregate concrete. However, the addition of stainless steel fibers to RAC can notably improve its compressive strength. Based on the data presented in Table 3, Figure 3 illustrates the cube compressive strength of each group of specimens after a 28-day curing period. As depicted in Figure 3, the compressive strength of SSFRAC demonstrates varying performance under different fiber dosage conditions. The introduction of stainless steel fibers leads to a rapid initial enhancement followed by a gradual plateau in SSFRAC’s compressive strength. When the dosage of fibers reaches 2%, the compressive strength of SSFRAC reaches 54.73 MPa, which is 11.1 MPa higher than that of RAC, with an increase of 25.4%. This is attributed to the generation of microcracks within SSFRAC when subjected to loading forces and the dispersion of stainless steel fibers throughout the concrete matrix, which impedes crack development within the matrix by altering their original trajectory. Due to their random distribution within the concrete, cracks propagate along complex paths around or through the fibers, necessitating more energy and consequently enhancing SSFRAC’s compressive strength.

3.2. Destructive Features

Figure 4 presents the compressive failure morphologies of RAC and 1.5% SSFRAC. Both materials initially exhibit longitudinal cracks during the early stage of loading. At the late stage, RAC undergoes rapid fragmentation due to the absence of fiber reinforcement, whereas SSFRAC retains integrity and residual load-bearing capacity because of the bridging and tensile effects of stainless steel fibers.

4. RSM Model Establishment

4.1. Response Surface Model Selection

The RSM is a technique used to approximate a function that cannot be explicitly expressed by creating a series of design points based on random variables and analyzing experimental data to fit an explicit function. It enables the assessment of the relationship between one or more responses of measurable variables through regression fitting, response surfaces, and contour lines. In this study, the central composite design (CCD) method will be employed for response surface design [21,22,23,24].

By employing the CCD method offered by the Design-Expert software, a more accurate second-order model was chosen, and a quadratic response surface equation was formulated, encompassing all first-order, second-order, and two-way interaction terms [25], as follows:

$$\mathrm{Y}={\mathsf{\beta }}_0+\sum _{\mathrm{i}=1}^{\mathrm{k}}{\mathsf{\beta }}_{\mathrm{i}}{\mathrm{X}}_{\mathrm{i}}+\sum _{\mathrm{i}=1}^{\mathrm{k}}{\mathsf{\beta }}_{\mathrm{i}\mathrm{i}}{\mathrm{X}}_{\mathrm{i}}^2+\sum _{\mathrm{i}<\mathrm{j}}^{\mathrm{k}}{\mathsf{\beta }}_{\mathrm{i}\mathrm{j}}{\mathrm{X}}_{\mathrm{i}}{\mathrm{X}}_{\mathrm{j}}+\mathrm{e}\left({\mathrm{X}}_{\mathrm{i}}\right.,{\mathrm{X}}_{\mathrm{i}},\cdots ,\left.{\mathrm{X}}_{\mathrm{i}}\right)$$

(1)

In Equation (1), Y denotes the response value which, in this study, refers to the compressive strength durability coefficient (S_c) or the flexural strength durability coefficient (S_f), both of which are dimensionless. X represents the independent variables, namely the number of dry–wet cycles (cycles), the stainless steel fiber content (vol.%), and the Na₂SO₄ concentration (mass%). The regression coefficients (β) are dimensionless parameters derived from model fitting. The term e denotes the residual error, defined as the deviation between the experimentally observed values and those predicted by the regression model.

4.2. Factors Levels and Response

A three-factor two-level experiment was conducted, combining the external dry–wet cycle frequency (A), the amount of stainless steel fibers in recycled concrete (B), and the concentration of Na₂SO₄ solution (C). The factors and levels are detailed in

Table 4. RSM factor levels.

Factor	Code	Code Levels
		−1	0	1
The number of dry–wet cycles	A	30	60	90
Fiber content	B	1	1.5	2
Na2SO4 Concentration	C	1	3	5

. The response values selected were the compressive strength retention coefficient $S_c$ and flexural strength retention coefficient $S_f$. Formulas (2) and (3) were utilized to calculate the strength change in SSFRAC after undergoing a specific number of dry–wet cycles.

$${\mathrm{S}}_{\mathrm{c}}={\displaystyle \frac{{\mathrm{c}}_{\mathrm{i}}}{\mathrm{c}}}\times 100\mathrm{\%}$$

(2)

$${\mathrm{S}}_{\mathrm{f}}={\displaystyle \frac{{\mathrm{f}}_{\mathrm{i}}}{\mathrm{f}}}\times 100\mathrm{\%}$$

(3)

In the equation, $S_c$ ($S_f$) represents the coefficient of compressive (flexural) strength corrosion resistance; $c_i$ ($f_i$) denotes the compressive (flexural) strength of SSFRAC after undergoing, measured in MPa; and c(f) signifies the compressive (flexural) strength of SSFRAC from the same batch and age as the test specimen, standard conditioned and cured under standard conditions, also in MPa.

4.3. Coupling Test Design and Results

Considering that the quantity of stainless steel fibers is an internal factor influencing concrete performance, and that the concentration of Na₂SO₄ solution and the number of dry–wet cycles are the external factors, the integration of internal and external factors in concrete constitutes the focal point of this study. The experimental design and response values for fiber tests are detailed in

Table 5. CCD test design and results.

Test Serial Number	Test Design			Test Results
	A: Period	B: Fiber Content	C: Na2SO4 Concentration	${\mathit{S}}_{\mathit{c}}$ /%	${\mathit{S}}_{\mathit{f}}$ /%
1	30	1	1	1	0.81
2	90	1	1	0.73	0.77
3	30	2	1	1.02	0.83
4	90	2	1	0.84	0.73
5	30	1	5	1.02	0.76
6	90	1	5	0.7	0.66
7	30	2	5	1.01	0.89
8	90	2	5	0.74	0.76
9	30	1.5	3	1.04	0.78
10	90	1.5	3	0.84	0.71
11	60	1	3	0.83	0.74
12	60	2	3	0.87	0.81
13	60	1.5	5	0.8	0.68
14	60	1.5	1	0.85	0.71
15	60	1.5	3	0.88	0.75
16	60	1.5	3	0.84	0.74
17	60	1.5	3	0.85	0.73
18	60	1.5	3	0.83	0.74
19	60	1.5	3	0.85	0.74

. Experiments numbered 1–14 represent factorial experiments, whereas 15–19 denote center experiments, resulting in a total of 19 test points. Among these, numbers 1–14 correspond to factorial points, representing fixed three-dimensional points formed by assigning values to A, B, and C as response factors. Numbers 15–19 pertain to repeated test points where the average value from three repetitions is calculated for each group to minimize experimental error.

5. RSM Model Verification

Using the Design-Expert software, the experimental data in Table 5 was integrated and processed to establish models for each response value. The data in Table 5 was subjected to second-order multivariate regression based on Formula (1), followed by optimization of the fitted data. As a result, second-order polynomial models for $S_{\mathrm{c}}$ and $S_f$ concerning the number of dry–wet cycles (A), the number of stainless steel fibers in recycled concrete (B), and Na₂SO₄ solution concentration (C) were obtained.

5.1. Compressive Strength Index $S_C$

The quadratic polynomial model of $S_C$ is

$${\mathrm{S}}_{\mathrm{c}}=0.857-0.119\mathrm{A}+0.023\mathrm{B}+0.002\mathrm{C}+0.018\mathrm{A}\mathrm{B}-0.022\mathrm{A}\mathrm{C}-0.016\mathrm{B}\mathrm{C}+0.078{\mathrm{A}}^2-0.012{\mathrm{B}}^2-0.058{\mathrm{C}}^2$$

(4)

Table 6. Analysis of variance of S_c.

	Sum of Squares	df	Mean Square	F-Value	p-Value
Model	0.1843	9	0.0205	50.68	<0.0001	significant
Residual	0.0036	9	0.0004
Lack of fit	0.0022	5	0.0004	1.28	0.418	not significant
Pure error	0.0014	4	0.0004
Cor total	0.1879	18

and

Table 7. Significance of regression coefficients of S_c..

	Coefficient Estimate	Standard Error	95% CI Low	95% CI High	p-Value
A	−0.1196	0.0066	−0.1346	−0.1047	<0.0001
B	0.0231	0.0066	0.0082	0.0381	0.0067
C	0.0019	0.011	−0.023	0.0268	0.8657
AB	0.0175	0.0071	0.0014	0.0336	0.036
AC	−0.0219	0.0089	−0.042	−0.0018	0.036
BC	−0.0156	0.0089	−0.0357	0.0045	0.1124
A2	0.0779	0.0122	0.0504	0.1054	0.0001
B2	−0.0121	0.0122	−0.0396	0.0154	0.3471
C2	−0.0579	0.019	−0.1009	−0.0149	0.0138

present the analysis of variance and regression coefficient significance, respectively. An adjusted R² = 0.9613 suggests that the model can account for 96.13% of the changes in response values, indicating a strong fit. The F value and p value in Table 6 serve as indicators to assess the effectiveness and significance of $S_c$. With an F value of 50.68 and a p value of less than both 0.0001 and 0.05, it is evident that the model for $S_c$ adheres to reliability and significance criteria; furthermore, with a residual term of 1.28 exceeding 0.05, it signifies a significant association with $S_c$ while maintaining high reliability.

Figure 5 displays the normal distribution of the residuals of $S_c$, with all data points aligning closely to a straight line, indicating a strong fit. In Figure 6, the residuals vs. predictions plot for $S_c$ reveals random distribution on both sides of zero. Additionally, Figure 7 illustrates the predictions vs. actual plot for $S_c$, demonstrating that all data points are tightly clustered around a straight line; closer proximity to this line signifies better performance. The high accuracy of the model is evident from the distribution pattern of these data points. In conclusion, Equation (4) effectively captures the relationship between $S_c$ and the three factors.

5.2. Flexural Strength Index $S_f$

The quadratic polynomial model of $S_f$ is

$${\mathrm{S}}_{\mathrm{f}}=0.734-0.041\mathrm{A}+0.020\mathrm{B}+0.006\mathrm{C}-0.011\mathrm{A}\mathrm{B}-0.014\mathrm{A}\mathrm{C}+0.039\mathrm{B}\mathrm{C}+0.020{\mathrm{A}}^2+0.050{\mathrm{B}}^2-0.046{\mathrm{C}}^2$$

(5)

Table 8. Analysis of variance of S_f..

	Sum of Squares	df	Mean Square	F-Value	p-Value
Model	0.0503	9	0.0056	35.87	<0.0001	significant
Residual	0.0014	9	0.0002
Lack of fit	0.0012	5	0.0002	4.81	0.0767	not significant
Pure error	0.0002	4	0.0001
Cor total	0.0517	18

and

Table 9. Significance of regression coefficients of S_f..

	Coefficient Estimate	Standard Error	95% CI Low	95% CI High	p-Value
A	−0.0412	0.0041	−0.0505	−0.0319	<0.0001
B	0.0202	0.0041	0.0109	0.0295	0.0008
C	0.0061	0.0068	−0.0094	0.0215	0.398
AB	−0.0112	0.0044	−0.0212	−0.0013	0.0312
AC	−0.0141	0.0055	−0.0265	−0.0016	0.0312
BC	0.0391	0.0055	0.0266	0.0515	<0.0001
A2	0.0203	0.0075	0.0032	0.0374	0.0248
B2	0.0503	0.0075	0.0332	0.0674	<0.0001
C2	−0.0464	0.0118	−0.0731	−0.0197	0.0034

present the analysis of variance and regression coefficient significance, respectively. An adjusted R² = 0.9457 indicates that the model can account for 94.57% of the changes in response values, suggesting a strong fit. The F value and p value in Table 8 serve as indicators to assess the effectiveness and significance of $S_f$. With an F value of 35.87 and a p value of less than both 0.0001 and 0.05, it is evident that the model for $S_f$ adheres to reliability and significance criteria; furthermore, with a residual term of 4.81 exceeding 0.05, it signifies a significant association with $S_f$ while maintaining high reliability.

Figure 8 illustrates the normal distribution of the residuals of $S_f$, with all data points aligning closely to a straight line, indicating a strong fit. In Figure 9, the residuals vs. predictions plot for $S_f$ reveals random distribution on both sides of zero. Additionally, Figure 10 depicts the predictions vs. actual plot for $S_f$, demonstrating that all data points are tightly clustered around a straight line; closer proximity to this line signifies better performance. The high accuracy of the model is evident from the distribution pattern of these data points. In conclusion, Equation (5) effectively captures the relationship between $S_f$ and the three factors.

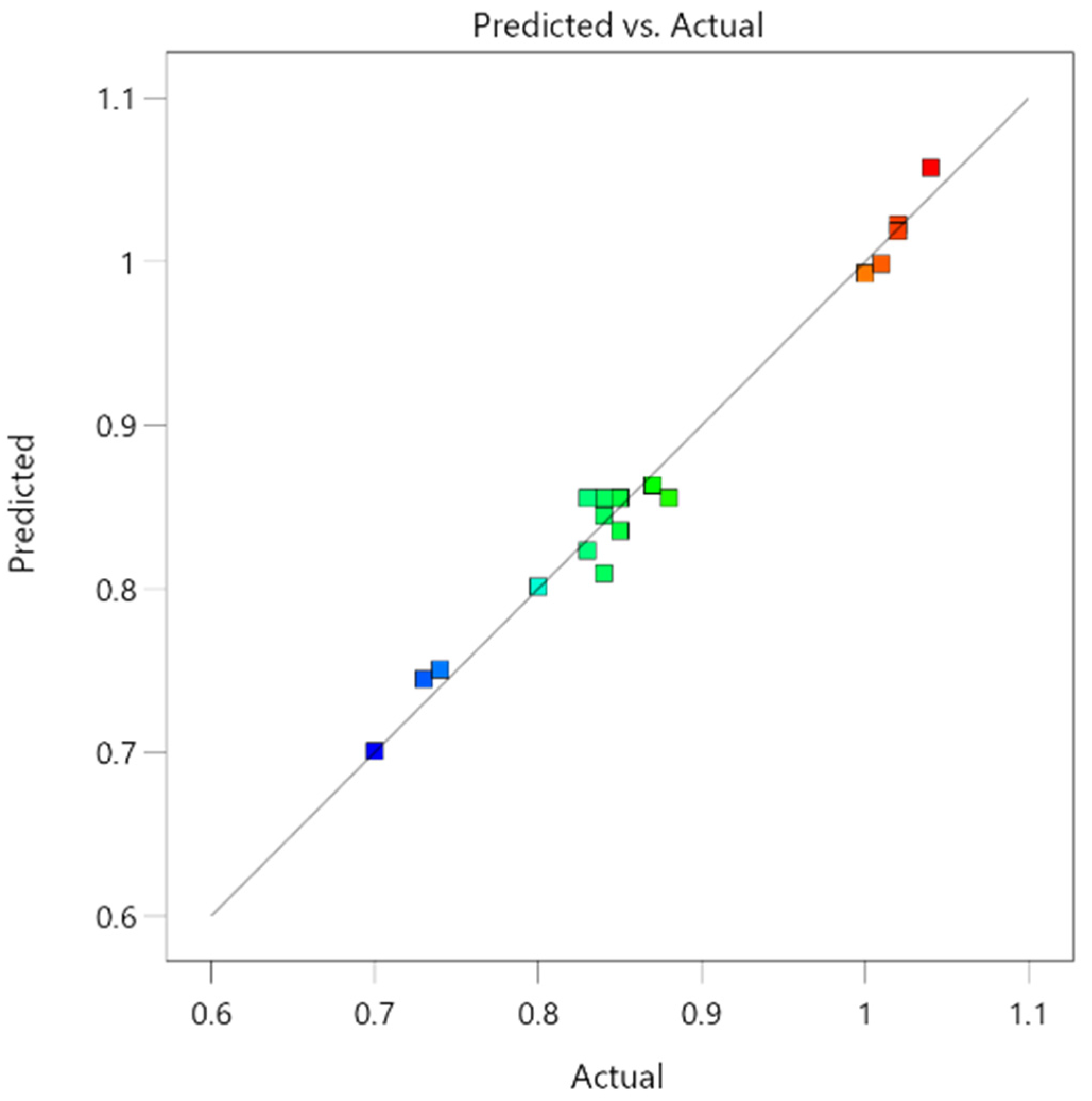
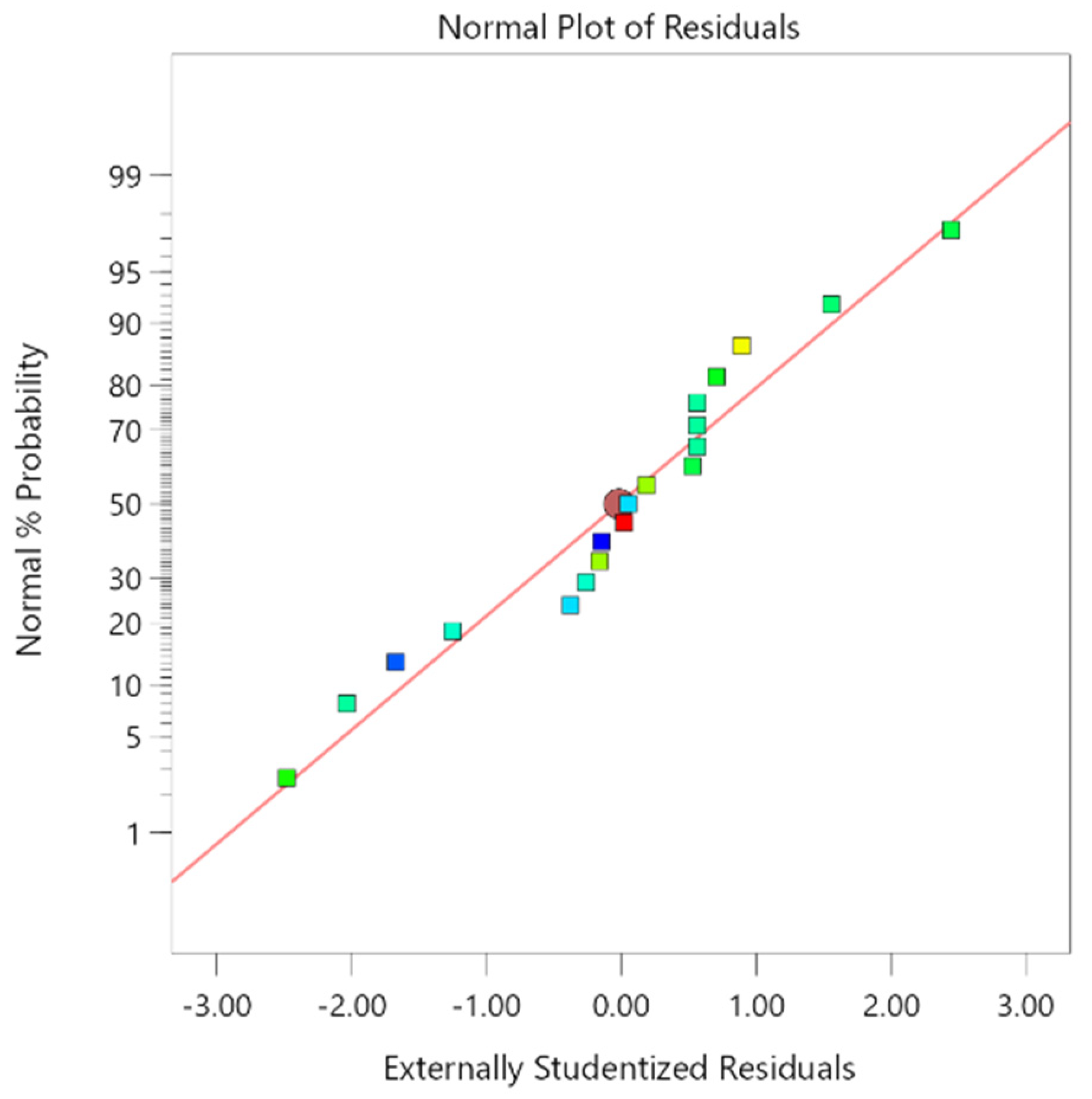
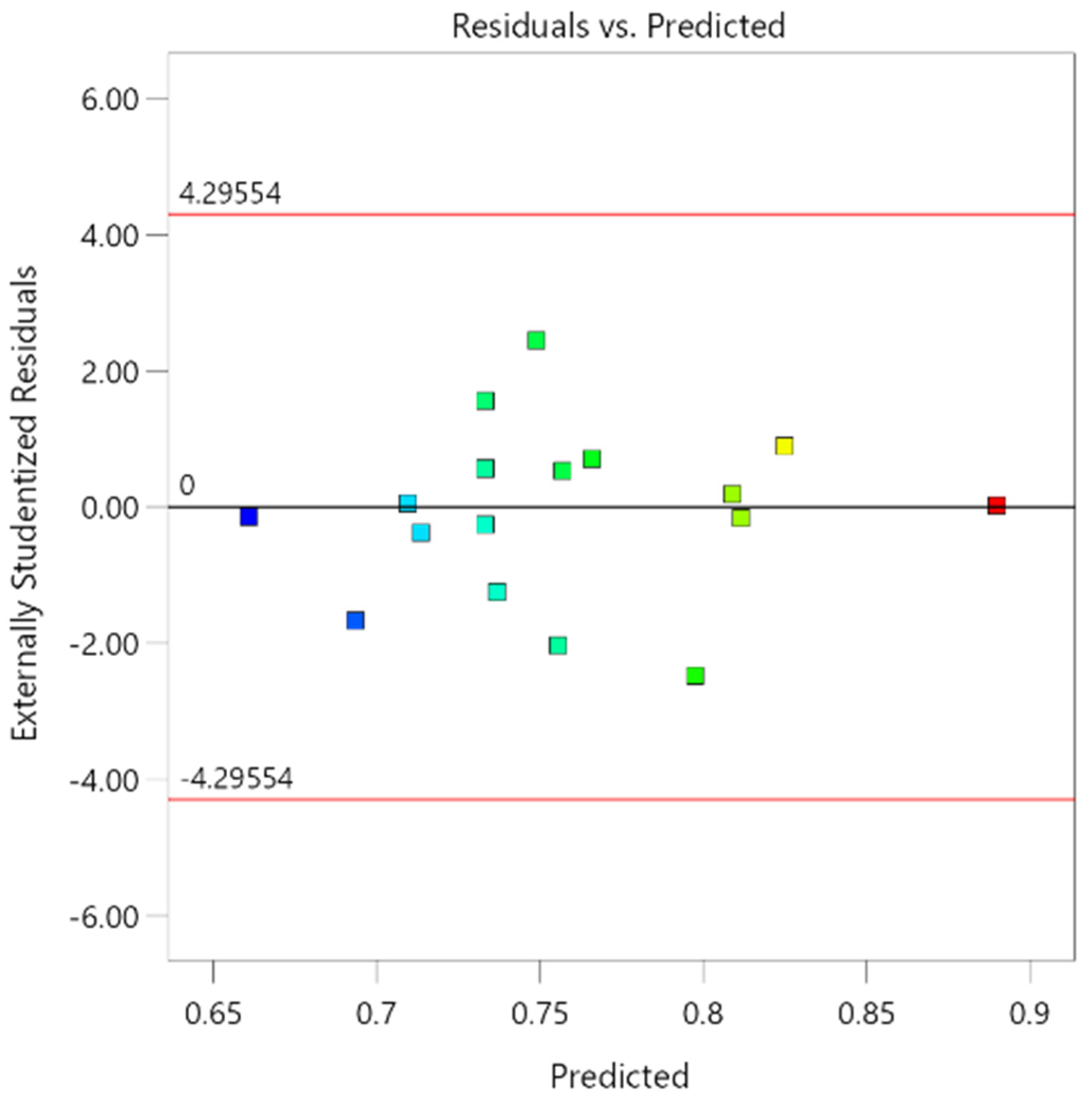
6. Analysis and Discussion of RSM Model Results

6.1. Influences of Various Factors and Their Interaction on $S_c$

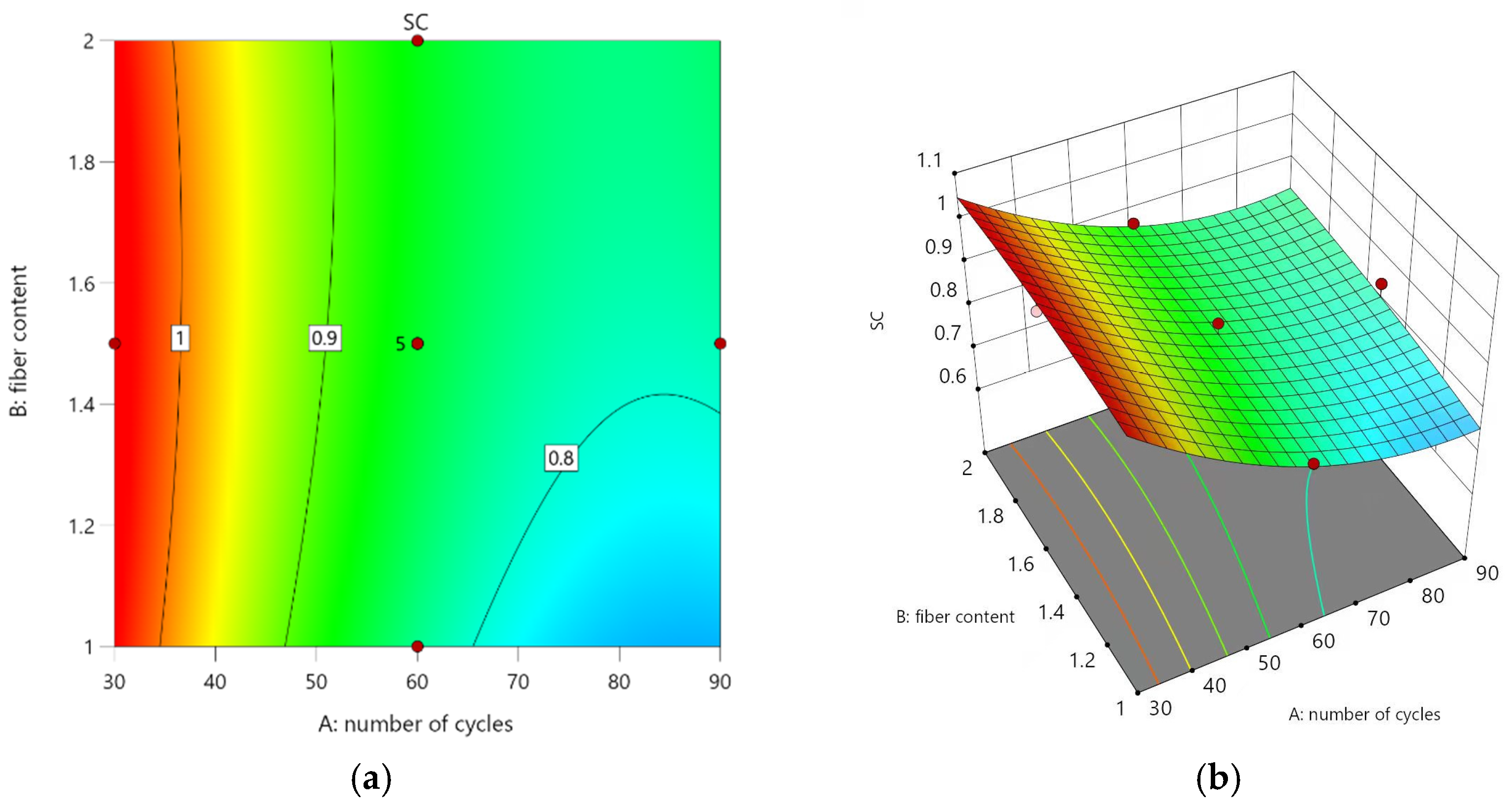
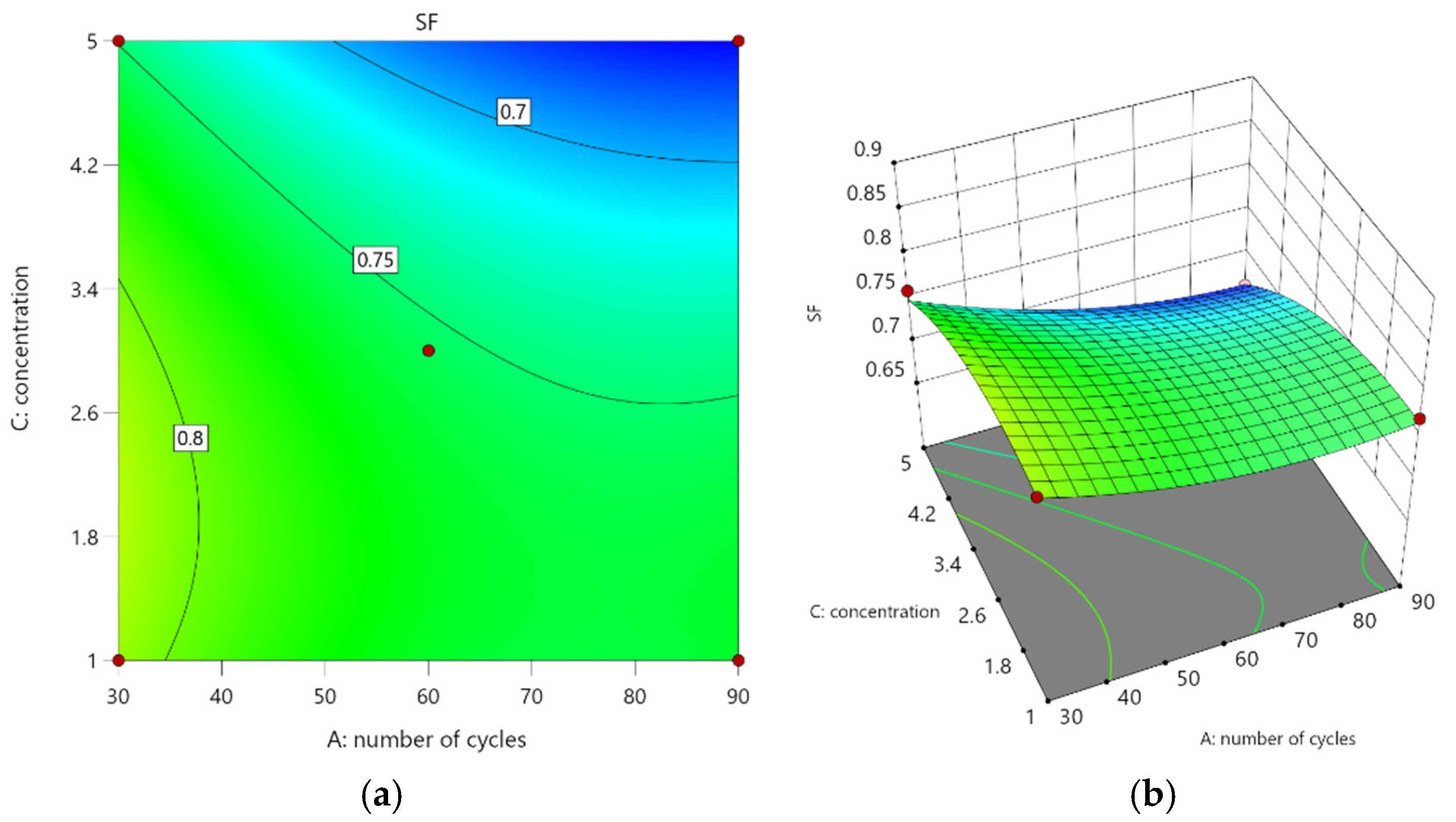
Figure 11a presents contour plots, depicting $S_c$ versus the number of dry–wet cycles and stainless steel fiber content, along with a three-dimensional response surface plot 11b ased on Equation (4). The density of the contour lines in 11a reveals that the vertical coordinate representing stainless steel fiber content is less densely populated than the horizontal coordinate denoting dry–wet cycle count, indicating that the influence of stainless steel fiber content on $S_c$ is comparatively less significant than that of dry–wet cycle count.

In 11b, the three-dimensional response surface can be described as follows: When the fixed number of dry–wet cycles is considered, an increase in stainless steel fiber content leads to a sustained upward trend in SSFRAC’s $S_{\mathrm{c}}$. This observation suggests that within the 1%–2% range, higher fiber content results in enhanced compressive strength due to the bridge-like action of fibers, which inhibits the formation and expansion of macroscopic cracks. Conversely, when maintaining constant fiber content, an increase in dry–wet cycles causes a continuous decline in SSFRAC’s $S_{\mathrm{c}}$, indicating that an increased number of dry–wet cycles weakens SSFRAC’s resistance to pressure.

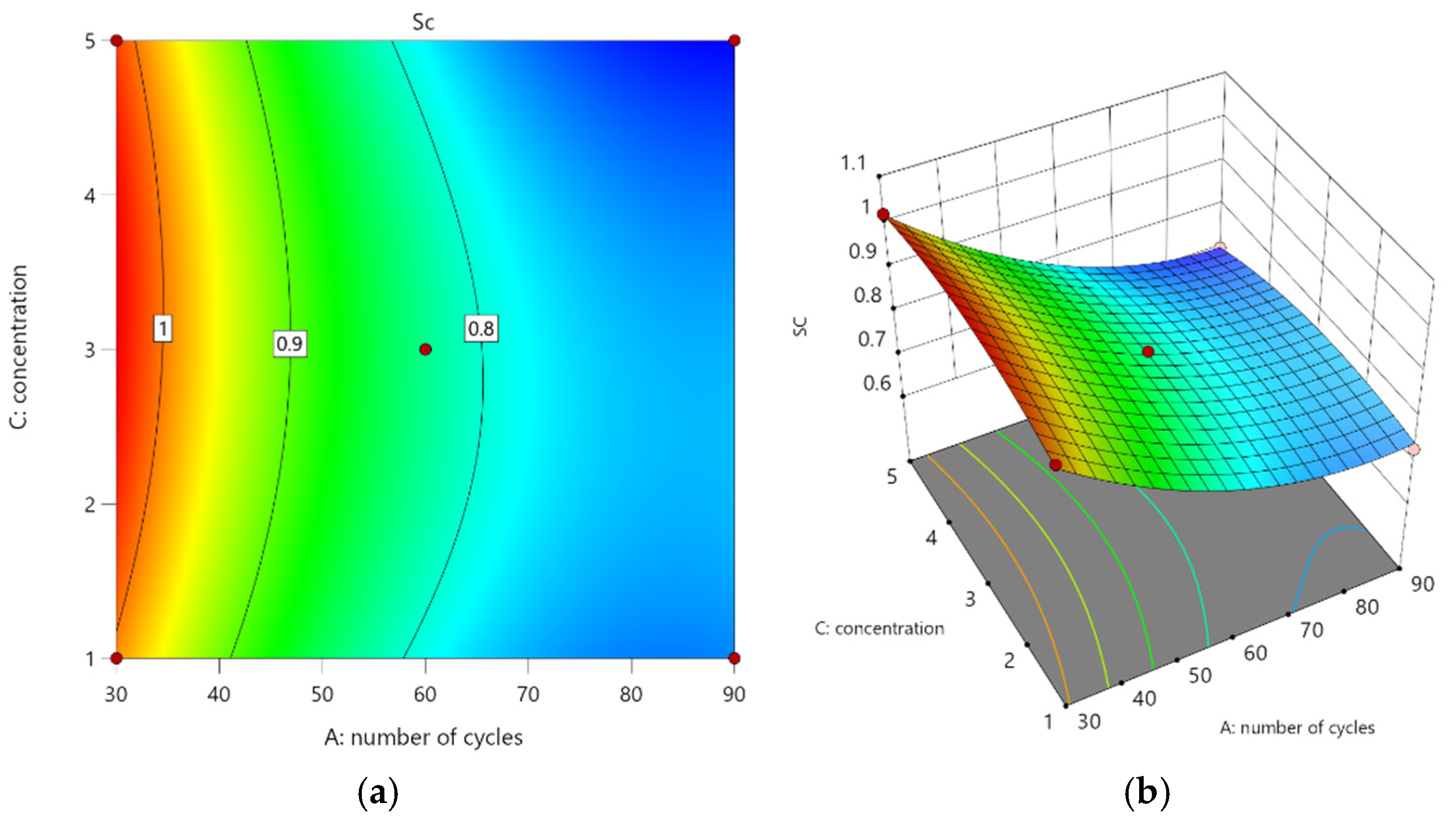
Figure 12a presents contour maps, depicting $S_{\mathrm{c}}$ concerning the number of dry–wet cycles and Na₂SO₄ concentration, along with a three-dimensional response surface plot Figure 12b based on Equation (4). The density of the contour lines in Figure 12a reveals that the Na₂SO₄ concentration contour lines are less dense than those representing dry–wet cycles, indicating that the influence of Na₂SO₄ concentration on $S_{\mathrm{c}}$ is comparatively less significant than that of dry–wet cycles.

In 12b, the three-dimensional response surface can be described as follows: The increase in the concentration of Na₂SO₄ solution is related to the increase in the number of cycles, leading to a declining trend in $S_{\mathrm{c}}$. This indicates that as the cycle progresses, the concrete’s salt solution attains saturation, triggering crystallization and precipitation. Subsequently, this mechanism exacerbates erosion on the concrete surface and results in a significant reduction in SSFRAC’s compressive strength.

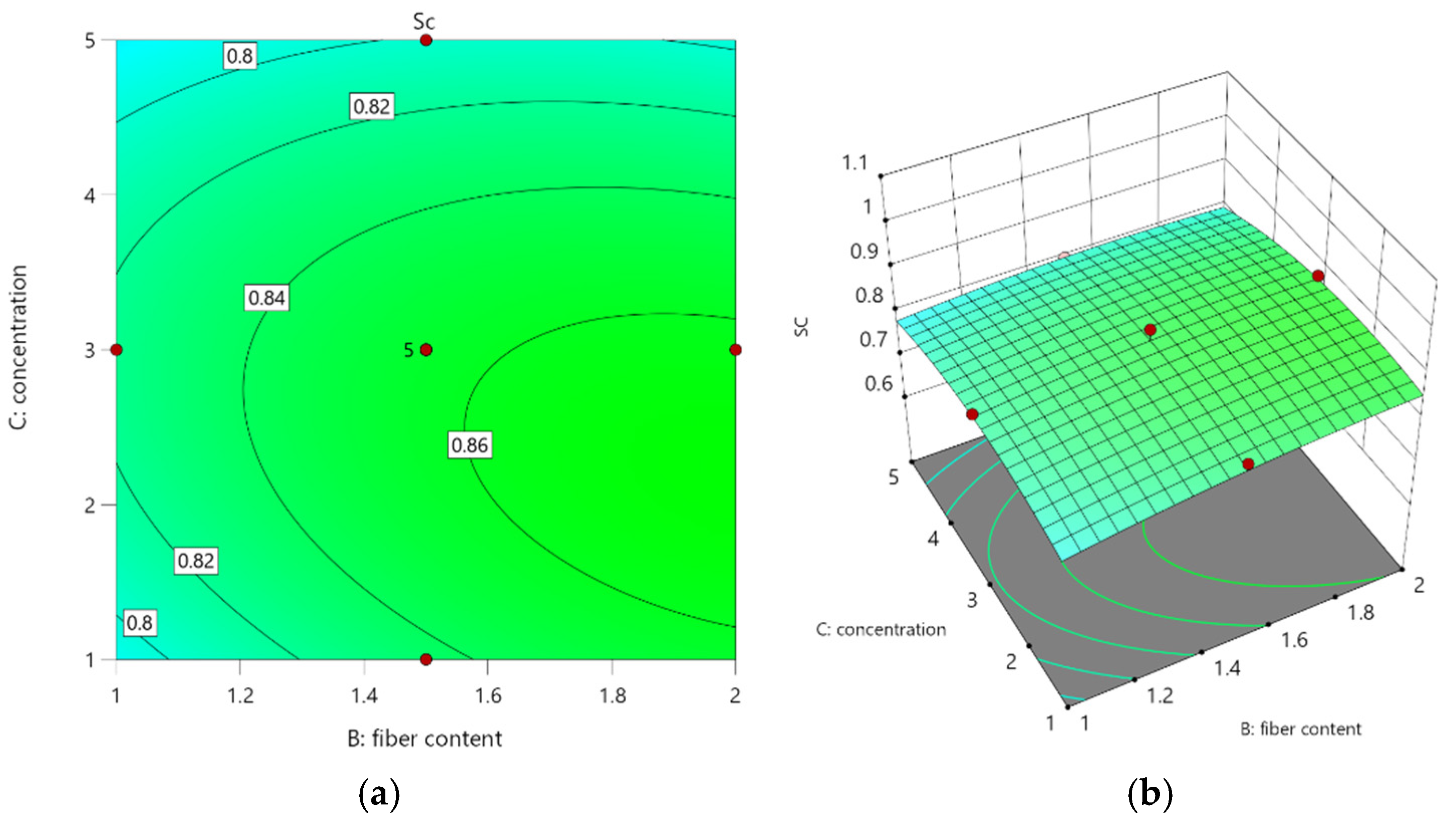
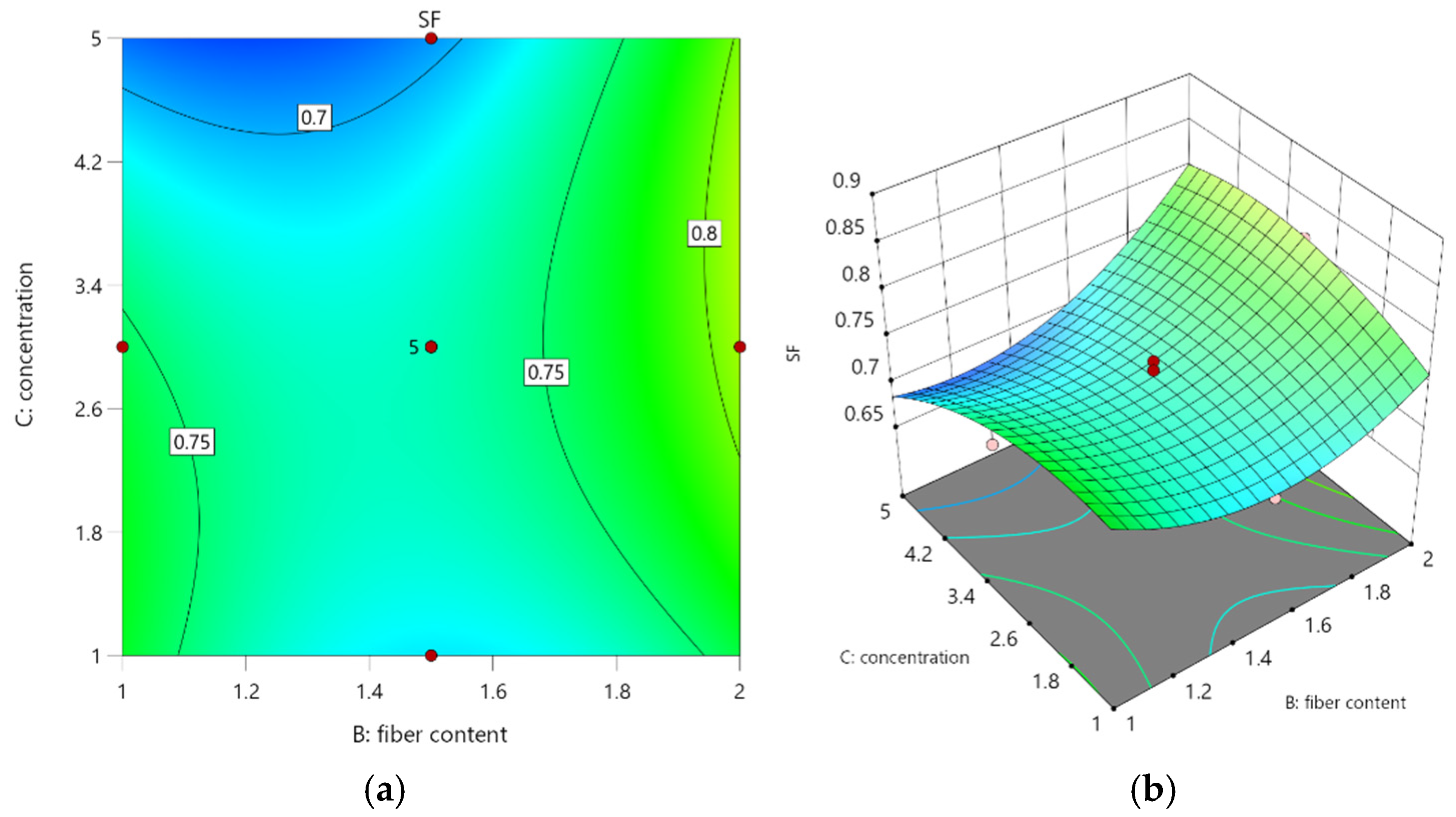
Figure 13 displays contour plots and 3D response surfaces of $S_{\mathrm{c}}$ concerning stainless steel fiber content and Na₂SO₄ concentration based on Equation (4). The figure illustrates that the contour lines representing fiber content on the horizontal axis in Figure 13a are less dense than those depicting Na₂SO₄ concentration on the vertical axis, suggesting that the impact of fiber content on $S_{\mathrm{c}}$ is comparatively less significant than that of Na₂SO₄ concentration. In Figure 13b, the 3D response surface can be described as follows:

When the Na₂SO₄ concentration remains constant, the trend of SSFRAC’s $S_{\mathrm{c}}$ consistently rises with increasing stainless steel fiber content, suggesting that within the 1%–2% range, higher fiber content leads to improved pressure resistance. Conversely, when the fiber content is held constant, the trend of SSFRAC’s $S_{\mathrm{c}}$ declines with increasing Na₂SO₄ concentration, indicating that higher Na₂SO₄ concentrations result in reduced pressure resistance for SSFRAC.

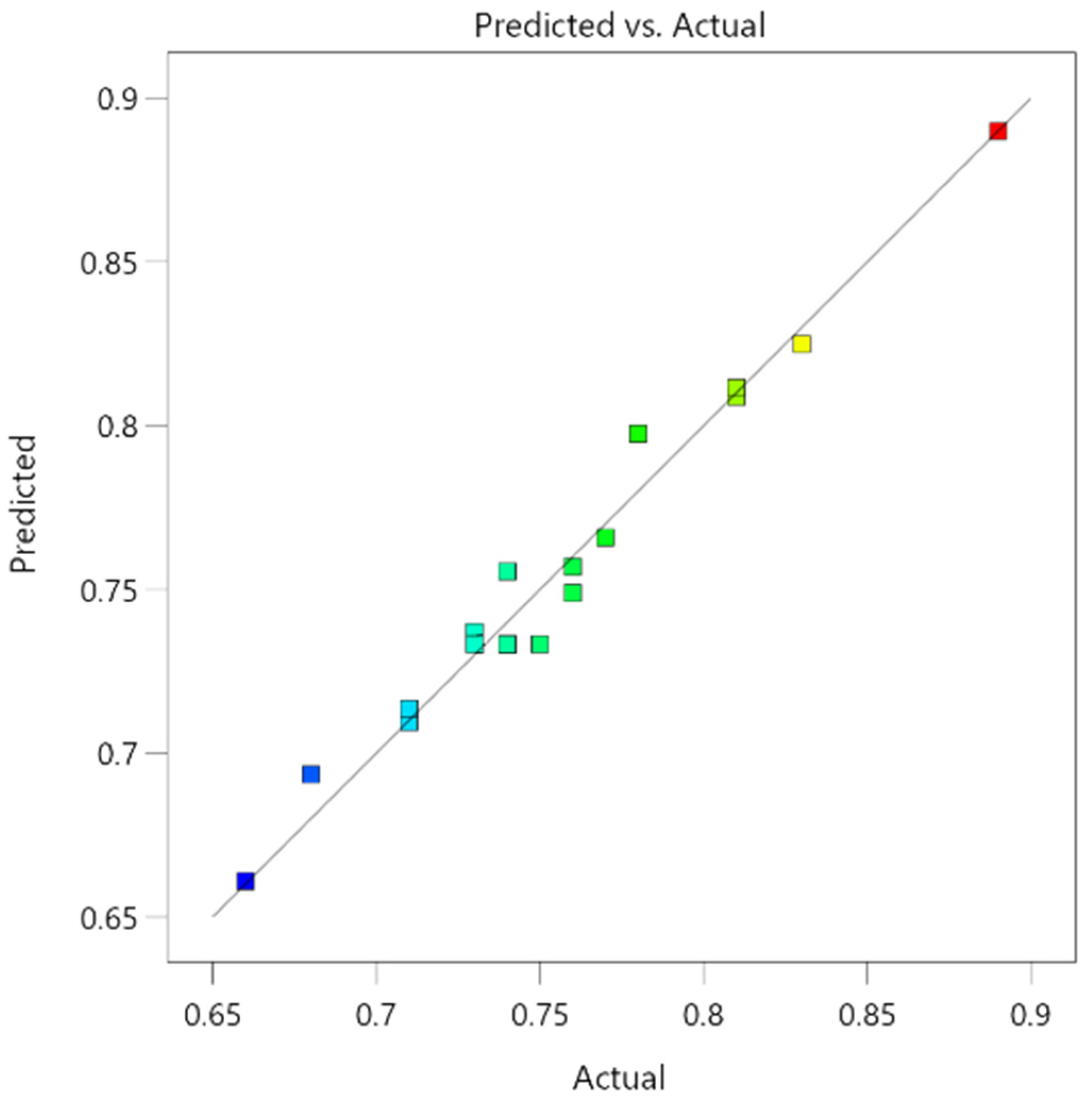
6.2. Influences of Various Factors and Their Interaction on $S_f$

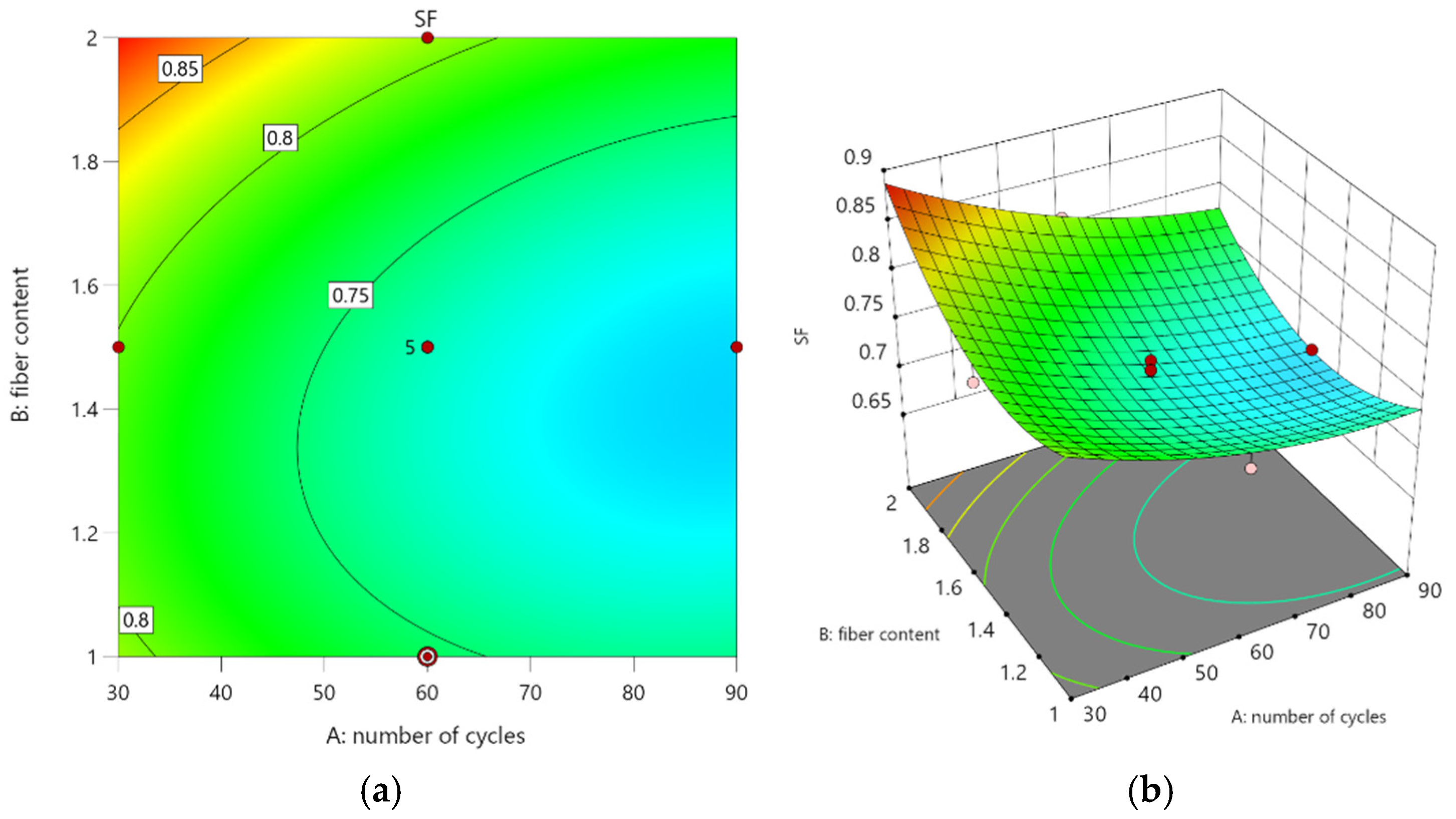
Figure 14a presents contour plot, illustrating $S_f$ concerning the number of dry–wet cycles and stainless steel fiber content, along with a three-dimensional response surface plot Figure 14b based on Equation (5). The density of the contour lines in Figure 14a reveals that the vertical coordinate representing fiber content is more densely packed than the horizontal coordinate depicting dry–wet cycle count, indicating that the influence of fiber content on $S_f$ is more significant than that of dry–wet cycle count. In Figure 14b, a concave three-dimensional response surface is depicted, which can be described as follows:

When the number of dry–wet cycles is held constant, the trend of $S_f$ consistently rises with increasing stainless steel fiber content, suggesting that higher fiber content within the 1%–2% range leads to improved bending resistance. Conversely, when the fiber content is kept constant, the trend of $S_f$ declines with increasing dry–wet cycle count, indicating that a greater number of dry–wet cycles results in reduced bending resistance.

Figure 15a presents contour plot illustrating $S_f$ concerning the number of dry–wet cycles and Na₂SO₄ concentration, along with a three-dimensional response surface plot Figure 15b based on Equation (5). The density of the contour lines in Figure 15a reveals that the Na₂SO₄ concentration contour lines are more densely packed than the dry–wet cycle contour lines, indicating that the influence of Na₂SO₄ concentration on $S_f$ is more significant than the number of dry–wet cycles. In Figure 15b, a concave three-dimensional response surface is depicted, which can be described as follows:

When the Na₂SO₄ concentration remains constant, the three-dimensional response surface of $S_f$ exhibits a decreasing trend with an increase in dry–wet cycling times, indicating that higher dry–wet cycling times lead to reduced bending resistance for SSFRAC. Conversely, when the number of dry–wet cycling times is held constant, the three-dimensional response surface of $S_f$ demonstrates an initial upward trend followed by a downward trend with increasing Na₂SO₄ solution concentration. This suggests that during the secondary hydration stage, Na₂SO₄ accelerates the generation of hydration products, filling pores and compacting the internal structure of SSFRAC while enhancing its strength. However, as the concentration of Na₂SO₄ increases, concrete’s internal salt solution easily reaches saturation and crystallizes; subsequently eroding surface crystals further degrade concrete. Therefore, an increase in Na₂SO₄ concentration results in decreased flexural strength for SSFRAC.

Figure 16 depicts a contour plot and a 3D response surface plot of $S_f$ as a function of stainless steel fiber content and Na₂SO₄ concentration, derived from Equation (5). The density of contour lines in Figure 16a’s horizontal axis, representing the fiber content, closely mirrors that in the vertical axis, which signifies the Na₂SO₄ concentration. This observation suggests that both factors exert a comparable influence on $S_f$ when assessing its performance. In Figure 16b, the 3D response surface is presented as follows:

When a small amount of Na₂SO₄ solution is added and the concentration of Na₂SO₄ solution is 1%, the $S_f$ curve exhibits a gradual increase with rising stainless steel fiber content. However, as the concentration of Na₂SO₄ solution increases, the curve demonstrates an upward trend that is more pronounced than at lower concentrations, indicating that an appropriate Na₂SO₄ concentration can synergistically enhance the effect of stainless steel fiber content.

6.3. Corrosion of SSFRAC by Na₂SO₄

Figure 17 illustrates the observed alterations in the test specimens under a 5% Na₂SO₄ concentration, 2% stainless steel fiber content, and dry–wet cycling for 30, 60, and 90 cycles. The cracks were detected using PS and depicted. It is evident that with an increase in the number of dry–wet cycles from Figure 17a–c, there is a corresponding escalation in both the quantity and width of cracks on the specimen surface. Utilizing the KS-105 wireless crack width gauge alongside advanced electronic imaging technology, the original state of the specimen surface was displayed on a tablet screen, enabling automatic measurement of crack widths using a high-precision ruler. The measured crack widths on the specimen surface after 90 dry–wet cycles were found to be 0.49 mm; after 60 cycles they were recorded at 0.23 mm, while after just 30 cycles they measured only at 0.03 mm. There is a varying degree of precipitation on the surface, indicating a violent chemical reaction within the concrete. The hydration product Ca(OH)₂ reacts with Na₂SO₄ solution to form gypsum, leading to the gradual formation of cracks in both the interior and surface of the concrete. As dry–wet cycling times increase, crack width and connectivity continue to expand, accompanied by precipitation of gypsum crystals that reduce bonding material between aggregates. Visible cracks can be observed on aggregate surfaces as well. At this stage, the bending resistance of the test piece decreases. Furthermore, higher stainless steel fiber content results in more internal pores and faster deterioration, explaining why higher stainless steel fiber content leads to faster decline compared to lower content. Figure 18 illustrates apparent changes in test pieces after 90 dry–wet cycles with 2% stainless steel fiber content and Na₂SO₄ concentrations at 1%, 3%, and 5%. From Figure 17c, it is evident that at a Na₂SO₄ concentration of 5%, there is increased precipitation and more pronounced deterioration on the test piece surface.

6.4. Theoretical Analysis of Na₂SO₄ for SSFRAC

Sulfate attack primarily involves two stages: the initial stage occurs when sulfate ions infiltrate SSFRAC and react with the hydration products of cement, Ca(OH)₂, to form gypsum, which fills the pores within SSFRAC. The subsequent stage occurs as some sulfate ions penetrate further, leading to the formation of ettringite (AFt), which induces internal stress expansion upon contact with the pore wall. Once this internal stress expansion reaches the tensile strength of concrete aggregate, microcracks are generated, thereby facilitating salt precipitation [26,27,28,29].

In the experiment, a dark red substance was observed on the surface of the sample immersed in the solution and on the concrete specimen in the dry–wet cycling tank, indicating the presence of Fe₂O₃. While stainless steel fibers did not exhibit visible corrosion, microscopic corrosion products had already formed internally, with iron elements detected within these products. Equation (6) depicts the chemical reaction of sulfate ions penetrating the specimen during testing, while Equation (7) illustrates how this reaction involving Cr₂O₃ unique to stainless steel fibers differs from that of common steel fibers.

$$3\mathrm{C}\mathrm{a}\mathrm{O}·{\mathrm{A}\mathrm{l}}_2{\mathrm{O}}_3·\mathrm{C}\mathrm{a}\mathrm{S}{\mathrm{O}}_4·12{\mathrm{H}}_2\mathrm{O}+2{\mathrm{C}\mathrm{a}}^{2+}+2{{\mathrm{S}\mathrm{O}}_4}^{2-}+16{\mathrm{H}}_2\to 3\mathrm{C}\mathrm{a}\mathrm{O}·{\mathrm{A}\mathrm{l}}_2{\mathrm{O}}_3·3{\mathrm{C}\mathrm{a}\mathrm{S}\mathrm{O}}_4·32{\mathrm{H}}_2\mathrm{O}$$

(6)

$$\mathrm{C}{\mathrm{r}}_2{\mathrm{O}}_3+3\mathrm{N}{\mathrm{a}}_2\mathrm{S}{\mathrm{O}}_4\to \mathrm{C}{\mathrm{r}}_2(\mathrm{S}{\mathrm{O}}_4{)}_3+3{\mathrm{H}}_2\mathrm{O}$$

(7)

It should be noted that the feasibility of the reaction expressed in Equation (7) is also governed by thermodynamic principles. According to reported thermodynamic data of the relevant oxides and sulfates (ΔG and ΔH values), the reaction between Cr₂O₃ in stainless steel fibers and sulfate ions is thermodynamically permissible under aqueous conditions. This indicates that the reaction can proceed spontaneously, although the rate may be limited by kinetic factors such as ion diffusion and local concentration gradients during dry–wet cycling. Therefore, Equation (7) is not only a hypothetical mechanism but is also supported by thermodynamic considerations, which distinguishes the corrosion resistance mechanism of stainless steel fibers from that of ordinary steel fibers.

7. Conclusions and Prospect

7.1. Conclusions

The mechanical properties of recycled concrete reinforced with stainless steel fibers were evaluated through sulfate dry–wet cyclic tests, and a three-factor two-level experiment based on RSM was designed to obtain the response values. The following conclusions were derived:

(1)

The addition of stainless steel fibers to the cementitious gel matrix effectively offsets the deficiencies in the compressive strength of RAC. The compressive strength of SSFRAC gradually increases with the increase in the fiber content, and finally stabilizes at 1.5% fiber content, Therefore, the optimal content of stainless steel fibers is 1.5%.

(2)

In the S_c model, the factors are ranked in order of significance as follows: dry–wet cycling times > Na₂SO₄ concentration > stainless steel fiber content. For the S_f model, the ranking is stainless steel fiber content > dry–wet cycling times > Na₂SO₄ concentration. The interaction between dry–wet cycling times and Na₂SO₄ concentration has the most significant impact on S_c, while the interaction between fiber content and Na₂SO₄ concentration most significantly influences S_f. These findings underscore the complex interplay between environmental conditions and material composition in hybrid gel–metal systems.

(3)

Micro-cracks induced by dry–wet cycles predominantly manifest on the concrete surface, with their abundance and width increasing with the number of cycles. This phenomenon reflects the degradation of the gel network under cyclic environmental stress, emphasizing the need for optimized metal–gel composites to enhance durability in aggressive conditions.

7.2. Prospect

The present study offers several notable strengths, including the novelty of incorporating stainless steel fibers into recycled aggregate concrete subjected to sulfate dry–wet cycling, combined with a systematic application of response surface methodology. This approach provides valuable quantitative insights into the interactive effects of fiber content, sulfate concentration, and cycling frequency. Nevertheless, certain limitations should be acknowledged. First, recycled aggregates originate from diverse sources, with variations in composition, original mix proportions, and service environments. These differences lead to significant fluctuations in particle morphology, surface roughness, porosity, water absorption, and strength [30]. Second, the mix design of recycled concrete is inherently more complex than that of ordinary concrete. In addition to conventional factors such as cement, aggregates, and water, it must also account for the replacement rate of recycled aggregates, the dosage and aspect ratio of stainless steel fibers, and their mutual interactions. Finally, discrepancies exist between the controlled laboratory conditions and real-world engineering environments. Actual service conditions are highly complex, and examining only the mechanical properties of recycled aggregate concrete under sulfate dry–wet cycling cannot fully capture the multifaceted deterioration processes encountered in practice.

Therefore, in future work, we can further improve our research. First, we can optimize the experimental design, such as expanding the range of factor levels, introducing more key variables, or conducting cross-validation by combining other numerical simulation methods with the response surface method. Second, we can increase the complexity and authenticity of the simulation environment, for example, by superimposing freeze–thaw cycles, temperature and humidity fluctuations, and other multi-factor coupling effects on the basis of dry–wet cycles, to make the conclusions more valuable for engineering reference. Third, we can enhance the universality of the research results by conducting multiple response surface modeling studies on recycled aggregates from different sources and with different substitution rates, as well as on stainless steel fibers of different types and dosages, summarizing the common laws among the variables, and constructing a general prediction model applicable to a wider range of material parameters.