A Study of HiPIMS Process Characteristics in SiO2 Deposition
Abstract
1. Introduction
2. Materials and Methods
3. Results
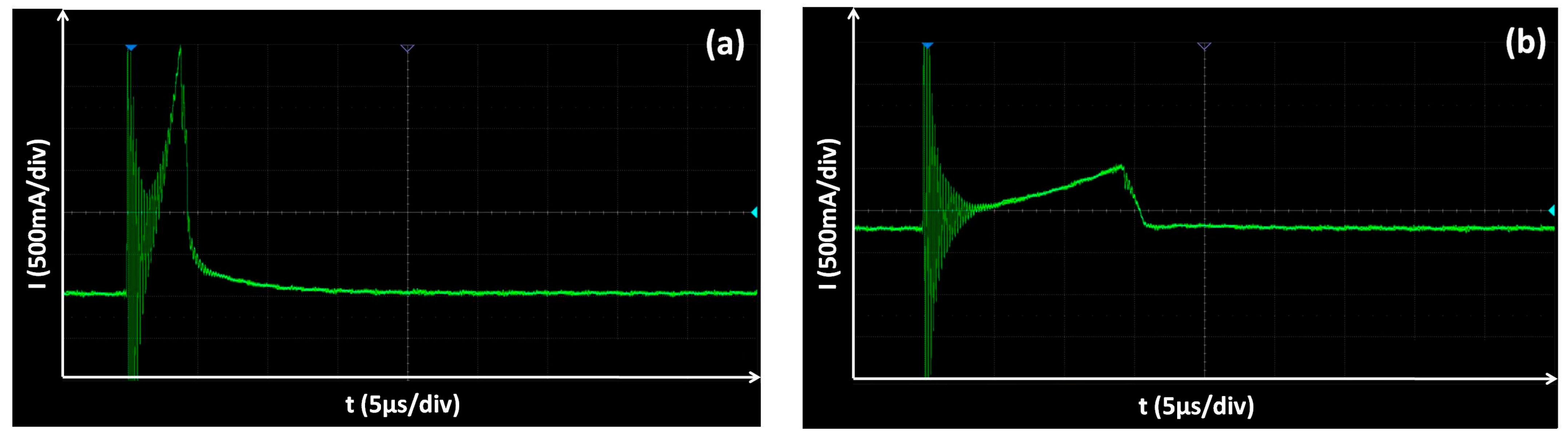
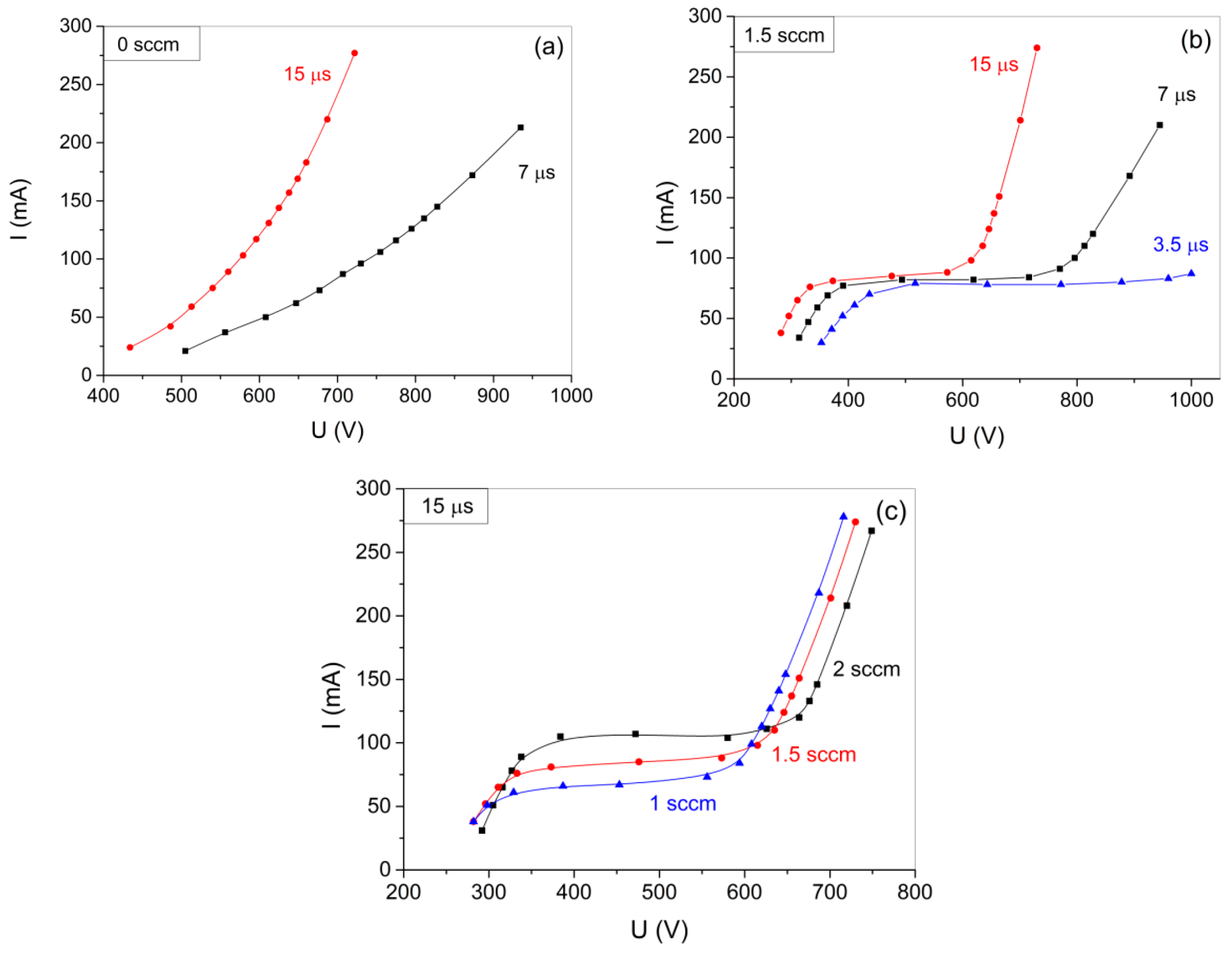
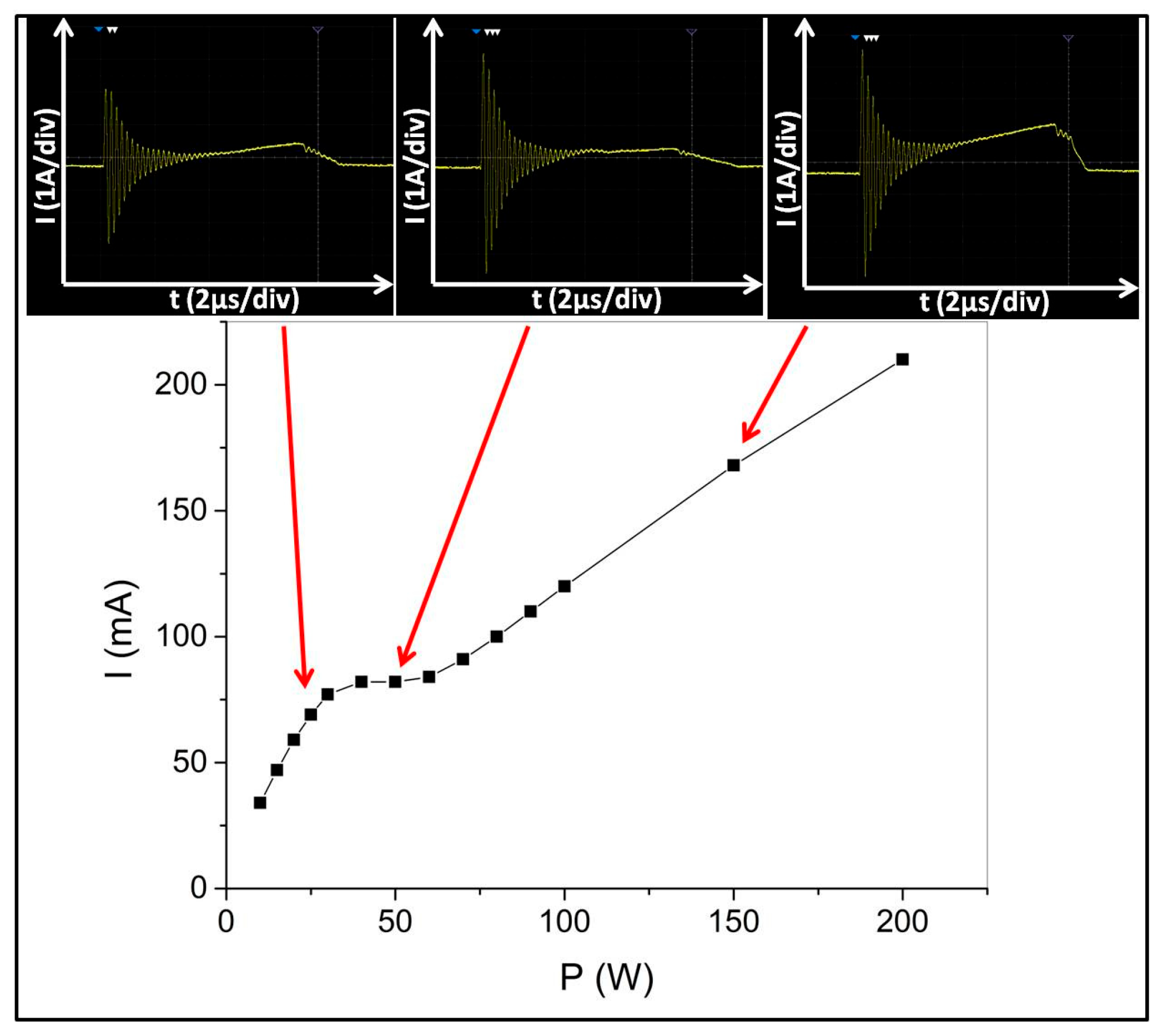
3.1. Electrical Characterization of the Discharge
3.2. Model of the Discharge Characteristic
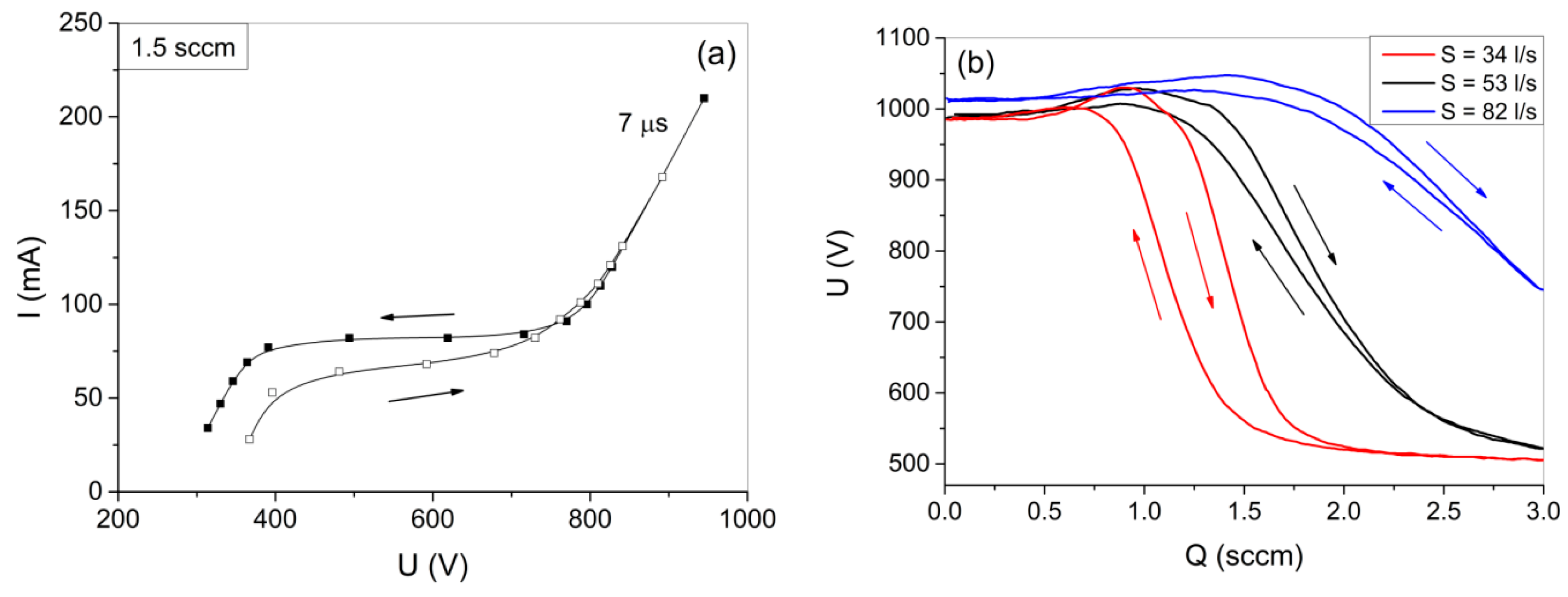
3.3. Investigation of the Hysteresis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Ym | 0.6 |
| Yc | 0.02 |
| αt = αs | 0.007 |
| X | 50 |
| ry | 0.033 |
| At | 20 cm2 |
| As | 1160 cm2 |
| Ar | 58 |
References
- Li, S.; Liu, C.; Zhu, T.; Wang, Y.; He, J.; Yang, G.; Sun, P.; Li, H.; Liu, H.; Jiang, N. Effects of the Thermal Treatments on the Optical Properties of SiO2 Anti-Reflective Coatings on Sapphire Windows. Infrared Phys. Technol. 2024, 137, 105151. [Google Scholar] [CrossRef]
- Mazur, M.; Wojcieszak, D.; Kaczmarek, D.; Domaradzki, J.; Song, S.; Gibson, D.; Placido, F.; Mazur, P.; Kalisz, M.; Poniedzialek, A. Functional Photocatalytically Active and Scratch Resistant Antireflective Coating Based on TiO2 and SiO2. Appl. Surf. Sci. 2016, 380, 165–171. [Google Scholar] [CrossRef]
- Ruud, C.J.; Cleri, A.; Maria, J.-P.; Giebink, N.C. Ultralow Index SiO2 Antireflection Coatings Produced via Magnetron Sputtering. Nano Lett. 2022, 22, 7358–7362. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Xu, J.; Wang, L.; Yang, N.; Ye, X.; Yuan, X.; Xiang, H.; Liu, C.; Li, H. Effect of Post-Deposition Annealing on Atomic Layer Deposited SiO2 Film for Silicon Surface Passivation. Mater. Sci. Semicond. Process. 2020, 106, 104777. [Google Scholar] [CrossRef]
- Aktas, S.; Caglar, M. Effect of SiO2 Gate Insulator on Electrical Performance of Solution Processed SnO2-Based Thin Film Phototransistor. Phys. B Condens. Matter 2023, 670, 415337. [Google Scholar] [CrossRef]
- Bhatt, V.; Chandra, S. Silicon Dioxide Films by RF Sputtering for Microelectronic and MEMS Applications. J. Micromech. Microeng. 2007, 17, 1066. [Google Scholar] [CrossRef]
- Cannon, P.; McGlynn, E.; O’Neill, D.; Darcy, C.; Rouse, E.; O’Connor, R.; Freeland, B.; O’Connell, B.; Gaughran, J. Deposition of High-Quality, Nanoscale SiO2 Films and 3D Structures. Appl. Mater. Today 2024, 38, 102175. [Google Scholar] [CrossRef]
- Zheng, J.; Yang, J.; Cao, W.; Huang, Y.; Zhou, Z.; Huang, Y.-X. Fabrication of Transparent Wear-Resistant Superhydrophobic SiO2 Film via Phase Separation and Chemical Vapor Deposition Methods. Ceram. Int. 2022, 48, 32143–32151. [Google Scholar] [CrossRef]
- Rebib, F.; Tomasella, E.; Dubois, M.; Cellier, J.; Sauvage, T.; Jacquet, M. SiOxNy Thin Films Deposited by Reactive Sputtering: Process Study and Structural Characterisation. Thin Solid Film. 2007, 515, 3480–3487. [Google Scholar] [CrossRef]
- Waite, M.M.; Shah, S.I. Target Poisoning during Reactive Sputtering of Silicon with Oxygen and Nitrogen. Mater. Sci. Eng. B 2007, 140, 64–68. [Google Scholar] [CrossRef]
- Carneiro, J.O.; Machado, F.; Rebouta, L.; Vasilevskiy, M.I.; Lanceros-Méndez, S.; Teixeira, V.; Costa, M.F.; Samantilleke, A.P. Compositional, Optical and Electrical Characteristics of SiOx Thin Films Deposited by Reactive Pulsed DC Magnetron Sputtering. Coatings 2019, 9, 468. [Google Scholar] [CrossRef]
- Hála, M.; Vernhes, R.; Zabeida, O.; Klemberg-Sapieha, J.-E.; Martinu, L. Reactive HiPIMS Deposition of SiO2/Ta2O5 Optical Interference Filters. J. Appl. Phys. 2014, 116, 213302. [Google Scholar] [CrossRef]
- Kim, K.; Kim, S.; An, S.; Lee, G.-H.; Kim, D.; Han, S. Anti-Reflection Porous SiO2 Thin Film Deposited Using Reactive High-Power Impulse Magnetron Sputtering at High Working Pressure for Use in a-Si:H Solar Cells. Sol. Energy Mater. Sol. Cells 2014, 130, 582–586. [Google Scholar] [CrossRef]
- Tiron, V.; Velicu, I.-L.; Matei, T.; Cristea, D.; Cunha, L.; Stoian, G. Ultra-Short Pulse HiPIMS: A Strategy to Suppress Arcing during Reactive Deposition of SiO2 Thin Films with Enhanced Mechanical and Optical Properties. Coatings 2020, 10, 633. [Google Scholar] [CrossRef]
- Arif, M.; Eisenmenger-Sittner, C. In Situ Assessment of Target Poisoning Evolution in Magnetron Sputtering. Surf. Coat. Technol. 2017, 324, 345–352. [Google Scholar] [CrossRef]
- Fekete, M.; Bernátová, K.; Klein, P.; Hnilica, J.; Vašina, P. Influence of Sputtered Species Ionisation on the Hysteresis Behaviour of Reactive HiPIMS with Oxygen Admixture. Plasma Sources Sci. Technol. 2020, 29, 025027. [Google Scholar] [CrossRef]
- Boivin, D.; Najah, A.; Jean-Marie-Désirée, R.; Noël, C.; Henrion, G.; Cuynet, S.; De Poucques, L. Towards Control of TiO2 Thickness Film in R-HiPIMS Process with a Coupled Optical and Electrical Monitoring of Plasma. Surf. Coat. Technol. 2022, 433, 128073. [Google Scholar] [CrossRef]
- Depla, D.; Mahieu, S.; De Gryse, R. Magnetron Sputter Deposition: Linking Discharge Voltage with Target Properties. Thin Solid Film. 2009, 517, 2825–2839. [Google Scholar] [CrossRef]
- Wang, Q.; Fang, L.; Liu, Q.; Chen, L.; Wang, Q.; Meng, X.; Xiao, H. Target Voltage Hysteresis Behavior and Control Point in the Preparation of Aluminum Oxide Thin Films by Medium Frequency Reactive Magnetron Sputtering. Coatings 2018, 8, 146. [Google Scholar] [CrossRef]
- Oniszczuk, A.W.; Owen, D.S.; Loch, D.A.L.; Hovsepian, P.E.; Ehiasarian, A.P. Reverse Pulse Strategies for Silicon Dioxide Thin Films Deposition by High Power Impulse Magnetron Sputtering. Surf. Coat. Technol. 2025, 505, 132117. [Google Scholar] [CrossRef]
- Arosa, Y.; de la Fuente, R.; Lobato, Y. Refractive Index Spectroscopy and Material Dispersion in Fused Silica Glass. Opt. Lett. 2020, 45, 4268–4271. [Google Scholar] [CrossRef]
- Jonsson, L.B.; Nyberg, T.; Katardjiev, I.; Berg, S. Frequency Response in Pulsed DC Reactive Sputtering Processes. Thin Solid Film. 2000, 365, 43–48. [Google Scholar] [CrossRef]
- Kelly, P.J.; Arnell, R.D. Magnetron Sputtering: A Review of Recent Developments and Applications. Vacuum 2000, 56, 159–172. [Google Scholar] [CrossRef]
- Lieberman, M.A.; Lichtenberg, A.J. Principles of Plasma Discharges and Materials Processing; Wiley-Interscience: New York, NY, USA, 2005; ISBN 978-0-471-72001-0. [Google Scholar]
- Westwood, W.D.; Maniv, S.; Scanlon, P.J. The Current-voltage Characteristic of Magnetron Sputtering Systems. J. Appl. Phys. 1983, 54, 6841–6846. [Google Scholar] [CrossRef]
- Takagi, S.; Nakaegawa, T.; Hsiao, S.-N.; Sekine, M. Estimations of Secondary Electron Emission Coefficients of Si, SiO2, and Polyimide Electrodes in Dual-Frequency Capacitively Coupled Discharge. Jpn. J. Appl. Phys. 2022, 62, SA1009. [Google Scholar] [CrossRef]
- Anders, A. Tutorial: Reactive High Power Impulse Magnetron Sputtering (R-HiPIMS). J. Appl. Phys. 2017, 121, 171101. [Google Scholar] [CrossRef]
- Gudmundsson, J.T.; Lundin, D. 1—Introduction to Magnetron Sputtering. In High Power Impulse Magnetron Sputtering; Lundin, D., Minea, T., Gudmundsson, J.T., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 1–48. ISBN 978-0-12-812454-3. [Google Scholar]
- Gudmundsson, J.T. Physics and Technology of Magnetron Sputtering Discharges. Plasma Sources Sci. Technol. 2020, 29, 113001. [Google Scholar] [CrossRef]
- Mu, Z.; Li, G.; Che, L.; Huang, K.; Liu, C. Studies of the Discharge Properties of Unbalanced Magnetron Sputtering System. Surf. Coat. Technol. 2005, 193, 46–49. [Google Scholar] [CrossRef]
- Pflug, A.; Siemers, M.; Szyszka, B.; Kappertz, O.; Nyberg, T.; Berg, S.; Severin, D.; Wuttig, M. Modeling of the Plasma Impedance in Reactive Magnetron Sputtering for Various Target Materials. In Proceedings of the Annual Technical Conference—Society of Vacuum Coaters, Denver, CO, USA, 23–28 April 2005; pp. 298–301. [Google Scholar]
- Wallin, E.; Helmersson, U. Hysteresis-Free Reactive High Power Impulse Magnetron Sputtering. Thin Solid Film. 2008, 516, 6398–6401. [Google Scholar] [CrossRef]
- Aiempanakit, M.; Kubart, T.; Larsson, P.; Sarakinos, K.; Jensen, J.; Helmersson, U. Hysteresis and Process Stability in Reactive High Power Impulse Magnetron Sputtering of Metal Oxides. Thin Solid Film. 2011, 519, 7779–7784. [Google Scholar] [CrossRef]
- Čapek, J.; Kadlec, S. Return of Target Material Ions Leads to a Reduced Hysteresis in Reactive High Power Impulse Magnetron Sputtering: Experiment. J. Appl. Phys. 2017, 121, 171911. [Google Scholar] [CrossRef]
- Strijckmans, K.; Moens, F.; Depla, D. Perspective: Is There a Hysteresis during Reactive High Power Impulse Magnetron Sputtering (R-HiPIMS)? J. Appl. Phys. 2017, 121, 080901. [Google Scholar] [CrossRef]
- Kadlec, S.; Musil, J.; Vyskocil, H. Hysteresis Effect in Reactive Sputtering: A Problem of System Stability. J. Phys. D Appl. Phys. 1986, 19, L187. [Google Scholar] [CrossRef]
- Berg, S.; Nyberg, T. Fundamental Understanding and Modeling of Reactive Sputtering Processes. Thin Solid Film. 2005, 476, 215–230. [Google Scholar] [CrossRef]
- Gajdics, M.; Hegedűs, N.; Olasz, D.; Serényi, M. Assistance to Determine the Stability State of a Reactive Sputtering Process Based on the Analytical Solution of the Classical Berg Model. Coatings 2025, 15, 499. [Google Scholar] [CrossRef]



| J (A/m2) | d (nm) | n | O/Si at Conc. Ratio |
|---|---|---|---|
| 100 | 137 | 1.465 | 1.85 |
| 175 | 282 | 1.463 | 1.99 |
| 200 | 333 | 1.462 | 2.01 |
| 235 | 392 | 1.461 | 2.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gajdics, M.; Olasz, D.; Sáfrán, G.; Serényi, M. A Study of HiPIMS Process Characteristics in SiO2 Deposition. Coatings 2025, 15, 1023. https://doi.org/10.3390/coatings15091023
Gajdics M, Olasz D, Sáfrán G, Serényi M. A Study of HiPIMS Process Characteristics in SiO2 Deposition. Coatings. 2025; 15(9):1023. https://doi.org/10.3390/coatings15091023
Chicago/Turabian StyleGajdics, Marcell, Dániel Olasz, György Sáfrán, and Miklós Serényi. 2025. "A Study of HiPIMS Process Characteristics in SiO2 Deposition" Coatings 15, no. 9: 1023. https://doi.org/10.3390/coatings15091023
APA StyleGajdics, M., Olasz, D., Sáfrán, G., & Serényi, M. (2025). A Study of HiPIMS Process Characteristics in SiO2 Deposition. Coatings, 15(9), 1023. https://doi.org/10.3390/coatings15091023







