Spatiotemporal Thermal Analysis of Large-Volume Concrete Girders: Distributed Fiber Sensing and Hydration Heat Simulation
Abstract
1. Introduction
2. Experimental Programs
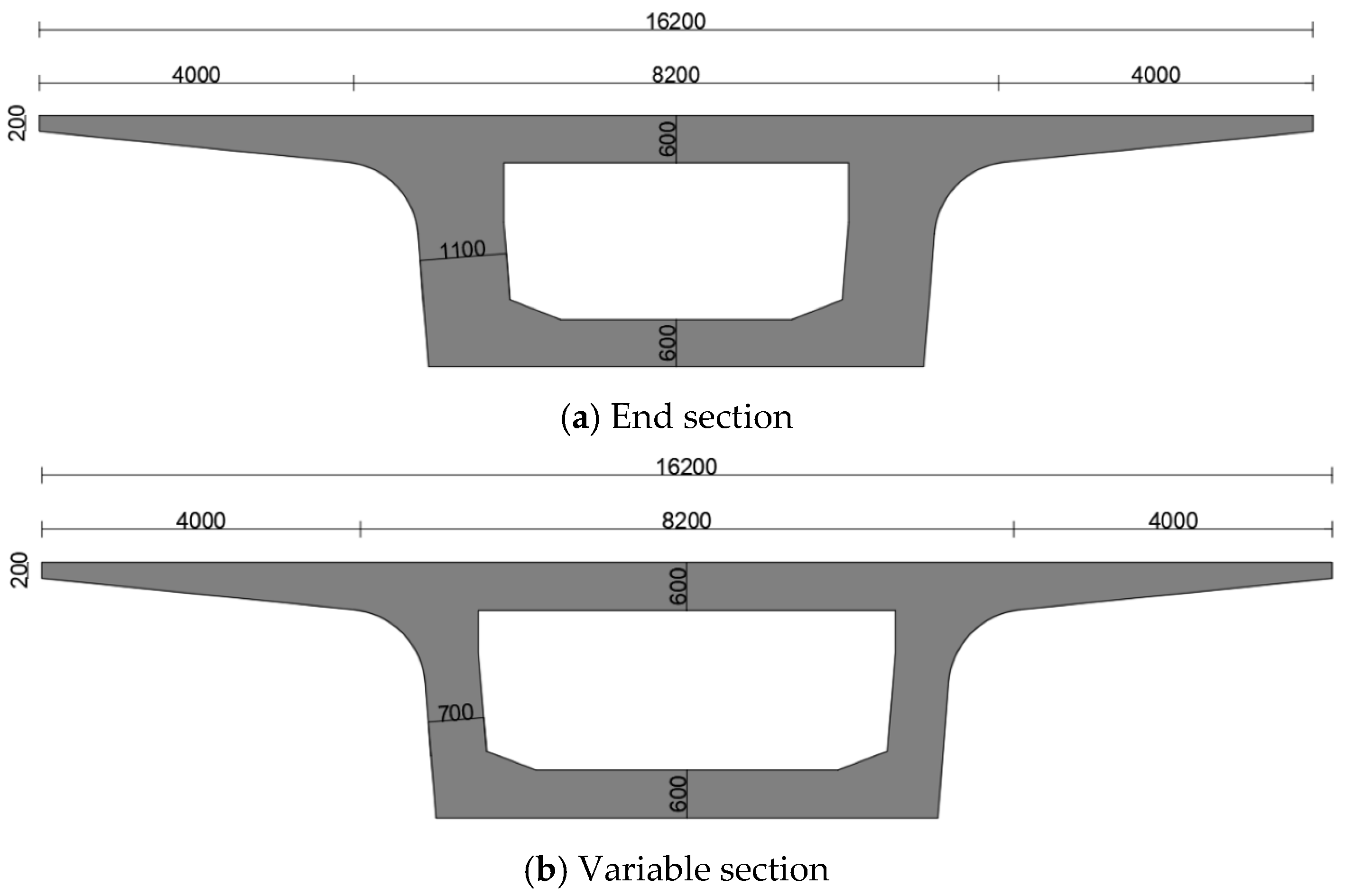
2.1. Project Overview
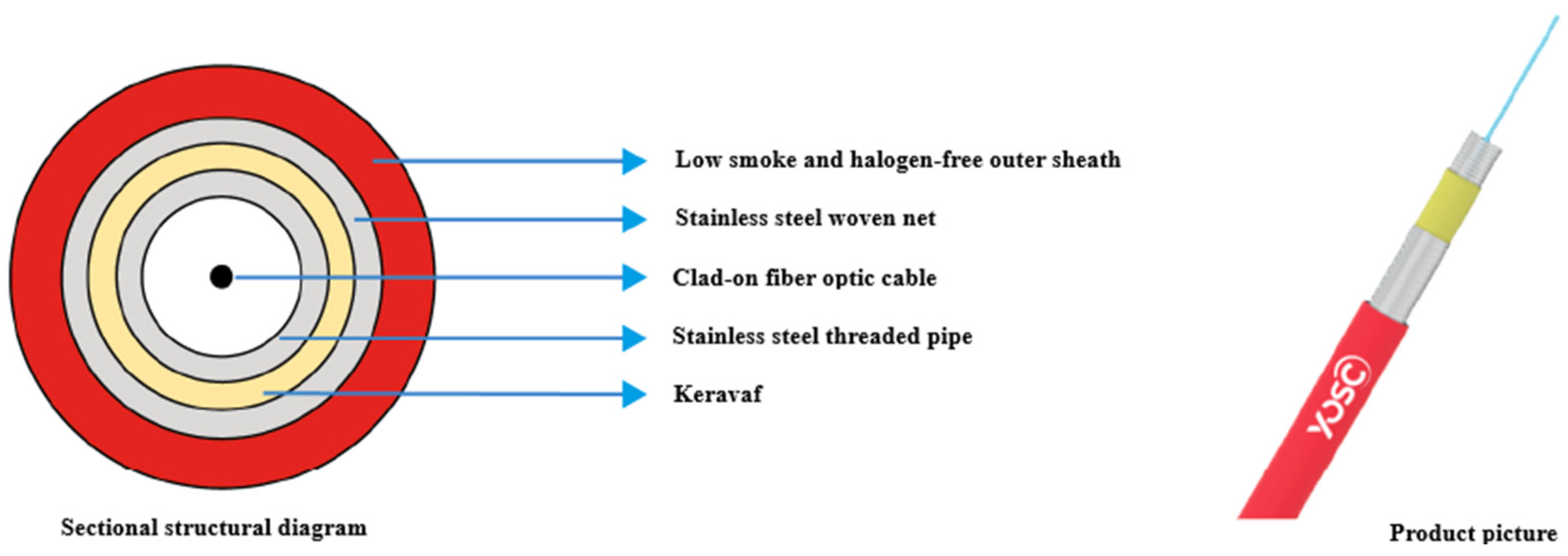
2.2. Instrumentation Layout
2.3. Measurement Program
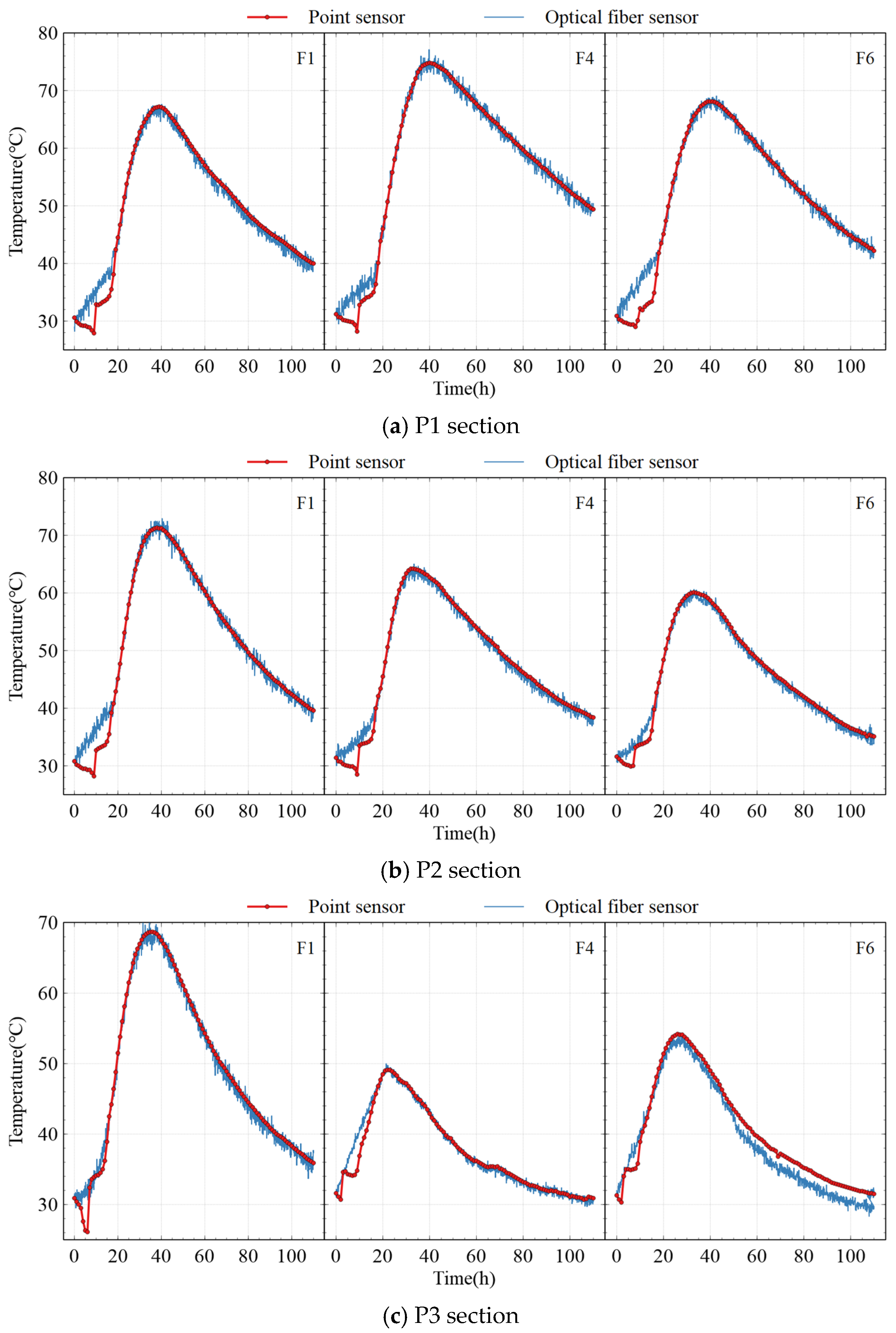
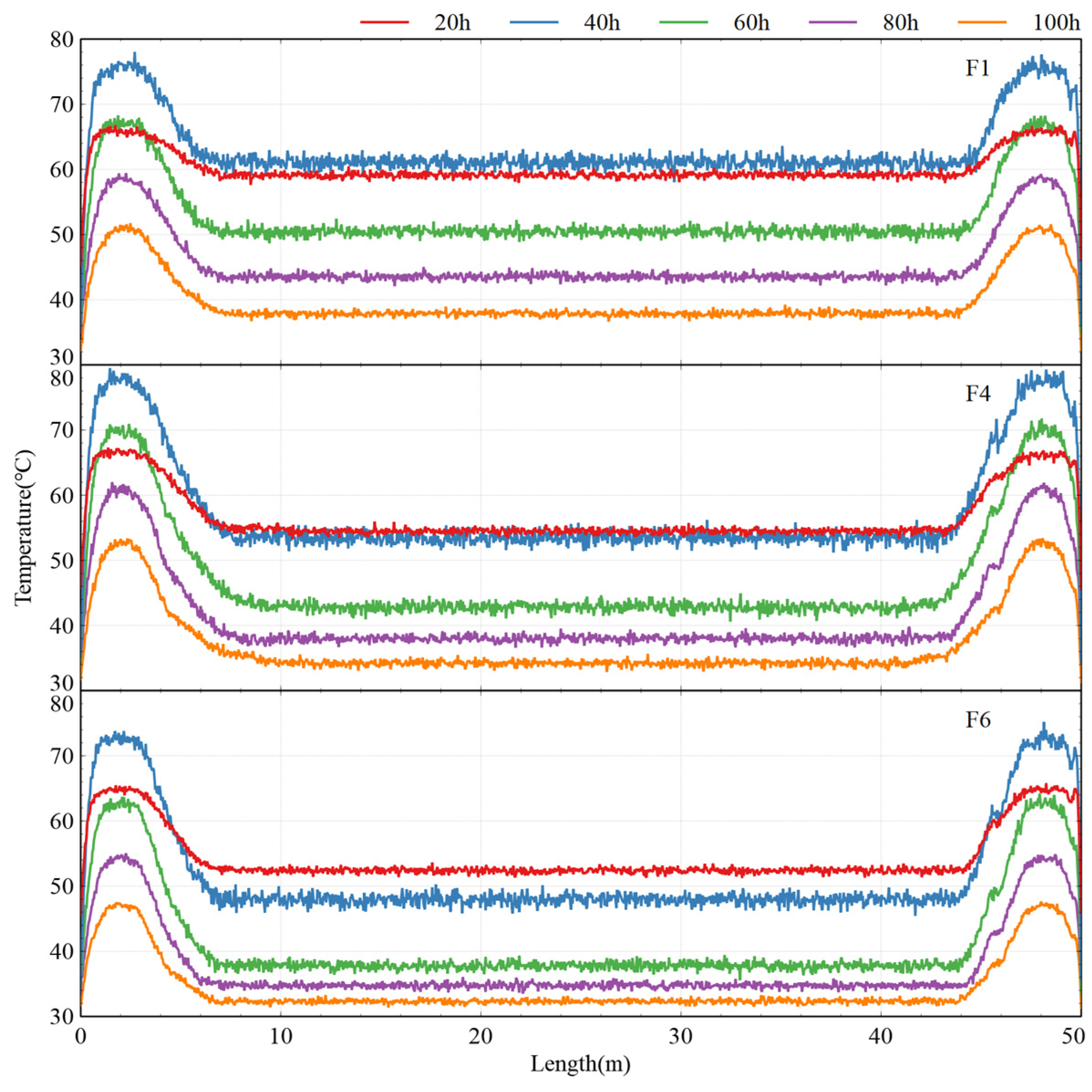
3. Field Test Results
4. Parametric Analysis of Residual Stress
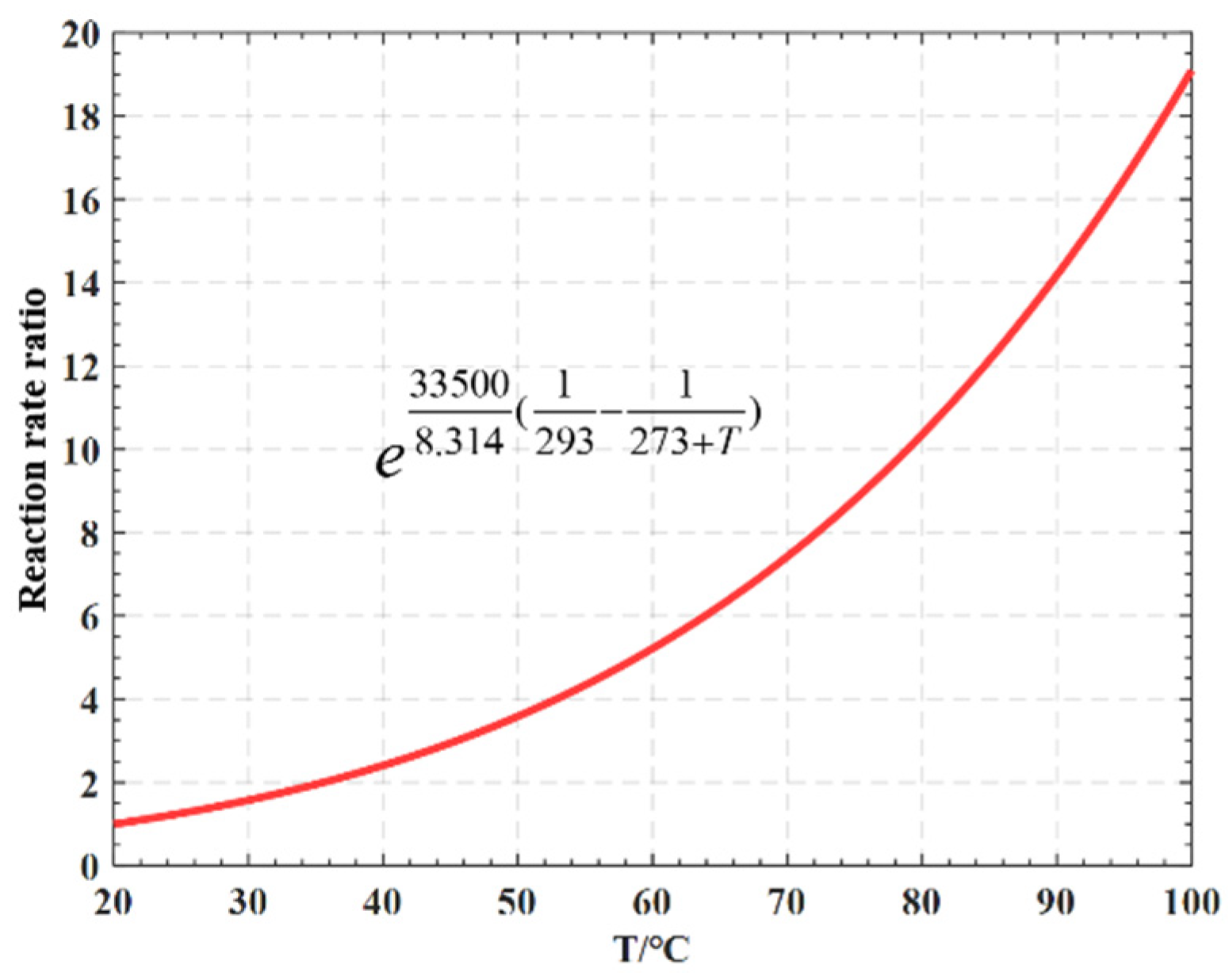
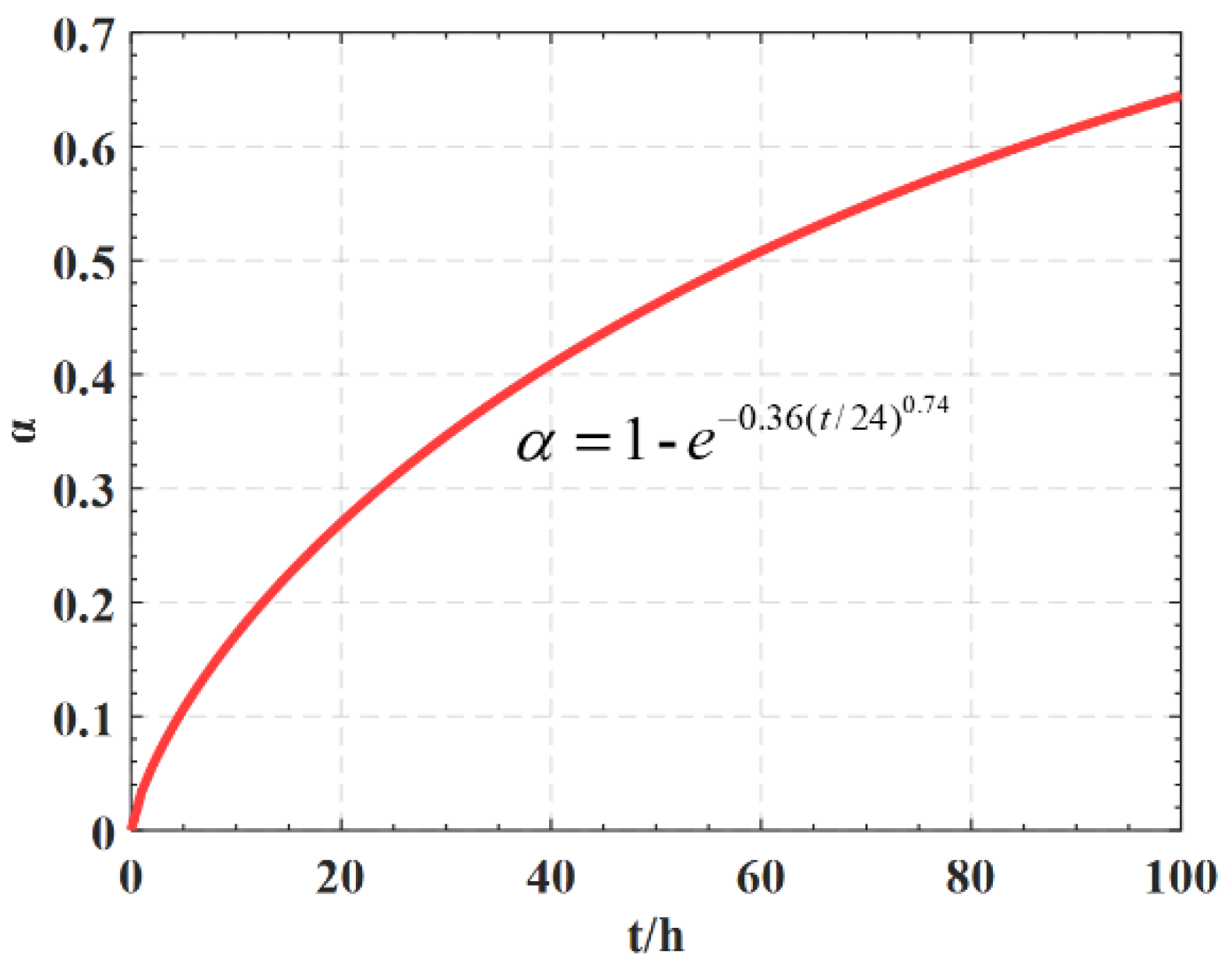
4.1. Principle of Temperature Field Calculation
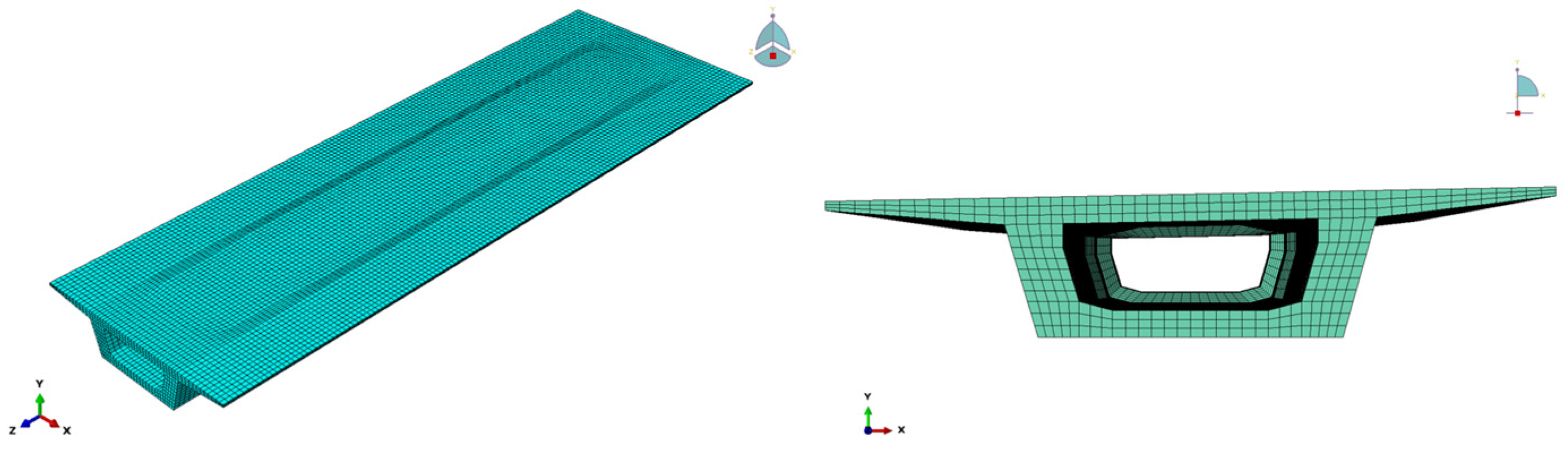
4.2. FEM
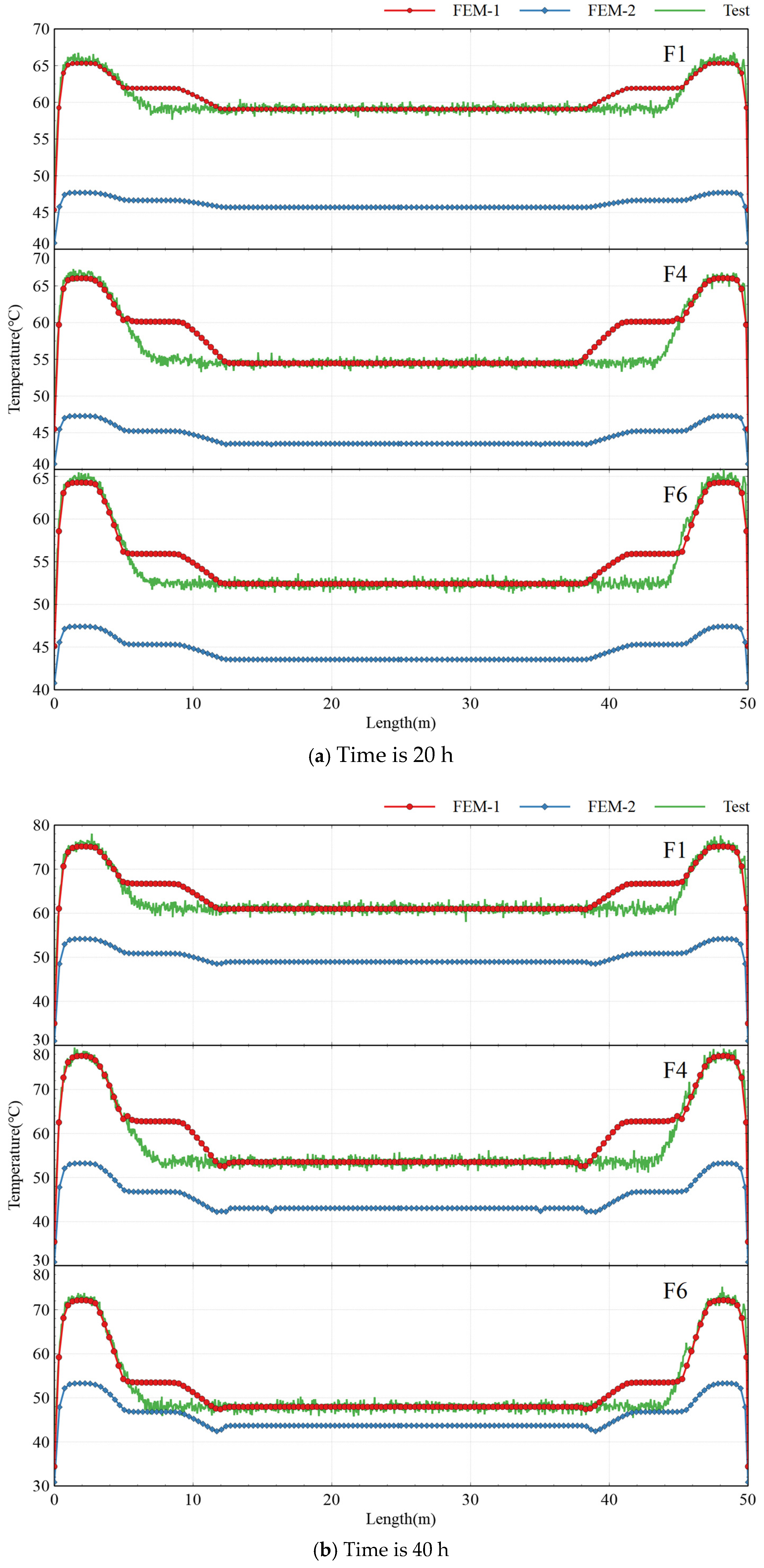
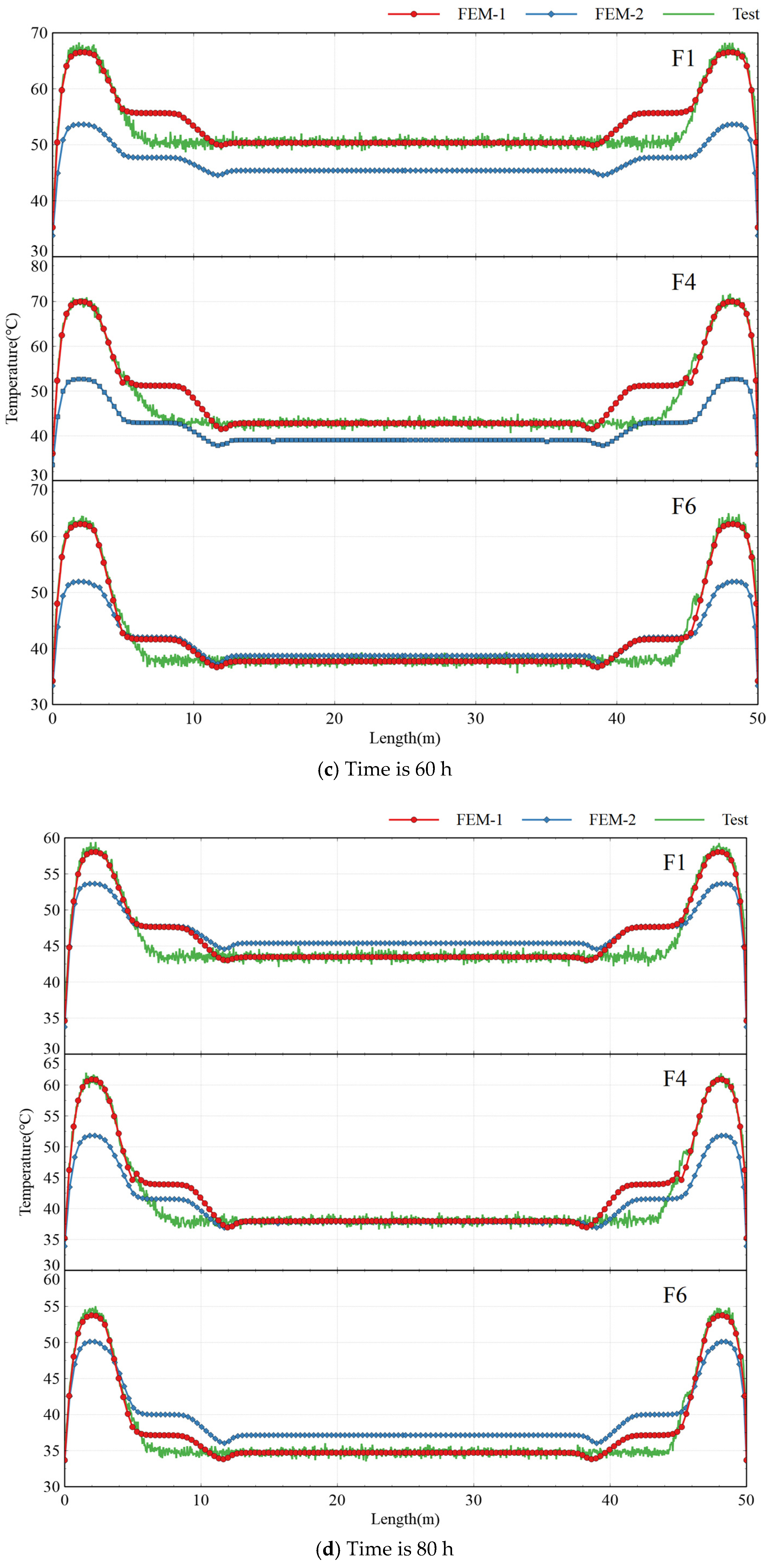
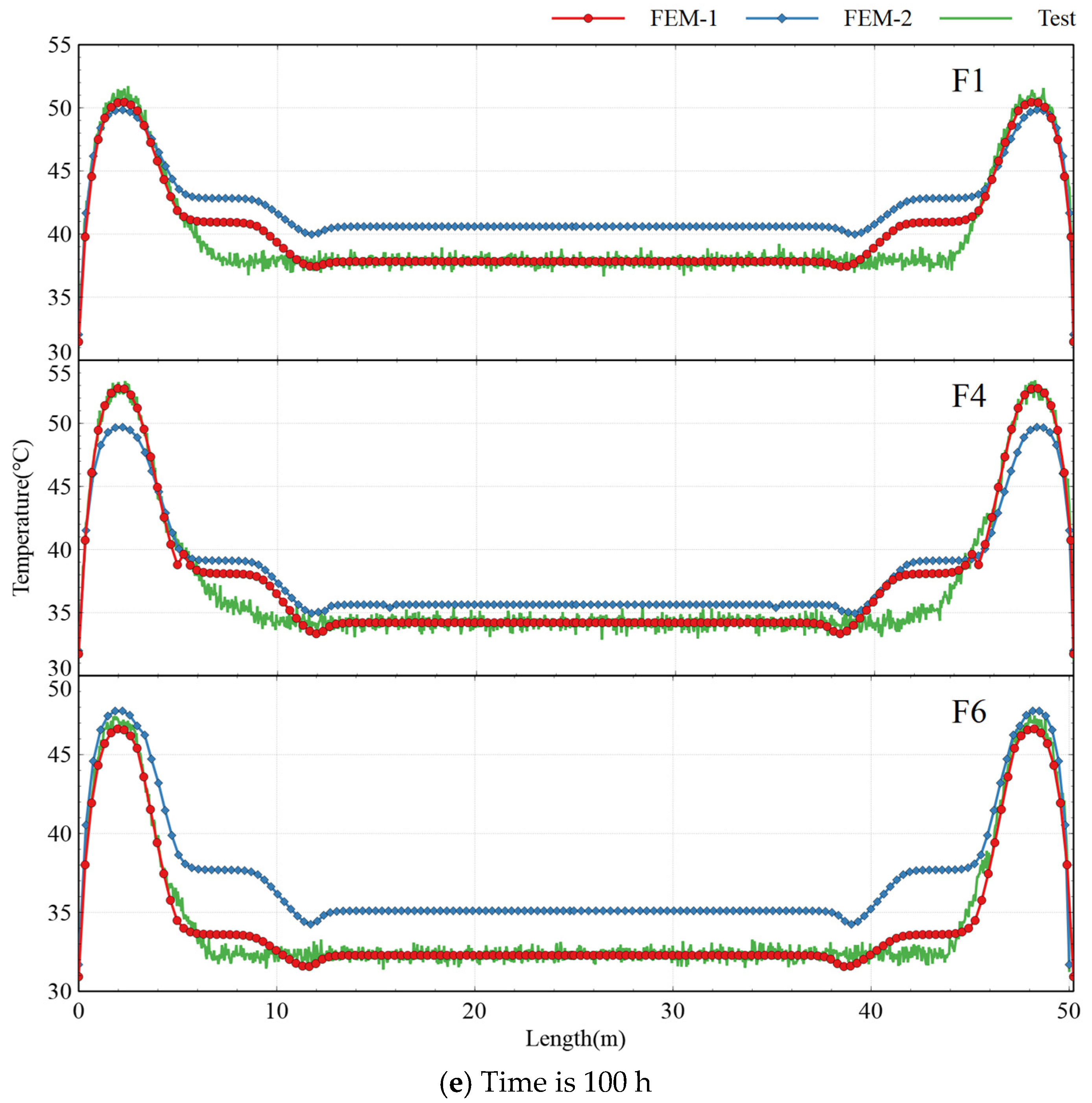
4.3. Model Validation
5. Conclusions
- DFOS demonstrated significant advantages over conventional point-type sensors, enabling comprehensive, real-time temperature monitoring across the entire structure with high spatial resolution (±0.5 °C accuracy). The alignment between DFOS measurements and validation data confirmed its reliability in capturing critical thermal gradients, particularly in complex geometries.
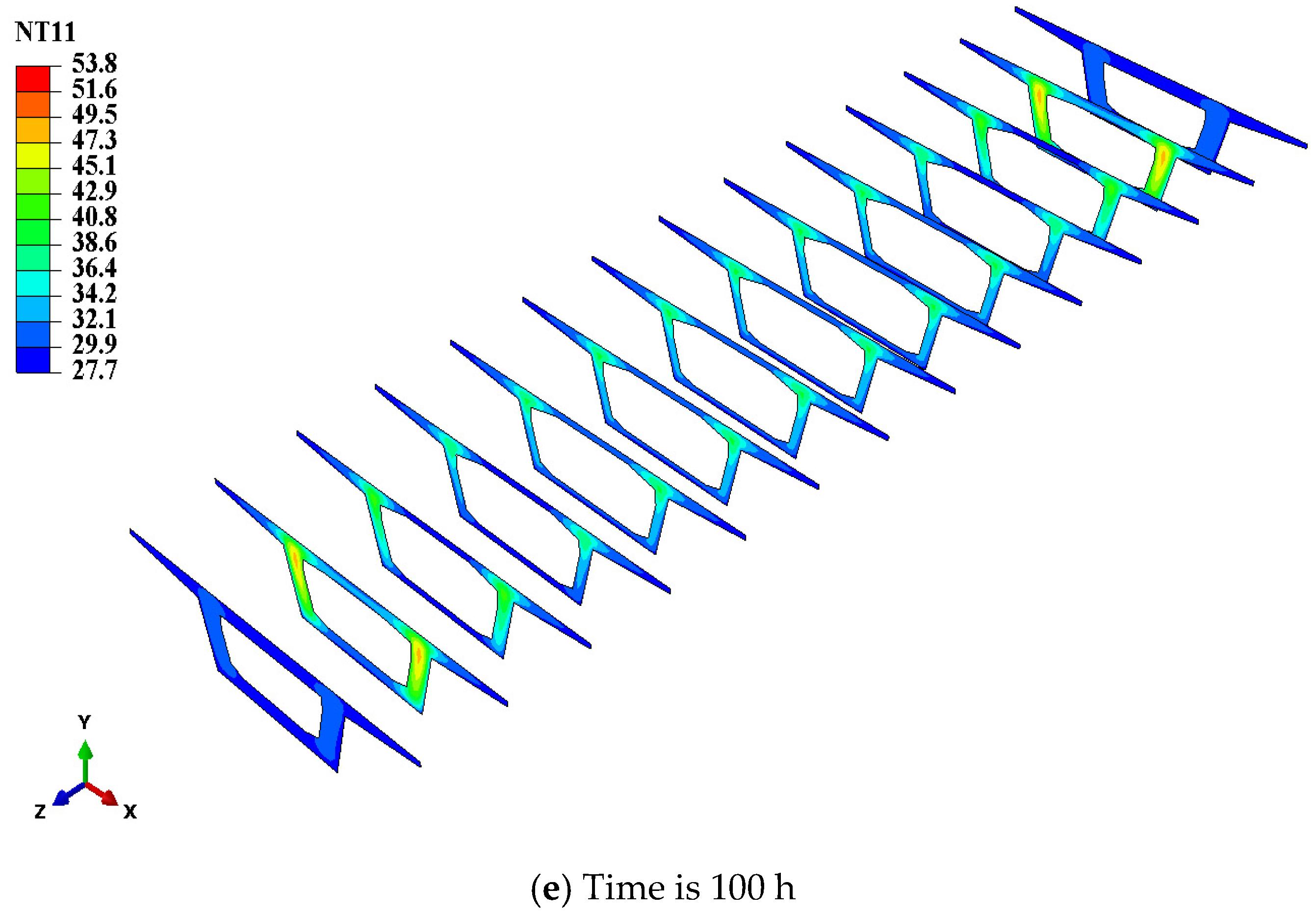
- Distinct temperature profiles were observed among cross-sections. The end section exhibited the highest peak temperature (74.8 °C) due to reduced heat dissipation in thicker web regions (110 cm), while the mid-span section showed lower peak values (53.8 °C) due to efficient surface cooling, emphasizing the vulnerability of web-core zones to thermal stress.
- The proposed finite element model (FEM), incorporating thermal parameters through equivalent age framework and UMATHT subroutine, demonstrated high-fidelity alignment with experimental data. The model accurately replicated the three-phase thermal evolution—rapid heating (0–40 h, peak 79.4 °C), sustained high-temperature plateau (40–60 h, >75 °C), and gradual cooling (60–100 h, 0.45 °C/h)—in geometrically complex LVBG, outperforming conventional static-parameter models by reducing prediction errors by up to 40%. This validated framework offers a robust computational tool for optimizing thermal management strategies to mitigate early-age cracking risks in large-scale concrete structures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DFOS | Distributed fiber optic sensing |
| FEM | Finite element model |
| LVBG | Large-volume concrete box girder |
References
- Xie, J.; Wang, X.; Qiao, W. In Situ Monitoring and Analysis of the Development Characteristics of Separation in Internal Overburden. Appl. Sci. 2024, 14, 6935. [Google Scholar] [CrossRef]
- Wang, J.; Garg, A.; Satyam, N.; Zhussupbekov, A.; Sushkova, S. DFOS Technology in Geoengineering Monitoring in the Past 35 Years: A Bibliometric Analysis. Sensors 2024, 24, 5051. [Google Scholar] [CrossRef] [PubMed]
- Weisbrich, M.; Messerer, D.; Holzer, F.; Trommler, U.; Roland, U.; Holschemacher, K. The Impact of Liquids and Saturated Salt Solutions on Polymer-Coated Fiber Optic Sensors for Distributed Strain and Temperature Measurement. Sensors 2024, 24, 4659. [Google Scholar] [CrossRef]
- Tyler, S.W.; Silvia, M.E.; Jakuba, M.V.; Durante, B.M.; Winebrenner, D.P. Impacts of Hydrostatic Pressure on Distributed Temperature-Sensing Optical Fibers for Extreme Ocean and Ice Environments. Photonics 2024, 11, 630. [Google Scholar] [CrossRef]
- Jiang, X.; Ban, X.; Ma, L.; Su, Y.; Cao, Q.; Zhang, Z.; Guo, J. Prestressed Concrete Box Girder with High-Capacity Strands-Monitoring and Analysis during Fabrication. Buildings 2022, 12, 911. [Google Scholar] [CrossRef]
- Nassr, A.A.; Abd-el-Rahim, H.H.A.; Kaiser, F.; El-sokkary, A.E. Topology optimization of horizontally curved box girder diaphragms. Eng. Struct. 2022, 256, 113959. [Google Scholar] [CrossRef]
- Zhang, P.; Xiong, H.; Wang, R. Measurements and numerical simulations for cast temperature field and early-age thermal stress in zero blocks of high-strength concrete box girders. Adv. Mech. Eng. 2022, 14, 168781322210915. [Google Scholar] [CrossRef]
- Schackow, A.; Effting, C.; Gomes, I.R.; Patruni, I.Z.; Vicenzi, F.; Kramel, C. Temperature variation in concrete samples due to cement hydration. Appl. Therm. Eng. 2016, 103, 1362–1369. [Google Scholar] [CrossRef]
- Wang, J.Q.; Fang, Z.; Liu, J. Measurement and Analysis of Hydration Heat of Long Span PC Box Girders. Bridge Constr. 2016, 46, 29–34. (In Chinese) [Google Scholar]
- Zhang, Z.; Liu, Y.; Liu, J.; Zhang, N. Thermo-mechanical behavior simulation and cracking risk evaluation on steel-concrete composite girders during hydration process. Structures 2021, 33, 3912–3928. [Google Scholar] [CrossRef]
- Yu, F.; Tong, J.; Peng, Y.; Chen, L.; Wang, S. A Case Study on the Application of 3D Scanning Technology in Deformation Monitoring of Slope Stabilization Structure. Buildings 2023, 13, 1589. [Google Scholar] [CrossRef]
- Li, H.; Yang, M. Application Study of Distributed Optical Fiber Seepage Monitoring Technology on Embankment Engineering. Appl. Sci. 2024, 14, 5362. [Google Scholar] [CrossRef]
- Zeng, Y.; Zeng, Y.; Jiang, D.; Liu, S.; Tan, H.; Zhou, J. Curing parameters’ influences of early-age temperature field in concrete continuous rigid frame bridge. J. Clean. Prod. 2021, 313, 127571. [Google Scholar] [CrossRef]
- Chen, B.; Guan, B.; Lu, X.; Tian, B.; Li, Y. Thermal conductivity evolution of early-age concrete under variable curing temperature: Effect mechanism and prediction model. Constr. Build. Mater. 2022, 319, 126078. [Google Scholar] [CrossRef]
- Dai, J.; Wang, Q.; Bi, R.; Wang, C.; Han, Z.; Du, W.; Chen, Z. Research on influencing factors and time-varying model of thermal conductivity of concrete at early age. Constr. Build. Mater. 2022, 315, 125638. [Google Scholar] [CrossRef]
- Zhuang, Z. Finite Element Analysis and Application Based on ABAQUS, 1st ed.; Tsinghua University Publishing House Co., Ltd.: Beijing, China, 2009. [Google Scholar]
- Zhang, X.; Zhu, H.; Jiang, X.; Broere, W. Distributed fiber optic sensors for tunnel monitoring: A state-of-the-art review. J. Rock Mech. Geotech. Eng. 2024, 16, 3841–3863. [Google Scholar] [CrossRef]
- Sun, J.; Meng, F.B.; Gu, Q.L. Analysis and Control Method of Hydration Heat Crack of 1000-Ton Whole-Hole Precast Box Girder Concrete. Qual. Eng. 2024, 42, 32–40. (In Chinese) [Google Scholar]
- Schindler, A.K. Concrete Hydration, Temperature Development, and Setting at Early-Ages. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2002. [Google Scholar]
- Van Breugel, K. Simulation of Hydration and Formation of Structure in Hardening Cement-Based Materials; Delft University Press: Delft, NL, USA, 1997. [Google Scholar]
- Zhu, B.F. Temperature Stresses and Temperature Control in Mass Concrete, 2nd ed; China Water Conservancy and Hydropower Press: Beijing, China, 2012. (In Chinese) [Google Scholar]
- Almeida Del Savio, A.; La Torre Esquivel, D.; Pasquel Carbajal, E.; De Andrade Silva, F. Experimental and Analytical Study of Temperatures Developed by the Heat of Hydration of High-Strength Self-Compacting Mass Concrete. Case Stud. Constr. Mater. 2025, 22, e04098. [Google Scholar] [CrossRef]






| Parameter | Material Composition | Quantity (kg/m3) |
|---|---|---|
| Binder system | Cement | 236 |
| Fly Ash | 118 | |
| Slag | 118 | |
| Aggregate gradation | Coarse aggregate (crushed stone) | 1045 |
| Fine aggregate (sand) | 727 | |
| Water-to-binder ratio | Water-to-binder ratio | 0.39 (Water content: 156 kg/m3) |
| Workability | Polycarboxylate superplasticizer | 0.23% (5.66 kg/m3) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Y.; Xiong, D.; Hong, D.; Wang, F.; Feng, X.; Yang, Q. Spatiotemporal Thermal Analysis of Large-Volume Concrete Girders: Distributed Fiber Sensing and Hydration Heat Simulation. Coatings 2025, 15, 453. https://doi.org/10.3390/coatings15040453
Fan Y, Xiong D, Hong D, Wang F, Feng X, Yang Q. Spatiotemporal Thermal Analysis of Large-Volume Concrete Girders: Distributed Fiber Sensing and Hydration Heat Simulation. Coatings. 2025; 15(4):453. https://doi.org/10.3390/coatings15040453
Chicago/Turabian StyleFan, Yuanji, Danyang Xiong, Deng Hong, Fei Wang, Xu Feng, and Qiuwei Yang. 2025. "Spatiotemporal Thermal Analysis of Large-Volume Concrete Girders: Distributed Fiber Sensing and Hydration Heat Simulation" Coatings 15, no. 4: 453. https://doi.org/10.3390/coatings15040453
APA StyleFan, Y., Xiong, D., Hong, D., Wang, F., Feng, X., & Yang, Q. (2025). Spatiotemporal Thermal Analysis of Large-Volume Concrete Girders: Distributed Fiber Sensing and Hydration Heat Simulation. Coatings, 15(4), 453. https://doi.org/10.3390/coatings15040453






