Thermal Analysis and Parameter Optimization of the Ironing Process for FDM-Printed PLA and ABS Parts

Abstract

The surface roughness of fused deposition modeling (FDM) parts severely limits their applications. Ironing, as an effective method to enhance surface quality, exhibits unclear interactions among its process parameters and lacks defined optimal process windows for different materials. To address this, this study employs a simulation to reveal the influence of ironing speed on the temperature field. Combining single-factor experiments with response surface methodology, predictive models for the surface roughness of PLA and ABS are established. Results indicate significant parameter interactions: PLA roughness is primarily governed by the interaction between ironing speed and ironing flow, while ABS roughness is co-influenced by the main effects of all three parameters (ironing speed, ironing flow, and ironing line spacing) as well as the interactions between speed and flow, and speed and line spacing. After optimization, the optimal surface roughness Ra values for PLA and ABS parts reached 0.852 μm and 1.014 μm, respectively. This study clarifies the dependence of ironing process effectiveness on material properties at the experimental optimization level, providing a theoretical basis for precise control of the FDM ironing process.

1. Introduction

Additive manufacturing (3D printing) enables rapid and precise fabrication of complex components through sequential material layering. In recent years, this technology has found extensive applications across various sectors, including aerospace, automotive manufacturing, and biomedical sectors [1,2,3,4].

Among numerous additive manufacturing techniques, Fused Deposition Modeling (FDM) technology has garnered significant attention for its distinct advantages of low cost, high flexibility, and rapid prototyping [5,6,7,8]. The process is based on the thermal fusion and solidification of thermoplastics, constructing parts by depositing molten filament through a controlled extrusion system [9,10], as shown in Figure 1. However, in addition to mechanical properties that can lag behind those from conventional manufacturing [11,12], FDM parts inherently exhibit pronounced staircase effects and high surface roughness due to the layer-by-layer deposition principle [13,14,15,16,17]. This surface quality issue has become a critical bottleneck restricting the technology’s expansion into higher-end application domains [18,19].

To address the surface quality limitations of FDM, researchers have adopted two primary approaches: printing parameter optimization and post-processing techniques. Extensive studies have confirmed that printing parameters such as layer height, printing speed, infill density, and nozzle temperature significantly influence the surface roughness of FDM parts [20,21,22,23,24,25]. Beyond FDM parameter optimization, various post-processing techniques have been developed to actively enhance surface quality, including chemical, mechanical grinding, and heat treatment methods. However, these conventional methods often improve surface finish at the expense of compromising dimensional accuracy, limiting applicability to complex geometries, and introducing potential defects such as residual stresses [26,27,28].

In contrast, ironing, as a novel post-processing method integrated within the FDM process itself, offers a straightforward and cost-effective alternative. It utilizes the printer’s own heated nozzle to re-melt and flatten the top surface with minimal material extrusion, effectively reducing roughness without the need for additional equipment.

Butt et al. [29] demonstrated that optimizing ironing parameters significantly enhances the surface smoothness of ABS and ASA, with ASA showing higher sensitivity to parameter variations. Targeting the needs of electronic device integration, Neuhaus et al. [30] achieved a 96.6% reduction in surface roughness through the ironing path optimization, enabling high-resolution strain sensor application. Alzyod and Ficzere [31], employing a Box–Behnken design, not only reduced surface roughness by 69% but also significantly improved the mechanical properties of the fabricated parts. Sardinha et al. [32] reported that ironing post-processing reduced surface roughness and warping in FDM-printed ABS parts by up to 60% and 30%, respectively. Alzyod et al. [33] systematically quantified the effects of path speed, ironing spacing, and flow rate on the surface quality of PLA samples using both contact and non-contact measurement methods, further validating the significant improvement achievable with the ironing process.

Despite confirming the effectiveness of ironing, the aforementioned studies exhibit notable limitations. On one hand, current research predominantly focuses on the experimental optimization of process parameters, overlooking the underlying thermal mechanisms involved in the ironing process. On the other hand, comparative studies on the ironing behavior of different materials are scarce, and the complex interactions among process parameters have yet to be systematically elucidated. In particular, there is a lack of research integrating transient thermal simulation with systematic experimental design to reveal the physical mechanisms underlying parameter interactions in the ironing process.

Compared to existing ironing process research, the novelty of this study is primarily reflected in the following three aspects:

• Combined Simulation and RSM Approach: This study addresses the lack of integrated thermal and experimental analysis in ironing by combining transient thermal simulation with RSM. The simulation qualitatively reveals the temperature field and heat-affected zone, providing mechanistic insight into the process, while the RSM is used to establish a predictive model for the parameter-response relationship.
• Mechanistic Understanding: We elucidate the material-dependent nature of ironing effectiveness by linking the statistical findings to the divergent rheological properties of PLA and ABS, offering fundamental insights beyond case-specific results.
• Material-Specific Optimization Frameworks: Building on this mechanistic understanding, we demonstrate how the contrasting rheologies of PLA and ABS lead to divergent parameter responses and unique optimal ironing conditions. This systematic comparison provides clear, material-specific frameworks for process design and optimization.

Combining thermal simulation with statistical modeling, this study elucidates the ironing mechanisms and parameter interactions for PLA and ABS, thereby providing a foundational framework for the precision surface treatment of FDM parts.

2. Ironing Process Analysis and Simulation

2.1. Ironing Principle and Thermal Fundamentals

The ironing process, as a surface treatment in FDM, remelts and flattens the surface material using a high-temperature nozzle while co-extruding a minimal amount of filament to fill surface voids. The operational principle involves a dedicated post-printing procedure where the nozzle is programmed to scan the top surface of the printed part at a consistent height, utilizing reduced flow, finer line spacing, and slower printing speed. At this maintained height, the applied heat remelts the top-layer paths while the extruded material permeates inter-path gaps, thereby achieving a leveled and consolidated surface.

Consequently, the ironing process that softens, spreads, and consolidates the material involves coupled multiphysics phenomena, including heat transfer, stress, and fluid flow. Herein, thermal action serves as the key controlling factor. The transfer of thermal energy directly influences the temperature distribution within the printed part, which in turn dictates the material’s phase state, viscosity, and flow deformation behavior, ultimately determining the final outcome of the ironing process.

The heat diffusion from the high-temperature ironing nozzle into the interior of the printed part is governed by Fourier’s law of heat conduction. This law states that the heat flux through a unit area per unit time is proportional to the temperature gradient normal to that area, and that the direction of heat flow is opposite to the direction of temperature increase. It is mathematically expressed by Equation (1).

$$\mathrm{q}=-\mathrm{k}\nabla \mathrm{T}$$

(1)

where $q$ is the heat flux density (W·m⁻²), $k$ is the thermal conductivity coefficient (W·m⁻¹·K⁻¹), and $\nabla T$ represents the temperature gradient. The negative sign indicates that heat flows from high-temperature regions to low-temperature regions, opposite to the direction of the temperature gradient.

To predict the temperature field distribution $T\left(x,y,z,t\right)$ throughout the printed part at any location and time during the ironing process, the transient heat conduction partial differential equation satisfying the energy conservation criterion must be solved, as shown in Equation (2).

$$\rho C_p{\displaystyle \frac{\partial T}{\partial t}}=\nabla ·\left(k\nabla T\right)+{\dot{Q}}_{gen}$$

(2)

where $\rho$ is the material density (kg·m⁻³), $C_p$ is the specific heat capacity at constant pressure (J·kg⁻¹·K⁻¹), and ${\displaystyle \frac{\partial T}{\partial t}}$ denotes the partial derivative of temperature with respect to time, representing the local temperature change rate. The term $\nabla ·\left(k\nabla T\right)$ describes the divergence of the conductive heat flux, characterizing the net heat flow into or out of a point. ${\dot{Q}}_{gen}$ represents the internal heat generation rate per unit volume (W·m⁻³), which equals zero in this ironing process.

Equation (2) constitutes the theoretical core for simulating the ironing thermal process, indicating that the temperature rise rate at any point within the printed part depends on the convergence or divergence of the surrounding heat flux. Within the actual ironing context, solving this governing equation requires implementing specific boundary conditions. Accordingly, the subsequent finite element analysis will develop a simplified numerical model based on this heat conduction theory to qualitatively reveal how ironing speed influences the temperature field distribution and the extent of the heat-affected zone.

2.2. Temperature Field-Based Modeling of the Ironing Thermal Process

To qualitatively analyze the thermal processes during the ironing procedure, this study employed COMSOL Multiphysics 6.2 software with the Heat Transfer Module to establish a two-dimensional transient heat conduction model. The governing equations were solved using a time-dependent solver based on the Backward Differentiation Formula (BDF) scheme. To accurately resolve the rapid heat transfer, adaptive time stepping was used with a conservative initial time step of 0.001 s, and a relative tolerance of 0.001 was set for the convergence criterion.

The printed part was simplified to a 30 mm × 2 mm rectangle, as shown in Figure 2. Given that the nozzle moves along a single path during the ironing process, the most significant thermal effects are manifested primarily in the plane formed by the direction of nozzle movement and the thickness direction of the part. Therefore, a two-dimensional computational domain is a reasonable and efficient simplification. While this approach neglects out-of-plane heat conduction compared to a 3D simulation, it effectively captures the in-plane thermal gradients, which are essential for a qualitative analysis of ironing speed. Computational costs are also significantly lower. The polymer material used in the model was PLA, and its thermophysical properties, obtained from the literature [34,35], are listed in

Table 1. Thermal properties of PLA material used in simulation.

Thermal Properties	Value	Unit
Density	1250	$\mathrm{k}\mathrm{g}·{\mathrm{m}}^{-3}$
Thermal conductivity coefficient	0.2	$\mathrm{W}·{\mathrm{m}}^{-1}·{\mathrm{K}}^{-1}$
Specific heat capacity	1800	$\mathrm{J}·{\mathrm{k}\mathrm{g}}^{-1}·{\mathrm{K}}^{-1}$

.

In this simulation model, several simplifying assumptions were adopted, including constant thermophysical properties, neglect of phase change, and omission of nozzle contact pressure. These simplifications are justified as the core objective is to qualitatively analyze the impact of ironing speed on the temperature field distribution, rather than to make precise quantitative predictions. This approach sufficiently meets the study’s objective while greatly reducing computational complexity.

The ironing nozzle was modeled as a planar heat source moving at a constant velocity along the X-direction. The spatial distribution of this heat source was defined by a two-dimensional Gaussian function, as expressed in Equation (3), representing the thermal footprint of the nozzle orifice on the part surface. It traversed along the top surface from the left end to the right end of the 30 mm × 2 mm rectangle.

$$q\left(x,y,t\right)=Q_0·exp\left(-{\displaystyle \frac{{\left(x-vt\right)}^2+y^2}{2R^2}}\right)$$

(3)

where $Q_0$ is the heat source intensity (W/m²), related to the temperature of the ironing nozzle; $v$ is the ironing speed (mm/s); $R$ is the characteristic radius of the heat source’s thermal footprint, modeling the effective heat conduction area. Its value is derived from the physical size of the nozzle outlet. A schematic diagram of the nozzle is provided in Figure 3 for clarity. It features a circular outlet with a diameter of 0.4 mm, which corresponds to the nozzle diameter used in the experimental.

To this end, the influence of ironing speed on the temperature field was examined by systematically varying this parameter within a defined range. A summary of the simulation parameters is provided in

Table 2. Simulation parameters.

Parameter Name	Values	Unit
Ironing speed	10, 30, 50	$\mathrm{mm}·{\mathrm{s}}^{-1}$
Heat source intensity	5.0 × 105	$\mathrm{W}·{\mathrm{m}}^{-2}$
characteristic radius	0.2	mm
Convective heat transfer coefficient	25	$\mathrm{W}·{\mathrm{m}}^{-2}·{\mathrm{K}}^{-1}$
Ambient temperature	35	$℃$
part bottom temperature	55	$℃$
Initial part top temperature	100	$℃$

.

A linear temperature gradient was established along the Y-direction of the printed part to represent its initial post-printing state, with the bottom temperature fixed at the build plate temperature of 55 °C and the top temperature at 100 °C. Convective heat transfer boundary conditions are applied to the top and sides of the printed part to simulate heat exchange with the surrounding air. A constant-temperature boundary condition is applied to the bottom to simulate the thermal stabilization effect of the build platform.

To enhance simulation efficiency, this model employs a mapped mesh partitioning approach. In the thickness direction (Y-direction), 60 uniformly distributed elements are allocated to better resolve the significant temperature decay from the surface to the interior of the printed part. Along the length direction (X-direction, corresponding to the heat source movement direction), 140 elements are assigned. The final generated mesh comprises 8400 domain elements with an average element quality of 1 and a total surface area of 60 mm².

A mesh independence study confirmed that the key simulation metrics were insensitive to mesh density. The complete results, including the analysis of both peak temperature and heat-affected zone extent, are provided in the Supplementary Material (Table S1 and Figure S1). Based on this study, the final mesh configuration of 140 (X) × 60 (Y) elements was selected for all simulations.

2.3. Temperature Field Simulation Analysis

Based on the aforementioned model, this study focuses on analyzing the influence of ironing speed on the temperature field developed in the PLA-printed part. Figure 4 presents the resulting temperature distribution nephograms and contour plots at the moment when the ironing heat source reaches the top center of the printed part under different ironing speeds.

As shown in Figure 4a,b, at the slow ironing speed of 10 mm/s, the prolonged dwell time of the heat source resulted in more thorough heat input and a broader diffusion range. The corresponding temperature nephogram exhibited the most extensive high-temperature zone, while the contour plot revealed noticeably elliptical, expanding isotherms. Under this condition, the simulated peak temperature of the printed part reached approximately 230 °C, and the spatial extent of the region exceeding 150 °C was the largest.

When the ironing speed increases to 30 mm/s (Figure 4c,d), the significantly reduced dwell time of the heat source over a given area markedly diminishes the heat accumulation effect, resulting in the simulated peak temperature drop to about 176 °C. Concurrently, the high-temperature zone contracted considerably, and the contour lines became more densely packed, indicating an increased temperature gradient and a narrowed heat-affected zone.

With a further increase in speed to 50 mm/s (Figure 4e,f), the relatively short interaction time between the heat source and the material prevented deep heat penetration into the printed part. Consequently, the high-temperature zone shrank further and became concentrated within a shallow region directly beneath the heat source. The isotherms in this area were the most densely packed, indicating the steepest temperature gradient and a significantly narrower heat-affected zone. Under these conditions, the simulated peak temperature decreased to approximately 158 °C.

In summary, as the ironing speed increases, the peak temperature of the printed part decreases significantly, and the heat-affected zone shrinks simultaneously. This phenomenon occurs because the energy input per unit area from the heat source reduces with increasing speed. The faster speed results in a shorter contact time between the heat source and the material, leading to less accumulated heat and consequently a lower peak temperature. At the same time, it must be acknowledged that the quantitative values of the peak temperatures mentioned above depend on the model and should therefore be regarded as comparative indicators. Nevertheless, the consistent qualitative trends offer valuable insights into the thermal behavior and help interpret the parameter effects observed in the experiments. This finding suggests that during the ironing process, an excessively low speed can easily overheat the surface material, causing excessive melting, flow, and accumulation. Conversely, an excessively high speed may provide insufficient heat input, preventing adequate softening and remelting of the surface material to eliminate the staircase effect, thus yielding suboptimal ironing results. Therefore, an intermediate speed window exists that enables rapid and effective material leveling for improved surface quality while avoiding the risks of overheating.

3. Experimental Materials and Methods

3.1. Experimental Platform and Specimen Preparation

The experimental apparatus platform is shown in Figure 5. All experimental test specimens were produced using a Bambu Lab X1-Carbon 3D printer. The surface roughness and microscopic morphology of the specimens were measured and characterized by a contact-type surface profilometer (JITAI810, JITAI KEYI, Beijing, China) and a super-depth-of-field microscope (HM-FD600E, AOSVI, Shenzhen, China), respectively.

The materials used in this experiment were PLA and ABS filaments, both with a diameter of 1.75 mm. The specific data for these materials are listed in

Table 3. Three-dimensional printing materials used in this study.

Material	Manufacturer	Recommended Printing Temperature [°C]	Color
PLA	Bambu Lab (Shenzhen, China)	190–230	white
ABS	Bambu Lab (Shenzhen, China)	240–270	white

.

The test specimens were fabricated as square blocks with dimensions of 30 mm × 30 mm × 2 mm. The three-dimensional model and photograph of the printed specimen are shown in Figure 6a,b, respectively. The detailed processing parameters for the square block specimens are listed in Table 4.

Table 4. Standard printing parameter settings.

Printing Parameter	Value
Infill density (%)	100
Infill pattern	Line
Layer height (mm)	0.2
Nozzle diameter (mm)	0.4
Printing speed (mm/s)	50
$\mathrm{Build} \mathrm{plate} \mathrm{temperature} (°\mathrm{C})$	55 (for PLA), 90 (for PLA)
$\mathrm{Nozzle} \mathrm{temperature} (°\mathrm{C})$	220 (for PLA), 270 (for PLA)
Flow (%)	98 (for PLA), 95 (for PLA)
Fan speed (%)	100 (for PLA), 10 (for PLA)

Table 4. Standard printing parameter settings.

Printing Parameter	Value
Infill density (%)	100
Infill pattern	Line
Layer height (mm)	0.2
Nozzle diameter (mm)	0.4
Printing speed (mm/s)	50
$\mathrm{Build} \mathrm{plate} \mathrm{temperature} (°\mathrm{C})$	55 (for PLA), 90 (for PLA)
$\mathrm{Nozzle} \mathrm{temperature} (°\mathrm{C})$	220 (for PLA), 270 (for PLA)
Flow (%)	98 (for PLA), 95 (for PLA)
Fan speed (%)	100 (for PLA), 10 (for PLA)

The “Line” infill pattern (as specified in Table 4) produced unidirectional diagonal lines within each layer, with the line orientation alternating at 90° between adjacent layers. Additionally, all specimens were printed using a peripheral structure composed of two layers of wall.

3.2. Ironing Experiment Design

To investigate the influence of various ironing parameters on surface roughness and provide reliable parameter ranges and trend references for subsequent Response Surface Methodology (RSM), this study conducted single-factor experiments targeting three parameters: ironing speed, ironing flow, and ironing line spacing. The experimental parameters for ironing speed were 10 mm/s, 20 mm/s, 30 mm/s, 40 mm/s, and 50 mm/s. Ironing flow parameters: 10%, 15%, 20%, 25%, 30%. Ironing line spacing parameters: 0.1 mm, 0.15 mm, 0.2 mm, 0.25 mm, 0.3 mm.

Following the single-factor experiments, to further investigate the interaction effects of these factors on surface roughness, a three-factor, three-level Box–Behnken design (BBD) was employed. Ironing speed, ironing flow, and ironing line spacing were selected as independent variables, with surface roughness (Ra) as the response variable for parameter analysis. Each material underwent 17 response surface experiments, including 5 replicate experiments at the center point. The selected parameters and their levels for the response surface experiments are shown in

Table 5. BBD parameter design.

Level	A: Ironing Speed (mm/s)	B: Ironing Flow (%)	C: Ironing Line Spacing (mm)
−1	10	10	0.1
0	30	20	0.2
1	50	30	0.3

.

In the response surface experiments, A, B, and C represent the ironing speed, ironing flow, and ironing line spacing, respectively. Surface roughness data for the aforementioned experiments were collected using a contact-type surface profilometer, with the probe movement direction perpendicular to the ironing direction on the specimen surface. The ironing direction, defined as the relative angle between the ironing path and the top-layer printing path, was fixed at 45°. To ensure data reliability and quantify process variability, each test condition was repeated three times (n = 3). For each repetition, five distinct locations (top, upper-middle, center, lower-middle, and bottom) were uniformly sampled along the ironing direction on the square specimen. The average value of these five measurements served as the final surface roughness value for that test specimen. The parameters of the profilometer were configured as follows: the evaluation length was 12.5 mm, the cutoff length was 2.5 mm, and the number of sampling segments was five. The schematic of the surface roughness measurement strategy is shown in Figure 7.

4. Results and Discussion

4.1. Analysis of Single-Factor Experimental Results

4.1.1. Effect of Ironing Speed on Surface Roughness

Ironing speed is a critical parameter that determines the interaction time between the nozzle and the surface of the printed part, influencing the flow and spreading behavior of the molten material and directly affecting the final surface quality. To investigate the individual effect of ironing speed, the ironing flow and ironing line spacing were fixed at 20% and 0.2 mm, respectively. The influence of ironing speed on the surface roughness (Ra and Rz) of PLA and ABS specimens is shown in Figure 8.

As shown in Figure 8, as the ironing speed increased from 10 to 50 mm/s, the surface roughness values (both Ra and Rz) of the PLA specimens exhibited a trend of initial significant decrease followed by gradual stabilization. In contrast, the surface roughness of the ABS specimens demonstrated a distinct decrease-then-increase trend, with the Rz parameter showing a more pronounced variation.

For PLA (Figure 8a), as the speed increased from 10 to 30 mm/s, the Rz decreased from 41.52 μm to 13.52 μm, and the Ra decreased from 10.22 μm to 1.57 μm, showing a significant downward trend in surface roughness. When the speed further increased to 50 mm/s, both Ra and Rz exhibited only minor fluctuations, with the surface roughness changes becoming stable. In this stage, the relatively small error ranges for Ra and Rz indicate that the ironing process for PLA exhibits good stability in the medium-to-high speed range. For ABS (Figure 8b), within the 10–30 mm/s speed range, the Rz decreased from 19.48 μm to 10.49 μm, while the Ra slightly decreased from 2.48 μm to 1.27 μm. However, when the speed further increased to 50 mm/s, the Rz sharply increased to 33.25 μm, and the Ra also increased slightly to 2.5 μm. Notably, the error range for Rz at 50 mm/s increased substantially to ±12.05 μm. This substantial increase implies severely compromised surface uniformity and poor process reproducibility for ABS during high-speed ironing.

In the low-speed range (10–20 mm/s), both materials exhibited high surface roughness resulting from prolonged nozzle dwell time. However, the underlying mechanisms differed due to their rheological characteristics [36,37,38]. PLA, characterized by its lower melt viscosity and more pronounced shear-thinning behavior [36,37], tended to undergo localized over-melting and unstable flow under extended thermal exposure. In contrast, ABS, with its higher melt strength and elasticity [36,38], primarily exhibited excessive extrusion and material accumulation under the extended thermal exposure. Therefore, although these two materials exhibited different behaviors at low ironing speeds, both showed a significant increase in Ra and Rz values.

In the high-speed range (40–50 mm/s), the surface roughness of PLA stabilized, indicating that a dynamic equilibrium had been reached between the ironing flow and the nozzle travel speed. The material’s stacking and stretching behaviors became consistent, resulting in no significant further changes in surface quality. In contrast, the surface roughness of ABS deteriorated markedly within this speed range. This degradation was due to excessive speed, causing insufficient material extrusion, which led to inadequate filling of the top surface layer and localized material shortages. Concurrently, the excessively short thermal exposure time prevented sufficient softening of the material. This impaired the material’s flowability and its ability to fill inter-layer gaps, ultimately leading to an increase in surface roughness.

Collectively, the results demonstrate that ironing speed significantly impacts surface quality by governing both the thermal exposure time and material deposition behavior. Both PLA and ABS achieved optimal surface quality around 30 mm/s, yet their responses to higher speeds diverged markedly. Owing to its superior melt flowability, PLA exhibited stable stretching behavior at high speeds, leading to gradual roughness variations. In contrast, the high melt strength and poor flowability of ABS resulted in insufficient filling under high-speed conditions, causing a sharp deterioration in roughness. These findings indicate that ABS is more sensitive to high-speed ironing than PLA, and consequently possesses a narrower optimal processing window.

4.1.2. Effect of Ironing Flow on Surface Roughness

Ironing flow is a key parameter influencing surface filling efficacy and material deposition behavior. To investigate its individual effect on surface roughness, the ironing speed and line spacing were fixed at 30 mm/s and 0.2 mm, respectively. The resulting influence of ironing flow on the surface roughness (Ra and Rz) of PLA and ABS specimens is shown in Figure 9.

As shown in Figure 9, under the fixed ironing speed and line spacing conditions, the surface roughness values (both Ra and Rz) for both materials initially decreased and then increased as the ironing flow was raised from 10% to 30%. More importantly, when the ironing flow deviates from the optimal range—whether too low or too high—it significantly widens the error range of the surface roughness, particularly for the Rz value, thereby reducing process stability.

For PLA (Figure 9a), as the ironing flow increased from 10% to 15%, the Rz decreased from 17.61 μm to 7.96 μm, and the Ra saw a slight reduction from 1.57 μm to 0.89 μm. This represents a significant declining trend in surface roughness for both Ra and Rz, during which their error ranges also reached a minimum (Rz: ±2.02 μm, Ra: ±0.15 μm). However, when the flow was further increased to 30%, the Rz surged sharply to 44.69 μm and the Ra increased substantially to 7.54 μm, marking a significant upward trend in surface roughness. Concurrently, the error ranges for both Rz and Ra expanded considerably. For ABS (Figure 9b), within the 10%–20% ironing flow range, the surface roughness improved notably: the Rz decreased from 31.59 μm to 10.49 μm, and the Ra slightly decreased from 3.16 μm to 1.27 μm, with their error ranges narrowing correspondingly (from ±0.86 μm to ±0.37 μm for Ra, and from ±9.48 μm to ±3.11 μm for Rz, respectively). In contrast, within the 20%–30% flow range, the Rz increased markedly to 26.78 μm, and the Ra also rose slightly to 4.34 μm, indicating a significant upward trend in surface roughness, accompanied by a clear expansion in the error range of Rz (the standard deviation of Rz expanded to ±6.22 μm).

Specifically, for PLA, the low-flow window is 10%–15%. At an ironing flow of 10%, insufficient extrusion volume led to poor inter-layer bonding and localized material deficiency on the surface, resulting in high surface roughness. Simultaneously, the large error range for Rz indicated significant fluctuations in surface peak-to-valley height and poor process stability. Increasing the ironing flow to 15% achieved optimal material filling, which significantly improved surface roughness and narrowed the error range, indicating excellent process stability. When the flow was further increased to 20%, the roughness exhibited a slight rebound alongside a marginally expanded error range, suggesting that the flow slightly exceeded the optimal value, with minor extrusion excess causing material accumulation. Upon entering the high-flow range of 25%–30%, the extrusion volume far exceeded the capacity of the line spacing (0.2 mm), triggering severe material buildup and nozzle-dragging-induced overflow, which drastically deteriorated the roughness. Concurrently, the error ranges for both Rz and Ra widened significantly, indicating highly unstable process conditions under high ironing flow.

ABS exhibits patterns similar to PLA. In the low ironing flow range of 10%–15%, insufficient filling leads to poor surface quality and a larger Rz error range. When the ironing flow increases to 15%, surface quality improves but remains suboptimal. At 20% ironing flow, surface quality reaches its peak with the smallest error range and the best process stability. In the high ironing flow range of 25%–30%, excessive extrusion volume causes noticeable material accumulation and overflow on the specimen surface, leading to a sharp increase in roughness. Simultaneously, the error range of Rz expands significantly, further indicating markedly deteriorated surface uniformity and worsened process stability under high-flow conditions.

In summary, ironing flow significantly impacts the surface ironing effectiveness. Both PLA and ABS achieve optimal surface quality within specific flow intervals (approximately 15% for PLA and 20% for ABS), where the error range is minimal and process robustness is the highest. Excessively low flow causes insufficient filling, while excessively high flow triggers material accumulation and overflow. Both scenarios result in a significant expansion of the surface roughness error ranges and poor process stability.

4.1.3. Effect of Ironing Line Spacing on Surface Roughness

Ironing line spacing governs the overlap degree between adjacent ironing paths. To investigate its isolated influence, this experiment fixed the ironing speed and ironing flow at 30 mm/s and 20%, respectively. The influence of different ironing line spacings on the surface roughness (Ra and Rz) of PLA and ABS specimens is depicted in Figure 10.

As shown in Figure 10, under fixed ironing speed and flow conditions, the influence of ironing line spacing on surface roughness exhibits distinctly different trends for PLA and ABS, highlighting a clear material dependency.

For PLA (Figure 10a), as the line spacing increased, the surface roughness generally exhibited a trend of first decreasing and then increasing. Both Ra and Rz reached their minimum values (Ra = 1.57 μm, Rz = 13.52 μm) at a line spacing of 0.20 mm, with relatively small error ranges (Ra: ±0.31 μm, Rz: ±2.66 μm). However, for ABS (Figure 10b), the surface roughness generally showed a gradual increase with increasing line spacing. The optimal surface roughness (Ra = 1.27 μm, Rz = 10.49 μm) was achieved at a line spacing of 0.1 mm, with a relatively narrow error range (Ra: ±0.08 μm, Rz: ±1.62 μm). Overall, the variation in surface roughness across the tested line spacing range was modest, with Ra fluctuating within a narrow band of only 0.25 μm. This minimal fluctuation confirms a stable process response for ABS under varying ironing line spacing.

Specifically, for PLA, when the line spacing was 0.1 mm, since this distance was significantly smaller than the 0.4 mm nozzle outlet diameter, adjacent paths overlapped excessively. This caused surface material to accumulate and form localized protrusions, thereby increasing surface roughness. Even when the line spacing was increased to 0.15 mm, the surface roughness remained high due to persistent partial material overlap, with the accumulation phenomenon continuing. Notably, within the 0.1–0.15 mm range, the surface roughness error range was significantly larger, further demonstrating the challenge of maintaining surface uniformity under small line spacing conditions. However, when the line spacing was further increased to the 0.25–0.3 mm range, the surface roughness (particularly the Rz value) exhibited a significant rebound. This indicates that the excessively large line spacing in this range (exceeding half of the 0.4 mm nozzle diameter) surpassed the effective action range of the nozzle, resulting in untreated gaps between adjacent paths and inadequate surface filling.

ABS exhibited a trend distinct from that of PLA, with its surface roughness increasing gradually as the line spacing widened. This behavior is attributed to the higher melt strength and lower flowability of ABS. At the small line spacing of 0.1 mm, the high melt strength of ABS made it less prone to flow instability caused by the compression from subsequent ironing paths. Consequently, the benefit of high path overlap was fully realized, allowing for repeated ironing of the same area, and material accumulation was suppressed. As the line spacing increased, the negative impact of reduced path overlap became dominant, leading to a gradual rise in surface roughness. This deterioration occurred because the increasing line spacing exceeded the coverage capability of the 0.4 mm nozzle, and the material’s inherently poor flowability could not bridge the resulting gaps. The overall variation in surface roughness ( $∆$R $\approx$ 0.25 μm) was significantly smaller than that of PLA ( $∆$Ra $\approx$ 1.24 μm), and the associated error range was relatively narrow. This demonstrates that ABS, owing to its higher melt strength, has lower sensitivity to line spacing variations and consequently a wider process window.

In conclusion, the impact of ironing line spacing on surface quality exhibits significant material dependency. PLA demonstrates a distinct optimal ironing line spacing at 0.20 mm, whereas ABS shows broader process adaptability, achieving stable and superior surface quality at smaller line spacings due to its high melt strength.

4.2. Analysis of Response Surface Methodology Results

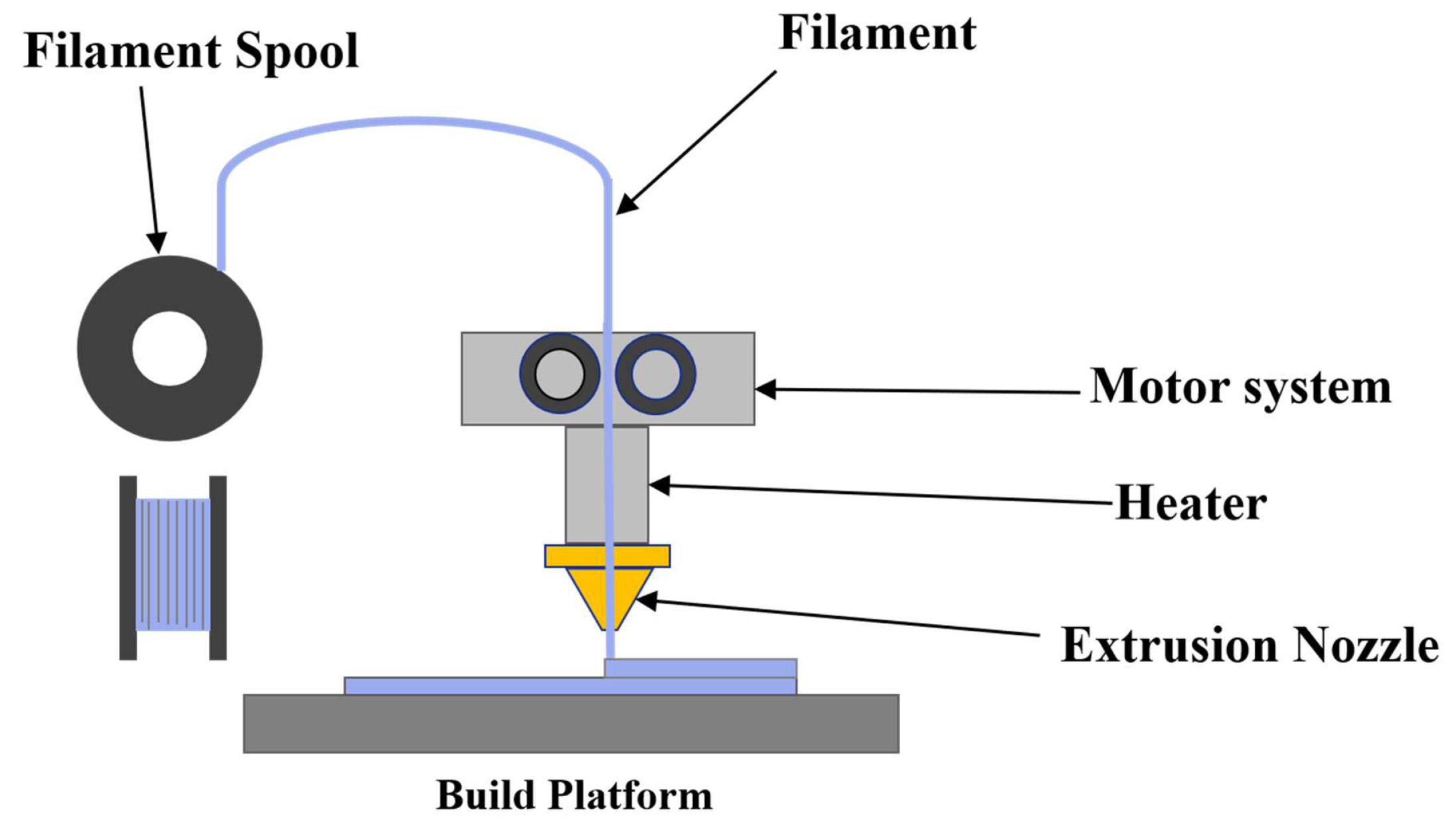
4.2.1. Model Establishment and Significance Analysis

Based on the results obtained from the Box–Behnken experimental design, this study employed Design-Expert software to perform quadratic regression fitting on the surface roughness (Ra) of PLA and ABS, resulting in reliable predictive models. The complete experimental design and response values are provided in Appendix A 

Table A1. All parameter combinations of the Box–Behnken experimental design and response values for surface roughness (Ra) of PLA and ABS.

Run No.	A	B	C	Ra (μm)
				PLA	ABS
1	−1	−1	0	1.6985	2.0445
2	+1	−1	0	9.6187	8.1080
3	−1	+1	0	18.9062	15.8370
4	+1	+1	0	2.1843	1.8430
5	−1	0	−1	7.2302	3.8747
6	+1	0	−1	1.6771	1.6483
7	−1	0	+1	5.6891	8.6345
8	+1	0	+1	1.3676	1.4268
9	0	−1	−1	1.2738	2.3517
10	0	+1	−1	4.8734	4.8386
11	0	−1	+1	1.9407	3.4384
12	0	+1	+1	7.5770	5.0600
13	0	0	0	1.1402	0.8640
14	0	0	0	1.7858	1.0210
15	0	0	0	2.5257	1.3630
16	0	0	0	1.6974	1.9890
17	0	0	0	1.2378	1.5720

. The analysis of variance (ANOVA) for the regression models of both materials is presented in

Table 6. ANOVA and Goodness-of-Fit for the regression models.

Source	PLA Model		ABS Model
	p-Value	Significance	p-Value	Significance
Model	<0.0001	Significant	<0.0001	Significant
A	<0.0001	Significant	<0.0001	Significant
B	<0.0001	Significant	0.0009	Significant
C	0.5371	Not Significant	0.0270	Significant
AB	<0.0001	Significant	<0.0001	Significant
AC	0.4813	Not Significant	0.0121	Significant
BC	0.2586	Not Significant	0.5779	Not Significant
A2	<0.0001	Significant	0.0001	Significant
B2	0.0001	Significant	0.0001	Significant
C2	0.0535	Not Significant	0.5100	Not Significant
Lack of Fit	0.1092	Not Significant	0.0754	Not Significant
Goodness-of-Fit
R2	0.9859		0.9839
Adjusted R2	0.9677		0.9632
Predicted R2	0.8257		0.7910

, with detailed ANOVA data available in Appendix A,

Table A2. ANOVA and significance test for the PLA experimental model.

Source	Sum of Squares	df	Mean Square	F-Value	p-Value	Significance
Model	335.44	9	37.27	54.34	<0.0001	Significant
A	43.60	1	43.60	63.57	<0.0001	Significant
B	45.17	1	45.17	65.86	<0.0001	Significant
C	0.2888	1	0.2888	0.4210	0.5371	Not Significant
AB	151.81	1	151.81	221.34	<0.0001	Significant
AC	0.3792	1	0.3792	0.5529	0.4813	Not Significant
BC	1.04	1	1.04	1.51	0.2586	Not Significant
A2	44.46	1	44.46	64.83	<0.0001	Significant
B2	42.44	1	42.44	61.88	0.0001	Significant
C2	3.69	1	3.69	5.38	0.0535	Not Significant
Residual	4.80	7	0.6859
Lack of Fit	3.59	3	1.20	3.94	0.1092	Not Significant
Pure Error	1.21	4	0.3034
Cor Total	340.24	16
R2 = 0.9859	Adjusted R2 = 0.9677	Predicted R2 = 0.8257

and

Table A3. ANOVA and significance test for the ABS experimental model.

Source	Sum of Squares	df	Mean Square	F-Value	p-Value	Significance
Model	235.47	9	26.16	47.57	<0.0001	Significant
A	37.69	1	37.69	68.54	<0.0001	Significant
B	16.92	1	16.92	30.78	0.0009	Significant
C	4.27	1	4.27	7.77	0.0270	Significant
AB	100.58	1	100.58	182.88	<0.0001	Significant
AC	6.20	1	6.20	11.28	0.0121	Significant
BC	0.1872	1	0.1872	0.3404	0.5779	Not Significant
A2	32.66	1	32.66	59.39	0.0001	Significant
B2	33.28	1	33.28	60.51	0.0001	Significant
C2	0.2649	1	0.2649	0.4817	0.5100	Not Significant
Residual	3.85	1	0.5499
Lack of Fit	3.05	7	1.02	5.07	0.0754	Not Significant
Pure Error	0.8015	3	0.2004
Cor Total	239.32	4
R2 = 0.9839	Adjusted R2 = 0.9632	Predicted R2 = 0.7910

.

As shown in Table 6, the regression models developed for both PLA and ABS were highly significant (p < 0.0001), while their lack-of-fit terms were not significant (p > 0.05), indicating that the models are valid and well-fitted. The determination coefficients R² and adjusted R² for both models were above 0.96, proving that the models explain over 96% of the variation in response values and possess excellent predictive capability. Furthermore, significance analysis of the individual factors and their interactions revealed distinct patterns: For PLA, the linear terms of ironing speed (A) and flow (B), as well as their interaction (AB), exerted extremely significant effects on Ra (p < 0.0001), whereas the main effect of ironing line spacing (C) and its related interactions were not significant. For ABS, the main effects of all three factors—ironing speed (A), flow (B), and line spacing (C)—as well as the interactions between ironing speed and flow (AB) and between ironing speed and line spacing (AC), were all significant.

It is noteworthy that the significance of factors revealed by the response surface analysis differs from the preliminary understanding derived from single-factor experiments. While single-factor experiments indicated that ironing line spacing (C) affects the surface quality of PLA, the response surface model showed its main effect to be insignificant (p = 0.5371). This suggests that the line spacing effect observed under fixed ironing speed and ironing flow conditions was dominated and masked by the highly significant speed-flow interaction (AB) in the response surface experiments. This finding highlights the limitations of relying solely on single-factor experiments and underscores the necessity of investigating parameter interactions.

The quadratic polynomial regression equations derived from the models are given by Equations (4) and (5).

Ra [μm] = 1.68 − 2.33A + 2.38B + 0.1900C − 6.16AB + 0.3079AC + 0.5092BC + 3.25A² + 3.17B² − 0.9360C² (for PLA)

(4)

Ra [μm] = 1.36 − 2.17A + 1.45B + 0.7308C − 5.01AB − 1.25AC − 0.2163BC + 2.79A² + 2.81B² − 0.2508C² (for ABS)

(5)

The above analysis demonstrates that the models established in this study possess high significance and predictive reliability, making them suitable for subsequent interaction analysis and parameter optimization. Furthermore, the significant factors differ between PLA and ABS. The following section will employ response surface plots to provide a focused analysis of the interactions between parameters on surface quality, thereby clarifying the optimal process optimization pathways for each material.

4.2.2. Analysis of Parameter Interactions

Using the Design-Expert software system, we analyzed the effects of interactions among three factors—ironing speed, ironing flow, and ironing line spacing—on the surface roughness Ra of PLA and ABS specimens. The results are shown in Figure 11.

As shown in Figure 11a,b, the interaction between ironing speed and flow (AB) exerted a highly significant influence on surface roughness. Specifically, for PLA (Figure 11a), the response surface exhibited a distinct steep-to-gentle transition. In the low-speed region (A < 25 mm/s), Ra values rose sharply with increasing ironing flow, resulting in a steep response surface. This indicated that the excessive material, delivered by the high flow, cannot be sufficiently spread and leveled by the low ironing speed, leading to material buildup. In the medium-high-speed region (A > 30 mm/s), Ra first slightly decreased and then gradually increased with increasing ironing flow, while its sensitivity to flow changes diminished significantly, resulting in a flatter response surface. This suggested that a moderate increase in material supply at high speeds could fill interlayer gaps and improve surface finish. However, when the flow continued to increase beyond the optimal value, even at high speeds, the excessive material supply eventually surpassed the leveling capacity, leading to slight material over-accumulation and a subsequent rise in Ra. The optimal process window for PLA was located in the combination zone of medium-high speeds and medium-low flows, where the process demonstrated good robustness. For ABS (Figure 11b), the response surface morphology was similar to that of PLA. In the low-ironing speed range, high ironing flow also caused Ra to increase, while in the high-ironing speed range, the sensitivity of Ra to flow changes was reduced, though excessive ironing flow still degraded surface quality. The optimal process window for ABS was also found in the combination zone of medium-to-high ironing speed and medium-to-low ironing flow.

As observed in Figure 11c,d, the influence of ironing line spacing (C) differed markedly between PLA and ABS, highlighting a clear material-dependent behavior. For PLA (Figure 11c), the response surface exhibited pronounced variation along the ironing speed axis while showing extremely gradual changes along the ironing line spacing axis. This aligns with the ANOVA results, where the AC interaction term was not significant (p = 0.4813). At a fixed ironing line spacing, the Ra value decreased sharply and then increased with rising ironing speed, indicating that both excessively long thermal exposure at low speeds and insufficient thermal exposure at high speeds led to deteriorated surface quality. For ABS (Figure 11d), the response surface morphology resembled that of PLA but exhibited more pronounced variation along the ironing line spacing axis, displaying a distinct inclination. In the low-to-medium speed range (A < 30 mm/s), Ra increased with larger line spacing, whereas in the medium-to-high speed range, the change in Ra with increasing line spacing became relatively gradual. These results demonstrate that ironing line spacing is a key controllable parameter in the ABS ironing process, and its optimal setting is closely related to ironing speed, requiring coordinated optimization.

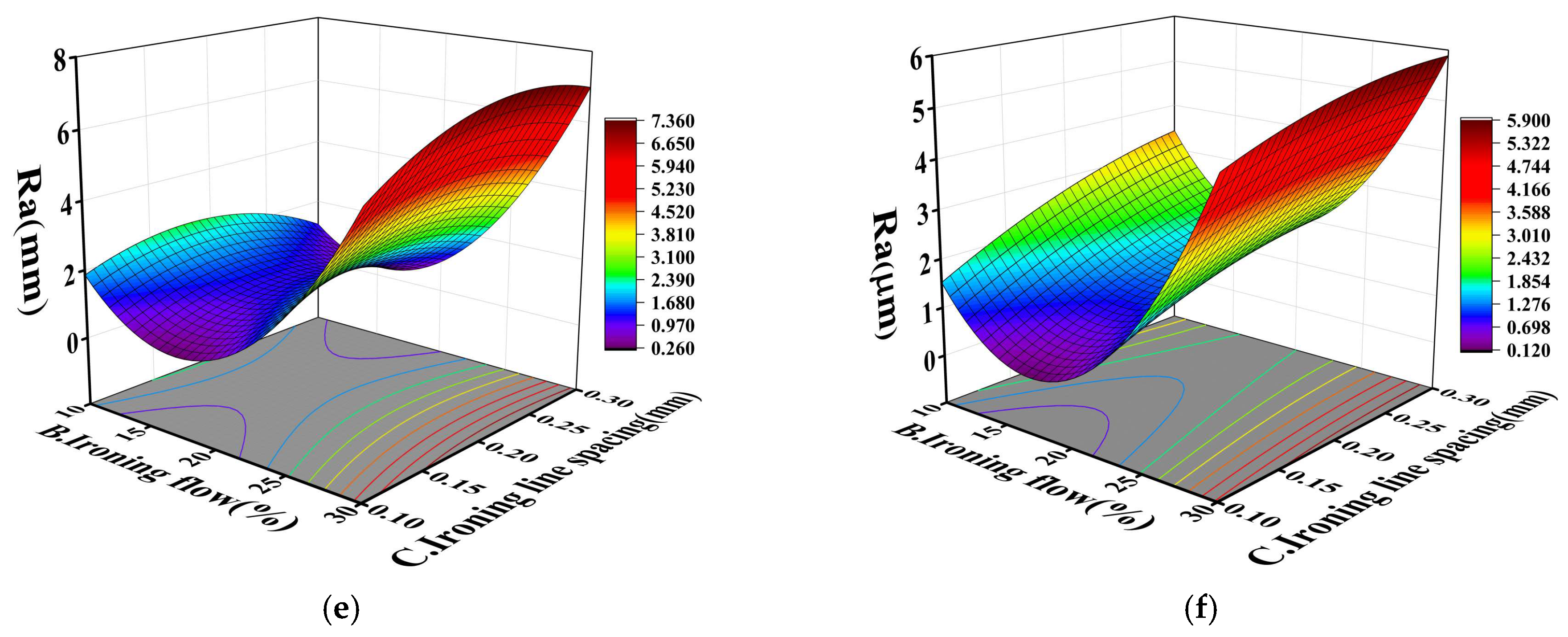
As shown in Figure 11e,f, the interaction between ironing flow and ironing line spacing (BC) had a relatively weak effect on both materials. For PLA (Figure 11e), the main effect of ironing flow (B) was highly significant and dominated the response surface trend, whereas the independent effect of ironing line spacing (C) was relatively weak. This aligned with the ANOVA conclusion that the BC term was not significant (p = 0.2586). At a fixed ironing line spacing, the Ra value first decreased and then increased significantly with increasing flow. This indicated that insufficient ironing flow failed to provide adequate material to cover the layer lines, leading to degraded surface quality (elevated Ra). Conversely, excessive flow caused material over-accumulation and overflow, resulting in surface irregularities (sharply increased Ra). For ABS (Figure 11f), the response surface characteristics resembled those of PLA. At a fixed ironing line spacing, Ra first decreased and then increased sharply with increasing ironing flow, with the main effect of ironing flow (B) being highly significant. However, the independent effect of ironing line spacing (C) is weaker compared to PLA, as evidenced by the flatter variation in the response surface along the C-axis direction.

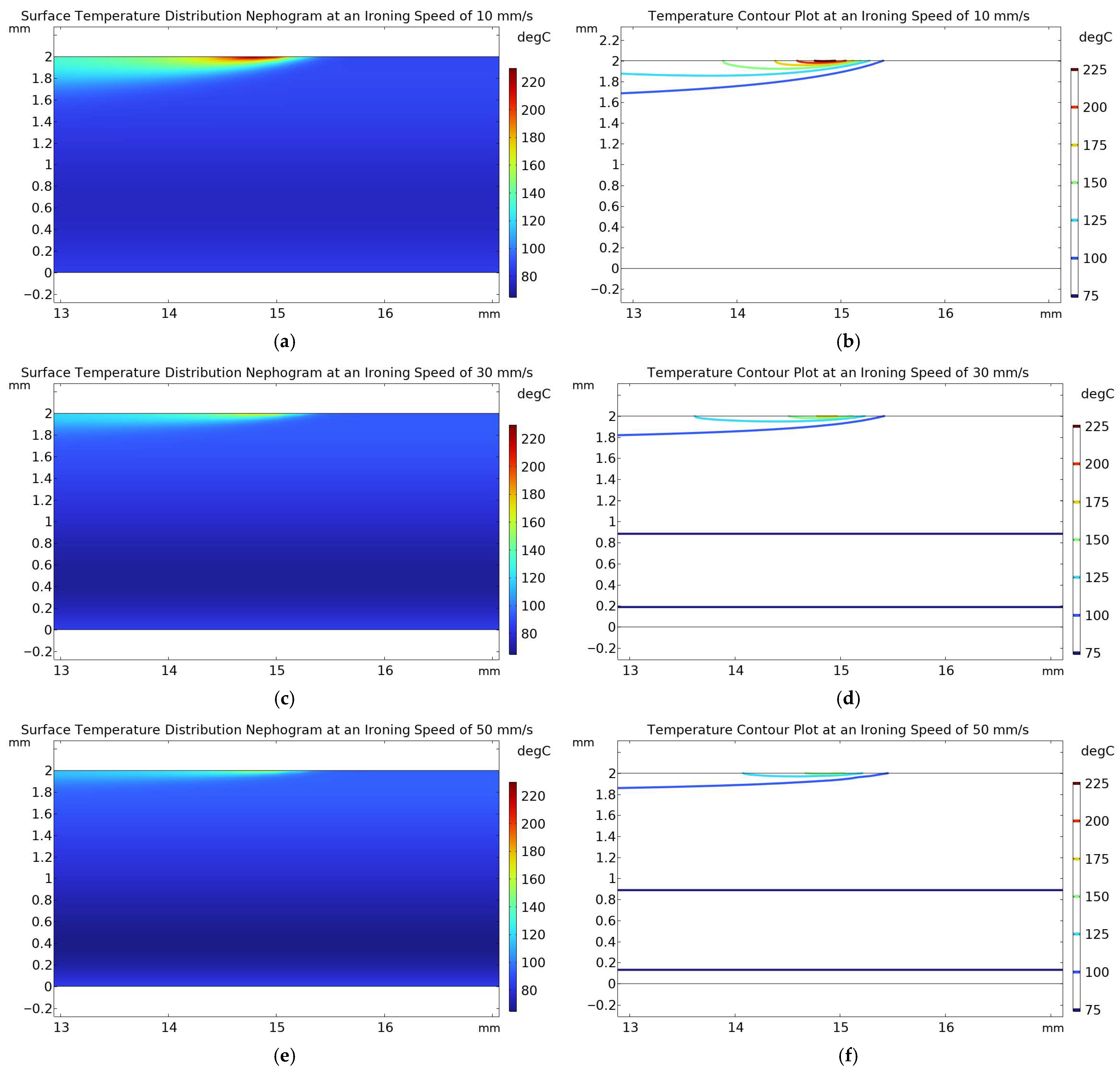
The significant AB and AC interactions for ABS, as shown in Figure 11b,d, can be interpreted through the fundamental mechanism of thermal input. In this study, this mechanism was qualitatively illustrated by the thermal simulations for PLA in Figure 4. Although ABS and PLA possess different rheological properties, the ironing speed governed the thermal energy input for both materials during the ironing process. For the AB interaction (Figure 11b), at a low speed of 10 mm/s, the prolonged thermal exposure (as indicated by the extensive heat-affected zones in Figure 4a,b) combined with a high flow of 30% allowed excessive material to be extruded, leading to accumulation. However, at a high speed of 50 mm/s, the brief thermal exposure (as indicated by the shallow heat-affected zones in Figure 4e,f) combined with a low flow of 10% failed to sufficiently soften and spread the material, resulting in insufficient filling. For the AC interaction (Figure 11d), at a low speed of 10 mm/s, despite sufficient heat input and a larger heat-affected zone, an excessively wide line spacing of 0.3 mm exceeded the material’s flow capacity, preventing effective gap filling and leading to increased surface roughness. However, at a high speed of 50 mm/s, even with a small line spacing of 0.1 mm, insufficient heat input and a shallow heat-affected zone hindered effective material flow and filling. The high melt strength of ABS severely restricted its flow, making it highly sensitive to both interactions influenced by ironing speed.

In summary, PLA and ABS exhibit fundamentally different sensitivities to ironing process parameters, a distinction rooted in their divergent rheological properties. The surface quality of PLA is primarily governed by the interaction between ironing speed and flow, indicating that its low-viscosity melt is highly sensitive to material supply. In contrast, ABS is significantly influenced by ironing speed, flow, and line spacing simultaneously, exhibiting more complex parameter coupling effects closely related to its high melt strength-induced flow resistance. Regarding optimization strategies, a combination of medium-to-high ironing speed and medium-to-low ironing flow represents a clearly effective approach for PLA. For ABS, however, the stronger parameter coupling narrows the optimal process window, necessitating strict coordination of ironing speed, flow, and line spacing during optimization.

4.2.3. Parameter Optimization and Validation

Based on the established response surface models, this study employed the optimization module of Design-Expert software to perform parameter optimization of ironing speed (A), flow (B), and line spacing (C), aiming to minimize surface roughness (Ra). To balance surface quality and production efficiency, the optimization range for speed (A) was constrained between 20 and 40 mm/s, while the other factors remained continuously adjustable within their experimental ranges. Subsequently, based on the predicted optimal parameter combinations, three replicate experiments were conducted for each PLA and ABS specimen, with the average values serving as the final measured results. The predictive accuracy of the models was evaluated by comparing the predicted and measured values. The optimal process parameter combinations for both materials, along with a comparison between the predicted and experimentally validated Ra values, are presented in

Table 7. Optimal process parameter combinations with corresponding predicted and measured Ra values.

Material	Ironing Speed (mm/s)	Ironing Flow (%)	Ironing Line Spacing (mm)	Predicted Ra (μm)	Measured Ra (μm)	Relative Error (%)
PLA	28.64	19.89	0.122	1.125	0.852	32.04
ABS	30.25	17.23	0.169	0.900	1.014	11.24

.

The comparison of the predicted results with the experimental results indicated that the two material models exhibit differences in predictive accuracy. For ABS, the validation experiments yielded a measured Ra of 1.014 μm, representing a relative error of 11.24% against the predicted value (0.900 μm). This error margin fell within the reasonable expectation range of the model’s predictive coefficient of determination (Pred R² = 0.7910), confirming the high predictive accuracy and reliability of the ABS regression model. For PLA, the larger relative error (32.04%) underscored a limitation of the model. While it excelled at identifying the correct optimization direction and the significant parameter interactions, its accuracy in predicting the absolute Ra value for a new parameter set was limited. This divergence between the high R² (0.9859) and the lower Pred R² (0.8257) quantified this limitation, indicating that the model explained the experimental design variance well but had reduced predictive power for new data. The superior actual measured Ra value (0.852 μm) suggested the presence of unmodeled interactions between the process conditions and the material behavior. Therefore, the primary utility of the PLA model lies in its proven ability to reliably guide parameter optimization towards the global optimum, rather than in providing precise point forecasts. The plots of predicted versus actual values for PLA and ABS models provided in the Supplementary Materials (Figure S2) further corroborate the above explanation.

4.3. Microstructural Analysis

To investigate the mechanism by which the ironing process improves surface quality and to compare the distinct surface characteristics of PLA and ABS resulting from their differing flow properties, this study employed a super-depth-of-field microscope to observe and contrast the surface topography of representative specimens from both materials, as shown in Figure 12. The selected specimens included: the original unironed surface, the surface treated with optimized ironing parameters, and typical specimens exhibiting poor surface roughness from the response surface experiments. The specimens with poor roughness corresponded to two typical defect conditions: low ironing speed with high ironing flow (10 mm/s, 30%) and high ironing speed with low ironing flow (50 mm/s, 10%), with the ironing line spacing fixed at 0.2 mm in both cases.

A comparison of surface topography before and after ironing reveals that both untreated PLA and ABS specimens exhibit distinct layered striations and pores. After ironing with optimized parameters, the surface texture of both materials became considerably finer and more uniform, with a significant reduction in layered striations and porosity. This provides clear visual evidence that the ironing process effectively enhances the surface quality of FDM-printed parts.

In terms of typical defect morphology, the two materials exhibited significant differences. Under low-speed, high-flow ironing conditions, PLA specimens developed distinct and continuous ridge-like protrusions, as shown in the marked area of Figure 12e. In contrast, the ABS specimen surface exhibited severe stringing and material overflow, where excess material accumulated into pronounced bulges and burrs, as indicated in the marked area of Figure 12f. This morphological disparity originated from the combined effect of prolonged local heating and material over-extrusion. Under these conditions, the high fluidity yet low melt strength of PLA led to unstable flow and accumulation, amplifying surface undulations. In contrast, the high melt strength and viscosity of ABS prevented the excess material from spreading evenly, causing localized accumulation and protrusion formation.

Under high-speed, low-flow ironing conditions, both materials exhibited surface pitting due to severe insufficiency in heat input and material filling. However, their morphological characteristics differed markedly: PLA specimens formed continuous, gully-like pits, as shown in the marked area of Figure 12g; whereas ABS exhibited discontinuous, yet larger and deeper isolated pits, as indicated in the marked area of Figure 12h. This phenomenon arises because PLA, with its superior melt flowability, tends to form relatively coherent depressed regions when underfilled. In contrast, ABS, characterized by high melt viscosity and poor flowability, struggles to flow and spread under the same brief thermal exposure. Consequently, it fails to achieve continuous filling and instead develops more isolated and severe pits under localized stress.

The aforementioned microstructural analysis indicates that optimizing the ironing process effectively eliminates layer lines, yielding a smooth surface. Furthermore, the analysis reveals that under non-optimized parameters, PLA and ABS exhibit distinctly different surface defects due to their varying material flow characteristics. Low-viscosity PLA tends to form continuous ridge-like elevations and pits due to uneven flow, while high-viscosity ABS, characterized by high melt strength and poor fluidity, primarily exhibits localized material buildup and isolated deep pits. These findings further underscore the dependence of the ironing process effectiveness on material properties.

The observed microstructures also offer an effective means to understand the mechanical and functional trade-offs introduced by the ironing process. The ridge-like protrusions in PLA and severe overflow in ABS could act as stress concentrators, potentially affecting fatigue life and dimensional accuracy. Conversely, the improved surface consolidation under optimal parameters suggests enhanced top-layer interlayer bonding. A comprehensive quantification of these effects, such as residual stress and mechanical strength, remains a key objective for future study.

5. Conclusions

This study systematically analyzed the impact of ironing process parameters on the surface quality of FDM-printed PLA and ABS parts through a combined simulation and experimental approach, yielding the following key conclusions:

(1)

A transient heat transfer simulation model was constructed using COMSOL to qualitatively reveal the influence of ironing speed on the temperature field. Results indicate that increasing ironing speed significantly reduces the maximum temperature on the printed part’s surface layer and shrinks the heat-affected zone. This provides a theoretical explanation for the phenomena observed during ironing: excessively low speeds may cause overheating, while excessively high speeds may result in insufficient melting.

(2)

Single-factor experiments reveal that the effects of ironing speed, ironing flow, and ironing line spacing on surface roughness (Ra, Rz) are not monotonically linear but instead exhibit distinct process windows. Furthermore, PLA and ABS show significantly different response trends to parameter variations. Specifically: the surface roughness of ABS readily deteriorates at high speeds (50 mm/s), while PLA remains relatively stable; The optimal ironing flow windows differ between PLA and ABS (approximately 15% for PLA and 20% for ABS); PLA exhibits an optimal line spacing (0.20 mm), whereas ABS shows a trend where smaller line spacing yields better surface quality.

(3)

Response surface analysis demonstrates that interactions between parameters significantly influence surface roughness. For PLA, the interaction between ironing speed and flow is the dominant factor. For ABS, the main effects of speed, flow, and line spacing, as well as the speed-flow and speed-line spacing interactions, must be considered. Based on the established reliable prediction models (R² = 0.9859 for PLA, R² = 0.9839 for ABS), the optimal parameter combinations were identified through optimization. Validation experiments confirmed that these optimized parameters significantly reduced surface roughness, with the resulting PLA and ABS specimens achieving surface roughness Ra values of 0.852 μm and 1.014 μm, respectively.

(4)

This study emphasizes that the effectiveness of the ironing process in improving surface quality strongly depends on material rheological properties. The low viscosity of PLA necessitates an optimization strategy centered on precisely matching speed and flow to control material flow. Conversely, the high viscosity and melt strength of ABS require a systematic balance of speed, flow, and line spacing to ensure better surface filling and formation. This work provides a comprehensive framework for the FDM ironing process, from mechanistic understanding to parameter optimization, offering clear guidance for the efficient production of high-surface-quality parts in practical manufacturing.

In summary, this study elucidates the influence of ironing process parameters on the surface roughness of PLA and ABS specimens, providing important insights for the surface quality control of FDM parts. While significant findings have been achieved, this work has limitations regarding the material systems and performance evaluation scope. Future research will extend to a wider range of engineering plastics and quantify key mechanical and functional properties, such as interlayer adhesion, tensile strength, and impact resistance, to fully elucidate the synergistic effects of the ironing process on the overall performance of printed parts.