Abstract
Biomimetic superhydrophobic surfaces have become a focal point of recent research, driven by their promise in diverse applications. Among these, the lotus and rose effects are of particular interest due to their contrasting adhesion characteristics. Given that superhydrophobicity is closely related to the hierarchical structures of these surfaces, investigating the effects of two-level roughness on superhydrophobicity is crucial. In our previous work, we introduced a wetting parameter (WRoughness), strongly correlated with the geometric characteristics of surface roughness, to elucidate the superhydrophobic behavior of solid surfaces. This parameter predicts the existence of a critical wetting parameter (WRoughness,c) during the Wenzel–Cassie transition. For two-level surface roughness composed of primary and secondary roughness, the WRoughness of the two-level surface is influenced by the geometric characteristics of both primary and secondary roughness. Furthermore, when secondary roughness is added to a primary roughness surface in the Wenzel state, the resulting two-level roughness can exhibit various superhydrophobic states, such as the Wenzel state, Wenzel–Cassie transition, or Cassie state, depending on the characteristics of the secondary roughness. To further investigate the influence of two-level roughness on superhydrophobicity, molecular dynamics (MD) simulations were also conducted.
1. Introduction
Wettability, a key characteristic of solid surfaces, is measured by the contact angle (CA, θ) [1], which is related to interfacial energies through Young’s Equation (1):
In this equation, γSL, γSG and γLG denote the interfacial energies associated with the solid–liquid, solid–gas (or solid–air), and liquid–gas (or liquid–air) interfaces, respectively. Superhydrophobic surfaces, characterized by CA exceeding 150° and contact angle hysteresis (CAH) less than 10°, have become a focus of intense investigation. This heightened attention stems from their promising utility across a diverse range of applications. These include, but are not limited to, self-cleaning coatings [2,3], corrosion resistance [4,5], ice prevention [6,7], anti-flashover treatments [8,9], controlled micro-droplet movement [10], enhanced vapor condensation and collection [11], and selective oil/water separation using membranes and meshes [12,13,14,15].
The hydrophobicity of a solid surface is understood to be influenced by both its chemical makeup and the geometrical attributes of its surface texture. The effects of surface roughness on the apparent CA (θ*) of liquid droplets are commonly explained using the Wenzel model [16,17] and the Cassie–Baxter model [18]. Additionally, experimental evidence suggests that liquid droplets in the Wenzel state exhibit stronger adhesion to structured surfaces compared to those in the Cassie state [19,20]. Consequently, Cassie state is often favored for various practical applications.
Biomimetics utilizes designs, adaptations, or derivations inspired by biological systems [21]. Superhydrophobic surfaces are observed in various natural examples, including lotus leaves, rose petals, the legs of water striders, and butterfly wings [22,23,24,25,26]. Of these, the surfaces of lotus leaves and rose petals have been particularly well-studied [27,28,29,30]. While both possess high water CAs, they exhibit significantly different water adhesion characteristics. Lotus leaves display superhydrophobicity with low adhesion, allowing nearly spherical water droplets to form with contact angles exceeding 150° and to readily roll off [31]. This behavior, termed the Lotus Effect, is attributed to the dual-scale surface structure in conjunction with the waxy epicuticular layer. Rose petals also exhibit superhydrophobicity, achieving contact angles as high as 152.4°; however, water droplets remain pinned to the surface and do not roll off, a phenomenon known as the Petal Effect [32,33]. Therefore, understanding how hierarchical surface roughness affects superhydrophobicity is a key area of investigation.
The influence of hierarchical structures on superhydrophobicity has been extensively investigated through both experimental and theoretical approaches [34,35,36,37,38,39,40,41]. These investigations generally indicate that surfaces with hierarchical structuring can substantially reduce surface wettability, resulting in significantly increased CAs [37]. Compared to surfaces lacking hierarchical features, these structured surfaces exhibit enhanced hydrophobicity, thereby promoting the formation of droplets in the Cassie state [38,39]. Consequently, the presence of dual-scale roughness in hierarchical surfaces aids in preventing the transition from the Cassie state to the Wenzel state [40,41]. Furthermore, hierarchical structures can lead to the observation of superhydrophobic states beyond the traditional Wenzel and Cassie regimes. For instance, Wang and Jiang [42] proposed a classification of five superhydrophobic states, encompassing the Wenzel state, the Cassie state, the “Lotus” and “Gecko” states, as well as a transitional state between the Wenzel and Cassie configurations. Within this framework, the “Lotus effect” is equivalent to the Cassie–Baxter state, representing a droplet suspended on air pockets within the rough surface, while the “Petal effect” corresponds to the Cassie impregnating state, an intermediate condition between the Cassie–Baxter and Wenzel states. Given that varying surface morphologies result in differing wetting behaviors, the transition of liquid adhesion from the “Rose Petal Effect” to the “Lotus Effect” on a given surface is likely closely linked to the impact of hierarchical structures on superhydrophobicity. Therefore, for surfaces exhibiting two-level hierarchical roughness, it is essential to examine the individual contributions of the primary and secondary roughness features on the overall superhydrophobic characteristics.
In our recent work [43], a wetting parameter (WRoughness) is proposed, which is directly related to the geometric attributes of surface texture, and utilized it to elucidate the Wenzel–Cassie wetting transition. During the transition from the Wenzel state to the Cassie state, the existence of a critical wetting parameter (WRoughness,c) is expected (Figure 1). Specifically, the Cassie state is predicted to occur when WRoughness is below this critical value (WRoughness < WRoughness,c).
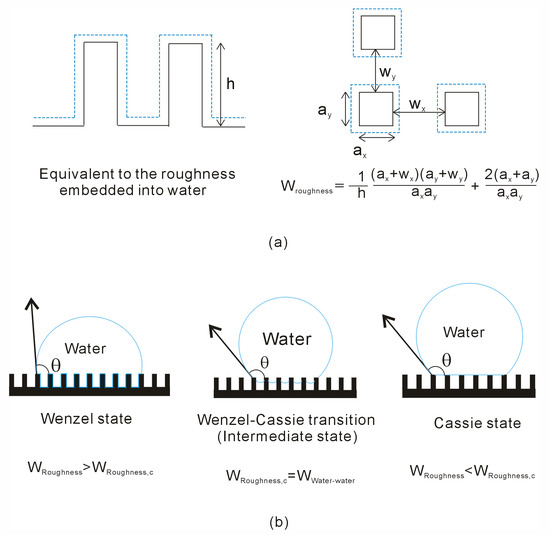
Figure 1.
(a) Surface roughness significantly influences the arrangement of water molecules at the interface. To quantitatively assess the impact of roughness on interfacial water, a wetting parameter, WRoughness, is proposed. (b) A critical wetting parameter, WRoughness,c, defines the onset of the Wenzel–Cassie transition, corresponding to specific geometric characteristics of the surface roughness. Above and below this critical value, the surface exhibits either the Wenzel or the Cassie state.
This work aimed to investigate the influence of two-level roughness on superhydrophobicity. For surfaces exhibiting two-level roughness, composed of primary and secondary roughness features, the overall WRoughness value is determined by the geometric properties of both the primary and secondary structures. Moreover, we propose that introducing secondary roughness to a primary roughness already in the Wenzel state can induce various superhydrophobic states, including the Wenzel–Cassie transition or a fully established Cassie state, depending on the specific characteristics of the secondary roughness. To further investigate the impact of two-level structures on superhydrophobicity, molecular dynamics (MD) simulations were also conducted.
2. Methods
2.1. MD Simulations
MD simulations were performed using GROMACS 2019 [44,45] to investigate the effect of two-level surface roughness on superhydrophobicity. The interactions between carbon atoms in the graphite material were modeled using the Optimized Potential for Liquid Simulations-All Atom (OPLS-AA) force field. Several water models are available for simulating water molecules; in these simulations, we chose to represent water molecules using the 4-site transferable intermolecular potential (TIP4P) model.
The Lennard-Jones potential was used to calculate van der Waals forces, which is mathematically defined as:
In this expression, εij represents the characteristic energy, σij the characteristic length, and rij the interatomic distance between atoms i and j. Within the framework of the OPLS force field, these parameters are derived from atomic values using the following geometric averaging rules:
During the simulations, both primary and secondary square pillars are used to represent the two-level surface roughness. This roughness is characterized by several parameters, including the pillar side lengths along the x and y axes (ax, ay), the groove widths separating the pillars along the x and y axes (wx, wy), and the pillar height (h) (as depicted in Figure 2). In the present study, we investigated the influence of two-level roughness on superhydrophobicity by systematically varying the geometric properties of either the primary or secondary surface roughness features, such as their side lengths, separations, or pillar heights.
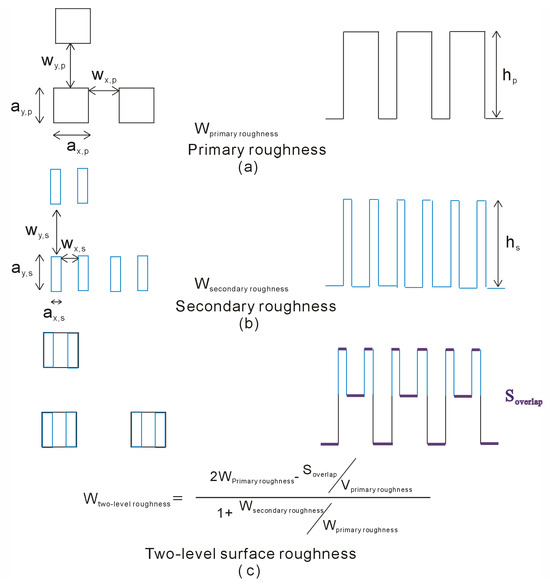
Figure 2.
(a,b) To simulate a two-level structure, primary and secondary square pillars were used to model the two-level surface roughness. The roughness is geometrically defined by the pillar side lengths (x, y), the groove widths between pillars (x, y), and the pillar height. (c) The wetting parameter (WTwo-level) for two-level surface roughness is related to both the primary surface roughness (WPrimary) and the secondary surface roughness (WSecondary).
In the MD simulations, we initially positioned a cubic water box, measuring 7.0 nm × 7.0 nm × 7.0 nm, above the graphite substrate, which was configured with varying degrees of surface roughness. Upon reaching thermodynamic equilibrium, the system was expected to transition to either the Wenzel state, characterized by wetting of the surface texture, or the Cassie state, where the water remained perched on the surface asperities. Furthermore, recognizing that superhydrophobicity may be influenced by the dimensions of the water droplet, we performed additional simulations employing cubic droplets with dimensions of 4.0 nm × 4.0 nm × 4.0 nm, 5.0 nm × 5.0 nm × 5.0 nm, and 6.0 nm × 6.0 nm × 6.0 nm. These simulations enabled us to explore the dependence of superhydrophobicity on droplet size.
The simulations were conducted within a simulation box measuring 21.0 nm × 21.0 nm × 20.0 nm, with the graphite substrate constrained to a fixed position. The simulations were performed using a canonical ensemble (NVT), and a Nosé–Hoover thermostat was used to carefully maintain a constant temperature of 300 K. Periodic boundary conditions were imposed in all three spatial dimensions. Lennard-Jones interactions were truncated at a cutoff distance of 1.0 nm, and the particle mesh Ewald (PME) method was employed for calculating long-range electrostatic interactions. Each simulation was run for a duration of 2 ns, with a time step of 2 fs.
2.2. CA Measurement
CAs were determined using the ImageJ software package (version 1.54g) [46] in conjunction with a contact angle plugin. Following the attainment of thermodynamic equilibrium in each simulated system, a near-spherical water droplet with a radius of approximately 4.0 nm was observed. To quantify the CA between the droplet and the substrate, a procedure involving manual selection was employed. This procedure required the identification of two points to define the baseline and three points along the droplet profile. These selected points were then utilized to define the droplet profile, which was subsequently used for CA calculation. In this study, the CA was measured three times for each droplet, resulting in an estimated uncertainty of approximately 3°.
2.3. Density Calculation
Upon deposition of a water droplet onto a solid surface, a solid–water interface is established. This interface can alter the characteristics of the liquid water, leading to deviations from those observed in bulk water. The wetting transition from the Wenzel state to the Cassie state is accompanied by the changes in the solid–water interface. To investigate the influence of surface roughness on the structure of water, water density distributions were calculated based on the MD simulation data. These calculations were performed utilizing the Visual Molecular Dynamics (VMD 1.9.1) software [47].
3. Results
According to this study, the CA between a water droplet and a smooth graphite surface was 66.0° (Figure 3). This value is lower than the CAs traditionally reported for graphite samples (75–95°) [48]. However, it is in agreement with Kozbail et al. [48] for highly ordered pyrolytic graphite (HOPG), who reported a water CA of 64.4 ± 2.9° measured within 10 s after exfoliation in air.
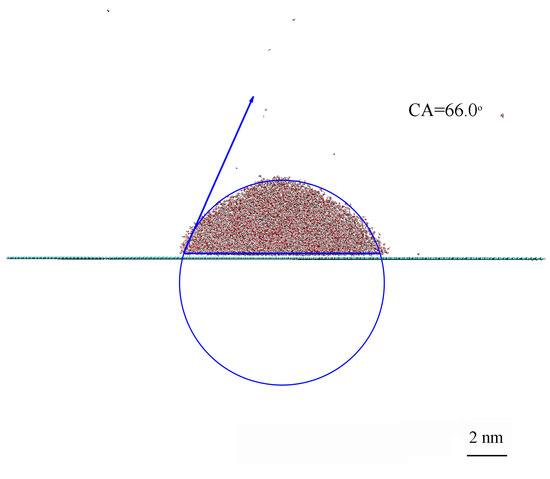
Figure 3.
CA measurements performed on a smooth surface.
During the simulations, primary and secondary square pillars are used to construct the two-level surface roughness. The geometric characteristics of the squared roughness are characterized by the pillar side lengths in the x and y axes (ax, ay), the groove widths between pillars in the x and y axes (wx, wy), and the pillar height (h) (Figure 2). To understand the effects of two-level roughness on superhydrophobicity, these characteristics are varied by modifying the geometric characteristics of either the primary or secondary surface roughness, such as side length, separations, or pillar height.
For primary surface roughness, increasing the height of the surface features resulted in an increase in CA from 66.0° to 139.7°. Furthermore, a sharp increase in CAs was observed during the wetting transition from the Wenzel state to the Cassie state (as illustrated in Figure 4 and detailed in Table 1).

Figure 4.
(a,b) The dependence of Wenzel–Cassie transition on geometric features of primary and secondary roughness. The relevant roughness parameters are presented in Table 1.

Table 1.
The wettability characteristics of primary and secondary surface roughness. The square pillars are designed to simulate the surface roughness of them. The wetting parameter (WRoughness) and revised parameter (r-WRoughness) are presented.
Superhydrophobicity is strongly linked to the geometric properties of surface roughness. Moreover, distinct solid–liquid contact configurations are associated with different superhydrophobic states (Figure 4). In the Wenzel state, the liquid phase entirely fills the spaces between surface roughness features. Conversely, in the Cassie state, the water droplet resides on top of the surface roughness elements, leaving the spaces on the surface unfilled by the liquid. Furthermore, during the Wenzel–Cassie transition, the lower surface of the penetrating liquid undergoes a gradual transformation from a conformal contact (complete penetration) to a final planar configuration (no penetration), indicative of a wetting transition from the Wenzel state to the Cassie state (partial penetration). This intermediate state can serve as a means of characterizing the Wenzel–Cassie wetting transition.
Water is often characterized as an anomalous liquid due to the formation of hydrogen bond. Upon the placement of a water droplet onto a solid surface, a solid–water interface is established. Drawing upon our previous studies [49,50,51] concerning the relationship between OH vibrations and hydrogen bonding, we observed that surface roughness primarily influences the structure of interfacial water (Figure 5). This conclusion is further supported by a range of experimental measurements detailed in the literature [52,53,54,55,56].
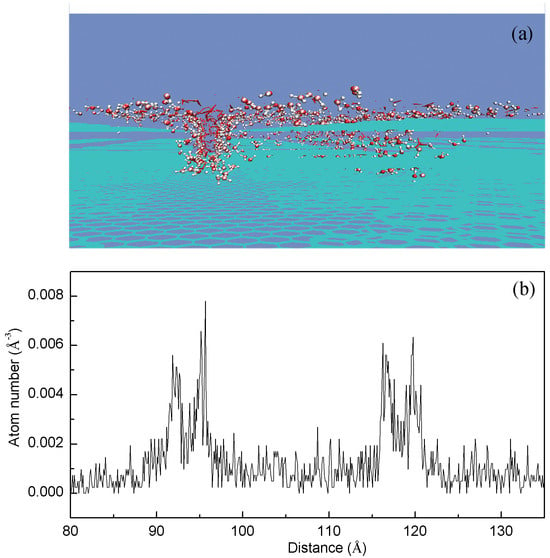
Figure 5.
Density distribution for water molecules filled in grooves between surface roughness. (a) Surface roughness significantly influences the organization of water molecules at the interface. These water molecules are depicted using CPK representation. (b) This arrangement is predicted to result in an increased density of the interfacial water.
Surface roughness exerts a primary influence on the structure of interfacial water. To elucidate the properties of this interfacial water, the density distribution is calculated for water molecules filled in grooves between surface roughness using MD simulations. The results show that the interfacial water layer exhibits a higher density compared to bulk water (Figure 5). This observation aligns with both experimental measurements [57] and theoretical simulations [58] on confined water. In combination with our recent studies [43,51], this phenomenon is attributed to the dominance of single donor-single acceptor (DA) hydrogen bonding in interfacial water.
Because hydrogen bonds are stronger than van der Waals interactions, the liquid water phase plays a significant role in the Wenzel–Cassie transition. To assess the impact of the roughness–water interface on water structure, a parameter, WRoughness, which is related to the ratio between the surface area and volume of the surface roughness, can be derived. Employing MD simulations, it was found that increasing the height of the surface roughness promotes the transition from the Wenzel state to the Cassie state (Figure 4). During the Wenzel–Cassie transition, this is accompanied by a reduction in WRoughness, and an increase in CA (Table 1).
For primary surface roughness (ax = 14.74 Å, ay = 12.76 Å, wx = 9.84 Å, wy = 8.51 Å), the wettability transition from the Wenzel to Cassie states is observed as the roughness height increases from 10.05 Å to 13.4 Å (Figure 4). This is due to the structural transition between interfacial and bulk water. This also suggests the existence of a critical height hc for the specific roughness. In combination with the above discussion, this can be represented by the critical wetting parameter of roughness, WRoughness,c (Table 1).
Based on the MD simulations, the WRoughness,c of primary roughness is determined to fall within the range of 0.49–0.56. This value is slightly larger than the theoretical WRoughness,c (0.47) at 0.1 MPa and 300 K [43]. From the definition of WRoughness, the molecular (or atomic) size of surface roughness is neglected. In combination with Figure 4, it is found that, with decreasing the separations between grooves, it is necessary to take into account the effects of atom size of surface roughness on WRoughness. Following the correction for the van der Waals radius of the substrate, the revised WRoughness, denoted as r-WRoughness, falls within the range of 0.37–0.41 for primary roughness. In the MD simulations conducted by Ren et al. [59], employing the TIP4P model for water molecules, the WRoughness,c parameter was determined to be in the range of 0.65–1.05, and the corresponding r-WRoughness,c lies in the range of 0.45–0.68 during the wetting transition from the Wenzel to Cassie states. Additionally, in our recent study [43], utilizing the SPC/E water model for water molecules, the WRoughness,c parameter was calculated to be in the range of 0.76–1.26, and the corresponding r-WRoughness,c lies in the range of 0.49–0.71 during the Wenzel–Cassie transition.
Based on the preceding discussion, we anticipate that the Cassie state will be favored when WRoughness is less than WRoughness,c. This relationship provides a framework for understanding the influence of surface roughness on hydrophobic states. In other words, the Cassie state is expected when the pillar height exceeds the critical height (=ac, =wc, >hc), the separation is less than the critical width (=ac, <wc, =hc), or the size of the pillar exceeds the critical size (>ac, =wc, =hc) [43]. This prediction aligns with the results obtained from our MD simulations. Furthermore, this understanding can also be applied to analyze other MD simulations [59,60] concerning the dependence of superhydrophobicity on the geometric characteristics of surface roughness.
In the simulations, to mimic two-level surface roughness, secondary square pillars were incorporated onto the primary roughness, thus creating a two-level surface roughness. The geometric characteristics of secondary roughness are characterized by the pillar side lengths in the x and y axes (ax, ay), the groove widths between pillars in the x and y axes (wx, wy), and the pillar height (h) (Figure 4 and Table 1). For the secondary roughness, increasing the height leads to an increase in the CA. Furthermore, the Wenzel–Cassie transition is observed as h increases from 10.05 Å to 13.4 Å. Consequently, during the Wenzel–Cassie transition, the corresponding WRoughness,c values were determined to fall within the range of 1.59–1.80, while r-WRoughness,c lies in the range of 0.67–0.73. It can be found that, with decreasing the roughness size, it may be necessary to take into account the effects of the molecular (or atomic) size of surface roughness on WRoughness,c.
To investigate the effects of two-level surface roughness on superhydrophobicity, secondary roughness is added to various primary roughness surfaces exhibiting either Wenzel or Cassie states. For two-level roughness built on a primary roughness surface in the Wenzel state (h = 6.7 Å), increasing the height of the secondary roughness leads to an increase in the CA and a decrease in the value of WRoughness (Figure 6 and Table 2). Furthermore, the addition of secondary roughness can influence the superhydrophobicity of the two-level surface, causing a change from the Wenzel state to the Wenzel–Cassie transition or Cassie state (Figure 6).
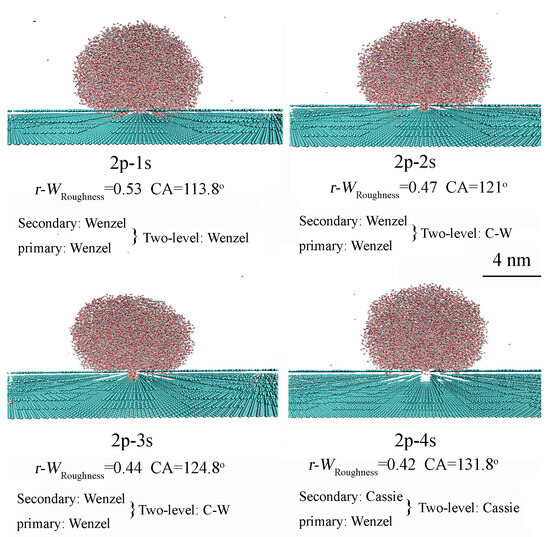
Figure 6.
For two-level roughness built on a primary roughness surface in the Wenzel state (h = 6.7 Å), increasing the height of the secondary roughness leads to an increase in the CA and a decrease in the value of WRoughness. The geometric characteristics of roughness are detailed in Table 2.

Table 2.
Two-level surface roughness. During the simulations, primary and secondary square pillars were used to model the two-level surface roughness. The wetting parameter (WRoughness) and revised WRoughness (r-WRoughness) are shown for primary, secondary, and two-level roughness.
Based on the MD simulations of primary and secondary surface roughness, these findings can be applied to investigate the dependence of superhydrophobicity in two-level roughness on both primary and secondary roughness characteristics. When the primary surface roughness is in the Wenzel state, the superhydrophobicity of the two-level surface can be related to either the Wenzel or Cassie state, depending on the characteristics of the secondary roughness. It is observed that the superhydrophobicity of the two-level roughness is influenced by both primary and secondary roughness features (Figure 6 and Table 2).
For two-level roughness built on a primary roughness surface exhibiting the Cassie state (h = 16.75 Å), increasing the height of the secondary roughness can also affect the CA of the two-level structure, which is reflected in the changes of WRoughness (Figure 7 and Table 2). Furthermore, compared to the primary roughness alone, the addition of secondary roughness can alter the superhydrophobicity of the two-level surface, causing a transition from the Wenzel state to the Wenzel–Cassie transition, or resulting in a Cassie state. The influence of secondary roughness on the superhydrophobicity of the two-level surface is closely related to the characteristics of the primary surface roughness.

Figure 7.
For two-level roughness built on a primary roughness surface in the Cassie state (h = 16.75 Å), increasing the height of the secondary roughness leads to an increase in the CA and a decrease in the value of WRoughness. Table 2 presents the geometric characteristics of the surface roughness.
Based on MD simulations, when the primary surface roughness exhibits the Cassie state, the superhydrophobicity of the two-level surface is influenced by the superhydrophobicity of the secondary roughness. The final state of the hierarchical surface is expected to be either Wenzel or Cassie, depending on whether the secondary roughness exhibits the Wenzel or Cassie state (Figure 7 and Table 2). However, when both primary and secondary roughness exhibit the Cassie state, the resulting superhydrophobicity of the two-level surface is definitively attributed to the Cassie state (Table 2).
In comparison with the Wenzel state, the Cassie state is often preferred in many practical applications. Therefore, it is important to study the superhydrophobicity of two-level roughness built upon a primary roughness surface in the Wenzel state. The superhydrophobicity of two-level roughness is related to the combined effects of primary and secondary roughness on superhydrophobicity. Based on the above discussion on two-level roughness, adding secondary roughness to primary roughness can decrease WRoughness. Unlike the Wenzel state for primary roughness alone, other superhydrophobic states, such as the Wenzel–Cassie transition and the Cassie states, can be achieved for two-level roughness (Figure 6). These principles can be utilized to rationally improve the superhydrophobicity of a solid surface.
In our recent study [43], the superhydrophobicity of solid roughness was found to be dependent on the size of the water droplet. To investigate this dependence, water droplets of varying cubic sizes were, respectively, placed on primary and secondary roughness, specifically 40 Å × 40 Å × 40 Å, 50 Å × 50 Å × 50 Å, 60 Å × 60 Å × 60 Å, and 70 Å × 70 Å × 70 Å (Figure 8). It was observed that increasing the size of the water droplet resulted in a wetting transition from the Wenzel to the Cassie state (Figure 8). The Wenzel–Cassie wetting transition was observed when the droplet diameter reached approximately 75 Å for primary roughness or 45 Å for secondary roughness, corresponding to an initial water box of 70 Å × 70 Å × 70 Å or 50 Å × 50 Å × 50 Å. Therefore, the Cassie state is expected where the droplet size significantly exceeds the geometric features of the surface roughness. To maintain the Cassie state, a lower size limit for the water droplet is expected. Given that the size of the secondary roughness is smaller than that of the primary roughness, it follows that the addition of secondary roughness may decrease this lower size limit for water droplet size. In other words, compared to primary roughness alone, the addition of secondary roughness reduces the dependency of superhydrophobicity on droplet size.
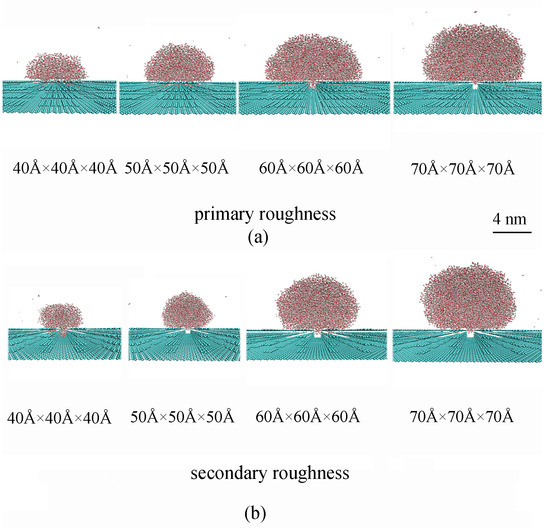
Figure 8.
The wettability of surfaces with primary (a) and secondary (b) roughness was studied as a function of water droplet size. Cubic water droplets with dimensions of 40 Å × 40 Å × 40 Å, 50 Å × 50 Å × 50 Å, 60 Å × 60 Å × 60 Å, and 70 Å × 70 Å × 70 Å were initially positioned on the rough surfaces for simulations.
4. Discussion
In the Wenzel state, the water phase completely occupies the surface indentations, effectively submerging the surface roughness elements within the liquid medium. This immersion has a direct effect on the local structure of the surrounding water. Conversely, the Cassie state is characterized by a liquid droplet that does not penetrate the cavities of the surface. Instead, air becomes trapped within these cavities, forming a heterogeneous interface. As a transition occurs from the Wenzel configuration to the Cassie configuration, the area of direct contact between the surface roughness and the water is reduced, while the proportion of water exhibiting bulk-like characteristics is increased. This suggests a correlation between Wenzel–Cassie transition and structural rearrangements within the water phase. Thus, it is necessary to study the structure of water and the modifying influence of surface roughness upon that structure.
The sensitivity of OH vibrations to hydrogen bonding makes them a valuable tool for investigating the structure of water. In our Raman spectroscopic studies [49,50,51], we observed that OH vibrations are primarily influenced by the hydrogen bonds within a water molecule’s immediate surroundings, reflecting its local hydrogen bonding environment. As a result, distinct OH vibrations correspond to OH groups participating in different local hydrogen-bonded networks. In contrast to both mixture and continuum models [61,62], our findings indicate that a water molecule interacts with neighboring water molecules through various local hydrogen-bonded arrangements [50,51], such as DDAA, DDA, DAA, and DA hydrogen bondings.
Given the primary dependence of OH vibrations on the local hydrogen-bonded networks surrounding a water molecule, surface roughness primarily influences the structure of interfacial water (Figure 1 and Figure 5). This is also demonstrated by experimental measurements concerning the structure and dynamics of water surrounding ions [52,53,54,55,56]. Additionally, based on our previous studies [63,64] on air–water interfaces and confined water, the formation of a roughness–water interface may be linked to the reduction in DDAA hydrogen bonding in interfacial water. Once the ratio of interfacial water to bulk water (RInterfacial water/Bulk water) is established, the Gibbs energy of interfacial water (ΔGRoughness-water) is given as, ΔGRoughness-water = RInterfacial water/Bulk water∙ΔGDDAA∙nHB, in which ΔGDDAA represents the Gibbs energy of DDAA hydrogen bonds, nHB indicates the average number of hydrogen bonds per water molecule [43].
As a droplet is placed on a solid surface, the water is divided into interfacial and bulk water. During the Wenzel–Cassie wetting transition, the structural rearrangement between interfacial and bulk water is expected, which is thermodynamically expressed as, ΔGRoughness-water = ΔGWater-water. For squared roughness (Figure 1), the following equation may be derived,
where WRoughness and WWater are defined as the wetting parameters related to surface roughness and water [43]. This relationship is predicated on the assumption that the size of the water droplet is significantly larger than the characteristic dimensions of the surface roughness, and that gravitational effects on wettability are negligible.
From Equation (4), a critical WRoughness (WRoughness,c) value is expected during the Wenzel–Cassie transition (Figure 1). With reference to WRoughness,c, it may be classified as exhibiting either the Wenzel or Cassie state (Figure 1). Furthermore, the WRoughness,c value is characterized by critical geometric parameters of the surface roughness, such as ac, wc, and hc [43]. This can be demonstrated by MD simulations discussed as above (Figure 4 and Table 1). This framework can be leveraged for the rational design of superhydrophobic surfaces with tailored properties.
Upon the placement of a water droplet onto a solid surface, it separates into interfacial and bulk water regions. In our recent work [43], it is found that, during the wetting transition from Wenzel to Cassie states, this leads to the decrease in interfacial water, and the increase in bulk water. Therefore, a transition between interfacial and bulk water may be expected during the Wenzel–Cassie transition. Indeed, this phenomenon arises from the higher degree of hydrogen bonding present in bulk water as compared to interfacial water [43]. This indicates that the Wenzel–Cassie wetting transition may be driven by the structural competition between interfacial and bulk water. Drawing upon our recent studies [51,65], we propose that hydrophobic interactions play a significant role in driving the Wenzel–Cassie transition.
Superhydrophobicity is dependent on the geometric characteristics of the roughness of a solid surface. This can be evaluated using the wetting parameter described above. This approach can also be extended to investigate the effects of two-level surface roughness on the superhydrophobicity of a solid surface. In this work, primary and secondary square pillars were used to model the two-level surface roughness. The geometric characteristics of the surface roughness are characterized by the pillar side lengths in the x and y axes (ax, ay), the groove widths between pillars in the x and y axes (wx, wy), and the pillar height (h) (Figure 2). To understand the dependence of superhydrophobicity on two-level roughness, the geometric characteristics of either the primary or secondary surface roughness, such as side length, separations, or pillar height, were varied.
For two-level roughness, the solid–liquid interface is influenced by both primary and secondary roughness. Unlike interfaces with single-level roughness, the Gibbs energy of the interfacial water of two-level roughness may be related to both primary and secondary roughness. Of course, this may be reflected on the wetting behavior of the water droplet. Additionally, various superhydrophobic states can exist for two-level surfaces, such as Wenzel, Cassie, and Wenzel–Cassie transition states. These states arise from the combined superhydrophobic characteristics related to primary and secondary roughness, such as the Wenzel–Wenzel (W-W) state, Wenzel–Cassie (W-C) state, Cassie–Wenzel (C-W) state, and Cassie–Cassie (C-C) state (Figure 9). Therefore, compared to the superhydrophobicity of single-level roughness, different Wenzel–Cassie transition states can be expected for two-level roughness.
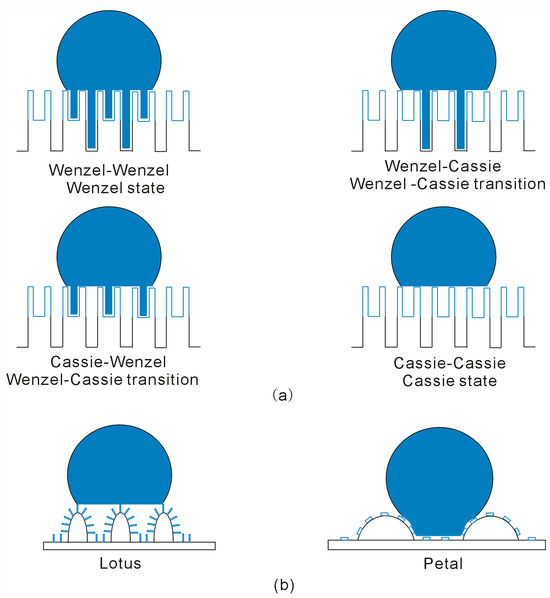
Figure 9.
(a) Various superhydrophobic states may be expected for two-level roughness, which is related to superhydrophobicity of both primary and secondary roughness. (b) The lotus effect is associated with the Cassie state, while the petal effect corresponds to the Wenzel–Cassie transition.
Based on the above discussion, a corresponding wetting parameter (WTwo-level) can be defined for two-level surface roughness (Figure 2), which can be expressed as follows,
where WPrimary and WSecondary represent the wetting parameters of the primary and secondary surface roughness, VPrimary and VSecondary mean the volume of primary and secondary roughness, respectively, SOverlap is the surface area overlapped by the primary and secondary roughness, and m is number of secondary roughness built upon per primary roughness (Figure 2). From the calculated WTwo-level, this may be applied to investigate the effects of two-level surface roughness on superhydrophobicity of solid surface.
As discussed above, the WRoughness parameter can be used to investigate the dependence of superhydrophobicity on the geometric characteristics of surface roughness. To understand the superhydrophobicity of two-level roughness, it is essential to study the influential factors of WTwo-level.
(I) Based on Equation (5), the WTwo-level parameter is related to the wetting parameters of primary and secondary roughness (WPrimary and WSecondary). Additionally, it is also influenced by the correlation between primary and secondary roughness (VSecondary/VPrimary, SOverlap/VPrimary). Therefore, it may be derived that the wetting parameter of two-level roughness, WTwo-level, mainly lies in the range from WPrimary to WSecondary. Of course, the value of WTwo-level may also be influenced by the relation between primary and secondary roughness, especially as WPrimary (or WSecondary) near to the critical wetting parameter.
(II) Furthermore, based on Equation (5), it is found that WTwo-level is also related to the ratio between SOverlap and VPrimary (SOverlap/VPrimary), or between SOverlap and VSecondary (SOverlap/(m∙VSecondary)). Increasing this ratio (SOverlap/VPrimary) decreases the value of the WTwo-level parameter, which can promote the Cassie state, especially as the wetting parameter of surface roughness near to critical value. This can be achieved by either increasing the area overlapped between the primary and secondary roughness or decreasing the volume of the primary surface roughness. This understanding may be used to understand and design the superhydrophobicity of two-level structured roughness.
According to the preceding discussion regarding the relationship between hydrophobicity and WRoughness, the Wenzel state is anticipated when WRoughness exceeds the critical value (WRoughness > WRoughness,c), while the Cassie state is observed when WRoughness is below the critical value (WRoughness < WRoughness,c). Based on Equation (5), this can be applied to investigate the relationship of superhydrophobicity between two-level, primary, and secondary surface roughness.
When the primary surface roughness is in the Wenzel state, the superhydrophobicity of the two-level surface is influenced by the characteristics of the secondary roughness. The resulting two-level surface is expected to exhibit Wenzel, Wenzel–Cassie transition, or Cassie states, depending on whether the secondary roughness is in the Wenzel or Cassie state (Figure 6 and Table 2).
Furthermore, if the primary surface roughness is in the Cassie state, the superhydrophobicity of the two-level surface roughness is influenced by the superhydrophobicity of the secondary roughness. If the secondary roughness is in the Wenzel state, the superhydrophobicity of the two-level surface can be in Wenzel, Wenzel–Cassie transition, or Cassie states. However, when both primary and secondary roughnesses are in the Cassie states, the resulting superhydrophobicity of the two-level surface will be the Cassie state (Figure 7 and Table 2).
Based on the discussion of superhydrophobicity in two-level surface roughness, these principles can also be extended to understand the difference between the Lotus and Petal effects. Although both Lotus and Petal effects are related to two-level hierarchically roughness, the Lotus effect is associated with the Cassie state, while the Petal effect is attributed to the Wenzel–Cassie transition state (Figure 9). This is due to the combined effects of primary and secondary roughness on superhydrophobicity, which are in turn related to structural differences in the primary and secondary roughness features. In fact, these differences can be explained by the ratio between the surface overlap (SOvelap) and the volume of the primary roughness (VRoughness,primary), i.e., SOverlap/VRoughness,primary. Compared to hierarchical roughness exhibiting the Petal effect, a larger SOverlap and a smaller VRoughness,primary are typically observed for the surface roughness exhibiting the Lotus effect [66,67] (Figure 9).
To understand the mechanism of hierarchical roughness on superhydrophobicity, various views have been proposed [68,69,70,71]. In combination with our recent work [43], roughness primarily affects the structure of interfacial water. This suggests that super-hydrophobicity arises from the competition between interfacial and bulk water, a phenomenon effectively described by the WRoughness. Consequently, the Wenzel–Cassie transition is significantly influenced by the ratio of surface area to volume of the roughness features. When comparing one-level and two-level roughness structures of the same volume, the improved superhydrophobicity observed in the two-level system is related to the increased surface area provided by the two-level structure.
In our recent work [43], a wetting parameter (WRoughness), closely related to the geometric characteristics of roughness, was proposed and used to understand the superhydrophobicity of a solid surface. During the Wenzel–Cassie wetting transition, a critical parameter, WRoughness,c, is expected. These parameters can also be applied to understand the effects of two-level roughness on superhydrophobicity. For two-level roughness composed of primary and secondary roughness, the WTwo-level of the two-level surface is related to the geometric characteristics of both primary and secondary roughness (Figure 10). In other words, the resulting superhydrophobicity of two-level structured roughness arises from the combined effects of primary and secondary roughness.

Figure 10.
(a,b) The WTwo-level of the two-level surface is related to the geometric characteristics of both primary and secondary roughness. Various superhydrophobic states are found for two-level surface roughness, which may be influenced by both primary and secondary roughness.
5. Conclusions
Building on our recent studies of superhydrophobicity on solid surfaces, this work investigates the effects of two-level surface roughness on superhydrophobicity. In our previous research, we proposed and applied a wetting parameter, WRoughness, closely related to the geometric characteristics of roughness, to understand the superhydrophobicity of solid surfaces. We also identified a critical WRoughness,c associated with the Wenzel–Cassie transition. For two-level roughness composed of primary and secondary roughness, the WTwo-level parameter is related to the wetting parameters of primary and secondary roughness (WPrimary and WSecondary). Additionally, it is also influenced by the correlation between primary and secondary roughness (VSecondary/VPrimary, SOverlap/VPrimary). Therefore, it may be derived that the wetting parameter of two-level roughness, WTwo-level, mainly lies in the range from WPrimary to WSecondary. Consequently, the WTwo-level of the two-level surface is related to the geometric characteristics of both primary and secondary roughness. Additionally, given that the size of the secondary roughness is less than that of the primary roughness, the addition of secondary roughness may lower the dependence of superhydrophobicity on droplet size compared to surfaces with only primary roughness. Additionally, regarding the mechanism of hierarchical roughness on superhydrophobicity, the enhanced superhydrophobicity observed in the two-level system results from the increased surface area provided by the two-level structure.
Author Contributions
Formal analysis, investigation, writing—review and editing, Y.W.; writing—review and editing, M.Y.; conceptualization, formal analysis, investigation, resources, data curation, writing—original draft preparation, supervision, writing—review and editing, Q.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant numbers 42430802).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The reviewers and editor are greatly appreciated for providing good suggestions to revise the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| WRoughness | Wetting parameter |
| WRoughness,c | Critical wetting parameter |
| WTwo-level | Wetting parameter of two-level roughness |
References
- Young, T. An essay on the cohesion of fluids. Philos. Trans. R. Soc. Lond. 1805, 95, 65–87. [Google Scholar] [CrossRef]
- Cai, H.; Duan, C.; Fu, M.; Zhang, J.; Huang, H.; Hu, Y.; Shi, J.; Ye, D. Scalable fabrication of superhydrophobic coating with rough coral reef-like structures for efficient self-cleaning and oil-water separation: An experimental and molecular dynamics simulation study. Small 2023, 19, 2207118. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.Z.; Militky, J.; Petru, M.; Tomková, B.; Ali, A.; Tören, E.; Perveen, S. Recent advances in superhydrophobic surfaces for practical applications: A review. Eur. Polym. J. 2022, 178, 111481. [Google Scholar] [CrossRef]
- Gateman, S.M.; Page, K.; Halimi, I.; Nascimento, A.R.C.; Savoie, S.; Schulz, R.; Moreau, C.; Parkin, I.P.; Mauzeroll, J. Corrosion of one-step superhydrophobic stainless-steel thermal spray coatings. ACS Appl. Mater. Interfaces 2020, 12, 1523–1532. [Google Scholar] [CrossRef]
- Nine, M.J.; Cole, M.A.; Johnson, L.; Tran, D.N.H.; Losic, D. Robust superhydrophobic graphene-based composite coatings with self-cleaning and corrosion barrier properties. ACS Appl. Mater. Interfaces 2015, 7, 28482–28493. [Google Scholar] [CrossRef] [PubMed]
- Lambley, H.; Graeber, G.; Vogt, R.; Gaugler, L.C.; Baumann, E.; Schutzius, T.M.; Poulikakos, D. Freezing-induced wetting transitions on superhydrophobic surfaces. Nat. Phys. 2023, 19, 649–655. [Google Scholar] [CrossRef]
- Hussain, S.; Muangnapoh, T.; Traipattanakul, B.; Lekmuenwai, M. Anti-icing property of superhydrophobic nanostructured brass via deposition of silica nanoparticles and nanolaser treatment. Nanomaterials 2023, 13, 1139. [Google Scholar] [CrossRef]
- Li, Y.; Jin, H.; Nie, S.; Zhang, P.; Gao, N. Dynamic behavior of water droplets and flashover characteristics on a superhydrophobic silicone rubber surface. Appl. Phys. Lett. 2017, 110, 201602. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, S.; Liu, S.; Zuo, Z.; Gao, Y.; Wu, C.; Liang, X. Super-hydrophobic silicone rubber for outdoor electrical insulation. Nano Today 2024, 58, 102406. [Google Scholar] [CrossRef]
- Chen, L.; Si, Y.; Guo, Z.; Liu, W. Superhydrophobic sand: A hope for desert water storage and transportation projects. J. Mater. Chem. A 2017, 5, 6416–6423. [Google Scholar] [CrossRef]
- Yin, K.; Du, H.; Dong, X.; Wang, C.; Duan, J.A.; He, J. A simple way to achieve bioinspired hybrid wettability surface with micro/nanopatterns for efficient fog collection. Nanoscale 2017, 9, 14620–14626. [Google Scholar] [CrossRef]
- Kota, A.K.; Kwon, G.; Choi, W.; Mabry, J.M.; Tuteja, A. Hygro-responsive membranes for effective oil–water separation. Nat. Commun. 2012, 3, 1025. [Google Scholar] [CrossRef]
- Gao, X.; Zhou, J.; Du, R.; Xie, Z.; Deng, S.; Liu, R.; Liu, Z.; Zhang, J. Robust superhydrophobic foam: A graphdiyne-based hierarchical architecture for oil/water separation. Adv. Mater. 2016, 28, 168–173. [Google Scholar] [CrossRef] [PubMed]
- Kang, L.; Wang, B.; Zeng, J.; Cheng, Z.; Li, J.; Xu, J.; Gao, W.; Chen, K. Degradable dual superlyophobic lignocellulosic fibers for high-efficiency oil/water separation. Green Chem. 2020, 22, 504–512. [Google Scholar] [CrossRef]
- Pang, Y.; Yu, Z.; Chen, H.; Xiang, Q.; Wang, Q.; Xie, C.; Liu, Y. Superhydrophobic polyurethane sponge based on sepiolite for efficient oil/water separation. J. Hazard. Mater. 2022, 434, 128833. [Google Scholar] [CrossRef]
- Wenzel, R.N. Resistance of solid surfaces to wetting by water. Ind. Eng. Chem. 1936, 28, 988–994. [Google Scholar] [CrossRef]
- Wenzel, R.N. Surface roughness and contact angle. J. Phys. Chem. 1949, 53, 1466–1467. [Google Scholar] [CrossRef]
- Cassie, A.B.D.; Baxter, S. Wettability of porous surfaces. Trans. Faraday Soc. 1944, 40, 546–550. [Google Scholar] [CrossRef]
- Koishi, T.; Yasuoka, K.; Fujikawa, S.; Ebisuzaki, T.; Zeng, X.C. Coexistence and transition between Cassie and Wenzel state on pillared hydrophobic surface. Proc. Natl. Acad. Sci. USA 2009, 106, 8435–8440. [Google Scholar] [CrossRef]
- Jeong, W.J.; Ha, M.Y.; Yoon, H.S.; Ambrosia, M. Dynamic behavior of water droplets on solid surfaces with pillar-type nanostructures. Langmuir 2012, 28, 5360–5371. [Google Scholar] [CrossRef]
- Bhushan, B. Biomimetics: Lessons from nature-An overview. Philos. Trans. R. Soc. A 2009, 367, 1445–1486. [Google Scholar] [CrossRef]
- Stanton, M.M.; Ducker, R.E.; MacDonald, J.C.; Lambert, C.R.; McGimpsey, W.G. Super-hydrophobic, highly adhesive, polydimethylsiloxane (PDMS) surfaces. J. Colloid Interface Sci. 2012, 367, 502–508. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B.; Tian, J.; Wang, C.; Gao, Y.; Wen, W. A facile and cost-effective approach to engineer surface roughness for preparation of large-scale superhydrophobic substrate with high adhesive force. Appl. Surf. Sci. 2016, 389, 679–687. [Google Scholar] [CrossRef]
- Hoefnagels, H.; Wu, D.; De With, G.; Ming, W. Biomimetic superhydrophobic and highly oleophobic cotton textiles. Langmuir 2007, 23, 13158–13163. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.C.; Hsu, S.H.; Chung, Y.C. Thermal imprint techniques for preparation of superhydrophobic polymer coatings. Surf. Coat. Technol. 2013, 231, 501–506. [Google Scholar] [CrossRef]
- Guo, Z.; Liu, W.; Su, B.L. Superhydrophobic surfaces: From natural to biomimetic to functional. J. Colloid Interface Sci. 2011, 353, 335–355. [Google Scholar] [CrossRef]
- Wang, P.; Zhao, T.; Bian, R.; Wang, G.; Liu, H. Robust superhydrophobic carbon nanotube film with lotus leaf mimetic multiscale hierarchical structures. ACS Nano 2017, 11, 12385–12391. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, Y.; Xiao, X.; Liu, G.; Xu, Z.; Wang, B.; Yu, C.; Ras, R.H.A.; Jiang, L. Efficient separation of immiscible oil/water mixtures using a perforated lotus leaf. Green Chem. 2019, 21, 6579–6584. [Google Scholar] [CrossRef]
- Allred, T.P.; Weibel, J.A.; Garimella, S.V. The petal effect of parahydrophobic surfaces offers low receding contact angles that promote effective boiling. Int. J. Heat Mass Transf. 2019, 135, 403–412. [Google Scholar] [CrossRef]
- Chen, Y.; Jie, Y.; Wang, J.; Ma, J.; Jia, X.; Dou, W.; Cao, X. Triboelectrification on natural rose petal for harvesting environmental mechanical energy. Nano Energy 2018, 50, 441–447. [Google Scholar] [CrossRef]
- Barthlott, W.; Neinhuis, C. Purity of the sacred lotus, or escape from contamination in biological surfaces. Planta 1997, 202, 1–8. [Google Scholar] [CrossRef]
- Feng, L.; Zhang, Y.; Xi, J.; Zhu, Y.; Wang, N.; Xia, F.; Jiang, L. Petal Effect: A superhydrophobic state with high adhesive force. Langmuir 2008, 24, 4114–4119. [Google Scholar] [CrossRef] [PubMed]
- Bhushan, B.; Her, E.K. Fabrication of superhydrophobic surfaces with high and low adhesion inspired from rose petal. Langmuir 2010, 26, 8207–8217. [Google Scholar] [CrossRef]
- Kavousanakis, M.E.; Chamakos, N.T.; Papathanasiou, A.G. Connection of intrinsic wettability and surface topography with the apparent wetting behavior and adhesion properties. J. Phys. Chem. C 2015, 119, 15056–15066. [Google Scholar] [CrossRef]
- Qiang, W.; Lan, Z.; Liu, Y.; Liu, Y.; Xu, W.; Wen, R.; Ma, X. Excellent hydrophobicity and high mobility of condensate droplets on hierarchical nanostructured surfaces: Insights from MD simulations. J. Mol. Liq. 2024, 407, 125139. [Google Scholar] [CrossRef]
- He, X.; Fan, J.; Cui, K.; Tian, Y.; Wang, T.; Wang, S. Wetting of nanoscale water films on hierarchically structured surfaces. Phys. Fluids 2024, 36, 052016. [Google Scholar] [CrossRef]
- Zhang, Z.; Ha, M.Y.; Jang, J. Contrasting water adhesion strengths of hydrophobic surfaces engraved with hierarchical grooves: Lotus leaf and rose petal effects. Nanoscale 2017, 9, 16200. [Google Scholar] [CrossRef] [PubMed]
- Kwon, T.W.; Jang, J.; Ambrosia, M.S.; Ha, M.Y. Molecular dynamics study on the hydrophobicity of a surface patterned with hierarchical nanotextures. Colloids Surf. A 2018, 559, 209–217. [Google Scholar]
- Zhang, M.Y.; Ma, L.J.; Wang, Q.; Hao, P.; Zheng, X. Wettability behavior of nanodroplets on copper surfaces with hierarchical nanostructures. Colloids Surf. A 2020, 604, 125291. [Google Scholar] [CrossRef]
- Li, H.; Yan, T. Importance of moderate size of pillars and dual-scale structures for stable superhydrophobic surfaces: A molecular dynamics simulation study. Comput. Mater. Sci. 2020, 175, 109613. [Google Scholar] [CrossRef]
- Whyman, G.; Bormashenko, E. How to make the cassie wetting state stable? Langmuir 2011, 27, 8171–8176. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Jiang, L. Definition of superhydrophobic states. Adv. Mater. 2007, 19, 3423–3424. [Google Scholar] [CrossRef]
- Sun, Q.; Chen, Y.N.; Liu, Y.Z. Wetting transition from Wenzel to Cassie states: Thermodynamic analysis. Materials 2025, 18, 543. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; van der Spoel, D.; van Drunen, R. GROMACS: A message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 1995, 91, 43–56. [Google Scholar] [CrossRef]
- van der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, flexible and free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef]
- Rasband, W.S. ImageJ Image Analysis Software; U.S. National Institutes of Health: Bethesda, MD, USA, 1997. Available online: https://imagej.net/ij/download.html (accessed on 6 July 2023).
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Kozbial, A.; Li, Z.; Sun, J.; Gong, X.; Zhou, F.; Wang, Y.; Xu, H.; Liu, H.; Li, L. Understanding the intrinsic water wettability of graphite. Carbon 2014, 74, 218–225. [Google Scholar] [CrossRef]
- Sun, Q. The Raman OH stretching bands of liquid water. Vib. Spectrosc. 2009, 51, 213–217. [Google Scholar] [CrossRef]
- Sun, Q. Local statistical interpretation for water structure. Chem. Phys. Lett. 2013, 568/569, 90–94. [Google Scholar] [CrossRef]
- Sun, Q. The hydrophobic effects: Our current understanding. Molecules 2022, 27, 7009. [Google Scholar] [CrossRef] [PubMed]
- Collins, K.D.; Neilson, G.W.; Enderby, J.E. Ions in water: Characterizing the forces that control chemical processes and biological structure. Biophys. Chem. 2007, 128, 95–104. [Google Scholar] [CrossRef]
- Cappa, C.D.; Smith, J.D.; Messer, B.M.; Cohen, R.C.; Saykally, R.J. Effects of cations on the hydrogen bond network of liquid water: New results from X-ray absorption spectroscopy of liquid microjets. J. Phys. Chem. B 2006, 110, 5301–5309. [Google Scholar] [CrossRef]
- Omta, A.W.; Kropman, M.F.; Woutersen, S.; Bakker, H.J. Negligible effect of ions on the hydrogen-bond structure in liquid water. Science 2003, 301, 347–349. [Google Scholar] [CrossRef] [PubMed]
- Moilanen, D.E.; Wong, D.; Rosenfeld, D.E.; Fenn, E.E.; Fayer, M.D. Ion–water hydrogen-bond switching observed with 2D IR vibrational echo chemical exchange spectroscopy. Proc. Natl. Acad. Sci. USA 2009, 106, 375–380. [Google Scholar] [CrossRef] [PubMed]
- Turton, D.A.; Hunger, J.; Hefter, G.; Buchner, R.; Wynne, K. Glasslike behavior in aqueous electrolyte solutions. J. Chem. Phys. 2008, 128, 161102. [Google Scholar] [CrossRef]
- Thompson, H.; Soper, A.K.; Ricci, M.A.; Bruni, F.; Skipper, N.T. The three–dimensional structure of water confined in nanoporous vycor glass. J. Phys. Chem. B 2007, 111, 5610–5620. [Google Scholar] [CrossRef]
- Giri, A.K.; Teixeira, F.; Cordeiro, M.N.D.S. Structure and kinetics of water in highly confined conditions: A molecular dynamics simulation study. J. Mol. Liq. 2018, 268, 625–636. [Google Scholar] [CrossRef]
- Ren, H.; Yang, F.; Li, C.; Deng, C. Controllable dewetting transition on graphene-based nanotextured surfaces. App. Surf. Sci. 2020, 520, 146374. [Google Scholar] [CrossRef]
- Niu, D.; Tang, G.H. Static and dynamic behavior of water droplet on solid surfaces with pillar–type microstructures from molecular dynamics simulation. Int. J. Heat Mass Transfer 2014, 79, 647–654. [Google Scholar] [CrossRef]
- Stanley, H.E.; Teixeira, J. Interpretation of the unusual behavior of H2O and D2O at low temperatures: Tests of a percolation model. J. Chem. Phys. 1980, 73, 3404–3422. [Google Scholar] [CrossRef]
- Nilsson, A.; Pettersson, L.G.M. Perspective on the structure of liquid water. Chem. Phys. 2011, 389, 1–34. [Google Scholar] [CrossRef]
- Sun, Q.; Guo, Y. Vibrational sum frequency generation spectroscopy of the air/water interface. J. Mol. Liq. 2016, 213, 28–32. [Google Scholar] [CrossRef]
- Sun, Q. The single donor-single acceptor hydrogen bonding structure in water probed by Raman spectroscopy. J. Chem. Phys. 2010, 132, 054507. [Google Scholar] [CrossRef]
- Sun, Q. The physical origin of hydrophobic effects. Chem. Phys. Lett. 2017, 672, 21–25. [Google Scholar] [CrossRef]
- Liu, M.; Wang, S.; Jiang, L. Nature-inspired superwettability systems. Nat. Rev. Mater. 2017, 2, 17036. [Google Scholar] [CrossRef]
- Teisala, H.; Butt, H. Hierarchical structures for superhydrophobic and superoleophobic surfaces. Langmuir 2019, 35, 10689–10703. [Google Scholar] [CrossRef]
- Patankar, N.A. Mimicking the Lotus effect: Influence of double roughness structures and slender pillars. Langmuir 2004, 20, 8209–8213. [Google Scholar] [CrossRef]
- Nosonovsky, M. Multiscale roughness and stability of superhydrophobic biomimetic interfaces. Langmuir 2007, 23, 3157–3161. [Google Scholar] [CrossRef]
- Boinovich, L.; Emelyanenko, A. Principles of design of superhydrophobic coatings by deposition from dispersions. Langmuir 2009, 25, 2907–2912. [Google Scholar] [CrossRef] [PubMed]
- Bittoun, E.; Marmur, A. The role of multiscale roughness in the Lotus effect: Is it essential for super-hydrophobicity? Langmuir 2012, 28, 13933–13942. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).