Mechanical Consequences of Gap-Graded Soils Subjected to Internal Erosion: The Effect of Mode of Removal of Fine Particles Using Discrete Element Method
Abstract
1. Introduction
2. Numerical Simulation
2.1. Model Establishment
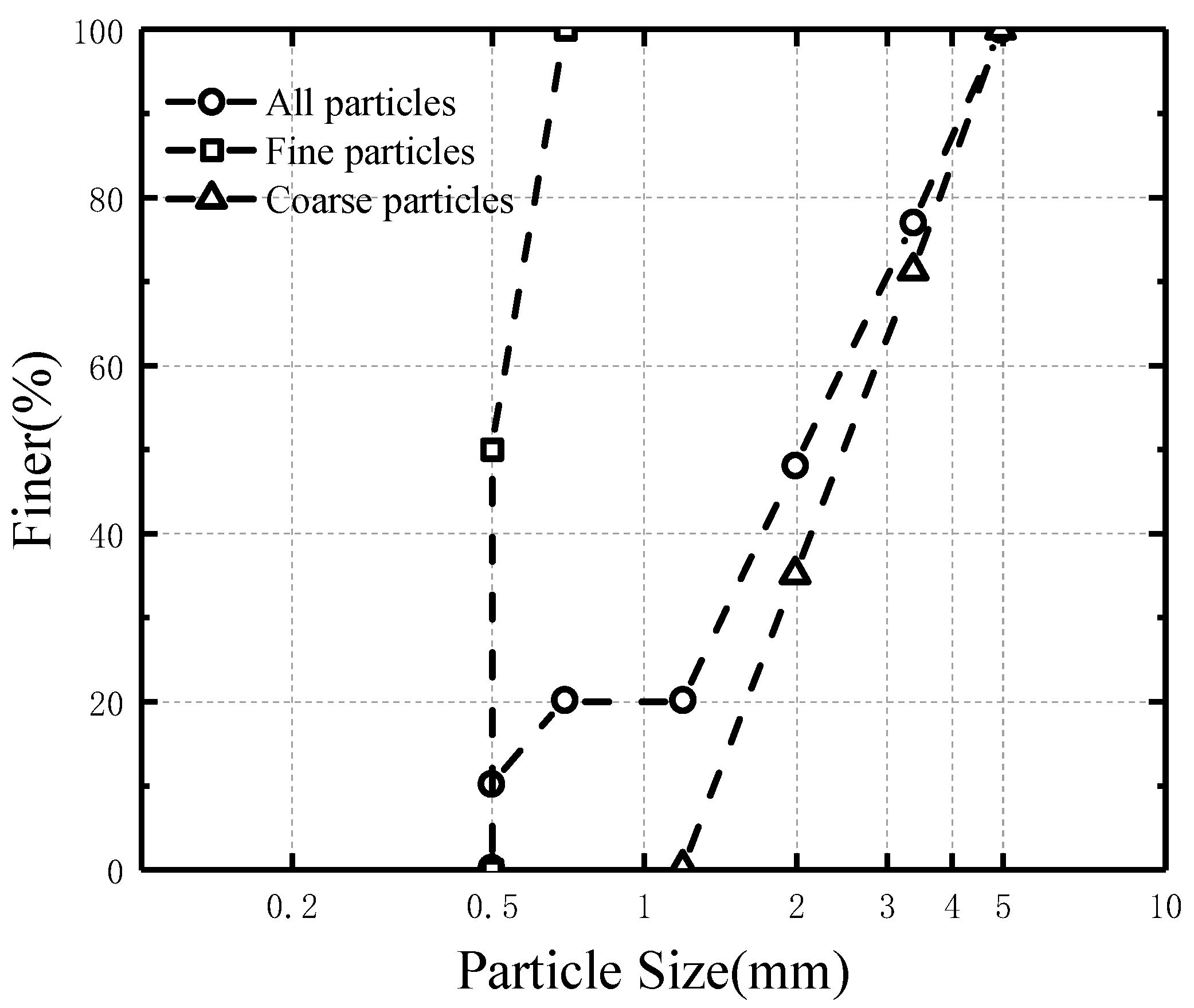
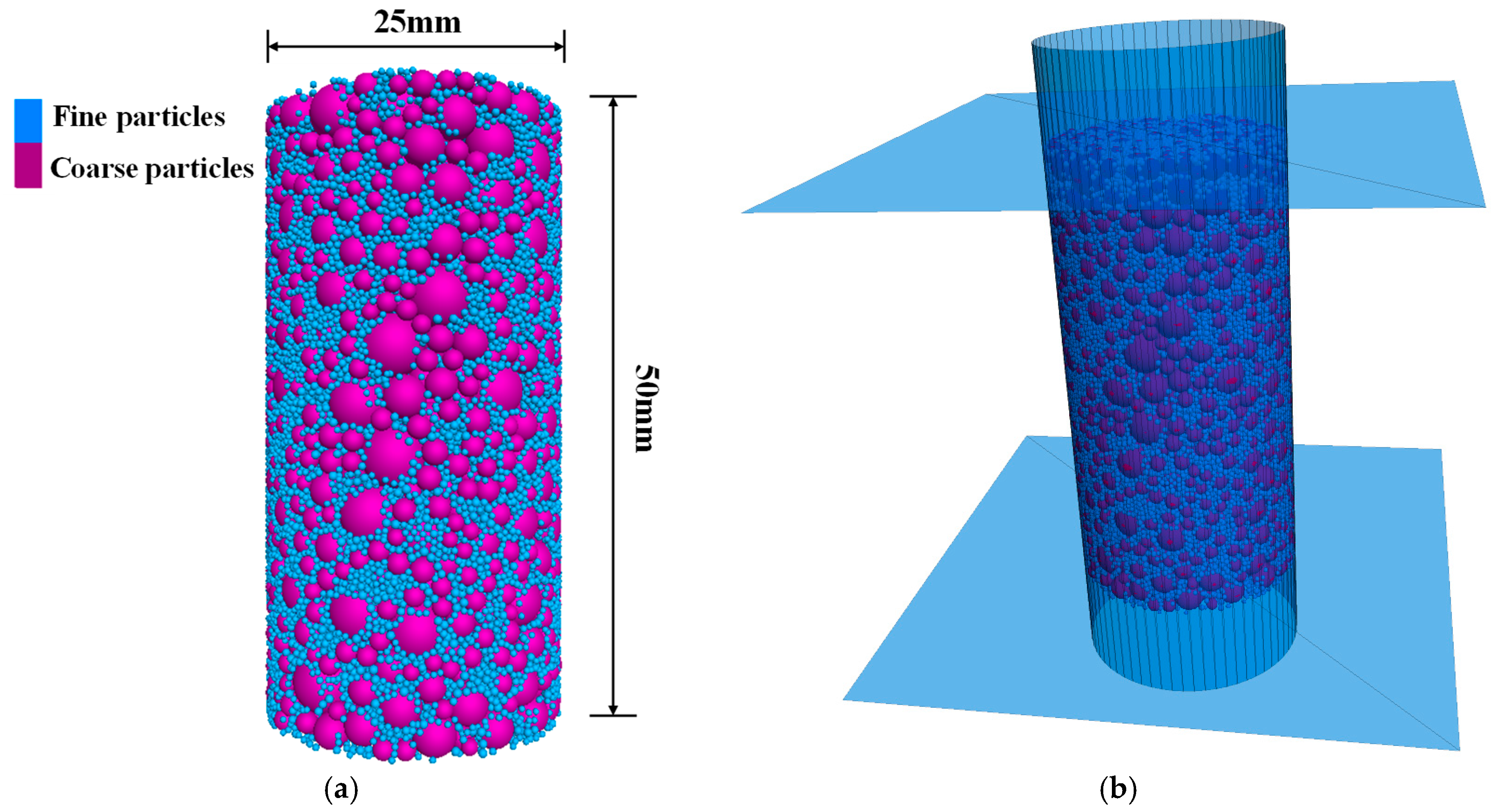
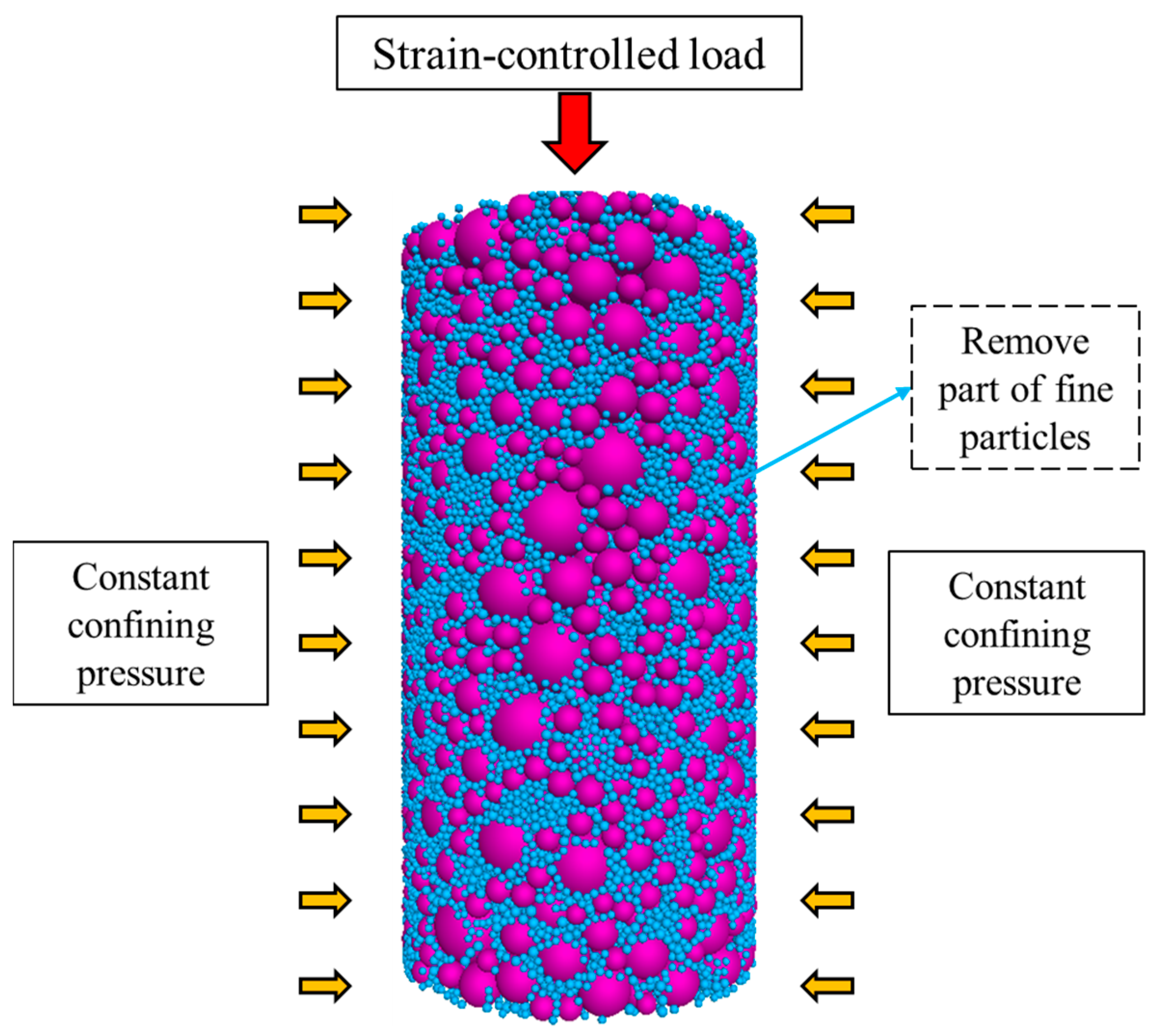
2.1.1. Sample Preparation
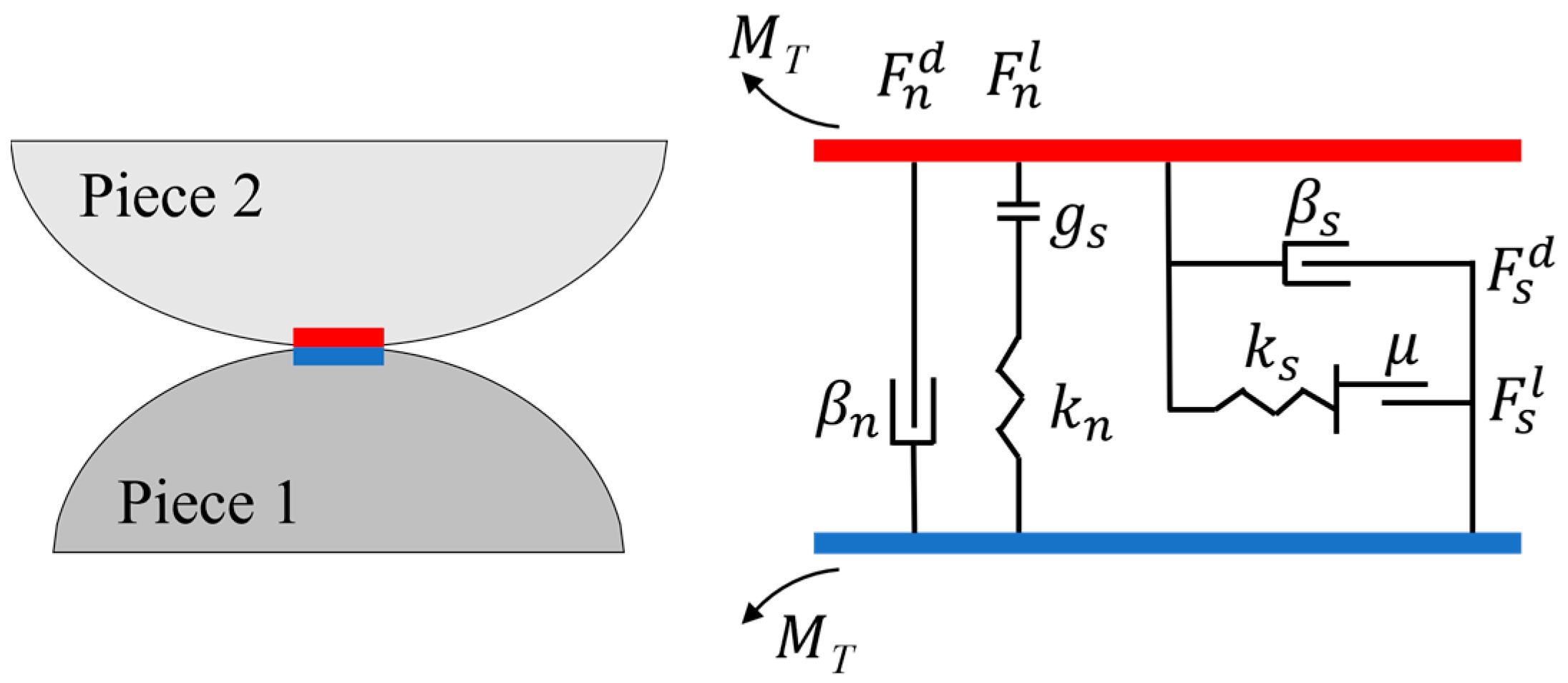
2.1.2. Contact Models
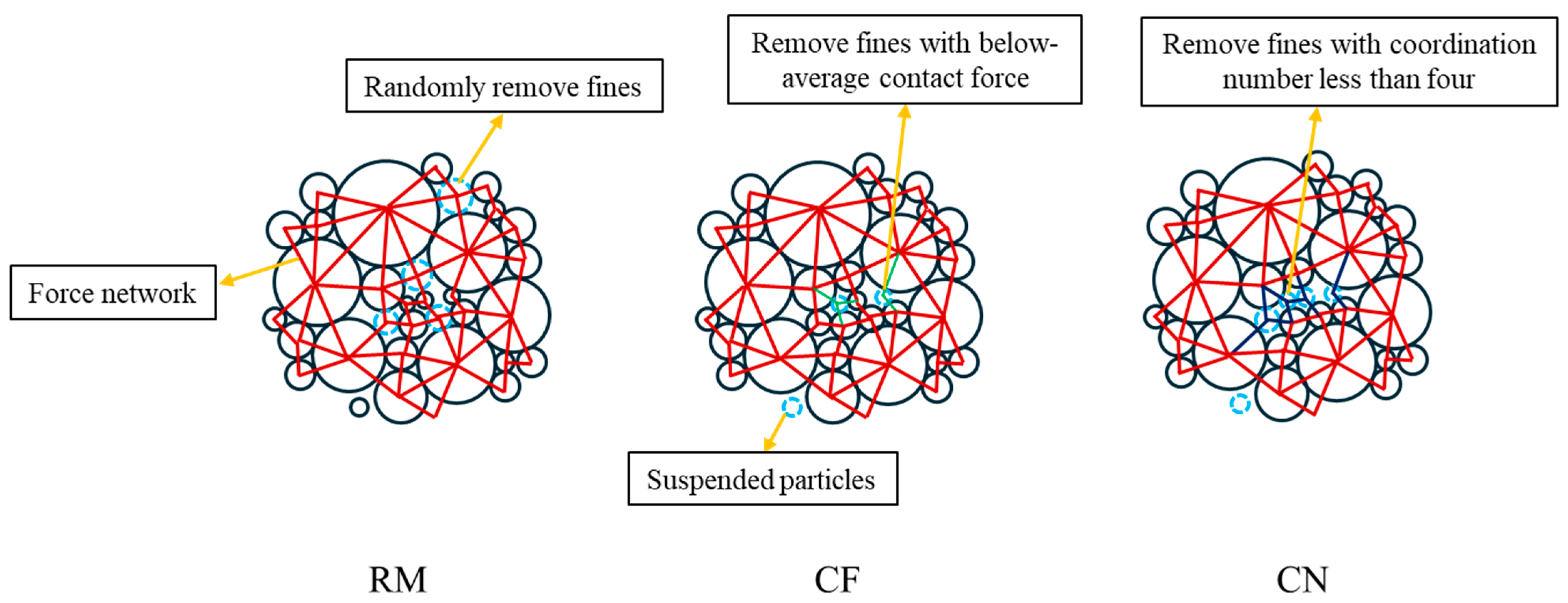
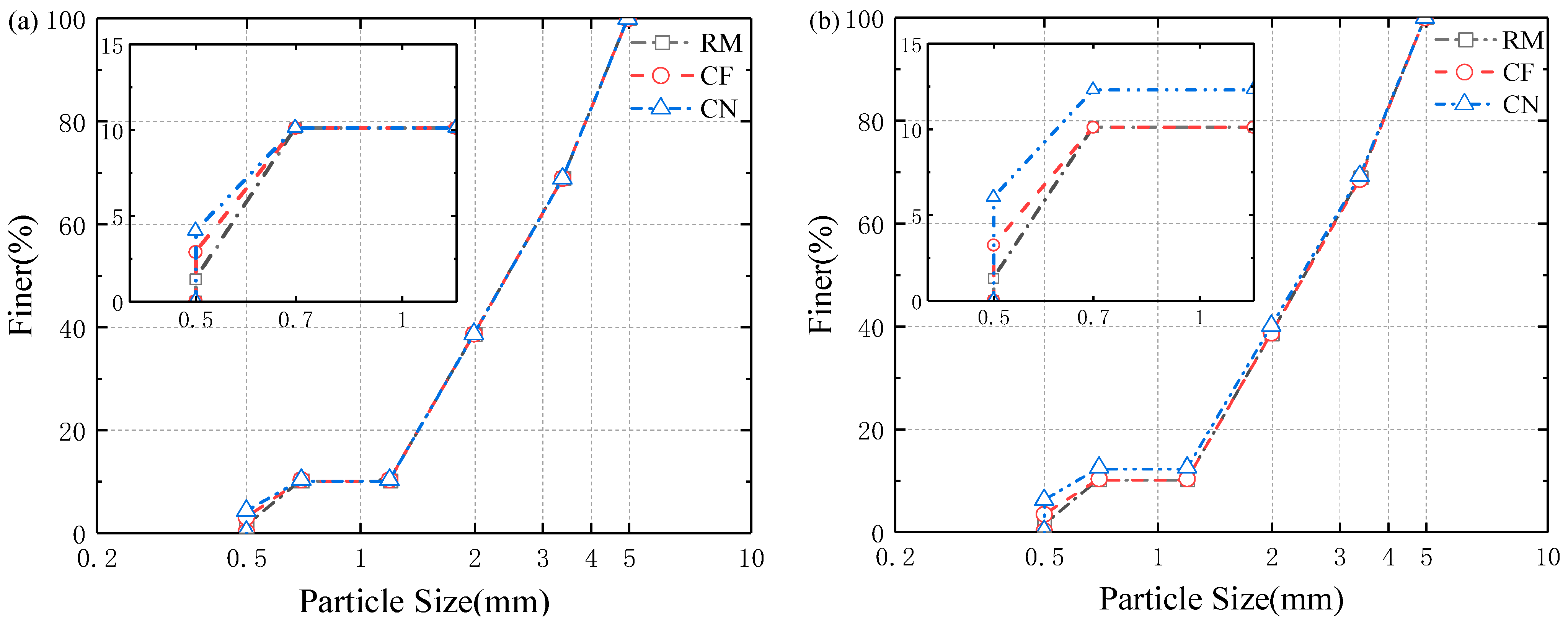
2.1.3. Three Different Modes of Internal Erosion
- (1)
- RM approach
- (2)
- CF approach
- (3)
- CN approach
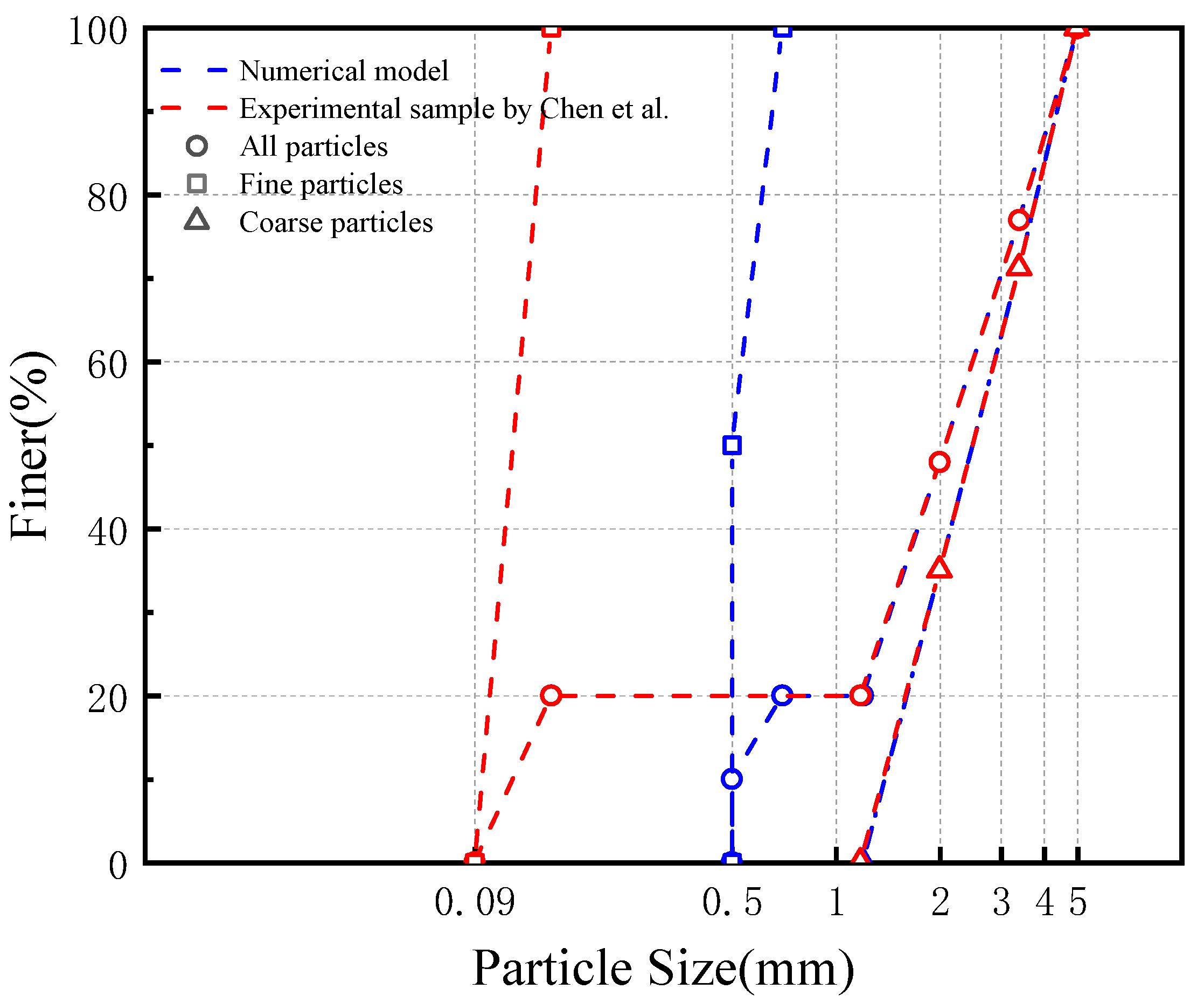
2.2. Calibration of Numerical Model
2.3. Numerical Experiment Scheme
3. Results and Discussion
3.1. Variations in Sample Properties
3.1.1. Evolution of PSD
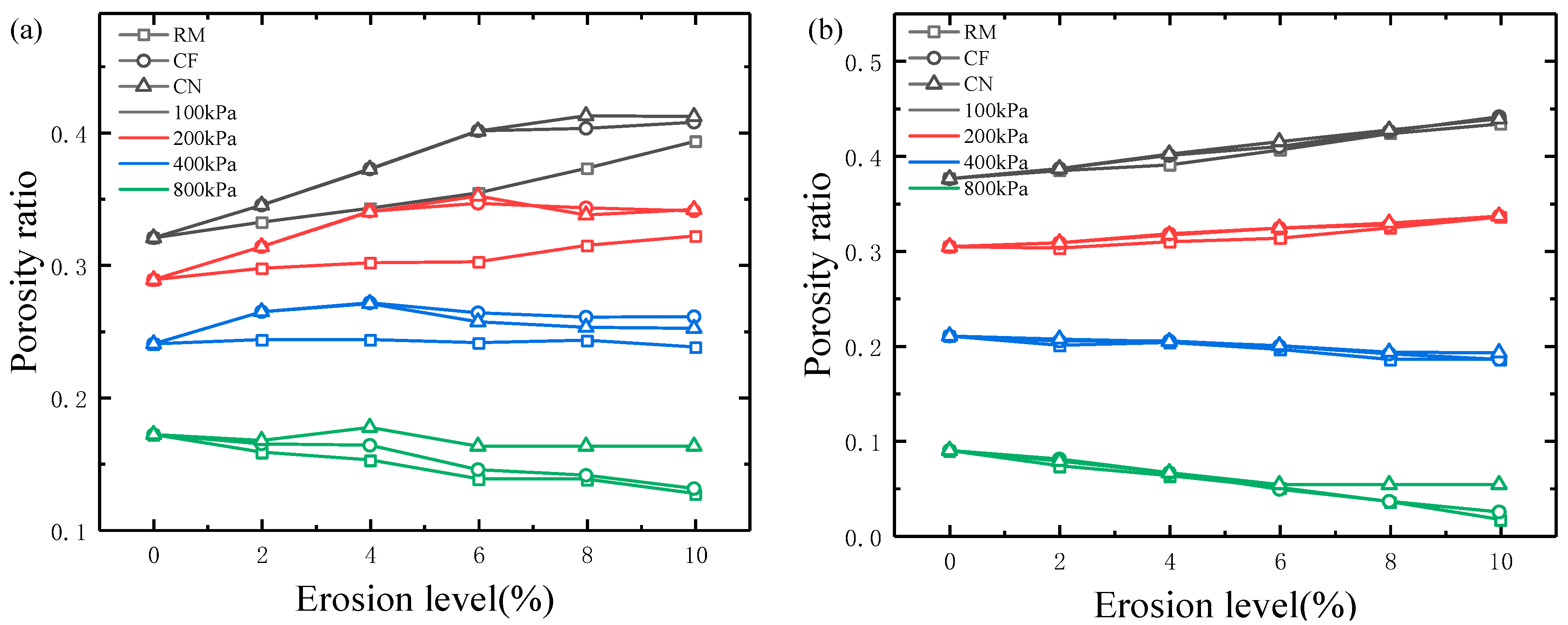
3.1.2. Evolution of Void Ratio
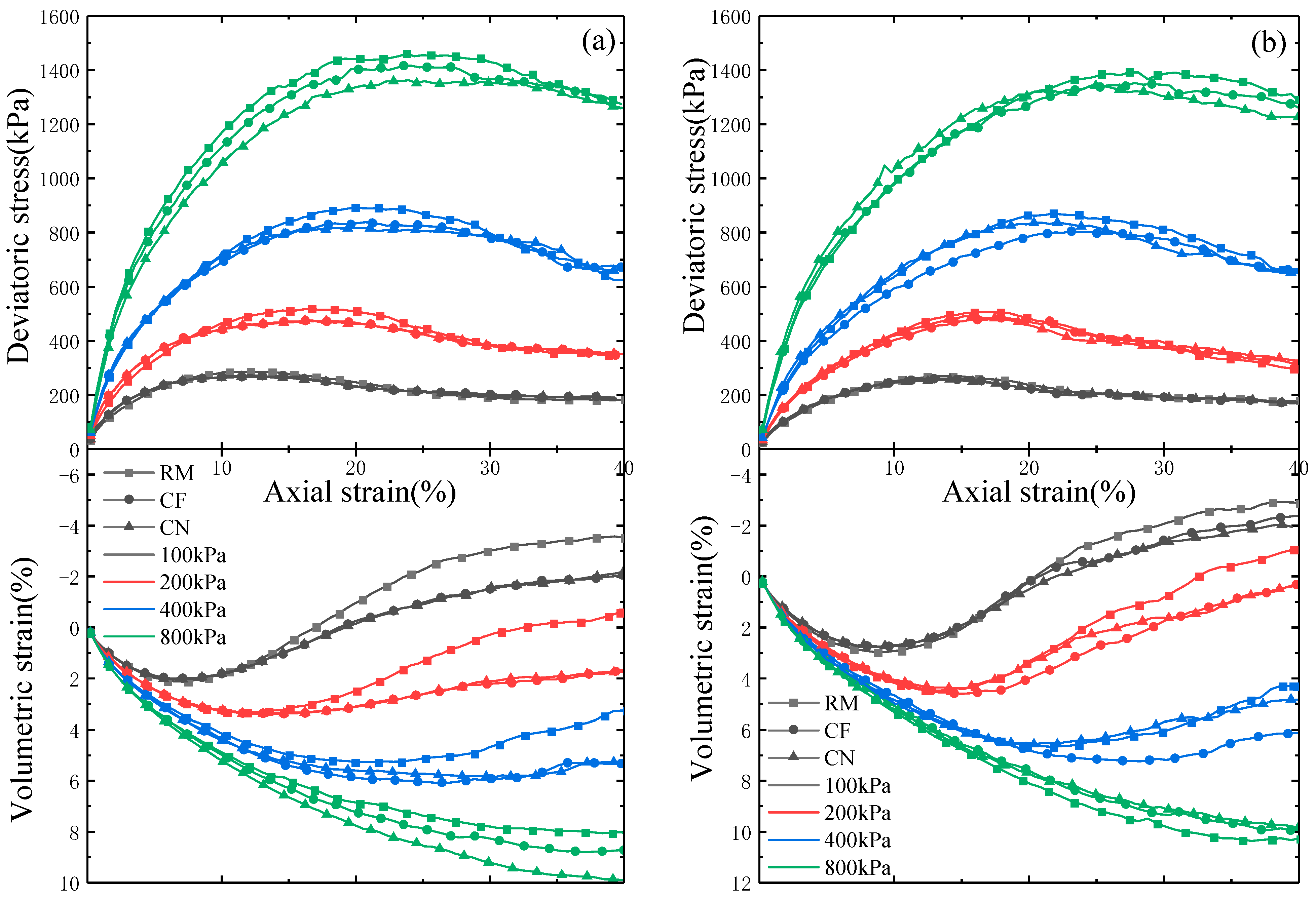
3.2. Stress–Strain Behavior
3.2.1. Effect of Degree of Internal Erosion
3.2.2. Effect of the Eroded Sample Preparation Method
3.3. Shear Secant Modulus
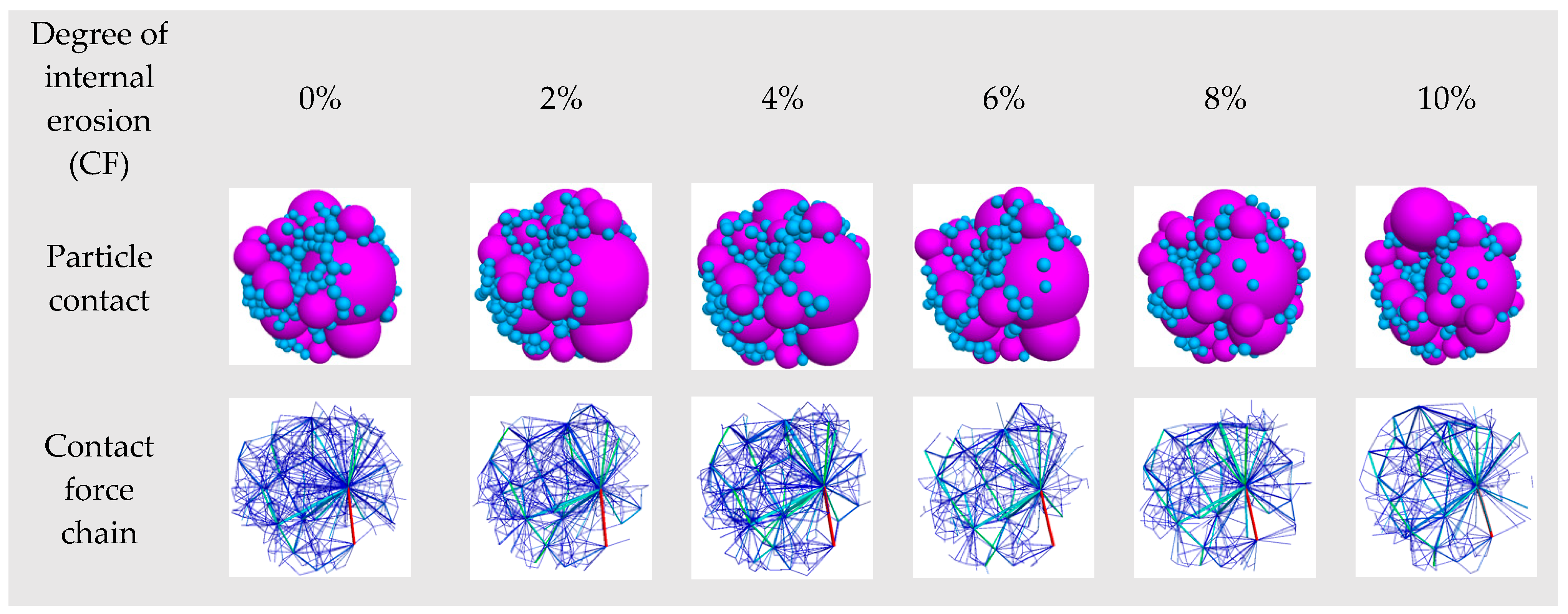
3.4. Micro-Mechanical Behavior
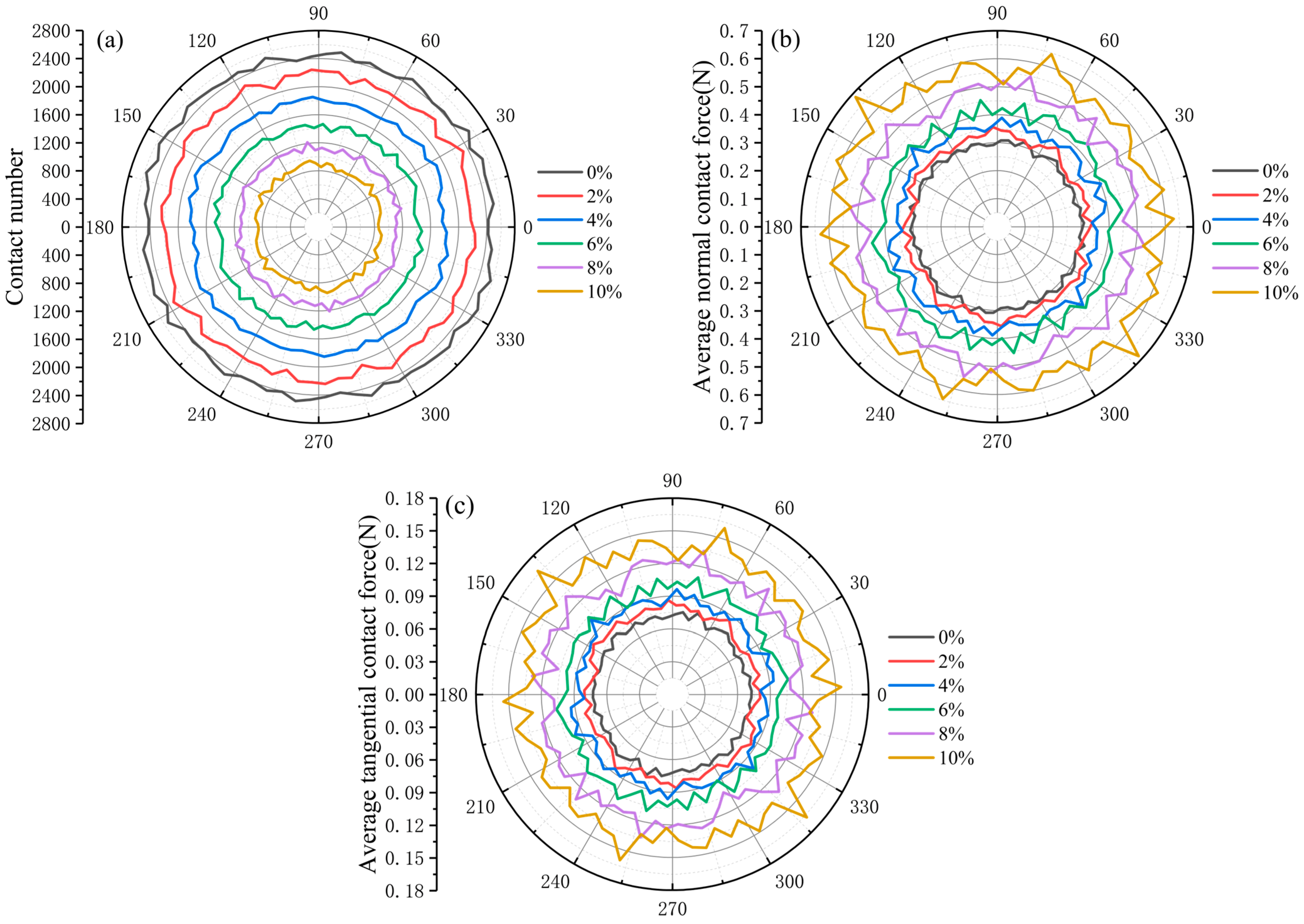
3.4.1. Evolution of Contact Number and Contact Force
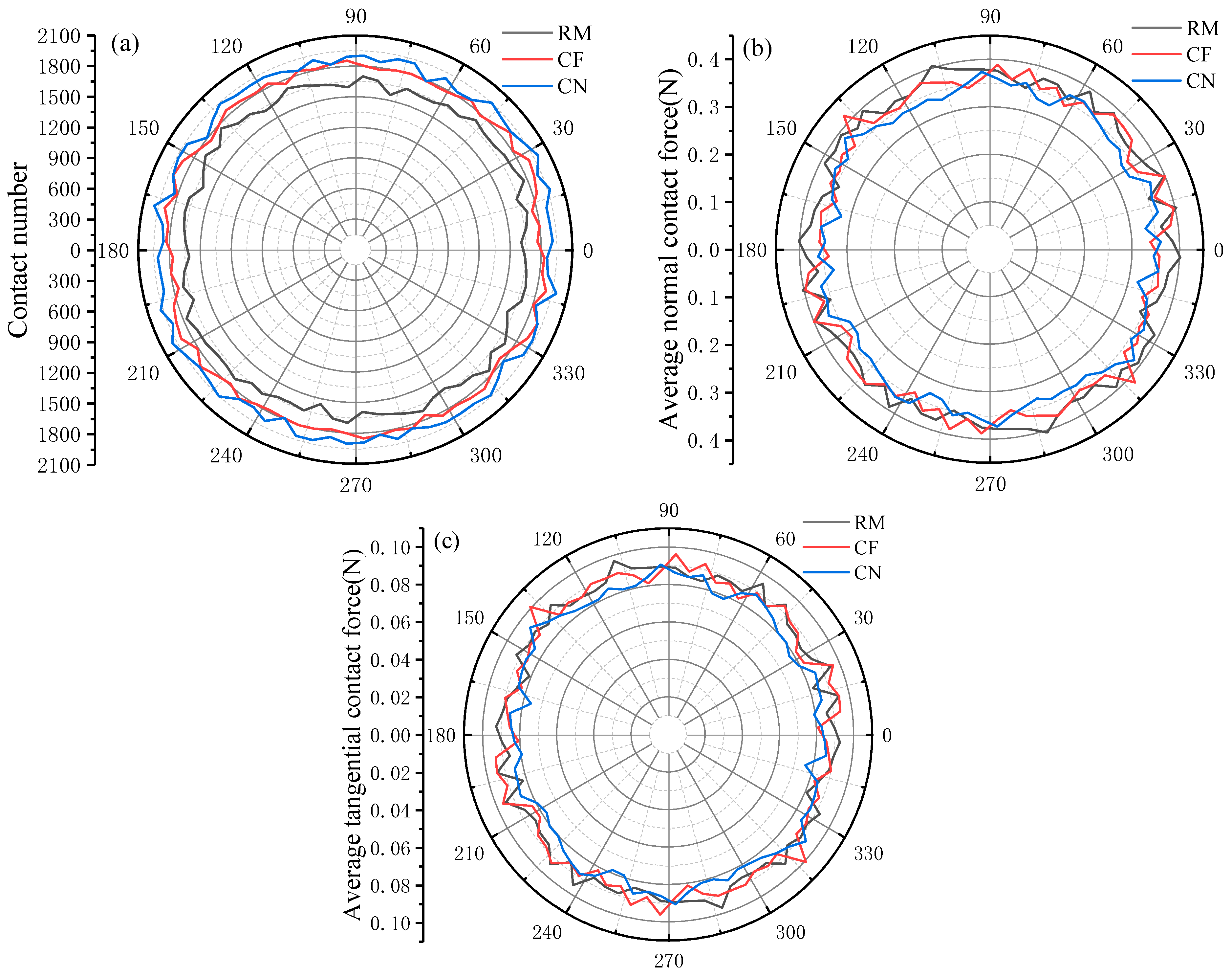
3.4.2. Effect of the Eroded Sample Preparation Method
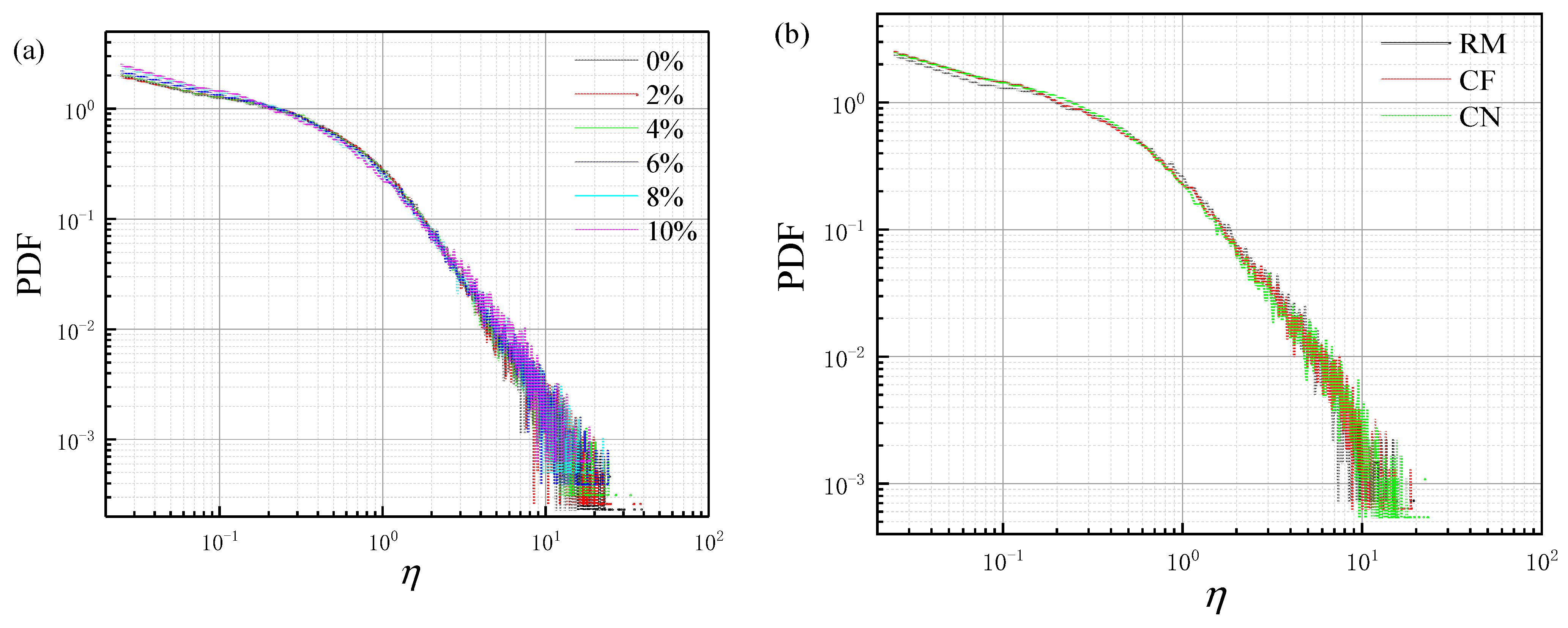
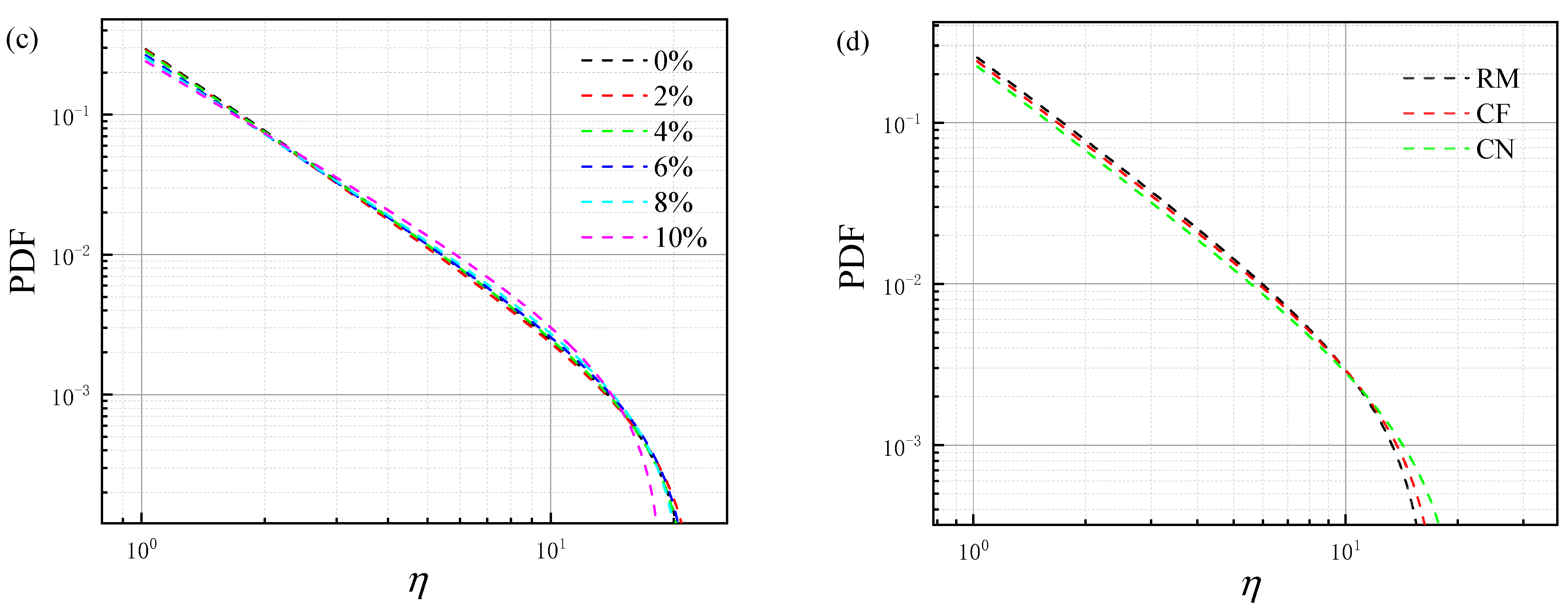
3.5. Probability Distribution Function of Contact Force
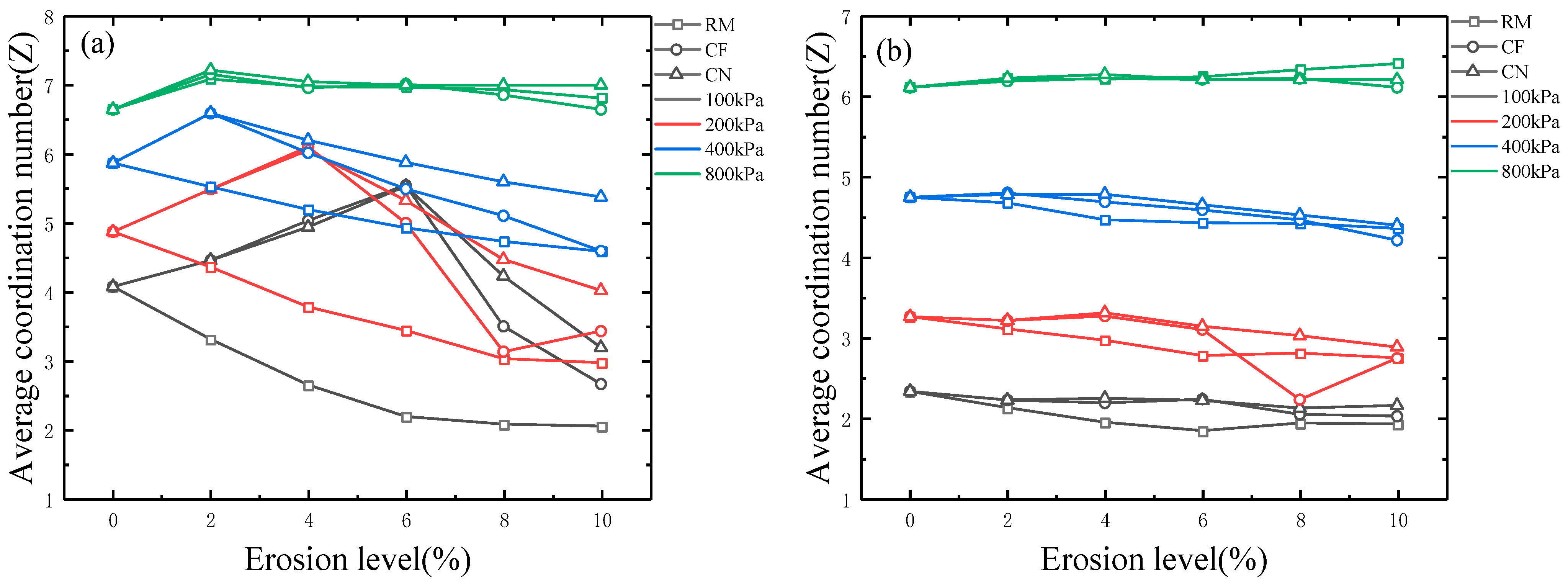
3.6. Average Coordination Number of Particles
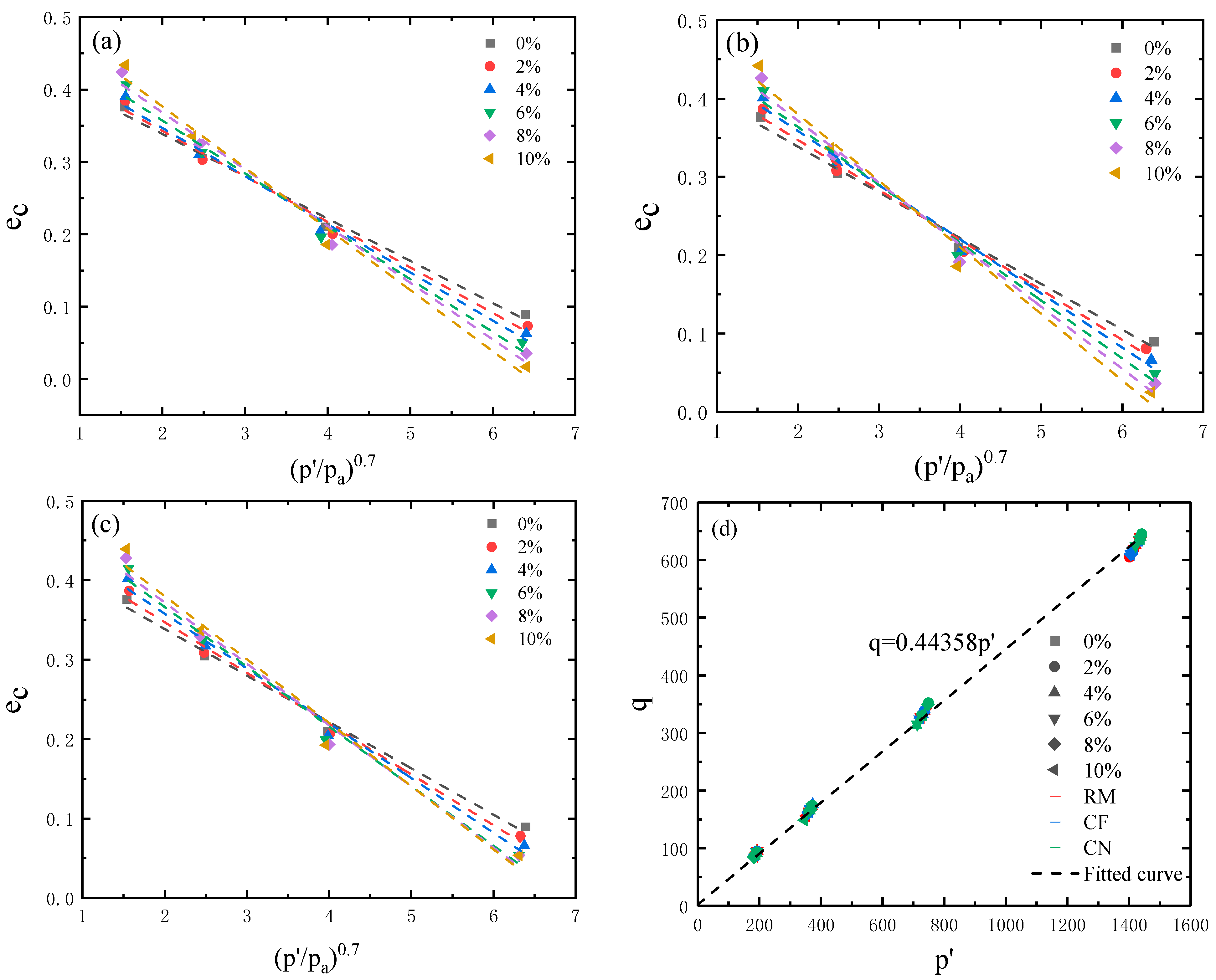
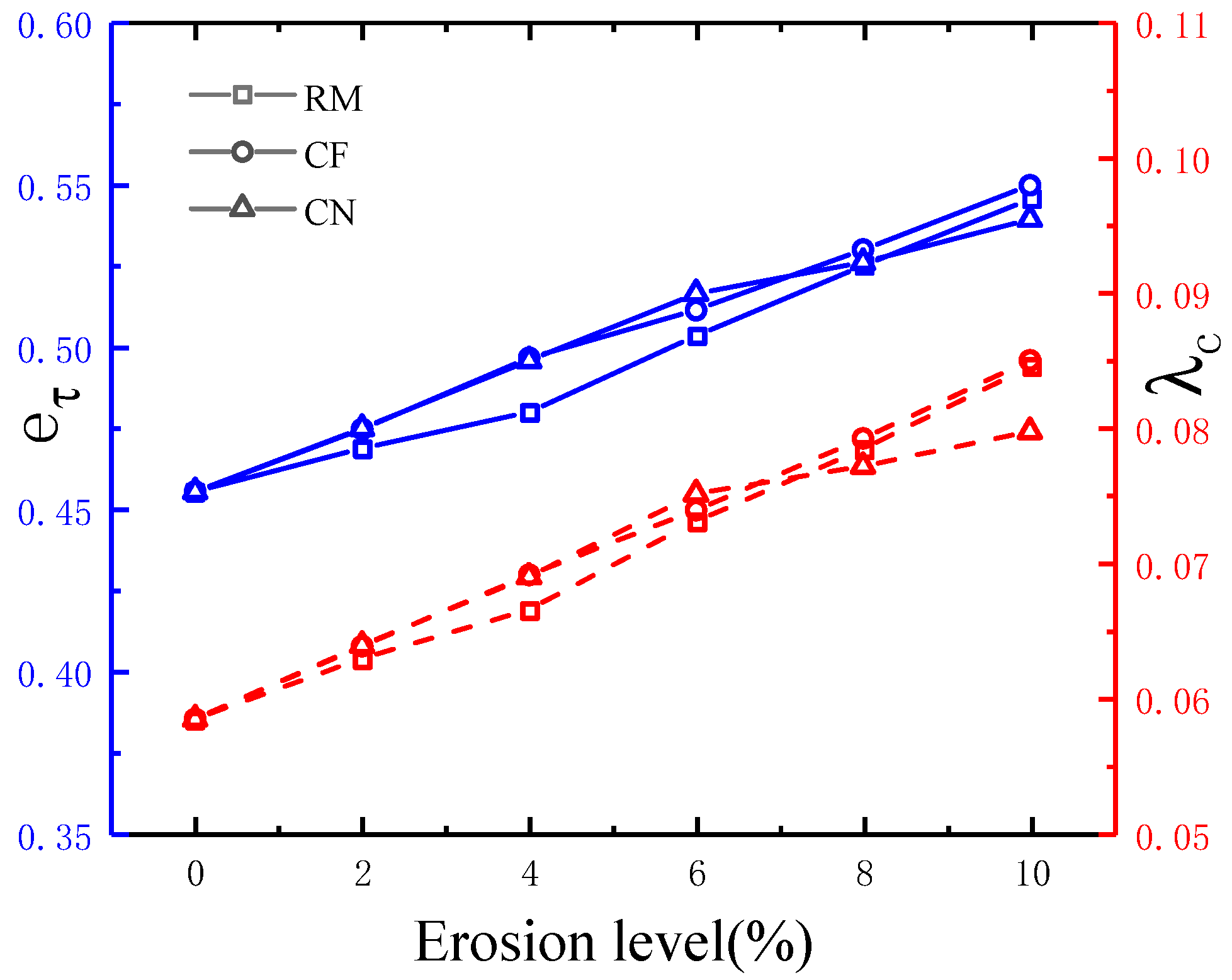
3.7. Influence of Internal Erosion on Critical State Line
4. Conclusions
- (1)
- Peak strength, stiffness, and deformation resistance have decreased, whereas residual strength has remained essentially constant with increasing internal erosion. RM-prepared specimens have exhibited larger peak strength, a smaller secant modulus E50, and more pronounced dilation. The choice of removal method has had a very limited influence on residual strength.
- (2)
- The total number of contacts has decreased markedly, while the average normal and tangential contact forces have increased as erosion has progressed. RM has produced the fewest contacts, the largest average normal contact forces, and the smallest average coordination number; CN has produced the most contacts, the smallest average contact forces, and the largest average coordination number. Differences in average coordination number between methods have become less pronounced after shearing.
- (3)
- Fine-particle loss has led to an upward shift and rotation of the CSL as internal erosion has developed, whereas its influence on the critical state friction angle has been less evident. The removal method has had only a limited effect on the CSL.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DEM | Discrete element method |
| RM | Random particle deletion |
| CF | Deletion by contact force magnitude |
| CN | Deletion by coordination number |
| PSD | Particle size distribution |
| Probability distribution functions | |
| D15 | Particle size below which 15% of the coarse/skeleton fraction lies by mass |
| d85 | Particle size below which 85% of the fine fraction lies by mass |
| Fl | Linear force |
| Fd | Damping force |
| MT | Rolling resistance moment |
| ∆θb | Relative bending-rotation increment |
| kr | Rolling resistance stiffness |
| Effective contact radius | |
| μr | Coefficient of rolling friction |
| Ekr | Rolling strain energy |
| Eur | Rolling slip energy |
| (MT)0 | Rolling resistance moment at the initial time step |
| ∆θbk | Elastic increment |
| ∆θbμr | Slip increment |
| E50 | Secant modulus |
| η | Ratio of contact force to average contact force |
| Z | Average coordination number of particles |
| Nc | Total number of contacts in the sample |
| Np | Total number of particles in the sample |
| ec | Critical state porosity |
| eτ | Critical state porosity corresponding to p′ = 0 |
| λc | Slope of the critical state line |
| p′ | Average effective stress |
| pa | A standard atmospheric pressure |
| ξ | Material parameter |
| R2 | Coefficient of determination |
References
- Muir Wood, D. The magic of sands—The 20th Bjerrum Lecture presented in Oslo, 25 November 2005. Can. Geotech. J. 2007, 44, 1329–1350. [Google Scholar] [CrossRef]
- Liu, Y.J.; Yang, J.; Yin, Z.Y. Numerical analysis of the impact of internal erosion on underground structures: Application to tunnel leakage. Rock Soil Mech. 2022, 43, 8. [Google Scholar] [CrossRef]
- Hu, W.; Hicher, P.Y.; Scaringi, G.; Xu, Q.; Van Asch, T.W.J.; Wang, G. Seismic precursor to instability induced by internal erosion in loose granular slopes. Geotechnique 2018, 68, 989–1001. [Google Scholar] [CrossRef]
- Qin, T.X.; Song, Z.; Wang, C.; Liang, F.Y. Two-point MPM study of fluidized grains in internal erosion around metro tunnel characterized by an erosion law. Comput. Geotech. 2025, 183, 107227. [Google Scholar] [CrossRef]
- Kenney, T.C.; Lau, D. Internal stability of granular filters. Can. Geotech. J. 1985, 22, 215–225. [Google Scholar] [CrossRef]
- Chang, D.S.; Zhang, L.M. Critical Hydraulic Gradients of Internal Erosion under Complex Stress States. J. Geotech. Geoenviron. Eng. 2013, 139, 1454–1467. [Google Scholar] [CrossRef]
- Chang, D.S.; Zhang, L.M. Extended internal stability criteria for soils under seepage. Soils Found. 2013, 53, 569–583. [Google Scholar] [CrossRef]
- Sterpi, D. Effects of the erosion and transport of fine particles due to seepage flow. Int. J. Geomech. 2003, 3, 111–122. [Google Scholar] [CrossRef]
- Zhang, S.; Li, Z.Q.; Tong, C.X.; Chen, C.; Chen, G.J.; Sheng, D.C. Suffusion of gravel-sand mixtures under cyclic hydraulic gradient with emphasis on tracking the migration of fine particles. Géotechnique, 2025; accepted. [Google Scholar]
- Dickinson, S.; Brachman, R.W.I. Permeability and internal erosion of a GCL beneath coarse gravel. Geosynth. Int. 2010, 17, 112–123. [Google Scholar] [CrossRef]
- Hicher, P.Y. Modelling the impact of particle removal on granular material behaviour. Geotechnique 2013, 63, 118–128. [Google Scholar] [CrossRef]
- Dai, S.H.; He, X.Z.; Tong, C.X.; Gao, F.; Zhang, S.; Sheng, D.C. Stability of sandy soils against internal erosion under cyclic loading and quantitatively examination of the composition and origin of eroded particles. Can. Geotech. J. 2024, 61, 732–747. [Google Scholar] [CrossRef]
- Sufian, A.; Bittner, T.; Bore, T.; Bajodek, M.; Scheuermann, A. Physical observations of the transient evolution of the porosity distribution during internal erosion using spatial time domain reflectometry. Can. Geotech. J. 2022, 59, 1443–1458. [Google Scholar] [CrossRef]
- Bi, J.F.; Zhang, H.T.; Luo, X.Q.; Shen, H.; Li, Z.M. Modeling of internal erosion using particle size as an extra dimension. Comput. Geotech. 2021, 133, 104021. [Google Scholar] [CrossRef]
- Yang, J.; Yin, Z.Y.; Laouafa, F.; Hicher, P.Y. Hydromechanical modeling of granular soils considering internal erosion. Can. Geotech. J. 2020, 57, 157–172. [Google Scholar] [CrossRef]
- Ke, L.; Takahashi, A. Strength reduction of cohesionless soil due to internal erosion induced by one-dimensional upward seepage flow. Soils Found. 2012, 52, 698–711. [Google Scholar] [CrossRef]
- Ouyang, M.; Takahashi, A. Influence of initial fines content on fabric of soils subjected to internal erosion. Can. Geotech. J. 2016, 53, 299–313. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, L.M.; Chang, D.S. Stress-Strain Behavior of Granular Soils Subjected to Internal Erosion. J. Geotech. Geoenviron. Eng. 2016, 142, 06016014. [Google Scholar] [CrossRef]
- Yang, Y.; Jiang, J.G.; Mao, W.W.; Xu, C. Investigation on the mechanical consequence of different internal erosion scenarios in gap-graded sandy soils. J. Eng. Geol. 2021, 29, 67–73. [Google Scholar] [CrossRef]
- Shi, X.S.; He, Z.H.; Zhao, J.D.; Liu, J.Y. Determination of the size of representative volume element for gap-graded granular materials. Powder Technol. 2024, 437, 119578. [Google Scholar] [CrossRef]
- Shi, X.S.; Nie, J.Y.; Zhao, J.D.; Gao, Y.F. A homogenization equation for the small strain stiffness of gap-graded granular materials. Comput. Geotech. 2020, 121, 103440. [Google Scholar] [CrossRef]
- Xiong, H.; Qiu, Y.Y.; Liu, J.Y.; Yin, Z.Y.; Chen, X.S. Macro-microscopic mechanism of suffusion in calcareous sand under tidal fluctuations by coupled CFD-DEM. Comput. Geotech. 2023, 162, 105676. [Google Scholar] [CrossRef]
- Zhang, F.S.; Wang, T.; Liu, F.; Peng, M.; Furtney, J.; Zhang, L.M. Modeling of fluid-particle interaction by coupling the discrete element method with a dynamic fluid mesh: Implications to suffusion in gap-graded soils. Comput. Geotech. 2020, 124, 103617. [Google Scholar] [CrossRef]
- Wang, T.; Chen, S.H.; Li, M.L.; An, M.K. A resolved CFD-DEM investigation of near-wellbore fine sand migration and production during methane hydrate extraction. Geomech. Energy Environ. 2024, 38, 100561. [Google Scholar] [CrossRef]
- Scholtès, L.; Hicher, P.Y.; Sibille, L. Multiscale approaches to describe mechanical responses induced by particle removal in granular materials. C. R. Mec. 2010, 338, 627–638. [Google Scholar] [CrossRef]
- Muir Wood, D.; Maeda, K.; Nukudani, E. Modelling mechanical consequences of erosion. Géotechnique 2010, 60, 447–457. [Google Scholar] [CrossRef]
- Zhang, F.S.; Li, M.L.; Peng, M.; Chen, C.; Zhang, L.M. Three-dimensional DEM modeling of the stress-strain behavior for the gap-graded soils subjected to internal erosion. Acta Geotech. 2019, 14, 487–503. [Google Scholar] [CrossRef]
- Taha, H.; Nguyen, N.S.; Marot, D.; Hijazi, A.; Abou-Saleh, K. A DEM study of the effect of the loss of fine particles on the mechanical behavior of gap-graded soils. Geomech. Energy Environ. 2022, 31, 100305. [Google Scholar] [CrossRef]
- Kézdi, Á. Soil Physics: Selected Topics; Elsevier: Amsterdam, The Netherlands, 2013; Volume 25. [Google Scholar]
- Itasca Consulting Group. PFC3D Documentation: Particle Flow Code, Ver. 6.0 Minneapolis, USA. Available online: https://docs.itascacg.com/pfc600/contents.html (accessed on 20 June 2025).
- Li, M.-W.; Hu, S.-L.; Tong, C.-X. Numerical Simulation of Mechanical Properties of Soil Considering the Effect of Internal Erosion. Mathematics 2023, 11, 2959. [Google Scholar] [CrossRef]
- Wan, S.F.; Pan, H.; Luo, G.Y.; Peng, S.G. Experimental study on the impact of water flow velocity on internal erosion of granite residual soil. Sci. Rep. 2025, 15, 28469. [Google Scholar] [CrossRef]
- Robbins, B.A.; Griffiths, D. Internal erosion of embankments: A review and appraisal. In Proceedings of the Rocky Mountain Geo-Conference 2018, Reston, VA, USA, 2 November 2018; pp. 61–75. [Google Scholar]
- Shire, T.; O’Sullivan, C.; Hanley, K.J. The influence of fines content and size-ratio on the micro-scale properties of dense bimodal materials. Granul. Matter 2016, 18, 52. [Google Scholar] [CrossRef]
- Tosun, H. Dynamic stability of large embankment dams and a case study. In Proceedings of the 6rd International Conference on Civil Structural and Transportation Engineering (ICCSTE21), Virtual Conference, Niagara Falls, ON, Canada, 17–19 May 2021; pp. 17–19. [Google Scholar]
- Mueth, D.M.; Jaeger, H.M.; Nagel, S.R. Force distribution in a granular medium. Phys. Rev. E 1998, 57, 3164. [Google Scholar] [CrossRef]
- Haq, S.; Indraratna, B.; Nguyen, T.T.; Rujikiatkamjorn, C. Micromechanical Analysis of Internal Instability during Shearing. Int. J. Geomech. 2023, 23, 04023078. [Google Scholar] [CrossRef]
- Roscoe, K.H.; Schofield, A.N.; Wroth, C.P. On the yielding of soils. Geotechnique 1958, 8, 22–53. [Google Scholar] [CrossRef]
- Tong, C.X.; Zhai, M.Y.; Li, H.C.; Zhang, S.; Sheng, D.C. Particle breakage of granular soils: Changing critical state line and constitutive modelling. Acta Geotech. 2022, 17, 755–768. [Google Scholar] [CrossRef]
- Li, X.S.; Wang, Y. Linear representation of steady-state line for sand. J. Geotech. Geoenviron. Eng. 1998, 124, 1215–1217. [Google Scholar] [CrossRef]
- Bandini, V.; Coop, M.R. The Influence of Particle Breakage on the Location of the Critical State Line of Sands. Soils Found. 2011, 51, 591–600. [Google Scholar] [CrossRef]



| Model Parameters | Value |
|---|---|
| Particle density (kg/m3) | 2650 |
| Normal stiffness of coarse particles (N/m) | 4.5 × 105 |
| Normal stiffness of fine particles (N/m) | 1.2 × 105 |
| Normal-to-shear stiffness ratio | 2.0 |
| Particle damping coefficient | 0.7 |
| Particle friction coefficient | 0.2 |
| Normal stiffness of wall (N/m) | 1 × 106 |
| Rolling friction coefficient | 0.1 |
| Particle-Deletion Method | Volume Fraction of Erosion (%) | Effective Confining Pressure σc (kPa) |
|---|---|---|
| No deletion | 0 | 100, 200, 400, 800 |
| RM | 2, 4, 6, 8, 10 | 100, 200, 400, 800 |
| CF | 2, 4, 6, 8, 10 | 100, 200, 400, 800 |
| CN | 2, 4, 6, 8, 10 | 100, 200, 400, 800 |
| Function | y = axb | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Erosion Degree | 0% | 2% | 4% | 6% | 8% | 10% | ||||
| Parameters | ||||||||||
| a | 0.30862 | 0.30509 | 0.29788 | 0.28005 | 0.26815 | 0.25258 | ||||
| b | −2.00051 | −2.03013 | −1.97658 | −1.93415 | −1.87352 | −1.75223 | ||||
| R2 | 0.99377 | 0.99475 | 0.99506 | 0.99331 | 0.99271 | 0.99346 | ||||
| Function | y = axb | |||
|---|---|---|---|---|
| Fines Deletion Methods | RM | CF | CN | |
| Parameters | ||||
| a | 0.26659 | 0.25241 | 0.23457 | |
| b | −1.73793 | −1.74604 | −1.78004 | |
| R2 | 0.99224 | 0.99348 | 0.99172 | |
| Parameters | Simulation Mode | 0% | 2% | 4% | 6% | 8% | 10% |
|---|---|---|---|---|---|---|---|
| eτ | RM | 0.45529 | 0.46865 | 0.47984 | 0.50341 | 0.52508 | 0.54564 |
| CF | 0.45529 | 0.47459 | 0.49659 | 0.51135 | 0.53003 | 0.54992 | |
| CN | 0.45529 | 0.47487 | 0.49574 | 0.51643 | 0.52617 | 0.53944 | |
| λc | RM | 0.05841 | 0.06288 | 0.06652 | 0.07308 | 0.0784 | 0.08455 |
| CF | 0.05841 | 0.0638 | 0.06909 | 0.07389 | 0.0792 | 0.08499 | |
| CN | 0.05841 | 0.06387 | 0.06894 | 0.07511 | 0.07714 | 0.07972 | |
| R2 | RM | 0.98812 | 0.98588 | 0.985 | 0.97989 | 0.9823 | 0.98284 |
| CF | 0.98812 | 0.98825 | 0.98792 | 0.98518 | 0.98057 | 0.97759 | |
| CN | 0.98812 | 0.98879 | 0.98586 | 0.98351 | 0.97631 | 0.96797 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, F.; Xu, H.; Xu, Y.; Hu, S.; Li, M.; Tong, C. Mechanical Consequences of Gap-Graded Soils Subjected to Internal Erosion: The Effect of Mode of Removal of Fine Particles Using Discrete Element Method. Coatings 2025, 15, 1218. https://doi.org/10.3390/coatings15101218
He F, Xu H, Xu Y, Hu S, Li M, Tong C. Mechanical Consequences of Gap-Graded Soils Subjected to Internal Erosion: The Effect of Mode of Removal of Fine Particles Using Discrete Element Method. Coatings. 2025; 15(10):1218. https://doi.org/10.3390/coatings15101218
Chicago/Turabian StyleHe, Feng, Haodong Xu, Yongqing Xu, Shengliang Hu, Maowen Li, and Chenxi Tong. 2025. "Mechanical Consequences of Gap-Graded Soils Subjected to Internal Erosion: The Effect of Mode of Removal of Fine Particles Using Discrete Element Method" Coatings 15, no. 10: 1218. https://doi.org/10.3390/coatings15101218
APA StyleHe, F., Xu, H., Xu, Y., Hu, S., Li, M., & Tong, C. (2025). Mechanical Consequences of Gap-Graded Soils Subjected to Internal Erosion: The Effect of Mode of Removal of Fine Particles Using Discrete Element Method. Coatings, 15(10), 1218. https://doi.org/10.3390/coatings15101218






