Phenomenological Analysis of Percolation Phenomena in Porous Low-k Dielectrics
Abstract
1. Introduction
- Section 2 examines mass transport mechanisms in porous low-k films, with a focus on how percolation controls diffusivity and reactive species infiltration, including the role of percolated networks in facilitating the diffusion of stable molecules, plasma radicals, and environmental contaminants.
- Section 3 explores how percolation affects key electrical properties, including permittivity, breakdown voltage, and dielectric degradation, particularly emphasizing how percolation alters dielectric breakdown strength, leakage currents, and long-term reliability.
- Section 4 discusses the mechanical consequences of percolation, including stress localization, fracture pathways, and mechanical failure modes, with an emphasis on how pore connectivity impacts elastic modulus, hardness, toughness, and reliability under mechanical stress.
- The conclusion highlights the broader implications of percolation for material design and outlines strategies for mitigating percolation-driven degradation while achieving ultra-low-k performance.
2. Mass Transport and the Role of Percolated Networks in Facilitating the Diffusion of Stable Molecules, Plasma Radicals, Positronium (Ps) and Environmental Contaminants
2.1. Fabrication of Porous Low-k Films
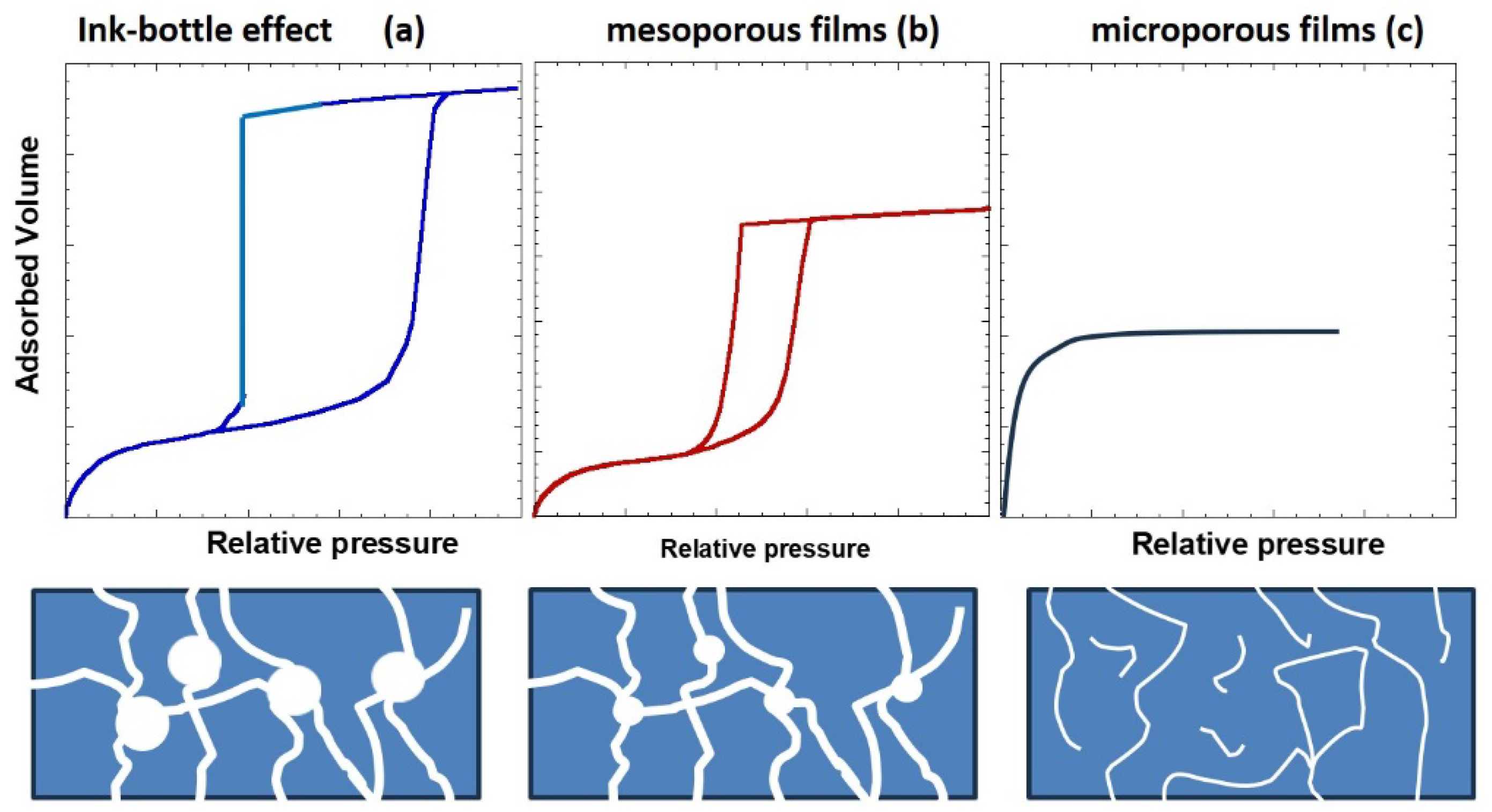
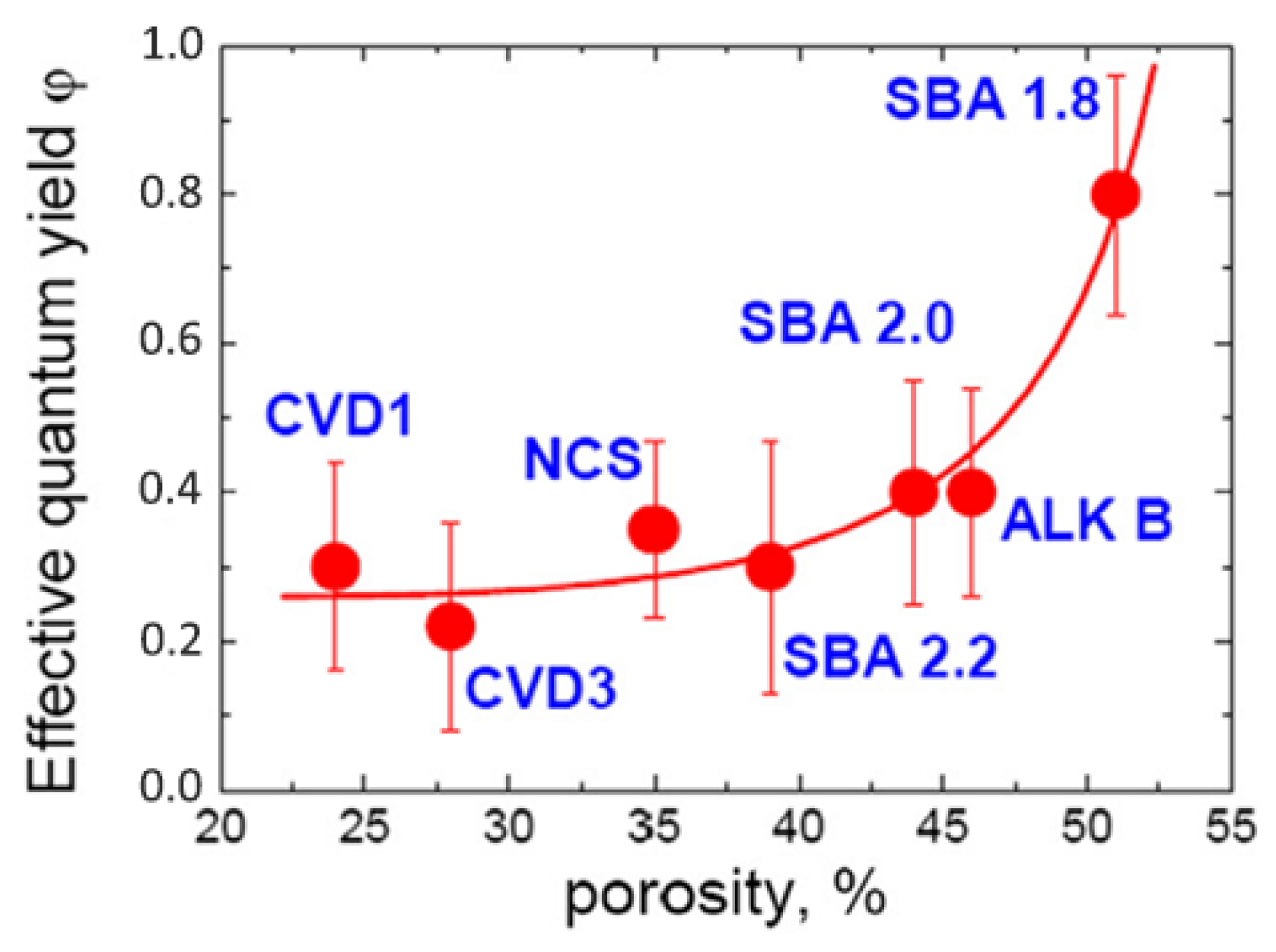
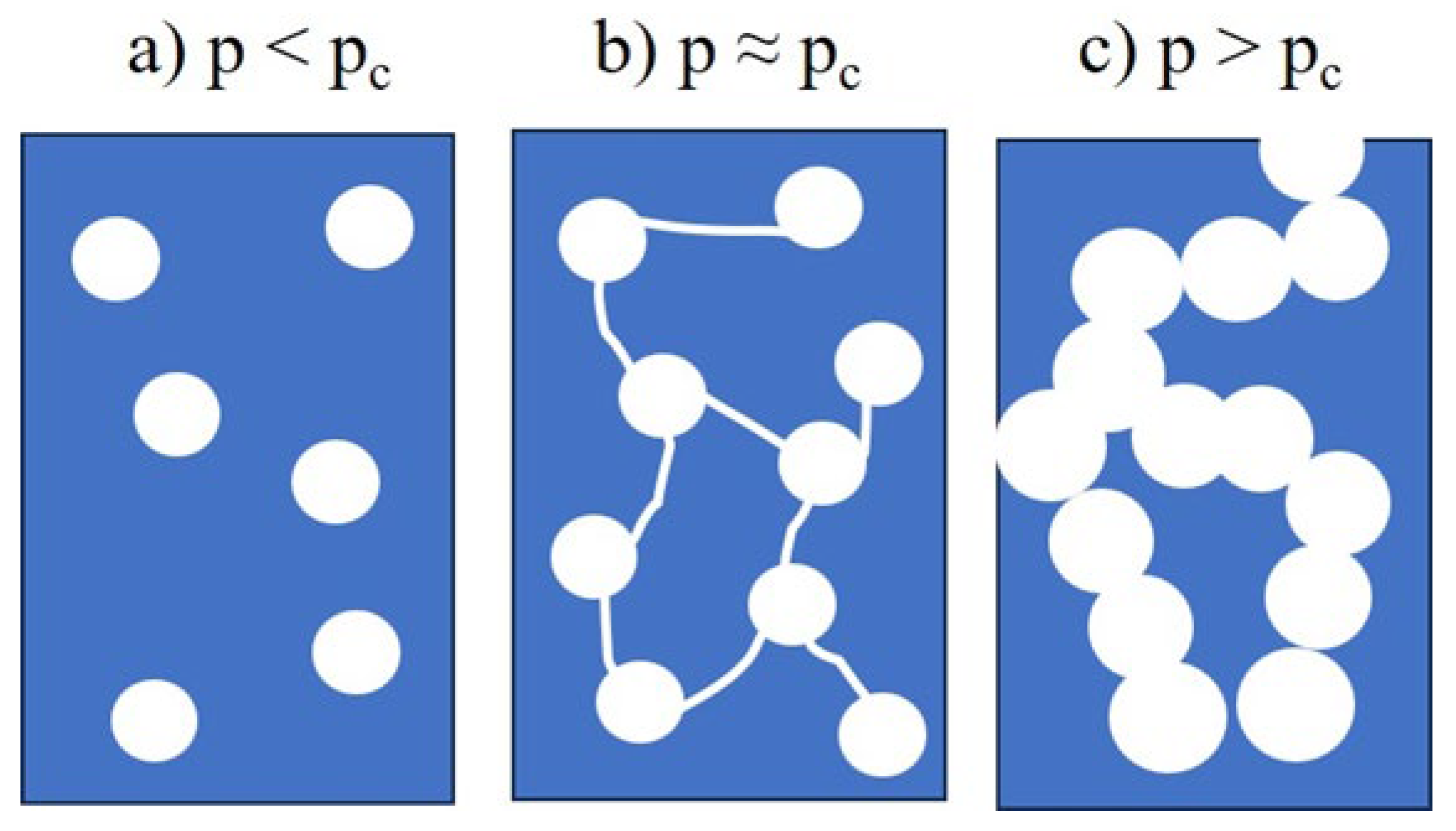
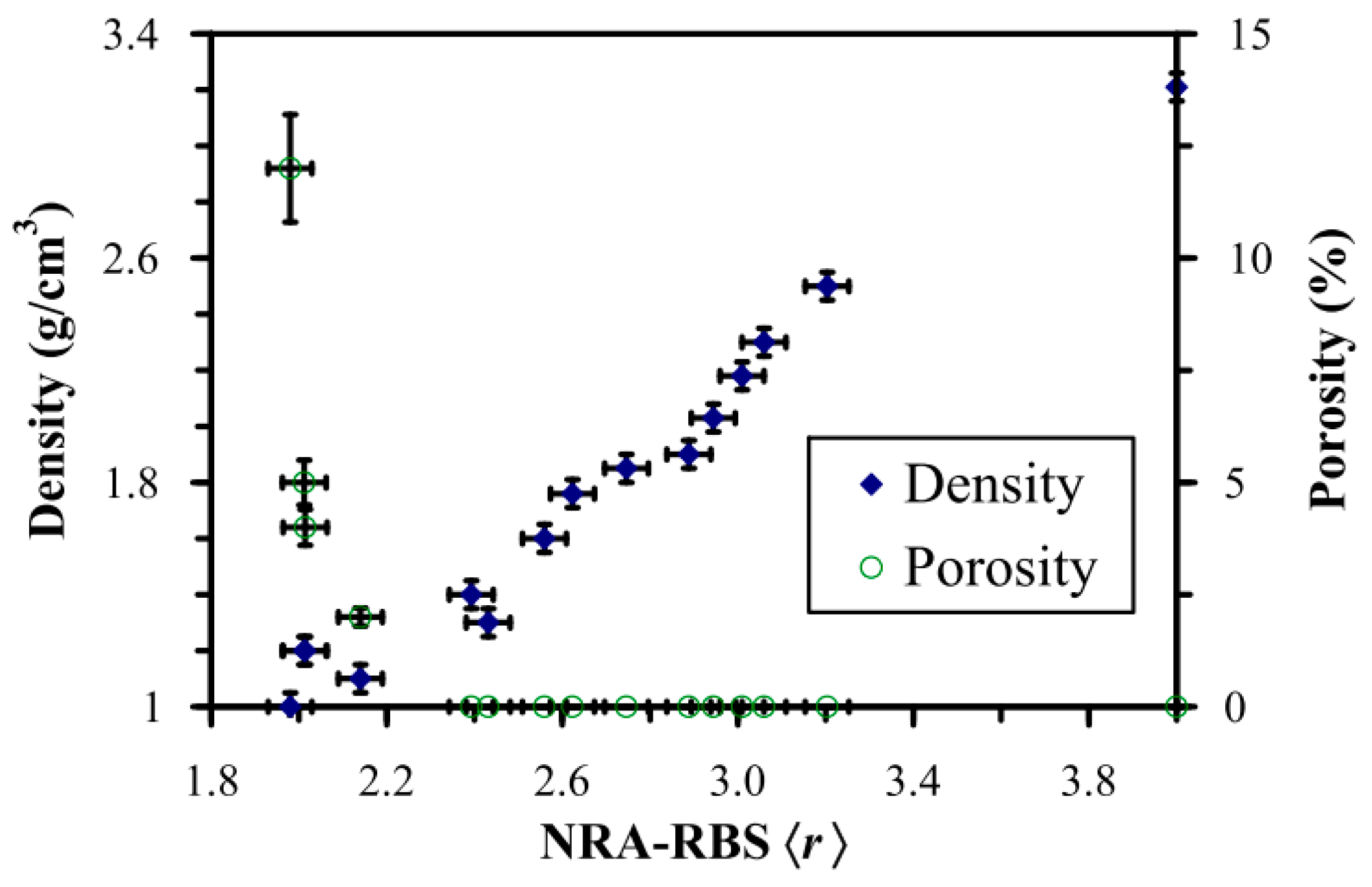
2.2. Types of Porosity and Mass Transport
- p < pc → no continuous path exists → macroscopic transport is effectively zero.
- p > pc → a connected network exists → transport becomes possible.
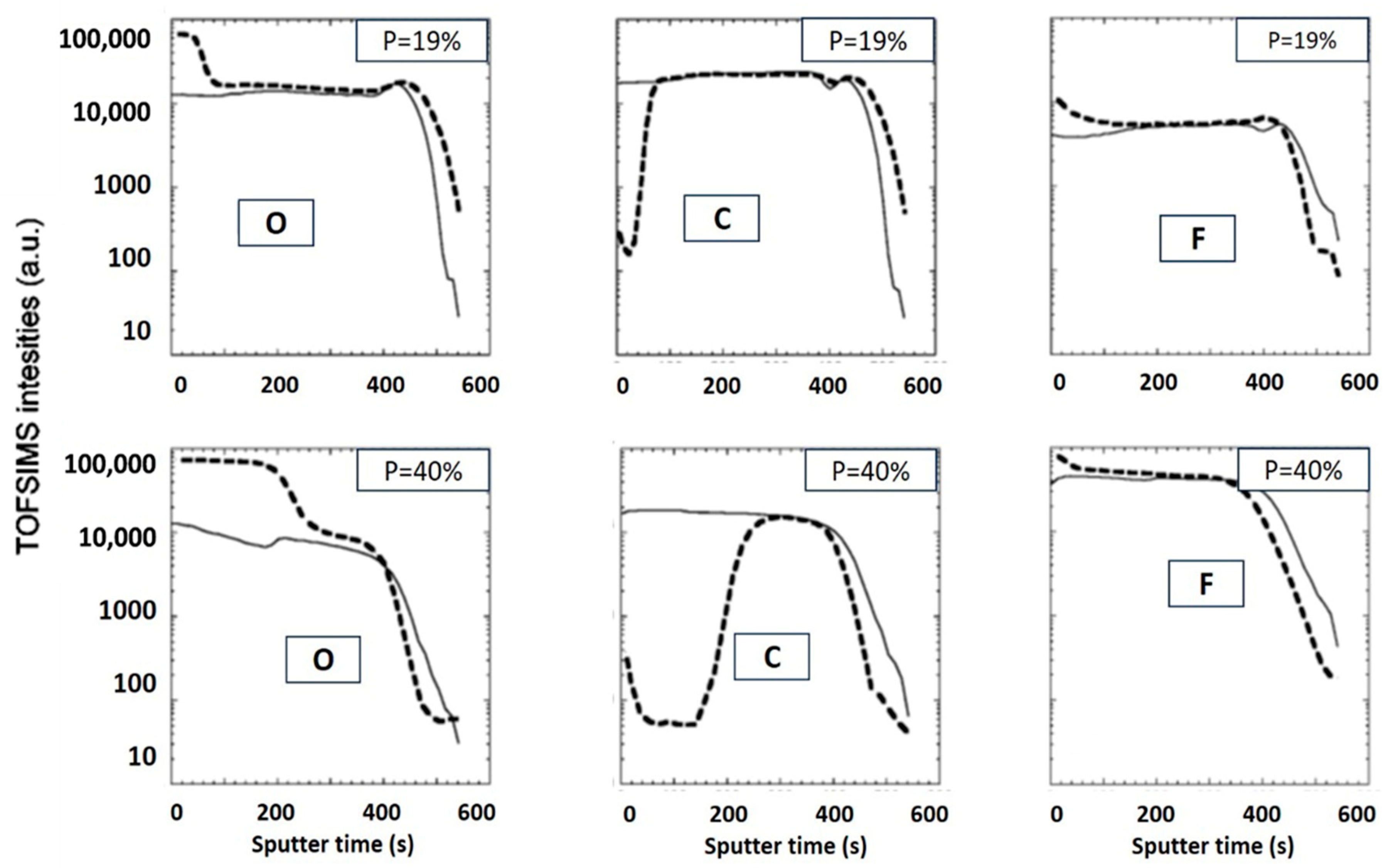
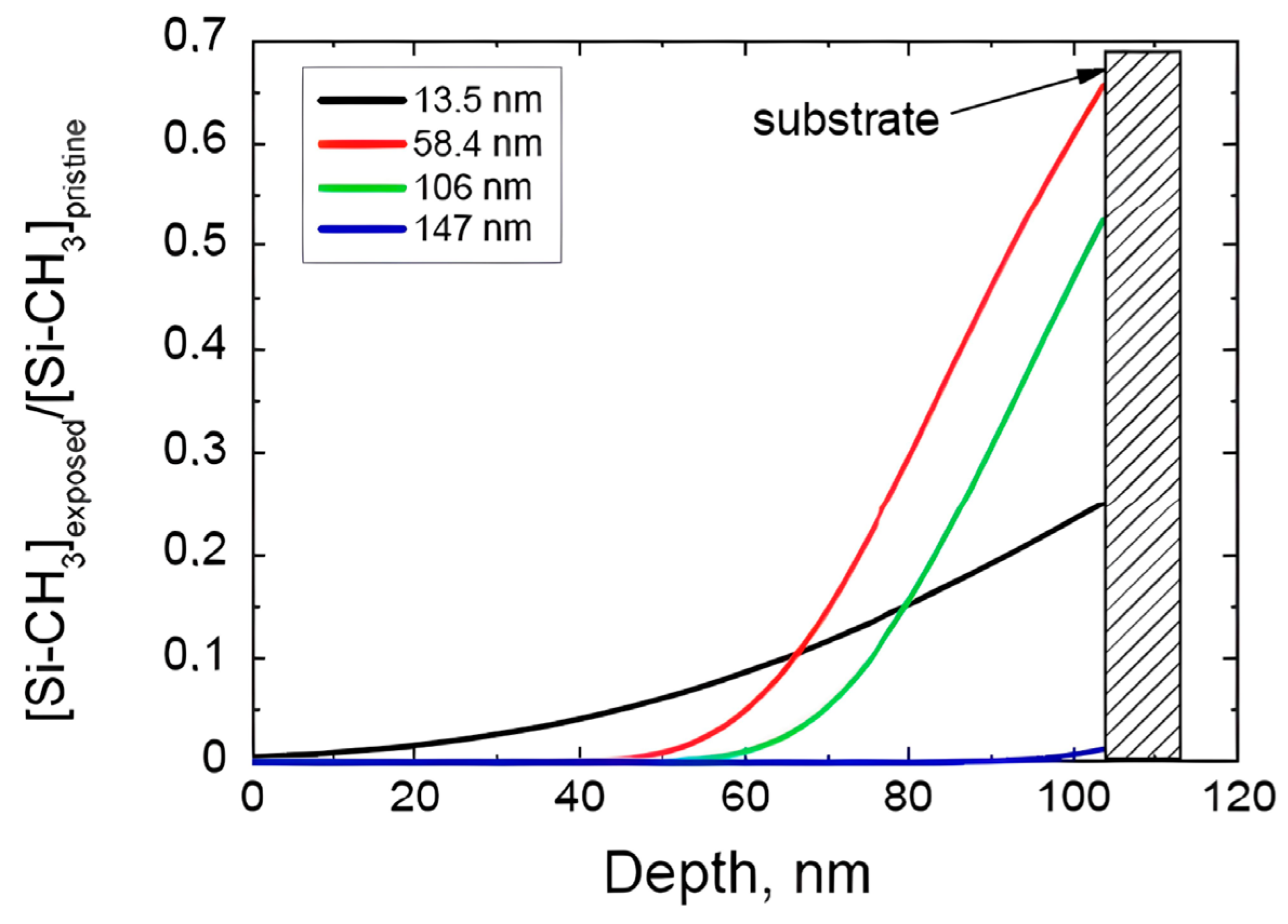
2.3. Depth Profile of Plasma-Induced Damage
2.3.1. Damage by Active Radicals
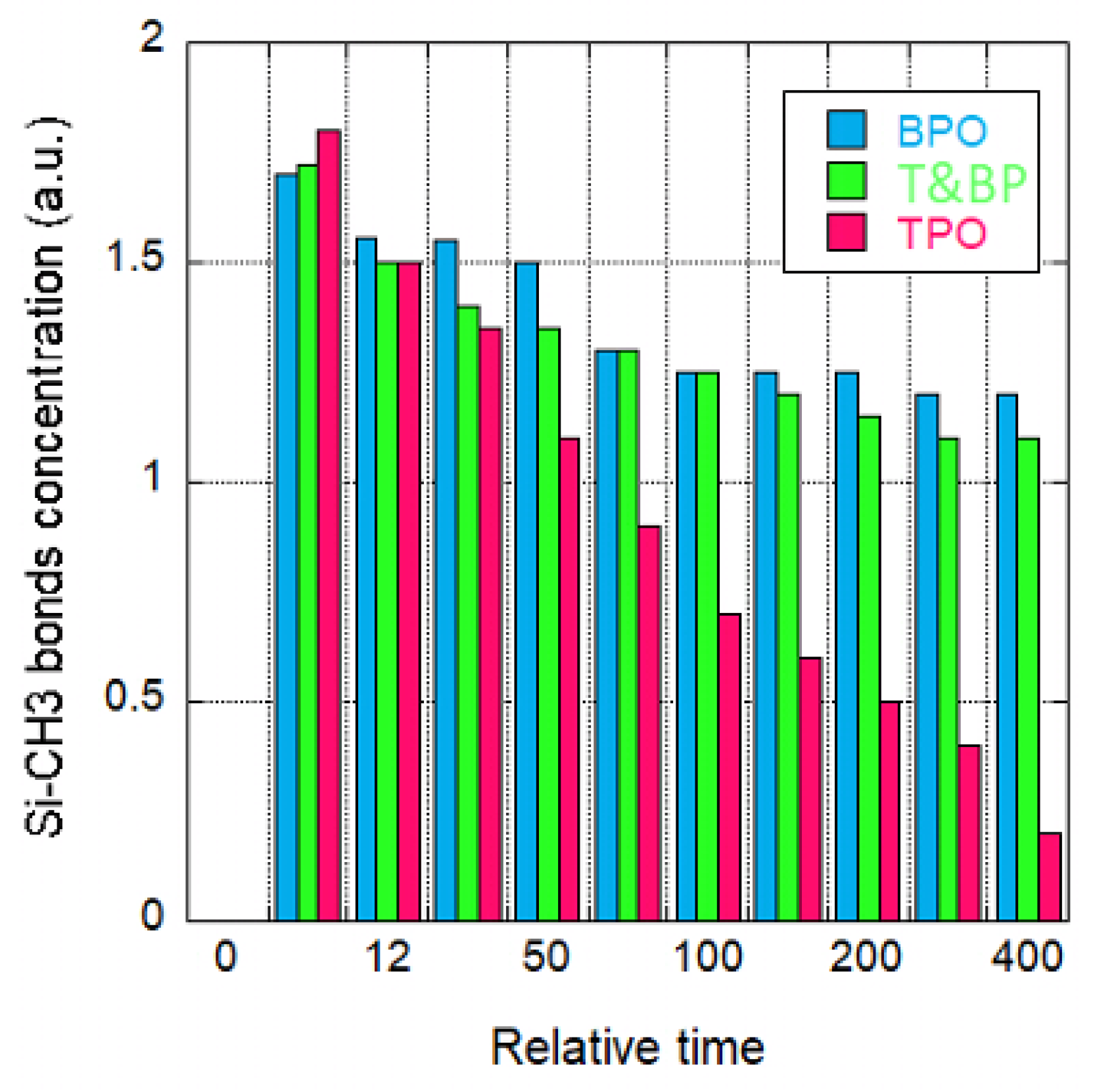
2.3.2. Damage by Ion Bombardment
- Top Power Only (TPO)—generating plasma radicals without ion bombardment;
- Bottom Power Only (BPO)—applying a bias to the bottom electrode, resulting in strong ion bombardment with minimal radical generation;
- Top and Bottom Power (T&BP)—combining both plasma radicals and ion bombardment.
2.3.3. VUV Damage
2.4. Concluding Remarks of Section 2
3. Percolation Phenomena Governing Electrical Failure in Low-k Films
3.1. General Overview of Percolation Phenomena in Porous OSG Low-k Films
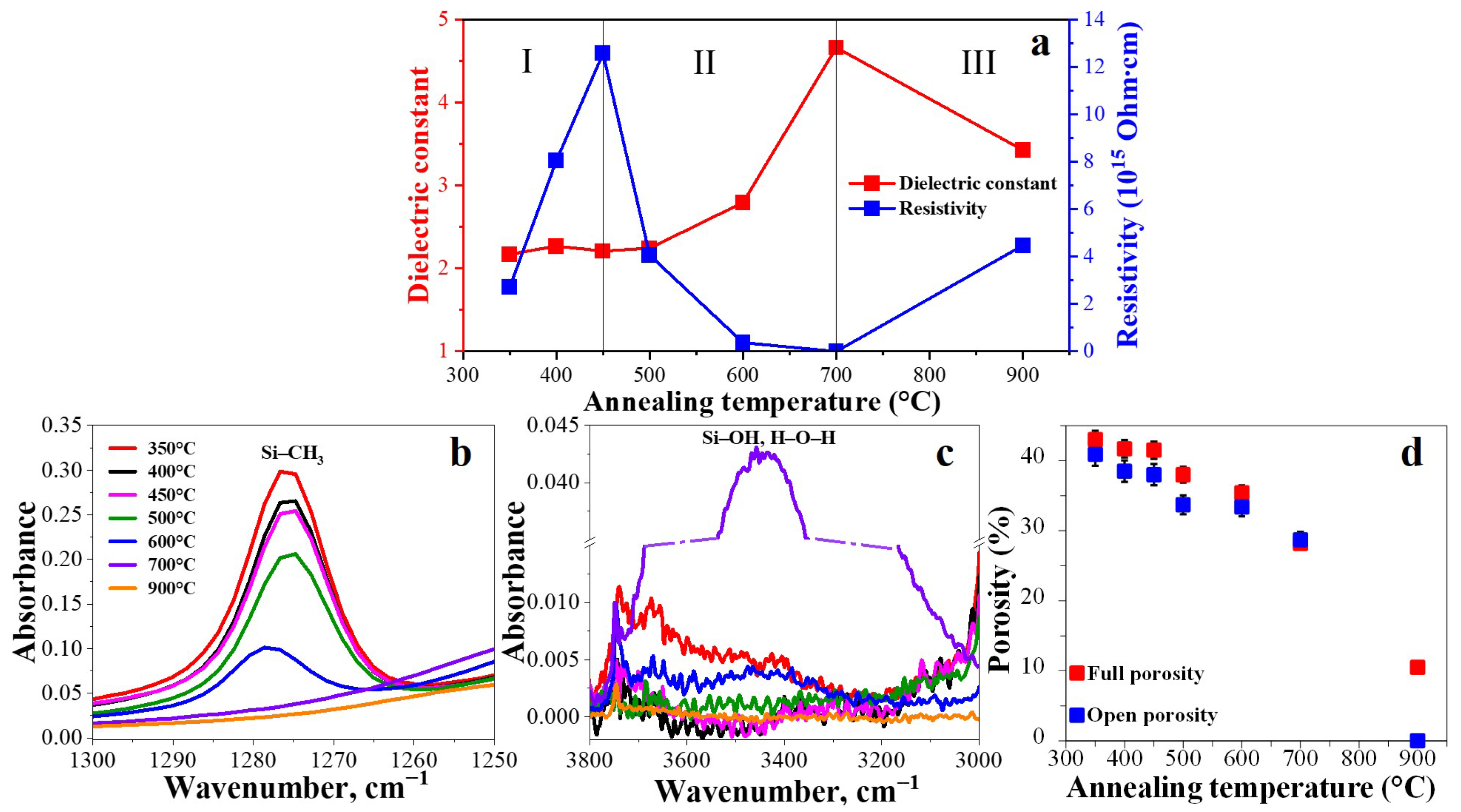
3.1.1. Dielectric Constant and Leakage Current vs. Porosity and Chemical Composition
- 350 °C–450 °C.
- 2.
- 450 °C–700 °C.
- 3.
- 700 °C–900 °C.
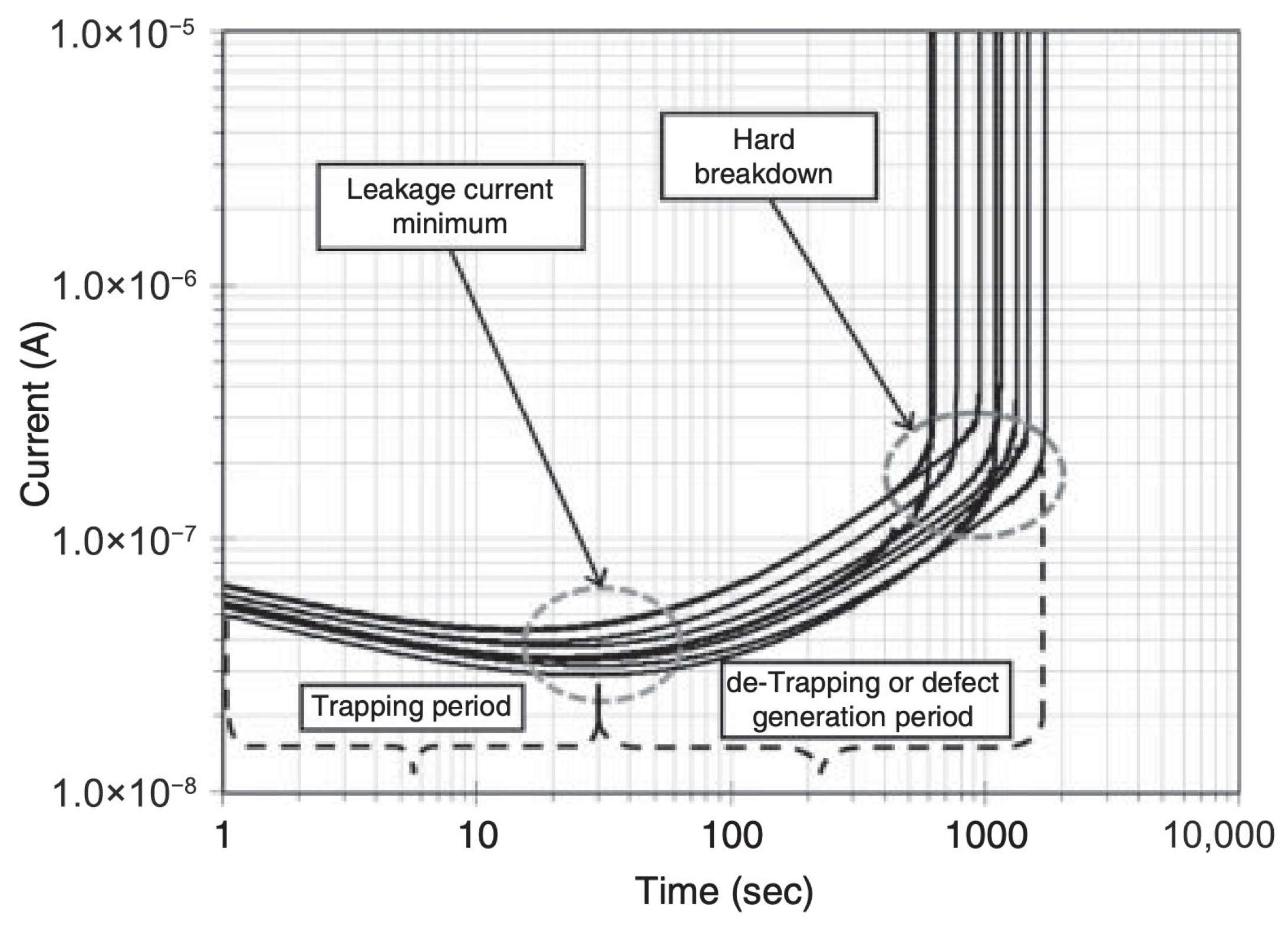
3.1.2. Leakage Current in Porous Low-k Films and Reliability
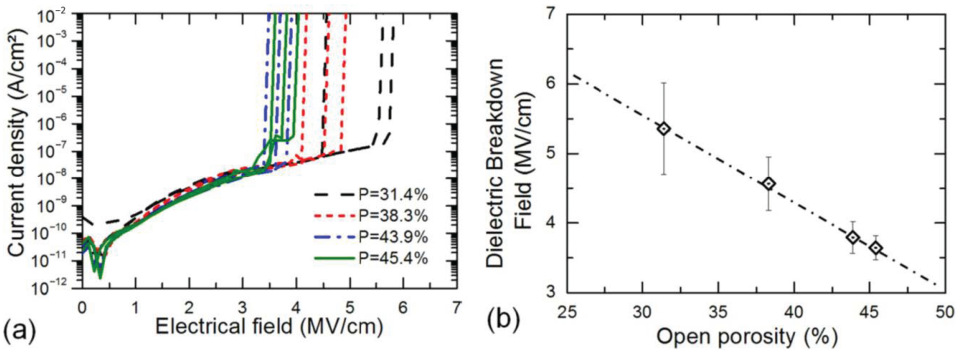
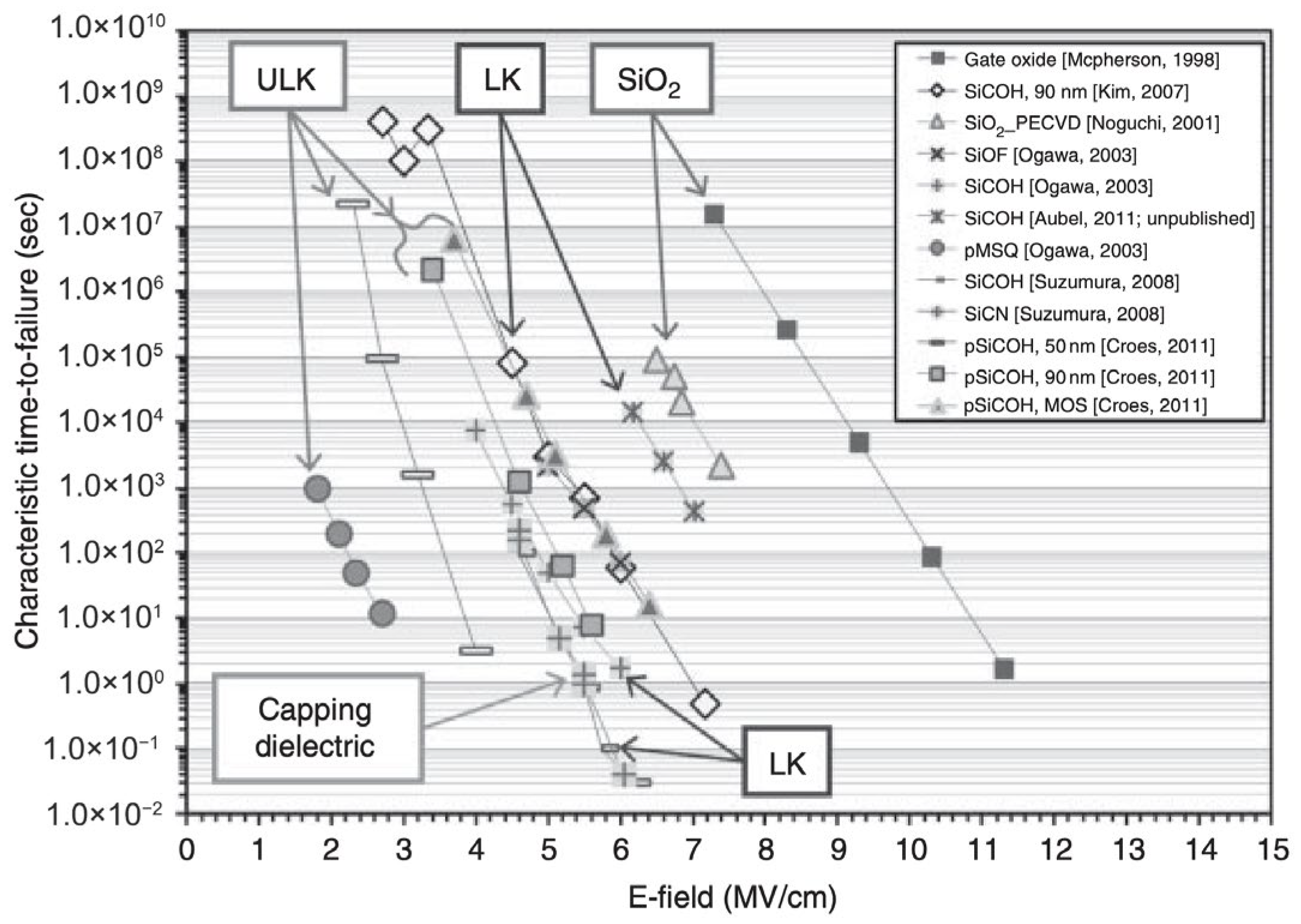
3.1.3. Breakdown Voltage
- Integration control: Pore stuffing (P4 approach) with pore protection by deposited polymers [82,83] and cryogenic etching (−100 °C), which condenses byproducts to minimize plasma damage [84], silylation passivates Si–OH traps, and stress-graded porosity design weakens field enhancement by 30%–50% [79]. These approaches collectively shift the percolation threshold, suppress defect connectivity, and restore dielectric robustness even at ULK regimes.
4. Mechanical Properties of Porous Low-k Materials
4.1. Mechanical Properties Versus Connectivity and Porosity
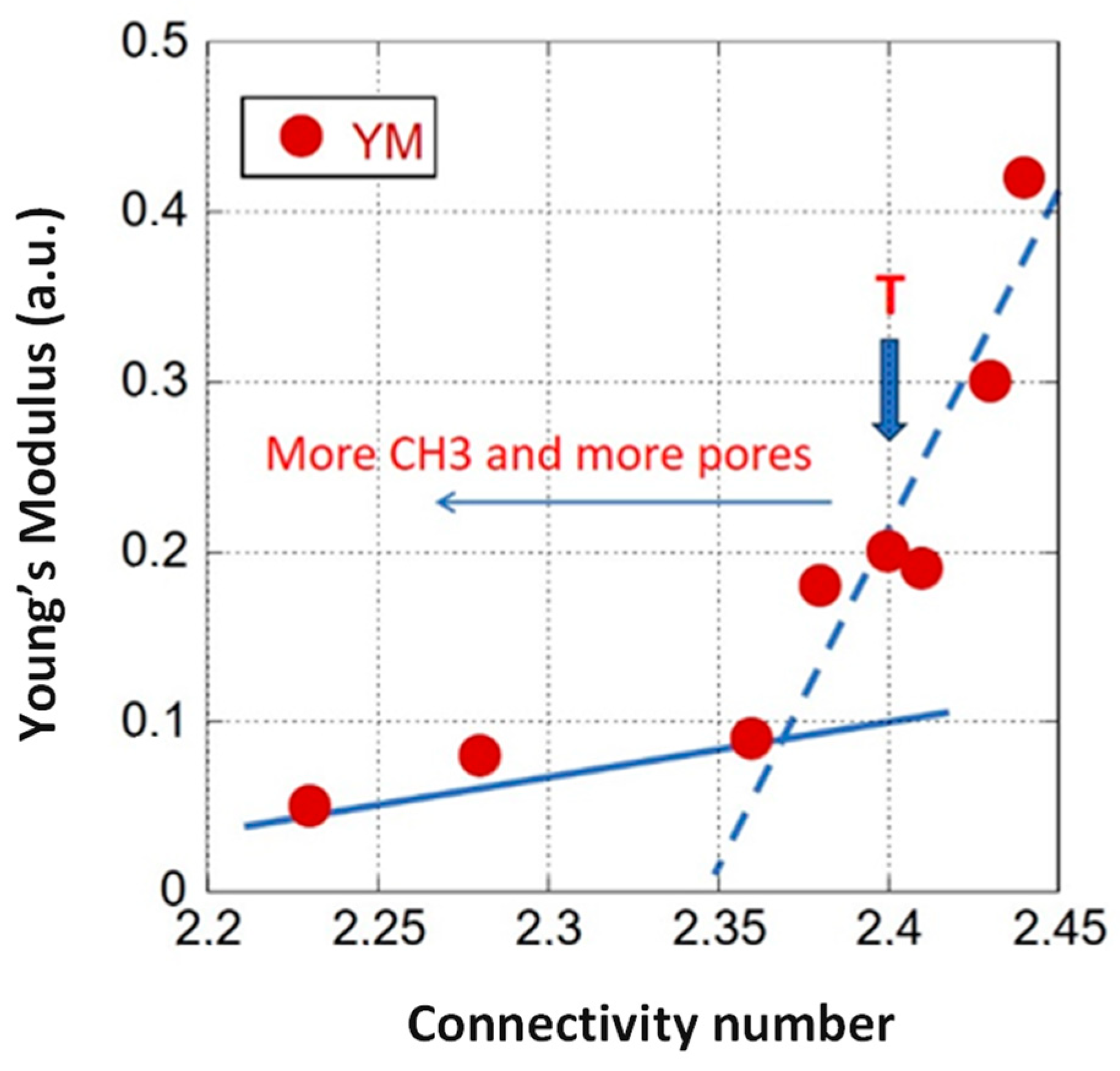
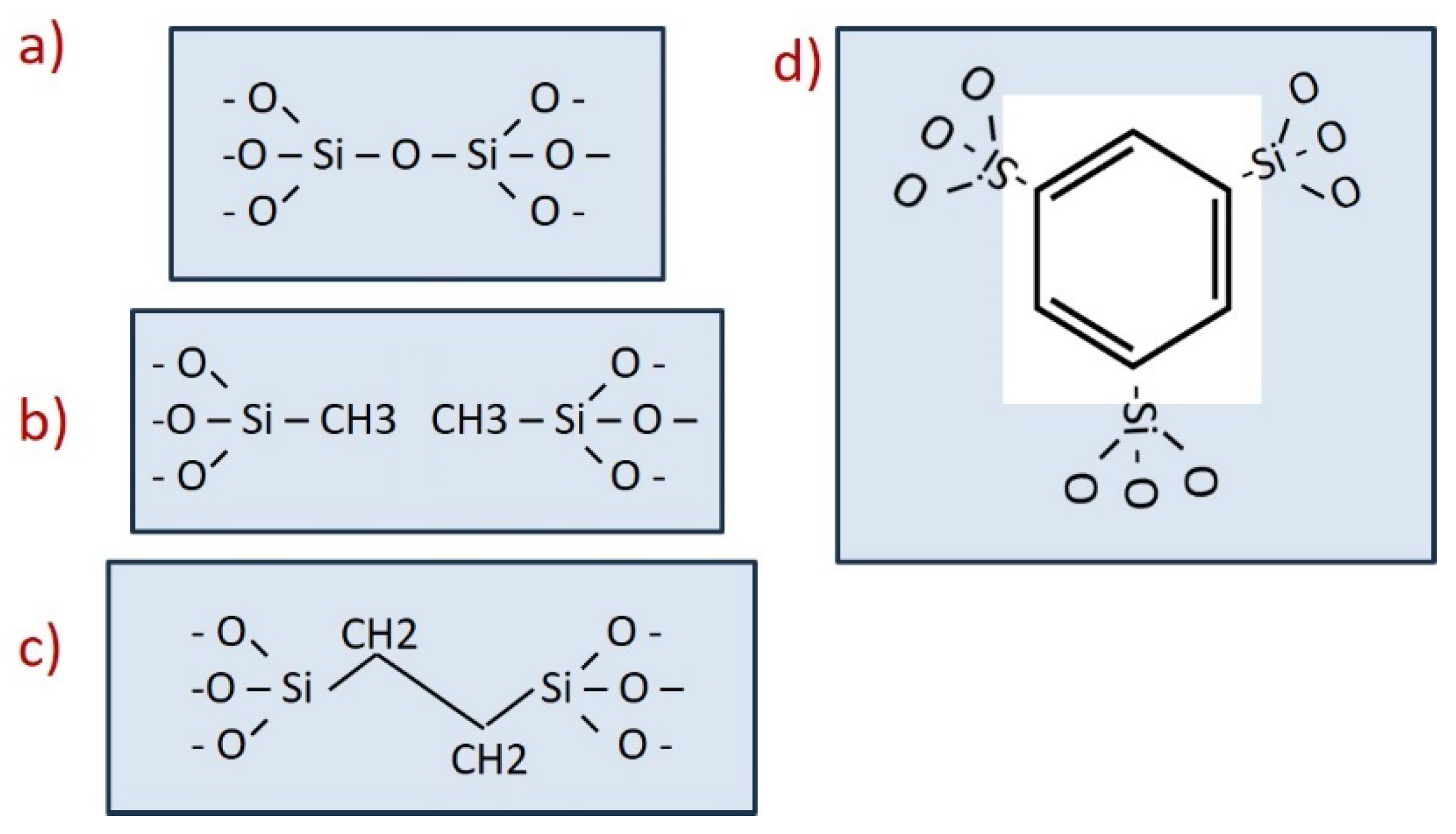
4.1.1. Mechanical Properties Versus the Matrix Connectivity (Dense OSG)
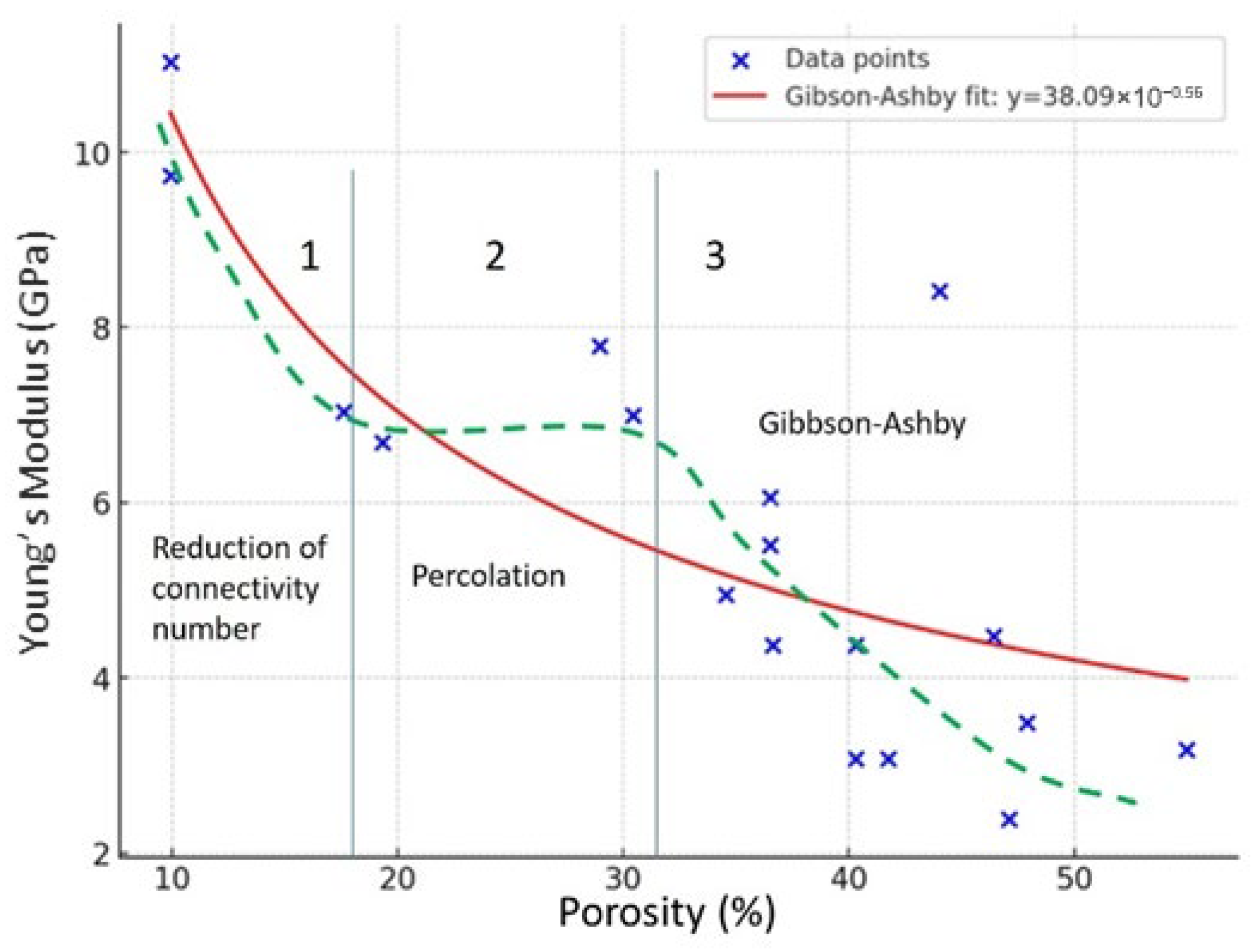
4.1.2. Mechanical Properties Versus Porosity (Porous OSG)
- E0—modulus of the dense matrix
- p—volume fraction porosity (0–1)
- n—exponent between ~2 and ~4 for silica-based films
- (a)
- Gibson–Ashby open-cell foam model (Equation (5)) [90]:
- (b)
- (c)
4.2. Stiffness Enhancement Strategies in Low-k and Hybrid Glasses
4.3. Non-Affine Deformations Control
5. Extended Summary of Experimental Trends
- Experimental Trends
- Leakage current rises sharply at relatively low porosity.
- Breakdown voltage and mechanical modulus collapse abruptly at higher porosity, typically in the range of 20%–30% (depending on pore size and connectivity), just above the percolation threshold for open pores.
- 2.
- Distinct Percolation Classes
- Transport phenomena: mass diffusion, electrical conduction, and leakage current.
- Mechanical phenomena: degradation of stiffness and strength.
- Nonlinear phenomena: dielectric breakdown.
- 3.
- Correlation Length and Timescales
- 4.
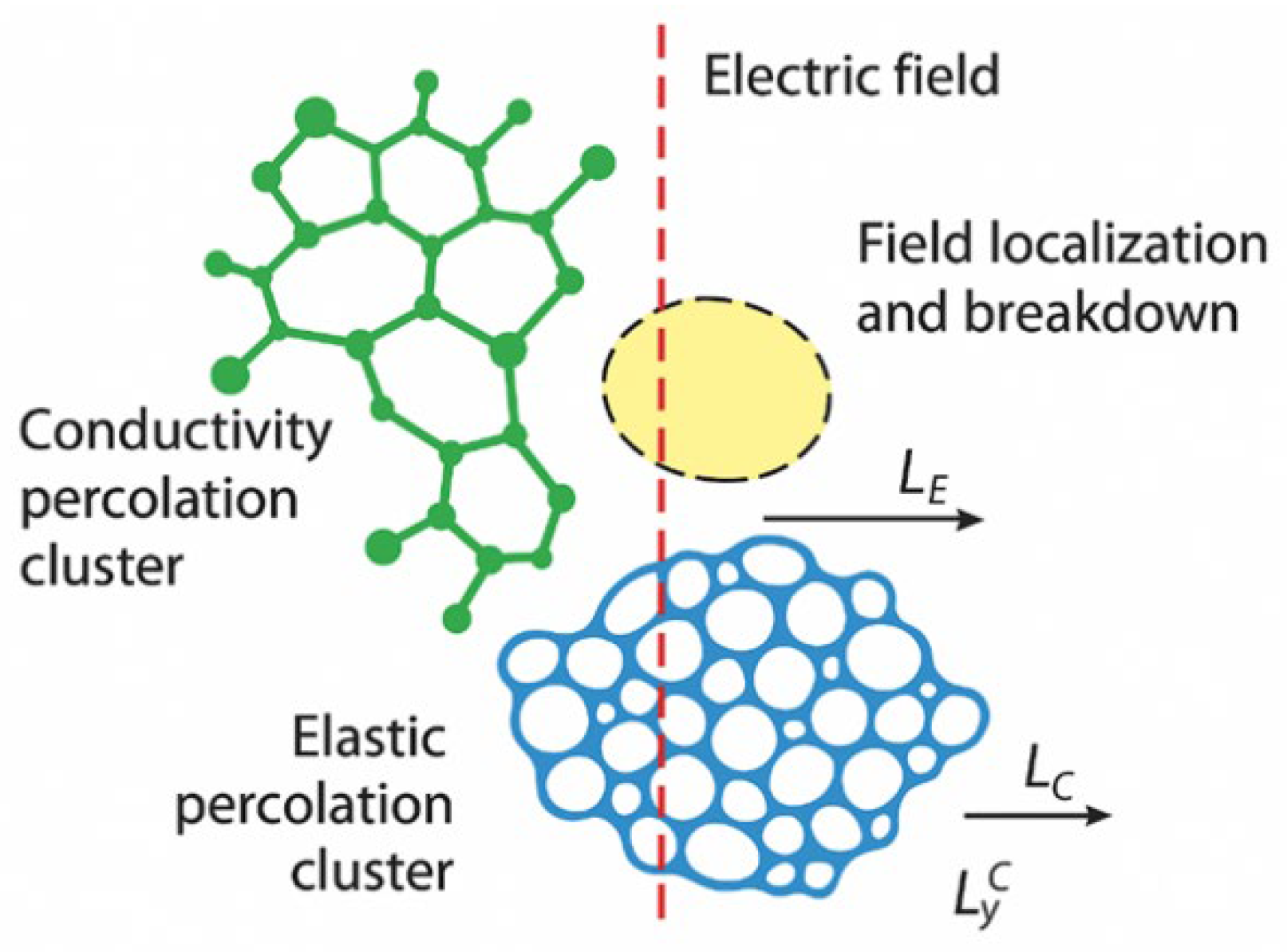
- Elastic and Breakdown Percolation
6. Conclusions
- Percolation Threshold for Leakage Current and mass transfer.
- 2.
- Percolation Threshold for Dielectric Breakdown
- local defect accumulation and hot-spot formation;
- field enhancement at pore edges;
- charge trapping;
- progressive filament growth.
- 3.
- Mechanical Percolation
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| OSG | Organosilica glass |
| ULSI | Ultra large scale integrated |
| RC | Resistance-Capacitance |
| CTE | Coefficient of thermal expansion |
| NTRS | National Technology Roadmap for Semiconductors |
| ITRS | International Technology Roadmap for Semiconductors |
| PECVD | Plasma-enhanced chemical vapor deposition |
| ULK | Ultralow-k |
| IRDS | International Roadmap of Devices and Systems |
| CMP | Chemical mechanical polishing |
| PALS | Positron annihilation lifetime spectroscopy |
| EP | Ellipsometric porosimetry |
| VUV | Vacuum ultraviolet |
| TPO | Top power only |
| BPO | Bottom power only |
| T&BP | Top and bottom power |
| PF | Poole-Frenkel |
| TDDB | Time-dependent dielectric breakdown |
| ODC | Oxygen-deficient centers |
| FSG | Fluorinated silica |
| NRA-RBS | Nuclear reaction analysis- Rutherford backscattering |
| P-MSQ | Methylsilsequioxane |
| ALD | Atomic layer deposition |
| FTIR | Fourier-transform infrared spectroscopy |
| HS | Hashin-Shtrikman |
| NI | Nanoindentation |
References
- Edelstein, D.; Heidenreich, J.; Goldblatt, R.; Cote, W.; Uzoh, C.; Lustig, N.; Roper, P.; McDevitt, T.; Motsiff, W.; Simon, A.; et al. Full copper wiring in a sub-0.25 μm CMOS ULSI technology. In Proceedings of the International Electron Devices Meeting (IEDM), Washington, DC, USA, 7–10 December 1997; pp. 773–776. [Google Scholar] [CrossRef]
- Andricacos, P.C.; Uzoh, C.; Dukovic, J.O.; Horkans, J.; Deligianni, H. Damascene copper electroplating for chip interconnections. IBM J. Res. Dev. 1998, 42, 567–574. [Google Scholar] [CrossRef]
- Havemann, R.H.; Hutchby, J.A. High-performance interconnects: An integration overview. Proc. IEEE 2001, 89, 586–601. [Google Scholar] [CrossRef]
- Ravindra, N.M. International Technology Roadmap for Semiconductors (ITRS). J. Electron. Mater. 2001, 30, 1478–1627. [Google Scholar]
- Ryan, E.T.; McKerrow, A.J.; Leu, J.; Ho, P.S. Materials issues and characterization of low-k dielectric materials. MRS Bull. 1997, 22, 49–54. [Google Scholar] [CrossRef]
- Harper, C. Electronic Packaging and Interconnection Handbook, 4th ed.; McGraw-Hill: New York, NY, USA, 2004. [Google Scholar]
- Ryan, E.T.; McKerrow, A.J.; Leu, J.; Ho, P.S. Materials issues and characterization of low-k dielectric materials. In Low Dielectric Constant Materials for IC Applications; Springer: Berlin/Heidelberg, Germany, 2003; pp. 23–74. [Google Scholar] [CrossRef]
- Hatton, B.D.; Landskron, K.; Hunks, W.J.; Bennett, M.R.; Shukaris, D.; Perovic, D.D.; Ozin, G.A. Materials chemistry for low-k materials. Mater. Today 2006, 9, 22–31. [Google Scholar] [CrossRef]
- Hong, N.; Zhang, Y.; Sun, Q.; Fan, W.; Li, M.; Xie, M.; Fu, W. The evolution of organosilicon precursors for low-k interlayer dielectric fabrication driven by integration challenges. Materials 2021, 14, 4827. [Google Scholar] [CrossRef]
- International Roadmap for Devices and Systems (IRDS). 2024 Update: More Moore; IEEE: Piscataway, NJ, USA, 2024; Available online: https://irds.ieee.org/images/files/pdf/2024/2024IRDS_MM.pdf (accessed on 25 August 2025).
- Baklanov, M.R.; Adelmann, C.; Zhao, L.; De Gendt, S. Advanced Interconnects: Materials, Processing, and Reliability. ECS J. Solid State Sci. Technol. 2015, 4, Y1–Y4. [Google Scholar] [CrossRef]
- Nakata, Y.; Ozaki, S.; Kudo, H. Multilevel interconnect technology for 45-nm node CMOS LSIs. Fujitsu Sci. Tech. J. 2010, 46, 120–127. [Google Scholar]
- Baklanov, M.R.; de Marneffe, J.F.; Shamiryan, D.; Urbanowicz, A.M.; Shi, H.; Rakhimova, T.V.; Huang, H.; Ho, P.S. Plasma processing of low-k dielectrics. J. Appl. Phys. 2013, 113, 041101. [Google Scholar] [CrossRef]
- Soulié, J.P.; Sankaran, K.; Van Troeye, B.; Leśniewska, A.; Pedreira, O.V.; Oprins, H.; Delie, G.; Fleischmann, C.; Boakes, L.; Rolin, C.; et al. Selecting Alternative Metals for Advanced Interconnects. J. Appl. Phys. 2024, 136, 171101. [Google Scholar] [CrossRef]
- Dull, T.L.; Frieze, W.E.; Gidley, D.W.; Sun, J.N.; Yee, A.F. Determination of pore size in mesoporous thin films from the annihilation lifetime of positronium. J. Phys. Chem. B 2001, 105, 4657–4662. [Google Scholar] [CrossRef]
- Baklanov, B.M.; Mogilnikov, K.P.; Polovinkin, V.G.; Dultsev, F.N. Determination of pore size distribution in thin films by el-lipsometric porosimetry. J. Vac. Sci. Technol. 2000, 18, 1385–1391. [Google Scholar] [CrossRef]
- Foran, B.J.; Kastenmeier, B.; Bright, D.S. Determination of pore-size distributions in low-k dielectric films by transmission electron microscopy. AIP Conf. Proc. 2003, 683, 556–561. [Google Scholar] [CrossRef]
- Sekhar, V.N. Mechanical characterization of black diamond (low-k) structures for 3D integrated circuit and packaging applications. In Nanoindentation in Materials Science; IntechOpen: London, UK, 2012. [Google Scholar] [CrossRef]
- Baklanov, M.; Ho, P.S.; Zschech, E. (Eds.) Advanced Interconnects for ULSI Technology; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Kresge, A.C.; Leonowicz, M.E.; Roth, W.J.; Vartuli, J.C.; Beck, J.S. Ordered mesoporous molecular sieves synthesized by a liquid-crystal template mechanism. Nature 1992, 359, 710–712. [Google Scholar] [CrossRef]
- Grill, A.; Perraud, L.; Patel, V.; Jahnes, C.; Cohen, S. Low dielectric constant SiCOH films as potential candidates for interconnect dielectrics. MRS Proc. 1999, 565, 107–116. [Google Scholar] [CrossRef]
- Grill, A. PECVD low and ultralow dielectric constant materials: From invention and research to products. J. Vac. Sci. Technol. B 2016, 34, 020801. [Google Scholar] [CrossRef]
- Iacopi, F.; Travaly, Y.; Eyckens, B.; Waldfried, C.; Abell, T.; Guyer, E.P.; Gage, D.M.; Dauskardt, R.H.; Sajavaara, T.; Houthoofd, K.; et al. Short-ranged structural rearrangement and enhancement of mechanical properties of organosilicate glasses induced by ultraviolet radiation. J. Appl. Phys. 2006, 99, 053511. [Google Scholar] [CrossRef]
- Baklanov, M.R.; Jousseaume, V.; Rakhimova, T.V.; Lopaev, D.V.; Mankelevich, Y.A.; Afanas’ev, V.V.; Shohet, J.L.; King, S.W.; Ryan, E.T. Impact of VUV photons on SiO2 and organosilicate low-k dielectrics: General behavior, practical applications, and atomic models. Appl. Phys. Rev. 2019, 6, 011301. [Google Scholar] [CrossRef]
- Chang, T.C.; Tsai, T.M.; Liu, P.T.; Chen, C.W.; Tseng, T.Y. Study on the effect of electron beam curing on low-k porous organosilicate glass (OSG) material. Thin Solid Films 2004, 469, 383–387. [Google Scholar] [CrossRef]
- Cho, S.M.; Papasouliotis, G.D.; Barnes, M. Method for Porogen Removal and Mechanical Strength Enhancement of Low-k Carbon Doped Silicon Oxide Using Low Thermal Budget Microwave Curing. U.S. Patent 7,892,985, 22 February 2011. [Google Scholar]
- Nguyen, P.T.; Fan, C.; Do, D.D.; Nicholson, D. On the cavitation-like pore blocking in ink-bottle pore: Evolution of hysteresis loop with neck size. J. Phys. Chem. C 2013, 117, 5475–5484. [Google Scholar] [CrossRef]
- Taylor, D.J.; Fleig, P.F.; Hietala, S.L. Technique for characterization of thin film porosity. Thin Solid Films 1998, 332, 257–261. [Google Scholar] [CrossRef]
- Furedi, M.; Manzano, C.V.; Marton, A.; Fodor, B.; Alvarez-Fernandez, A.; Guldin, S. Beyond the meso/macroporous boundary: Extending capillary condensation-based pore size characterization in thin films through tailored adsorptives. J. Phys. Chem. Lett. 2024, 15, 1420–1427. [Google Scholar] [CrossRef] [PubMed]
- Stassin, T.; Verbeke, R.; Cruz, A.J.; Rodríguez-Hermida, S.; Stassen, I.; Marreiros, J.; Krishtab, M.; Dickmann, M.; Egger, W.; Vankelecom, I.F.J.; et al. Porosimetry for thin films of metal–organic frameworks: A comparison of positron annihilation lifetime spectroscopy and adsorption-based methods. Adv. Mater. 2021, 33, 2006993. [Google Scholar] [CrossRef]
- Yim, J.H.; Seon, J.B.; Jeong, H.D.; Pu, L.S.; Baklanov, M.R.; Gidley, D.W. Morphological control of nanoporous films by the use of functionalized cyclodextrins as porogens. Adv. Funct. Mater. 2004, 14, 277–282. [Google Scholar] [CrossRef]
- Alvarez-Fernandez, A.; Reid, B.; Fornerod, M.J.; Taylor, A.; Divitini, G.; Guldin, S. Structural characterization of mesoporous thin film architectures: A tutorial overview. ACS Appl. Mater. Interfaces 2020, 12, 5195–5208. [Google Scholar] [CrossRef]
- Rasadujjaman, M.; Wang, Y.; Zhang, L.; Naumov, S.; Attallah, A.G.; Liedke, M.O.; Koehler, N.; Redzheb, M.; Vishnevskiy, A.S.; Seregin, D.S.; et al. A detailed ellipsometric porosimetry and positron annihilation spectroscopy study of porous organosilicate-glass films with various ratios of methyl terminal and ethylene bridging groups. Microporous Mesoporous Mater. 2020, 306, 110434. [Google Scholar] [CrossRef]
- Lépinay, M.; Djourelov, N.; Marinov, H.; Broussous, L.; Courouble, K.; Licitra, C.; Bertin, F.; Rouessac, V.; Ayral, A. Depth-resolved impact of integration process on porosity and solvent diffusion in a SiOCH low-k material. J. Porous Mater. 2014, 21, 475–484. [Google Scholar] [CrossRef]
- Vanstreels, K.; Wu, C.; Gonzalez, M.; Schneider, D.; Gidley, D.; Verdonck, P.; Baklanov, M.R. Effect of pore structure of nanometer scale porous films on the measured elastic modulus. Langmuir 2013, 29, 12025–12035. [Google Scholar] [CrossRef]
- Ben-Avraham, D. Diffusion and Reactions in Fractals and Disordered Systems; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Liu, L.; Zheng, L.; Chen, Y. Macroscopic and microscopic anomalous diffusion in comb model with fractional dual-phase-lag model. Appl. Math. Model. 2018, 62, 629–637. [Google Scholar] [CrossRef]
- Goworek, T.; Ciesielski, K.; Jasińska, B.; Wawryszczuk, J. Positronium in large voids. Silicagel. Chem. Phys. Lett. 1997, 272, 91–95. [Google Scholar] [CrossRef]
- Kunnen, E.; Baklanov, M.R.; Franquet, A.; Shamiryan, D.; Rakhimova, T.V.; Urbanowicz, A.M.; Struyf, H.; Boullart, W. Effect of energetic ions on plasma damage of porous SiCOH low-k materials. J. Vac. Sci. Technol. B 2010, 28, 450–459. [Google Scholar] [CrossRef]
- Shamiryan, D.; Baklanov, M.R.; Vanhaelemeersch, S.; Maex, K. Comparative study of SiOCH low-k films with varied porosity interacting with etching and cleaning plasma. J. Vac. Sci. Technol. B 2002, 20, 1923–1928. [Google Scholar] [CrossRef]
- Shi, H.; Huang, H.; Bao, J.; Liu, J.; Ho, P.S.; Zhou, Y.; Pender, J.T.; Armacost, M.D.; Kyser, D. Role of ions, photons, and radicals in inducing plasma damage to ultra low-k dielectrics. J. Vac. Sci. Technol. B 2012, 30, 011206. [Google Scholar] [CrossRef]
- Uchida, S.; Takashima, S.; Hori, M.; Fukasawa, M.; Ohshima, K.; Nagahata, K.; Tatsumi, T. Plasma damage mechanisms for low-k porous SiOCH films due to radiation, radicals, and ions in the plasma etching process. J. Appl. Phys. 2008, 103, 073303. [Google Scholar] [CrossRef]
- Takeda, K.; Miyawaki, Y.; Takashima, S.; Fukasawa, M.; Oshima, K.; Nagahata, K.; Tatsumi, T.; Hori, M. Mechanism of plasma-induced damage to low-k SiOCH films during plasma ashing of organic resists. J. Appl. Phys. 2011, 109, 033303. [Google Scholar] [CrossRef]
- Rakhimova, T.V.; Rakhimov, A.T.; Mankelevich, Y.A.; Lopaev, D.V.; Kovalev, A.S.; Vasil’eva, A.N.; Zyryanov, S.M.; Kurchikov, K.; Proshina, O.V.; Voloshin, D.G.; et al. Low-k films modification under EUV and VUV radiation. J. Phys. D Appl. Phys. 2013, 47, 025102. [Google Scholar] [CrossRef]
- Nichols, M.T.; Sinha, H.; Wiltbank, C.A.; Antonelli, G.A.; Nishi, Y.; Shohet, J.L. Time-dependent dielectric breakdown of plasma-exposed porous organosilicate glass. Appl. Phys. Lett. 2012, 100, 112905. [Google Scholar] [CrossRef]
- Nichols, M.T.; Mavrakakis, K.; Lin, Q.; Shohet, J.L. The effects of plasma exposure and vacuum ultraviolet irradiation on photopatternable low-k dielectric materials. J. Appl. Phys. 2013, 114, 104107. [Google Scholar] [CrossRef]
- Ren, H.; Nichols, M.T.; Jiang, G.; Antonelli, G.A.; Nishi, Y.; Shohet, J.L. Defects in low-k organosilicate glass and their response to processing as measured with electron-spin resonance. Appl. Phys. Lett. 2011, 98, 102903. [Google Scholar] [CrossRef]
- Bittel, B.C.; Lenahan, P.M.; King, S.W. Ultraviolet radiation effects on paramagnetic defects in low-k dielectrics for ultralarge scale integrated circuit interconnects. Appl. Phys. Lett. 2010, 97, 063506. [Google Scholar] [CrossRef]
- Sinha, H.; Ren, H.; Nichols, M.T.; Lauer, J.L.; Tomoyasu, M.; Russell, N.M.; Jiang, G.; Antonelli, G.A.; Fuller, N.C.; Engelmann, S.U.; et al. The effects of vacuum ultraviolet radiation on low-k dielectric films. J. Appl. Phys. 2012, 112, 111101. [Google Scholar] [CrossRef]
- Ogawa, E.T.; Aubel, O. Electrical breakdown in advanced interconnect dielectrics. In Advanced Interconnects for ULSI Technology; Baklanov, M., Ho, P.S., Zschech, E., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2012; pp. 369–434. [Google Scholar] [CrossRef]
- Y Barbarin, Y.; Croes, K.; Roussel, P.J.; Li, Y.; Verdonck, P.; Baklanov, M.; Tokei, Z.; Zhao, L. Reliability characteristics of thin porous low-k silica-based interconnect dielectrics. In Proceedings of the 2013 IEEE International Reliability Physics Symposium (IRPS), Monterey, CA, USA, 14–18 April 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 2F.3.1–2F.3.6. [Google Scholar] [CrossRef]
- Wu, C.; Li, Y.; Baklanov, M.R.; Croes, K. Electrical reliability challenges of advanced low-k dielectrics. ECS J. Solid State Sci. Technol. 2014, 4, N3065–N3070. [Google Scholar] [CrossRef]
- Suzumura, N.; Yamamoto, S.; Kodama, D.; Makabe, K.; Komori, J.; Murakami, E.; Maegawa, S.; Kubota, K. A new TDDB degradation model based on Cu ion drift in Cu interconnect dielectrics. In Proceedings of the 2006 IEEE International Reliability Physics Symposium, San Jose, CA, USA, 26–30 March 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 484–489. [Google Scholar] [CrossRef]
- Tokei, Z.; Sutcliffe, V.; Demuynck, S.; Iacopi, F.; Roussel, P.; Beyer, G.P.; Hoofman, R.J.O.M.; Maex, K. Impact of the barrier/dielectric interface quality on reliability of Cu porous-low-k interconnects. In Proceedings of the 2004 IEEE International Reliability Physics Symposium, Phoenix, AZ, USA, 25–29 April 2004; IEEE: Piscataway, NJ, USA, 2004; pp. 326–332. [Google Scholar] [CrossRef]
- Baklanov, M.R.; Gismatulin, A.A.; Naumov, S.; Perevalov, T.V.; Gritsenko, V.A.; Vishnevskiy, A.S.; Rakhimova, T.V.; Vorotilov, K.A. Comprehensive Review on the Impact of Chemical Composition, Plasma Treatment, and Vacuum Ultraviolet (VUV) Irradiation on the Electrical Properties of Organosilicate Films. Polymers 2024, 16, 2230. [Google Scholar] [CrossRef]
- Agmon, N. The Grotthuss mechanism. Chem. Phys. Lett. 1995, 244, 456–462. [Google Scholar] [CrossRef]
- King, S.W.; Bielefeld, J.; Xu, G.; Lanford, W.A.; Matsuda, Y.; Dauskardt, R.H.; Kim, N.; Hondongwa, D.; Olasov, L.; Daly, B.; et al. Influence of network bond percolation on the thermal, mechanical, electrical and optical properties of high and low-k a-SiC:H thin films. J. Non-Cryst. Solids 2013, 379, 67–79. [Google Scholar] [CrossRef]
- Gerelt-Od, M.; Kolesnikova, T.G.; Mokrushev, P.A.; Vishnevskiy, A.S.; Vorotilov, K.A.; Gismatulin, A.A.; Gritsenko, V.A.; Baklanov, M.R. Exploring the relationship between electrical characteristics and changes in chemical composition and structure of OSG low-k films under thermal annealing. Coatings 2024, 14, 1412. [Google Scholar] [CrossRef]
- Zheng, H.; Guo, X.; Pei, D.; Ryan, E.T.; Nishi, Y.; Shohet, J.L. Effects of vacuum ultraviolet irradiation on trapped charges and leakage currents of low-k organosilicate dielectrics. Appl. Phys. Lett. 2015, 106, 192902. [Google Scholar] [CrossRef]
- Ren, H.; Jiang, G.; Antonelli, G.A.; Nishi, Y.; Shohet, J.L. The nature of the defects generated from plasma exposure in pristine and ultraviolet-cured low-k organosilicate glass. Appl. Phys. Lett. 2011, 98, 251906. [Google Scholar] [CrossRef]
- Vanstreels, K.; Ciofi, I.; Barbarin, Y.; Baklanov, M.R. Influence of porosity on dielectric breakdown of ultralow-k dielectrics. J. Vac. Sci. Technol. B 2013, 31, 051202. [Google Scholar] [CrossRef]
- Urbanowicz, A.M.; Vanstreels, K.; Verdonck, P.; Shamiryan, D.; De Gendt, S.; Baklanov, M.R. Improving mechanical robustness of ultralow-k SiOCH plasma enhanced chemical vapor deposition glasses by controlled porogen decomposition prior to UV-hardening. J. Appl. Phys. 2010, 107, 104104. [Google Scholar] [CrossRef]
- Ogawa, E.T.; Kim, J.; Haase, G.S.; Mogul, H.C.; McPherson, J.W. Leakage, breakdown, and TDDB characteristics of porous low-k silica-based interconnect dielectrics. In Proceedings of the 2003 IEEE International Reliability Physics Symposium Proceedings, 41st Annual, Dallas, TX, USA, 30 March–4 April 2003; IEEE: Piscataway, NJ, USA, 2003; pp. 166–172. [Google Scholar] [CrossRef]
- Lee, S.C.; Oates, A.S. Reliability limitations to the scaling of porous low-k dielectrics. In Proceedings of the 2011 International Reliability Physics Symposium, Monterey, CA, USA, 10–14 April 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 2F.5.1–2F.5.5. [Google Scholar] [CrossRef]
- Li, Y.; Ciofi, I.; Carbonell, L.; Heylen, N.; Van Aelst, J.; Baklanov, M.R.; Groeseneken, G.; Maex, K.; Tőkei, Z. Influence of absorbed water components on SiOCH low-k reliability. J. Appl. Phys. 2008, 104, 034104. [Google Scholar] [CrossRef]
- Jinnai, B.; Nozawa, T.; Samukawa, S. Damage mechanism in low-dielectric (low-k) films during plasma processes. J. Vac. Sci. Technol. B 2008, 26, 1926–1932. [Google Scholar] [CrossRef]
- Van Besien, E.; Pantouvaki, M.; Zhao, L.; De Roest, D.; Baklanov, M.R.; Tőkei, Z.; Beyer, G. Influence of porosity on electrical properties of low-k dielectrics. Microelectron. Eng. 2012, 92, 59–61. [Google Scholar] [CrossRef]
- Hong, C.; Milor, L. Effect of porosity on charge transport in porous ultra-low-k dielectrics. In Proceedings of the 2006 International Interconnect Technology Conference, Burlingame, CA, USA, 5–7 June 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 140–142. [Google Scholar] [CrossRef]
- Lloyd, J.R.; Murray, C.E.; Ponoth, S.; Cohen, S.; Liniger, E. The effect of Cu diffusion on the TDDB behavior in low-k interlevel dielectrics. Microelectron. Reliab. 2006, 46, 1643–1647. [Google Scholar] [CrossRef]
- Michelon, J.; Hoofman, R.J. Moisture influence on porous low-k reliability. IEEE Trans. Device Mater. Reliab. 2006, 6, 169–174. [Google Scholar] [CrossRef]
- Lee, S.C.; Oates, A.S.; Chang, K.M. Fundamental understanding of porous low-k dielectric breakdown. In Proceedings of the 2009 IEEE International Reliability Physics Symposium, Montreal, QC, Canada, 26–30 April 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 481–485. [Google Scholar] [CrossRef]
- Miyazaki, H.; Kodama, D.; Suzumura, N. The observation of stress-induced leakage current of damascene interconnects after bias temperature aging. In Proceedings of the 2008 IEEE International Reliability Physics Symposium, Phoenix, AZ, USA, 27 April–1 May 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 150–157. [Google Scholar] [CrossRef]
- Wu, C.; Li, Y.; Barbarin, Y.; Ciofi, I.; Croes, K.; Bömmels, J.; De Wolf, I.; Tőkei, Z. Correlation between field dependent electrical conduction and dielectric breakdown in a SiCOH based low-k (k = 2.0) dielectric. Appl. Phys. Lett. 2013, 103, 032902. [Google Scholar] [CrossRef]
- Wu, E.Y.; Vollertsen, R.P. On the Weibull shape factor of intrinsic breakdown of dielectric films and its accurate experimental determination. Part I: Theory, methodology, experimental techniques. IEEE Trans. Electron Devices 2003, 49, 2131–2140. [Google Scholar] [CrossRef]
- Ogawa, E.T.; McPherson, J.W.; Rosal, J.A.; Dickerson, K.J.; Chiu, T.C.; Tsung, L.Y.; Jain, M.K.; Bonifield, T.D.; Ondrusek, J.C.; McKee, W.R. Stress-induced voiding under vias connected to wide Cu metal leads. In Proceedings of the 2002 IEEE International Reliability Physics Symposium, Dallas, TX, USA, 7–11 April 2002; Proceedings, 40th Annual (Cat. No. 02CH37320). IEEE: Piscataway, NJ, USA, 2002; pp. 312–321. [Google Scholar] [CrossRef]
- Hong, C.; Milor, L. Electric field enhancement caused by porosity in ultra-low-k dielectrics. In Proceedings of the ISSM 2005, IEEE International Symposium on Semiconductor Manufacturing, San Jose, CA, USA, 13–15 September 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 434–437. [Google Scholar] [CrossRef]
- Orlov, A.A.; Rezvanov, A.A.; Gvozdev, V.A.; Orlov, G.A.; Seregin, D.S.; Kuznetsov, P.I.; Blumberg, T.; Veselov, A.A.; Suzuki, T.; Morozov, E.N.; et al. Dielectric barrier in the subtractive process of formation of a copper metallization system. Russ. Microelectron. 2022, 51, 470–479. [Google Scholar] [CrossRef]
- Chen, F.; Li, B.; Lee, T.; Christiansen, C.; Gill, J.; Angyal, M.; Shinosky, M.; Burke, C.; Hasting, W.; Austin, R.; et al. Technology reliability qualification of a 65nm CMOS Cu/low-k BEOL interconnect. In Proceedings of the 2006 13th International Symposium on the Physical and Failure Analysis of Integrated Circuits, Singapore, 3–7 July 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 97–105. [Google Scholar] [CrossRef]
- Paquette, M.M.; Nordell, B.J.; Caruso, A.N.; Sato, M.; Fujiwara, H.; King, S.W. Optimization of amorphous semiconductors and low-/high-k dielectrics through percolation and topological constraint theory. MRS Bull. 2017, 42, 39–44. [Google Scholar] [CrossRef]
- Armini, S.; Prado, J.L.; Krishtab, M.; Swerts, J.; Verdonck, P.; Meersschaut, J.; Conard, T.; Blauw, M.; Struyf, H.; Baklanov, M.R. Pore sealing of k 2.0 dielectrics assisted by self-assembled monolayers deposited from vapor phase. Microelectron. Eng. 2014, 120, 240–245. [Google Scholar] [CrossRef]
- Zhao, L.; Tokei, Z.; Gischia, G.G.; Pantouvaki, M.; Croes, K.; Beyer, G. A novel test structure to study intrinsic reliability of barrier/low-k. In Proceedings of the 2009 IEEE International Reliability Physics Symposium, Montreal, QC, Canada, 26–30 April 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 848–850. [Google Scholar] [CrossRef]
- Frot, T.; Volksen, W.; Purushothaman, S.; Bruce, R.; Dubois, G. Application of the Protection/Deprotection Strategy to the Science of Porous Materials. Adv. Mater. 2011, 23, 2828–2832. [Google Scholar] [CrossRef]
- Frot, T.; Volksen, W.; Purushothaman, S.; Bruce, R.L.; Magbitang, T.; Miller, D.C.; Sherwood, M.H.; Dubois, G. Post Porosity Plasma Protection: Scaling of Efficiency with Porosity. Adv. Funct. Mater. 2012, 22, 3043–3050. [Google Scholar] [CrossRef]
- Zhang, L.; Ljazouli, R.; Lefaucheux, P.; Tillocher, T.; Dussart, R.; Mankelevich, Y.A.; de Marneffe, J.-F.; de Gendt, S.; Baklanov, M.R. Low damage cryogenic etching of porous organosilicate low-k materials using SF6/O2/SiF4. ECS J. Solid State Sci. Technol. 2013, 2, N131–N139. [Google Scholar] [CrossRef]
- Vanstreels, K.; Li, H.; Vlassak, J.J. Mechanical reliability of low-k dielectrics. In Advanced Interconnects for ULSI Technology, 1st ed.; Baklanov, M.R., Ho, P., Zschech, E., Eds.; Springer: New York, NY, USA, 2012; Volume 10, pp. 339–367. [Google Scholar] [CrossRef]
- Phillips, J.C.; Thorpe, M.F. Constraint Theory, Vector Percolation and Glass Formation. Solid State Commun. 1985, 53, 699–702. [Google Scholar] [CrossRef]
- Burkey, D.D.; Gleason, K.K. Structure and mechanical properties of thin films deposited from 1,3,5-trimethyl-1,3,5-trivinylcyclotrisiloxane and water. J. Appl. Phys. 2003, 93, 5143–5150. [Google Scholar] [CrossRef]
- Ross, D. Chemical Vapor Deposition of Organosilicon Composite Thin Films for Porous Low-k Films. Ph.D. Thesis, MIT, Cambridge, MA, USA, 2005. [Google Scholar]
- Plawsky, J.L.; Achanta, R.; Cho, W.; Rodriguez, O.; Saxena, R.; Gill, W.N. Mechanical and transport properties of low-k dielectrics. In Dielectric Films for Advanced Microelectronics; Baklanov, M.R., Green, M., Maex, K., Eds.; John Wiley & Sons: New York, NY, USA, 2007; pp. 137–197. [Google Scholar] [CrossRef]
- Ashby, M.F.; Gibson, L.J. Cellular Solids: Structure and Properties; Press Syndicate of the University of Cambridge: Cambridge, UK, 1997; pp. 175–231. [Google Scholar]
- Hashin, Z.; Shtrikman, S. A variational approach to the theory of the elastic behaviour of multiphase materials. J. Mech. Phys. Solids 1963, 11, 127–140. [Google Scholar] [CrossRef]
- Sa, Y.K.; Bang, J.; Son, J.; Yu, D.Y.; Kim, Y.C. Enhanced thermo–mechanical reliability of ultralow-k dielectrics with self-organized molecular pores. Materials 2021, 14, 2284. [Google Scholar] [CrossRef]
- Farago, O.; Kantor, Y. Entropic elasticity of phantom percolation networks. Europhys. Lett. 2000, 52, 413–419. [Google Scholar] [CrossRef]
- Rice, R.W. Use of normalized porosity in models for the porosity dependence of mechanical properties. J. Mater. Sci. 2005, 40, 983–989. [Google Scholar] [CrossRef]
- Kováčik, J. Correlation between Young’s modulus and porosity in porous materials. J. Mater. Sci. Lett. 1999, 18, 1007–1010. [Google Scholar] [CrossRef]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory; Taylor & Francis: London, UK, 2018. [Google Scholar]
- Yeap, K.B.; Kopycinska-Mueller, M.; Chen, L.; Chen, Y.; Jungmann, M.; Krause-Rehberg, R.; Mahajan, S.; Vlassak, J.; Gall, M.; Zschech, E. The effect of the pore topology on the elastic modulus of organosilicate glasses. J. Mater. Res. 2013, 28, 1262–1268. [Google Scholar] [CrossRef]
- Michalak, D.J.; Blackwell, J.M.; Torres, J.M.; Gleason, K.K.; Grill, A.; Le, Q.T.; Gates, S.M.; Neumayer, D.A.; Noori, A.M.; Smith, B.C.; et al. Porosity Scaling Strategies for Low-k Films. J. Mater. Res. 2015, 30, 3363–3385. [Google Scholar] [CrossRef]
- Li, H.; Lin, Y.; Tsui, T.Y.; Vlassak, J.J. The effect of porogen loading on the stiffness and fracture energy of brittle organosilicates. J. Mater. Res. 2009, 24, 107–116. [Google Scholar] [CrossRef][Green Version]
- Burg, J.A.; Oliver, M.S.; Frot, T.J.; Sherwood, M.; Lee, V.; Dubois, G.; Dauskardt, R.H. Hyperconnected molecular glass network architectures with exceptional elastic properties. Nat. Commun. 2017, 8, 1019. [Google Scholar] [CrossRef]
- Kilic, K.I.; Dauskardt, R.H. Design of Ultrastiff Organosilicate Hybrid Glasses. Adv. Funct. Mater. 2019, 29, 1904890. [Google Scholar] [CrossRef]
- Kilic, K.I.; Dauskardt, R.H. Mechanically Reliable Hybrid Organosilicate Glasses for Advanced Interconnects. J. Vac. Sci. Technol. B 2020, 38, 060601. [Google Scholar] [CrossRef]
- De Keer, L.; Kilic, K.I.; Van Steenberge, P.H.; Daelemans, L.; Kodura, D.; Frisch, H.; De Clerck, K.; Reyniers, M.-F.; Barner-Kowollik, C.; Dauskardt, R.H.; et al. Computational Prediction of the Molecular Configuration of Three-Dimensional Network Polymers. Nat. Mater. 2021, 20, 1422–1430. [Google Scholar] [CrossRef]
- Rasadujjaman, M.; Wang, X.; Wang, Y.; Zhang, J.; Arkhincheev, V.E.; Baklanov, M.R. Analytical study of porous organosilicate glass films prepared from mixtures of 1,3,5- and 1,3-alkoxysilylbenzenes. Materials 2021, 14, 1881. [Google Scholar] [CrossRef]
- Broadbent, S.R.; Hammersley, J.M. Percolation processes: I. Crystals and mazes. Math. Proc. Camb. Philos. Soc. 1957, 53, 629–641. [Google Scholar] [CrossRef]
- Kesten, H. The critical probability of bond percolation on the square lattice equals 1/21/21/2. Commun. Math. Phys. 1980, 74, 41–59. [Google Scholar] [CrossRef]
- Aizenman, M.; Barsky, D.J. Sharpness of the Phase Transition in Percolation Models. Commun. Math. Phys. 1987, 108, 489–526. [Google Scholar] [CrossRef]
- Grimmett, G.R. Inequalities and entanglements for percolation and random-cluster models. In Perplexing Problems in Probability: Festschrift in Honor of Harry Kesten; Birkhäuser: Boston, MA, USA, 1999; pp. 91–105. [Google Scholar] [CrossRef]
- Grassberger, P. On the Critical Behavior of the General Epidemic Process and Dynamical Percolation. Math. Biosci. 1983, 63, 157–172. [Google Scholar] [CrossRef]
- Cohen, R.; Havlin, S. Complex Networks: Structure, Robustness and Function; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Sahimi, M. Flow and Transport in Porous Media and Fractured Rock: From Classical Methods to Modern Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Newman, M.E.J. Spread of epidemic disease on networks. Phys. Rev. E 2002, 66, 016128. [Google Scholar] [CrossRef]
- Beggs, J.M.; Plenz, D. Neuronal avalanches in neocortical circuits. J. Neurosci. 2003, 23, 11167–11177. [Google Scholar] [CrossRef]
- Gupta, P.; Kumar, P.R. The capacity of wireless networks. IEEE Trans. Inf. Theory 2000, 46, 388–404. [Google Scholar] [CrossRef]
- Achlioptas, D.; D’Souza, R.M.; Spencer, J. Explosive percolation in random networks. Science 2009, 323, 1453–1455. [Google Scholar] [CrossRef] [PubMed]
- De Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar]
- Ashby, M.F.; Medalist, R.M. The Mechanical Properties of Cellular Solids; Pergamon Press: Oxford, UK, 1983. [Google Scholar] [CrossRef]
- Gibson, I.J.; Ashby, M.F. The Mechanics of Three-Dimensional Cellular Materials. Proc. R. Soc. Lond. A 1982, 382, 43–59. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F.; Schajer, G.S.; Robertson, C.I. The Mechanics of Two-Dimensional Cellular Materials. Proc. R. Soc. Lond. A 1982, 382, 25–42. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Ashby, M.F.; Fleck, N.A. Foam Topology: Bending versus Stretching Dominated Architectures. Acta Mater. 2001, 49, 1035–1040. [Google Scholar] [CrossRef]
- Efros, A.L.; Shklovskii, B.I. Critical Behaviour of Conductivity and Dielectric Constant Near the Metal-Non-Metal Transition Threshold. Phys. Status Solidi B 1976, 76, 475–485. [Google Scholar] [CrossRef]
- Clerc, J.P.; Giraud, G.; Laugier, J.M.; Luck, J.M. The Electrical Conductivity of Binary Disordered Systems, Percolation Clusters, Fractals and Related Models. Adv. Phys. 1990, 39, 191–309. [Google Scholar] [CrossRef]
- Bergman, D.J.; Stroud, D. Physical Properties of Macroscopically Inhomogeneous Media. In Solid State Physics; Academic Press: San Diego, CA, USA, 1992; Volume 46, pp. 147–269. [Google Scholar] [CrossRef]
- Kumar, A.; Vidhyadhiraja, N.S.; Kulkarni, G.U. Current distribution in conducting nanowire networks. J. Appl. Phys. 2017, 122, 045101. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Fractals: Form, Chance, and Dimension; W. H. Freeman and Company: New York, NY, USA, 2020. [Google Scholar]
- Richardson, L.F. The Problem of Contiguity: An Appendix to Statistics of Deadly Quarrels. Gen. Syst. Yearb. 1961, 6, 139–187. [Google Scholar]
- Addison, P.S. Fractals and Chaos: An Illustrated Course; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Weiss, G.H.; Havlin, S. Some properties of a random walk on a comb structure. Phys. A 1986, 134, 474–482. [Google Scholar] [CrossRef]
- Havlin, S.; Kiefer, J.E.; Weiss, G.H. Anomalous diffusion on a random comblike structure. Phys. Rev. A 1987, 36, 1403. [Google Scholar] [CrossRef]
- Murthy, K.P.N.; Kehr, K.W. Mean first-passage time of random walks on a random lattice. Phys. Rev. A 1989, 40, 2082. [Google Scholar] [CrossRef]
- Dhar, D. Diffusion and drift on percolation networks in an external field. J. Phys. A Math. Gen. 1984, 17, L257–L262. [Google Scholar] [CrossRef]
- Tateishi, A.A.; Ribeiro, H.V.; Sandev, T.; Petreska, I.; Lenzi, E.K. Quenched and annealed disorder mechanisms in comb models with fractional operators. Phys. Rev. E 2020, 101, 022135. [Google Scholar] [CrossRef]
- Lubashevskii, I.A.; Zemlyanov, A.A. Continuum description of anomalous diffusion on a comb structure. J. Exp. Theor. Phys. 1998, 87, 700–713. [Google Scholar] [CrossRef]
- Alexander, S.; Orbach, R. Density of states on fractals: “fractons”. J. Phys. Lett. 1982, 43, 625–631. [Google Scholar] [CrossRef]
- Gefen, Y.; Aharony, A.; Mandelbrot, B.B.; Kirkpatrick, S. Solvable fractal family, and its possible relation to the backbone at percolation. Phys. Rev. Lett. 1981, 47, 1771. [Google Scholar] [CrossRef]
- Chamon, C. Quantum glassiness in strongly correlated clean systems: An example of topological overprotection. Phys. Rev. Lett. 2005, 94, 040402. [Google Scholar] [CrossRef] [PubMed]
- Haah, J. Local stabilizer codes in three dimensions without string logical operators. Phys. Rev. A 2011, 83, 042330. [Google Scholar] [CrossRef]
- Nandkishore, R.M.; Hermele, M. Fractons. Annu. Rev. Condens. Matter Phys. 2019, 10, 295–313. [Google Scholar] [CrossRef]
- Hong, S.; Lee, C.S.; Lee, M.H.; Lee, Y.; Ma, K.Y.; Kim, G.; Yoon, S.I.; Ihm, K.; Kim, K.-J.; Shin, T.J.; et al. Ultralow-dielectric-constant amorphous boron nitride. Nature 2020, 582, 511–514. [Google Scholar] [CrossRef] [PubMed]
- Cao, L.; Guo, X.; Li, M. Research on the properties of low-k films grafted on Cu (111) surface via electrochemical reduction of aryl diazonium salts. Appl. Surf. Sci. 2025, 684, 161959. [Google Scholar] [CrossRef]
- Multia, J.; Kravchenko, D.E.; Rubio-Gimenez, V.; Philip, A.; Ameloot, R.; Karppinen, M. Nanoporous Metal–Organic Framework Thin Films Prepared Directly from Gaseous Precursors by Atomic and Molecular Layer Deposition: Implications for Microelectronics. ACS Appl. Nano Mater. 2023, 6, 827–831. [Google Scholar] [CrossRef]




| Material | Type | k-Value | Porosity (%) | Deposition | Integration | Technology Nodes |
|---|---|---|---|---|---|---|
| FOX | Fluorinated SiO2 | 3.0–3.6 | Dense | Spin-on | Yes | 180 nm, 130 nm |
| BDI | OSG | ~3.0 | <10 | PECVD | Yes | 90 nm, 65 nm |
| BDII | OSG | ~2.5 | ~25 | PECVD | Yes | 65 nm, 45 nm, 32 nm |
| SiLK, Flare | Organic polymer | ~2.6 | Dense | Spin-on | No | Rejected (too high CTE) |
| XLK, LKD | OSG | ~2.0–2.3 | ~50 | Spin-on | No | Experimental |
| NCS | OSG | ~2.0–2.3 | ~35–40 | Spin-on | Limited (Fujitsu) | Experimental |
| BDIII | OSG | ~2.2 | ~40–45 | PECVD | No | Experimental |
| Property | Dense OSG | Porous OSG |
|---|---|---|
| Dielectric constant (k) | 2.8–3.1 | <2.5 (ultra-low-k) |
| Breakdown field | High (4–8 MV/cm) | Moderate–low (2–4 MV/cm) |
| Leakage current | Very low | High (exponential surge at pc) |
| Moisture uptake | Minimal | High (hydrophilic pores) |
| Mechanical strength | High | Reduced (crack-prone) |
| Percolation threshold | None | 25%–35% porosity |
| Property | Typical Sensitivity to Porosity | Percolation Threshold in OSG | Main influencing Factors in OSG | Remarks |
|---|---|---|---|---|
| Mass transfer | Very High | ~15%–20% open porosity | Pore interconnectivity, hydrophilicity (Si–OH groups), plasma damage | Onset seen via vapor sorption, porosimetry |
| Moisture uptake | High | ~15%–20% | Surface silanol density, open pores, exposure to air or plasma | Leads to permittivity drift and leakage |
| Charge transfer/Leakage | High | ~15%–25% | Moisture condensation, hydrocarbon residues, electric field-induced transport | Strongly accelerated after percolation path is filled |
| Breakdown field (EBD) | Moderate | ~20%–30% | Pore alignment (vertical), moisture, carbon adsorption, Si–OH content | Degradation is nonlinear and field-assisted |
| Mechanical properties | High | ~25%–30% | Matrix crosslinking, Si–O–C vs. Si–O–Si ratio, pore clustering | Densely crosslinked films resist cracking longer |
| dielectric constant (k) | Moderate—(Clausius-Mossotti equation) | No sharp threshold | Total porosity, pore size | Decreases steadily with porosity |
| Mechanical Property | Typical Range | Integration Spec/Requirement | Failure Mode If Below Spec |
|---|---|---|---|
| Young’s Modulus | d-SiO2: ~70 GPa; d-OSG: 8–15 GPa; p-OSG: 3–10 GPa | ≥4–5 GPa for CMP and packaging survivability (sub-10 nm nodes often target ~5–6 GPa) | CMP dishing/erosion, deformation under capping/barrier stress, densification → k-value increase |
| Hardness | d-SiO2: ~8–10 GPa; p-OSG: 0.5–2 GPa | ≥0.5–1.0 GPa for surface wear resistance | Surface scratching, debris generation, CMP defects |
| Fracture Toughness (plane strain, KIC) | d-SiO2: ~0.8–1.0 MPa·m1/2; p-OSG: 0.2–0.4 MPa·m1/2 | ≥0.25–0.3 MPa·m1/2 to prevent crack propagation | Crack initiation/propagation from packaging stress, wafer handling, or thermal cycling |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gerelt-Od, M.; Rasadujjaman, M.; Arkhincheev, V.E.; Vorotilov, K.A.; Baklanov, M.R. Phenomenological Analysis of Percolation Phenomena in Porous Low-k Dielectrics. Coatings 2025, 15, 1138. https://doi.org/10.3390/coatings15101138
Gerelt-Od M, Rasadujjaman M, Arkhincheev VE, Vorotilov KA, Baklanov MR. Phenomenological Analysis of Percolation Phenomena in Porous Low-k Dielectrics. Coatings. 2025; 15(10):1138. https://doi.org/10.3390/coatings15101138
Chicago/Turabian StyleGerelt-Od, Mungunsuvd, Md Rasadujjaman, Valerii E. Arkhincheev, Konstantin A. Vorotilov, and Mikhail R. Baklanov. 2025. "Phenomenological Analysis of Percolation Phenomena in Porous Low-k Dielectrics" Coatings 15, no. 10: 1138. https://doi.org/10.3390/coatings15101138
APA StyleGerelt-Od, M., Rasadujjaman, M., Arkhincheev, V. E., Vorotilov, K. A., & Baklanov, M. R. (2025). Phenomenological Analysis of Percolation Phenomena in Porous Low-k Dielectrics. Coatings, 15(10), 1138. https://doi.org/10.3390/coatings15101138









