Evaluation of Steel Slag Optimal Replacement in Asphalt Mixture under Microwave Heating Based on 3D Polyhedral Aggregate Electromagnetic-Thermal Meso-Model

Abstract

Replacing conventional aggregate with steel slag waste can boost the microwave absorption properties of asphalt mixtures and reduce pollution to protect the environment. In order to achieve the best healing in steel slag asphalt mixture, the optimum particle size and content of steel slag are essential. For this purpose, a high-efficiency algorithm for the random growth and placement of convex polyhedron aggregate is proposed in this paper. The limestone aggregate is replaced with an equal volume of steel slag, and a three-dimensional mesoscale random model of steel slag asphalt mixture is developed. The process of microwave heating is simulated by FEM. The numerical simulations are compared with the reported experimental data, which proves that the model is reliable (R² = 99.40%). Both the volume average temperature and the uniformity of temperature distribution indicate that the steel slag replacement rate of 60% at 4.75–9.5 mm and 60% at 9.5–13.2 mm is optimal, among which the heat transfer of 4.75–9.5 mm steel slag is more uniform, and the temperature gradient is lower. Steel slag can dramatically increase the heating rate of an asphalt mixture, and the peak of the temperature gradient is around the boundary of steel slag. The reflection properties of steel slag may be related to the dielectric constant, permeability, and particle size. Excess steel slag will cause overheating in most zones of the specimen and will also depress the absorption efficiency of microwaves. The coefficient of variance for spherical (0.36) and polyhedral (0.32) aggregate specimen temperatures indicates that the aggregate’s shape has a negligible effect on the heat transfer of asphalt mixtures.

1. Introduction

Asphalt mixtures are prone to damage under changing environmental conditions such as temperature and humidity, combined with the action of long-term repeated traffic loads, resulting in a large number of microcracks [1,2]. If these microcracks are left unrepaired, they will continue to grow, and will eventually lead to the structural failure of the asphalt pavement. Therefore, regular maintenance and the repair of asphalt pavement are important. Some studies have found that asphalt molecules in the cracks inside the asphalt mixture will self-heal the microcracks by wetting and diffusion, which can restore their original strength level to a certain extent [3,4]. This characteristic of asphalt mixtures can significantly reduce maintenance costs, extend its service life, and ultimately reduce greenhouse gas emissions [5]. However, the self-healing process of asphalt mixtures is very slow and does not satisfy the demands of actual engineering.

As we all know, an asphalt mixture is a thermally induced self-healing material. Asphalt flows and fills cracks when in the temperature range of 30 °C to 70 °C [6]. Temperature is the main factor affecting its self-healing, and a relatively high temperature can speed up the healing process of the asphalt mixture. Previous research has shown that the asphalt material begins to heal itself at a temperature of 55 °C without interference from other factors [7]. Liu found that asphalt mixture specimens achieved 100% healing performance at temperatures ranging from 70 °C to 120 °C [8]. Thus, it is very effective to accelerate the healing of asphalt materials by increasing the temperature. Currently, induction heating and microwave heating are the two main technical methods [9,10]. Some scholars compared the recovery percentage of original mechanical properties after healing treatment and found that microwave heating was more effective in terms of healing rate than induction heating, and could recover most of the original mechanical properties of asphalt mixture [11]. In addition, compared with induction heating technology, microwave heating has excellent application prospects in pavement engineering, such as pavement de-icing and maintenance, due to its environmental protection, high heating efficiency, strong penetration, and selective heating [5,12,13].

In the process of microwave heating, the medium absorbs microwaves in a changing electromagnetic field, generating losses to heat the material. A conventional asphalt mixture has a low microwave absorption capacity; to improve its microwave absorption behavior, the addition of metal fibers, steel slag, and carbon nanomaterials can enhance the healing performance of asphalt mixtures [14,15]. Steel slag, as a solid waste generated abundantly in the steel production process, can be utilized as aggregate to save on the use of natural aggregate and can then reduce the construction cost of pavement [16]. Additionally, this solid waste disposal and recycling process can protect the ecological environment and promote sustainable development [17]. Steel slag is generally added to asphalt mixture as an equal-volume replacement for ordinary aggregate, which can improve the water sensitivity and stiffness of an asphalt mixture and prolong its fatigue life [18,19]. According to the research of some scholars, the particle size and volume content of steel slag had an impact on how well asphalt mixtures absorbed microwave efficiency. For instance, Gao’s research suggested that the 0.6 mm, 2.36 mm, and 9.5 mm particle sizes are suitable for steel slag [12]; Lou revealed that an asphalt mixture with 60% coarse aggregate replacement in the 4.75–9.5 mm range had better healing performance [20]; Chen indicated that the microwave heating efficiency of the asphalt mixture was optimal when 50% of the 4.75–9.5 mm and 50% of the 9.5–13.2 mm aggregates were replaced by steel slag [21]. These research results imply that the steel slag content is crucial to the healing performance of the asphalt mixture under microwave heating. However, there are few studies on the influence of steel slag particle size in terms of the electromagnetic field.

Numerical simulations have advantages for studying the electromagnetic behavior of specimens during microwave heating. At the same time, although laboratory tests can clearly describe the healing behavior of cracks in an asphalt mixture when heated by external macroscopic characteristics, there are few studies on the mechanism of the various phases of steel slag asphalt mixture under microwave heating. Therefore, a numerical model based on a mesoscopic scale has the potential to investigate the mechanism of internal crack healing within steel slag asphalt mixture in microwave heating. In this paper, in order to simulate the realistic mesoscopic scale of the asphalt mixture, we present a random algorithm to generate an approximate polyhedral aggregate system and develop a three-dimensional model containing steel slag, asphalt mortar, and aggregate particles. Then, the microwave heating performance of asphalt mixtures is explored with different steel slag replacement rates in various particle size intervals at the mesoscale.

2. Basic Assumptions

This paper attempts to study the behavior of steel slag contents on the asphalt mixture at different particle size intervals under microwave heating, by developing a meso-random model with a coupled electromagnetic field and solid heat transfer. This model should make it possible to describe the effects of shape, location distribution, and aggregate size on the microwave heating performance of the asphalt mixture. In particular, it should be able to describe the multi-physical field process of microwave heating. Therefore, we first compiled a random growth and placement algorithm to produce polyhedral aggregates and construct a 3D mesoscale numerical model. Then, we created a numerical model of microwave heating asphalt mixture for coupled electromagnetic field and solid heat transfer using COMSOL Multiphysics (version 5.6) to analyze this multi-field coupling problem.

In reality, the mesoscopic scale and composition of asphalt mixtures are very complicated, and specimens under microwave radiation are also subjected to quite complex physical and chemical effects. Thus, to simplify the numerical model, the following treatment and assumptions are employed:

• Aggregate with a particle size below 4.75 (mm), fine mineral powder as filler, and asphalt binder are homogenized into a uniform asphalt mortar. This simplification is reasonable since this mesoscopic model, based on polyhedral aggregates, already has high accuracy.
• To reduce the complexity of the calculation, we assume aggregate shapes can be treated as convex polyhedrons (hereafter referred to as polyhedrons). Despite the deviation of this assumption from reality, polyhedral aggregate still presents a much better approximation to the actual shapes of aggregate than mesoscale models based on spherical aggregate.
• The physical and chemical properties of the constituents in the specimen are kept constant, and the variations of these properties can be assumed to be negligible over a relatively small temperature range, so these are assumed to be constant in the model.
• We neglect voids in the mesoscopic scale of the asphalt mixture because the void ratio of an AC-type mix is small, usually below 4%.
• We treat the inner heat transfer of the components of the asphalt mixture specimen as perfect and ideal conditions, with no heat loss occurring during internal transfer, i.e., no consideration is made of the interface of thermal resistance.

3. Microwave Heating Model

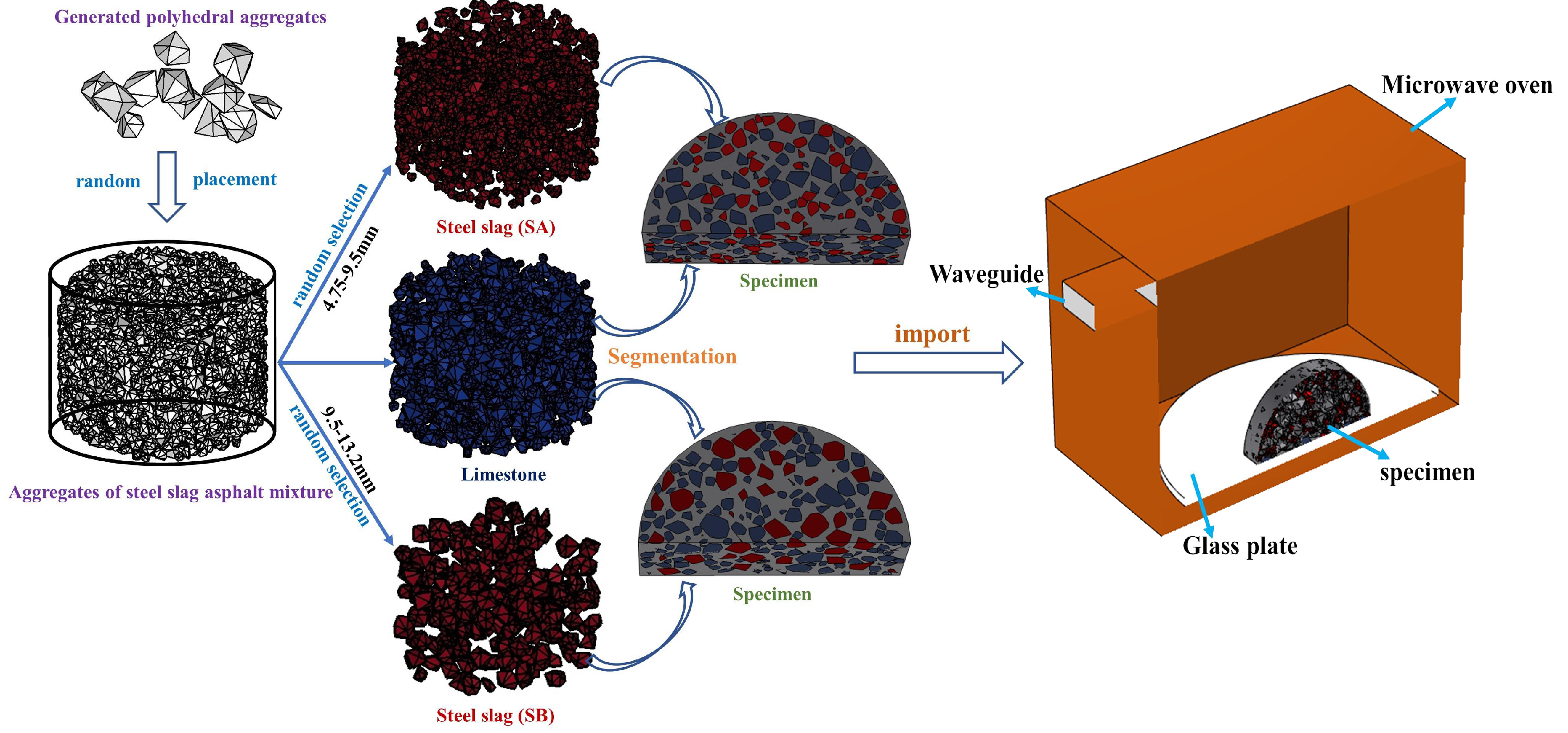
3.1. Meso-Random Geometry Model

Our previous work proposed a Gilbert–Johnson–Keerthi (GJK)-based algorithm for generating polyhedral aggregates by random placement [22]. In the current study, we also utilize the GJK algorithm to handle collisions between aggregate particles. The present polyhedral aggregate model is divided into two parts; these are the generation of aggregate and the random placement of aggregate, as follows:

• Random growth algorithm for aggregates. Firstly, we generate those spheres with the desired probability distribution, based on the modified Monte Carlo method proposed in our previous study [23], then, we generate elementary octahedral aggregates based on spheres. Four points of the octahedral aggregate are located on the horizontal plane of the sphere, and the other two points are located on the upper and lower sphere surfaces. Next, we search the longest side of the aggregate and expand it outward. After some 3D expansion, we connect all the edges and generate a polyhedral aggregate particle. This method can improve the selection of growing edges: it selects the sub-length edges to grow when the current edge is unable to keep growing and avoids a situation wherein the longest edge cannot grow.
• Random placement method, based on the GJK algorithm. We arrange all the generated aggregate geometry information from smallest to largest, then convert two convex hulls into a configuration space via Minkowski difference [24,25]. Subsequently, we transform the distance between two convex hulls into the distance between the configuration space. In the case that the nearest distance is greater than 0, it proves that the two aggregates are separated. When the nearest distance is equal to 0, it means that the edges of the two aggregates are coincident, while in the case that the nearest distance does not exist, the partial areas of the two objects overlap. Therefore, the random placement of aggregates is realized according to the distance between the two polyhedrons. Besides, this algorithm can achieve the random placement of a relatively high aggregate volume ratio, based on the given gradation.

Next, we export the geometric information of all polyhedral aggregate particles, which contains the coordinate position and the shape and size of each aggregate particle. Then, the geometric information of aggregate particles with intervals of 4.75–9.5 mm and 9.5–13.2 mm is randomly selected and replaced by steel slag. Note that this information will be used in the next step to generate aggregate in ABAQUS (version 2016, SIMULIA) by using parametric Python scripts. Since the generated aggregate particles in ABAQUS are mesh files, we import them into Hypermesh (version 13.0) to generate geometric parts, based on the mesh reconfiguration geometry of the aggregate system. In order to be consistent with the experimental situation reported in Ref. [26], we cut along two planes of the generated Marshall specimen to obtain a semi-circular sample. Finally, we import the obtained geometric parts into the microwave oven model and achieve the needed mesoscale geometry model. To sum up, Figure 1 shows the modeling process, and the geometrical parameters of microwave ovens can be found in Ref. [23].

3.2. Governing Equation

3.2.1. Electromagnetic Field

The radiation and interaction of rapidly varying electromagnetic fields in the asphalt mixture medium follow the system of Maxwell’s equations, while the electromagnetic constitutive relation of its macro behavior only considers linear polarization and magnetization. The governing equation in the electric field is shown in Equation (1):

$$\nabla \times {\mu }_m^{-1}\left(\nabla \times \mathit{E}\right)-k_0^2\left({\epsilon }_m-\frac{j\sigma }{\omega {\epsilon }_0}\right)\mathit{E}=0$$

(1)

where $\mathit{E}$ represents the electric field strength, ${\mu }_m$ and ${\epsilon }_m$ are the relative permittivity and permeability, $k_0$ denotes the wave numbers in free space, $j$ is an imaginary unit ($j^2$ = −1), $\omega$ represents the angular frequency, and ${\epsilon }_0$ represents the dielectric constant of free space. Note that once the electric field intensity in Equation (1) has been established, magnetic quantities can be easily derived from Maxwell’s equations.

3.2.2. Temperature Field

The medium generates heat in the electromagnetic field because of resistive loss and magnetic loss. The heat generated by the medium in microwave heating is coupled into the solid heat transfer equation as the heat source for simulating transient heat transfer, and the resulting Equation (2) is shown below:

$$Q_e=\frac{1}{2}Re\left(\mathit{J}·\mathit{E}\right)+\frac{1}{2}Re\left(i\omega \mathit{B}·\mathit{H}\right)$$

(2)

where $\mathit{J}$ is the current density, $\mathit{B}$ is the magnetic induction strength, $\mathit{H}$ is the magnetic field strength, and $Q_e$ is the heat source (absorbed power).

According to Fourier’s energy balance calculation, the governing equation for heat conduction in the conductor is:

$$\rho C\frac{\partial T}{\partial t}+\nabla \cdot \left(-k\nabla T\right)=Q_e$$

(3)

where $\rho$ is the density, $k$ is the thermal conductivity, $C$ represents the specific heat capacity of the material, and $\frac{\partial T}{\partial t}$ denotes the variation in temperature with time.

3.2.3. Boundary Conditions

For the electromagnetic field, noticing that the waveguide wall and the microwave oven wall are overlapped with copper, they are defined as impedance boundary conditions, which are solved in the frequency domain by Equation (4), as shown below:

$$\sqrt{\frac{{\mu }_0{\mu }_r}{{\epsilon }_0{\epsilon }_r-j\sigma /\omega }}\mathit{n}\times \mathit{H}+\mathit{E}-\left(\mathit{n}\cdot \mathit{E}\right)\mathit{n}=\left(\mathit{n}\cdot {\mathit{E}}_s\right)\mathit{n}-{\mathit{E}}_s$$

(4)

where $\sigma$ is the electrical conductivity, $\mathit{n}$ is the normal vector on the boundary, and ${\mathit{E}}_s$ is the electric field source.

The transverse electric (TE₁₀) wave excitation from the rectangular port boundary and the scattering parameters can be described as:

$$S=\frac{{{\displaystyle \int }}_p\left(\mathit{E}-{\mathit{E}}_1\right)\cdot {\mathit{E}}_1}{{{\displaystyle \int }}_p{\mathit{E}}_1\cdot {\mathit{E}}_1}$$

(5)

where ${\mathit{E}}_1$ represents the electric field in the rectangular port.

For the temperature field, the boundary of the asphalt mixture specimen is defined as a convective heat flux condition, where heat is exchanged with the air in the microwave oven cavity by convection. The corresponding equation is as follows:

$$-k\cdot \nabla T=h\left(T-T_a\right)$$

(6)

where $T$ is the transient temperature, $h$ represents the surface convective coefficient, and $T_a$ denotes the ambient temperature. It is assumed that the solid medium of the specimen is all in close contact. In addition, regardless of the interface’s thermal resistance, each solid medium’s temperature and the heat flux density at the interface are equal.

4. Simulation Method

4.1. Finite Element Model

The microwave heating process is simulated in COMSOL Multiphysics 5.6 using the finite element method (FEM). To solve the multi-physics field problem, we first analyze the electromagnetic field in the frequency domain and then couple the absorbed power as a heat source into the transient solid heat transfer. In the mesoscopic scale simulation study of an asphalt mixture, the accuracy and quality of the mesh have a crucial influence on the numerical simulation. In this paper, a free tetrahedral mesh with scaling geometry is adopted, and the maximum element is defined as 0.24 mm, which is 1/5 of the wavelength of the frequency 2.45 GHz. There are 1,613,229 mesh elements for the specimen (Figure 2). The average element quality of the model mesh is 0.61, meaning that the model meshing is regular and reliable [27].

4.2. Material Properties

This study uses the material and gradation from those previously reported in Ref. [20] to design the steel slag asphalt mixture, where the authors measured the microwave heating ability of basalt aggregate. The results revealed that basalt in a size range within 9.5–13.2 mm and 13.2–16 mm conducts heat well, so their aggregate particles above 9.5 mm were basalt. Moreover, the remaining aggregate particles and fillers employed in their study were all limestone, for economic reasons. The model is an AC-13 graded asphalt mixture with an asphalt content of 5.0%. The gradation curve of the specimen after random placement is plotted in Figure 3. For the detailed properties of the material, please refer to Ref. [23]. To make this model realistic, the parameters are chosen to be consistent with the actual situation as closely as possible. Since the limestone aggregate and asphalt below 4.75 mm are deemed to be homogeneous asphalt mortar, the electromagnetic and thermophysical properties of this asphalt mortar can be obtained via the mix rule.

Table 1. Thermal and electromagnetic parameters of asphalt mortar.

Component	Density (kg/m3)	Thermal Conductivity (W/(m·°C))	Specific Heat Capacity (J/(kg·°C))	Electrical Conductivity (S/m)	Relative Complex Permittivity
Asphalt mortar	2550.36	3.055	867.72	0.002	6.5–0.028 *j

*j is the imaginary unit (j² = −1).

shows the values obtained for the asphalt mortar by the volume averaging method.

4.3. Random Selection

The primary purpose of this study is to explore the effect of steel slag content in different particle size intervals on asphalt mixtures during microwave heating and to investigate the optimal steel slag replacement rate in the interval. Notice that in the original grading, the aggregates over 9.5 mm were basalt, while the rest were limestone. To avoid the influence of different aggregates for quantitative analysis, we altered all basalt aggregates to limestone and replaced the equal volume of limestone of 9.5–13.2 mm and 9.5–4.75 mm with steel slag, respectively. During the simulation, the steel slag asphalt mixture is heated for 100 s at 25 °C, with 2.45 GHz frequency and 700 W power.

The random replacement of steel slag is divided into two steps: selection and replacement. First, we implement an algorithm to randomly select limestone aggregates of equal volume in all particle size intervals in Python. The randomly selected aggregate particles have different sizes and uniform location distribution. After that, those selected limestone aggregates are replaced by steel slag. We then test 6 groups of specimens to eliminate the errors caused by random placement and ensure uniformity with the experimental results. The fine steel slag selected within the interval of 4.75–9.5 mm is recorded as SA, and the coarse steel slag selected within the interval of 9.5–13.2 mm is recorded as SB. All steel slag asphalt mixtures are designed as shown in

Table 2. Steel slag asphalt mixtures.

Replacement Ratio	With a Particle Size of 4.75–9.5 mm	With a Particle Size of 9.5–13.2 mm
0%	SA0	SB0
20%	SA20	SB20
40%	SA40	SB40
60%	SA60	SB60
80%	SA80	SB80
100%	SA100	SB100

.

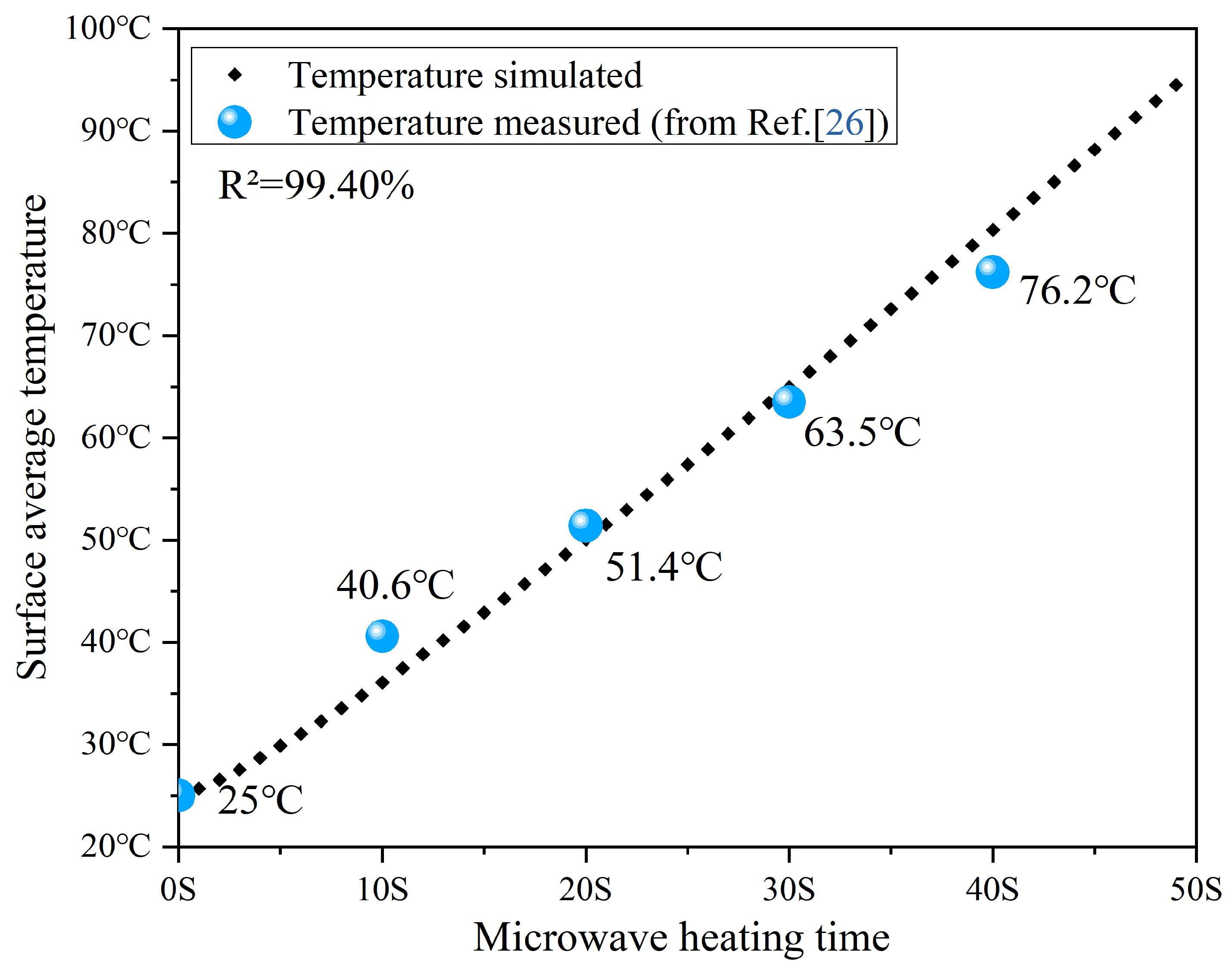
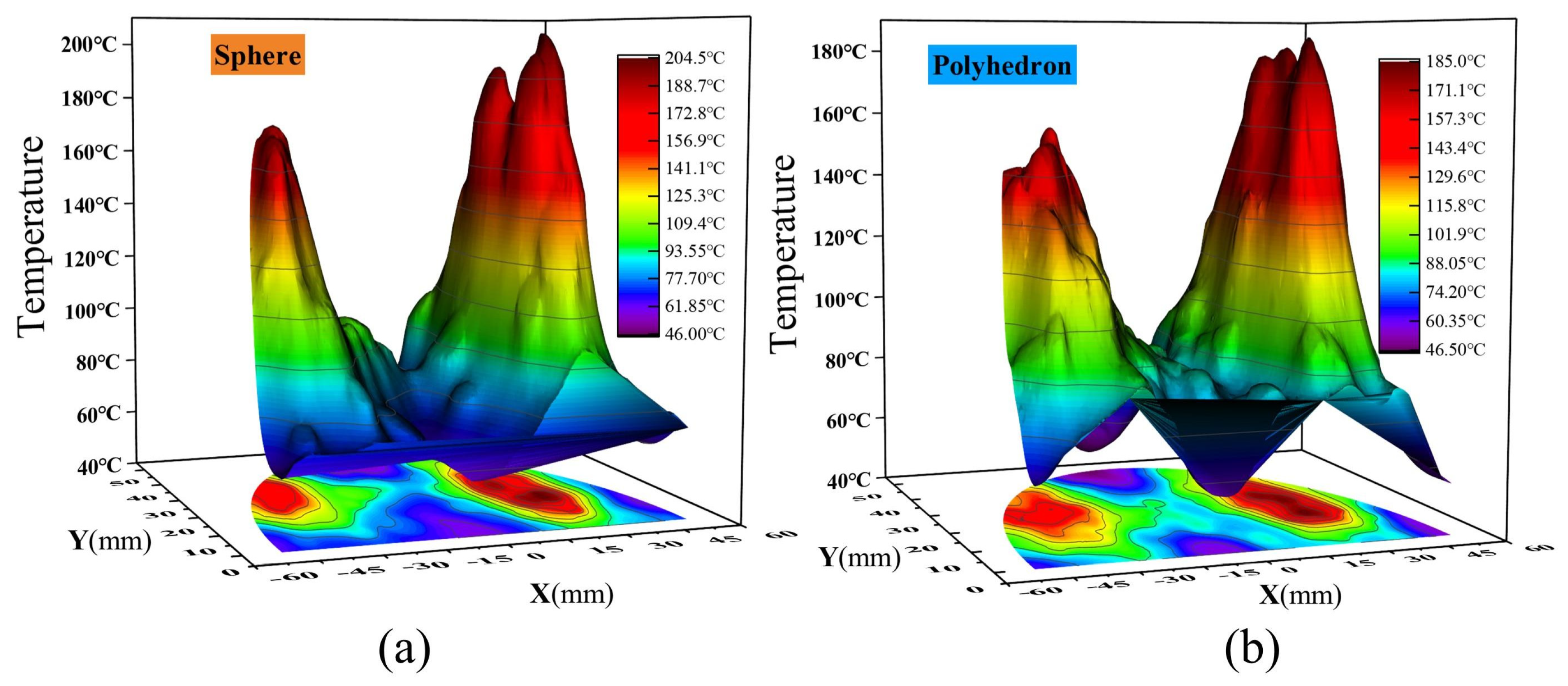
5. Model Validation from Experiment and Shape Effect

First, to compare with the reported experimental data, we also use the steel slag to replace 60% of the limestone within 4.75–9.5 mm for simulating the experiment. We calculate the average temperature of all surfaces of the asphalt mixture and compare it with the experimentally measured data from Ref. [26] to verify the reliability of the numerical simulation. As shown in Figure 4, the results of the numerical simulations correlate well with those of the reported experimental tests. Since we have been keeping the conditions as consistent as possible with those used in the references during the numerical simulation, it can be seen that the model describes the microwave heating process of steel slag asphalt mixtures well. The tiny discrepancies may be due to differences between the actual structure and the model, as well as to the effect of voids and moisture during heating.

In our previous work, we investigated the effect of different steel slag contents within a size range of 4.75–9.5 mm on microwave-heated asphalt mixtures based on spherical aggregates [23]. In order to explore the influence of aggregate shape on microwave heating, in particular for spherical aggregates and polyhedral aggregates, we have tried to display the difference in the temperature of the center slice of the asphalt mixture, where all the other parameters are chosen to be the same except the shape of the aggregates. We extract the temperature values of all data points in their central slices to plot the temperature field distribution, which is compared in Figure 5, where the x- and y-axes indicate the position of the specimen slice, and the z-axis represents the temperature magnitude. The results show that for the difference between the maximum and minimum temperatures, the polyhedral aggregate temperatures (138.5 °C) are lower than the spherical ones (158.5 °C). Then, we use the coefficient of variance to evaluate the uniformity of the temperature distribution. The specific method for this is described in Section 6.3.1. The coefficient of variance of polyhedral aggregates (0.32) is slightly lower than that of spherical aggregates (0.36). Nevertheless, both the spherical and the polyhedral aggregate specimens show visible temperature peaks on both sides, while their internal temperature distribution is not uniform. The shape of the aggregate has little effect on the heat transfer of the asphalt mixture under microwave heating.

6. Results and Discussions

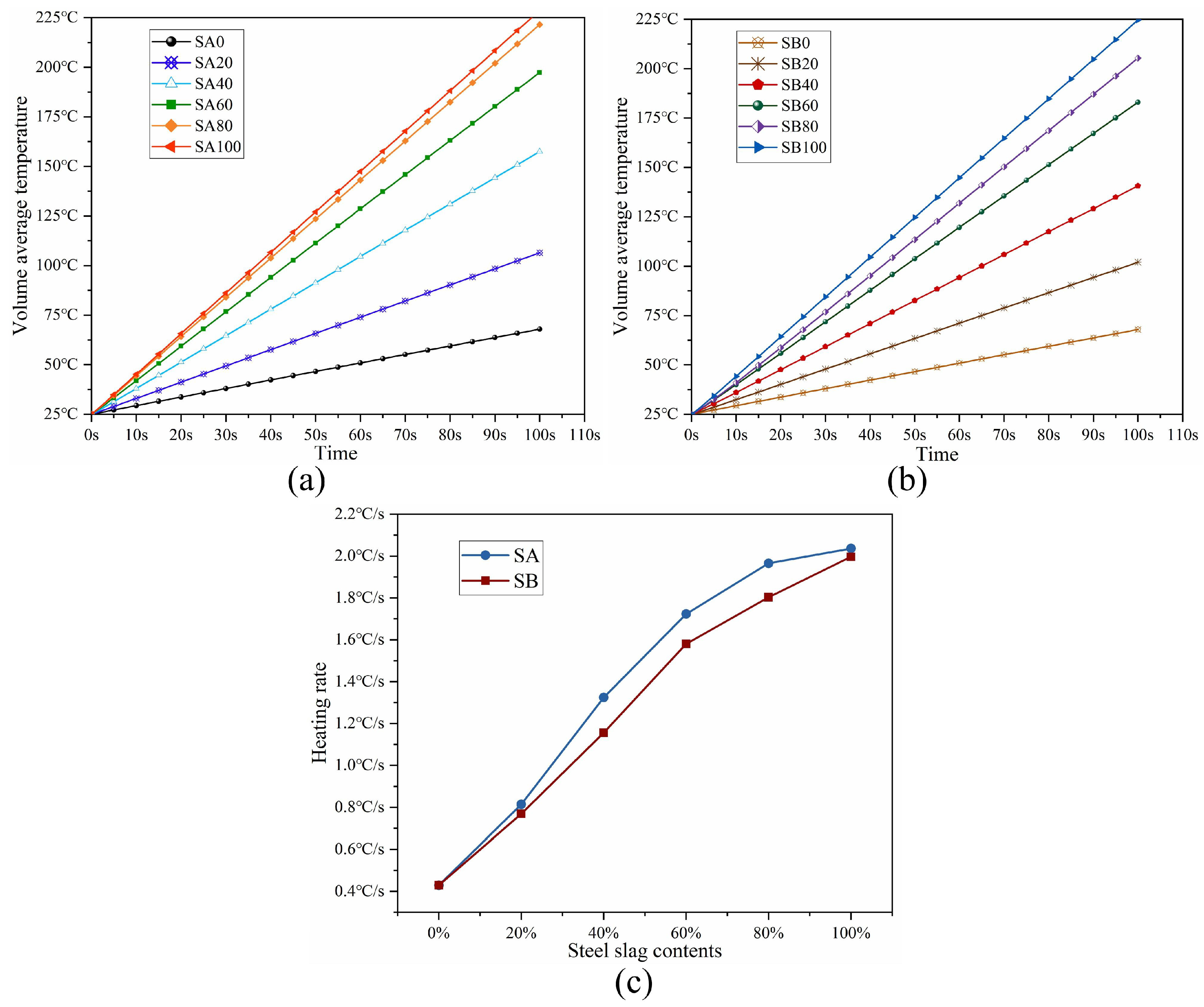
6.1. Effect of Different Particle Sizes of Steel Slag Contents on the Volume Average Temperature

We calculated the volume average temperature of the specimen, as shown in Figure 6a,b, and fitted the data linearly with the slope representing the heating rate of the specimen. The results in Figure 6c show that, compared with conventional aggregate, steel slag can remarkably increase the volume temperature of asphalt mixtures. Moreover, the heating rate of steel slag asphalt mixtures gradually slows down as steel slag contents reach more than 60%. This indicates that the heating rate does not increase linearly as the steel slag content increases. The higher heating rate for SA than SB may have resulted from the fact that more aggregate exists in the 4.75–9.5 mm range than that in the 9.5–13.2 mm range.

Temperature is one of the most critical factors in analyzing the healing of asphalt mixtures. An appropriate temperature allows the asphalt mixture to heal best and prevents asphalt from overheating. Based on previous studies, the optimum healing effect can be achieved when most zones of the asphalt mixture reach 90 °C, and crack healing can be obtained at this temperature without overheating [28]. Noticing that the time period of 40 s is the suitable time for microwave heating of asphalt mixture [29], we assessed the healing properties of steel slag asphalt mixtures by temperature and compared the volume average temperature of all specimens at the 40th s. The results demonstrate that at the 40th s, SA60 (93.99 °C) and SB60 (87.75 °C) have a volume average temperature closer to 90 °C than the other specimens and display better healing performance.

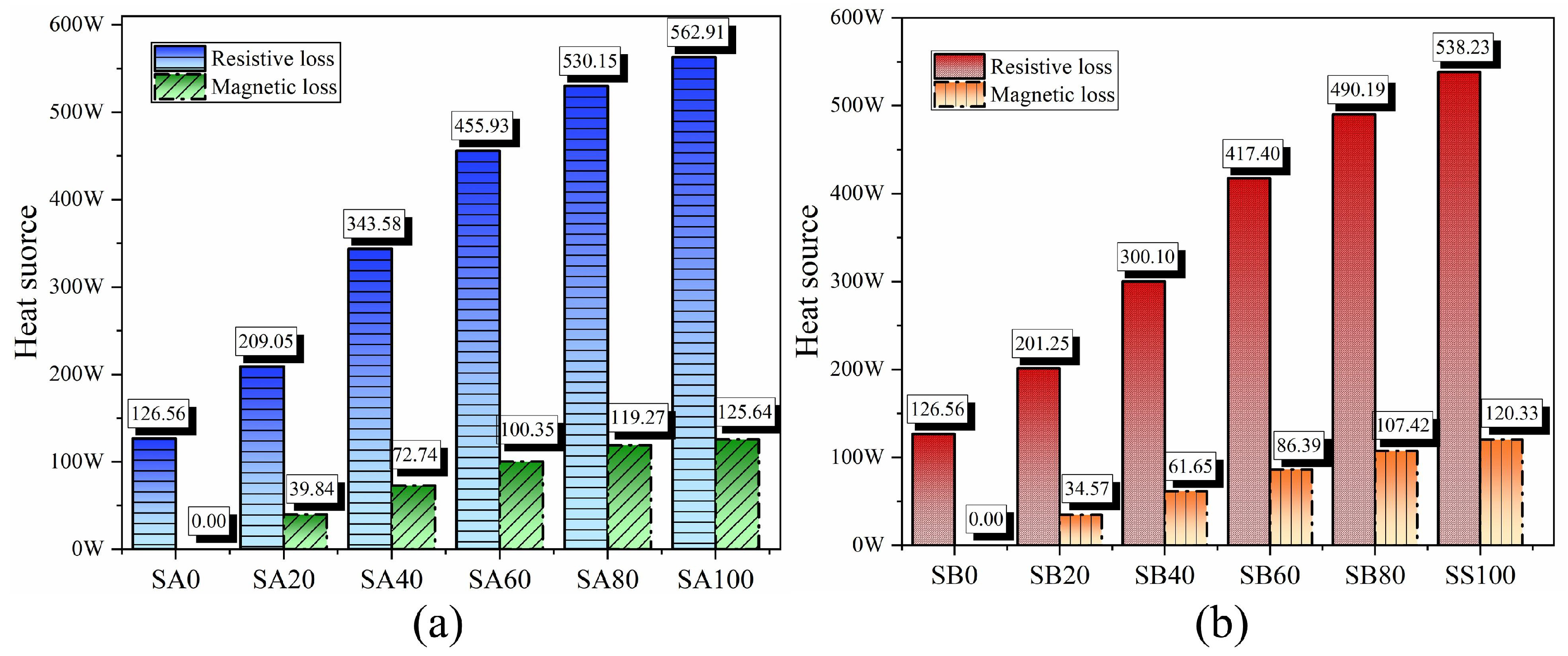
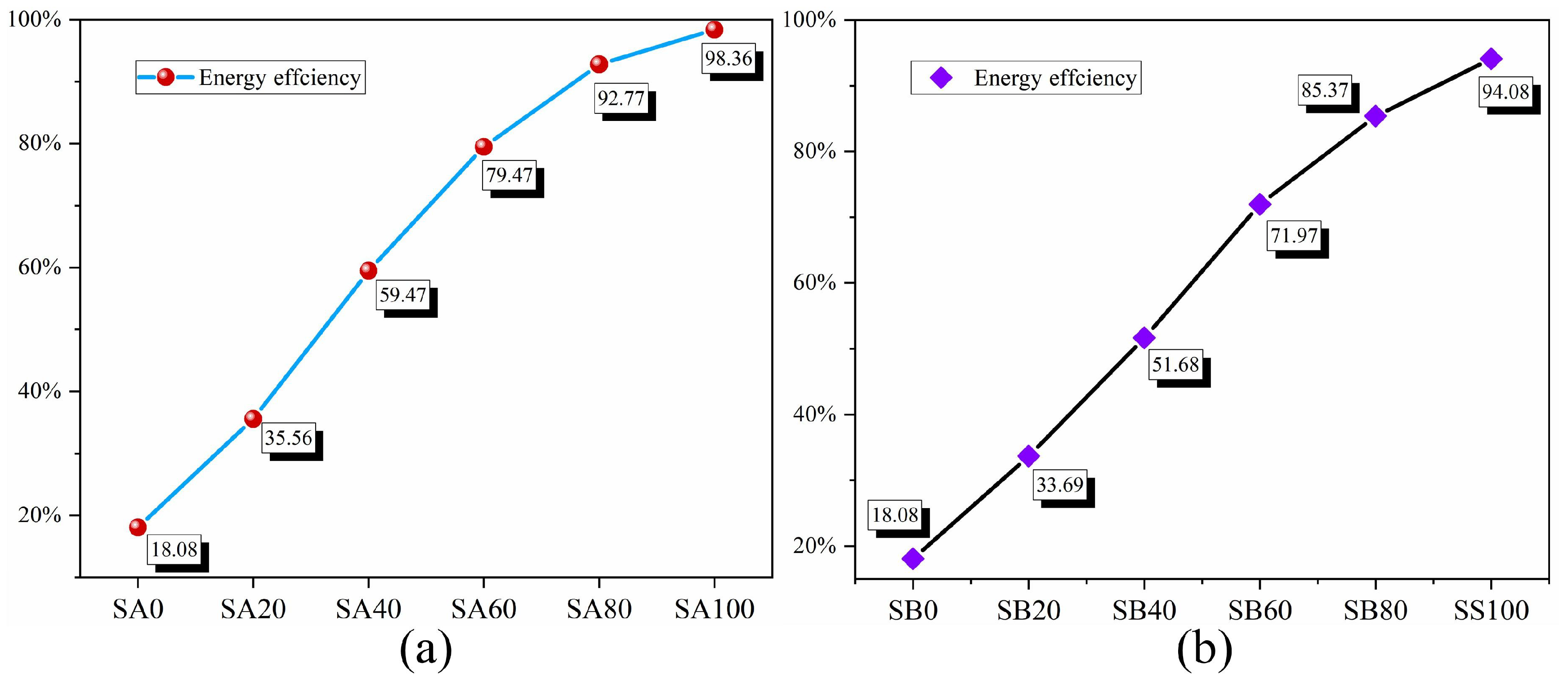
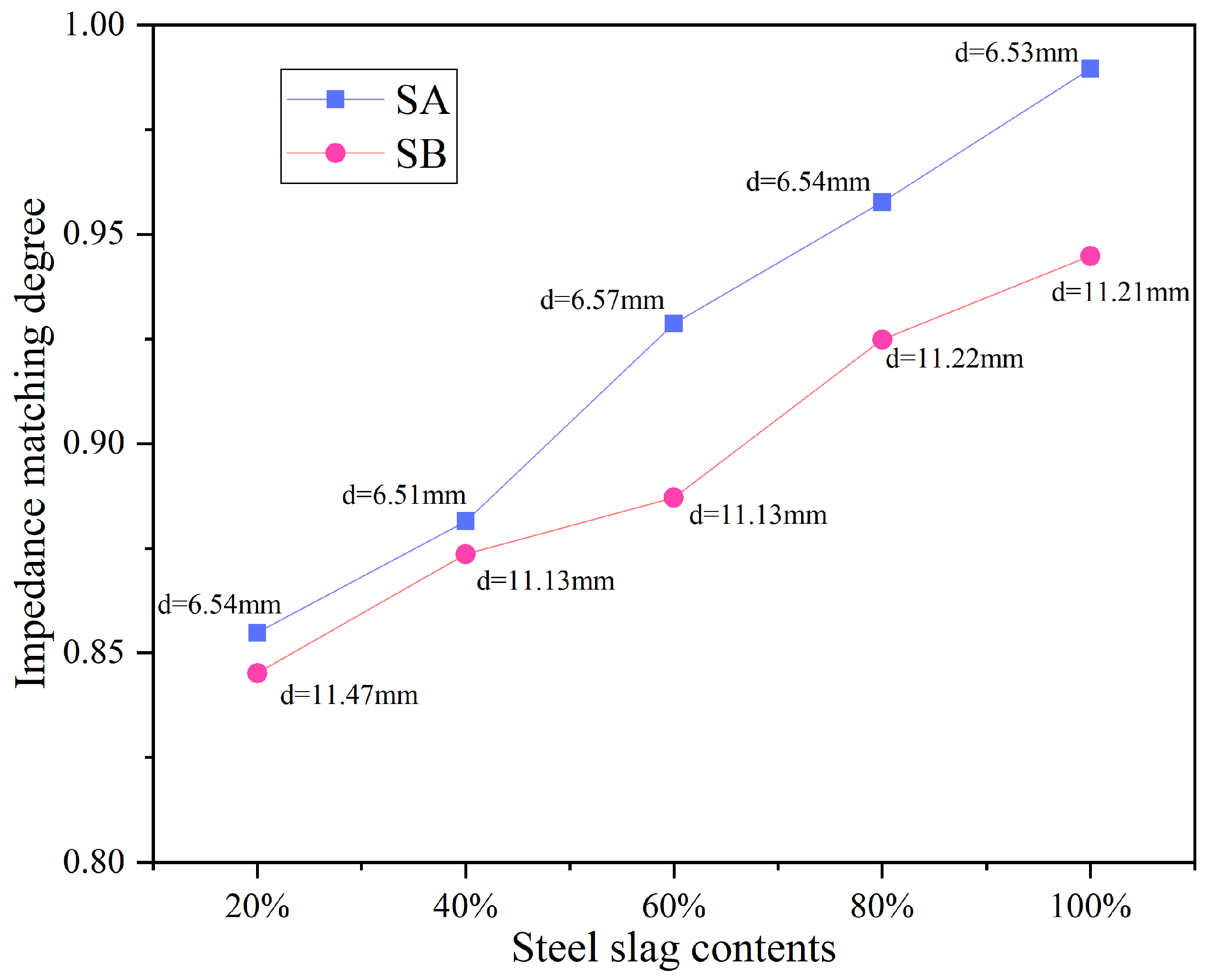
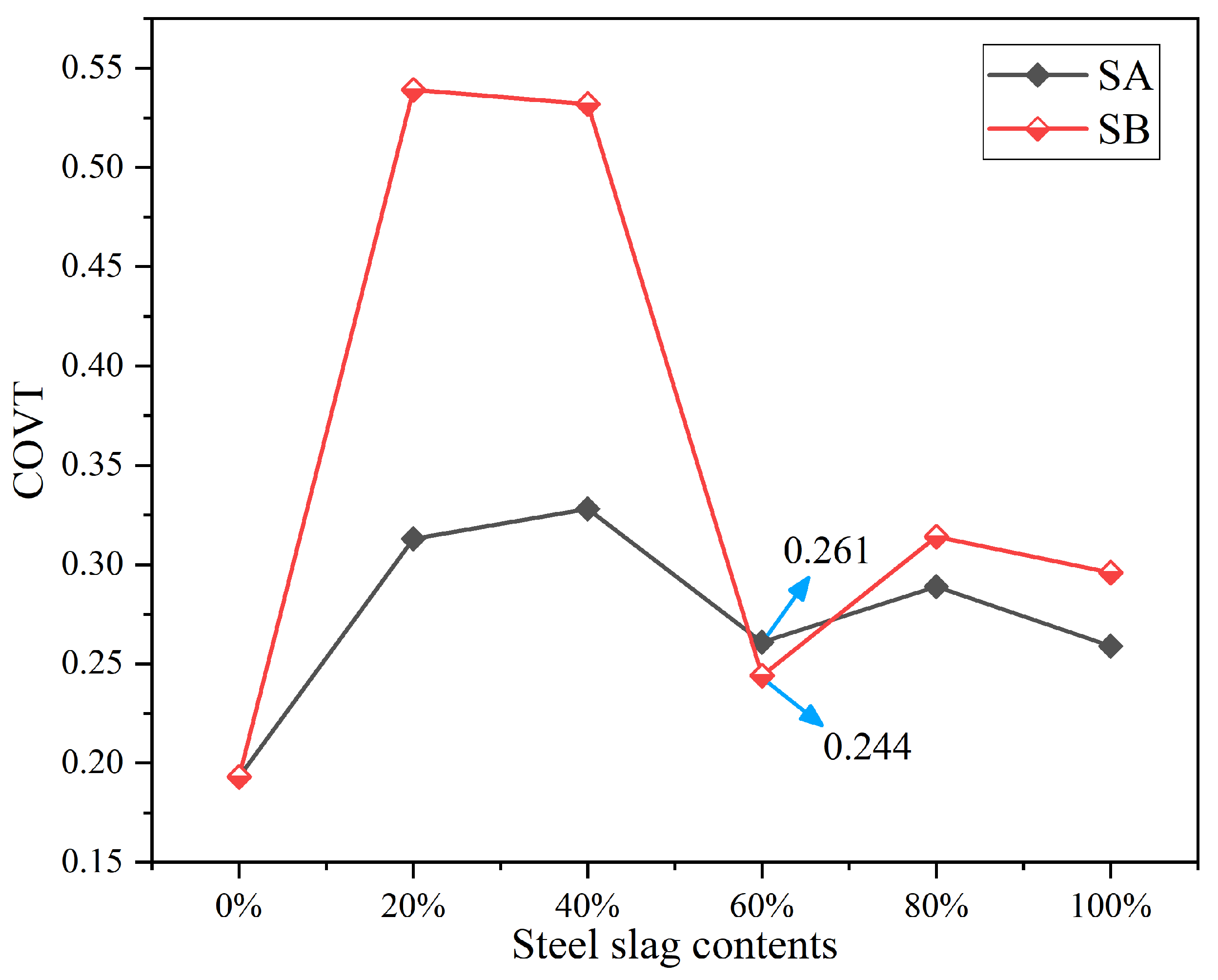
6.2. Effect of Steel Slag Contents of Asphalt Mixtures on Microwave Absorption Capacity

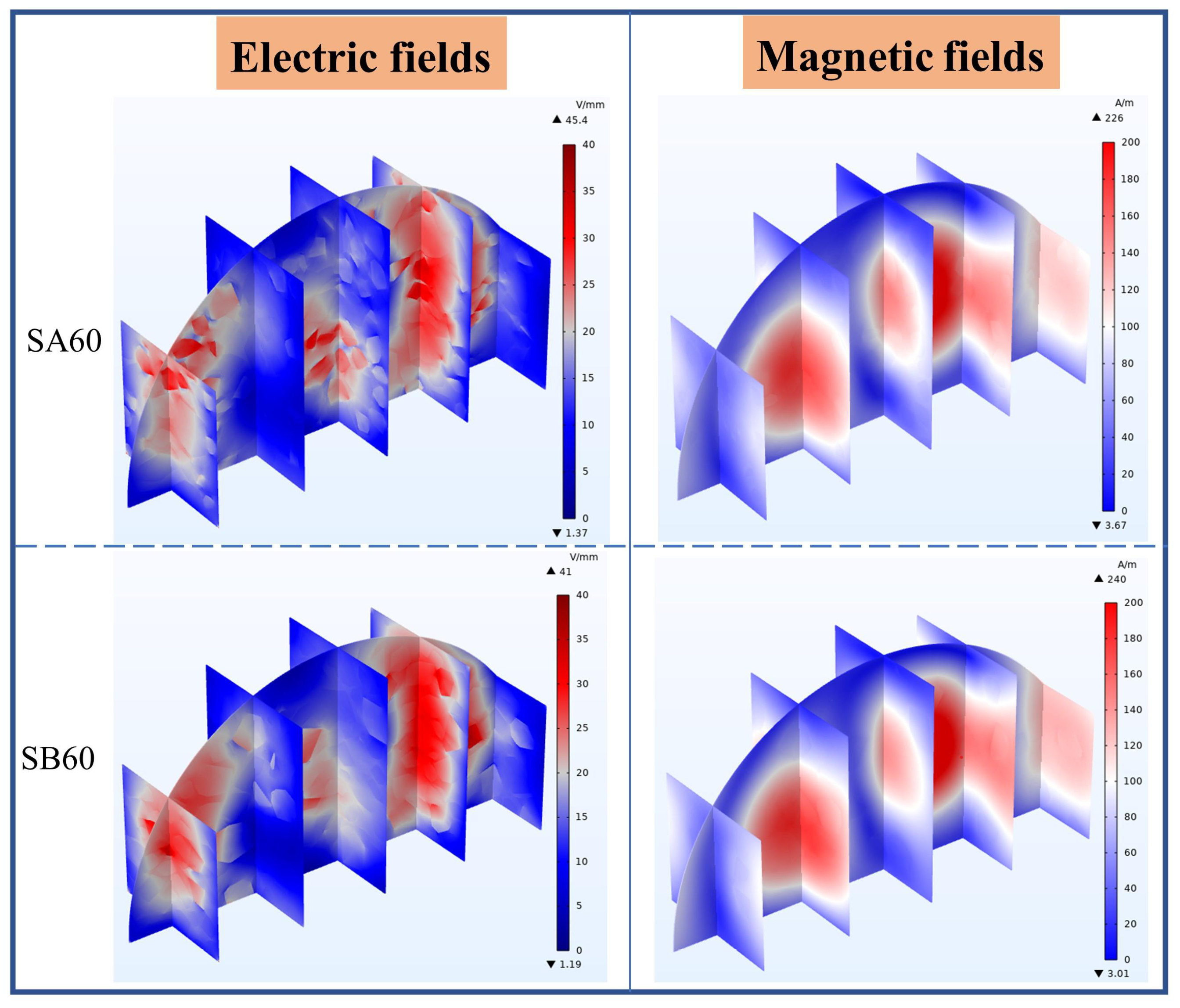
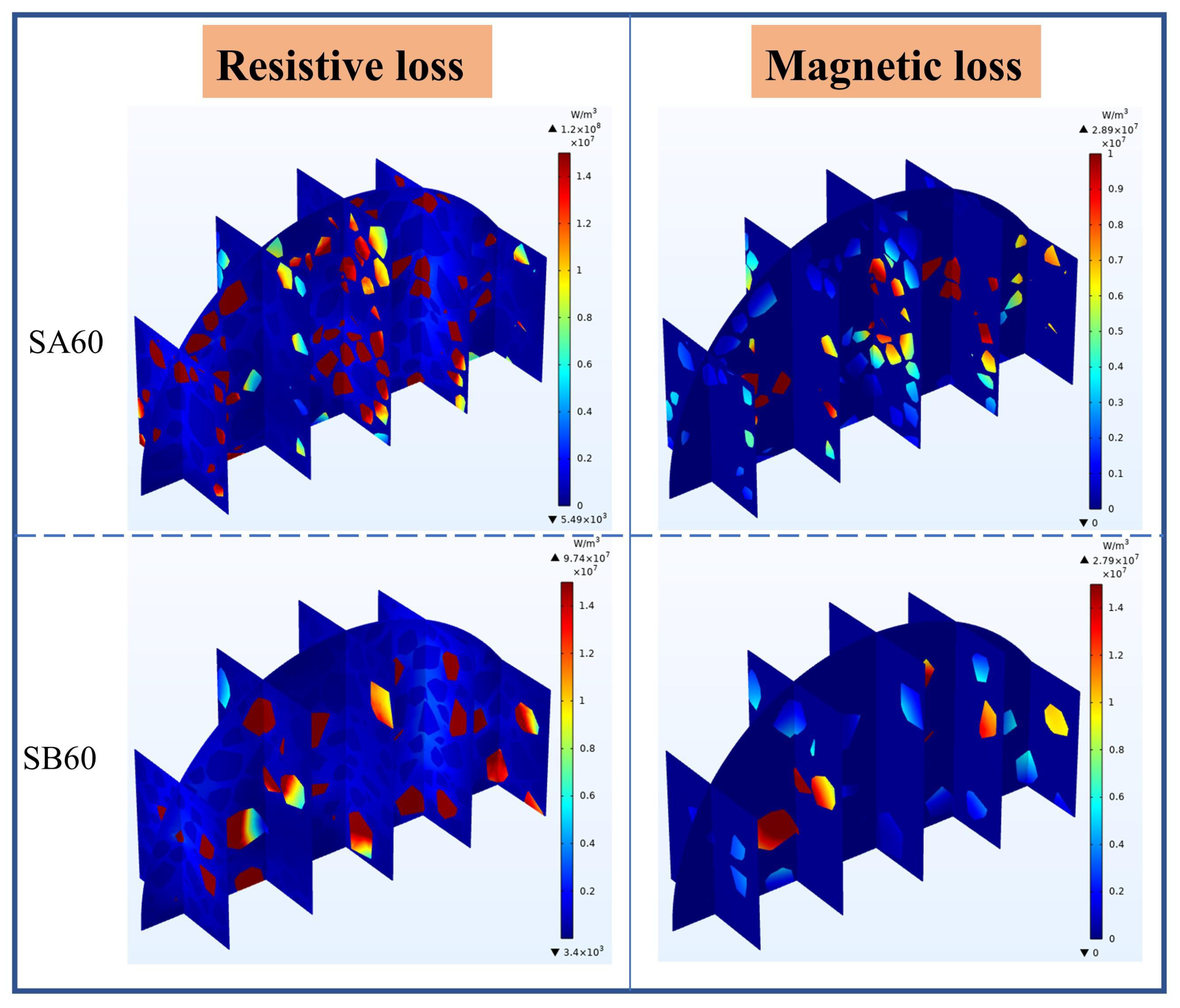
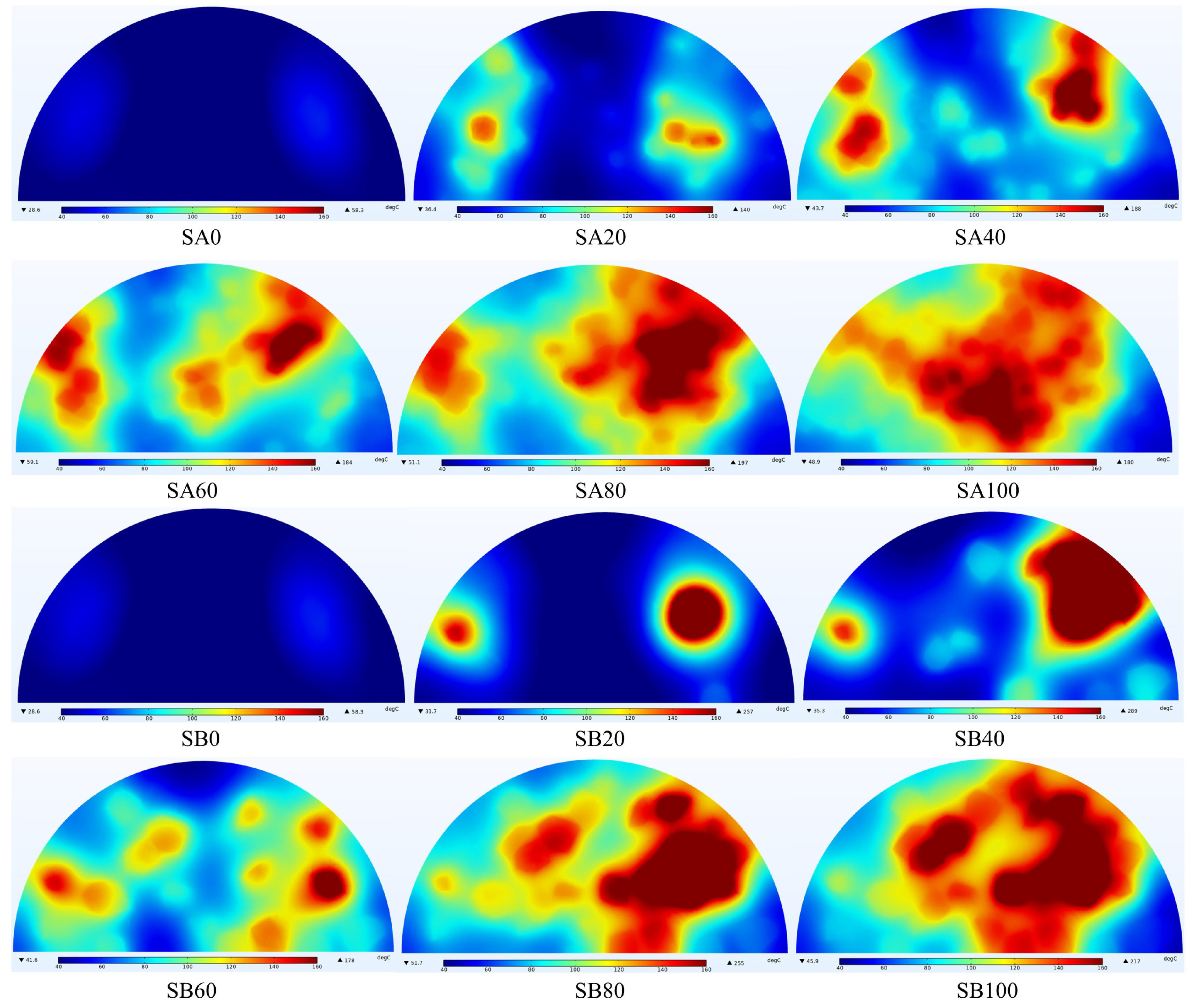
6.2.1. Electromagnetic Field and Heat Source Distribution of Asphalt Mixtures with Polyhedral Steel Slag

Steel slag can enhance the specimens’ thermal conductivity and electromagnetic properties, which gives it better microwave absorption performance than the conventional aggregate asphalt mixture. To probe the electromagnetic field and heat source distribution inside the asphalt mixture, multi-section diagrams of the electric and magnetic fields and heat sources of SA60 and SB60 are presented in Figure 7 and Figure 8. One can see that the electromagnetic field distribution within the specimen is uneven, and the peak of the electric field intensity is mainly concentrated around the steel slag. Asphalt mortar and limestone exhibit lower dielectric properties. The magnetic field of the steel slag asphalt mixture, in contrast to the electric field, displays a specific oscillatory pattern, owing to the distribution of electromagnetic wave propagation and reflection internal to the specimen.

We classified the heat sources ($Q_e$) into resistive loss and magnetic loss, which are generated by the absorption of microwaves of steel slag asphalt mixtures, including dielectric loss, eddy current loss, and hysteresis loss. Figure 8 shows that the heat source generated by the absorption of microwaves from the steel slag aggregate accounts for the majority. The uniformity of the heat source distribution of the specimen relies on the location distribution of steel slag.

6.2.2. Microwave Heating Efficiency Analysis and Optimal Replacement Rate Mechanism

As shown in Figure 9, we counted the resistive and magnetic loss for all specimens using the volume integration method. The results reveal that the primary heat source in specimens is resistive loss. Moreover, the greater the steel slag content, the greater the loss generated by the absorption of microwaves in the specimen.

The content of steel slag in different particle size intervals can remarkably influence the microwave performance of the asphalt mixture. In order to assess its performance, we employed the efficiency of steel slag asphalt mixture in terms of absorbing microwaves for evaluation; this is characterized by the ratio of the power absorbed by the specimen to the microwave input power (700 W). These are calculated as shown in Figure 10, where the highest microwave absorption efficiency is achieved when the steel slag replacement rate is 100% in the ranges of 4.75–9.5 mm and 9.5–13.2 mm. The microwave heating efficiency of steel slag replacement aggregates in the 4.75–9.5 mm range is higher than that in the 9.5–13.2 mm range, which is probably attributable to the higher aggregate volume content in the 4.75–9.5 mm interval in this gradation.

Notably, when the replacement rate is over 60%, the rate of increase in microwave heating efficiency slows down, which indicates that more and more of the microwaves have been reflected rather than absorbed. On the one hand, this ability to reflect electromagnetic waves is usually evaluated via impedance, which is influenced by the dielectric constant, the permeability, and the thickness of the material. On the other hand, the specimen does not reflect electromagnetic waves when the impedance of the material is equal to the impedance of free space. To quantitatively analyze these phenomena, we evaluated the impact of steel slag content on the reflection microwaves of asphalt mixtures, according to the equation proposed by Ma [30]. The detail function (Equation (7c)) represents the degree to which the impedance of the material deviates from the best match; the larger the value, the higher the reflection coefficient that the material exhibits. These equations are as follows:

$$K=\frac{4\pi \sqrt{{\mu }^{\prime }{\epsilon }^{\prime }}}{c}\frac{\sin \left[\left({\delta }_e+{\delta }_m\right)/2\right]}{\cos {\delta }_e\cos {\delta }_m}$$

(7a)

$$\begin{array}{c}M=[4{\mu }^{\prime }\cos {\delta }_e{\epsilon }^{\prime }\cos {\delta }_m]\cdot [{({\mu }^{\prime }\cos {\delta }_e-{\epsilon }^{\prime }\cos {\delta }_m)}^2\\ +{(\tan \frac{{\delta }_m-{\delta }_e}{2})}^2{\left({\mu }^{\prime }\cos {\delta }_e+{\epsilon }^{\prime }\cos {\delta }_m\right)}^2{]}^{-1}\end{array}$$

(7b)

$$\Delta =\left|{\sinh }^2\left(Kfd\right)-M\right|$$

(7c)

where ${\delta }_e$ is the dielectric loss angle ($\tan {\delta }_e={\mu }^{″}/{\mu }^{\prime }$), ${\delta }_m$ is the magnetic loss angle ($\tan {\delta }_m={\epsilon }^{″}/{\epsilon }^{\prime }$), $c$ is the speed of light, $f$ is the microwave frequency, ${\mu }^{\prime }$ and ${\epsilon }^{\prime }$ represent the real parts of relative complex permittivity and permeability, and ${\mu }^{″}$ and ${\epsilon }^{″}$ represent the magnetic loss imaginary parts of relative complex permittivity and permeability, respectively.

Noting that these electromagnetic properties are represented by the average relative complex permittivity and the average relative complex permeability of the asphalt mixture, which are obtained by volume averaging, we assume that the nominal thickness of the medium ($d$) is equal to the average particle size of the steel slag, therefore Equation (8) is shown below:

$$d=\frac{{\displaystyle \sum _{i=1}^{N}Ag{g}_i}}{Num}$$

(8)

where $Ag{g}_i$ is the particle size of the steel slag and $Num$ is the total number of steel slag particles in the interval.

As shown in Figure 11, SA denotes steel slag within 4.75–9.5 mm, SB denotes steel slag within 9.5–13.2 mm, and the horizontal coordinate represents the steel slag content in each interval. The impedance matching degree of the specimen is the lowest when the steel slag content is the least, which means that steel slag affects the impedance of the asphalt mixture. SA has a higher impedance-matching degree than SB, implying that steel slag with a 9.5–13.2 mm particle size may reflect fewer microwaves. Steel slag will also increase the degree of specimen impedance matching; the more steel slag there is, the higher the microwave reflectivity of the specimen. A high reflectivity means that more microwaves radiating on the steel slag’s surface are reflected. Chen’s study suggests that high-density steel slag aggregates reflect microwaves [21], whereas this study shows that the reflection properties of steel slag may be influenced not only by the density but also by the dielectric constant, permeability, and particle size.

6.3. Influence of Steel Slag Content on Temperature Distribution

6.3.1. Variation of Temperature Distribution in the Center Section

The steel slag in the asphalt mixture is initially heated in the heating process. Through the microwave’s radiation and the steel slag’s heat transfer, the asphalt and aggregate continuously warm up [23]. Until the asphalt reaches softening temperature and starts to flow, the microcracks in the specimen achieve the best self-healing effect through the flow of asphalt at an optimal temperature. However, a higher temperature than this will cause the asphalt to overheat and deteriorate. Consequently, we drew the temperature distribution of the center slice of the specimen in the 40th second. The temperature of the center slice can reflect the details of the temperature distribution inside the specimen and can be used to investigate the optimal volume replacement rate by comparing the temperature distribution in all instances.

As shown in Figure 12, compared to asphalt mixtures with conventional aggregate (SA0, SB0), the addition of steel slag to the specimens shows significant temperature peaks, which boosts the internal temperature heat transfer of the asphalt mixture. The temperature was highest in the left and right zones of the specimen because the microwave frequency, microwave power, and specimen location impacted the electromagnetic field distribution and, thus, influenced the temperature distribution. When SA20 and SB20 were heated to the 40th second, the middle of the specimen was distributed, with an evident low-temperature zone; in the center of the low-temperature zone, some isolated high-temperature peaks appeared when the added steel slag content reached 40%. SA40 had a more even distribution of light-colored high-temperature zones compared to SB40. The latter appeared to be overheating in some zones on the right side, but there were still a large number of low-temperature zones overall.

When the steel slag content increased to over 60%, most specimen interiors showed light-colored high-temperature zones. The original middle low-temperature zones were slowly covered, and the temperature inside the specimen was gradually upgraded. Meanwhile, the temperature of some zones exceeded 100 °C. As the steel slag content increased to more than 80%, the temperature in most zones of the asphalt mixture exceeded 100 °C as well. Asphalt is melted and aged at this high temperature, detaching from the aggregate, deteriorating the performance of the asphalt mixture, and finally affecting the healing level negatively [31].

In order to accurately assess the uniformity of the internal temperature heat transfer of specimens with different steel slag contents under microwave heating, we utilized the variance coefficient to evaluate the uniformity of temperature distribution:

$$\mathrm{COVT}=\frac{\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N{\left(T_i-\overline{T}\right)}^2}}}{\overline{T}}$$

(9)

where $T_i$ refers to the temperature (°C) at a data point at the center slice, $N$ represents the total data point, $\overline{T}$ represents the average temperature (°C) at the center slice.

We calculated the coefficient of variance by extracting the temperature values for each data point on this slice, depicted in Figure 13, with lower values denoting a more uniform distribution. The addition of steel slag will result in uneven heat transfer among the components within the specimen. In particular, the aggregate size in the 9.5–13.2 mm makes the internal temperature distribution of SB20 and SB40 very uneven compared to other specimens at the same replacement rate. Figure 13 shows that when the replacement rate is 60%, the variance coefficients of both specimens reach the lowest point, which means that the temperature distribution is relatively uniform. The uniformly distributed temperature helps the steel slag asphalt mixture to prevent local overheating from microwave heating and enhances the healing effect of microcracks.

6.3.2. Internal Temperature Gradients of Steel Slag Asphalt Mixtures

Internal temperature changes in the steel slag asphalt mixture during microwave heating are very complex. The different dielectric properties of asphalt mortar, limestone aggregates, and steel slag lead to different heating rates under the radiation of microwaves, resulting in temperature gradients. The temperature gradient reflects the direction and rate of the fastest change in temperature around a particular location, which can describe the difference in the heat transfer rate of each component within the specimen in a better way. In addition, temperature gradients trigger thermal stress; while high temperatures melt the asphalt, excessive thermal stress can lead to debonding at the interface between the asphalt and the aggregate. Figure 14 depicts the magnitude of the temperature gradient in the center slices of all specimens, with the peak of the temperature gradient occurring at the interface of the steel slag and diffusing outwards toward the asphalt mortar. Compared with SA (4.75–9.5 mm), SB (9.5–13.2 mm) has a higher magnitude of temperature gradient than the former, demonstrating that specimens containing 4.75–9.5 mm of steel slag aggregates exhibit better uniform temperature distribution during microwave heating. In addition, thermal stress variations due to stress differences and thermal expansion promote the interfacial debonding behavior of steel slag and asphalt. In this way, the higher temperature gradients generated by steel slag aggregates in the 9.5–13.2 mm range may harm the healing of the asphalt mixture.

7. Conclusions

To realistically simulate the shape of aggregates, this work first develops a meso-random model via an algorithm for the random growth and placement of polyhedral aggregate, which accounts for the particle size and location distribution of aggregate particles. Then, the effects of different steel slag contents in various particle size intervals on the healing performance and microwave heating efficiency of the steel slag asphalt mixture are evaluated via a microwave heating numerical model. The details of the electromagnetic and thermal field distributions are analyzed, and the models are validated with the reported experimental data. The following conclusions can be drawn:

• The algorithm for random growth and placement that is presented in this paper can generate a polyhedral aggregate model with a high volume ratio. The details of the internal temperature and electromagnetic fields of the asphalt mixture during microwave heating can be effectively described by the 3D mesoscale model that has been developed. The shape of the aggregate (sphere and polyhedron) has little effect on the uniformity of heat transfer within the asphalt mixture. The steel slag asphalt mixture’s surface temperature values accord well with the reported experimental findings, which demonstrates the validity of the model.
• When the steel slag replacement rate is 60% in both the 4.75–9.5 mm and 9.5–13.2 mm particle size intervals, the volume average temperature of the asphalt mixture is the closest to the optimal healing temperature, and the temperature distribution of the asphalt mixture is the most uniform. In particular, the temperature gradient around the boundary of the steel slag is the highest. The heat transfer is more uniform for the 4.75–9.5 mm steel slag compared to the 9.5–13.2 mm steel slag.
• The electromagnetic field of the asphalt mixture exhibits a specific oscillation pattern under microwave radiation. In addition, the dielectric constant, permeability, and particle size of steel slag may affect the properties of microwave reflection. Too much steel slag will increase the impedance of the specimen and hinder the absorption of microwaves.

The void ratio of an asphalt mixture is an important factor affecting heat transfer, and voids in the mesoscopic model should be considered in future research. At the same time, the effects of thermal stresses caused by the microwave heating process need to be explored in more depth.