A Joint Estimation Method Based on Kalman Filter of Battery State of Charge and State of Health
Abstract
:1. Introduction
2. Battery Modeling and Parameter Identification
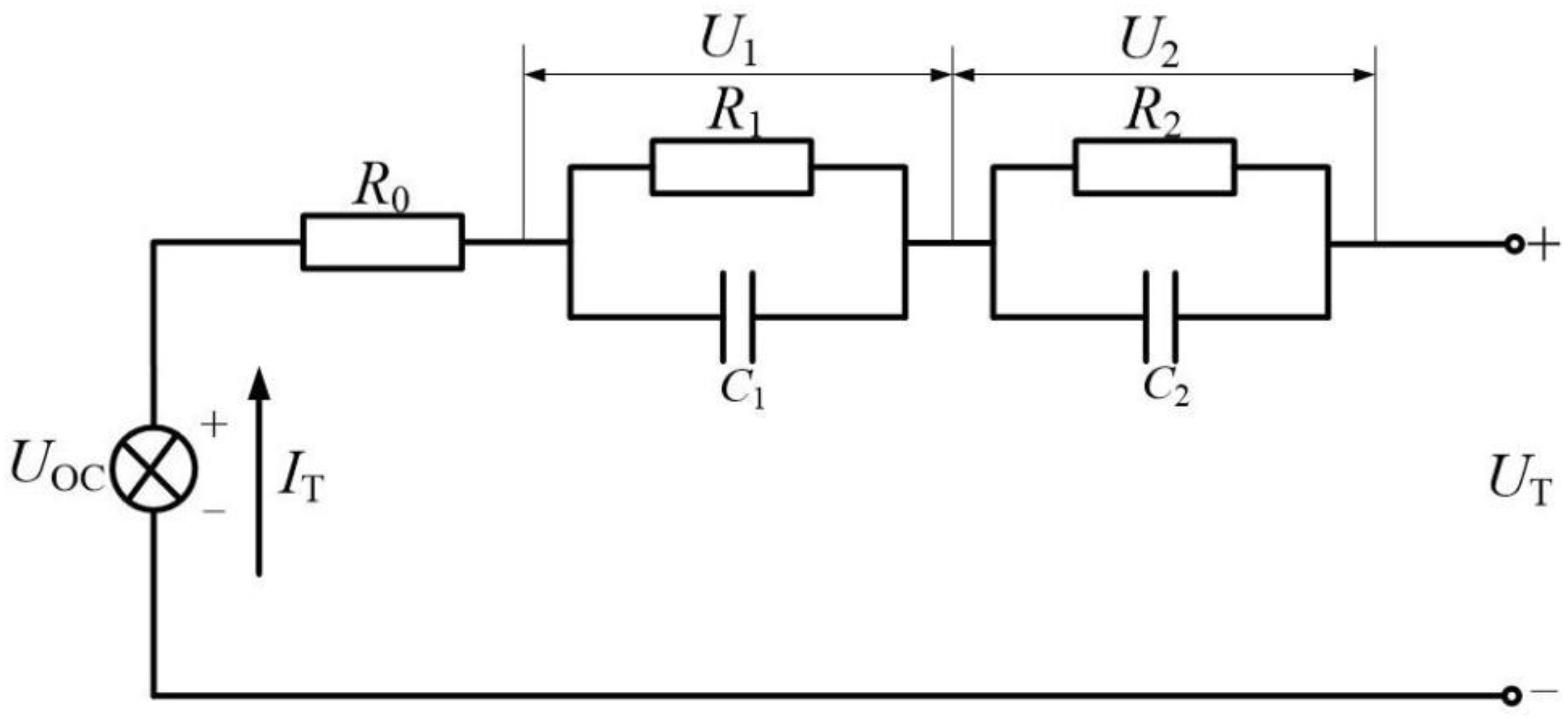
2.1. Equivalent Circuit Model of Lithium Battery
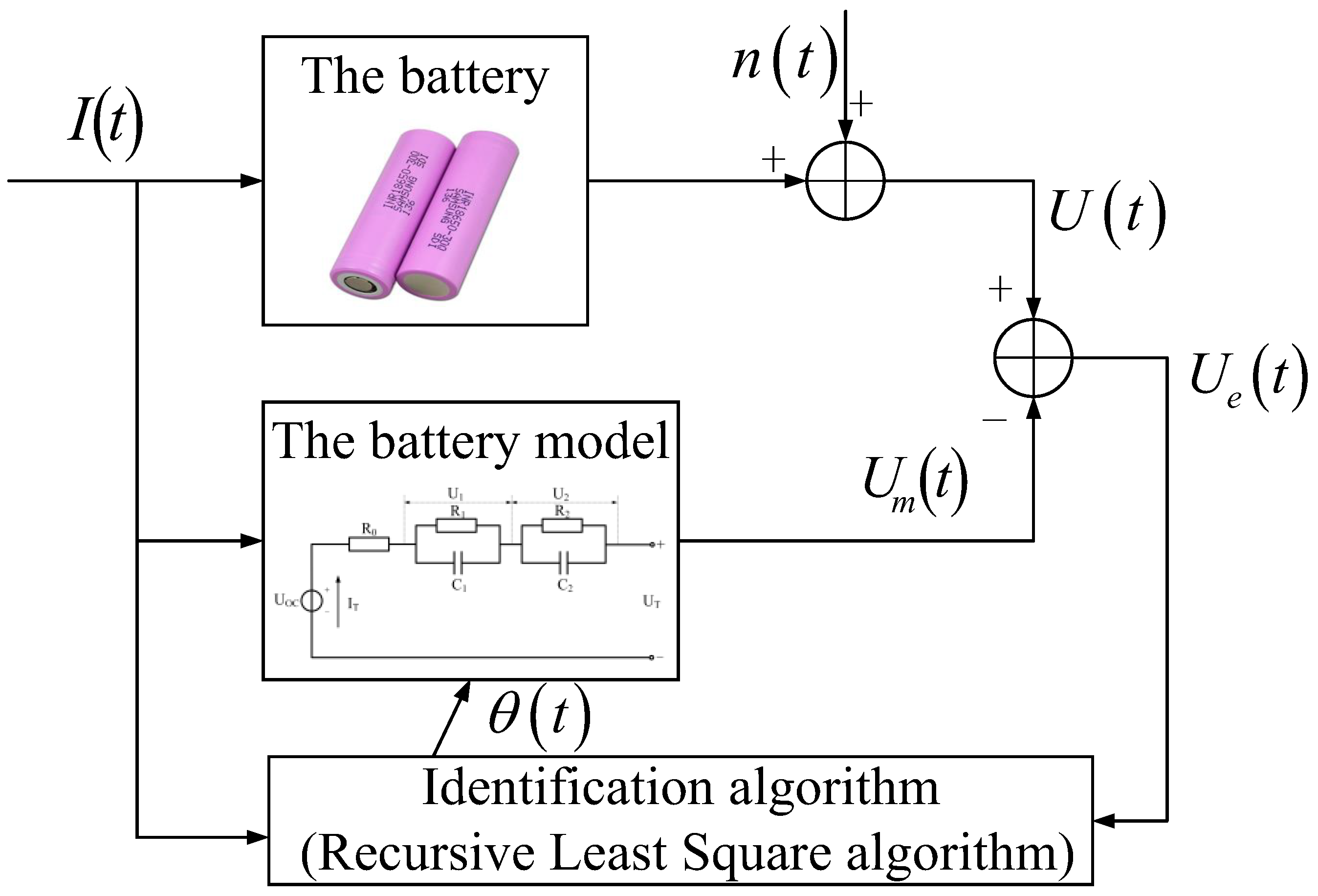
2.2. Online Parameter Identification of Lithium Battery
3. Joint State Estimation of Battery Power
3.1. UKF Algorithm Principle
3.2. UKPF Algorithm Principle
- (1)
- PF algorithm principle
- (2)
- UKPF algorithm principle
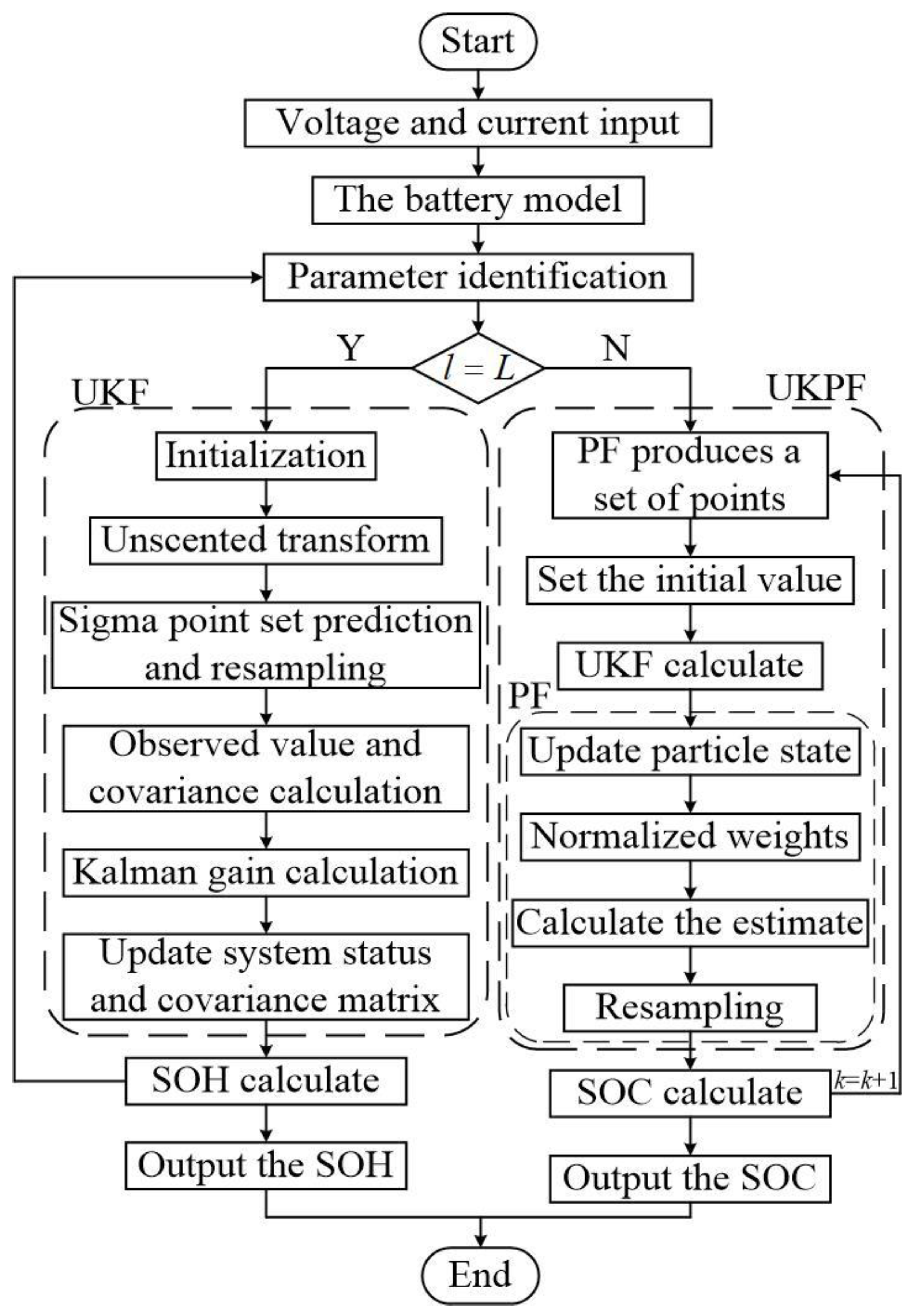
3.3. Multi-Time Scale Joint Estimation of Battery power State
- (1)
- Input the battery voltage and current data into the battery model for online parameter identification;
- (2)
- Determine whether the time scale transformation is met, if so, step (3) is carried out, otherwise, step (4) is carried out;
- (3)
- UKF estimates SOH and uses estimated results to update system parameters;
- (4)
- UKPF cycle estimation SOC;
- (5)
- Output the SOC and SOH estimation results.
4. Test Results and Analysis
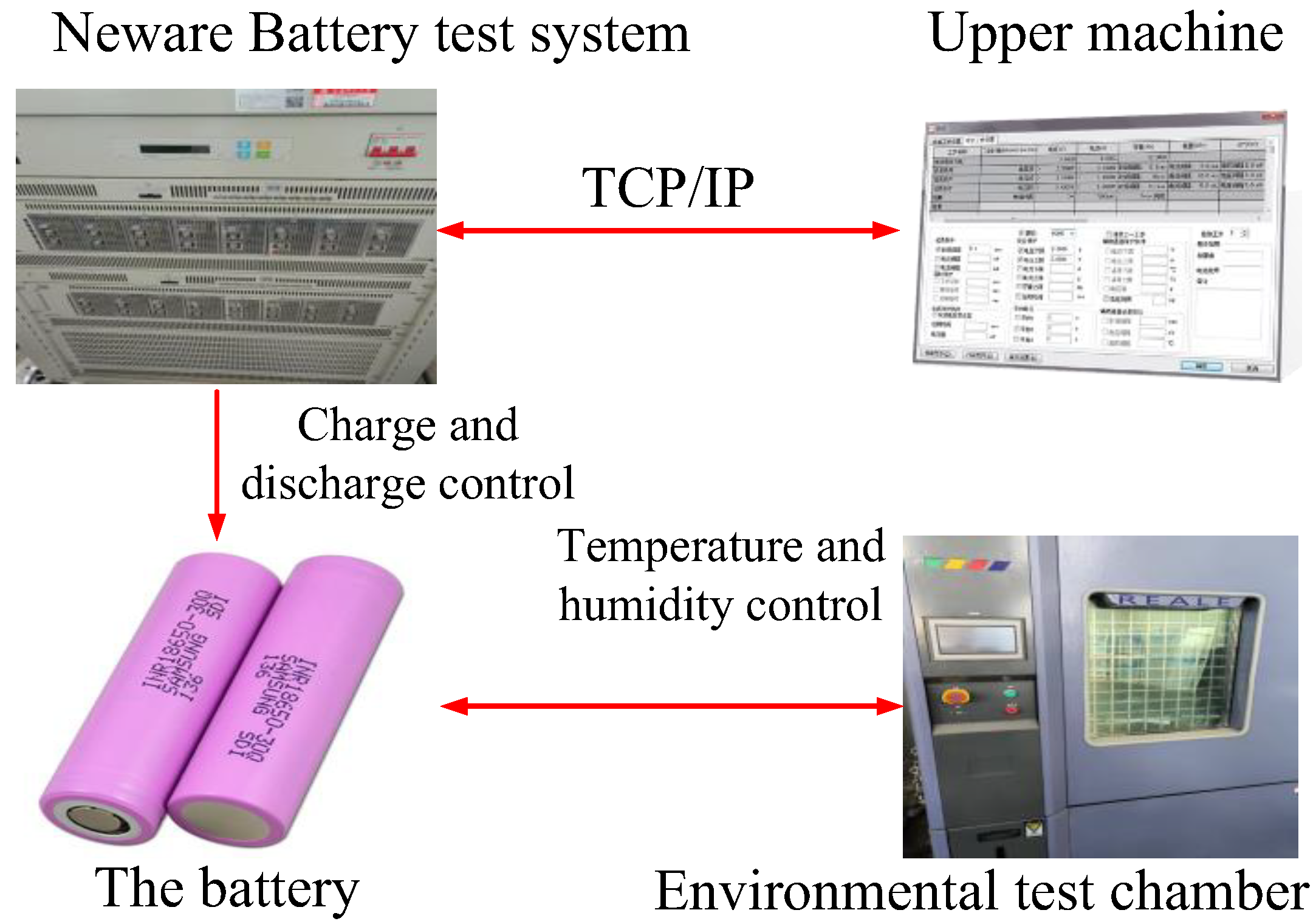
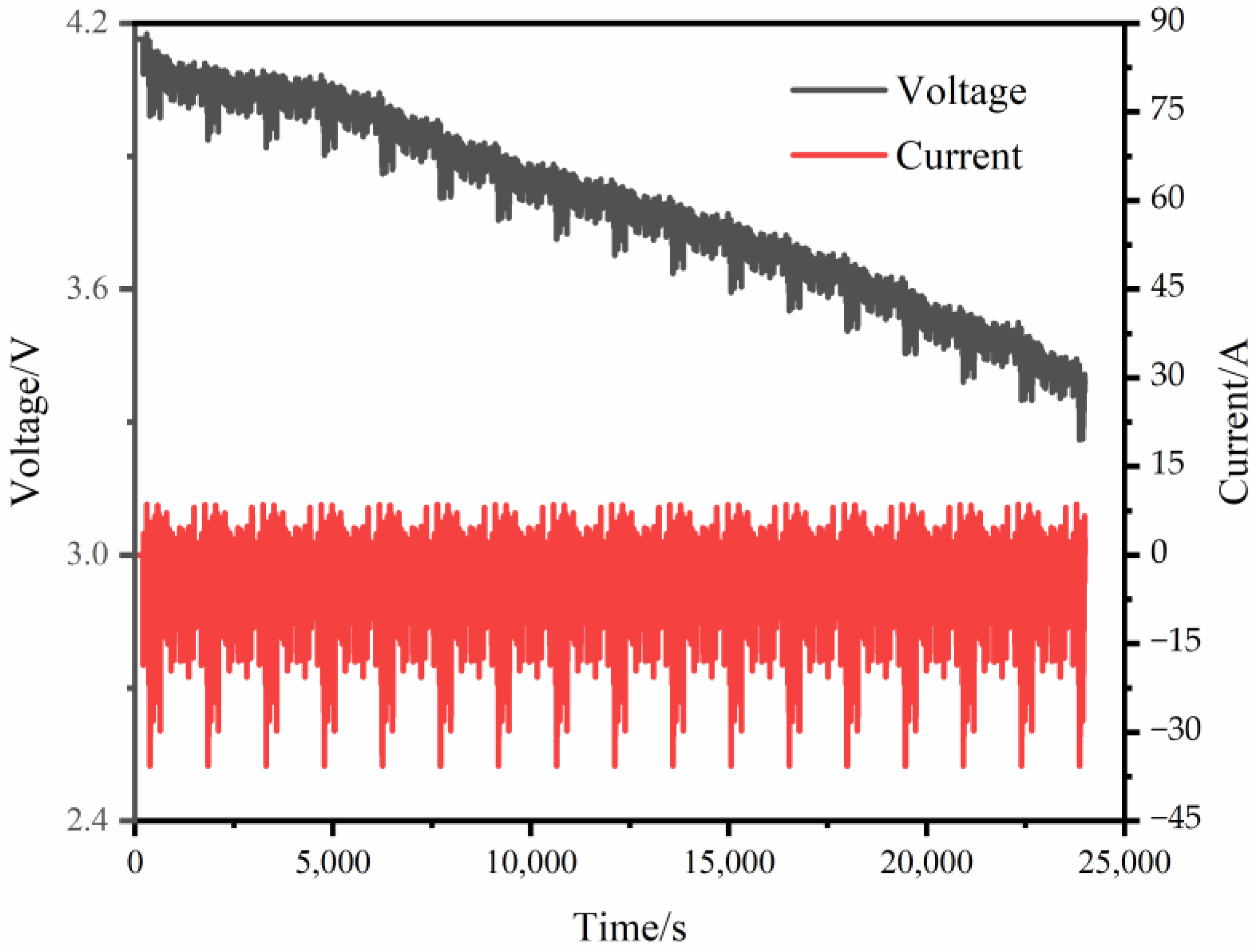
4.1. Test Platform Building and Test Data Collection
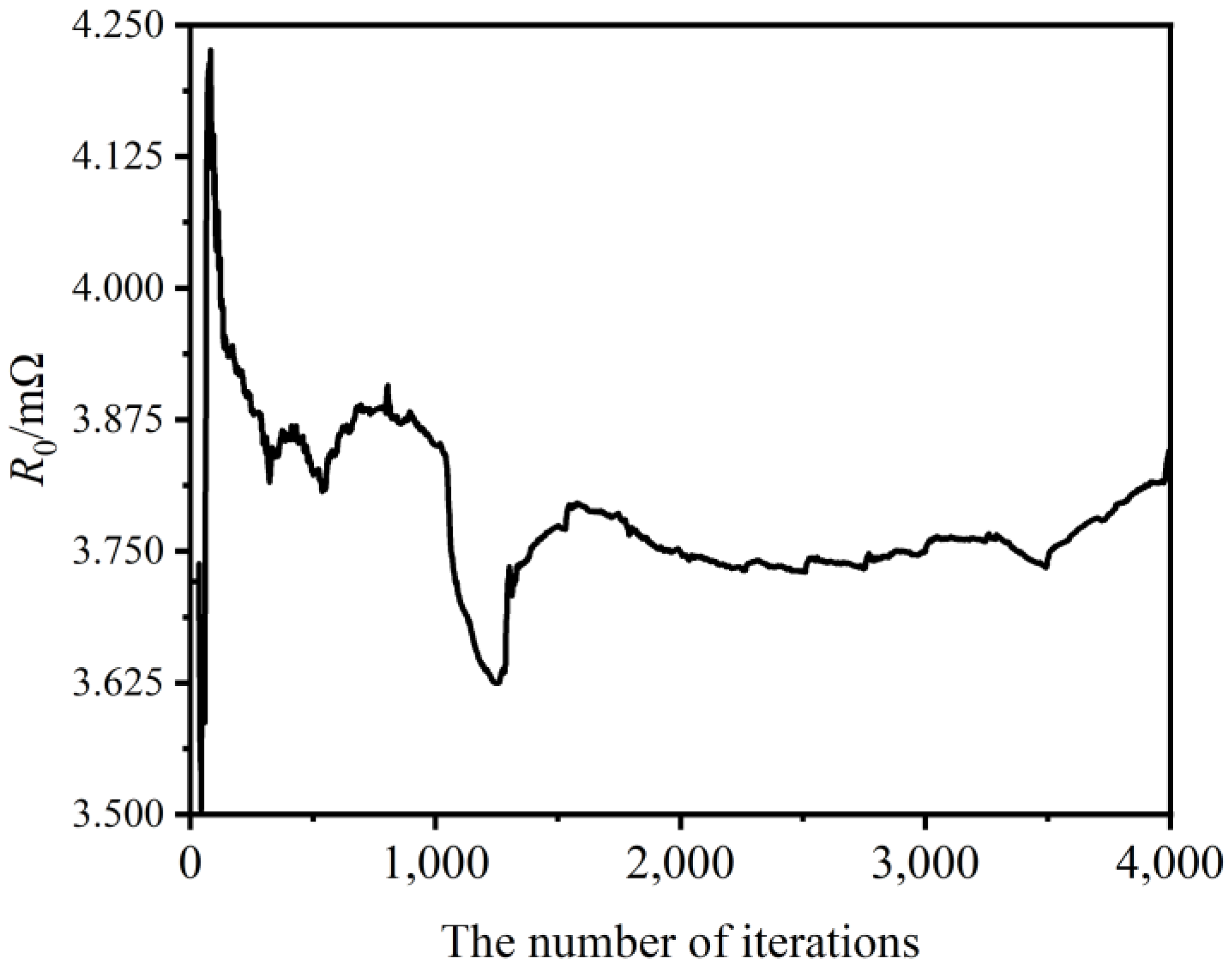
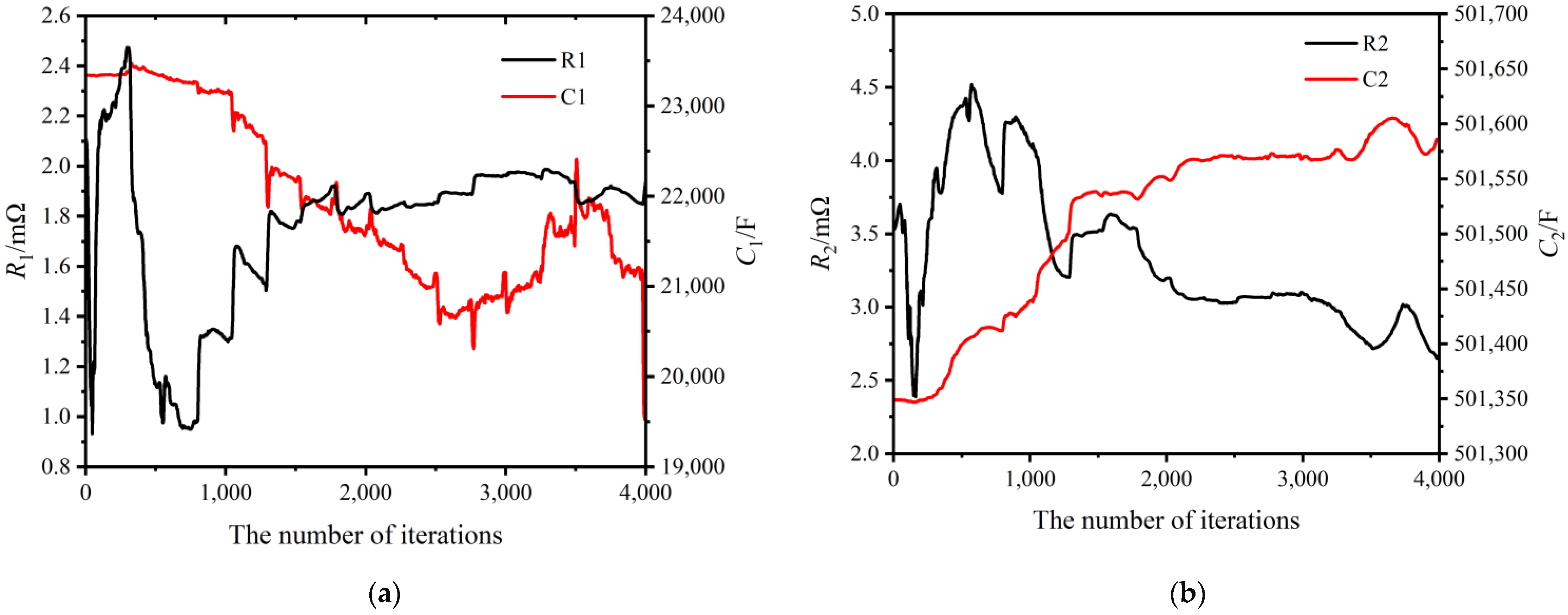
4.2. Parameter Identification Results
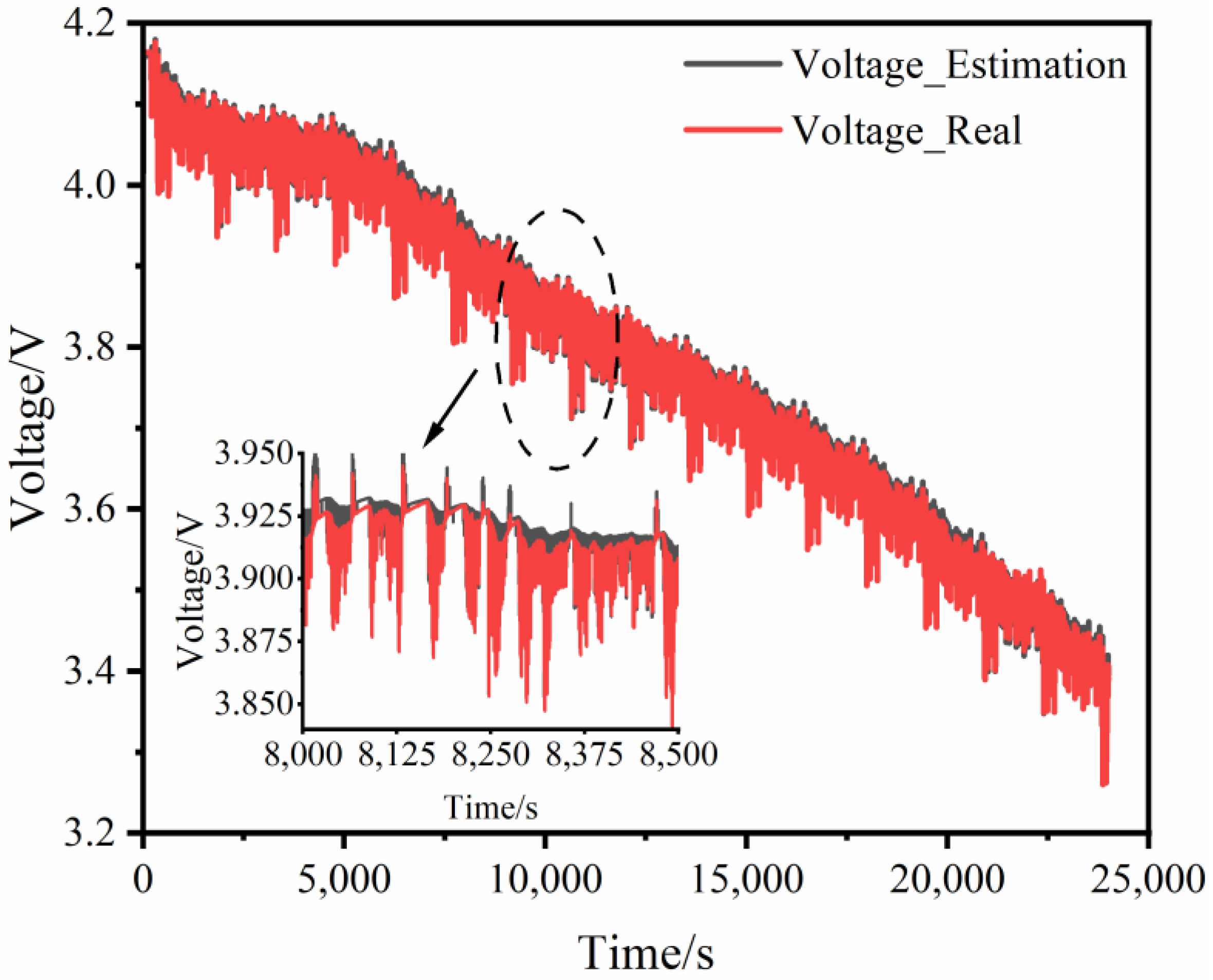
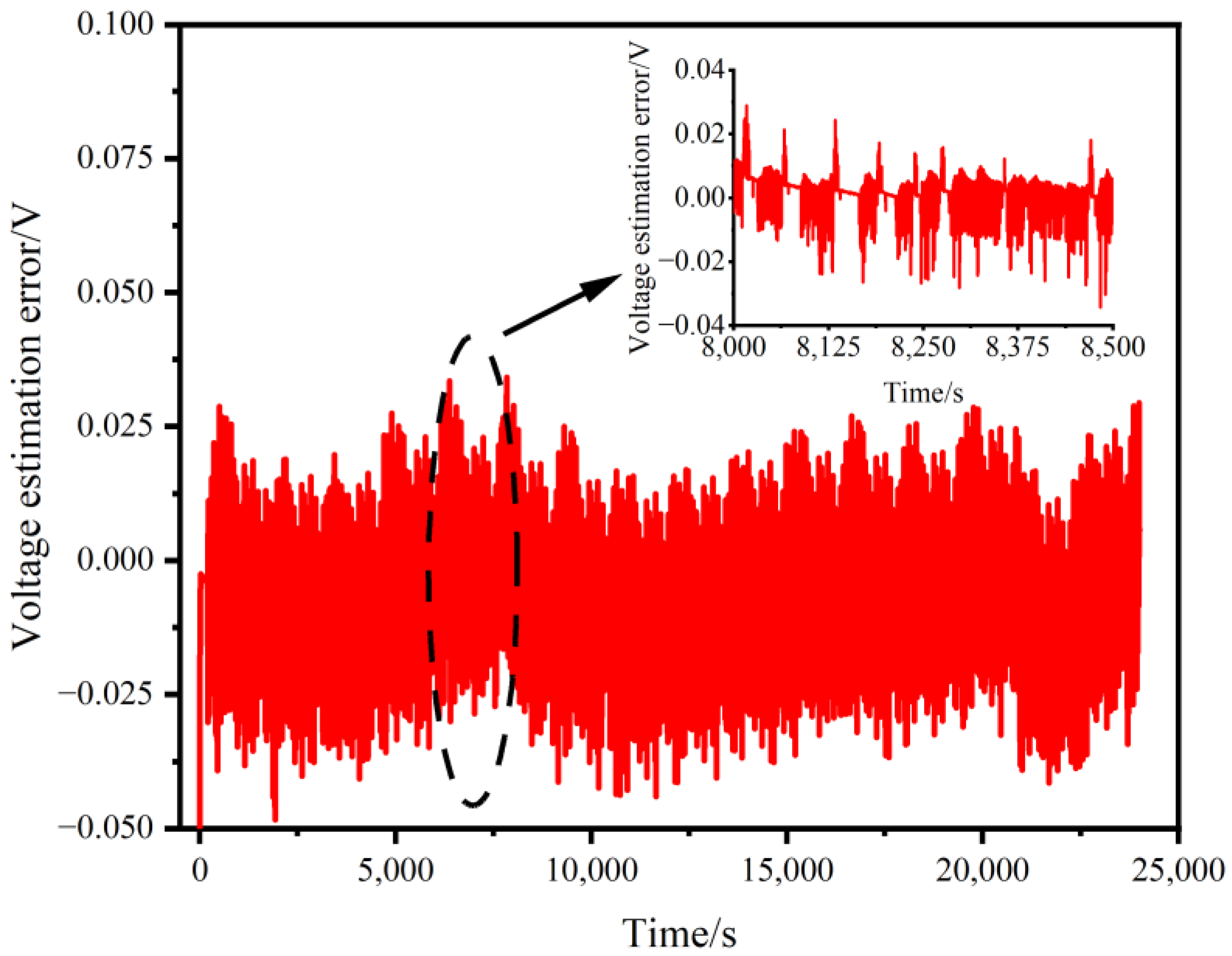
4.3. Multi-Time Scale Joint Estimation Results
- (1)
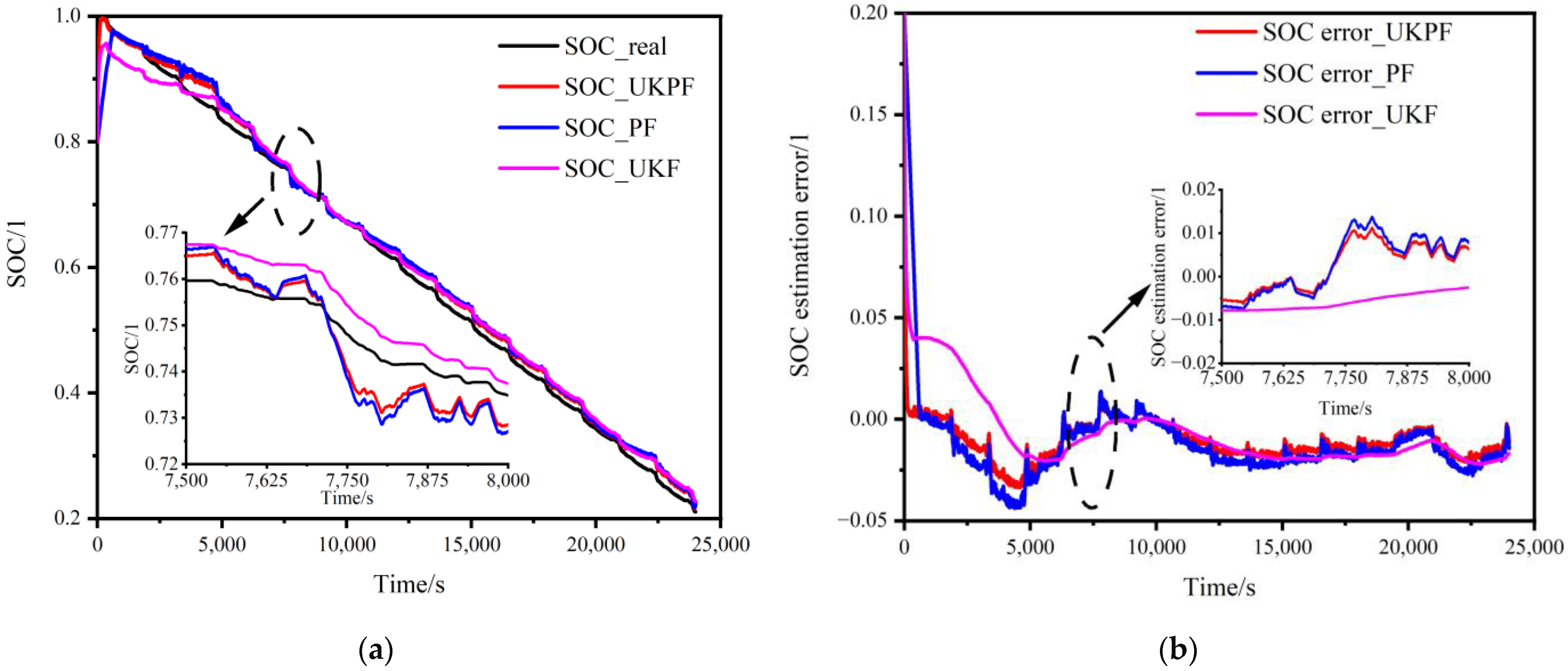
- UKPF algorithm estimation of SOC
- (2)
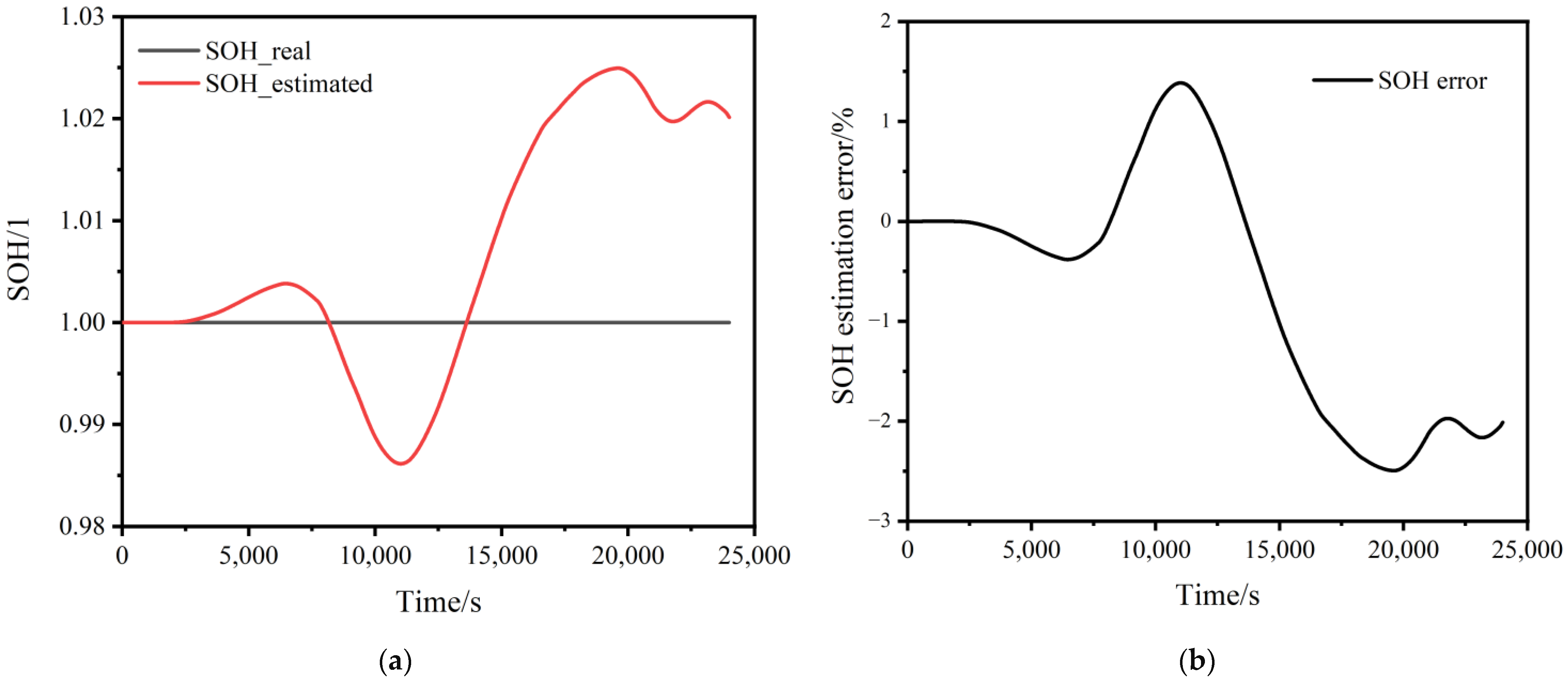
- UKF algorithm estimation of SOH
- (3)
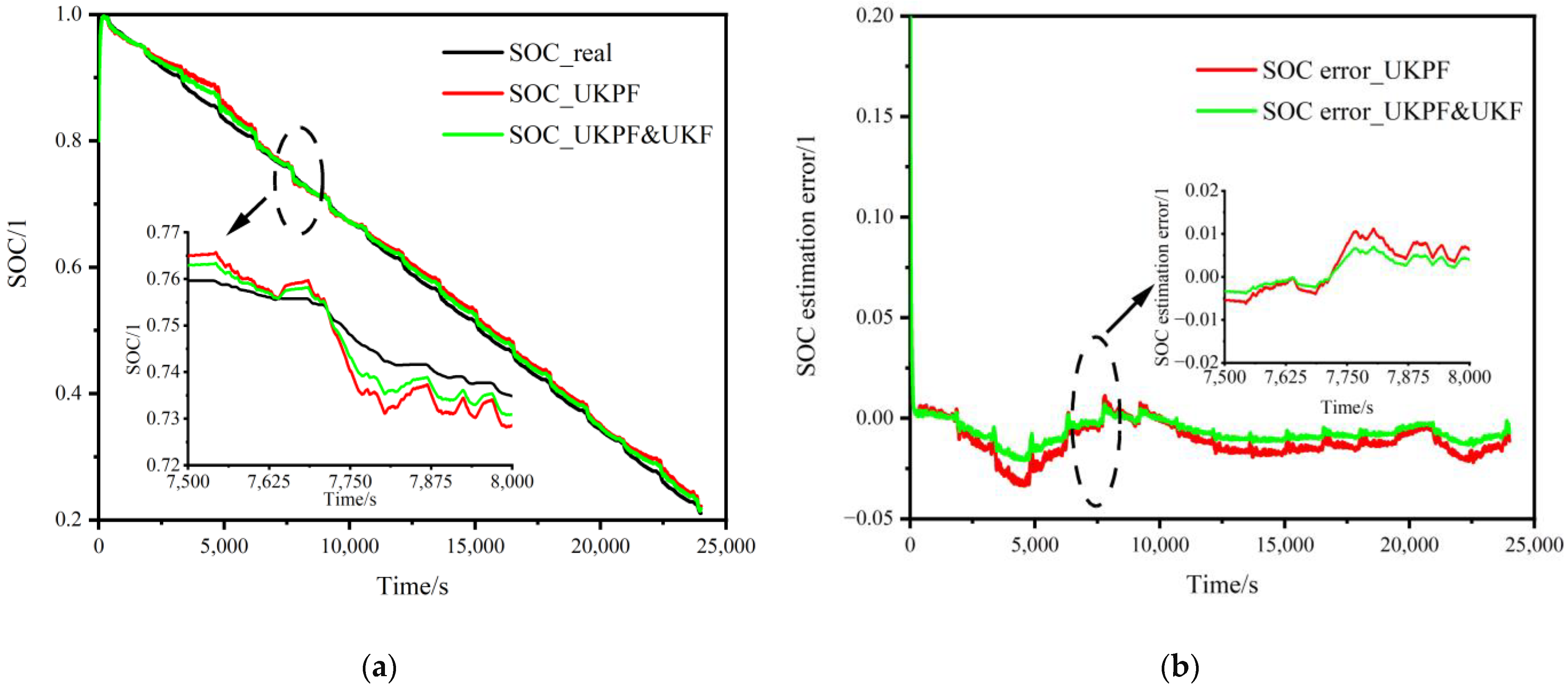
- Multi-time scale joint estimation results
5. Conclusions
- (1)
- The battery parameters can be identified online. The error of the parameter identification results is less than 5%, which verifies the validity and accuracy of the model. Therefore, this model can accurately represent the working process of a lithium battery and lays a foundation for the subsequent estimation of its battery state.
- (2)
- Compared with the UKF and the PF algorithm, the UKPF algorithm has higher robust accuracy and stability, and its estimation error of a lithium battery’s state of charge is less than 3.4%. The SOH error of the UKF algorithm is less than 2.5%, which can accurately and effectively estimate the SOH of the battery.
- (3)
- The multi-time scale joint estimation error is within 2.2%, which significantly improves the estimation accuracy of a battery’s SOC and ensures the long-term estimation performance of a battery.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, Q.; Xu, J.; Li, X.; Xu, D.; Cao, B. State-of-health estimation of lithium-ion battery based on fractional impedance model and interval capacity. Int. J. Electr. Power Energy Syst. 2020, 119, 105883. [Google Scholar] [CrossRef]
- Xiao, F.; Li, C.; Fan, Y.; Yang, G.; Tang, X. State of charge estimation for lithium-ion battery based on Gaussian process regression with deep recurrent kernel. Int. J. Electr. Power Energy Syst. 2020, 124, 106369. [Google Scholar] [CrossRef]
- Wang, B.; Xuan, D.; Zhao, X.; Chen, J.; Lu, C. Dynamic battery equalization scheme of multi-cell lithium-ion battery pack based on PSO and VUFLC. Int. J. Electr. Power Energy Syst. 2021, 136, 107760. [Google Scholar] [CrossRef]
- Trovò, A.; Saccardo, A.; Giomo, M.; Guarnieri, M. Thermal modeling of industrial-scale vanadium redox flow batteries in high-current operations. J. Power Sources 2019, 424, 204–214. [Google Scholar] [CrossRef] [Green Version]
- Deja, P.; Kurpiel, W. Systems for Protecting and Controlling the Lithium Cells. ECS Trans. 2019, 95, 337–347. [Google Scholar] [CrossRef]
- Sung, W.; Lee, J. Improved capacity estimation technique for the battery management systems of electric vehicles using the fixed-point iteration method. Comput. Chem. Eng. 2018, 117, 283–290. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Zhang, H.T. Design and Application of Lithium-ion Battery Management System: Review of New Energy Technology and Power Man-agement. Cell 2020, 50, 105–106. [Google Scholar]
- Moura, S.J.; Argomedo, F.B.; Klein, R.; Mirtabatabaei, A.; Krstic, M. Battery State Estimation for a Single Particle Model with Electrolyte Dynamics. IEEE Trans. Control. Syst. Technol. 2017, 25, 453–468. [Google Scholar] [CrossRef]
- Lu, J.; Wei, L.; Pour, M.M.; Mekonnen, Y.; Sarwat, A.I. Modeling discharge characteristics for predicting battery remaining life. In Proceedings of the 2017 IEEE Transportation Electrification Conference and Expo (ITEC), Chicago, IL, USA, 22–24 June 2017. [Google Scholar]
- Misyris, G.S. State-of-charge estimation for li-ion batteries: A more accurate hybrid approach. IEEE Trans. Energy Convers. 2019, 34, 109–119. [Google Scholar] [CrossRef] [Green Version]
- Mandli, A.R. Fast computational framework for optimal life management of lithium-ion batteries. Int. J. Energy Res. 2018, 42, 1973–1982. [Google Scholar] [CrossRef]
- Zheng, F.; Xing, Y.; Jiang, J.; Sun, B.; Kim, J.; Pecht, M. Influence of different open circuit voltage tests on state of charge online estimation for lithium-ion batteries. Appl. Energy 2016, 183, 513–525. [Google Scholar] [CrossRef]
- Khalid, A.; Stevenson, A.; Sarwat, A.I. Performance Analysis of Commercial Passive Balancing Battery Management System Operation Using a Hardware-in-the-Loop Testbed. Energies 2021, 14, 8037. [Google Scholar] [CrossRef]
- Bao, H.; Yu, Y. Error Correction of Battery SOC Estimation Based on Ampere-hour Integral Method. Comput. Simul. 2013, 30, 148–151. [Google Scholar]
- Chen, J.; Ouyang, Q.; Xu, C.; Su, H. Neural network based state of charge observer design for lithium-ion batteries. IEEE Trans. Control. Syst. Technol. 2017, 26, 1–9. [Google Scholar] [CrossRef]
- Guo, G.F.; Shui, L.; Wu, X.L.; Cao, B.G. SOC Estimation for Li-Ion battery using svm based on particle swarm optimization. Adv. Mater. Res. 2014, 1051, 1004–1008. [Google Scholar] [CrossRef]
- Khalid, A.; Sarwat, A.I. Unified Univariate-Neural Network Models for Lithium-Ion Battery State-of-Charge Forecasting Using Minimized Akaike Information Criterion Algorithm. IEEE Access 2021, 9, 39154–39170. [Google Scholar] [CrossRef]
- Afshar, S.; Morris, K.; Khajepour, A. State-of-charge estimation using an EKF-based adaptive observer. IEEE Trans. Control. Syst. Technol. 2019, 27, 1907–1923. [Google Scholar] [CrossRef]
- Jiang, C.; Taylor, A.; Duan, C.; Bai, K. Extended Kalman Filter based battery state of charge (SOC) estimation for electric vehicles. In Proceedings of the IEEE Transportation Electrification Conference and Expo, Detroit, MI, USA, 16–19 June 2013; pp. 1–5. [Google Scholar]
- Shi, P.; Zhao, Y.W. Application of unscented Kalman filter in the SOC estimation of Li-ion battery for autonomous mobile robot. In Proceedings of the IEEE International Conference on Information Acquisition, Veihai, China, 20–23 August 2006; pp. 1279–1283. [Google Scholar]
- Xia, B.; Sun, Z.; Zhang, R.; Cui, D.; Lao, Z.; Wang, W.; Sun, W.; Lai, Y.; Wang, M. A comparative study of three improved algorithms based on particle filter algorithms in SOC estimation of lithium-ion batteries. Energies 2017, 10, 114901–114914. [Google Scholar] [CrossRef]
- Kurpiel, W.; Deja, P.; Polnik, B.; Skóra, M.; Miedziński, B.; Habrych, M.; Debita, G.; Zamłyńska, M.; Falkowski-Gilski, P. Performance of Passive and Active Balancing Systems of Lithium Batteries in Onerous Mine Environment. Energies 2021, 14, 7624. [Google Scholar] [CrossRef]
- Wei, K.; Chen, Q.Y. States Estimation of Li-ion Power Batteries Based on Adaptive Unscented Kalman Filters. In Proceedings of the CSEE, Klagenfurt, Austria, 23–25 April 2014; pp. 445–452. [Google Scholar]
- Remmlinger, J.; Buchholz, M.; Meiler, M.; Bernreuter, P.; Dietmayer, K. State-of-health monitoring of lithium-ion batteries in electric vehicles by on-board internal resistance estimation. J. Power Sources 2011, 196, 5357–5363. [Google Scholar] [CrossRef]
| Battery Parameters | Nominal Capacity (mAh) | Charge Cut-Off Voltage (V) | Discharge Cut-Off Voltage (V) | Nominal Voltage (V) |
|---|---|---|---|---|
| INR18650-30Q | 3000 | 4.2 | 2.5 | 3.6 |
| SOC Estimated Method | SOC Estimated Mean Error | SOC Estimated MAXIMUM error |
|---|---|---|
| Joint estimation algorithm | 0.74% | 2.11% |
| UKPF algorithm | 1.19% | 3.37% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Q.; Ma, K.; Xu, L.; Song, L.; Li, X.; Li, Y. A Joint Estimation Method Based on Kalman Filter of Battery State of Charge and State of Health. Coatings 2022, 12, 1047. https://doi.org/10.3390/coatings12081047
Yang Q, Ma K, Xu L, Song L, Li X, Li Y. A Joint Estimation Method Based on Kalman Filter of Battery State of Charge and State of Health. Coatings. 2022; 12(8):1047. https://doi.org/10.3390/coatings12081047
Chicago/Turabian StyleYang, Qingxia, Ke Ma, Liyou Xu, Lintao Song, Xiuqing Li, and Yefei Li. 2022. "A Joint Estimation Method Based on Kalman Filter of Battery State of Charge and State of Health" Coatings 12, no. 8: 1047. https://doi.org/10.3390/coatings12081047
APA StyleYang, Q., Ma, K., Xu, L., Song, L., Li, X., & Li, Y. (2022). A Joint Estimation Method Based on Kalman Filter of Battery State of Charge and State of Health. Coatings, 12(8), 1047. https://doi.org/10.3390/coatings12081047







