A Practical Design Guide for Unbonded Jointed Plain Concrete Roads over Deteriorated HMA Roads: Realistic Traffic Loading
Abstract
1. Introduction
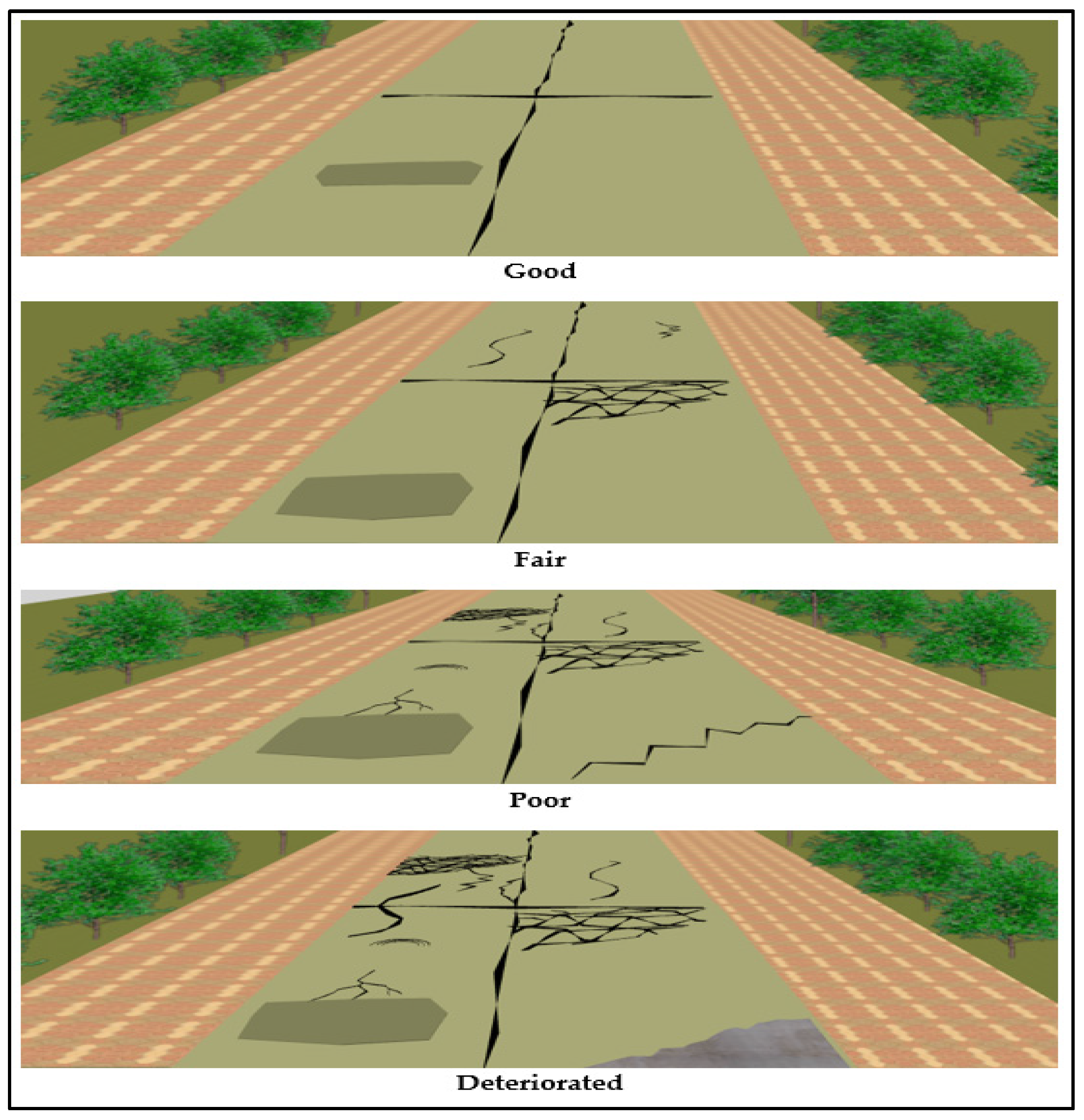
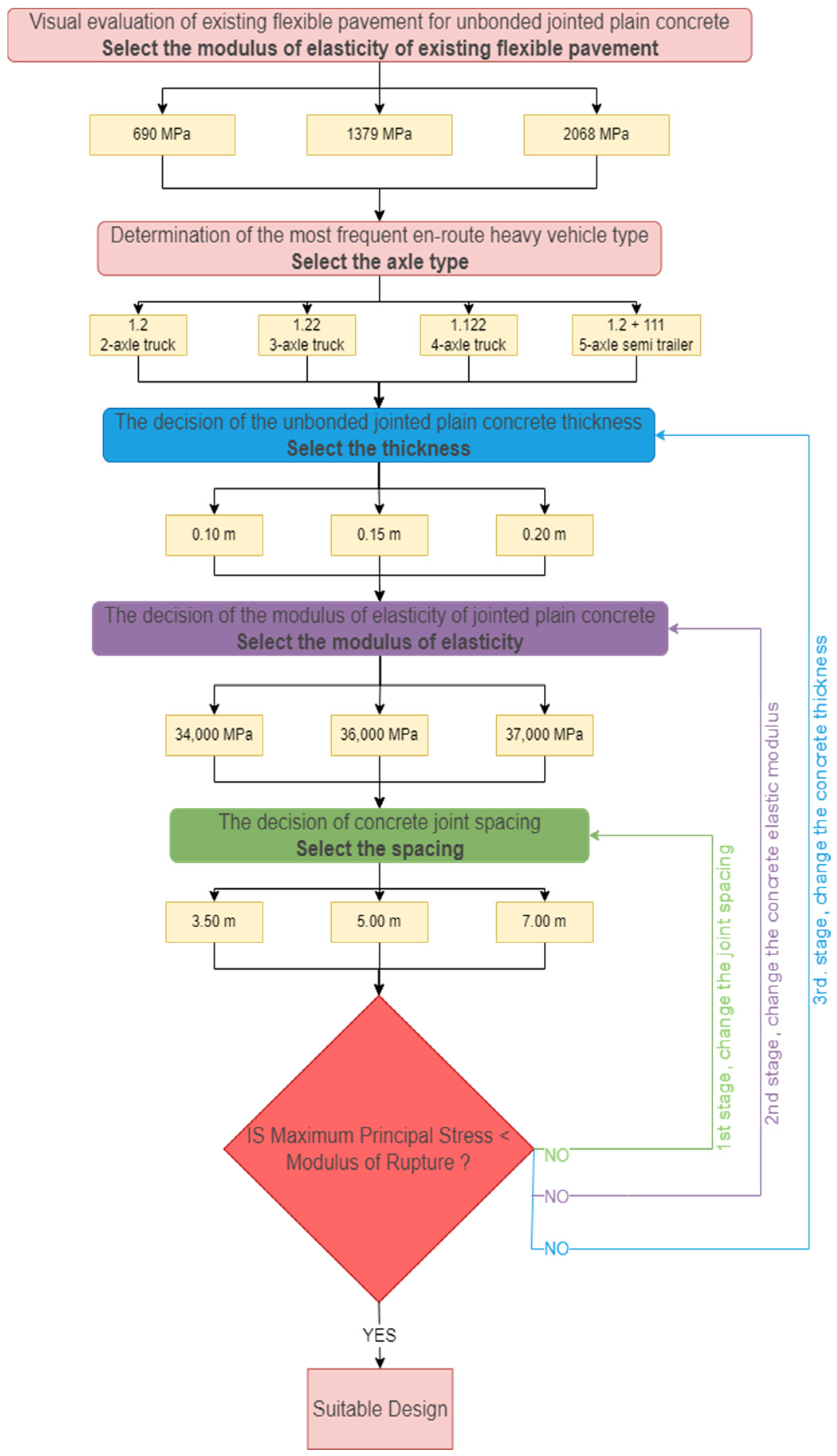
1.1. Visual Evaluation of HMA Pavement
1.2. Research Significance
2. Materials and Methods
2.1. Verification of the ANSYS Model Established with Literature Studies
2.1.1. Verification of Stresses Induced by Temperature Difference
2.1.2. Verification of Stresses Induced by Single Wheel Loads
2.2. Calculation of Unbonded Concrete Pavement Thickness on HMA Pavement with AASHTO Method
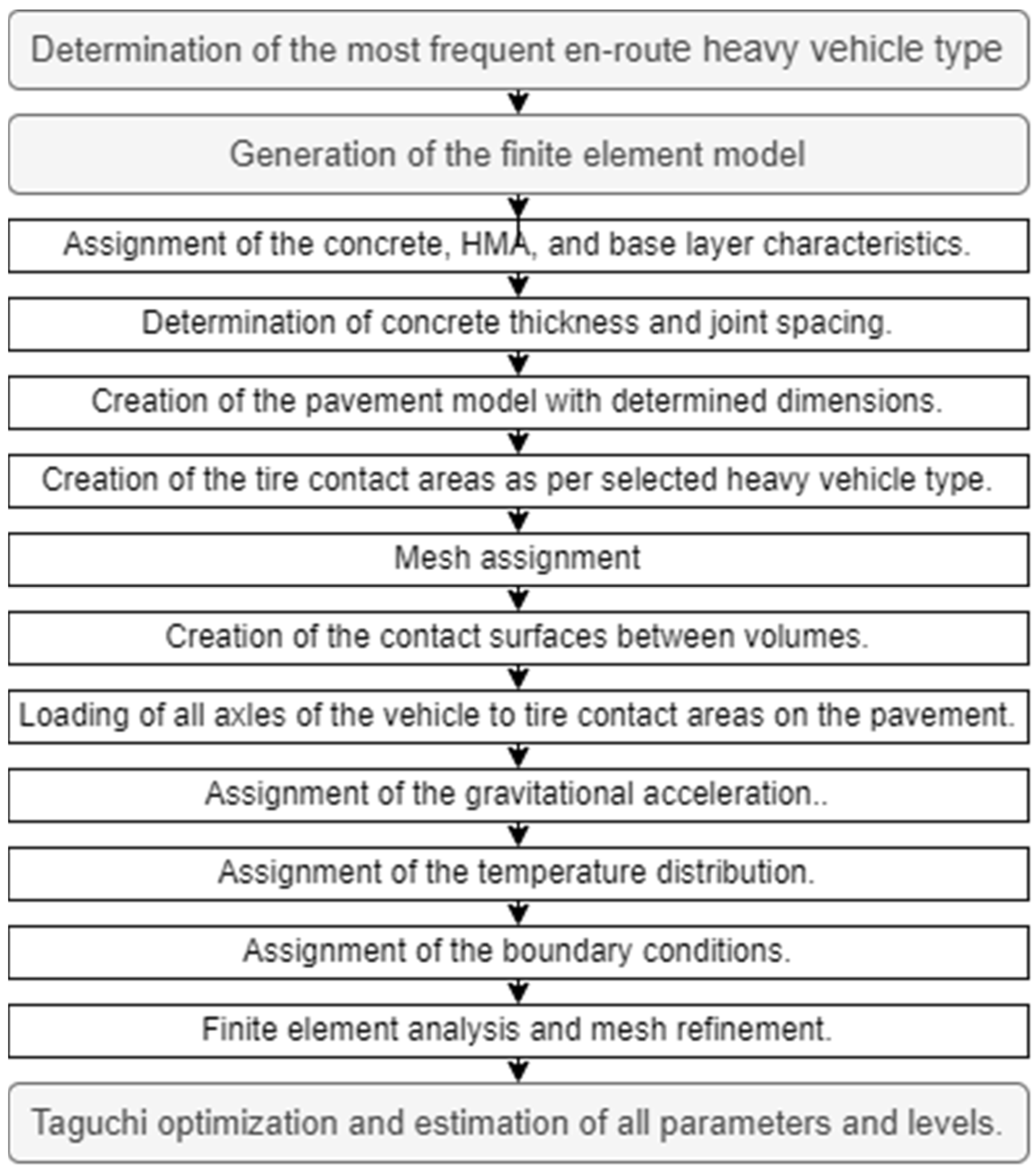
2.3. Finite Elements Model
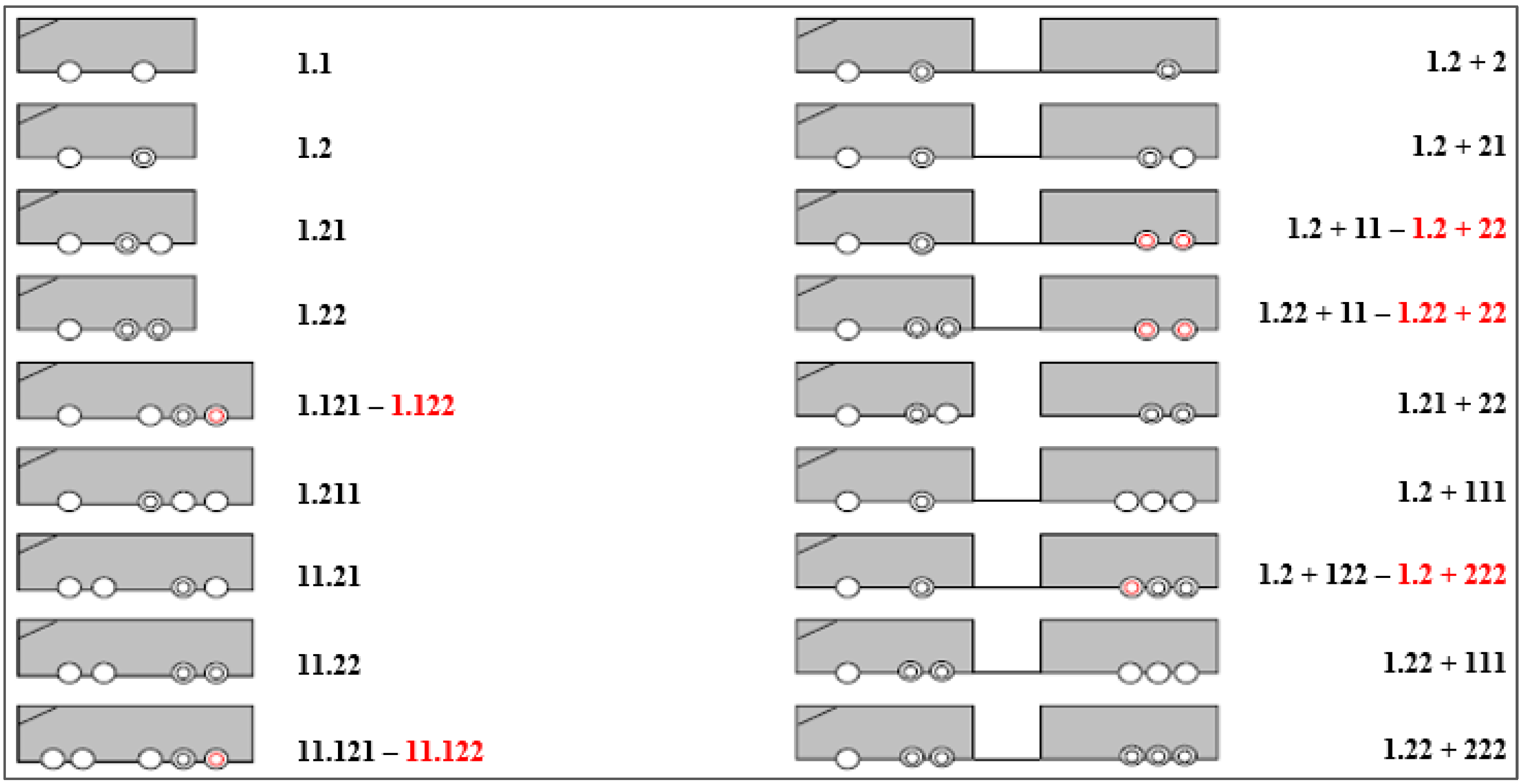
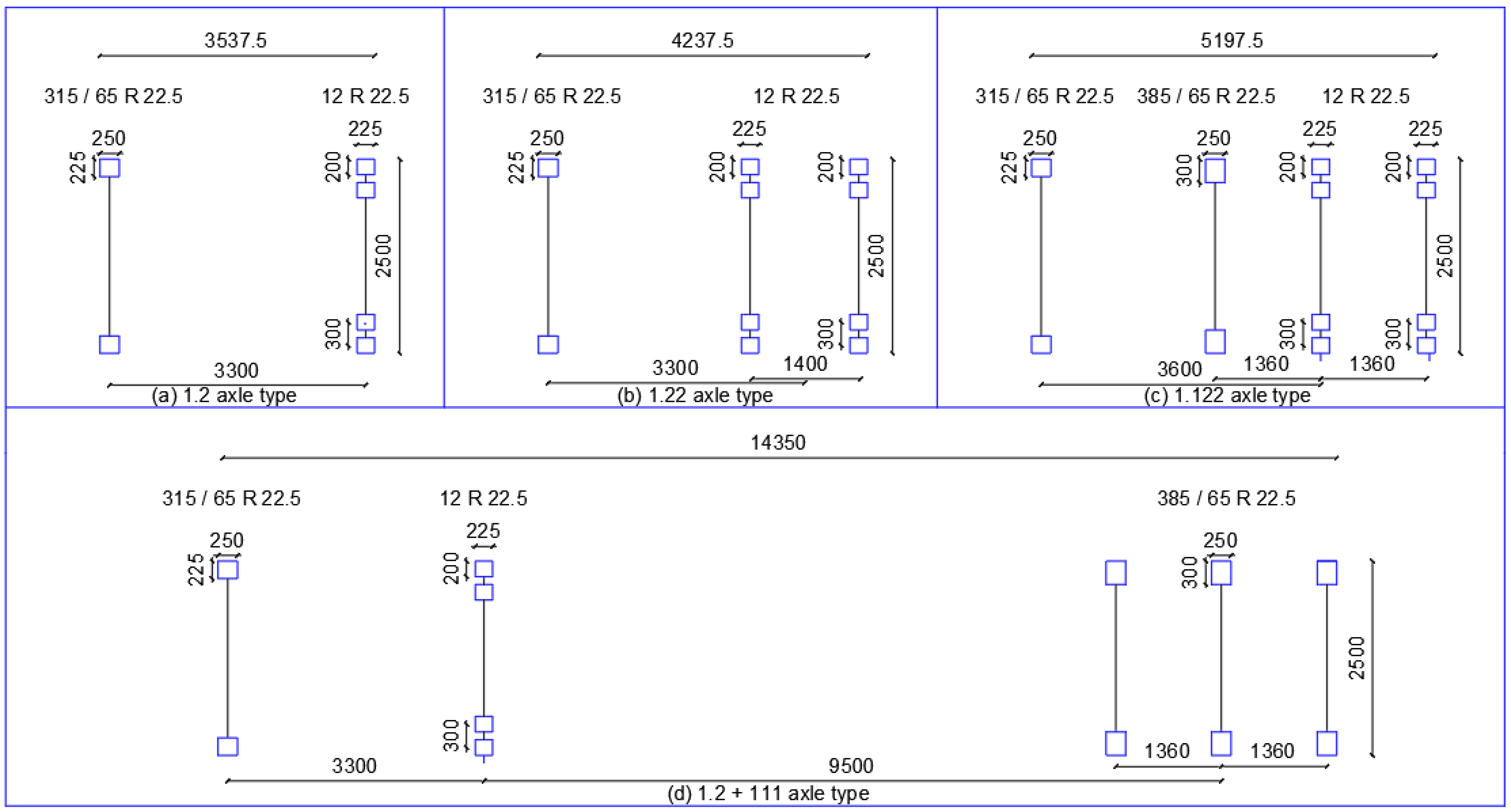
2.3.1. Axle Configurations
2.3.2. Tire–Pavement Contact Areas and Inflation Pressure
2.3.3. Pavement Layer Thicknesses and Material Properties
2.3.4. The Constitutive Finite Element Model
2.4. Taguchi Method
3. Results and Discussion
3.1. Bilinear Temperature Change in Concrete Slab
3.2. 3-Axle Truck Loading Analysis Results
3.3. Evaluation of Three-Axle Truck Loading Analysis Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Söderqvist, J. Design of Concrete Pavements: Design Criteria for Plain and Lean Concrete; KTH: Stockholm, Sweden, 2006. [Google Scholar]
- Ağar, E.; Sütaş, İ.; Öztaş, G. Beton Yollar: Rijit yol Üstyapıları; Malzeme-Tasarım-Üretim-Yapım-Bakım Teknikleri; İstanbul Teknik Üniversitesi: Istanbul, Turkey, 1998. [Google Scholar]
- Tunç, A. Yol Malzemeleri (Agrega, Asfalt, Bitümlü Karışımlar, Beton, Zemin) ve Uygulamaları (Kaplamalar ve Zemin Islahı-Dizayn ve Yapım Metotları); Atlas-Nobel Yayın Dağıtım: Ankara, Turkey, 2001. [Google Scholar]
- Institute, A. Pavement Rehabilitation—Preparation for Asphalt Overlays; Publication CL-5; Asphalt Institute: Lexington, KY, USA, 1996. [Google Scholar]
- Institute, A. Alternatives in Pavement Maintenance, Rehabilitation, and Reconstruction; Publication IS-178; Asphalt Institute: Lexington, KY, USA, 1994. [Google Scholar]
- Wen, H.; Titi, H.; Berry, D. Study of Best Practices for Pre-Overlay Repair and Asphalt Overlay. In Airfield and Highway Pavements, Proceedings of the 2006 Airfield and Highway Pavement Specialty Conference American Society of Civil Engineers; American Society of Civil Engineers: Atlanta, GA, USA, 2006. [Google Scholar]
- Harrington, D.; Fick, G.; Bordeleon, A.; Cable, J.; DeGraff, D.; Parkes, N.; Riley, R.; Rodden, R.; Roesler, J.; Vandenbossche, J. Guide to Concrete Overlays Sustainable Solutions for Resurfacing and Rehabilitating Existing Pavements, 3rd ed.; National Concrete Pavement Technology Center: Ames, IA, USA, 2014. [Google Scholar]
- Torres, H.; Roesler, J.; Rasmussen, R.O.; Harrington, D. Guide to the Design of Concrete Overlays Using Existing Methodologies; Iowa State University, National Concrete Pavement Technology Center: Ames, IA, USA, 2012. [Google Scholar]
- Branch, D. Guidelines for the Thickness Design of Bonded Whitetopping Pavement in the State of Colorado; Department of Transportation, Research Branch: Denver, CO, USA, 1998. [Google Scholar]
- Rea, R.C.; Jensen, W.G. A Concrete Overlay on an Asphalt Road. Int. J. Pavement Eng. 2005, 6, 111–114. [Google Scholar] [CrossRef]
- Rasmussen, R.; Rozycki, D.K. Thin and Ultra-Thin Whitetopping: A Synthesis of Highway Practice; Transportation Research Board: Washington, DC, USA, 2004. [Google Scholar]
- Sheehan, M.J.; Tarr, S.M.; Tayabji, S.D. Instrumentation and Field Testing of Thin Whitetopping Pavement in Colorado and Revision of the Existing Colorado Thin Whitetopping Procedure; Colorado Department of Transportation, Research Branch: Denver, CO, USA, 2004. [Google Scholar]
- Sultana, S. Extending Asphalt Pavement Life with Thin Whitetopping; Kansas State University: Manhattan, KS, USA, 2010. [Google Scholar]
- Zbiciak, A.; Graczyk, M.; Józefiak, K.; Brzeziński, K.; Michalczyk, R.J.R.; Mosty, B.-D. Assessment of the Effect of Concrete Slab Geometrical Parameters on the Distribution of Stresses in the Road Pavement Structure. Roads Bridges-Drogi Mosty 2019, 18, 171–180. [Google Scholar]
- Salman, M.M.; Patil, A.S. Analytical Study of Steel Fibre Reinforced Rigid Pavements under Moving Load. IJSRD–Int. J. Sci. Res. Dev. 2014, 2, 7. [Google Scholar]
- Çelik, M. Karadeniz Bölgesi köy Yolları için Rijit ve Esnek Kaplamanın Mekanistik ve Maliyet Açısından Karşılaştırılması; Karadeniz Teknik Üniversitesi/Fen Bilimleri Enstitüsü: Trabzon, Turkey, 2014. [Google Scholar]
- Kumara, W.; Tia, M.; Wu, C.-L.; Choubane, B. Evaluation of applicability of ultra-thin whitetopping (UTW) in Florida. In Proceedings of the 2003 Annual Transportation Research Board Meeting (CD-ROM), Washington, DC, USA, 12–16 January 2003. [Google Scholar]
- Hossain, M.; Sultana, S. Extending Asphalt Pavement Life Using Thin Whitetopping; MID-America Transportation Center: Lincoln, NE, USA, 2010. [Google Scholar]
- Hu, X.; Walubita, L.F. Effects of layer interfacial bonding conditions on the mechanistic responses in asphalt pavements. J. Transp. Eng. 2011, 137, 28–36. [Google Scholar] [CrossRef]
- Williamson, M.J. Finite Element Analysis of Hot-Mix Asphalt Layer Interface Bonding; Kansas State University: Manhattan, KS, USA, 2015. [Google Scholar]
- Ozer, H.; Al-Qadi, I.L.; Wang, H.; Leng, Z.J. Characterisation of interface bonding between hot-mix asphalt overlay and concrete pavements: Modelling and in-situ response to accelerated loading. Int. J. Pavement Eng. 2012, 13, 181–196. [Google Scholar] [CrossRef]
- Mansour, W. Numerical analysis of the shear behavior of FRP-strengthened continuous RC beams having web openings. Eng. Struct. 2021, 227, 111451. [Google Scholar] [CrossRef]
- Baraghith, A.T.; Mansour, W.; Behiry, R.N.; Fayed, S. Effectiveness of SHCC strips reinforced with glass fiber textile mesh layers for shear strengthening of RC beams: Experimental and numerical assessments. Constr. Build. Mater. 2022, 327, 127036. [Google Scholar] [CrossRef]
- Sakr, M.A.; Sleemah, A.A.; Khalifa, T.M.; Mansour, W.N. Behavior of RC beams strengthened in shear with ultra-high performance fiber reinforced concrete (UHPFRC). In Proceedings of the MATEC Web of Conferences 2018; EDP Sciences: Les Ulis, France, 2018. [Google Scholar]
- Hamoda, A.; Emara, M.; Mansour, W. Behavior of steel I-beam embedded in normal and steel fiber reinforced concrete incorporating demountable bolted connectors. Compos. Part B Eng. 2019, 174, 106996. [Google Scholar] [CrossRef]
- Mansour, W.; Sakr, M.A.; Seleemah, A.A.; Tayeh, B.A.; Khalifa, T.M. Bond behavior between concrete and prefabricated Ultra High-Performance Fiber-Reinforced Concrete (UHPFRC) plates. Struct. Eng. Mech. 2022, 81, 305–316. [Google Scholar]
- Mansour, W.; Fayed, S. Effect of interfacial surface preparation technique on bond characteristics of both NSC-UHPFRC and NSC-NSC composites. In Structures; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Basha, A.; Fayed, S.; Mansour, W. Flexural strengthening of RC one way solid slab with Strain Hardening Cementitious Composites (SHCC). Adv. Concr. Constr. 2020, 9, 511–527. [Google Scholar]
- Al Harki, B.Q.K.; Mal Jawahery, S.; Abdulmawjoud, A.A. Hybrid Steel Fiber of Rigid Pavements: A 3D Finite Element and Parametric Analysis. Coatings 2022, 12, 1478. [Google Scholar] [CrossRef]
- Kayıpmaz, M.T. Beton Yollarda Isıl Genleşmeye Bağlı Gerilmelerin Araştırılması; Karadeniz Teknik Üniversitesi Fen Bilimleri Enstitüsü İnşaat Mühendisliği Anabilim Dalı: Trabzon, Turkey, 2019. [Google Scholar]
- PI, Pavement Interactive. Modulus of Subgrade Reaction. Available online: https://pavementinteractive.org/reference-desk/design/design-parameters/modulus-of-subgrade-reaction/#:~:text=The%20modulus%20of%20subgrade%20reaction,by%20correlation%20with%20other%20tests (accessed on 15 September 2020).
- KGM. Karayolları Trafik ve Ulaşım Bilgileri, Otoyollar ve Devlet Yollarının Trafik Dilimlerine Göre Yıllık Ortalama Günlük Trafik Değerleri ve Ulaşım Bilgileri; Trafik Güvenliği Dairesi Başkanlığı Ulaşım Etütleri Şubesi Müdürlüğü: Ankara, Turkey, 2020. [Google Scholar]
- Özcanan, S.; Akpınar, M.V. Esnek Üstyapılarda Kritik Tekerlek ve Aks Konfigürasyonların Mekanistik Analizlere Göre Tespit Edilmesi. İMO Teknik Dergi 2014, 6625, 413. [Google Scholar]
- Moffatt, M. Guide to Pavement Technology: Part 2: Pavement Structural Design; Austroads: Sydney, Australia, 2017. [Google Scholar]
- Korkiala-Tanttu, L. Calculation Method for Permanent Deformation of Unbound Pavement Materials; VTT: Espoo, Finland, 2009. [Google Scholar]
- Ovalı, İ.; Esen, C. Ansys Workbench: Oku, İzle, Dinle, Öğren! Kodlab Yayın Dağıtım Yazılım ve Eğitim Hizmetleri San. ve Tic. Ltd. Şti.: Istanbul, Turkey, 2017. [Google Scholar]
- Shoukry, S.N.; Fahmy, M.; Prucz, J.; William, G. Validation of 3DFE analysis of rigid pavement dynamic response to moving traffic and nonlinear temperature gradient effects. Int. J. Geomech. 2007, 7, 16–24. [Google Scholar] [CrossRef]
- Ersoy, U.; Özcebe, G. Betonarme: Temel Ilkeler; TS-500 ve Türk Deprem Yönetmeliğine Göre Hesap, Bizim Büro Basımevi: Ankara, Turkey, 2001. [Google Scholar]
- Roesler, J.R.; Bordelon, A.C.; Ioannides, A.; Beyer, M.; Wang, D. Design and Concrete Material Requirements for Ultra-Thin Whitetopping; Illinois Center for Transportation: Rantoul, IL, USA, 2008. [Google Scholar]
- ACPA, American Concrete Pavement Association Bonded Concrete Overlay on Asphalt (BCOA) Thickness Designer. 2020. Available online: http://apps.acpa.org/apps/bcoa.aspx (accessed on 15 September 2020).
- Diallo, A.O. Beton yol Üstü Asfalt Kaplamaların Sonlu Elemanlar Yöntemi ile Mekanistik Analizi; Karadeniz Teknik Üniversitesi/Fen Bilimleri Enstitüsü: Trabzon, Turkey, 2019. [Google Scholar]
- STRUCT. Static Friction Coefficients. Available online: https://structx.com/Material_Properties_007.html (accessed on 15 September 2020).
- Teller, L.; Sutherland, E. Observed effects of variations in temperature and moisture on the size, shape and stress resistance of concrete pavement slabs. Public Roads 1935, 16, 169–197. [Google Scholar]
- Thomlinson, J. Temperature variations and consequent stresses produced by daily and seasonal temperature cycles in concrete slabs. Concr. Constr. Eng. 1940, 36, 298–307. [Google Scholar]
- Choubane, B.; Tia, M. Nonlinear temperature gradient effect on maximum warping stresses in rigid pavements. Transp. Res. Rec. 1992, 1370, 11. [Google Scholar]
- Armaghani, J.M.; Larsen, T.J.; Smith, L.L. Temperature Response of Concrete Pavements; Committee on Strength and Deformation Characteristics of Pavement Sections, National Academy of Sciences: Washington, DC, USA, 1987. [Google Scholar]
- Karunarathne, A.; Mampearachchi, W.; Nanayakkara, A. Modelling of Thermal Effects Due to Solar Radiation on Concrete Pavements; University of Moratuwa: Moratuwa, Sri Lanka, 2010. [Google Scholar]
- Yu, H.T.; Khazanovich, L.; Darter, M.I.; Ardani, A. Analysis of concrete pavement responses to temperature and wheel loads measured from intrumented slabs. Transp. Res. Rec. 1998, 1639, 94–101. [Google Scholar] [CrossRef]
- Siddique, Z.Q.; Hossain, M.; Meggers, D. Temperature and curling measurements on concrete pavement. In Proceedings of the 2005 Mid-Continent Transportation Research Symposium, Ames, IA, USA, 18–19 August 2005. [Google Scholar]
- Kim, S.-M.; Nam, J.-H. Measurements and experimental analysis of temperature variations in Portland cement concrete pavement systems. Road Mater. Pavement Des. 2010, 11, 745–771. [Google Scholar] [CrossRef]
- Kim, K. Enhanced Finiıte Element Analysis Tools and Instrumentation Method to Evaluate the Structural Behavior of Non-Conventıonal Concrete Pavements. Ph.D. Thesis, University of Florida, Gainesville, FL, USA, 2017. [Google Scholar]
- Richardson, J.M.; Armaghani, J.M. Stress Caused by Temperature Gradient in Portland Cement Concrete Pavements; Transportation Research Board: Washington, DC, USA, 1987. [Google Scholar]
- Shoukry, S.N.; Fahmy, M.R. Optimization of Concrete Slab Geometry for Enhanced Rigid Pavement Performance and Service Life; WVDOT Research Project No. 140; Department of Mechanical and Aerospace Engineering, College of Engineering and Mineral Resources, West Virginia University: Morgantown, WV, USA, 2002. [Google Scholar]
- Byrum, C.; Hansen, W. Influence function approach to analysis of jointed portland cement concrete pavement. Transp. Res. Rec. 1994, 1449, 148–158. [Google Scholar]
- Maitra, S.R.; Reddy, K.; Ramachandra, L. Estimation of critical stress in jointed concrete pavement. Procedia-Soc. Behav. Sci. 2013, 104, 208–217. [Google Scholar] [CrossRef]
- Dhananjay, M.; Abhilash, K. Study of thermal gradient in concrete slabs through experimental approach. Glob. J. Res. Eng. Civ. Struct. Eng. 2014, 14, 1–16. [Google Scholar]
- Kim, K.; Chun, S. Evaluation of internally cured concrete pavement using environmental responses and critical stress analysis. Int. J. Concr. Struct. Mater. 2015, 9, 463–473. [Google Scholar] [CrossRef]
- Pancar, E.B.; Akpınar, M.V. Temperature reduction of concrete pavement using glass bead materials. Int. J. Concr. Struct. Mater. 2016, 10, 39–46. [Google Scholar] [CrossRef]
- Kamalakara, G.K.; MSrikanth, N.; Sachin, B.K.; Vijaykumar, S.K.; Siddharam, B.W.; Sushmitha, M. Study of temperature differential in different types of concrete slabs. IJRAR- Int. J. Res. Anal. Rev. 2018, 5, 1022–1028. [Google Scholar]
- Bas, F.İ. Bozulmuş BSK Yol Üzeri Derzli Donatısız beton Yolların Mekanistik Değerlendirilmesi; Atatürk Üniversitesi: Erzurum, Turkey, 2020; p. 202. [Google Scholar]
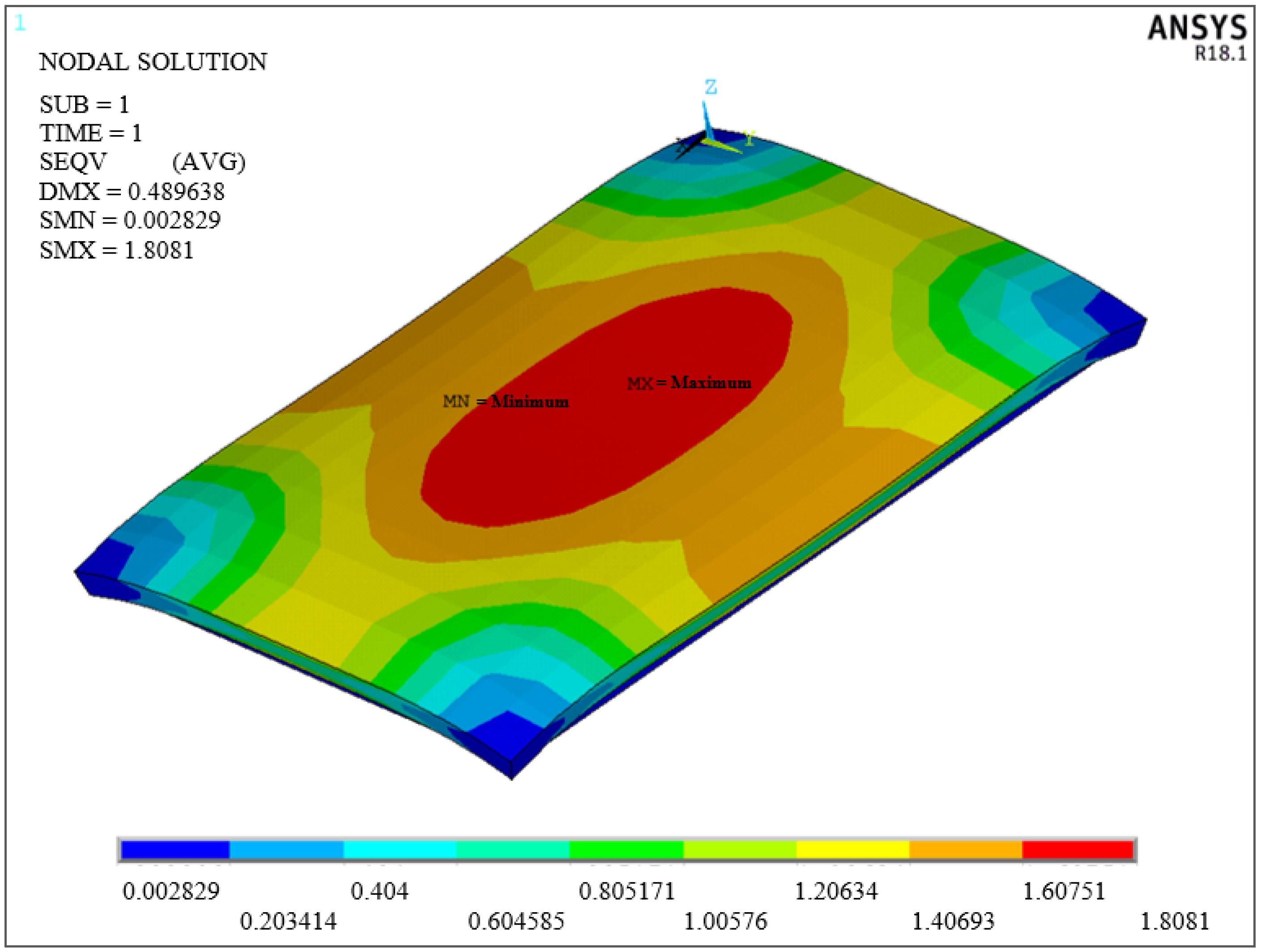
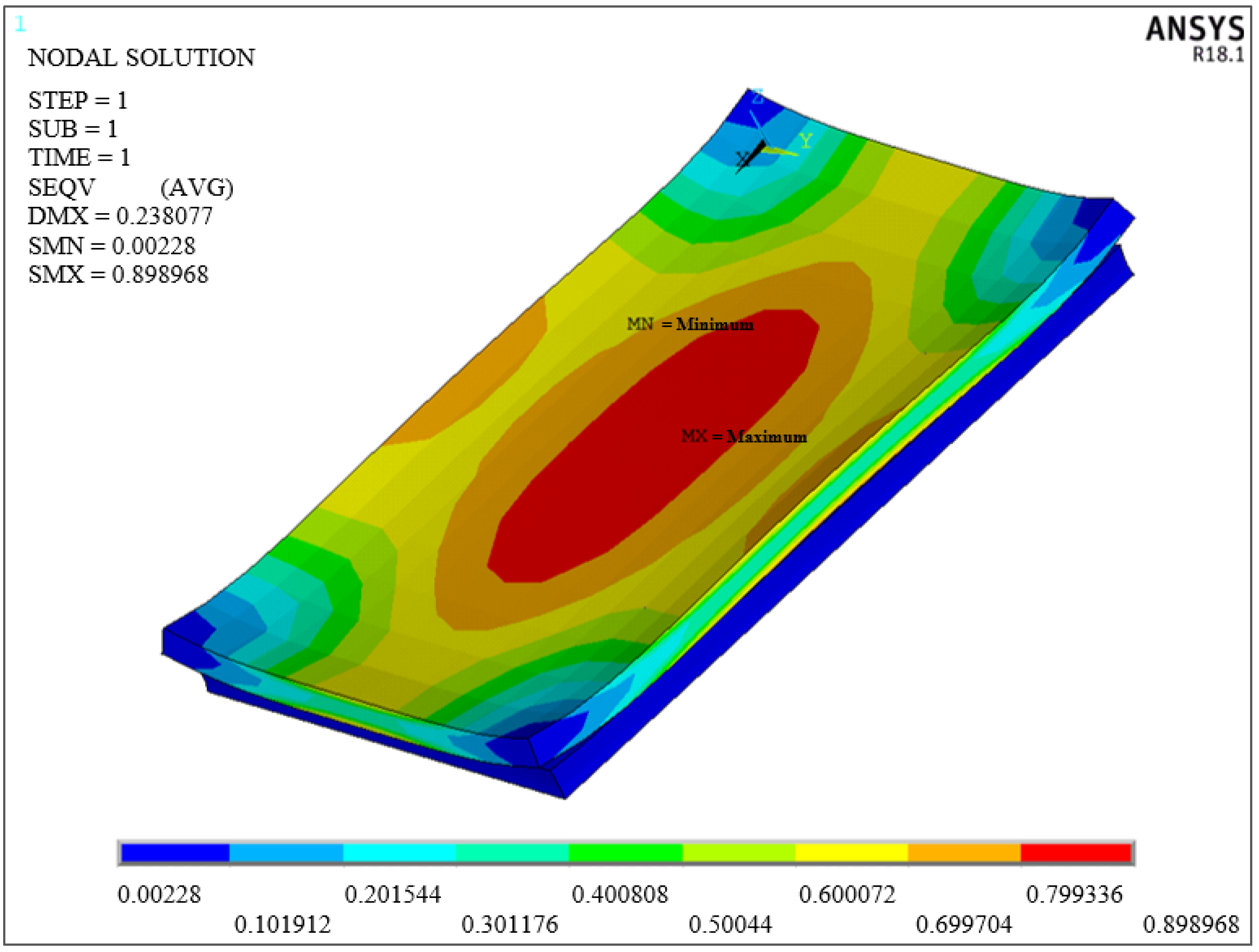
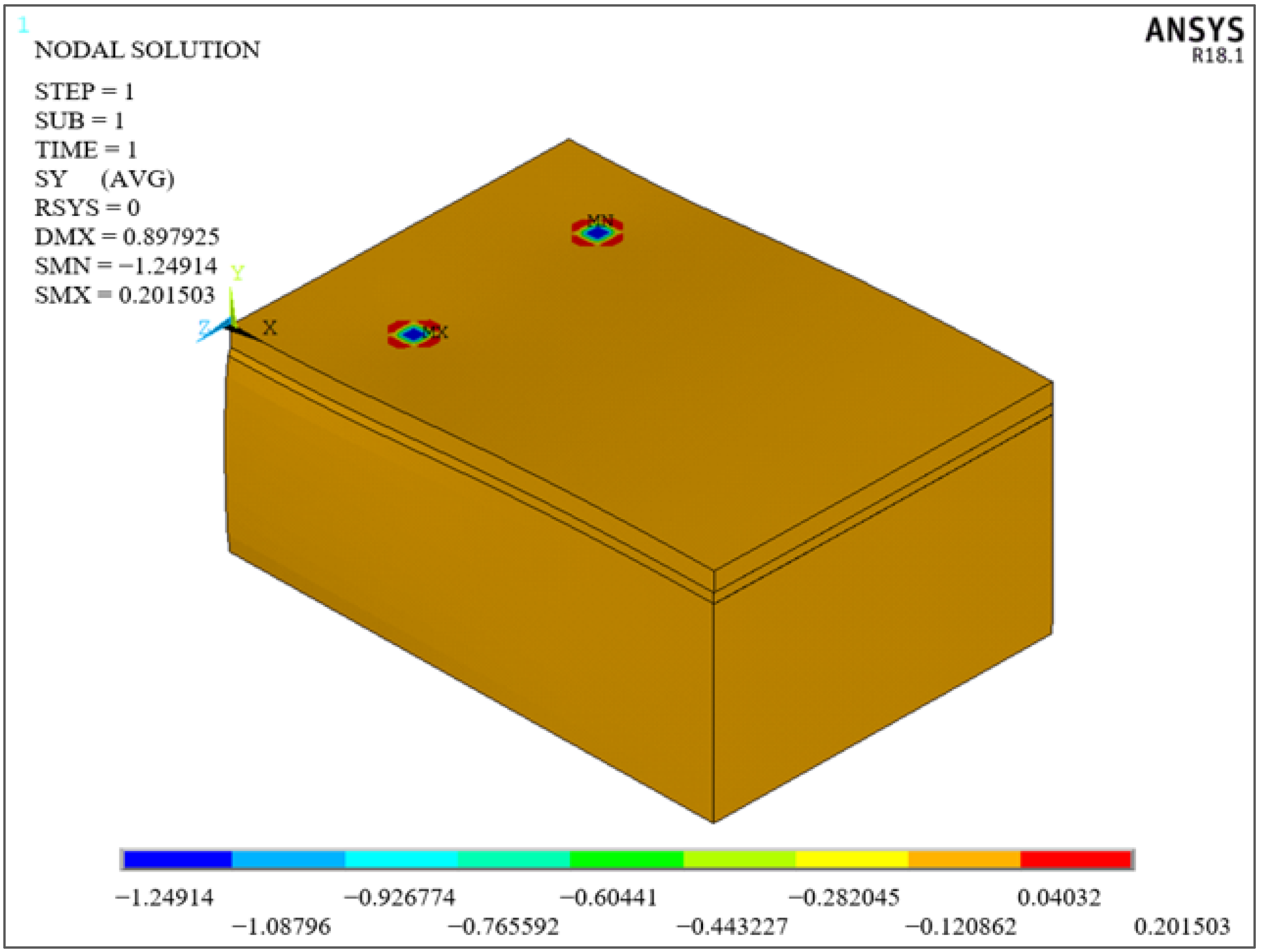
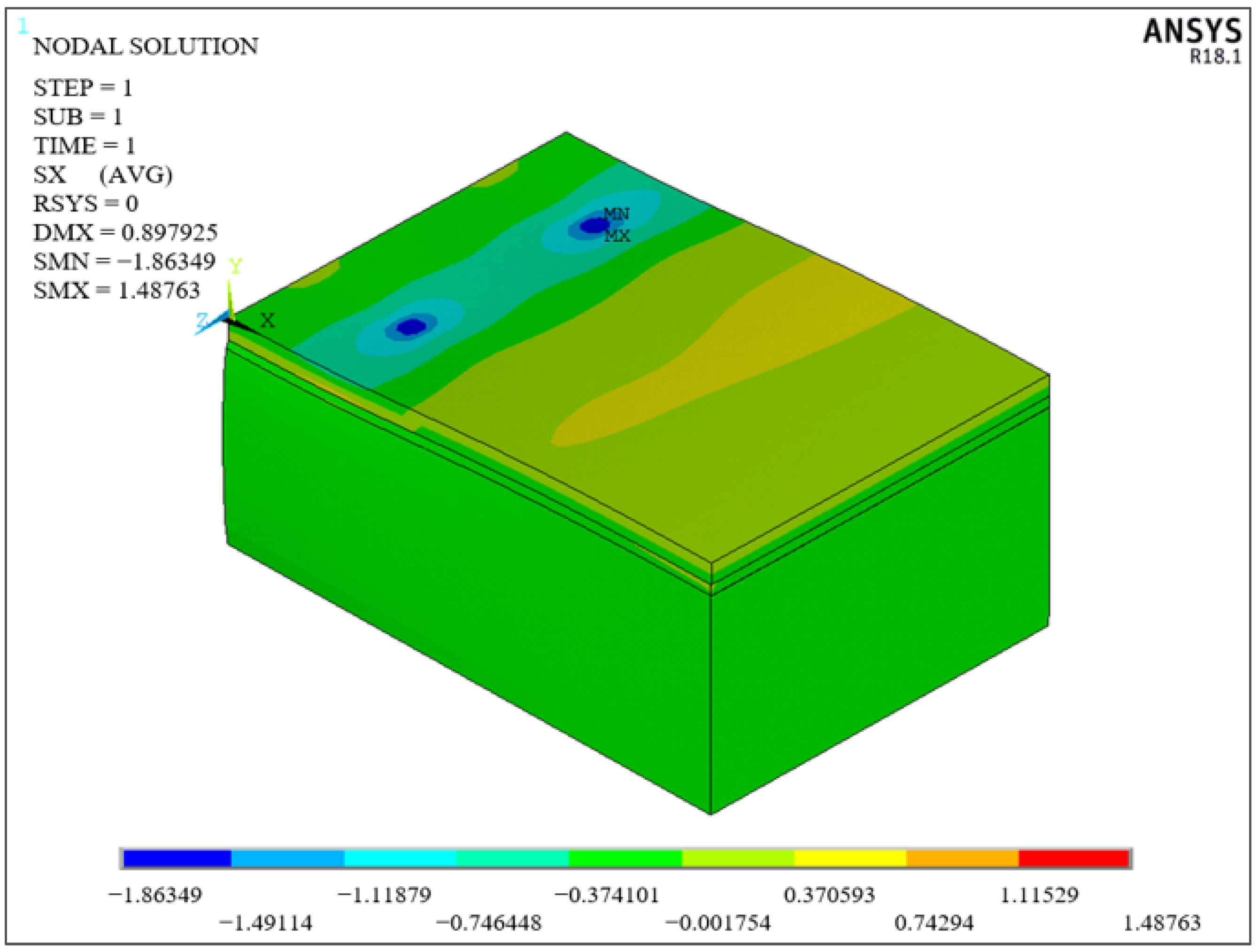




| The Study | Total Deformation mm | Deformation in Y Direction mm | Deformation in X Direction mm | Tension in Y Direction MPa | Tension in X Direction MPa | ||||
|---|---|---|---|---|---|---|---|---|---|
| DMX | SMN | SMX | SMN | SMX | SMN | SMX | SMN | SMX | |
| Çelik [16] | 0.889 | −0.889 | 0.090 | −0.038 | 0.143 | −1.219 | 0.301 | −1.823 | 1.039 |
| ANSYS Verification Model | 0.898 | −0.898 | 0.081 | −0.037 | 0.122 | −1.249 | 0.202 | −1.864 | 1.488 |
| Concrete Class | C20/25 | C25/30 | C30/37 | C35/45 | C40/50 | C45/55 | C50/60 |
|---|---|---|---|---|---|---|---|
| 18 kip (8,2 t) W8,2 | 3 × 106 | 3 × 106 | 3 × 106 | 3 × 106 | 3 × 106 | 3 × 106 | 3 × 106 |
| R | 95% | 95% | 95% | 95% | 95% | 95% | 95% |
| ZR | −1.645 | −1.645 | −1.645 | −1.645 | −1.645 | −1.645 | −1.645 |
| S0 | 0.35 | 0.35 | 0.35 | 0.35 | 0.35 | 0.35 | 0.35 |
| Pt | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| P0 | 4.5 | 4.5 | 4.5 | 4.5 | 4.5 | 4.5 | 4.5 |
| Modulus of rupture of PCC—Sc (psi) | 464 | 522 | 551 | 609 | 638 | 667 | 725 |
| Cd | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Load transfer coefficient—J | 3.8 | 3.8 | 3.8 | 3.8 | 3.8 | 3.8 | 3.8 |
| Modulus of elasticity of concrete—Ec (psi) | 4.06 × 106 | 4.35 × 106 | 4.64 × 106 | 4.79 × 106 | 4.93 × 106 | 5.22 × 106 | 5.37 × 106 |
| Modulus of subgrade reaction—k (PCI) | 500 | 500 | 500 | 500 | 500 | 500 | 500 |
| log10W8,2 | 6.477 | 6.477 | 6.477 | 6.477 | 6.477 | 6.477 | 6.477 |
| Overlay thickness—D (inch) | 10.44 | 9.78 | 9.51 | 8.97 | 8.73 | 8.54 | 8.12 |
| Overlay thickness—D (m) | 0.265 | 0.248 | 0.242 | 0.228 | 0.222 | 0.217 | 0.206 |
| Type of Vehicle | Type of Axle | Wheelbase (mm) | |||||
|---|---|---|---|---|---|---|---|
| Mercedes | Ford | Man | Volvo | DAF | Renault | ||
| Two-axle truck | 1.2 | 3300 to 6600 | 4750–5500 | 3900 to 5100 | 3400 to 6700 | 3450 to 7300 | 3400 to 6700 |
| Three-axle truck | 1.22 | 3600 to 5700 | 4460–5410 | 3300 to 5100 | 3885 to 6685 | 4500 to 6600 | 3500 to 6000 |
| Four-axle truck | 1.122 | 3600 to 5700 | 5100–5200–5900 | 3600 to 5700 | 4300 to 5885 | 4700–5300 | 4300 to 6400 |
| Five-axle semi-trailer | 1.2 + 111 | 3300–3600–3900 | 3600 | 3600–3900 | 3500–3600–3700–3800 | 3600–3800 | 3500–3700–3800–3900 |
| Type of Tire | Wheel Load (kg) | Tire Inflation Pressure (kPa) | Tire Contact Area Length (mm) × Width (mm) | Placement |
|---|---|---|---|---|
| 315/80 R 22.5 | 4100 | 700 | 250 × 225 | Front Tires on Trucks and Tow Trucks |
| 385/65 R 22.5 | 4100 | 700 | 250 × 300 | Tires on Semi-Trailers |
| 12 R 22.5 | 4100 | 700 | 225 × 200 + 225 × 200 | Dual Tires |
| Parameter | Level | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| Slab Thickness (m) | 0.10 | 0.15 | 0.20 |
| Transverse Joint Spacing (m) | 3.50 | 5.00 | 7.00 |
| Modulus of Elasticity of Concrete (MPa) | 34,000 | 36,000 | 37,000 |
| Modulus of Elasticity of HMA (MPa) | 690 | 1379 | 2068 |
| 4 Parameter 3 Level | ||||
|---|---|---|---|---|
| Experiment No | Slab Thickness (m) | Transverse Joint Spacing (m) | Modulus of Elasticity of Concrete (MPa) | Modulus of Elasticity of HMA (MPa) |
| 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 2 | 2 |
| 3 | 1 | 3 | 3 | 3 |
| 4 | 2 | 1 | 2 | 3 |
| 5 | 2 | 2 | 3 | 1 |
| 6 | 2 | 3 | 1 | 2 |
| 7 | 3 | 1 | 3 | 2 |
| 8 | 3 | 2 | 1 | 3 |
| 9 | 3 | 3 | 2 | 1 |
| Author | Temperature Differences | Thickness (mm) | Measured Temperature (°C) | Calculated Temperature (°C) |
|---|---|---|---|---|
| Armaghani et al. [46] | Negative | 64 | 18.1 | 18.2 |
| 114 | 19.9 | 20.0 | ||
| 165 | 21.7 | 21.3 | ||
| Positive | 64 | 32.6 | 32.8 | |
| 114 | 29.0 | 29.0 | ||
| 165 | 26.4 | 27.0 | ||
| Karunarathne et al. [47] | Negative | 25 | 34.4 | 34.5 |
| 50 | 34.8 | 34.9 | ||
| 75 | 35.4 | 35.3 | ||
| 100 | 35.8 | 36.0 | ||
| 125 | 36.2 | 36.6 | ||
| Positive | 25 | 44.6 | 44.0 | |
| 50 | 44.0 | 42.8 | ||
| 75 | 43.0 | 41.6 | ||
| 100 | 41.9 | 40.4 | ||
| 125 | 40.6 | 39.1 | ||
| Yu et al. [48] | Negative | 118 | 18.2 | 18.1 |
| 177 | 20.2 | 20.0 | ||
| 236 | 21.6 | 21.4 | ||
| Positive | 118 | 32.3 | 32.4 | |
| 177 | 28.0 | 28.2 | ||
| 236 | 25.2 | 26.0 | ||
| Siddique et al. [49] | Negative | 76 | 27.5 | 27.4 |
| 152 | 29.0 | 28.8 | ||
| 229 | 31.0 | 29.9 | ||
| Positive | 76 | 36.5 | 38.0 | |
| 152 | 33.5 | 34.6 | ||
| 229 | 32.0 | 32.8 | ||
| Kim and Nam [50] | Negative | 70 | 30.1 | 30.1 |
| 119 | 31.1 | 30.7 | ||
| 172 | 31.6 | 31.0 | ||
| 224 | 32.1 | 31.7 | ||
| 274 | 32.1 | 32.5 | ||
| Positive | 70 | 39.0 | 39.4 | |
| 119 | 37.1 | 36.7 | ||
| 172 | 35.5 | 35.5 | ||
| 224 | 34.0 | 33.1 | ||
| 274 | 32.5 | 30.8 | ||
| Choubane and Tia [45] | Negative | 64 | 28.9 | 28.9 |
| 114 | 30.4 | 30.2 | ||
| 165 | 31.5 | 31.2 | ||
| Positive | 64 | 43.8 | 43.8 | |
| 114 | 39.4 | 39.6 | ||
| 165 | 36.8 | 37.5 |
| Previous Studies | Thickness (cm) | Max. Pos. Temp. Difference °C | Max. Pos. Temp. Linear Gradient °C/cm | Max. Neg. Temp. Difference °C | Study Area | Measurement Time for Pos. Temp. Difference | Measurement Time for Neg. Temp. Difference |
|---|---|---|---|---|---|---|---|
| Armaghani and Larsen [46] | 23 | 11.0 | 0.48 | −6.1 | Site | Summer | Summer |
| Richardson and Armaghani [52] Shoukry and Fahmy [53] | 22.5 | 10.0 | 0.44 | Site | Summer | ||
| Choubane and Tia [45] | 20.3 | 12.7 | 0.63 | −4.6 | Site | Summer | Summer |
| Byrum and Hansen [54] | 17.8 | 15.5–19.4 | 0.87–1.09 | −7.8 to −11.6 | Site | Summer | |
| Yu et al. [48] | 29.5 | 12.8 | 0.43 | −6.7 | Site | Summer | Summer |
| Siddique et al. [49] | 30.5 | 10.5 | 0.34 | −5.0 | Site | Summer | Summer |
| Karunarathne et al. [47] | 15 | 7.9 | 0.53 | −2.6 | Site | Summer | Summer |
| Kim and Nam [50] | 32.6 | 10.0 | 0.31 | −2.5 | Site | Summer | Summer |
| Maitra et al. [55] | 30 | 26.8 | 0.89 | Laboratory Conditions | |||
| Salman and Patil [15] | 20.32 | 13.4 | 0.66 | −6.7 | Finite Element Analysis | ||
| Dhananjay and Abhilash [56] | 25 | 13.2 | 0.53 | −3.5 | Site | Summer | Summer |
| Kim and Chun [57] | 23 | 5.0 | 0.22 | −4.4 | Site | Winter | Winter |
| Pancar and Akpınar [58] | 25 | 14.0 | 0.56 | −9.8 | Site | Summer | Winter |
| Kamalakara et al. [59] | 30 | 15.0 | 0.5 | −6.0 | Site | Summer | Summer |
| Second Model Three-Axle Heavy Vehicle Loading | ||||||
|---|---|---|---|---|---|---|
| Experiment No | Maximum Principal Stresses and Displacements Induced by Temperature Differences | Maximum Principal Stresses and Displacements Induced by Temperature Differences and Loading | ||||
| ANSYS | Bradbury | ANSYS | ||||
| Max Displacement | Transverse Joint | Longitudinal Joint Bottom | Longitudinal Joint Bottom | Max Displacement | Transverse Joint | |
| DMX (mm) | S1MAX (MPa) | S1 (MPa) | S1 (MPa) | DMX (mm) | S1MAX (MPa) | |
| 1 | 0.15 | 1.13 | 1.10 | 0.96 | 0.80 | 7.13 |
| 2 | 0.15 | 1.23 | 1.20 | 1.01 | 0.77 | 6.65 |
| 3 | 0.15 | 1.26 | 1.24 | 1.04 | 0.77 | 7.16 |
| 4 | 0.24 | 3.45 | 1.68 | 1.45 | 0.65 | 4.16 |
| 5 | 0.24 | 3.39 | 1.83 | 1.44 | 0.67 | 4.70 |
| 6 | 0.23 | 3.41 | 1.74 | 1.33 | 0.67 | 4.36 |
| 7 | 0.34 | 4.43 | 2.35 | 2.08 | 0.65 | 4.45 |
| 8 | 0.33 | 3.76 | 2.19 | 1.78 | 0.65 | 3.92 |
| 9 | 0.34 | 4.12 | 2.34 | 1.87 | 0.69 | 4.06 |
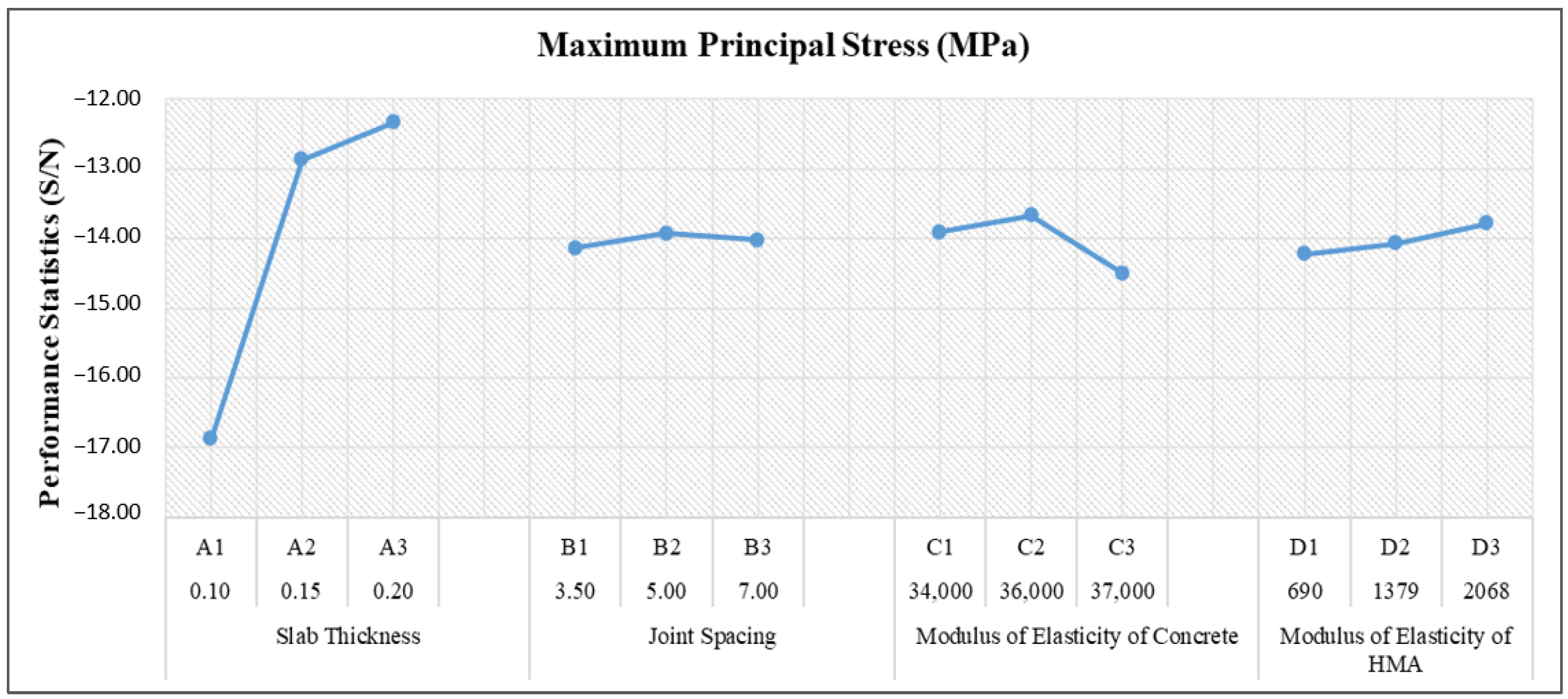
| Average S/N Effects | ||||
|---|---|---|---|---|
| Slab Thickness | Joint Spacing | Modulus of Elasticity of Concrete | Modulus of Elasticity of HMA | |
| 1st Level | −16.872 | −14.137 | −13.906 | −14.225 |
| 2nd Level | −12.871 | −13.921 | −13.670 | −14.071 |
| 3rd Level | −12.334 | −14.020 | −14.502 | −13.782 |
| Factors | Level | Contribution upon S/N |
|---|---|---|
| Slab Thickness | A3 | 1.692 |
| Joint Spacing | B2 | 0.105 |
| Modulus of Elasticity of Concrete | C2 | 0.356 |
| Modulus of Elasticity of HMA | D3 | 0.244 |
| Contribution of All Factors (S/N) | 2.397 | |
| Average Performance Statistics (S/N) | −14.026 | |
| Expected Value at Optimum Conditions (S/N) | −11.629 | |
| Verification Test Result (S/N)/(MPa) | −12,320/4.13 | |
| Confidence Interval (α = 95%) (S/N) | −12,517/−11.233 |
| Elasticity Mod. of HMA (MPa) | Heavy Vehicle Axle Type | Concrete Thickness (m) | Elasticity Mod. of Concrete (MPa) | Joint Spacing (m) | Maximum Principal Stress (MPa) | Rupture Mod. of Concrete (MPa) | Result |
|---|---|---|---|---|---|---|---|
| 690 | 1.22 | 0.10 | 34,000 | 3.50 | 7.13 | 4.40 | Not Suitable |
| 690 | 1.22 | 0.10 | 34,000 | 5.00 | 6.96 | 4.40 | Not Suitable |
| 690 | 1.22 | 0.10 | 34,000 | 7.00 | 7.03 | 4.40 | Not Suitable |
| 690 | 1.22 | 0.10 | 36,000 | 3.50 | 6.94 | 4.60 | Not Suitable |
| 690 | 1.22 | 0.10 | 36,000 | 5.00 | 6.77 | 4.60 | Not Suitable |
| 690 | 1.22 | 0.10 | 36,000 | 7.00 | 6.85 | 4.60 | Not Suitable |
| 690 | 1.22 | 0.10 | 37,000 | 3.50 | 7.64 | 5.00 | Not Suitable |
| 690 | 1.22 | 0.10 | 37,000 | 5.00 | 7.45 | 5.00 | Not Suitable |
| 690 | 1.22 | 0.10 | 37,000 | 7.00 | 7.53 | 5.00 | Not Suitable |
| 690 | 1.22 | 0.15 | 34,000 | 3.50 | 4.39 | 4.40 | Suitable |
| 690 | 1.22 | 0.15 | 34,000 | 5.00 | 4.39 | 4.40 | Suitable |
| 690 | 1.22 | 0.15 | 34,000 | 7.00 | 4.38 | 4.40 | Suitable |
| 690 | 1.22 | 0.15 | 36,000 | 3.50 | 4.38 | 4.60 | Suitable |
| 690 | 1.22 | 0.15 | 36,000 | 5.00 | 4.27 | 4.60 | Suitable |
| 690 | 1.22 | 0.15 | 36,000 | 7.00 | 4.32 | 4.60 | Suitable |
| 690 | 1.22 | 0.15 | 37,000 | 3.50 | 4.82 | 5.00 | Suitable |
| 690 | 1.22 | 0.15 | 37,000 | 5.00 | 4.70 | 5.00 | Suitable |
| 690 | 1.22 | 0.15 | 37,000 | 7,00 | 4.75 | 5.00 | Suitable |
| 690 | 1.22 | 0.20 | 34,000 | 3.50 | 4.23 | 4.40 | Suitable |
| 690 | 1.22 | 0.20 | 34,000 | 5.00 | 4.12 | 4.40 | Suitable |
| 690 | 1.22 | 0.20 | 34,000 | 7.00 | 4.17 | 4.40 | Suitable |
| 690 | 1.22 | 0.20 | 36,000 | 3.50 | 4.12 | 4.60 | Suitable |
| 690 | 1.22 | 0.20 | 36,000 | 5.00 | 4.01 | 4.60 | Suitable |
| 690 | 1.22 | 0.20 | 36,000 | 7.00 | 4.06 | 4.60 | Suitable |
| 690 | 1.22 | 0.20 | 37,000 | 3.50 | 4.53 | 5.00 | Suitable |
| 690 | 1.22 | 0.20 | 37,000 | 5.00 | 4.42 | 5.00 | Suitable |
| 690 | 1.22 | 0.20 | 37,000 | 7.00 | 4.47 | 5.00 | Suitable |
| 1379 | 1.22 | 0.10 | 34,000 | 3.50 | 7.00 | 4.40 | Not Suitable |
| 1379 | 1.22 | 0.10 | 34,000 | 5.00 | 6.83 | 4.40 | Not Suitable |
| 1379 | 1.22 | 0.10 | 34,000 | 7.00 | 6.91 | 4.40 | Not Suitable |
| 1379 | 1.22 | 0.10 | 36,000 | 3.50 | 6.82 | 4.60 | Not Suitable |
| 1379 | 1.22 | 0.10 | 36,000 | 5.00 | 6.65 | 4.60 | Not Suitable |
| 1379 | 1.22 | 0.10 | 36,000 | 7.00 | 6.73 | 4.60 | Not Suitable |
| 1379 | 1.22 | 0.10 | 37,000 | 3.50 | 7.50 | 5.00 | Not Suitable |
| 1379 | 1.22 | 0.10 | 37,000 | 5.00 | 7.32 | 5.00 | Not Suitable |
| 1379 | 1.22 | 0.10 | 37,000 | 7.00 | 7.40 | 5.00 | Not Suitable |
| 1379 | 1.22 | 0.15 | 34,000 | 3.50 | 4.35 | 4.40 | Suitable |
| 1379 | 1.22 | 0.15 | 34,000 | 5.00 | 4.31 | 4.40 | Suitable |
| 1379 | 1.22 | 0.15 | 34,000 | 7.00 | 4.36 | 4.40 | Suitable |
| 1379 | 1.22 | 0.15 | 36,000 | 3.50 | 4.30 | 4.60 | Suitable |
| 1379 | 1.22 | 0.15 | 36,000 | 5.00 | 4.20 | 4.60 | Suitable |
| 1379 | 1.22 | 0.15 | 36,000 | 7.00 | 4.24 | 4.60 | Suitable |
| 1379 | 1.22 | 0.15 | 37,000 | 3.50 | 4.73 | 5.00 | Suitable |
| 1379 | 1.22 | 0.15 | 37,000 | 5.00 | 4.62 | 5.00 | Suitable |
| 1379 | 1.22 | 0.15 | 37,000 | 7.00 | 4.67 | 5.00 | Suitable |
| 1379 | 1.22 | 0.20 | 34,000 | 3.50 | 4.15 | 4.40 | Suitable |
| 1379 | 1.22 | 0.20 | 34,000 | 5.00 | 4.05 | 4.40 | Suitable |
| 1379 | 1.22 | 0.20 | 34,000 | 7.00 | 4.10 | 4.40 | Suitable |
| 1379 | 1.22 | 0.20 | 36,000 | 3.50 | 4.04 | 4.60 | Suitable |
| 1379 | 1.22 | 0.20 | 36,000 | 5.00 | 3.94 | 4.60 | Suitable |
| 1379 | 1.22 | 0.20 | 36,000 | 7.00 | 3.99 | 4.60 | Suitable |
| 1379 | 1.22 | 0.20 | 37,000 | 3.50 | 4.45 | 5.00 | Suitable |
| 1379 | 1.22 | 0.20 | 37,000 | 5.00 | 4.34 | 5.00 | Suitable |
| 1379 | 1.22 | 0.20 | 37,000 | 7.00 | 4.39 | 5.00 | Suitable |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baş, F.İ.; Bayrak, O.Ü.; Bayata, H.F. A Practical Design Guide for Unbonded Jointed Plain Concrete Roads over Deteriorated HMA Roads: Realistic Traffic Loading. Coatings 2022, 12, 1817. https://doi.org/10.3390/coatings12121817
Baş Fİ, Bayrak OÜ, Bayata HF. A Practical Design Guide for Unbonded Jointed Plain Concrete Roads over Deteriorated HMA Roads: Realistic Traffic Loading. Coatings. 2022; 12(12):1817. https://doi.org/10.3390/coatings12121817
Chicago/Turabian StyleBaş, Fatih İrfan, Osman Ünsal Bayrak, and Halim Ferit Bayata. 2022. "A Practical Design Guide for Unbonded Jointed Plain Concrete Roads over Deteriorated HMA Roads: Realistic Traffic Loading" Coatings 12, no. 12: 1817. https://doi.org/10.3390/coatings12121817
APA StyleBaş, F. İ., Bayrak, O. Ü., & Bayata, H. F. (2022). A Practical Design Guide for Unbonded Jointed Plain Concrete Roads over Deteriorated HMA Roads: Realistic Traffic Loading. Coatings, 12(12), 1817. https://doi.org/10.3390/coatings12121817






