Analytical Simulation for Magnetohydrodynamic Maxwell Fluid Flow Past an Exponentially Stretching Surface with First-Order Velocity Slip Condition
Abstract
:1. Introduction
2. Problem Formulation
3. HAM Solution
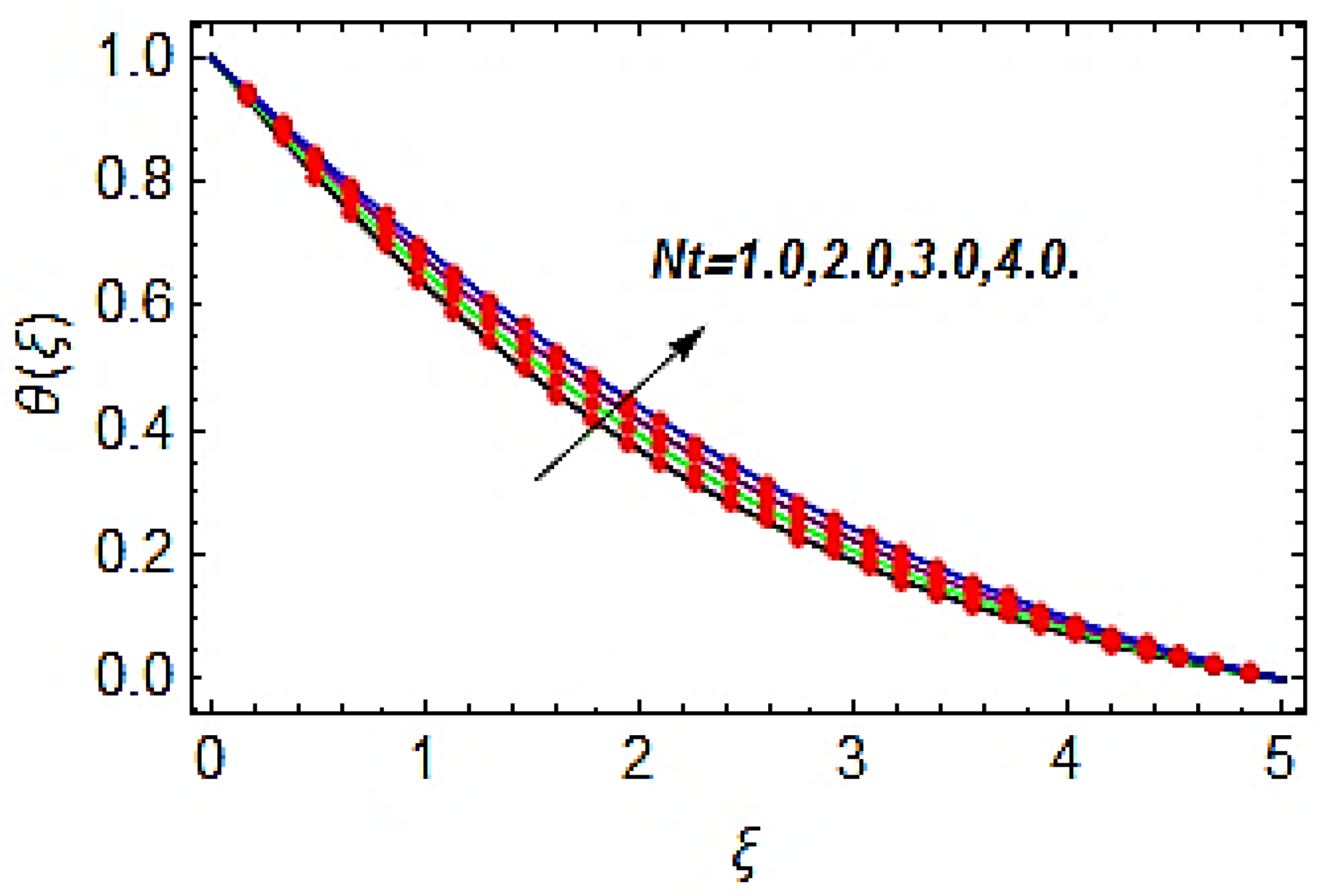
4. Results and Discussion
5. Conclusions
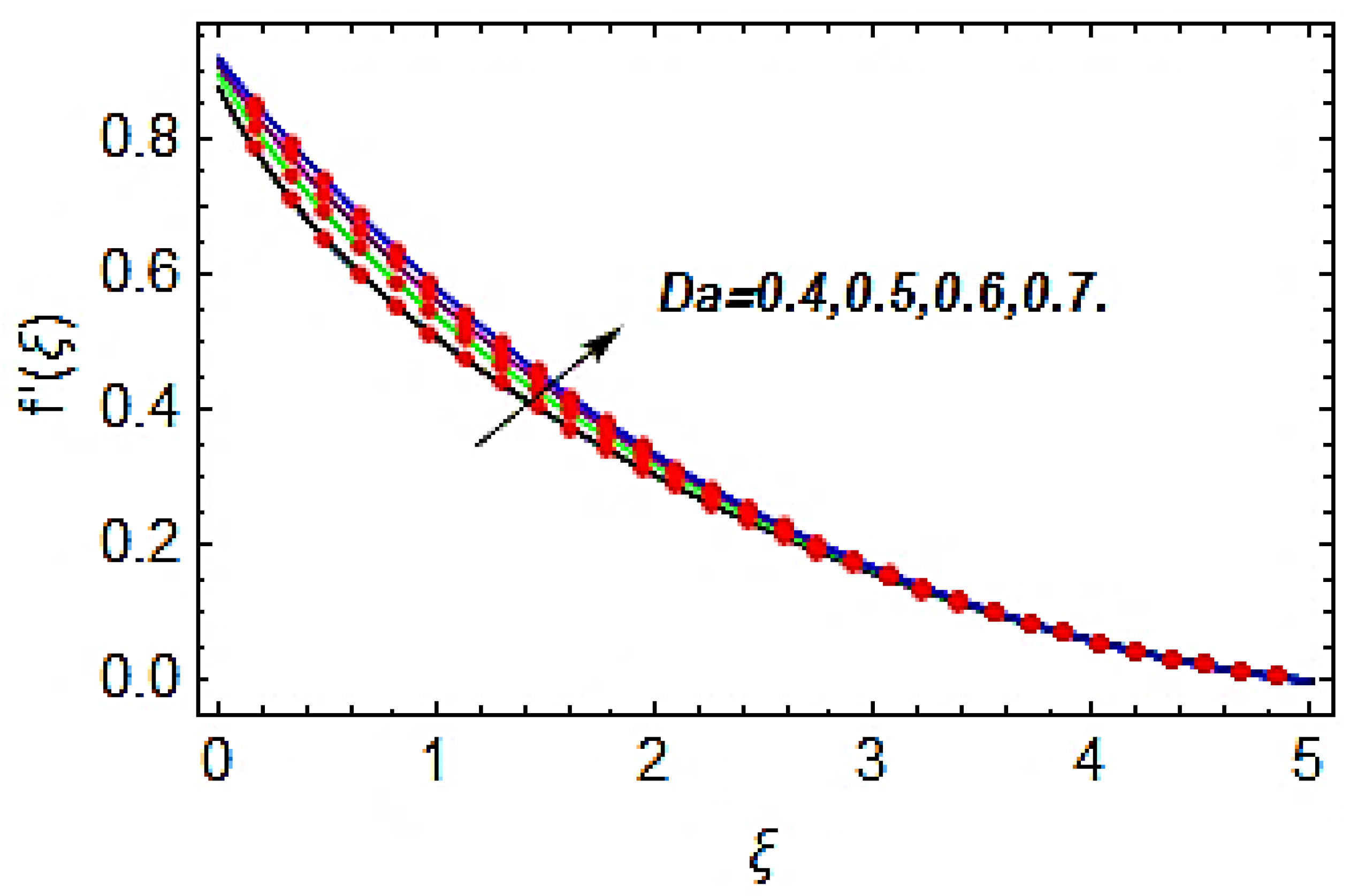
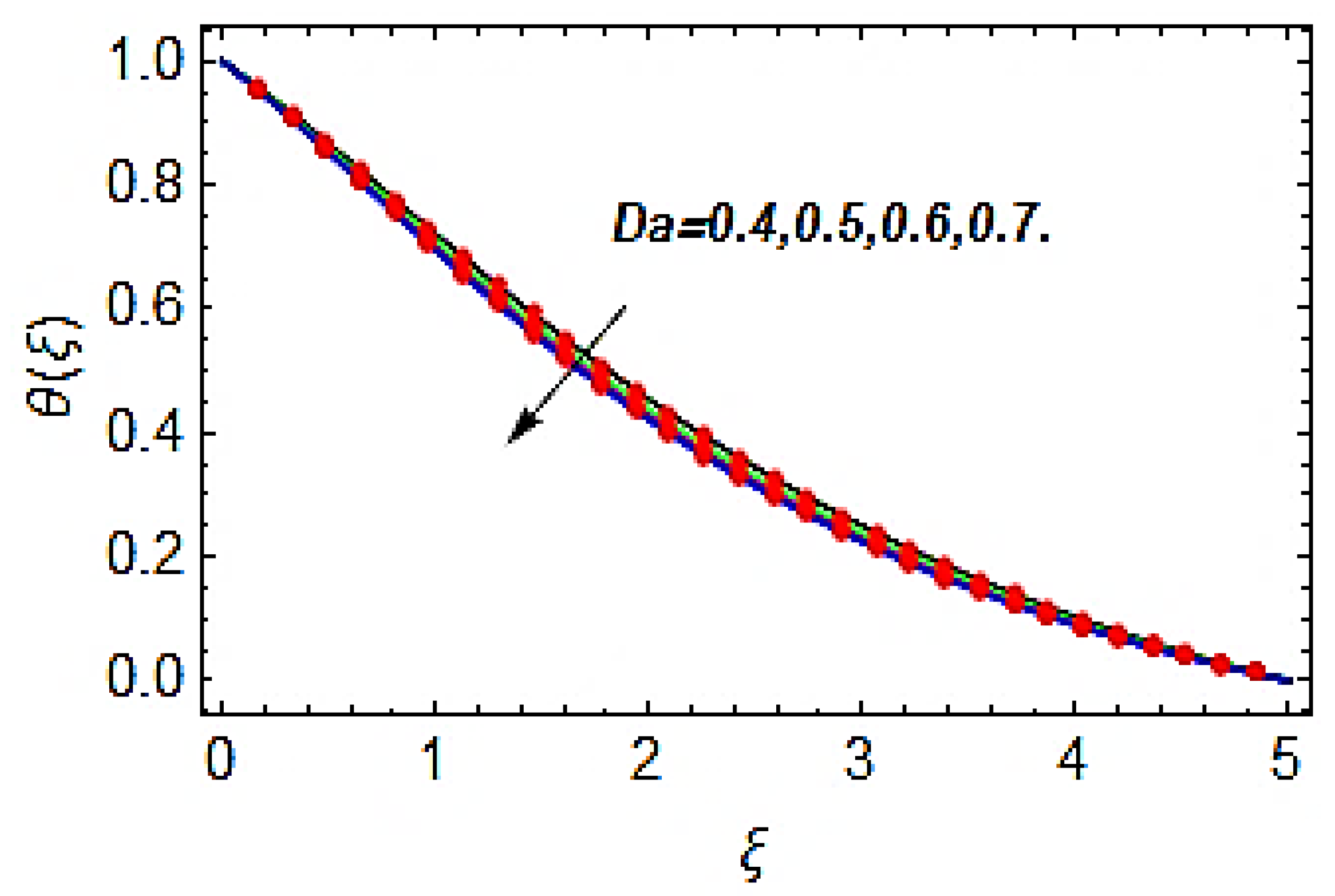
- The flow profile increases while the thermal and concentration profiles reduce with greater Darcy number.
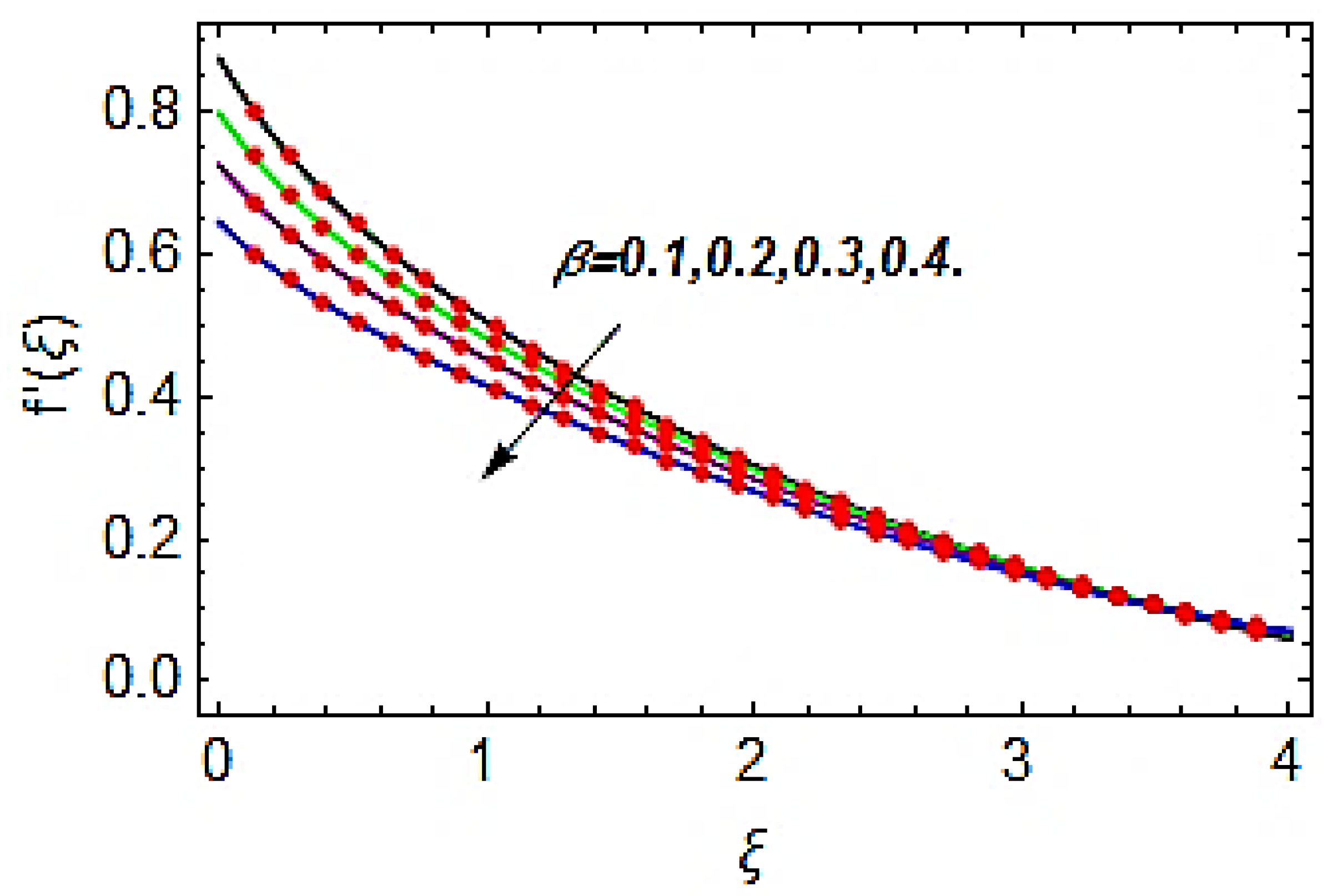
- The greater Deborah number augments the velocity profile.
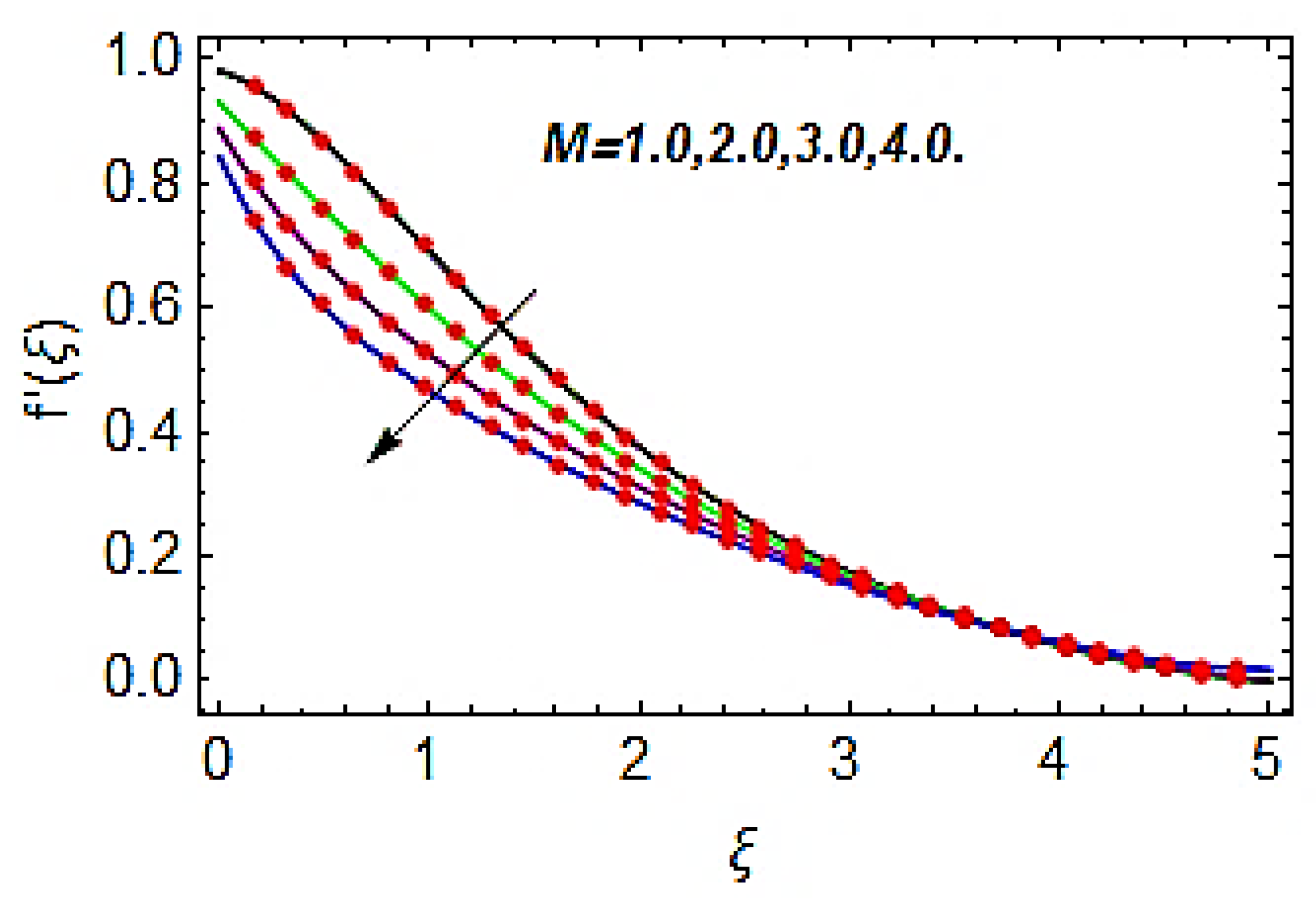
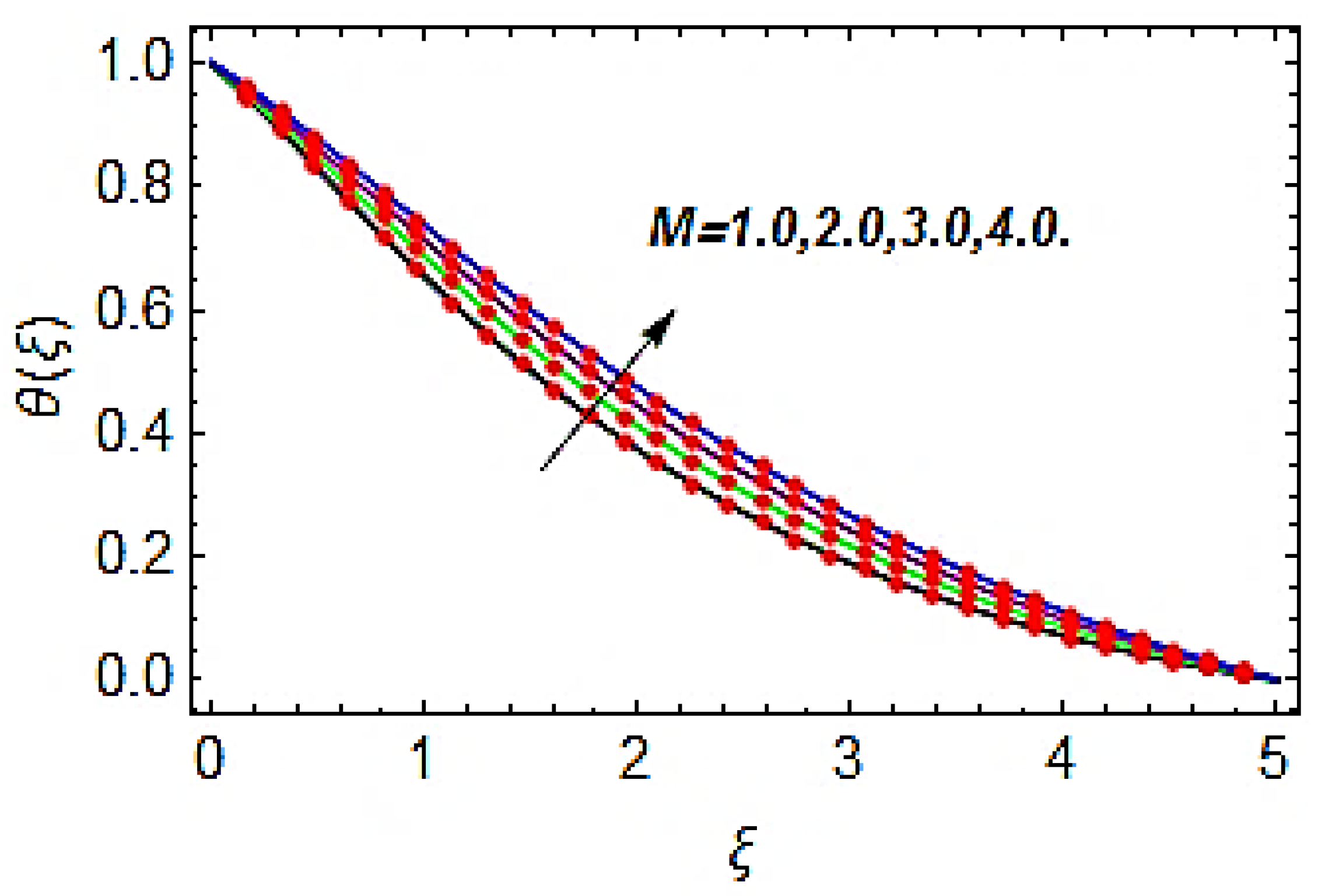
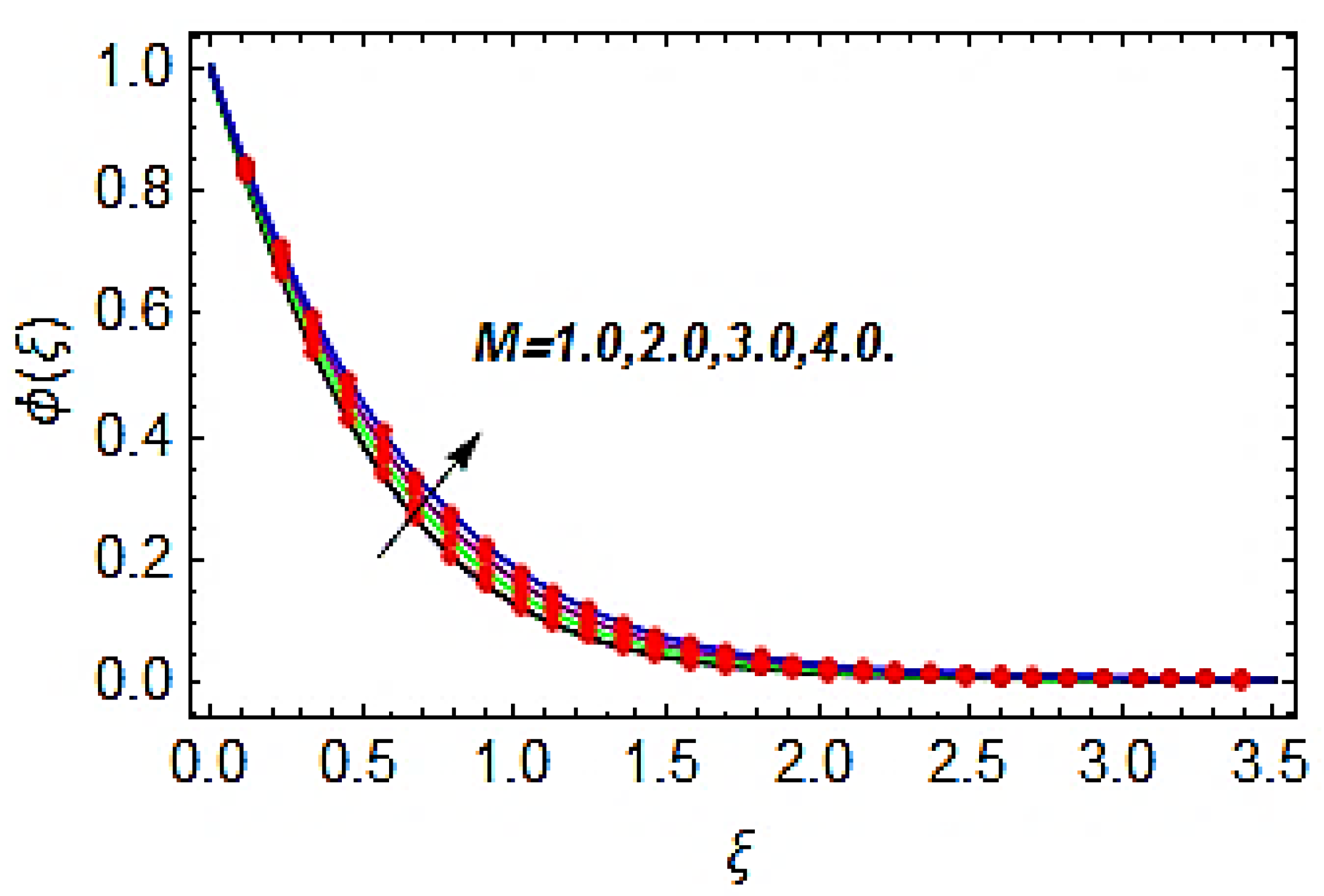
- The augmentation in magnetic parameter reduces the velocity profile, while the temperature and concentration profile increases with the increasing magnetic parameter.
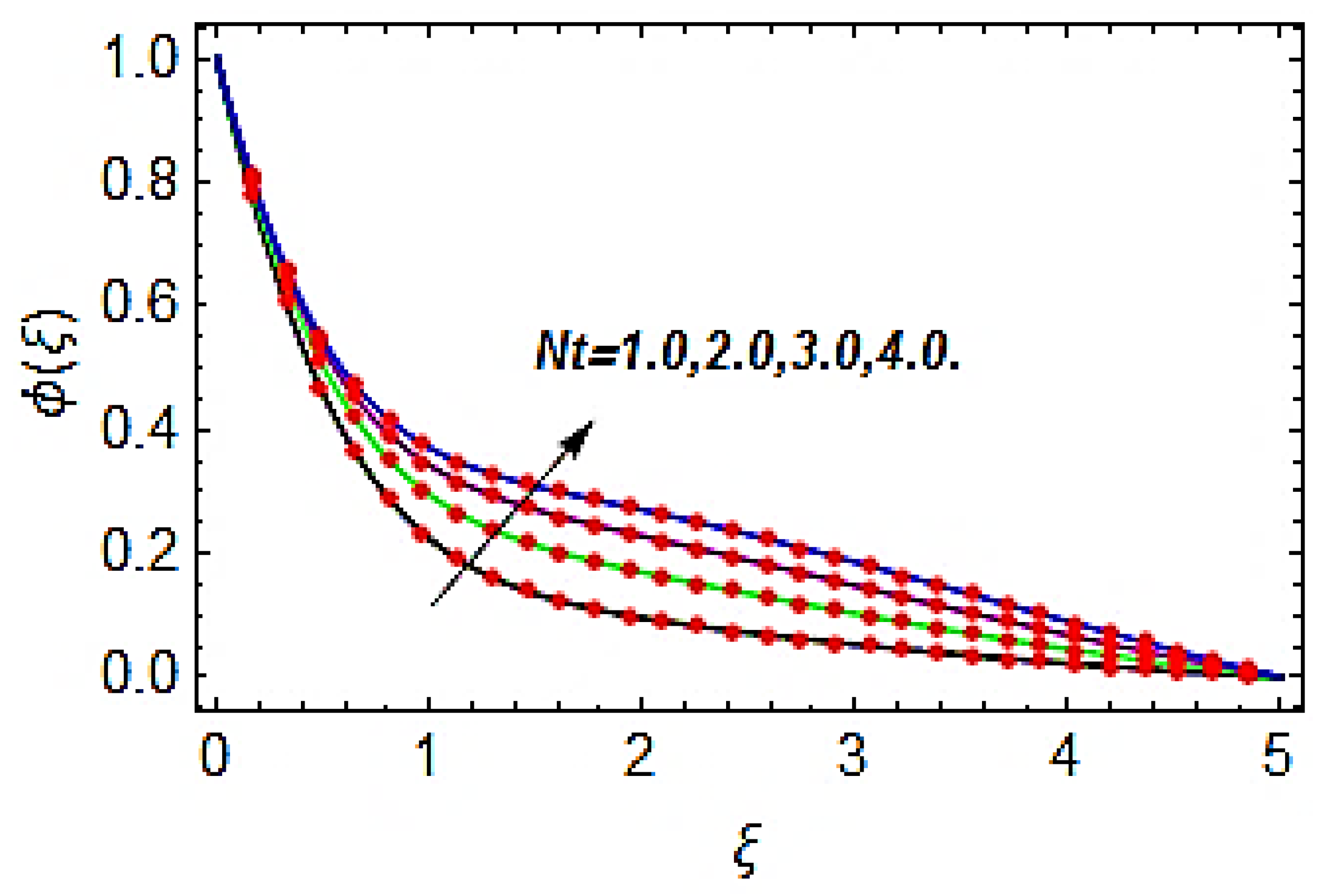
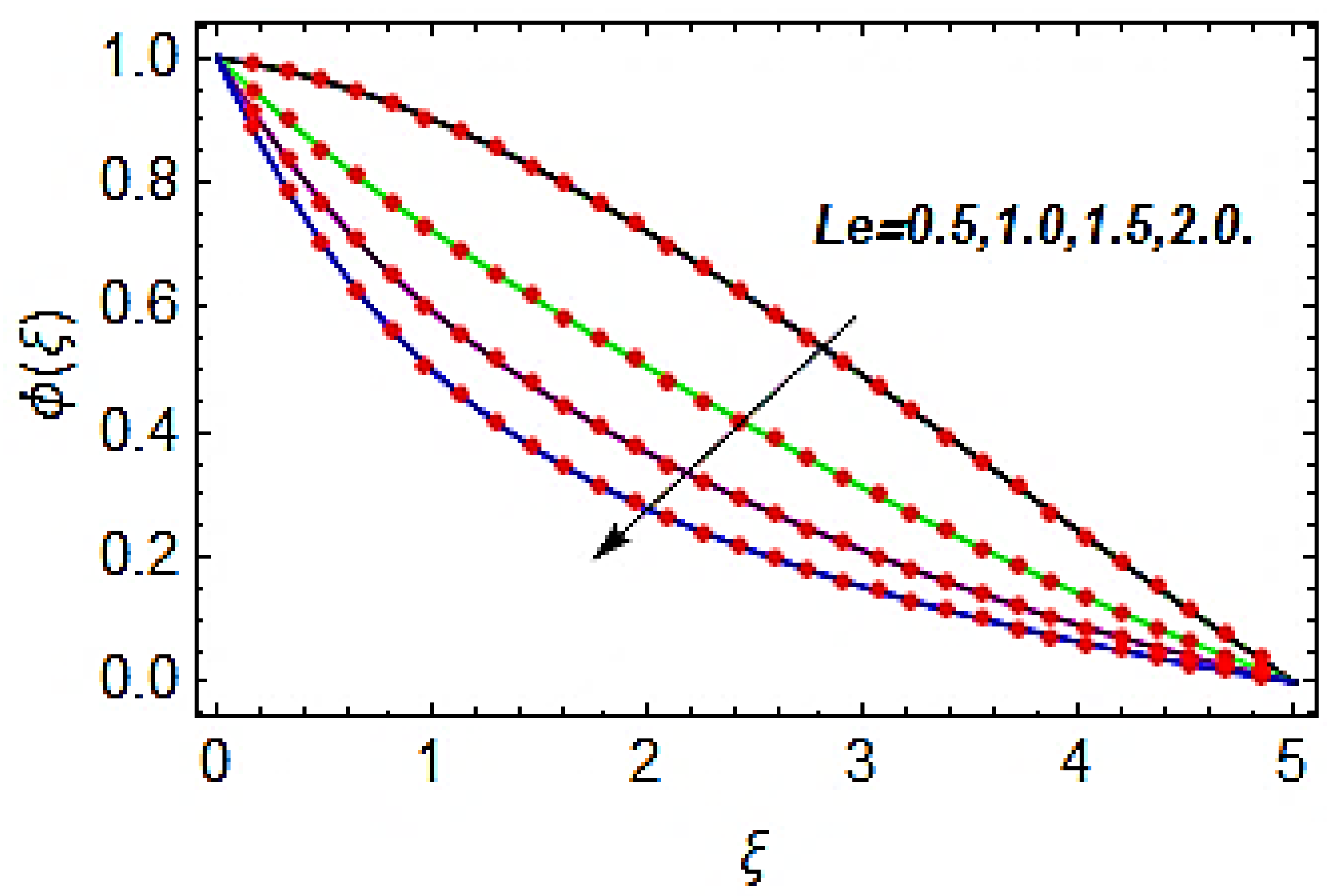
- Both the thermal and concentration profiles are the increasing functions of the thermophoresis parameter.
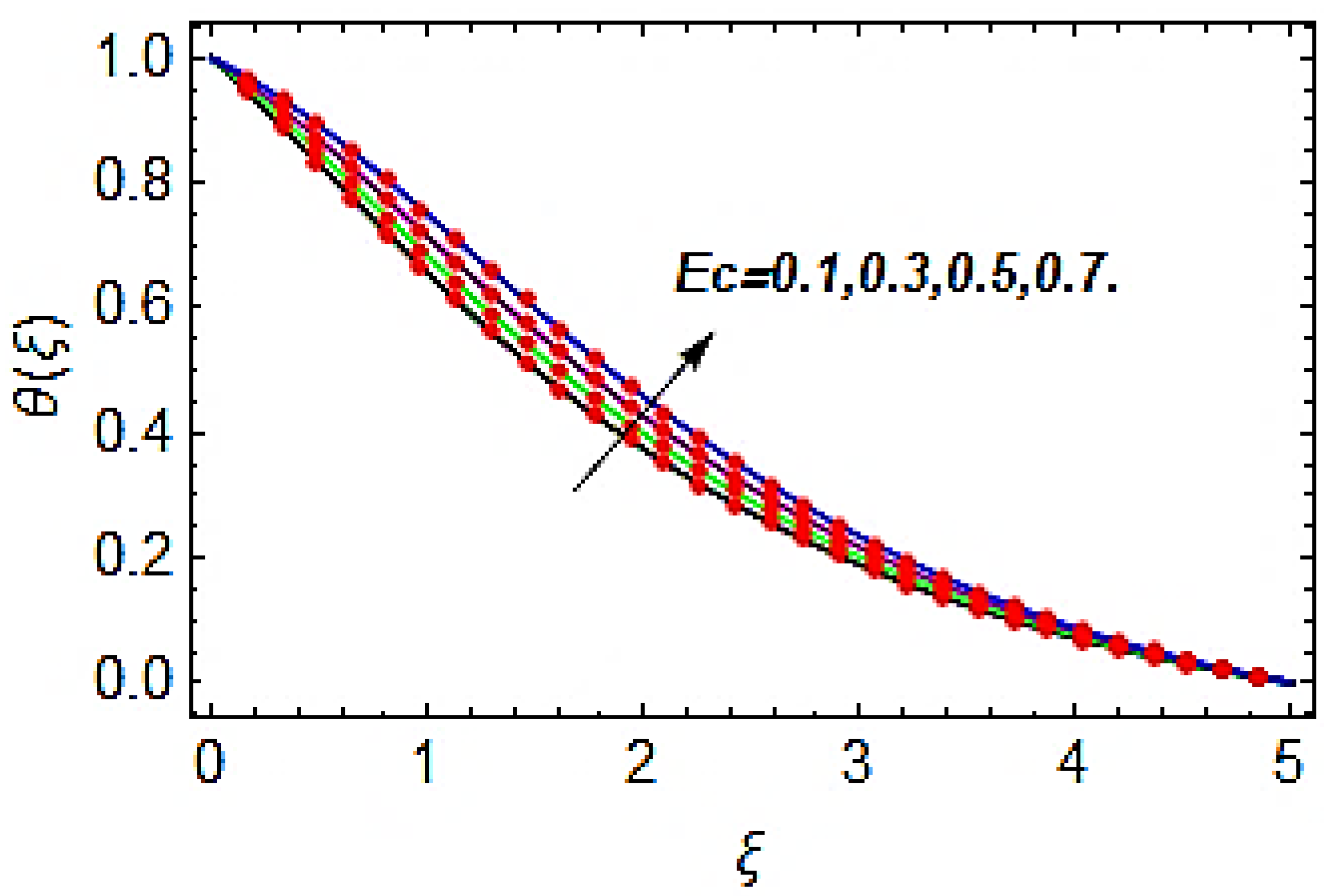
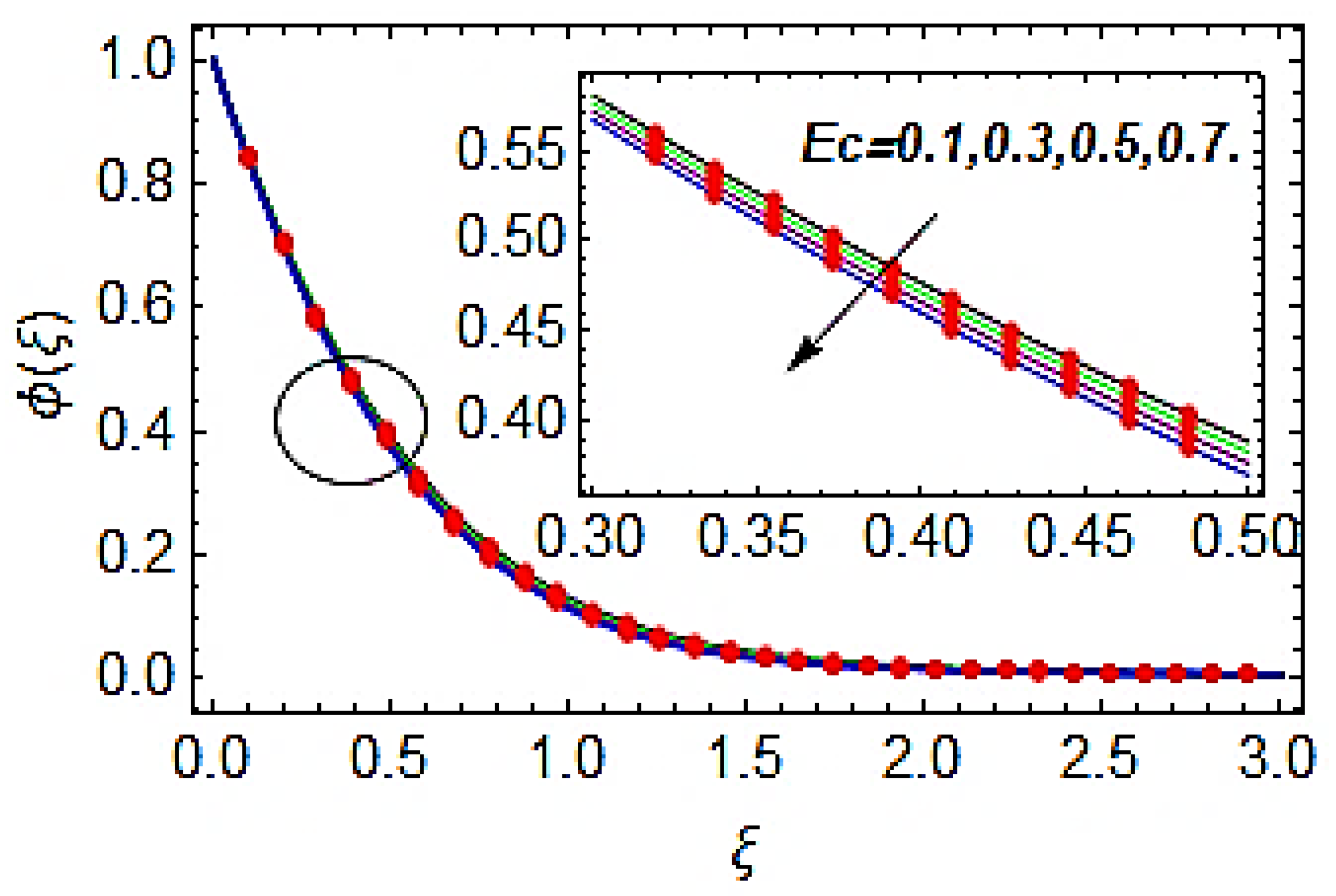
- The thermal profile is the increasing function of the Brownian motion parameter and Eckert number, whereas the concentration profile is the reducing function of the Brownian motion parameter and Eckert number.
- With the augmentation in Darcy number, the permeability strength of porous media increases, which concludes the increasing conduct of thermal and mass transportation.
- In this investigation, the higher Eckert number reduces the heat and mass transfer rates.
- Growth in magnetic parameter reduces the heat transfer rate while it increases the mass transfer rate.
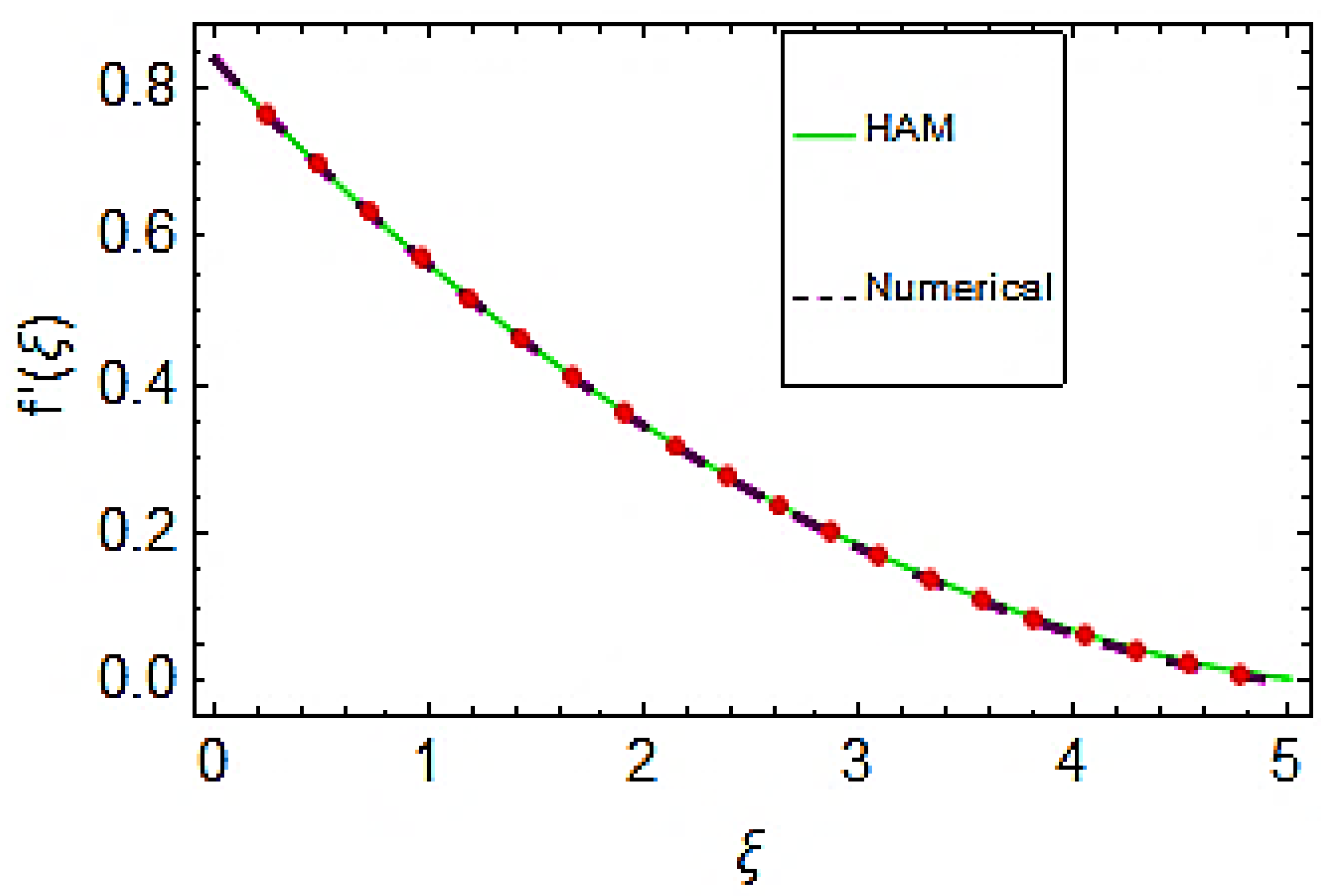
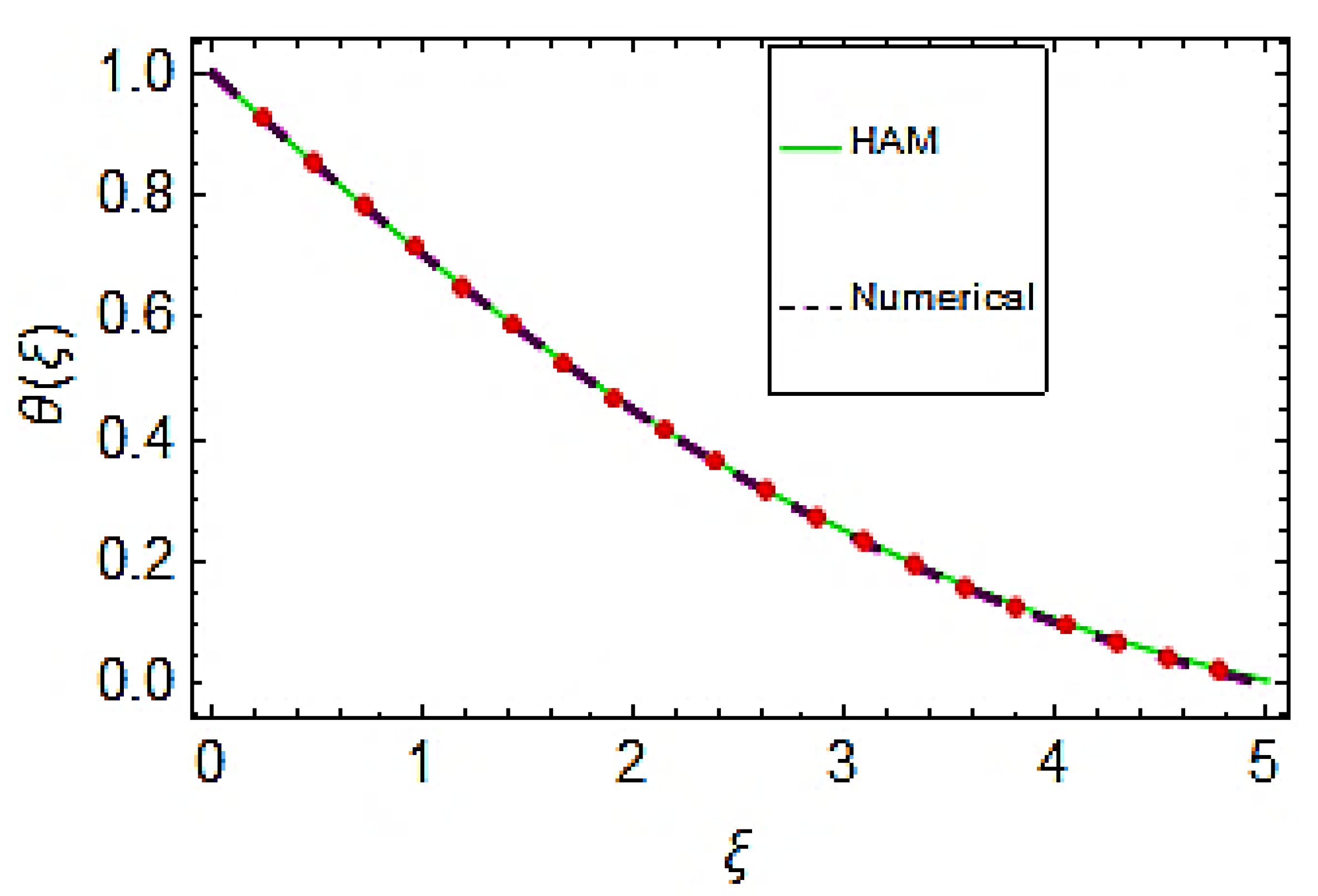
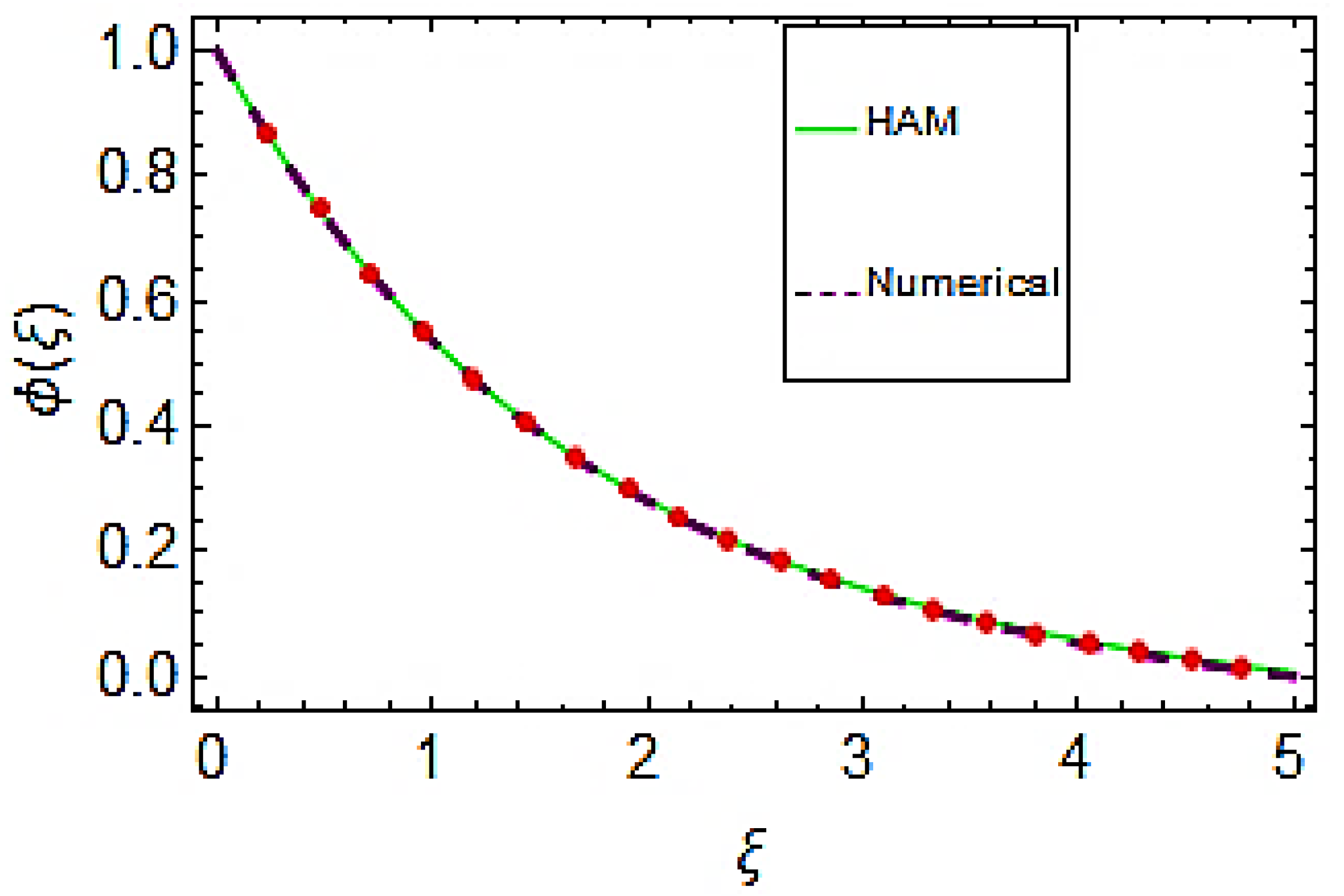
- The comparison between HAM and numerical solutions ensures the validity of the solution.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Description |
| velocity components | |
| Fluid density | |
| relaxation time | |
| Force of gravity | |
| thermal diffusivity | |
| Heat capacitance | |
| Thermophoresis coefficient | |
| Temperature | |
| Ambient temperature | |
| Reference Concentration | |
| Maxwell parameter | |
| Magnetic parameter | |
| Brownian parameter | |
| Darcy’s number | |
| Heat source/sink parameter | |
| Local Reynolds number | |
| strength of magnetic effects | |
| Stretchable velocity | |
| Permeability | |
| specific heat | |
| thermal conductivity | |
| Brownian coefficient | |
| Reference temperature | |
| Reference velocity | |
| Concentration | |
| Ambient concentration | |
| Prandtl number | |
| Thermophoresis parameter | |
| Lewis number | |
| Eckert number | |
| Radiation parameter | |
| Reference length |
References
- Alfvén, H. Existence of Electromagnetic-Hydrodynamic Waves. Nature 1942, 150, 405–406. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. MHD fluid flow and heat transfer due to a stretching rotating disk. Int. J. Therm. Sci. 2012, 51, 195–201. [Google Scholar] [CrossRef]
- Kumar, K.A.; Sugunamma, V.; Sandeep, N. Effect of thermal radiation on MHD Casson fluid flow over an exponentially stretching curved sheet. J. Therm. Anal. Calorim. 2019, 140, 2377–2385. [Google Scholar] [CrossRef]
- Khan, A.; Kumam, W.; Khan, I.; Saeed, A.; Gul, T.; Kumam, P.; Ali, I. Chemically reactive nanofluid flow past a thin moving needle with viscous dissipation, magnetic effects and hall current. PLoS ONE 2021, 16, e0249264. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.; Shah, Z.; Alzahrani, E.; Islam, S. Entropy generation and thermal analysis for rotary motion of hydromagnetic Casson nanofluid past a rotating cylinder with Joule heating effect. Int. Commun. Heat Mass Transf. 2020, 119, 104979. [Google Scholar] [CrossRef]
- Levin, M.L.; Miller, M.A. Maxwell a treatise on electricity and magnetism. Uspekhi Fizicheskikh Nauk 1981, 135, 425–440. [Google Scholar] [CrossRef]
- Islam, S.; Khan, A.; Kumam, P.; Alrabaiah, H.; Shah, Z.; Khan, W.; Zubair, M.; Jawad, M. Radiative mixed convection flow of maxwell nanofluid over a stretching cylinder with joule heating and heat source/sink effects. Sci. Rep. 2020, 10, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Shehzad, S.; Mabood, F.; Rauf, A.; Tlili, I. Forced convective Maxwell fluid flow through rotating disk under the thermophoretic particles motion. Int. Commun. Heat Mass Transf. 2020, 116, 104693. [Google Scholar] [CrossRef]
- Khan, M.N.; Nadeem, S.; Ahmad, S.; Saleem, A. Mathematical analysis of heat and mass transfer in a Maxwell fluid. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020. [Google Scholar] [CrossRef]
- Ahmad, M.; Muhammad, T.; Ahmad, I.; Aly, S. Time-dependent 3D flow of viscoelastic nanofluid over an unsteady stretching surface. Phys. A Stat. Mech. Appl. 2020, 551, 124004. [Google Scholar] [CrossRef]
- Farooq, U.; Lu, D.; Munir, S.; Ramzan, M.; Suleman, M.; Hussain, S. MHD flow of Maxwell fluid with nanomaterials due to an exponentially stretching surface. Sci. Rep. 2019, 9, 1–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sakiadis, B.C. Boundary-layer behavior on continuous solid surfaces: I. Boundary-layer equations for two-dimensional and axisymmetric flow. AIChE J. 1961, 7, 26–28. [Google Scholar] [CrossRef]
- Sakiadis, B.C. Boundary-layer behavior on continuous solid surfaces: III. The boundary layer on a continuous cylindrical surface. AiChE J. 1961, 7, 467–472. [Google Scholar] [CrossRef]
- Nadeem, S.; Khan, M.; Abbas, N. Transportation of slip effects on nanomaterial micropolar fluid flow over exponentially stretching. Alex. Eng. J. 2020, 59, 3443–3450. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Baleanu, D.; Nisar, K.S. Convective Effect on Magnetohydrodynamic (MHD) Stagnation Point Flow of Casson Fluid over a Vertical Exponentially Stretching/Shrinking Surface: Triple Solutions. Symmetry 2020, 12, 1238. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Mixed convection flow over an exponentially stretching/shrinking vertical surface in a hybrid nanofluid. Alex. Eng. J. 2020, 59, 1881–1891. [Google Scholar] [CrossRef]
- Patil, P.; Kulkarni, M.; Hiremath, P. Effects of surface roughness on mixed convective nanofluid flow past an exponentially stretching permeable surface. Chin. J. Phys. 2019, 64, 203–218. [Google Scholar] [CrossRef]
- Shah, Z.; Kumam, P.; Deebani, W. Radiative MHD Casson Nanofluid Flow with Activation energy and chemical reaction over past nonlinearly stretching surface through Entropy generation. Sci. Rep. 2020, 10, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.N.; Nadeem, S.; Ullah, N.; Saleem, A. Theoretical treatment of radiative Oldroyd-B nanofluid with microorganism pass an exponentially stretching sheet. Surf. Interfaces 2020, 21, 100686. [Google Scholar] [CrossRef]
- Manjunatha, S.; Kuttan, B.A.; Ramesh, G.K.; Gireesha, B.J.; Aly, E.H. 3D flow and heat transfer of micropolar fluid suspended with mixture of nanoparticles (Ag-CuO/H2O) driven by an exponentially stretching surface. Multidiscip. Modeling Mater. Struct. 2020, 16, 1691–1707. [Google Scholar] [CrossRef]
- Muhammad, T.; Rafique, K.; Asma, M.; Alghamdi, M. Darcy–Forchheimer flow over an exponentially stretching curved surface with Cattaneo–Christov double diffusion. Phys. A Stat. Mech. Appl. 2020, 556, 123968. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow towards a stagnation point on an exponentially stretching/shrinking vertical sheet with buoyancy effects. Int. J. Numer. Methods Heat Fluid Flow 2020, 31, 216–235. [Google Scholar] [CrossRef]
- Li, Y.-X.; Alshbool, M.H.; Lv, Y.-P.; Khan, I.; Khan, M.R.; Issakhov, A. Heat and mass transfer in MHD Williamson nanofluid flow over an exponentially porous stretching surface. Case Stud. Therm. Eng. 2021, 26, 100975. [Google Scholar] [CrossRef]
- Alazmi, B.; Vafai, K. Analysis of fluid flow and heat transfer interfacial conditions between a porous medium and a fluid layer. Int. J. Heat Mass Transf. 2001, 44, 1735–1749. [Google Scholar] [CrossRef]
- Fatunmbi, E.O.; Ogunseye, H.A.; Sibanda, P. Magnetohydrodynamic micropolar fluid flow in a porous medium with multiple slip conditions. Int. Commun. Heat Mass Transf. 2020, 115, 104577. [Google Scholar] [CrossRef]
- Krishna, M.V.; Ahamad, N.A.; Chamkha, A.J. Hall and ion slip effects on unsteady MHD free convective rotating flow through a saturated porous medium over an exponential accelerated plate. Alex. Eng. J. 2020, 59, 565–577. [Google Scholar] [CrossRef]
- Hayat, T.; Haider, F.; Alsaedi, A.; Ahmad, B. Unsteady flow of nanofluid through porous medium with variable characteristics. Int. Commun. Heat Mass Transf. 2020, 119, 104904. [Google Scholar] [CrossRef]
- Asjad, M.I.; Ikram, M.D.; Akgül, A. Analysis of MHD viscous fluid flow through porous medium with novel power law fractional differential operator. Phys. Scr. 2020, 95, 115209. [Google Scholar] [CrossRef]
- Khan, Z.H.; Khan, W.A.; Tang, J.; Sheremet, M.A. Entropy generation analysis of triple diffusive flow past a horizontal plate in porous medium. Chem. Eng. Sci. 2020, 228, 115980. [Google Scholar] [CrossRef]
- Jafar, A.B.; Shafie, S.; Ullah, I. MHD radiative nanofluid flow induced by a nonlinear stretching sheet in a porous medium. Heliyon 2020, 6, e04201. [Google Scholar] [CrossRef] [PubMed]
- Bidin, B.; Nazar, R. Numerical solution of the boundary layer flow over an exponentially stretching sheet with thermal radiation. Eur. J. Sci. Res. 2009, 33, 710–717. [Google Scholar]
- Mukhopadhyay, S. Upper-convected maxwell fluid flow over an unsteady stretching surface embedded in porous medium subjected to suction/blowing. Z. Für Nat. A 2012, 67, 641–646. [Google Scholar] [CrossRef] [Green Version]



| Ref. [31] | Ref. [32] | Present Values | |
|---|---|---|---|
| 1.0 | 0.9547 | 0.9547 | 0.9548 |
| 2.0 | 1.4714 | 1.4714 | 1.4715 |
| 3.0 | 1.8961 | 1.8961 | 1.8961 |
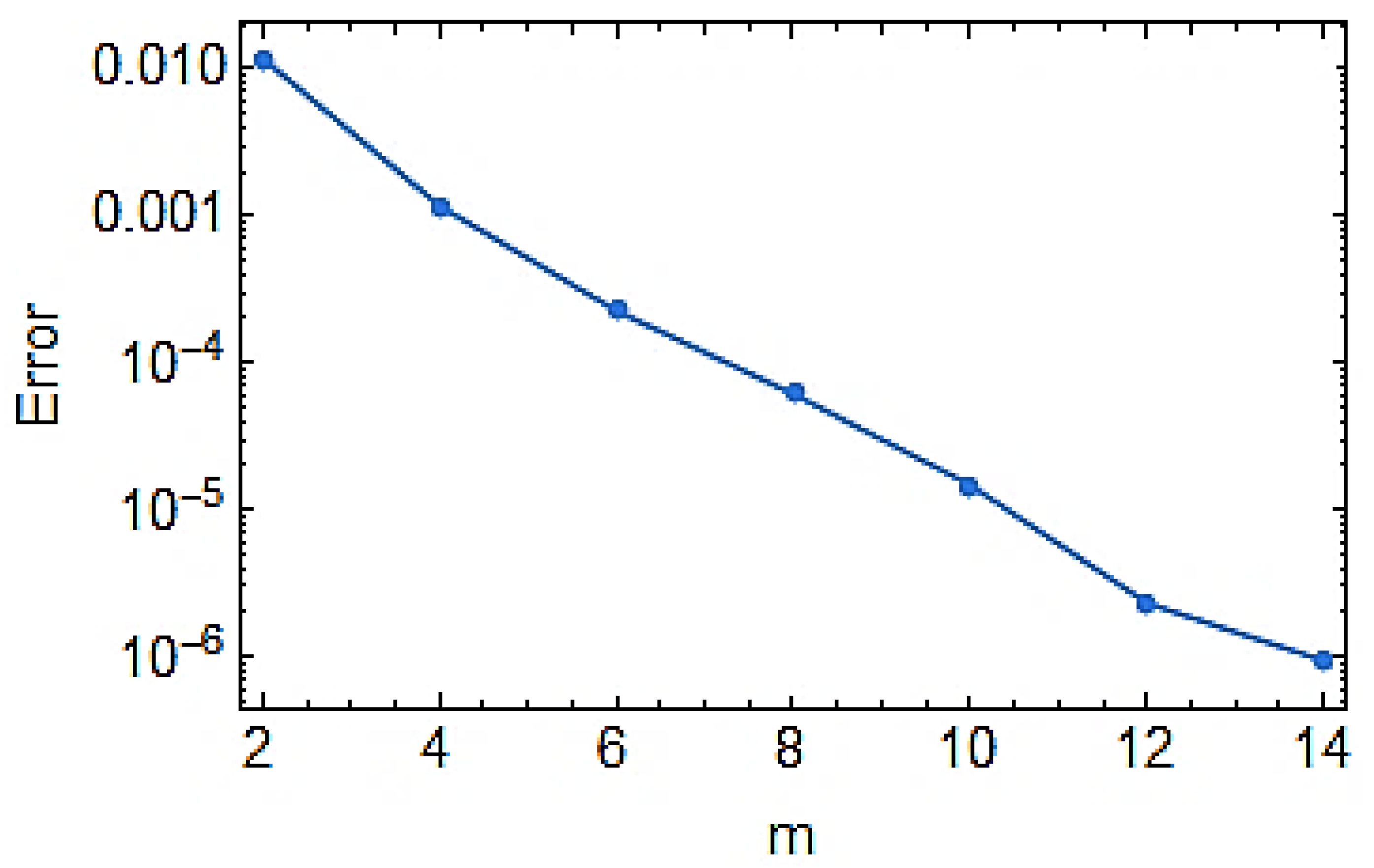
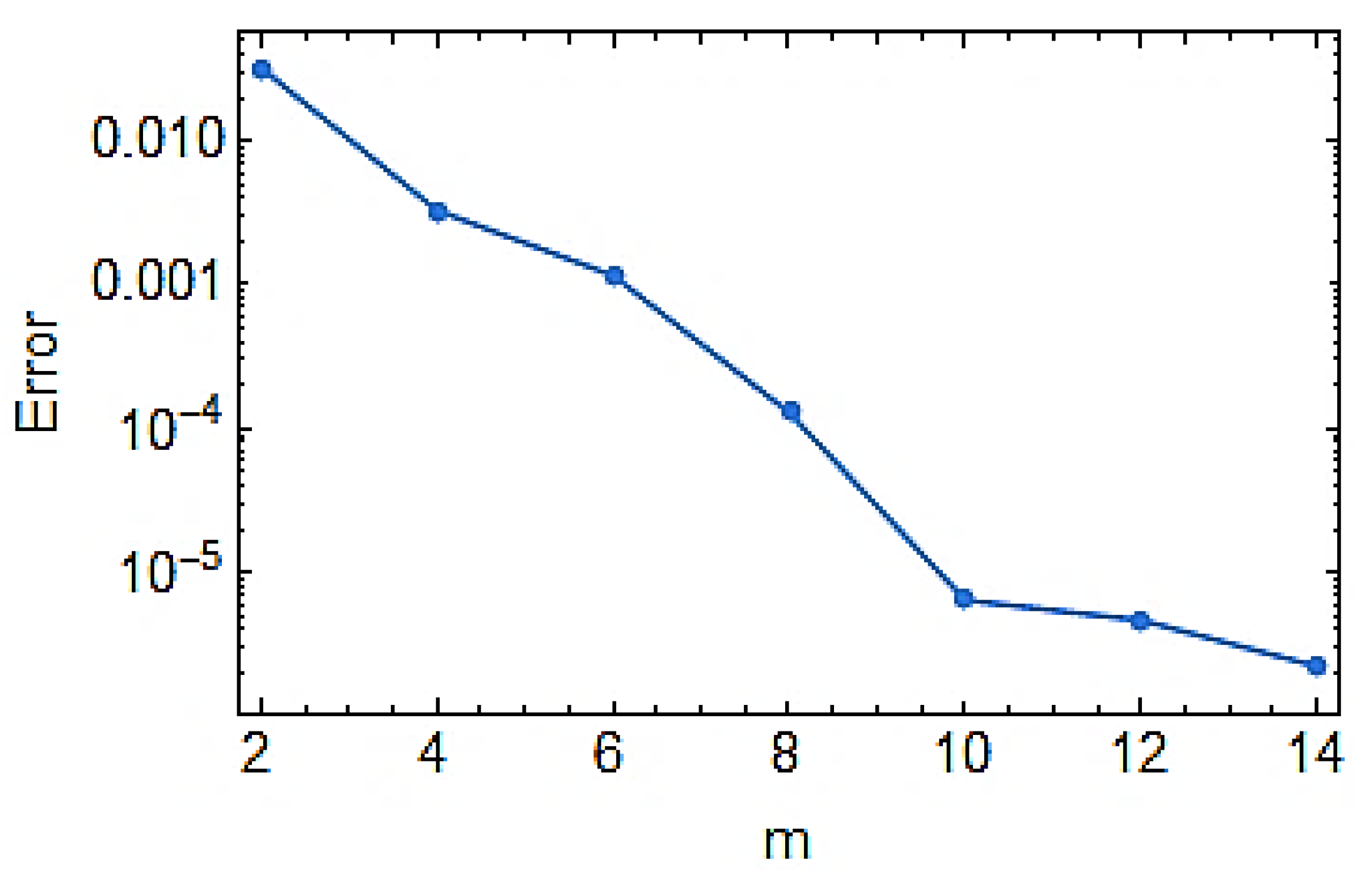
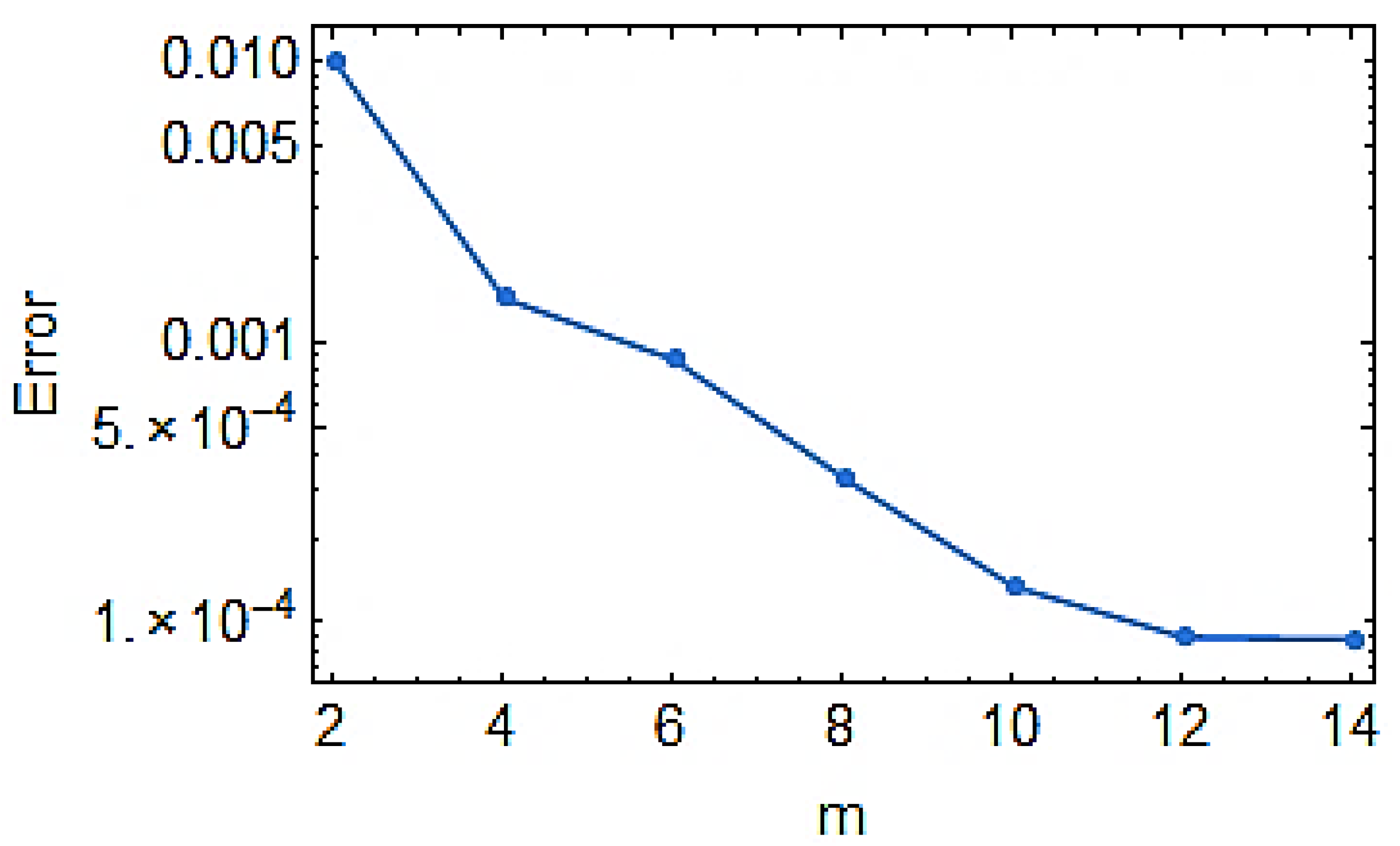
| Order of Approximations | CPU Time (in Seconds) | Velocity Function | Temperature Function | Concentration Function |
|---|---|---|---|---|
| 1 | 0.1404 | 0.007052 | 0.003414 | 0.000974 |
| 3 | 1.6224 | 0.001049 | 0.000100 | 0.000046 |
| 5 | 7.8936 | 0.000245 | 0.000018 | 0.000014 |
| 7 | 22.0584 | 0.000041 | 2.1494 × 10−6 | 4.0166 × 10−6 |
| 9 | 52.3537 | 0.000015 | 3.8766 × 10−7 | 7.6049 × 10−7 |
| 11 | 111.166 | 2.8658 × 10−6 | 7.1641 × 10−8 | 1.3424 × 10−8 |
| 13 | 218.307 | 5.8343 × 10−7 | 1.0756 × 10−8 | 3.1915 × 10−8 |
| 15 | 324.307 | 5.8343 × 10−8 | 1.0756 × 10−8 | 3.1915 × 10−8 |
| 20 | 932.471 | 5.8343 × 10−8 | 1.0756 × 10−8 | 3.1915 × 10−8 |
| 0.1 | 0.887516 | |||||
| 0.2 | 1.010560 | |||||
| 0.3 | 1.175030 | |||||
| 0.1 | 0.957536 | |||||
| 0.2 | 0.543257 | |||||
| 0.3 | 0.295332 | |||||
| 0.1 | 0.943168 | |||||
| 0.2 | 0.558536 | |||||
| 0.3 | 0.296429 | |||||
| 0.1 | 0.347954 | |||||
| 0.2 | 0.360895 | |||||
| 0.3 | 0.386636 | |||||
| 0.1 | 0.469674 | |||||
| 0.2 | 0.396361 | |||||
| 0.3 | 0.336873 | |||||
| 0.1 | 0.465363 | |||||
| 0.2 | 0.446376 | |||||
| 0.3 | 0.420874 |
| 0.1 | 0.373181 | |||||
| 0.2 | 0.351389 | |||||
| 0.3 | 0.345457 | |||||
| 0.1 | 0.423488 | |||||
| 0.2 | 0.409932 | |||||
| 0.3 | 0.380207 | |||||
| 0.1 | 0.359858 | |||||
| 0.2 | 0.371503 | |||||
| 0.3 | 0.405051 | |||||
| 0.1 | 0.405019 | |||||
| 0.2 | 0.457856 | |||||
| 0.3 | 0.511508 | |||||
| 0.1 | 0.358505 | |||||
| 0.2 | 0.363773 | |||||
| 0.3 | 0.372853 | |||||
| 0.1 | 0.697364 | |||||
| 0.2 | 0.664374 | |||||
| 0.3 | 0.635633 |
| HAM | Numerical | Absolute Error | |
|---|---|---|---|
| 0.0 | 0.828818 | 0.795797 | 0.033021 |
| 0.5 | 0.448207 | 0.347478 | 0.100729 |
| 1.0 | 0.253278 | 0.146868 | 0.106410 |
| 1.5 | 0.147001 | 0.061207 | 0.085794 |
| 2.0 | 0.086806 | 0.025356 | 0.061451 |
| 2.5 | 0.051930 | 0.010475 | 0.041456 |
| 3.0 | 0.031469 | 0.004316 | 0.027153 |
| 3.5 | 0.019403 | 0.001766 | 0.017638 |
| 4.0 | 0.012300 | 0.000699 | 0.011601 |
| 4.5 | 0.008160 | 0.000232 | 0.007929 |
| 5.0 | 0.005809 | −0.000013 | 0.005821 |
| HAM | Numerical | Absolute Error | |
|---|---|---|---|
| 0.0 | 1.000000 | 1.000000 | 0.000000 |
| 0.5 | 0.861734 | 0.890063 | 0.028329 |
| 1.0 | 0.742111 | 0.790668 | 0.048557 |
| 1.5 | 0.322220 | 0.692580 | 0.060360 |
| 2.0 | 0.528143 | 0.592819 | 0.064677 |
| 2.5 | 0.428540 | 0.491288 | 0.062748 |
| 3.0 | 0.333315 | 0.389007 | 0.055692 |
| 3.5 | 0.242911 | 0.287353 | 0.044442 |
| 4.0 | 0.157949 | 0.187751 | 0.029802 |
| 4.5 | 0.079048 | 0.091556 | 0.012508 |
| 5.0 | 0.006738 | −7.975410 × 10−7 | 0.006739 |
| HAM | Numerical | Absolute Error | |
|---|---|---|---|
| 0.0 | 1.000000 | 1.000000 | 2.220450 × 10−16 |
| 0.5 | 0.833150 | 0.833913 | 0.000762 |
| 1.0 | 0.694178 | 0.694714 | 0.000536 |
| 1.5 | 0.574847 | 0.574322 | 0.000525 |
| 2.0 | 0.470337 | 0.468678 | 0.001659 |
| 2.5 | 0.377196 | 0.374759 | 0.002437 |
| 3.0 | 0.292759 | 0.289950 | 0.002809 |
| 3.5 | 0.214934 | 0.211942 | 0.002993 |
| 4.0 | 0.142097 | 0.138718 | 0.003379 |
| 4.5 | 0.073006 | 0.068553 | 0.004453 |
| 5.0 | 0.006738 | −6.874450 × 10−8 | 0.006738 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dawar, A.; Saeed, A.; Shah, Z.; Kumam, W.; Islam, S.; Kumam, P. Analytical Simulation for Magnetohydrodynamic Maxwell Fluid Flow Past an Exponentially Stretching Surface with First-Order Velocity Slip Condition. Coatings 2021, 11, 1009. https://doi.org/10.3390/coatings11081009
Dawar A, Saeed A, Shah Z, Kumam W, Islam S, Kumam P. Analytical Simulation for Magnetohydrodynamic Maxwell Fluid Flow Past an Exponentially Stretching Surface with First-Order Velocity Slip Condition. Coatings. 2021; 11(8):1009. https://doi.org/10.3390/coatings11081009
Chicago/Turabian StyleDawar, Abdullah, Anwar Saeed, Zahir Shah, Wiyada Kumam, Saeed Islam, and Poom Kumam. 2021. "Analytical Simulation for Magnetohydrodynamic Maxwell Fluid Flow Past an Exponentially Stretching Surface with First-Order Velocity Slip Condition" Coatings 11, no. 8: 1009. https://doi.org/10.3390/coatings11081009
APA StyleDawar, A., Saeed, A., Shah, Z., Kumam, W., Islam, S., & Kumam, P. (2021). Analytical Simulation for Magnetohydrodynamic Maxwell Fluid Flow Past an Exponentially Stretching Surface with First-Order Velocity Slip Condition. Coatings, 11(8), 1009. https://doi.org/10.3390/coatings11081009









