A New Strong Form Technique for Thermo-Electro-Mechanical Behaviors of Piezoelectric Solids
Abstract
1. Introduction
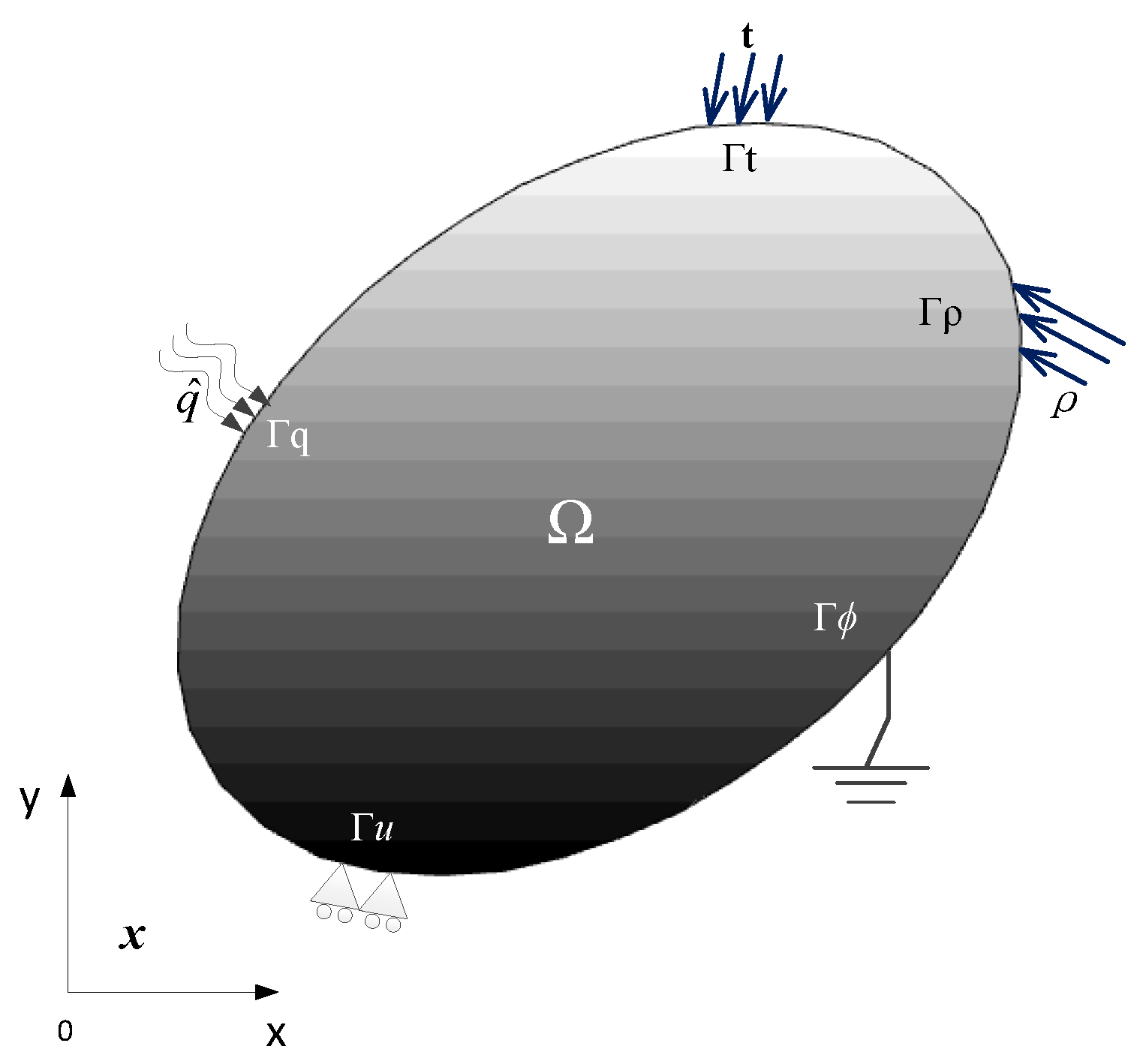
2. Unified Governing Equations for Thermo-Electro-Mechanical Problems
3. Elemental Differential Method for Thermo-Electro-Mechanical Problems
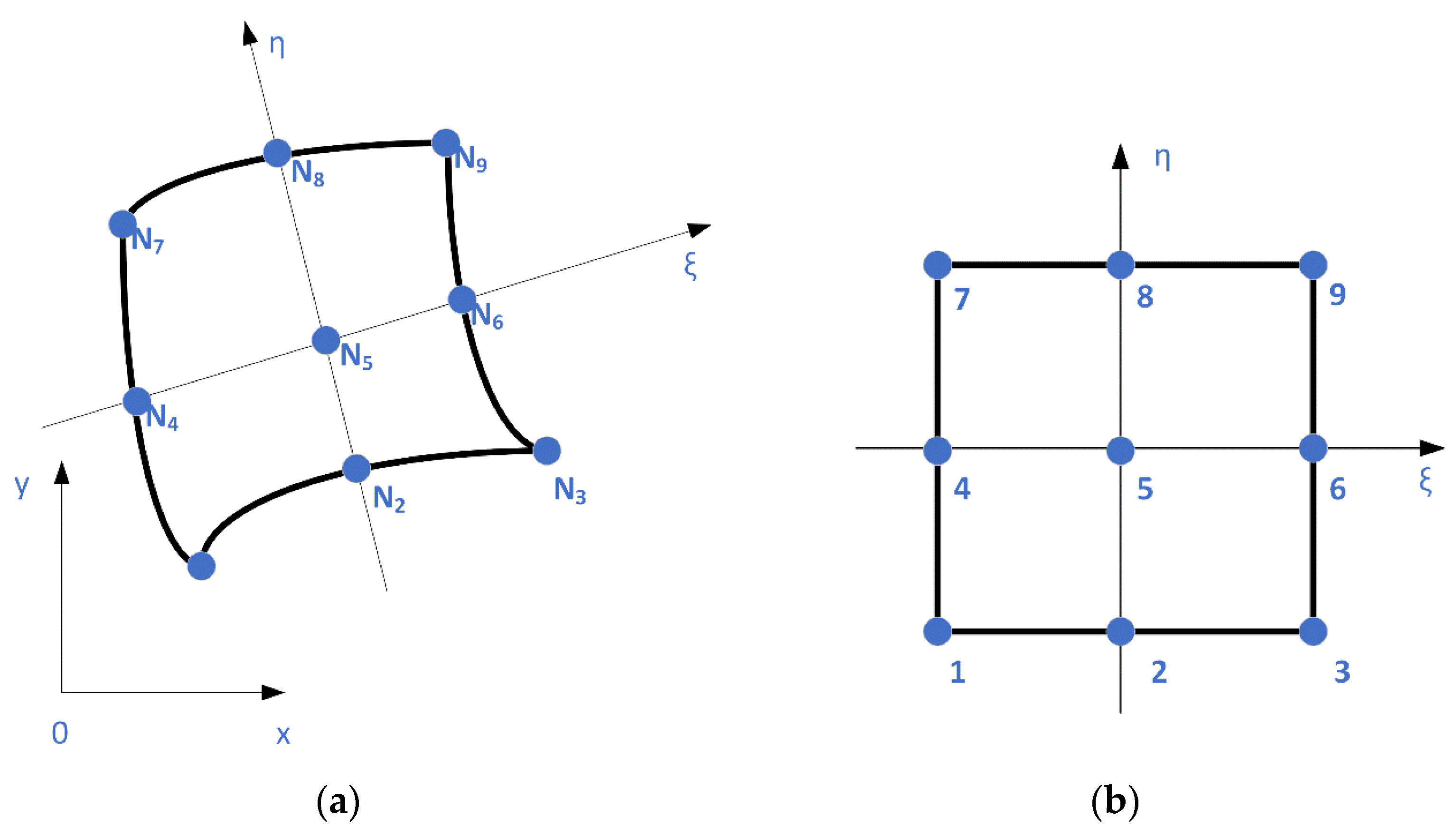
3.1. Lagrange Isoparametric Elements
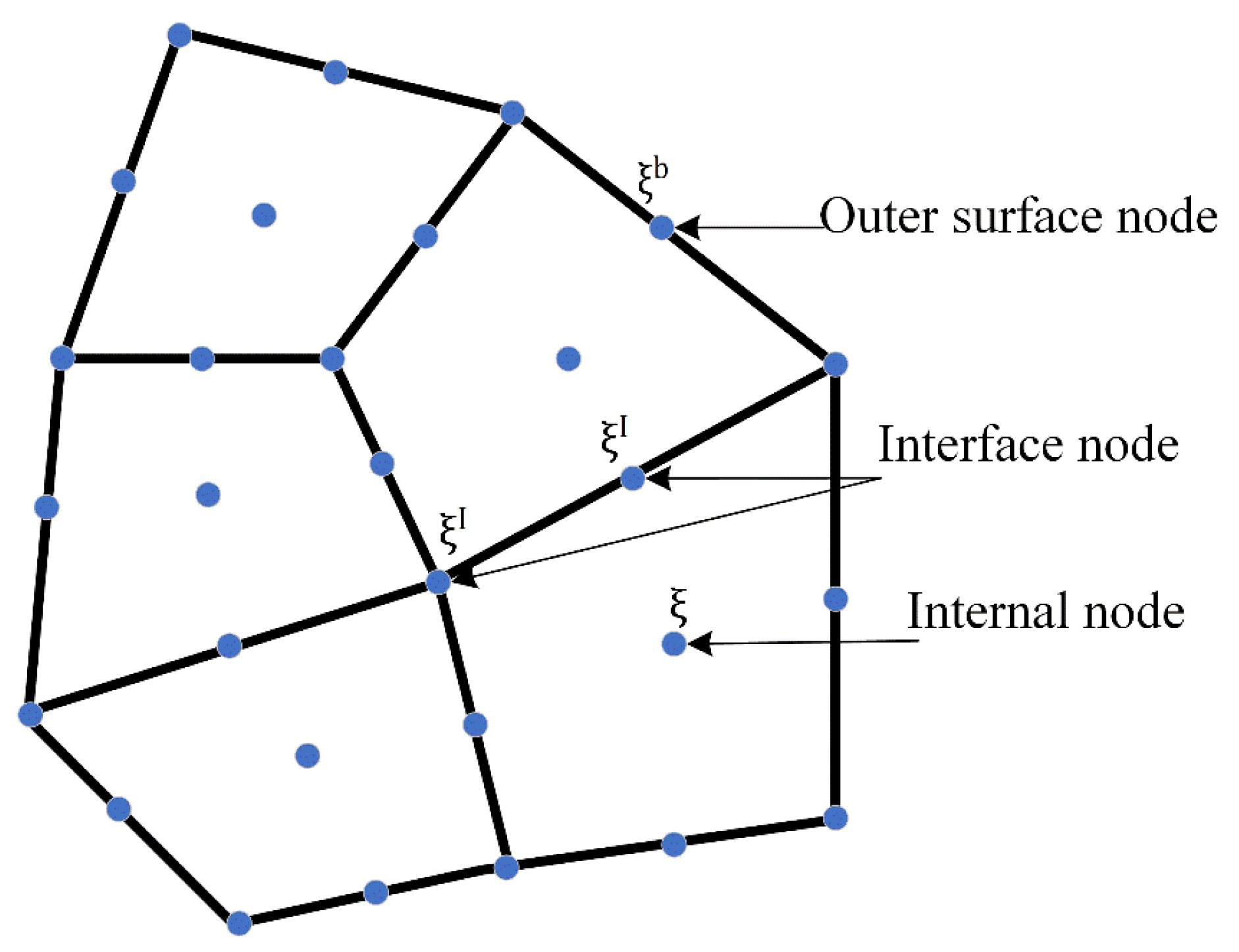
3.2. Point Collocation Technique
3.2.1. Point Collocation Technique for Thermal Conductions
3.2.2. Point Collocation Techniques for the Thermal Elastic Problems
3.2.3. The Final System of Equations for the Coupled Problem
4. Numerical Examples
4.1. Piezoelectric Composite Structure Composed of Periodical Unit Cells
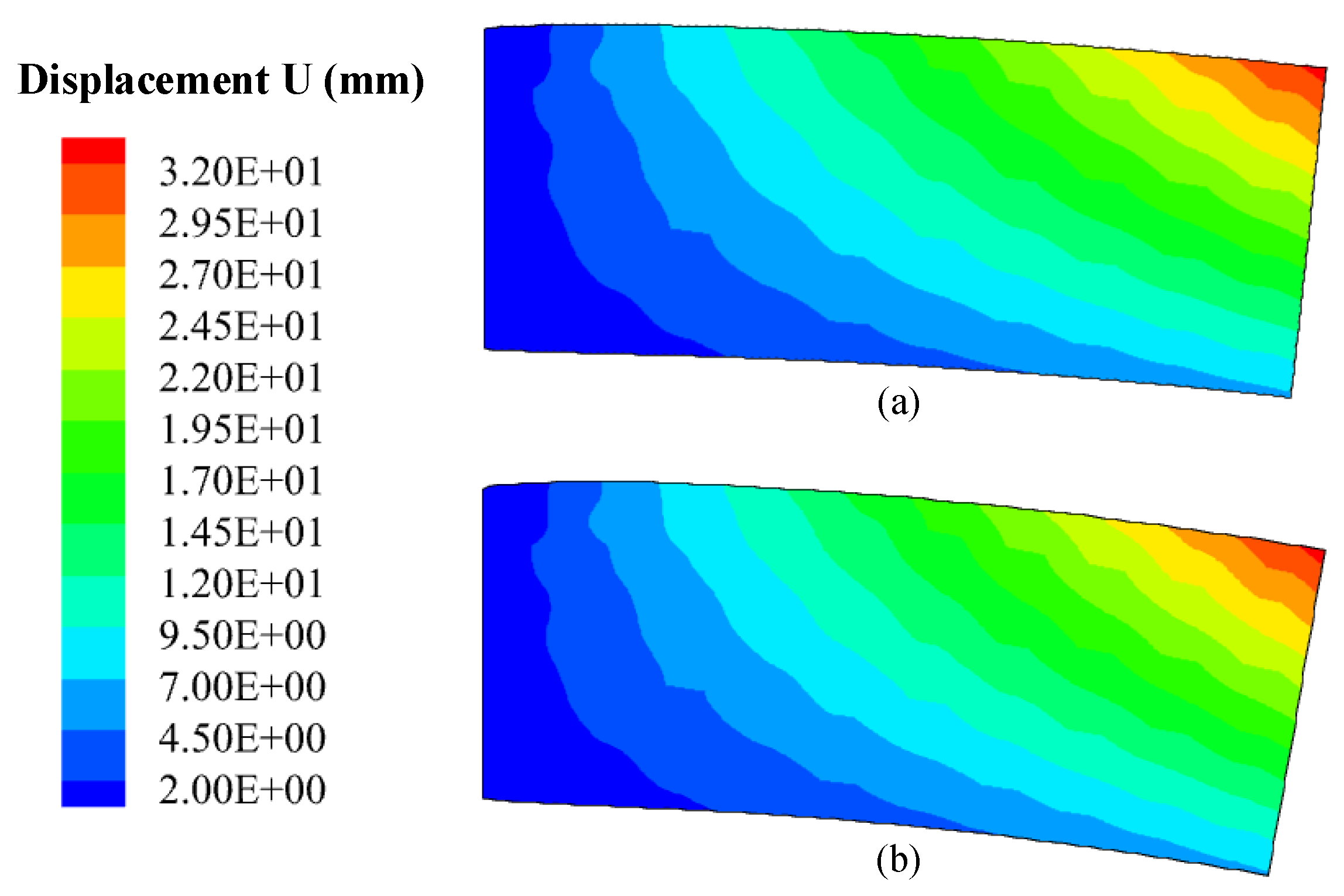
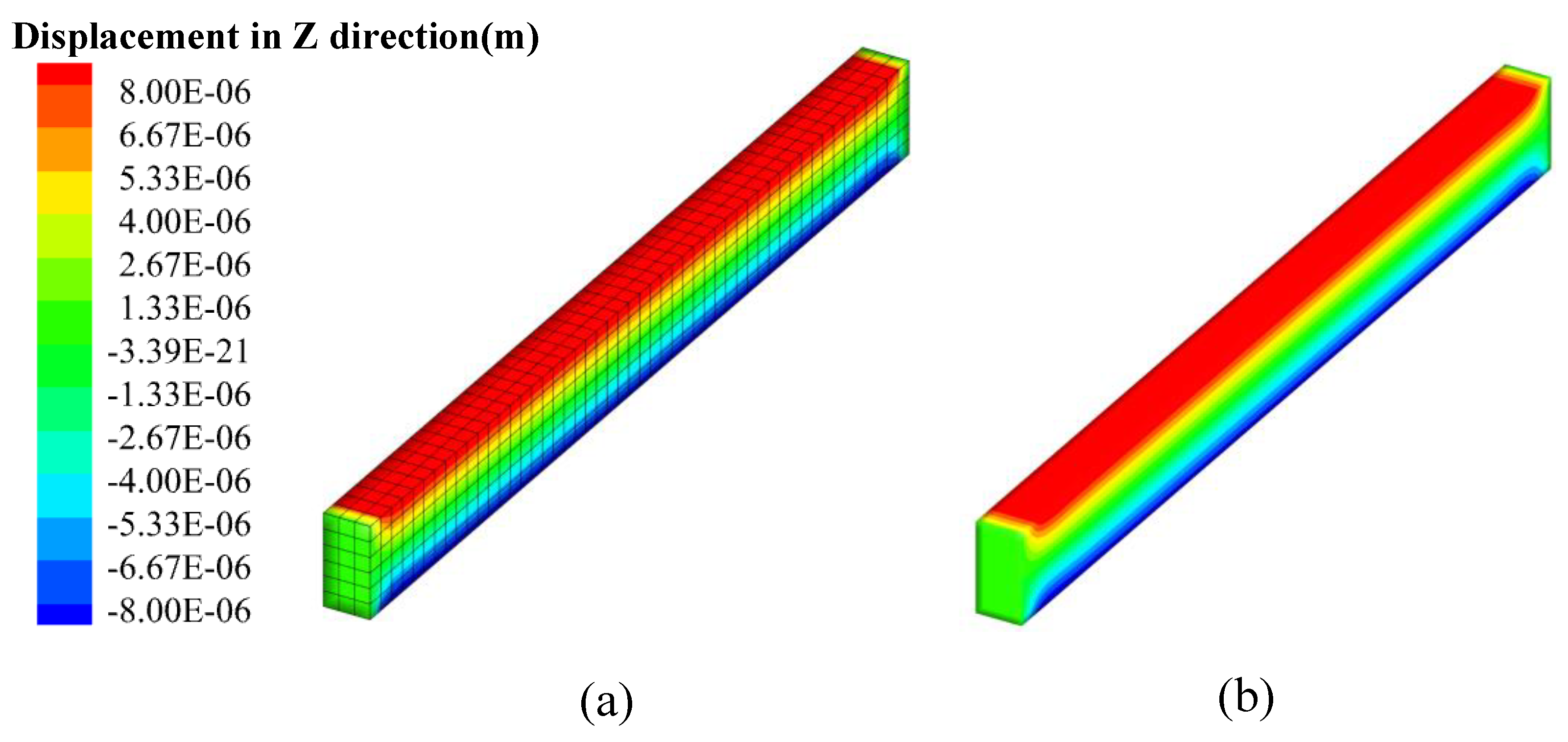
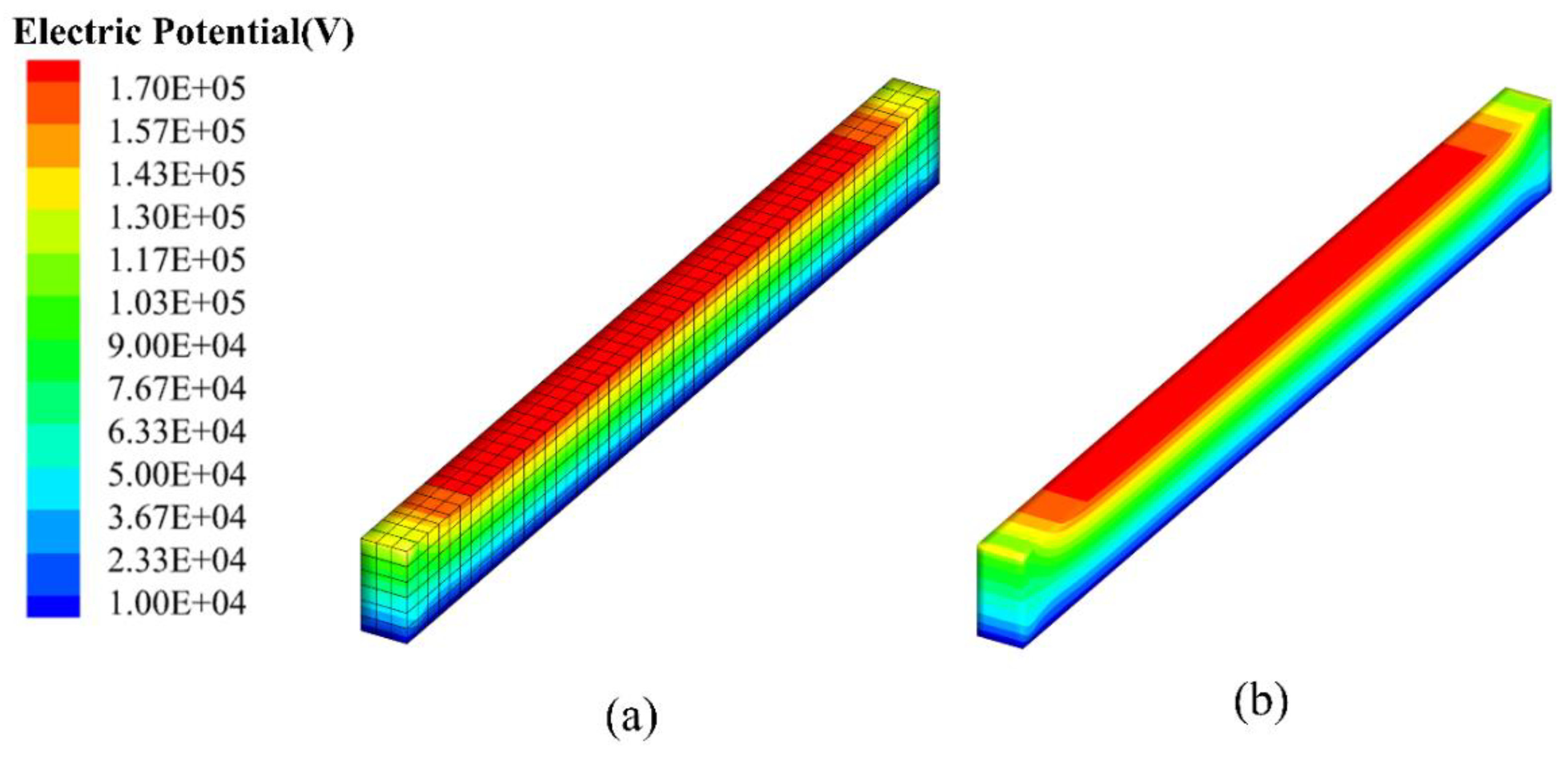
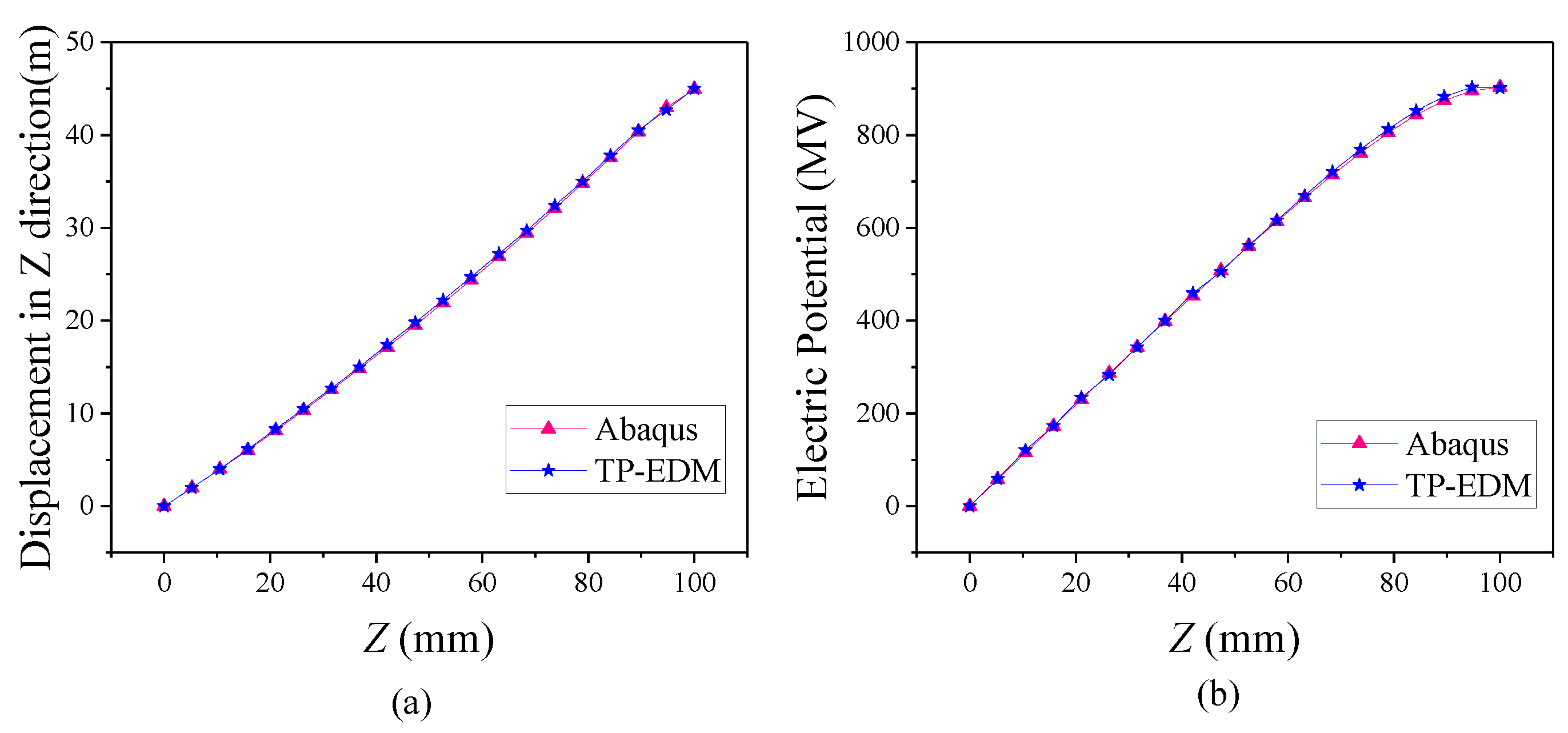
4.2. Clamped Thermal Piezoelectric 3D Beam
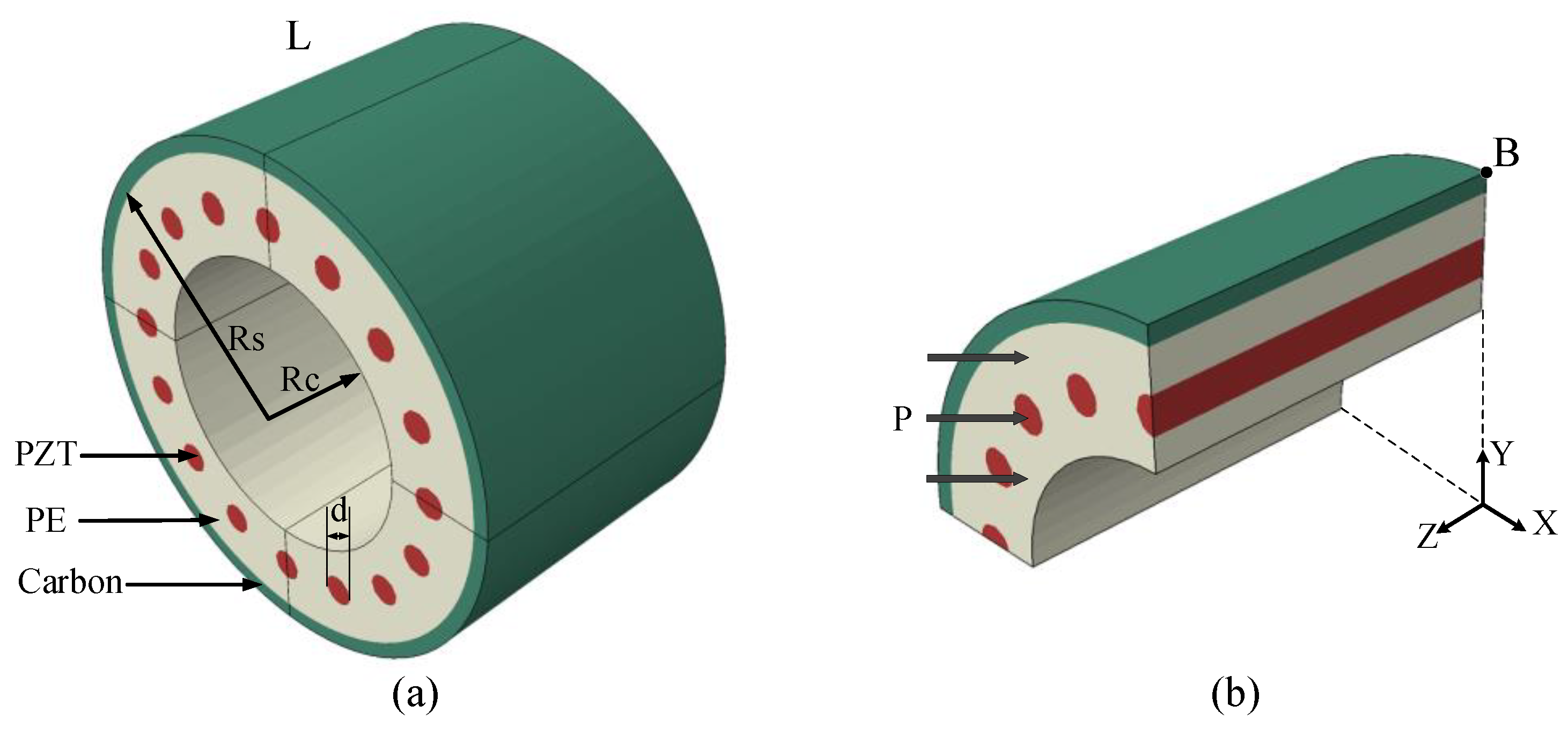
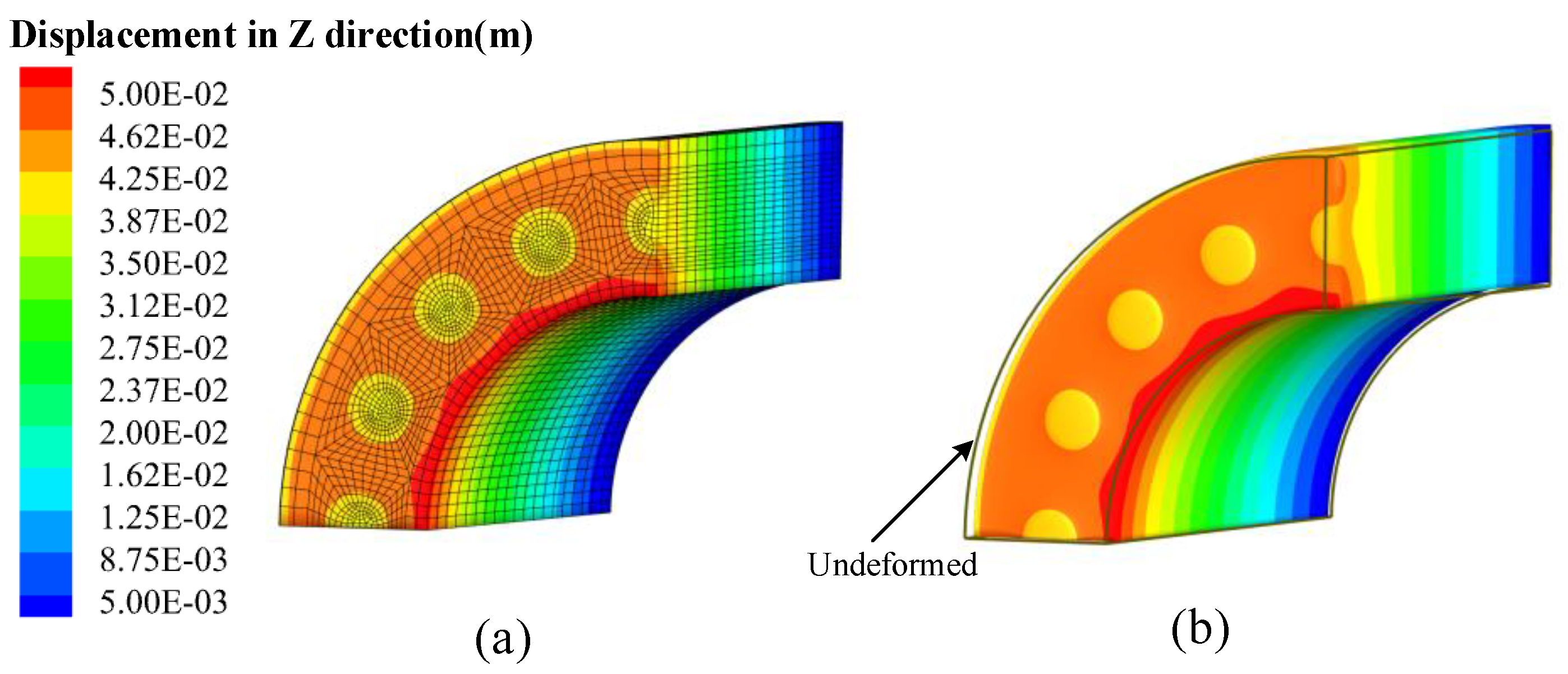
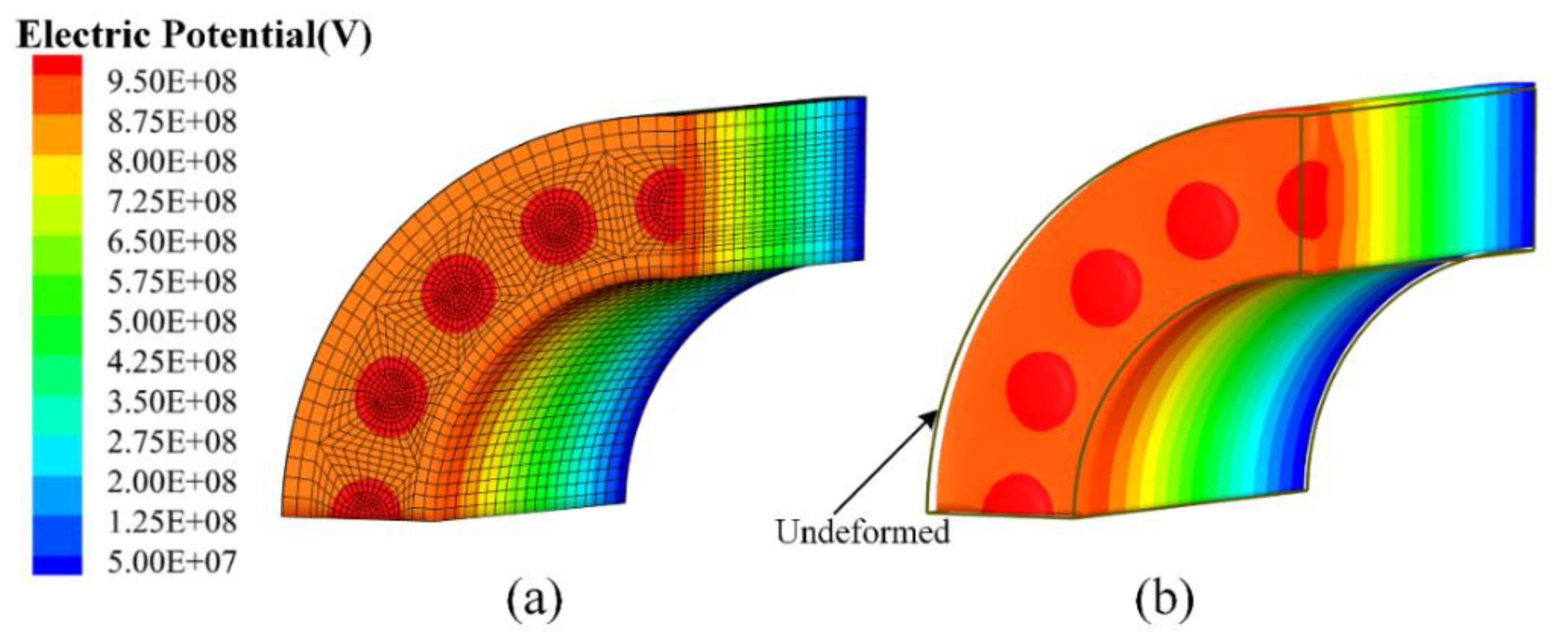
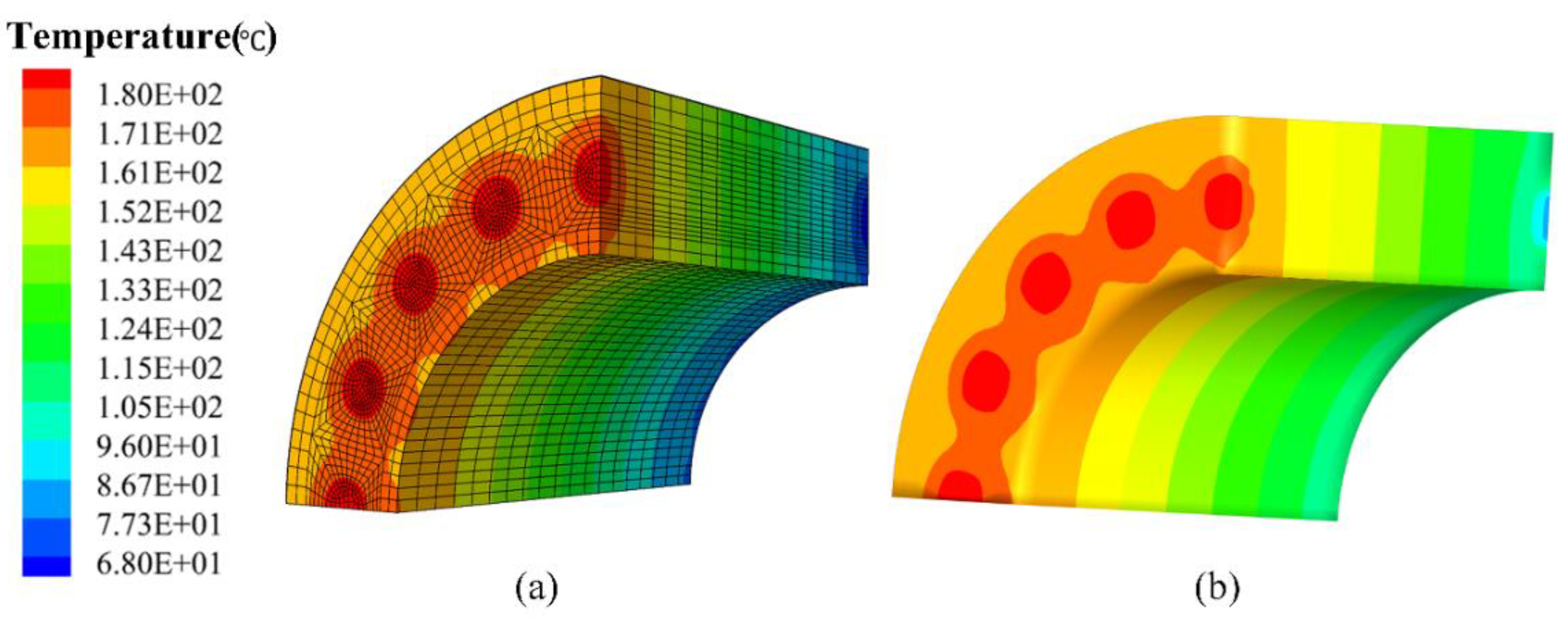
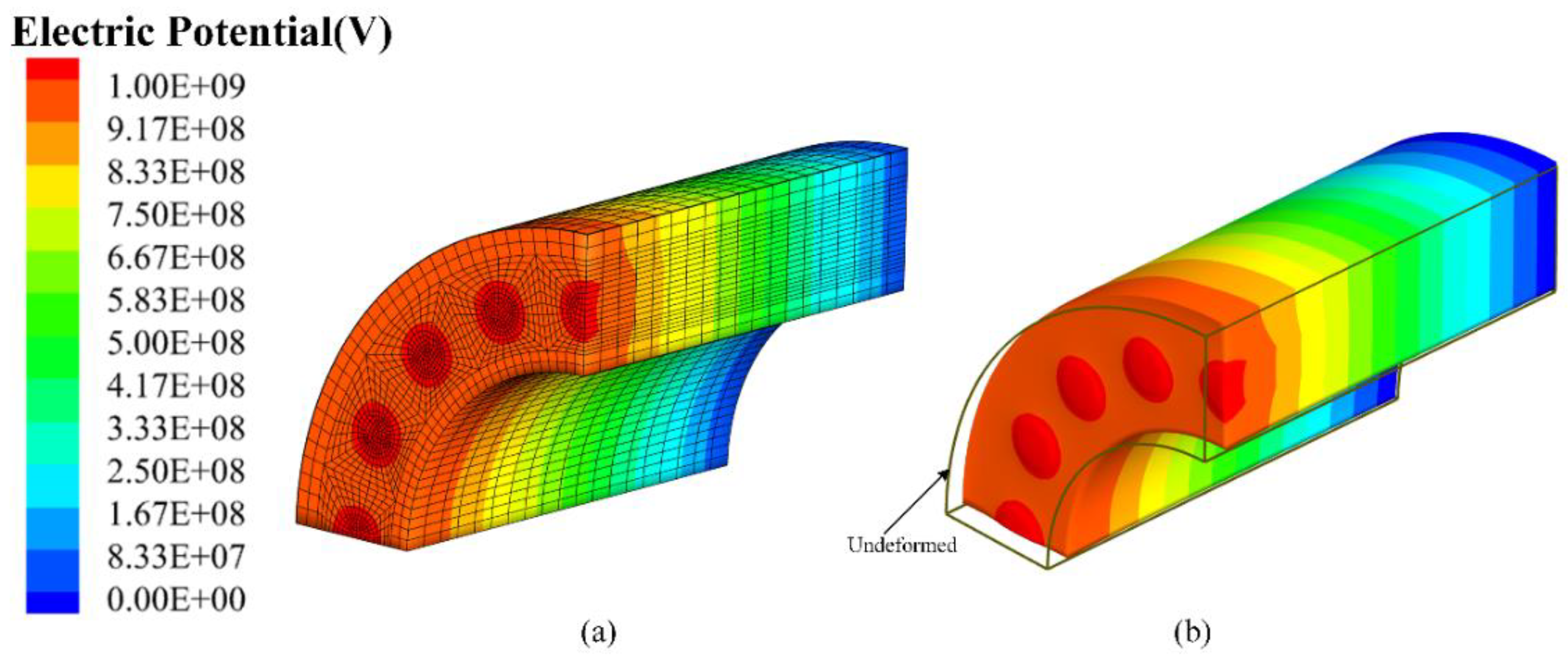
4.3. Cylindrical Structure Reinforced by Piezoelectric Fiber
| PZT: | |
| PE: | |
| Carbon: | |
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, X.; Wang, H.; Ning, X. Needle-shaped ultrathin piezoelectric microsystem for guided tissue targeting via mechanical sensing. Nat. Biomed. Eng. 2018, 2, 165–172. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, L.; Wang, L. Skin-Integrated graphene-embedded lead Zirconate Titanate rubber for energy harvesting and mechanical sensing. Adv. Mater. Technol. 2019, 4, 1900744. [Google Scholar] [CrossRef]
- Tariq, M.H.; Younas, U.; Dang, H.; Ren, J. A general solution for three dimensional steady-state transversely isotropic hygro-thermo-magneto-piezoelectric media. Appl. Math. Model. 2020, 80, 625–646. [Google Scholar] [CrossRef]
- Gülay, A.M.; Cengiz, D. Certain hygrothermopiezoelectric multi-field variational principles for smart elastic laminae. Mech. Adv. Mater. Struct. 2008, 15, 21–32. [Google Scholar] [CrossRef]
- Wang, X.Q.; Fu, T.C.; Chan, K.H. In-built thermo-mechanical cooperative feedback mechanism for self-propelled multimodal locomotion and electricity generation. Nat. Commun. 2018, 9, 3438. [Google Scholar] [CrossRef]
- Wang, X.Q.; Chan, K.H.; Cheng, Y. Somatosensory, Light-Driven, Thin-Film Robots Capable of Integrated Perception and Motility. Adv. Mater. 2020, 32, 2000351. [Google Scholar] [CrossRef]
- Song, K.; Zhao, R.; Wang, Z.L. Conjuncted Pyro-Piezoelectric Effect for Self-Powered Simultaneous Temperature and Pressure Sensing. Adv. Mater. 2019, 31, 1902831.1–1902831.9. [Google Scholar] [CrossRef] [PubMed]
- Fantoni, F.; Bacigalupo, A.; Paggi, M. Design of thermo-piezoelectric microstructured bending actuators via multi-field asymptotic homogenization. Int. J. Mech. Sci. 2018, 146–147, 319–336. [Google Scholar] [CrossRef]
- Batra, A.; Aggarwal, M. Pyroelectric Materials: Infrared Detectors, Particle Accelerators and Energy Harvesters; SPIE Press: Bellingham, WA, USA, 2013; Chapter 1; ISBN 9780819493316. [Google Scholar]
- Nan, C.; Bichurin, M.; Dong, S.; Viehland, D.; Srinivasan, G. Multiferroic magnetoelectric composites: Historical perspective, status, and future directions. J. Appl. Phys. 2008, 103, 031101. [Google Scholar] [CrossRef]
- Tan, P.; Tong, L. Modeling for the electro-magneto-thermo-elastic properties of piezoelectric-magnetic fiber reinforced composites. Compos. Part A Appl. Sci. Manuf. 2002, 33, 631–645. [Google Scholar] [CrossRef]
- Ashida, F.; Sakata, S.I.; Matsumoto, K. Structure design of a poiezoelectric composite disk for control of thermal stress. J. Appl. Mech. 2008, 75, 061009. [Google Scholar] [CrossRef]
- Taya, N.M.; Namli, O.C. Design of piezo-SMA composite for thermal energy harvester under fluctuating temperature. J. Appl. Mech. 2011, 78, 2388–2399. [Google Scholar] [CrossRef]
- Srivastava, V.; Song, Y.; Bhatti, K.; James, R.D. The direct conversion of heat to electricity using multiferroic alloys. Adv. Energy Mater. 2011, 1, 97–104. [Google Scholar] [CrossRef]
- Ang, S.; Brachelet, F.; Breaban, F.; Defer, D. Defect detection in CFRP by infrared thermography with CO2 Laser excitation compared to conventional lock-in infrared thermography. Compos. Part B 2015, 69, 1–5. [Google Scholar] [CrossRef]
- Sladek, J.; Sladek, V.; Wunsche, M.; Tan, C.-L. Crack analysis of size-dependent piezoelectric solids under a thermal load. Eng. Fract. Mech. 2017, 182, 187–220. [Google Scholar] [CrossRef]
- Rahman, A.A.A. Influence of the Perforation Configuration on the Dynamic Behavior of Multilayered Beam Structure. Structures 2020, 28, 1413–1426. [Google Scholar] [CrossRef]
- Jiang, J.P.; Li, D.X. A new finite element model for piezothermoelastic composite beam. J. Sound Vib. 2007, 306, 849–864. [Google Scholar] [CrossRef]
- Amini, Y.; Emdad, H.; Farid, M. Finite element modeling of functionally graded piezoelectric harvesters. Compos. Struct. 2015, 129, 165–176. [Google Scholar] [CrossRef]
- Yan, Z.; Jiang, L. On a moving dielectric crack in a piezoelectric interface with spatially varying properties. Eng. Fract. Mech. 2009, 76, 560–579. [Google Scholar] [CrossRef]
- Shi, J.; Akbarzadeh, A.H. Architected cellular piezoelectric metamaterials: Thermo-electro-mechanical properties. Acta Mater. 2019, 163, 91–121. [Google Scholar] [CrossRef]
- Lv, J.; Yang, K.; Zhang, H.; Yang, D.; Huang, Y. A hierarchical multiscale approach for predicting thermo-electro-mechanical behavior of heterogeneous piezoelectric smart materials. Comput. Mater. Sci. 2014, 87, 88–99. [Google Scholar] [CrossRef]
- Wang, D.D.; Wang, J.R.; Wu, J.C. Superconvergent gradient smoothing meshfree collocation method. Comput. Methods Appl. Mech. Eng. 2018, 340, 728–766. [Google Scholar] [CrossRef]
- Gu, Y.T.; Liu, G.R. A meshfree weak-strong (MWS) form method for time dependent problems. Comput. Mech. 2005, 35, 134–145. [Google Scholar] [CrossRef]
- Gao, X.W.; Li, Z.Y.; Yang, K. Element differential method and its application in thermal-mechanical problems. Int. J. Numer. Methods Eng. 2018, 113, 82–108. [Google Scholar] [CrossRef]
- Moradi-Dastjerdi, R.; Radhi, A.; Behdinan, K. Damped dynamic behavior of an advanced piezoelectric sandwich plate. Compos. Struct. 2020, 243, 12243. [Google Scholar] [CrossRef]
- Liew, K.M.; Yang, J.; Kitipornchai, S. Postbuckling of piezoelectric FGM plates subject to thermo-electro-mechanical loading. Int. J. Solids Struct. 2003, 40, 3869–3892. [Google Scholar] [CrossRef]
- Alashti, R.A.; Khorsand, M. Three-dimensional thermo-elastic analysis of a functionally graded cylindrical shell with piezoelectric layers by differential quadrature method. Int. J. Press. Vessel. Pip. 2011, 88, 167–180. [Google Scholar] [CrossRef]
- Lv, J.; Shao, M.J.; Cui, M.; Gao, X.W. An efficient collocation approach for piezoelectric problems based on the element differential method. Compos. Struct. 2019, 230, 111483. [Google Scholar] [CrossRef]
- Gao, X.W.; Huang, S.Z.; Cui, M. Element differential method for solving general heat conduction problems. Int. J. Heat Mass Transfer. 2017, 115, 882–894. [Google Scholar] [CrossRef]
- Mosallaie, B.A.A.; Ghorbanpour, A.A.; Kolahchi, R.; Mozdianfard, M.R. Electro-thermo-mechanical torsional buckling of a piezoelectric polymeric cylindrical shell reinforced by DWBNNTs with an elastic core. Appl. Math. Model. 2012, 36, 2983–2995. [Google Scholar] [CrossRef]

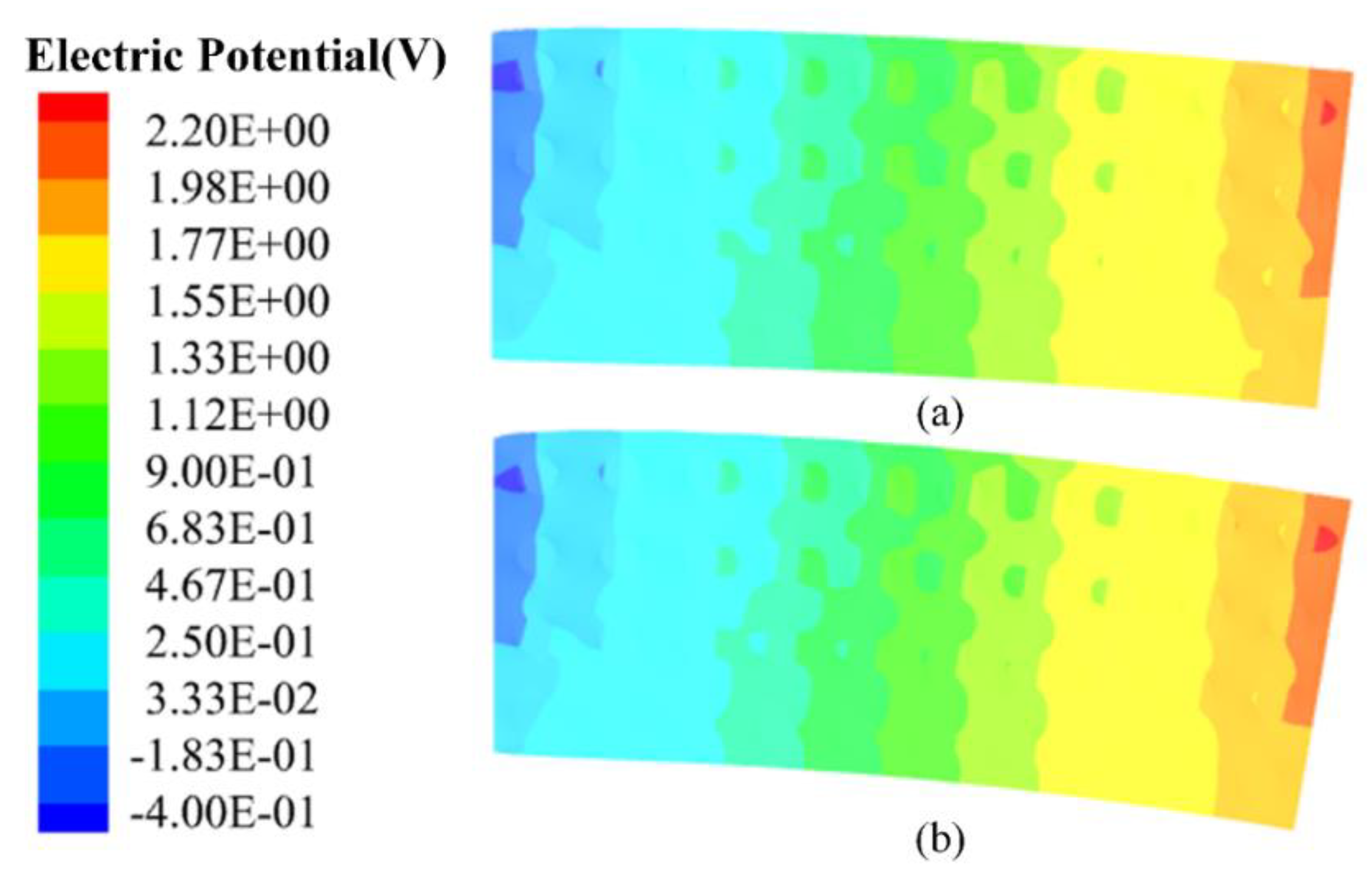
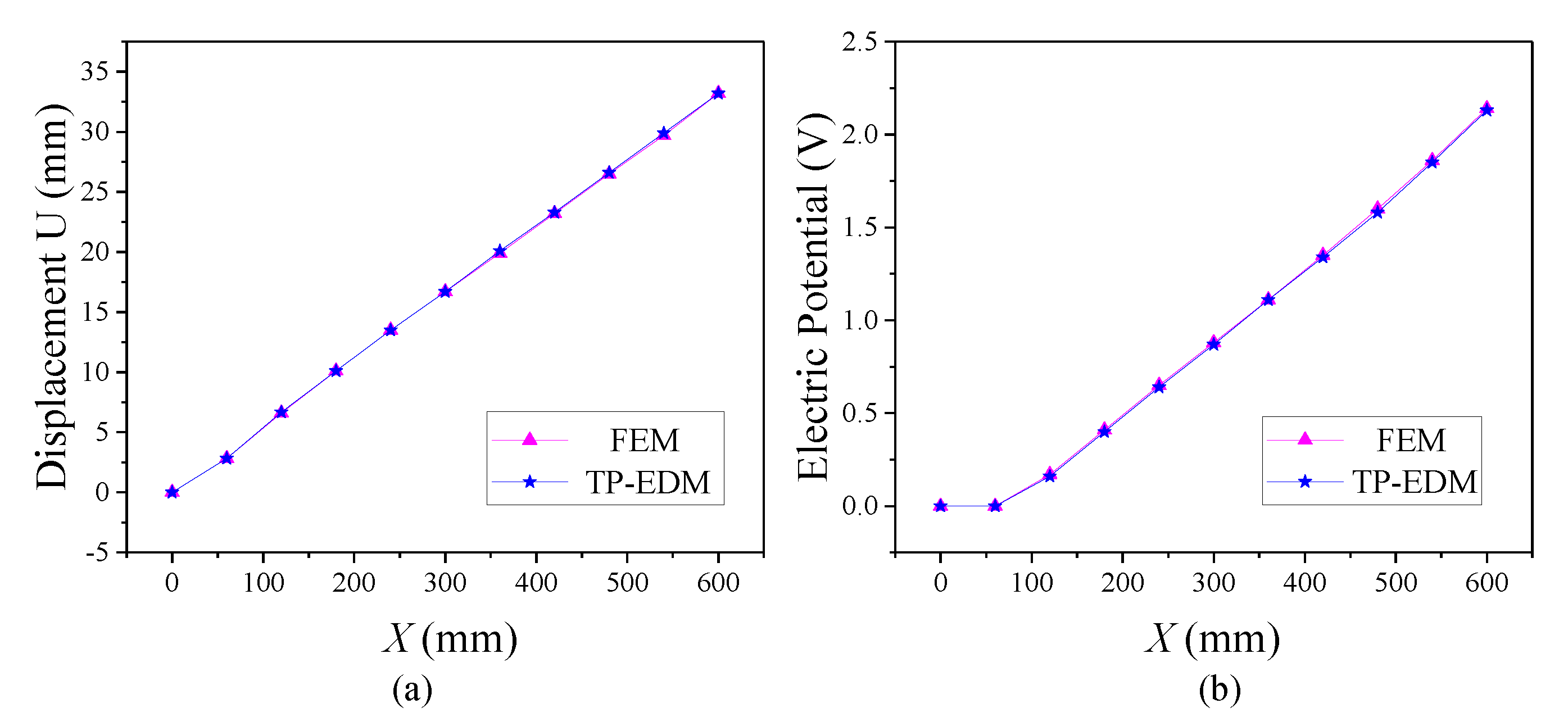


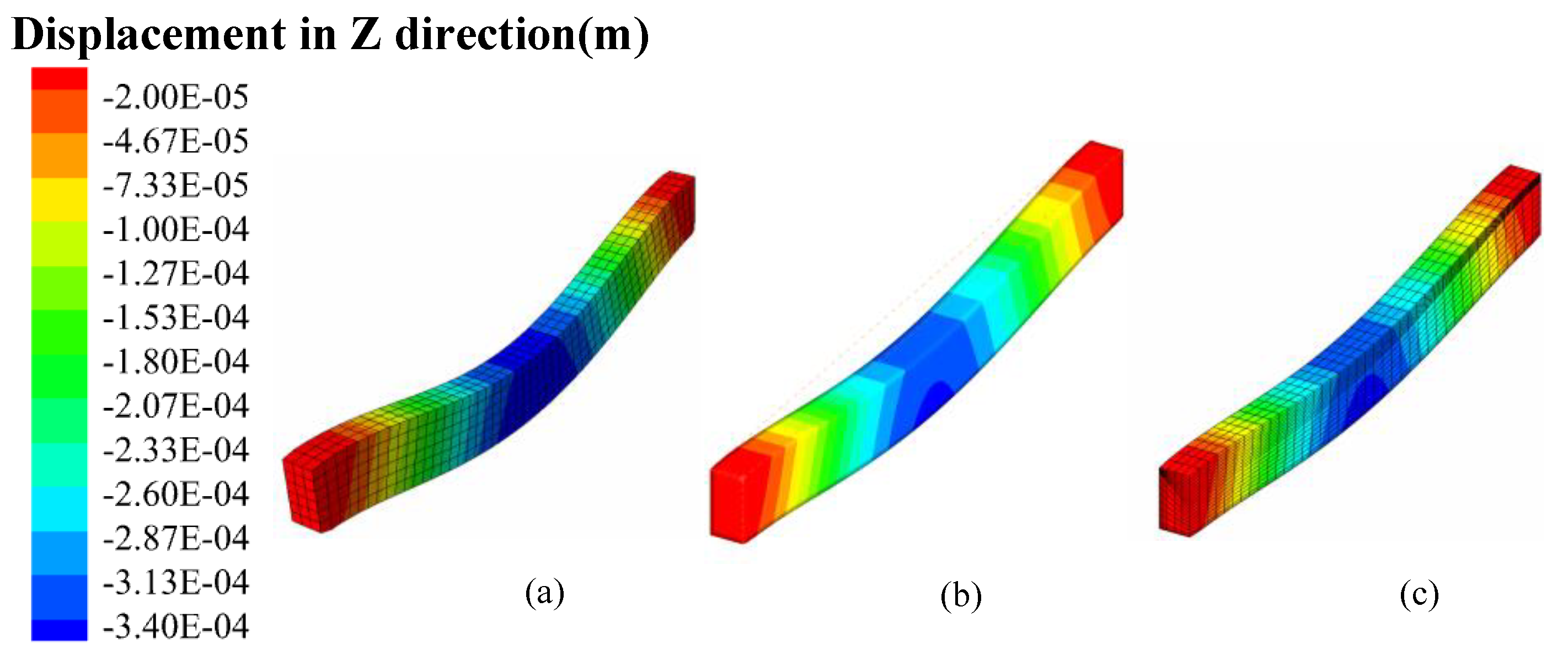
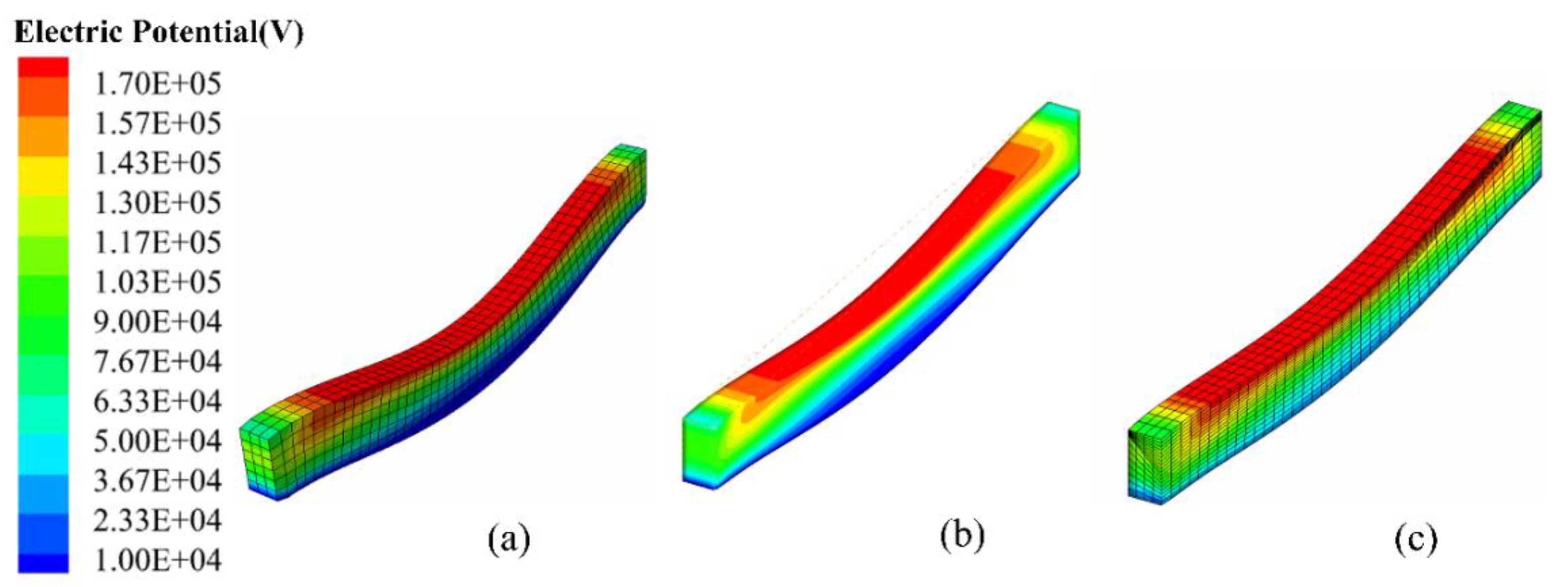
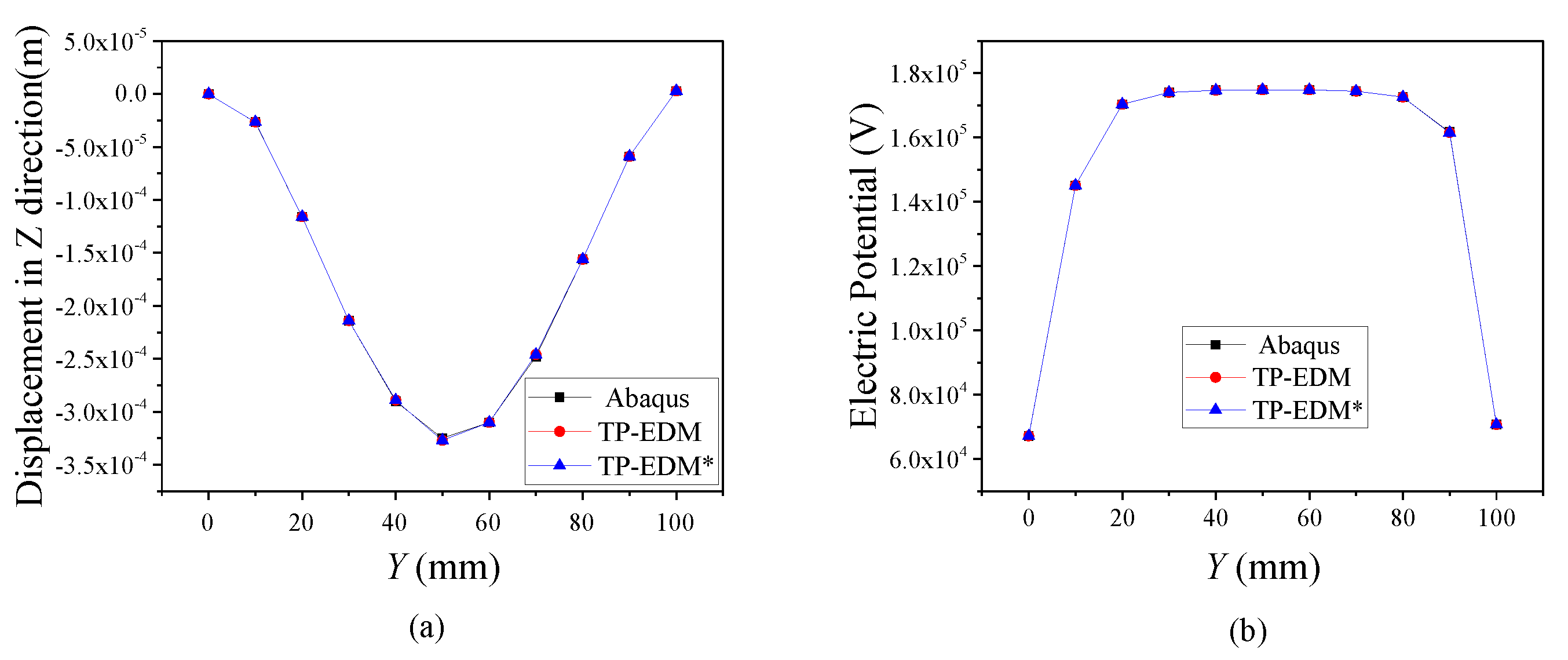

| Method | u (mm) | φ (V) |
|---|---|---|
| FEM | 33.29 | 2.26 |
| TP-EDM | 33.23 | 2.18 |
| Methods | w (m) | φ (V) |
|---|---|---|
| Abaqus | 1.02 × 10−5 | 1.76 × 105 |
| TP-EDM | 1.01 × 10−5 | 1.76 × 105 |
| Number of Mesh Grids | w (FEM) | w (TP-EDM) | φ (FEM) | φ (TP-EDM) |
|---|---|---|---|---|
| 900 | 3.44 × 10−4 | 3.48 × 10−4 | 1.75 × 10−5 | 1.76 × 10−5 |
| 5000 | 3.48 × 10−4 | 3.49 × 10−4 | 1.75 × 10−5 | 1.75 × 10−5 |
| 12103 | 3.48 × 10−4 | 3.49 × 10−4 | 1.74 × 10−5 | 1.75 × 10−5 |
| Method | w (m) | φ (V) |
|---|---|---|
| Abaqus | 4.49 × 10−2 | 9.03 × 108 |
| TP-EDM | 4.47 × 10−2 | 9.02 × 108 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, J.; Shao, M.; Xue, Y.; Gao, X.; Xie, Z. A New Strong Form Technique for Thermo-Electro-Mechanical Behaviors of Piezoelectric Solids. Coatings 2021, 11, 687. https://doi.org/10.3390/coatings11060687
Lv J, Shao M, Xue Y, Gao X, Xie Z. A New Strong Form Technique for Thermo-Electro-Mechanical Behaviors of Piezoelectric Solids. Coatings. 2021; 11(6):687. https://doi.org/10.3390/coatings11060687
Chicago/Turabian StyleLv, Jun, Minjie Shao, Yuting Xue, Xiaowei Gao, and Zhaoqian Xie. 2021. "A New Strong Form Technique for Thermo-Electro-Mechanical Behaviors of Piezoelectric Solids" Coatings 11, no. 6: 687. https://doi.org/10.3390/coatings11060687
APA StyleLv, J., Shao, M., Xue, Y., Gao, X., & Xie, Z. (2021). A New Strong Form Technique for Thermo-Electro-Mechanical Behaviors of Piezoelectric Solids. Coatings, 11(6), 687. https://doi.org/10.3390/coatings11060687







