A Comprehensive Numerical Study on Friction Reduction and Wear Resistance by Surface Coating on Cam/Tappet Pairs under Different Conditions
Abstract
1. Introduction
2. Methodological Outline
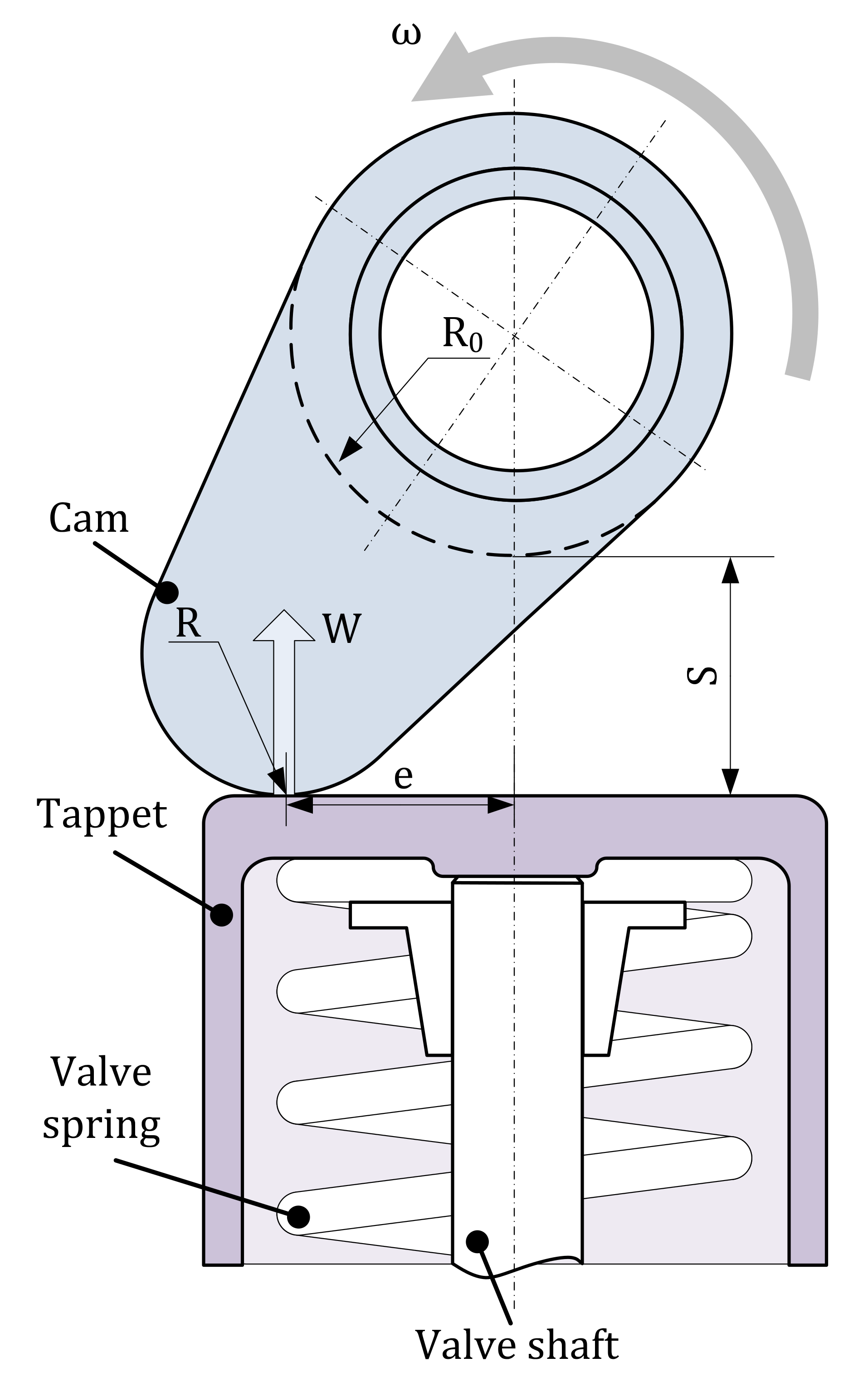
2.1. Kinematics and Dynamics
2.2. Lubrication Analysis
2.2.1. Average Reynolds Equation
2.2.2. Rheology Relation
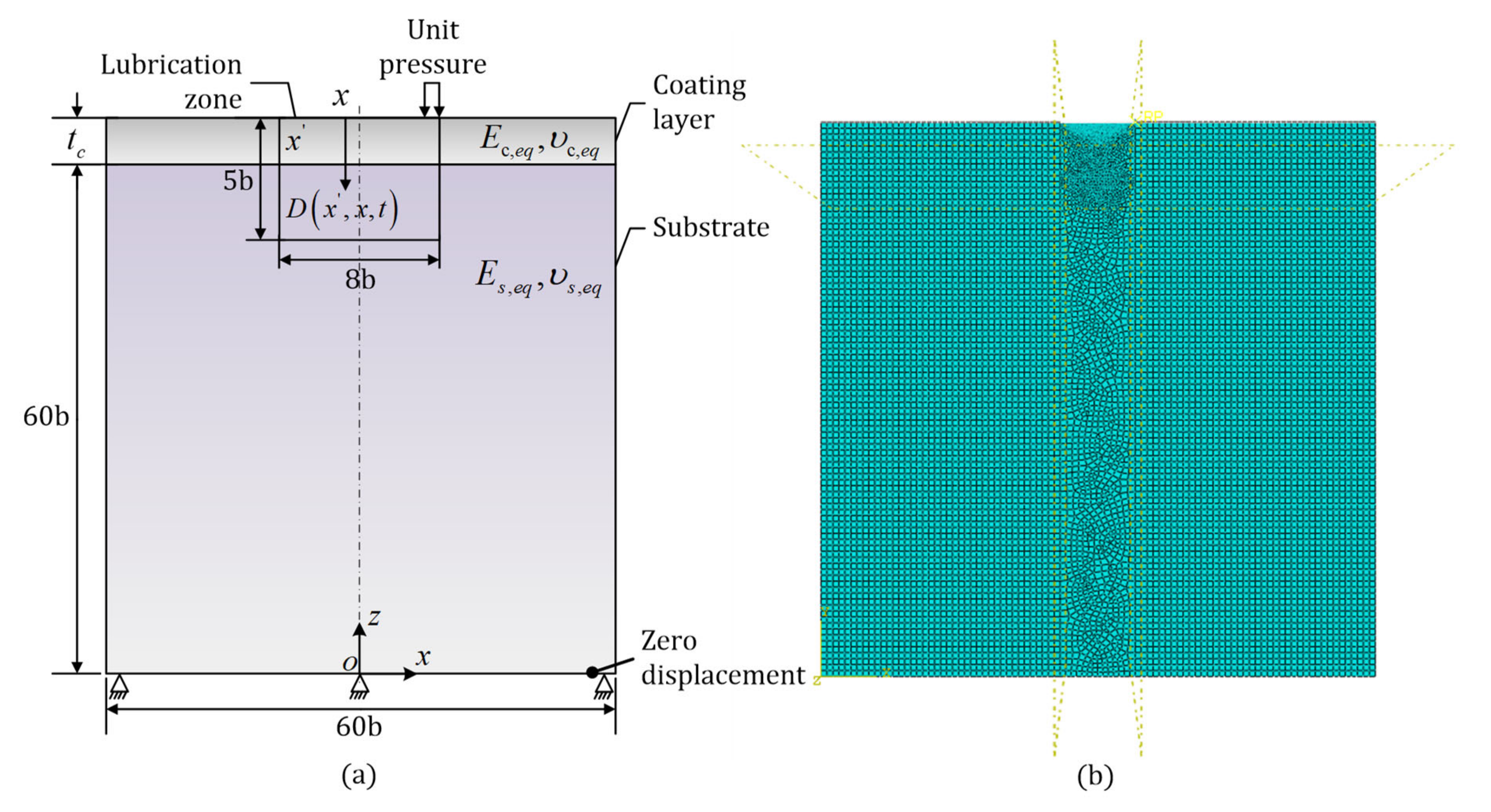
2.2.3. Elastic Deformation Calculation
2.2.4. Load Balance Equation
2.3. Asperity Contact Model
2.4. Thermal Analysis
2.4.1. Lubricant Energy Equation
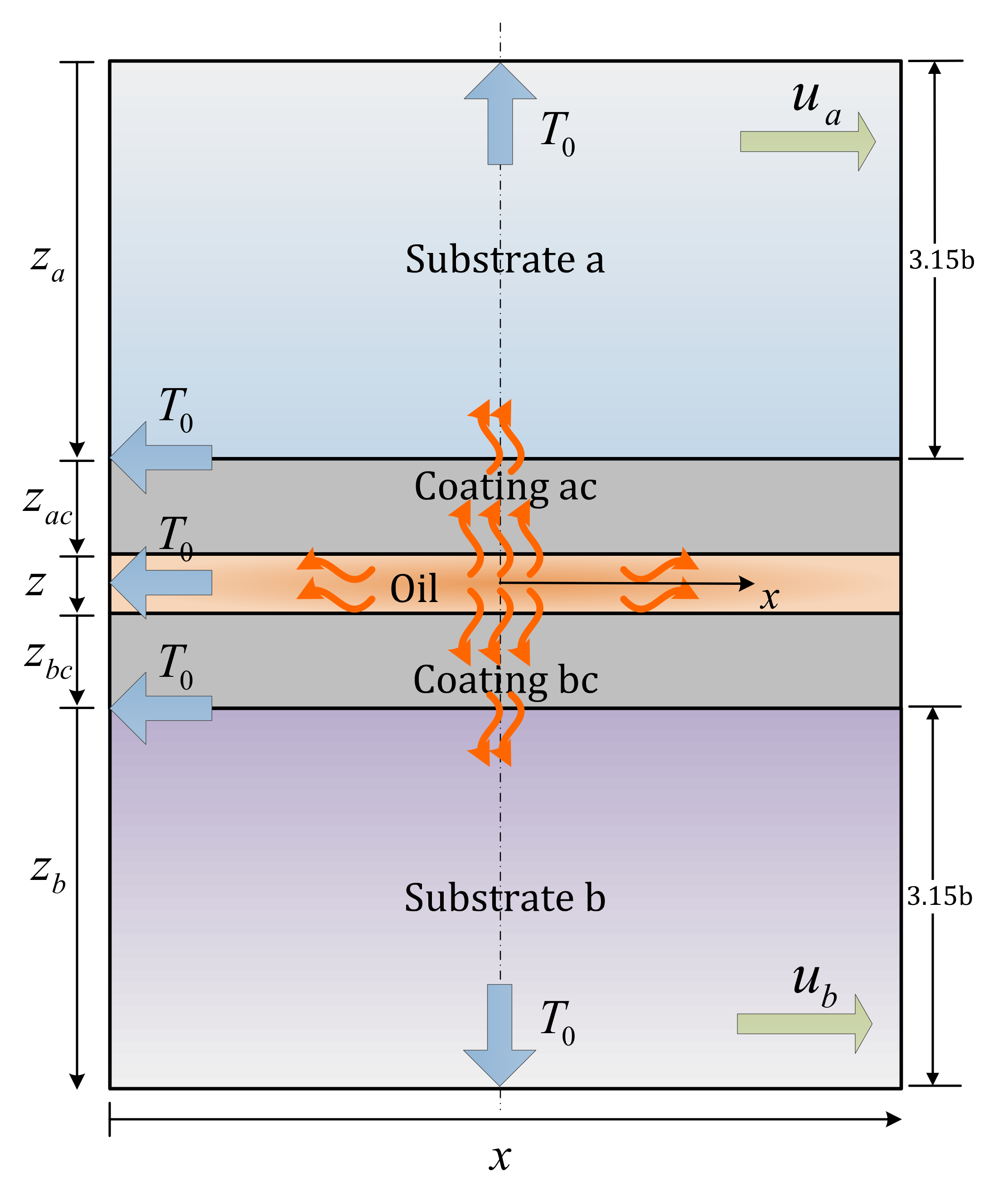
2.4.2. Substrate and Coating Energy Equations
2.4.3. Heat Flux Continuity Equations
2.4.4. Boundary Conditions
2.5. Friction Loss and Wear Evaluation
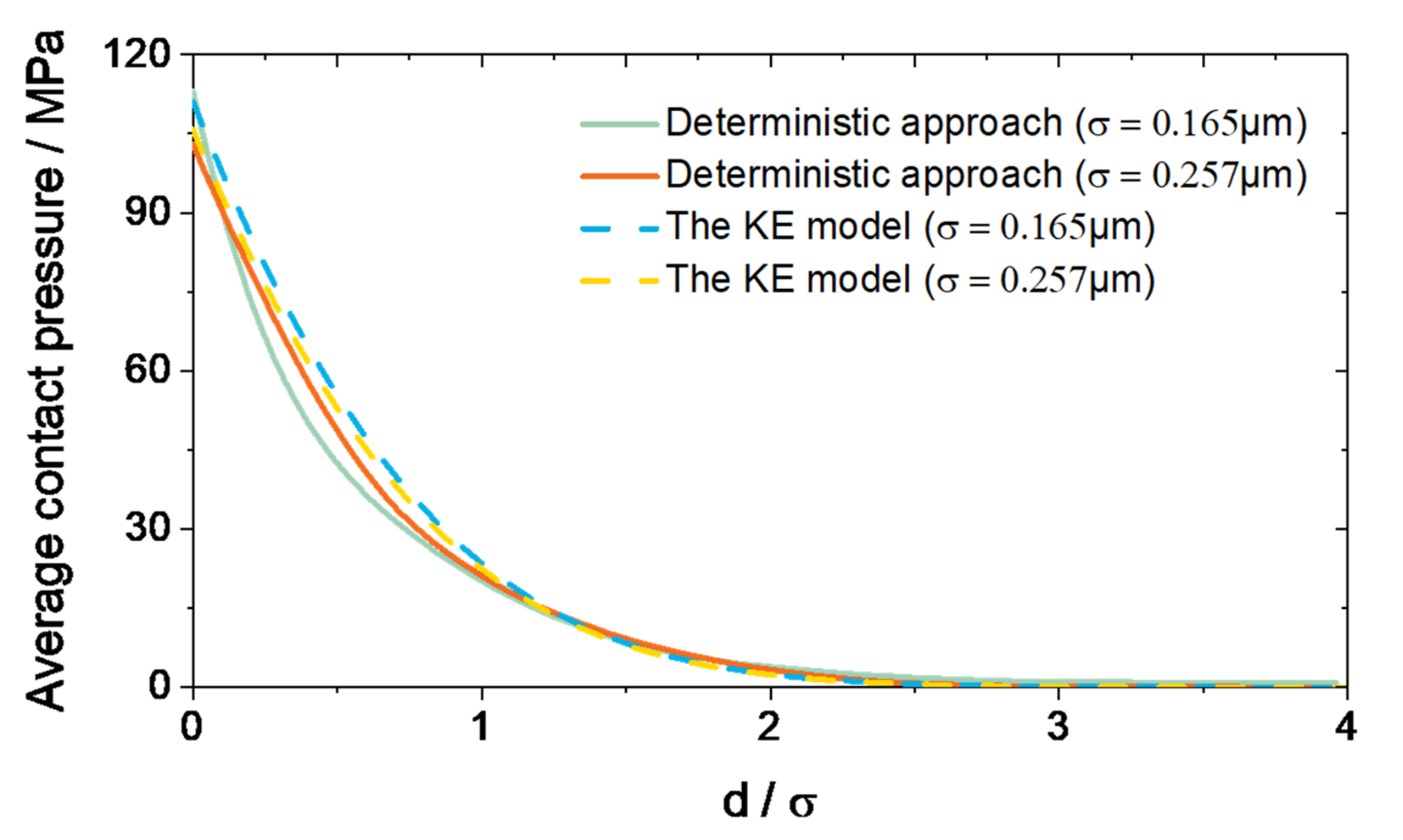
3. Results and Discussion
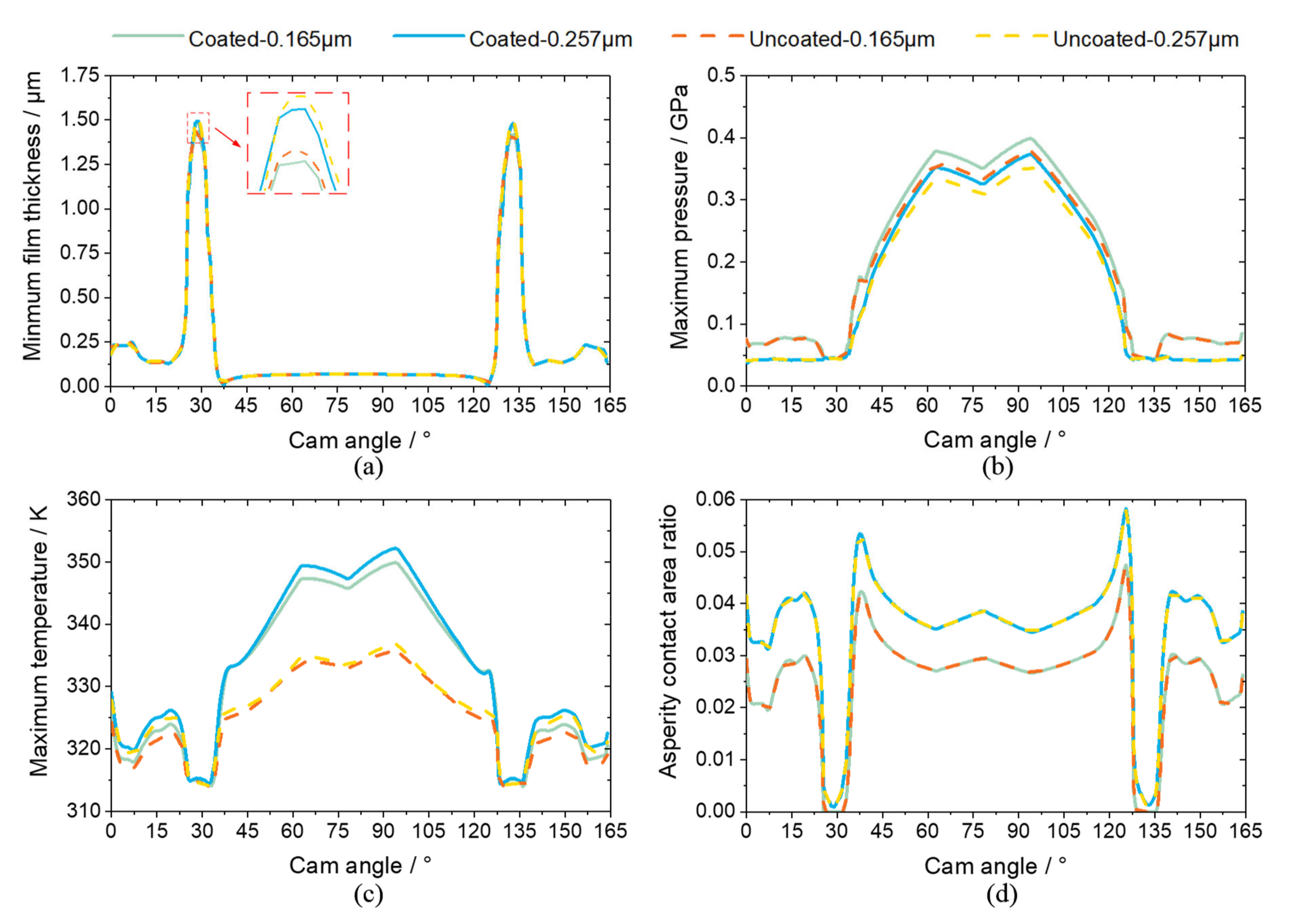
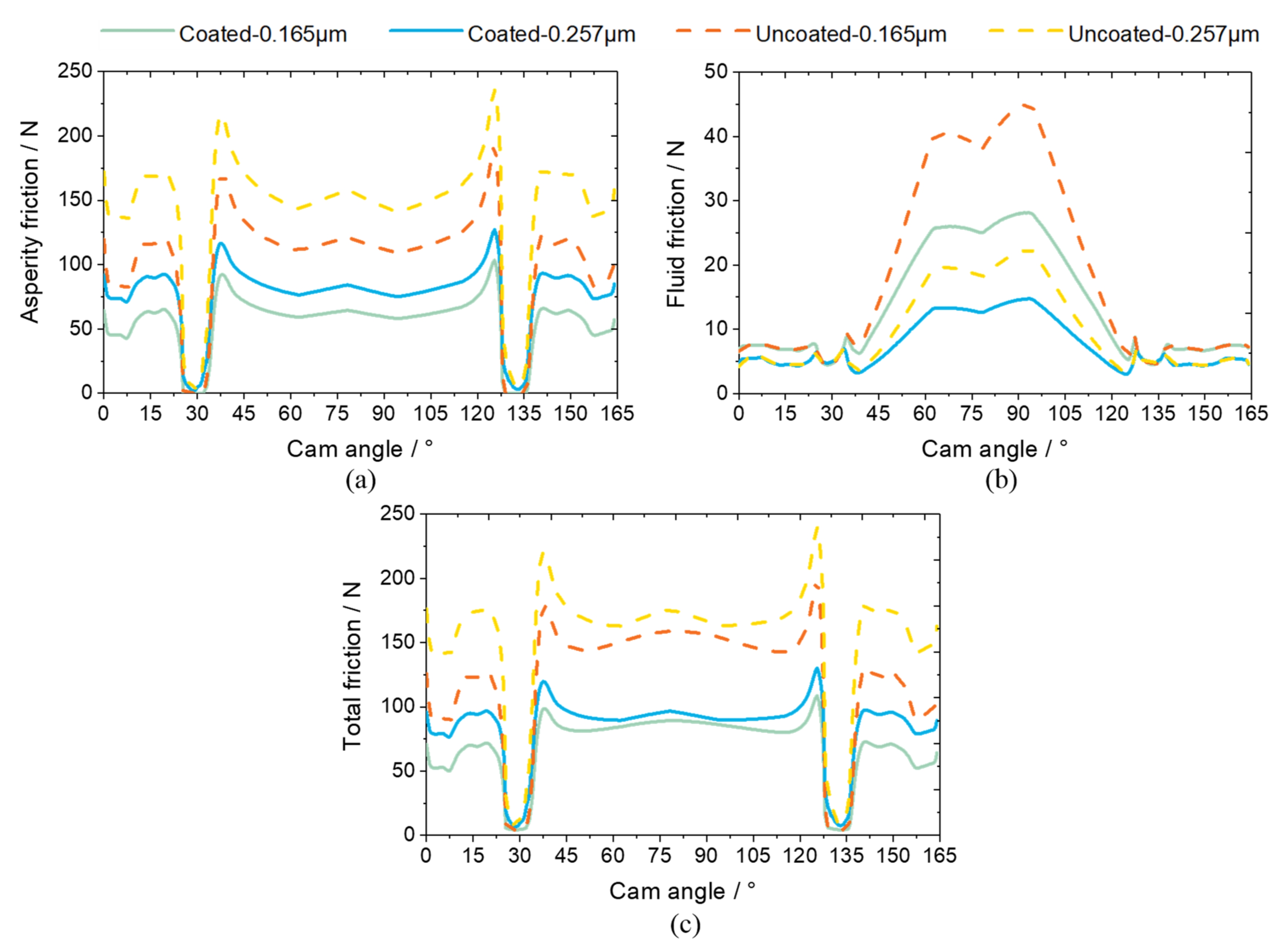
3.1. Normal-Load Conditions
3.2. Heavy-Load Conditions
4. Conclusions
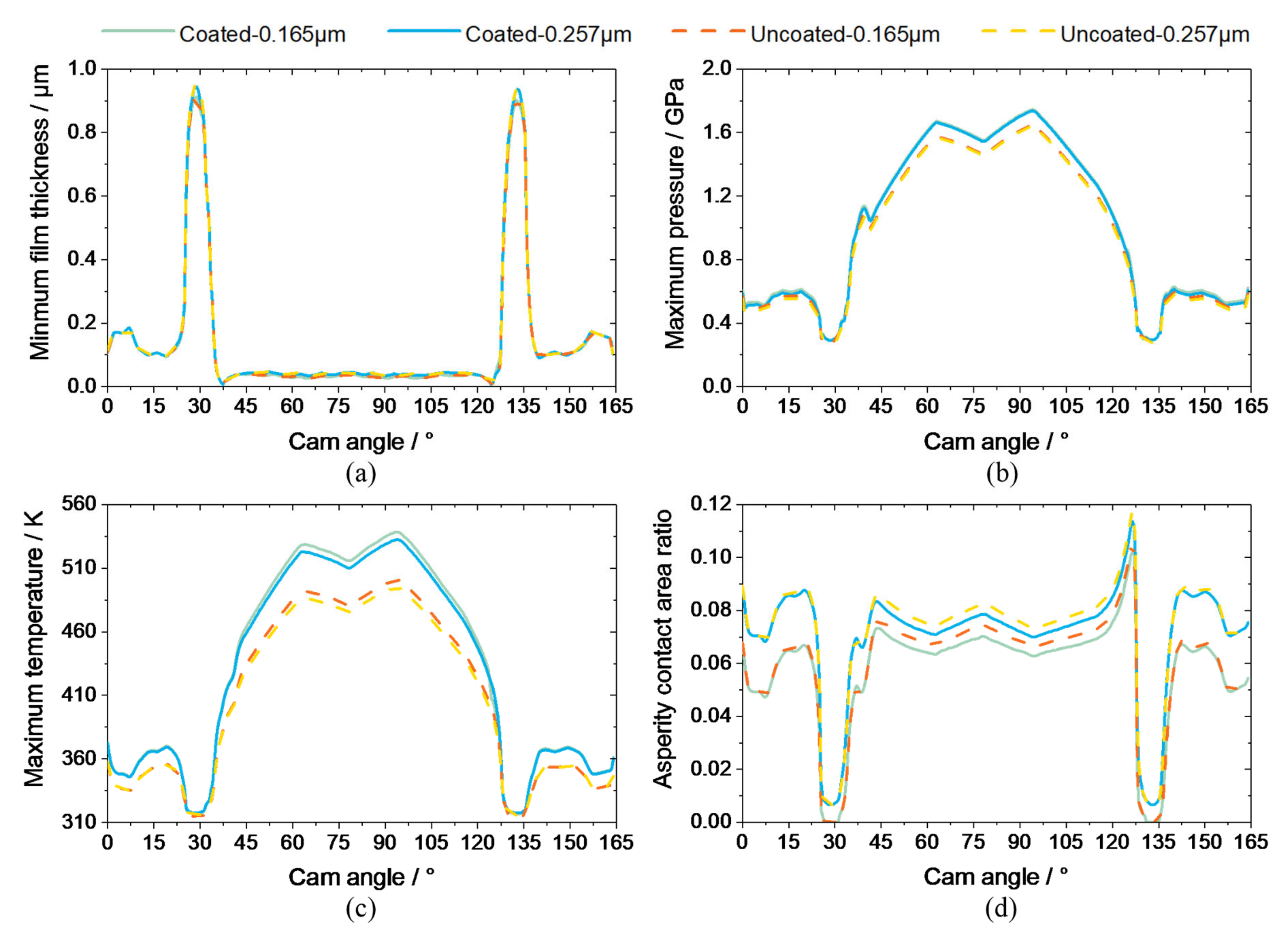
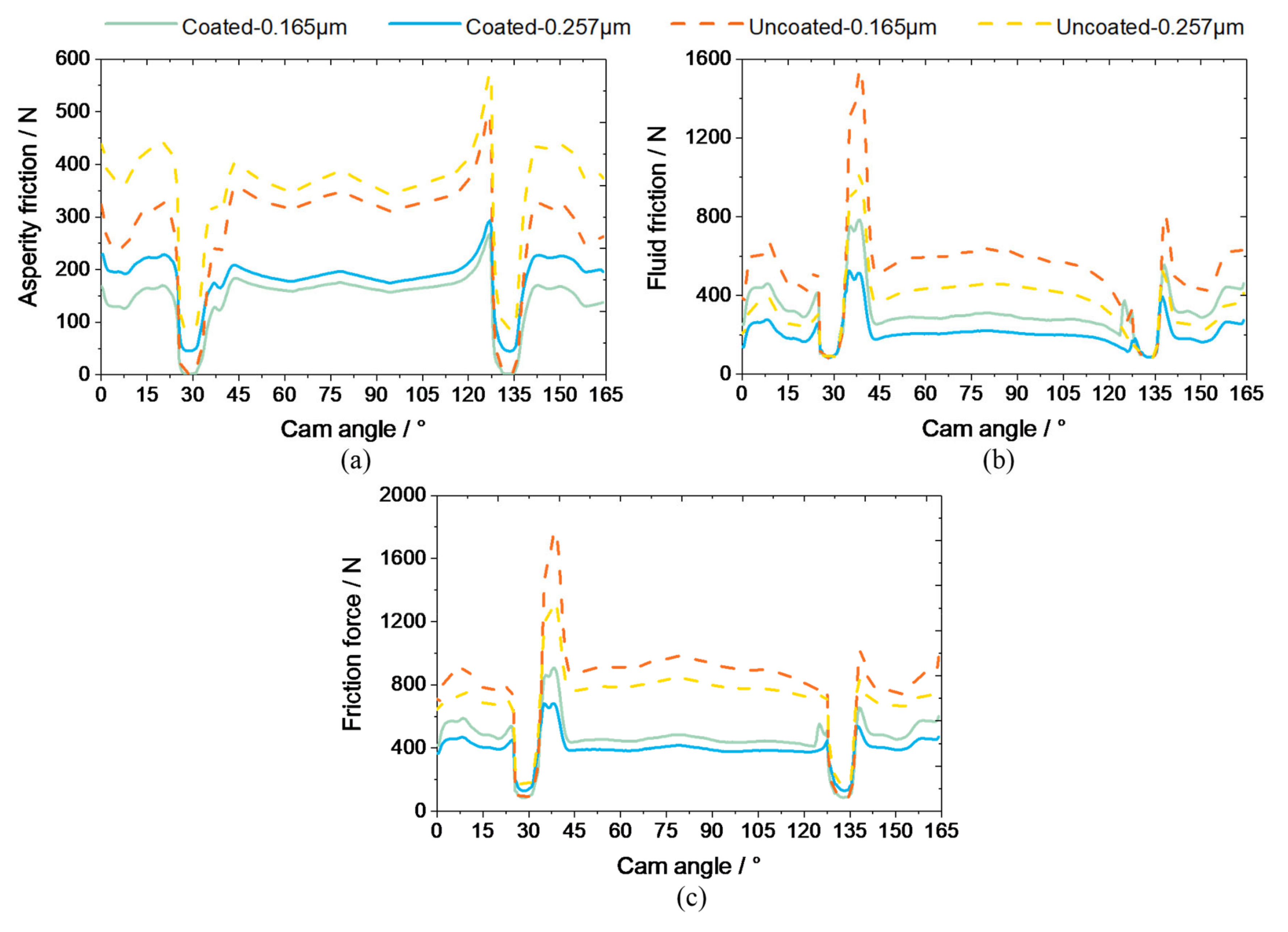
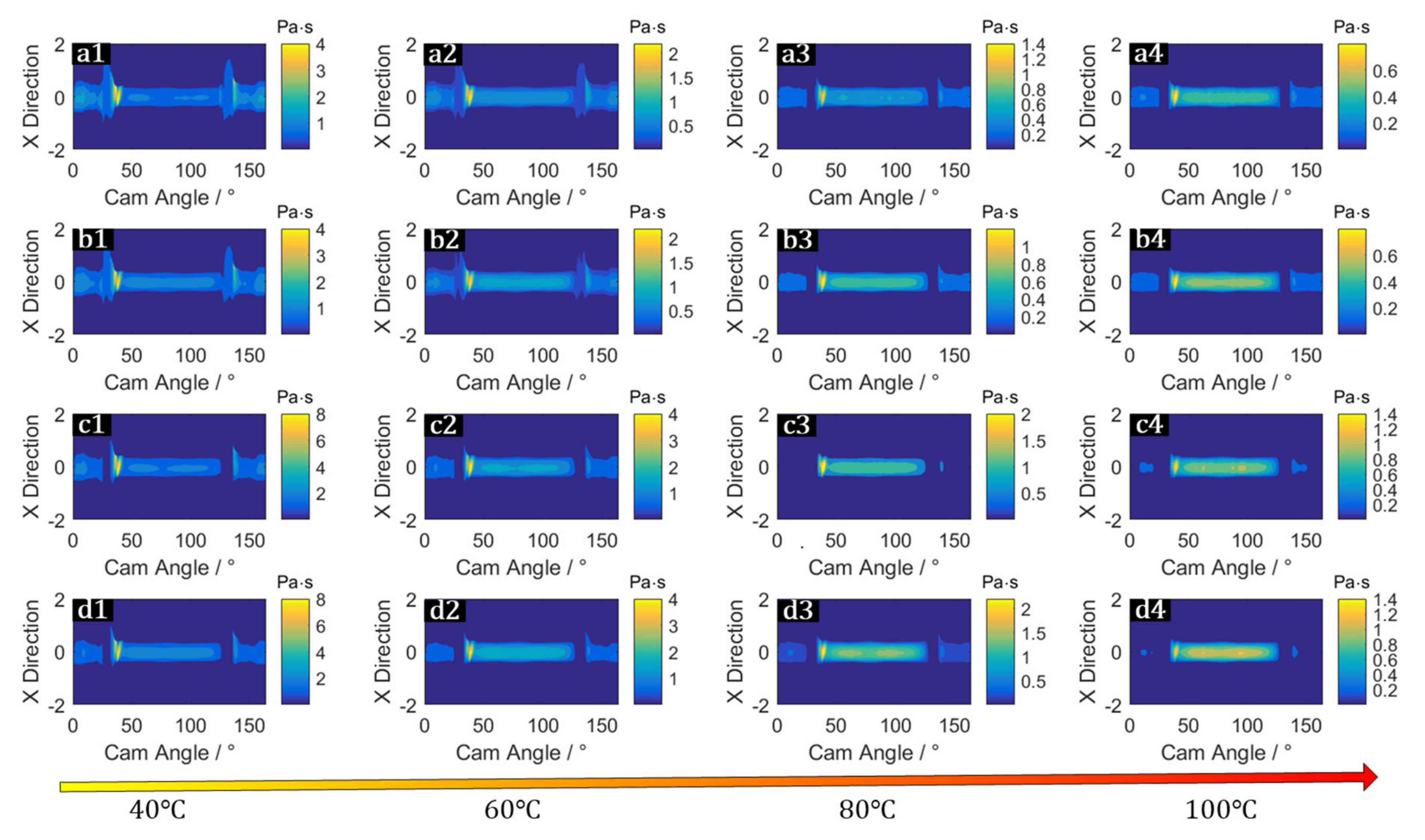
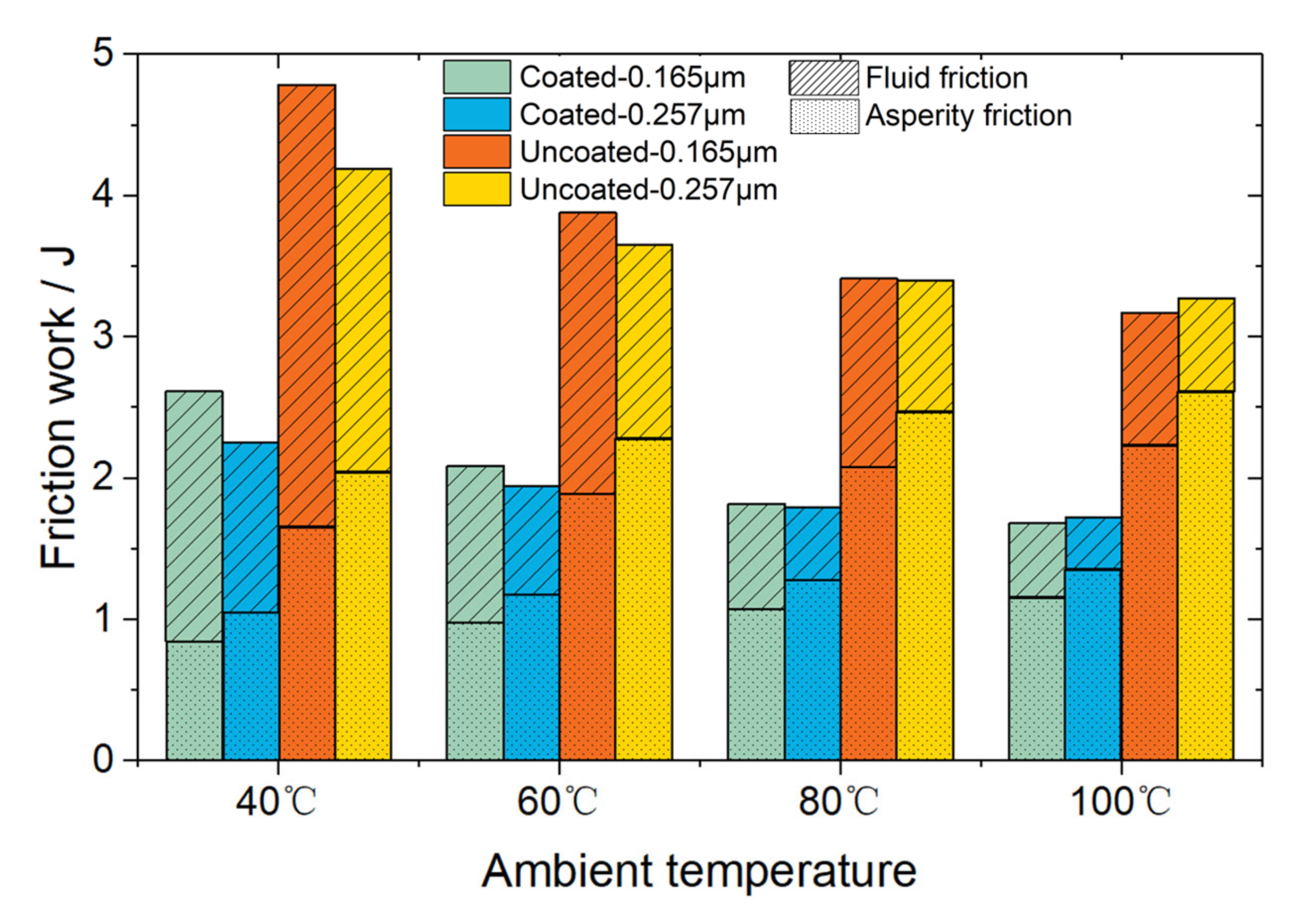
- The anti-friction effect of coatings is mainly reflected in two aspects. On the one hand, the fluid friction for the coated surface is reduced due to its low thermal inertia, which services as a thermal barrier and results in high lubricant temperature and low shear force. Moreover, the asperity contact friction for the coated surface is also lower owing to its favourable friction coefficient, despite a slightly higher asperity contact.
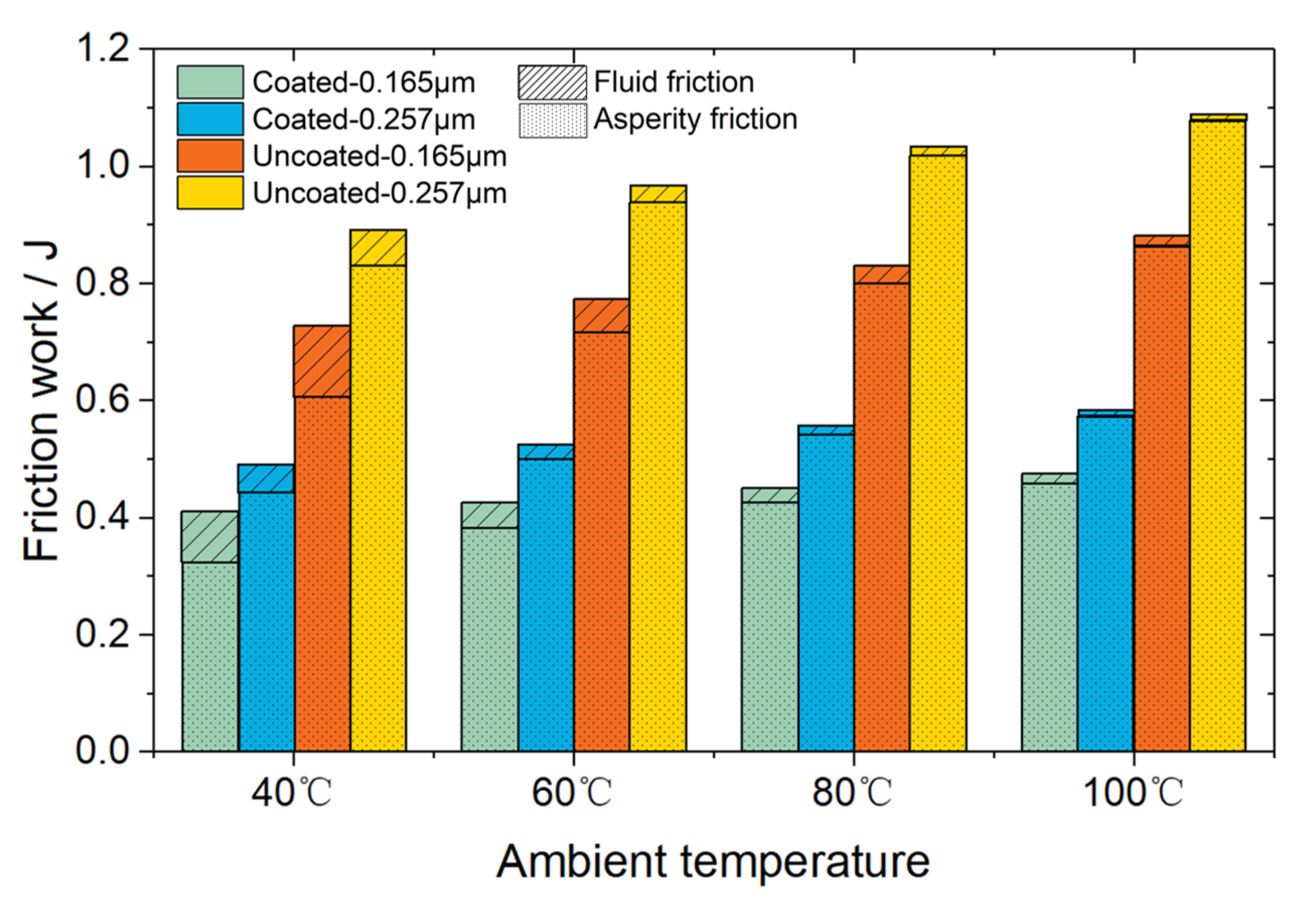
- The friction loss during a cam cycle of the coated cam/tappet is noticeably decreased by almost 40%. With the rising ambient temperature, the friction loss increases gradually, where the fluid friction consumption shrinks continuously, while the asperity friction consumption manifests an expanding trend.
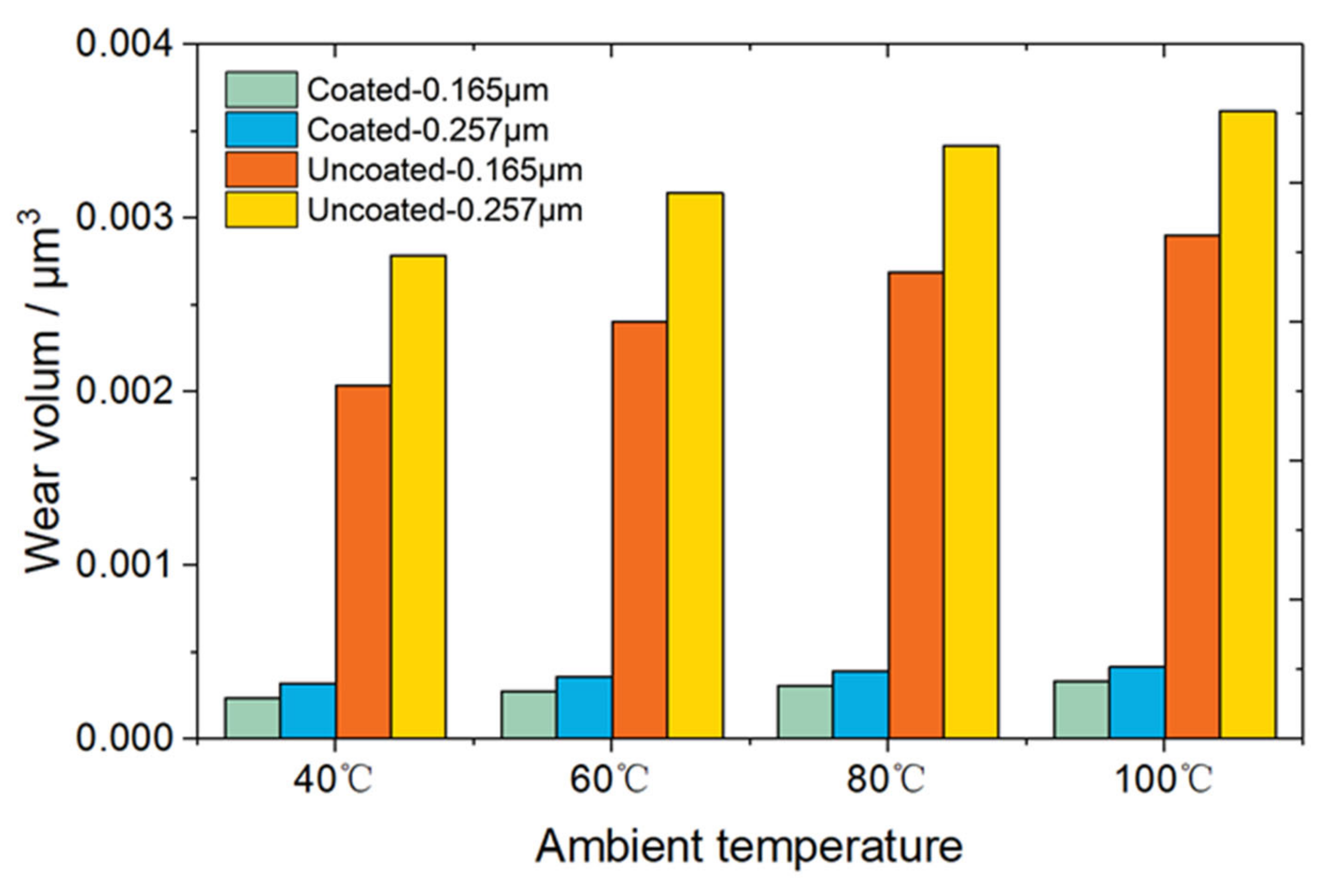
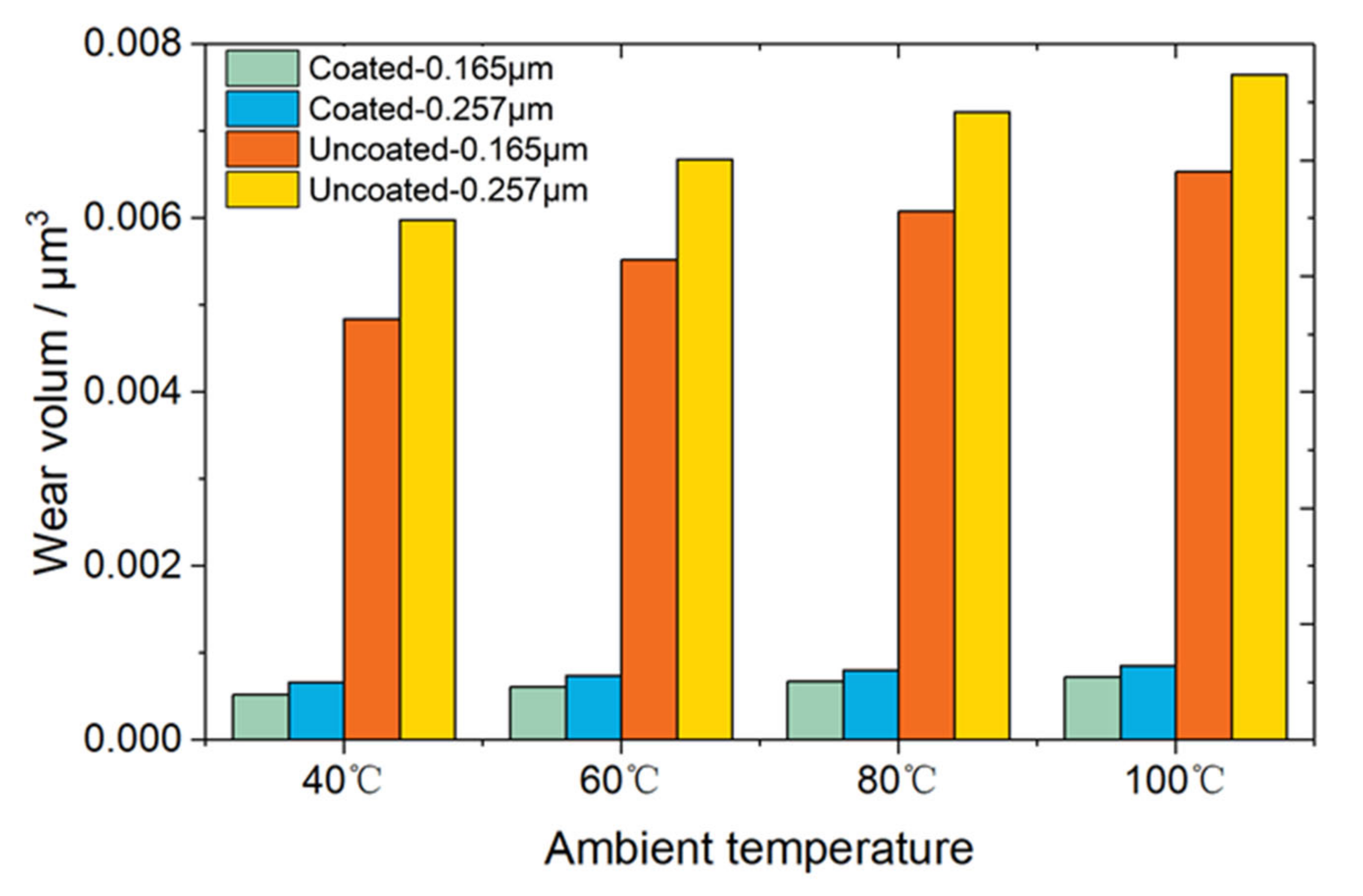
- The wear volume of the coated surface is substantially lower than that of the uncoated, which can be attributed to its high hardness and low wear coefficient. Besides, higher ambient temperature and roughness will result in more severe wear volume.
- The friction reduction and wear-resistance effect of coatings on cam/tappet pairs under a much heavier load are still valid, and a reduced friction loss up to 45% is achieved in the coated cases. However, the total friction consumption is decreased when the ambient temperature rises from 40C to 100C. The wear volume is more than twice that under the normal load, and thus it is predictable that the wear durability will be much shorter.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Ambient temperature (K) | |
| c | Specific heat of lubricant (J/(kgK)) |
| , | Specific heat of substrates and coatings (J/(kgK)) |
| Clearance between the rough surfaces (m) | |
| D | Influence coefficient |
| , | Modulus of elasticity for substrates and coatings (GPa) |
| , , | Total, lubricant viscous, and asperity contact friction (N) |
| h | Film thickness (m) |
| Wear depth (m) | |
| Hardness (GPa) | |
| geometrical acceleration (m) | |
| k | Thermal conductivity of lubricant W/(m K) |
| , | Thermal conductivity of substrates and coatings W/(mK) |
| Wear coefficient | |
| L | Cm thickness (m) |
| p | Film pressure (Pa) |
| Asperity contact pressure (Pa) | |
| Base circle radius of cam (m) | |
| Equivalent contact radius (m) | |
| s | Cam lift (m) |
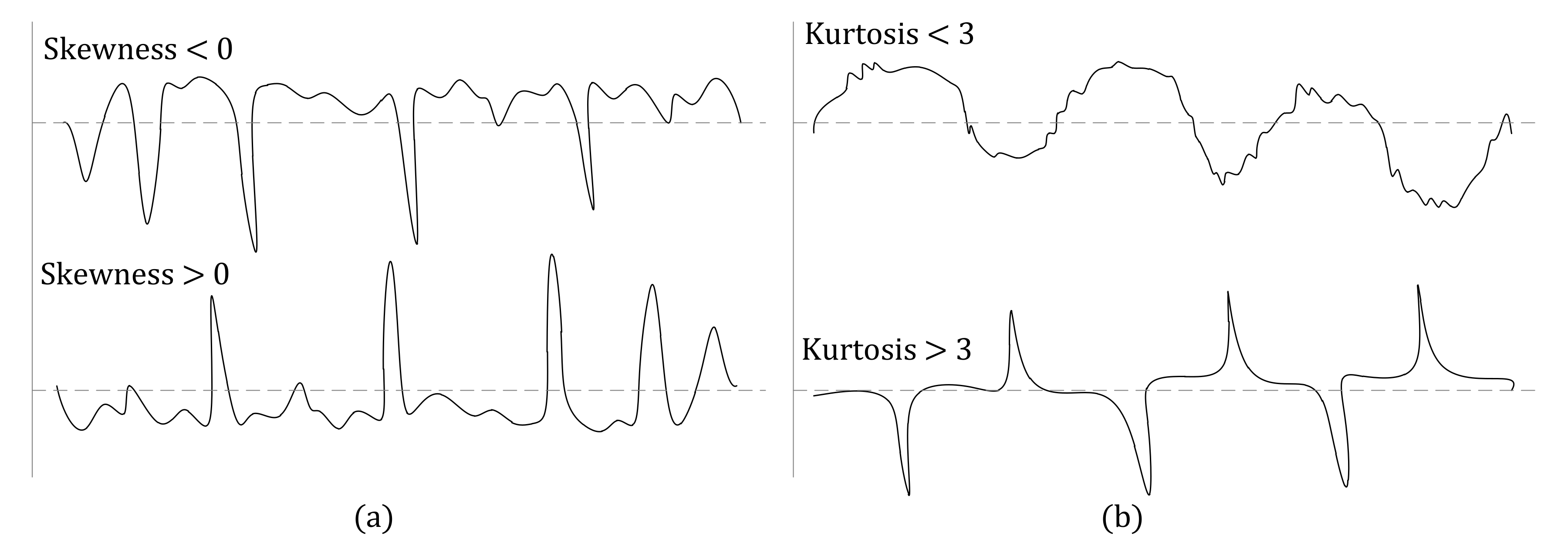
| Kurtosis | |
| Skewness | |
| Slide distance (m) | |
| t | Time (s) |
| T | Lubricant temperature (K) |
| , | Velocities of the control volumes in and directions (m/s) |
| , | Velocities of the cam and tappet (m/s) |
| Entrainment velocity (m/s) | |
| Elastic deformation of surfaces (m) | |
| , | Poisson’s ratio for substrates and coatings |
| Friction work (J) | |
| Applied load (N/m) | |
| x | Coordinate in rolling direction |
| , | Leading and trailing edges |
| Coordinate in film thickness direction | |
| Thermal expansion coefficient, () | |
| Arithmetic mean asperity curvature () | |
| Root mean square height (m) | |
| Lubricant viscosity (Pas) | |
| Initial lubricant viscosity (Pas) | |
| Density of asperities () | |
| friction coefficient of the dry contact surface | |
| Lubricant density (kg/m3) | |
| Initial lubricant density (kg/m3) | |
| , | Substrates and coatings density (kg/m3) |
| Root mean square height (m) | |
| , | Composite roughness () |
| Viscous shear force (Pa) | |
| , , , , , | Flow factors |
| Angular velocity of the cam (rad/s) |
Appendix A
References
- Kalghatgi, G. Is it really the end of internal combustion engines and petroleum in transport? Appl. Energy 2018, 225, 965–974. [Google Scholar] [CrossRef]
- Dolatabadi, N.; Forder, M.; Morris, N.; Rahmani, R.; Rahnejat, H.; Howell-Smith, S. Influence of advanced cylinder coatings on vehicular fuel economy and emissions in piston compression ring conjunction. Appl. Energy 2020, 259, 114129. [Google Scholar] [CrossRef]
- Serrano, J.R.; Novella, R.; Piqueras, P. Why the Development of Internal Combustion Engines Is Still Necessary to Fight against Global Climate Change from the Perspective of Transportation. Appl. Sci. 2019, 9, 4597. [Google Scholar] [CrossRef]
- Buchal, C.; Karl, H.-D.; Sinn, H.-W. Kohlemotoren, Windmotoren und Dieselmotoren: Was zeigt die CO2-Bilanz? ifo Schnelldienst. 2019, 72, 40–54. [Google Scholar]
- Holmberg, K.; Andersson, P.; Erdemir, A. Global energy consumption due to friction in passenger cars. Tribol. Int. 2012, 47, 221–234. [Google Scholar] [CrossRef]
- Gangopadhyay, A.; McWatt, D.G.; Zdrodowski, R.J.; Simko, S.J.; Matera, S.; Sheffer, K.; Furby, R.S. Valvetrain Friction Reduction through Thin Film Coatings and Polishing. Tribol. Trans. 2012, 55, 99–108. [Google Scholar] [CrossRef]
- Dowson, D.; Taylor, C.M.; Zhu, G. A transient elastohydrodynamic lubrication analysis of a cam and follower. J. Phys. D Appl. Phys. 1992, 25, A313–A320. [Google Scholar] [CrossRef]
- Chong, W.W.F.; Teodorescu, M.; Rahnejat, H. Mixed thermo-elastohydrodynamic cam-tappet power loss in low-speed emission cycles. Int. J. Engine Res. 2012, 15, 153–164. [Google Scholar] [CrossRef]
- Torabi, A.; Akbarzadeh, S.; Salimpour, M.R.; Khonsari, M.M. On the running-in behavior of cam-follower mechanism. Tribol. Int. 2018, 118, 301–313. [Google Scholar] [CrossRef]
- Teodorescu, M.; Taraza, D.; Henein, N.A.; Bryzik, W. Experimental Analysis of Dynamics and Friction in Valve Train Systems. SAE Tech. Pap. Ser. 2002, 2002, 1027–1037. [Google Scholar] [CrossRef]
- Green, D.A.; Lewis, R.; Dwyer-Joyce, R.S. Wear of Valve Train Components Due to Soot Contaminated Lubricant. SAE Tech. Pap. Ser. 2006. [Google Scholar] [CrossRef]
- Ohr, R.; Jacoby, B.; Gradowski, M.; Schug, C.; Hilgers, H. Analytical and functional characterization of ultrathin carbon coatings for future magnetic storage devices. Surf. Coat. Technol. 2003, 173, 111–115. [Google Scholar] [CrossRef]
- Kasemo, B. Biological surface science. Surf. Sci. 2002, 500, 656–677. [Google Scholar] [CrossRef]
- Robertson, J. Diamond-like amorphous carbon. Mater. Sci. Eng. R Rep. 2002, 37, 129–281. [Google Scholar] [CrossRef]
- Martin, P. Review of the filtered vacuum arc process and materials deposition. Thin Solid Films 2001, 394, 1–14. [Google Scholar] [CrossRef]
- Kano, M. Super low friction of DLC applied to engine cam follower lubricated with ester-containing oil. Tribol. Int. 2006, 39, 1682–1685. [Google Scholar] [CrossRef]
- Dobrenizki, L.; Tremmel, S.; Wartzack, S.; Hoffmann, D.C.; Brögelmann, T.; Bobzin, K.; Bagcivan, N.; Musayev, Y.; Hosenfeldt, T. Efficiency improvement in automobile bucket tappet/camshaft contacts by DLC coatings – Influence of engine oil, temperature and camshaft speed. Surf. Coatings Technol. 2016, 308, 360–373. [Google Scholar] [CrossRef]
- Habchi, W. A numerical model for the solution of thermal elastohydrodynamic lubrication in coated circular contacts. Tribol. Int. 2014, 73, 57–68. [Google Scholar] [CrossRef]
- Habchi, W. Influence of thermo-mechanical properties of coatings on friction in elastohydrodynamic lubricated contacts. Tribol. Int. 2015, 90, 113–122. [Google Scholar] [CrossRef]
- Bobzin, K.; Brögelmann, T.; Stahl, K.; Michaelis, K.; Mayer, J.; Hinterstoißer, M. Friction reduction of highly-loaded rolling-sliding contacts by surface modifications under elasto-hydrodynamic lubrication. Wear 2015, 328, 217–228. [Google Scholar] [CrossRef]
- Yu, C.; Meng, X.; Xie, Y. Numerical simulation of the effects of coating on thermal elastohydrodynamic lubrication in cam/tappet contact. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2016, 231, 221–239. [Google Scholar] [CrossRef]
- Marian, M.; Weikert, T.; Tremmel, S. On Friction Reduction by Surface Modifications in the TEHL Cam/Tappet-Contact-Experimental and Numerical Studies. Coatings 2019, 9, 843. [Google Scholar] [CrossRef]
- Hauert, R. An overview on the tribological behavior of diamond-like carbon in technical and medical applications. Tribol. Int. 2004, 37, 991–1003. [Google Scholar] [CrossRef]
- Yoshida, Y.; Kunitsugu, S. Friction wear characteristics of diamond-like carbon coatings in oils containing molybdenum dialkyldithiocarbamate additive. Wear 2018, 414, 118–125. [Google Scholar] [CrossRef]
- Steiner, L.; Bouvier, V.; May, U.; Hegadekatte, V.; Huber, N. Modelling of unlubricated oscillating sliding wear of DLC-coatings considering surface topography, oxidation and graphitisation. Wear 2010, 268, 1184–1194. [Google Scholar] [CrossRef]
- Gangopadhyay, A.; Sinha, K.; Uy, D.; McWatt, D.G.; Zdrodowski, R.J.; Simko, S.J. Friction, Wear, and Surface Film Formation Characteristics of Diamond-Like Carbon Thin Coating in Valvetrain Application. Tribol. Trans. 2010, 54, 104–114. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. An Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication. J. Lubr. Technol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. Application of Average Flow Model to Lubrication Between Rough Sliding Surfaces. J. Lubr. Technol. 1979, 101, 220–229. [Google Scholar] [CrossRef]
- Roelands, C.J.A.; Winer, W.O.; Wright, W.A. Correlational Aspects of the Viscosity-Temperature-Pressure Relationship of Lubricating Oils (Dr In dissertation at Technical University of Delft, 1966). J. Lubr. Technol. 1971, 93, 209–210. [Google Scholar] [CrossRef]
- Dowson, D.; Higginson, G.R. Elasto-Hydrodynamic Lubrication: International Series on Materials Science and Technology; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Habchi, W.; Eyheramendy, D.; Vergne, P.; Morales-Espejel, G. Stabilized fully-coupled finite elements for elastohydrodynamic lubrication problems. Adv. Eng. Softw. 2012, 46, 4–18. [Google Scholar] [CrossRef]
- Chu, L.-M.; Chen, C.-Y.; Tee, C.-K.; Chen, Q.-D.; Li, W.-L. Elastohydrodynamic Lubrication Analysis for Transversely Isotropic Coating Layer. J. Tribol. 2014, 136, 031502. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J.B.P. Contact of nominally flat surfaces. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1966, 295, 300–319. [Google Scholar]
- Greenwood, J.A.; Tripp, J.H. The Contact of Two Nominally Flat Rough Surfaces. In Proceedings of the Institution of Mechanical Engineers; SAGE Publications: London, UK, 1970; Volume 185, pp. 625–633. [Google Scholar]
- Chang, W.-R.; Etsion, I.; Bogy, D.B. An Elastic-Plastic Model for the Contact of Rough Surfaces. J. Tribol. 1987, 109, 257–263. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. A Finite Element Based Elastic-Plastic Model for the Contact of Rough Surfaces. Tribol. Trans. 2003, 46, 383–390. [Google Scholar] [CrossRef]
- Tian, X.; Bhushan, B. A Numerical Three-Dimensional Model for the Contact of Rough Surfaces by Variational Principle. J. Tribol. 1996, 118, 33–42. [Google Scholar] [CrossRef]
- Liu, Z.; Meng, X.; Wen, C.; Yu, S.; Zhou, Z. On the oil-gas-solid mixed bearing between compression ring and cylinder liner under starved lubrication and high boundary pressures. Tribol. Int. 2019, 140, 105869. [Google Scholar] [CrossRef]
- Ai, X.; Sawamiphakdi, K. Solving Elastic Contact Between Rough Surfaces as an Unconstrained Strain Energy Minimization by Using CGM and FFT Techniques. J. Tribol. 1999, 121, 639–647. [Google Scholar] [CrossRef]
- Yang, P.; Qu, S.; Kaneta, M.; Nishikawa, H. Formation of Steady Dimples in Point TEHL Contacts. J. Tribol. 2000, 123, 42–49. [Google Scholar] [CrossRef]
- Masjedi, M.; Khonsari, M.M. Theoretical and experimental investigation of traction coefficient in line-contact EHL of rough surfaces. Tribol. Int. 2014, 70, 179–189. [Google Scholar] [CrossRef]
- Wang, J.; Yang, P. A Numerical Analysis for TEHL of Eccentric-Tappet Pair Subjected to Transient Load. J. Tribol. 2003, 125, 770–779. [Google Scholar] [CrossRef]
- Kim, N.-W.; Kim, K.-W. Effects of sliding velocity and ambient temperature on the friction and wear of a boundary-lubricated, multi-layered DLC coating. Wear 2014, 315, 95–102. [Google Scholar] [CrossRef]
- Meng, X.; Gu, C.; Zhang, D. Modeling the wear process of the ring/liner conjunction considering the evaluation of asperity height distribution. Tribol. Int. 2017, 112, 20–32. [Google Scholar] [CrossRef]
- Archard, J.F. Contact and Rubbing of Flat Surfaces. J. Appl. Phys. 1953, 24, 981. [Google Scholar] [CrossRef]
- Zabala, B.; Igartua, A.; Fernández, X.; Priestner, C.; Ofner, H.; Knaus, O.; Abramczuk, M.; Tribotte, P.; Girot, F.; Roman, E.; et al. Friction and wear of a piston ring/cylinder liner at the top dead centre: Experimental study and modelling. Tribol. Int. 2017, 106, 23–33. [Google Scholar] [CrossRef]
- Teodorescu, M.; Rahnejat, H.; Gohar, R.; Dowson, D. Harmonic decomposition analysis of contact mechanics of bonded layered elastic solids. Appl. Math. Model. 2009, 33, 467–485. [Google Scholar] [CrossRef]
- Esen, H.; Inalli, M. ANN and ANFIS models for performance evaluation of a vertical ground source heat pump system. Expert Syst. Appl. 2010, 37, 8134–8147. [Google Scholar] [CrossRef]
- Gu, C.; Meng, X.; Wang, S.; Ding, X. Research on Mixed Lubrication Problems of the Non-Gaussian Rough Textured Surface with the Influence of Stochastic Roughness in Consideration. J. Tribol. 2019, 141, 1–36. [Google Scholar] [CrossRef]
- Ye, X.; Tse, Z.T.; Tang, G.; Li, X.; Song, G. Retraction notice to: “Effect of electropulsing treatment on microstructure and mechanical properties of cold-rolled pure titanium strips” [Journal of Materials Processing Technology, Volume 222, August 2015, Pages 27-32]. J. Mater. Process. Technol. 2019, 268, 223. [Google Scholar] [CrossRef]


| Base Circle Radius of Cam, mm | Maximum Lift of Cam, mm | Cam Depth, mm | Spring Stiffness, N/mm | Initial Tension of Spring, N |
|---|---|---|---|---|
| 16.5 | 8.0041 | 12 | 16.6 | 172 |
| Parameter | Surface 1 | Surface 2 | Unit |
|---|---|---|---|
| Root mean square height, | 0.165 | 0.2517 | μm |
| Kurtosis, | 10.6186 | 23.0696 | - |
| Skewness, | 2.5958 | −1.0278 | - |
| Density of asperities, | 0.4545 | 0.6224 | |
| Arithmetic mean asperity curvature, | 0.8521 | 0.4972 |
| Parameters | Value | Unit |
|---|---|---|
| Young’s modulus of substrates, | 210 | GPa |
| Poisson ratio of substrates, | 0.3 | - |
| Young’s modulus of coatings, | 305 | GPa |
| Poisson ratio of coatings, | 0.3 | - |
| Coating thickness, | 4 | |
| Density of substrates, | 7850 | Kg/ |
| Density of coatings, | 3500 | Kg/ |
| Specific heat of substrates, | 470 | J/(kgK) |
| Specific heat of coatings, | 200 | J/(kgK) |
| Thermal conductivity of substrates, | 46 | W/(mK) |
| Thermal conductivity of coatings, | 5 | W/(mK) |
| Parameters | Value | Unit |
|---|---|---|
| Viscosity of lubricant at 313 K, | 0.01 | Pas |
| Density of lubricant at 313 K, | 875 | Kg/ |
| Specific heat of lubricant, | 2000 | J/(kgK) |
| Thermal conductivity of lubricant, | 0.14 | W/(mK) |
| Thermal expansion coefficient, |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyu, B.; Meng, X.; Zhang, R.; Cui, Y. A Comprehensive Numerical Study on Friction Reduction and Wear Resistance by Surface Coating on Cam/Tappet Pairs under Different Conditions. Coatings 2020, 10, 485. https://doi.org/10.3390/coatings10050485
Lyu B, Meng X, Zhang R, Cui Y. A Comprehensive Numerical Study on Friction Reduction and Wear Resistance by Surface Coating on Cam/Tappet Pairs under Different Conditions. Coatings. 2020; 10(5):485. https://doi.org/10.3390/coatings10050485
Chicago/Turabian StyleLyu, Bugao, Xianghui Meng, Rui Zhang, and Yi Cui. 2020. "A Comprehensive Numerical Study on Friction Reduction and Wear Resistance by Surface Coating on Cam/Tappet Pairs under Different Conditions" Coatings 10, no. 5: 485. https://doi.org/10.3390/coatings10050485
APA StyleLyu, B., Meng, X., Zhang, R., & Cui, Y. (2020). A Comprehensive Numerical Study on Friction Reduction and Wear Resistance by Surface Coating on Cam/Tappet Pairs under Different Conditions. Coatings, 10(5), 485. https://doi.org/10.3390/coatings10050485




