Drug Combinations to Prevent Antimicrobial Resistance: Various Correlations and Laws, and Their Verifications, Thus Proposing Some Principles and a Preliminary Scheme
Abstract
1. Introduction
2. Results
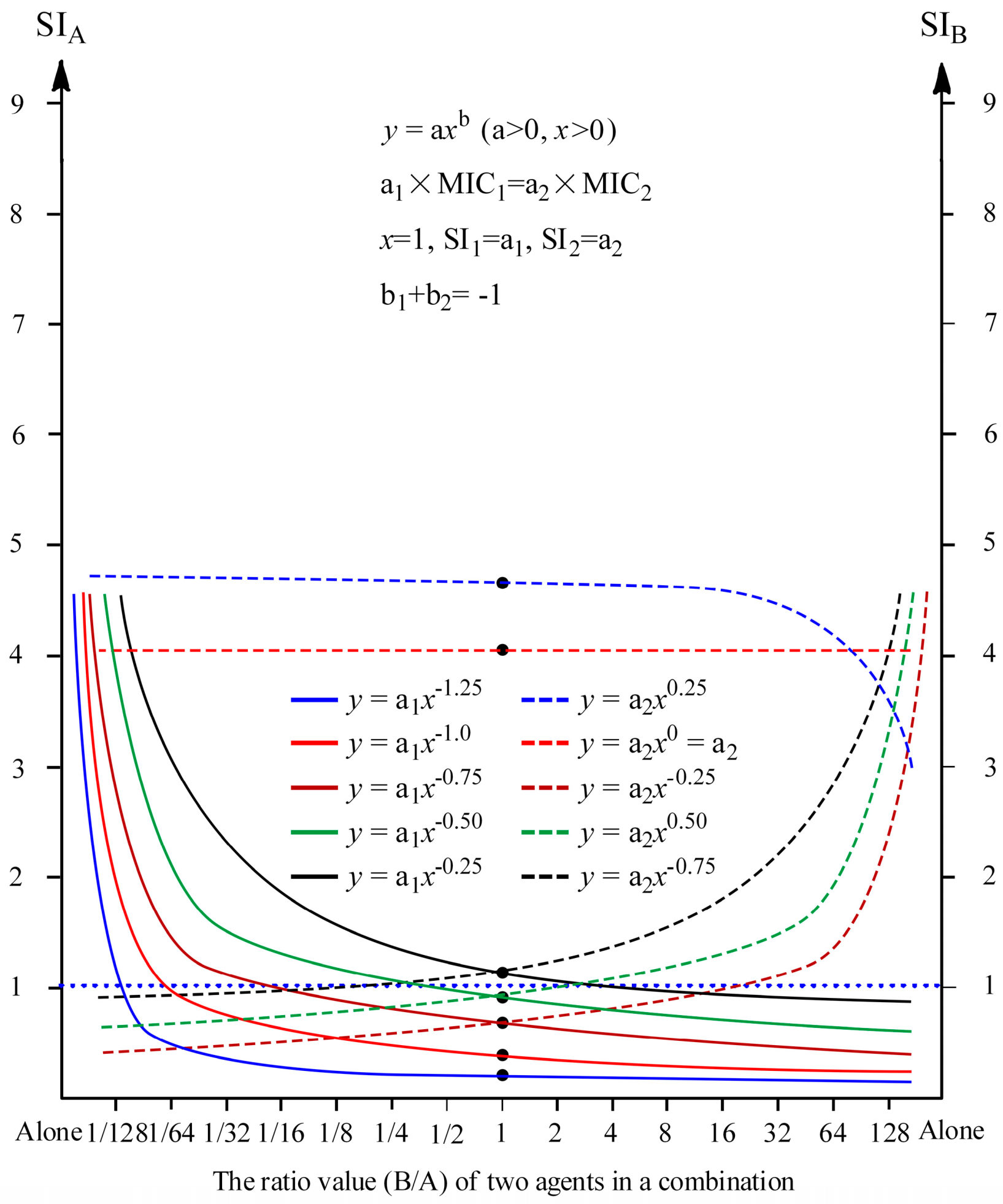
2.1. Correlation between the SI of One Agent and the Ratio of Two Agents, in a Drug Combination
2.2. Correlation between the MPSI and the MIC, MPC or SI Ratio of Two Agents in an Antimicrobial Combination
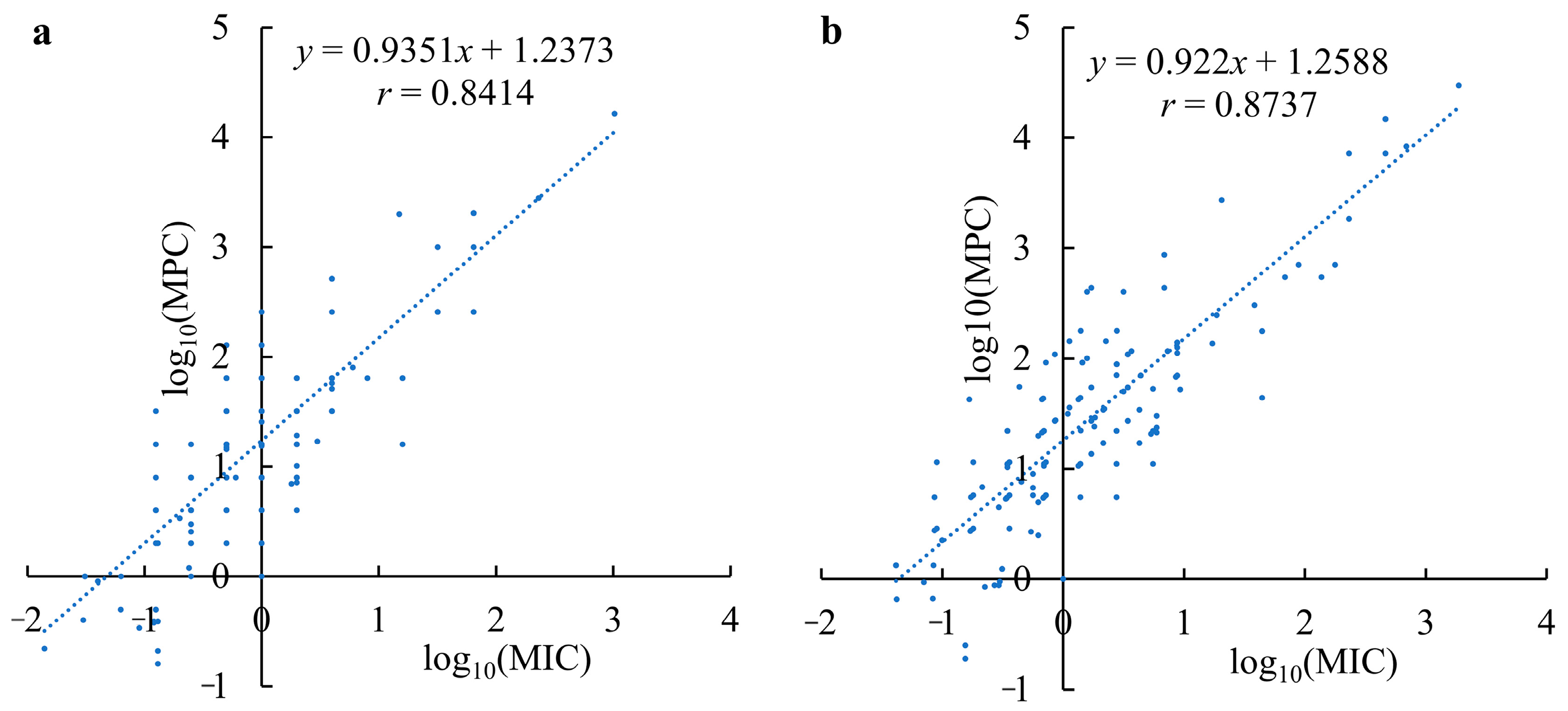
2.3. Correlation between the MPC and the MIC of an Antimicrobial Agent
2.4. Verification and Improvement for Regularity Conclusion by Antibiotic Exposure Experiments
2.4.1. Susceptibility Changes of MRSA to Antibiotics after Exposed to Reported Combinations
2.4.2. Susceptibility Changes of MRSA to Antibiotics after Exposed to Designed Combinations
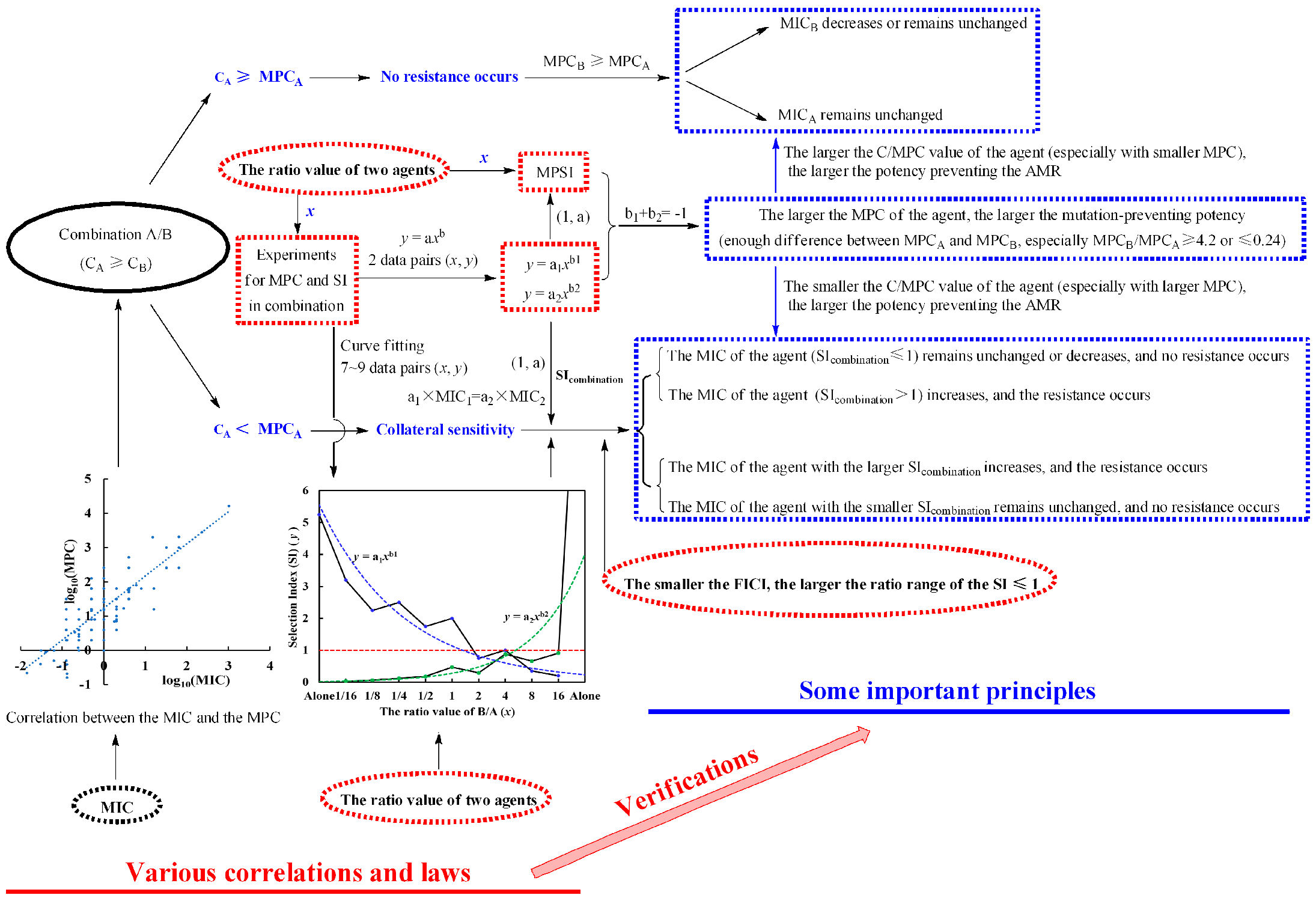
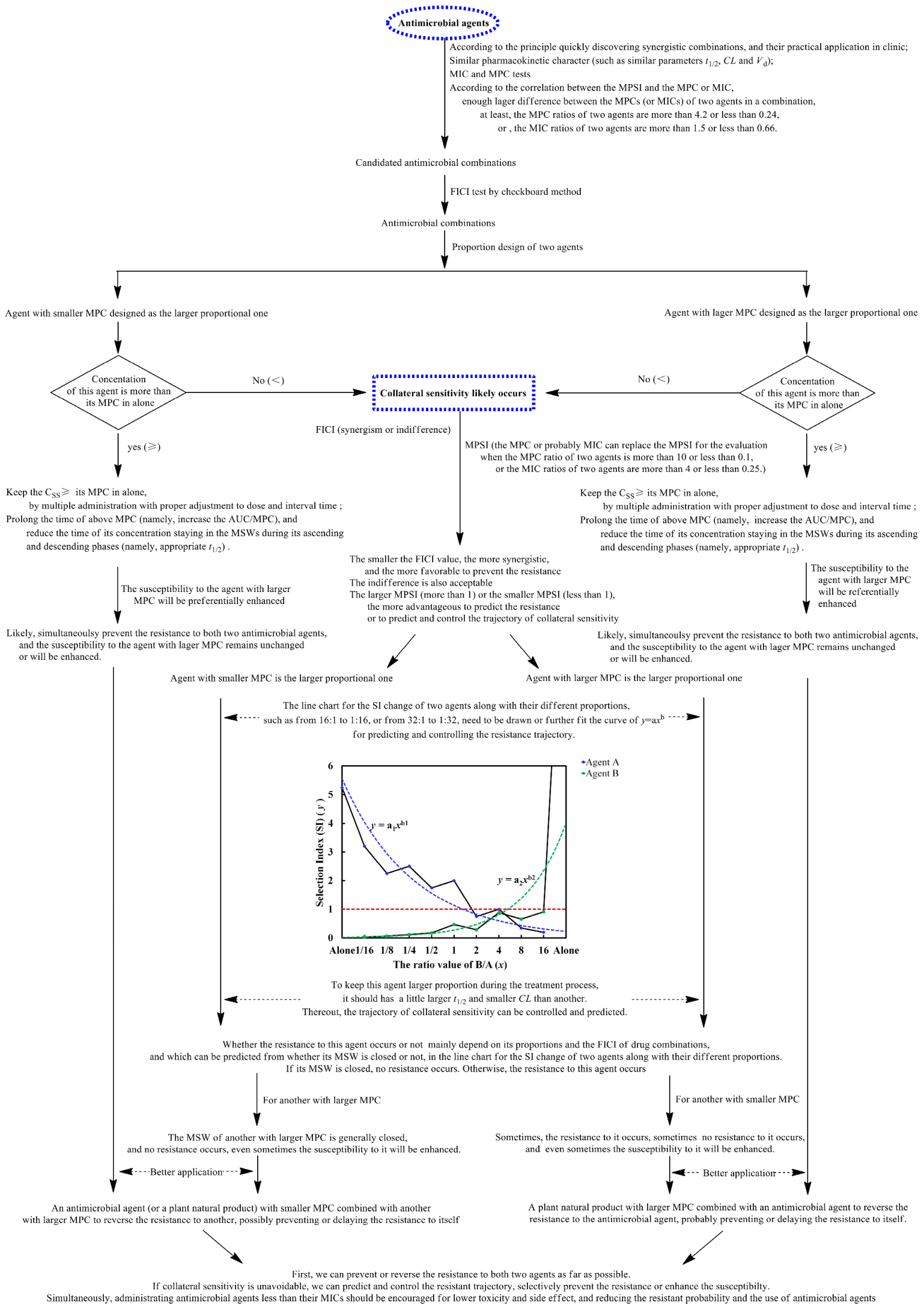
3. Discussion
4. Materials and Methods
4.1. Analyses for the Data Reported by Us
4.1.1. Correlation between the SI of One Agent and the Ratio of Two Agents in a Combination
4.1.2. MPSI and Correlations between the MPSI and the MIC, MPC or SI Ratio of Two Antimicrobial Agents in a Drug Combination
4.1.3. Correlation between the MPC and the MIC of an Antimicrobial Agent
4.1.4. Statistical Analysis
4.2. Verification and Improvement for Regularity Conclusion by Antibiotic Exposure Experiments
4.2.1. Antimicrobial Agents
4.2.2. Isolates and Media
4.2.3. Susceptibility Test
4.2.4. Antibiotic Exposures
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- MacLean, R.C.; Millan, A.S. The evolution of antibiotic resistance. Science 2019, 365, 1082–1083. [Google Scholar] [CrossRef]
- Laxminarayan, R.; Sridhar, D.; Blaser, M.; Wang, M.; Woolhouse, M. Achieving global targets for antimicrobial resistance. Science 2016, 353, 874–875. [Google Scholar] [CrossRef]
- Murray, C.J.L.; Ikuta, K.S.; Sharara, F.; Swetschinski, L.; Aguilar, G.R.; Gray, A.; Han, C.; Bisignano, C.; Rao, P.; Wool, E.; et al. Global burden of bacterial antimicrobial resistance in 2019, a systematic analysis. Lancet 2022, 399, 629–655. [Google Scholar] [CrossRef]
- Wright, G.D. Opportunities for natural products in 21st century antibiotic discovery. Nat. Prod. Rep. 2017, 34, 694–701. [Google Scholar] [CrossRef]
- Fischbach, M.A. Combination therapies for combating antimicrobial resistance. Curr. Opin. Microbiol. 2011, 14, 519–523. [Google Scholar] [CrossRef]
- Bush, K. Improving known classes of antibiotics, an optimistic approach for the future. Curr. Opin. Pharmacol. 2012, 12, 527–534. [Google Scholar] [CrossRef]
- Theuretzbacher, U.; Piddock, L.J. Non-traditional antibacterial therapeutic options and challenges. Cell Host Microbe 2019, 26, 61–72. [Google Scholar] [CrossRef]
- Tyers, M.; Wright, G.D. Drug combinations, a strategy to extend the life of antibiotics in the 21st century. Nat. Rev. Microbiol. 2019, 17, 141–155. [Google Scholar] [CrossRef]
- Tepekule, B.; Uecker, H.; Derungs, I.; Frenoy, A.; Bonhoeffer, S. Modeling antibiotic treatment in hospitals, A systematic approach shows benefits of combination therapy over cycling, mixing, and mono-drug therapies. PLoS Comput. Biol. 2017, 13, e1005745. [Google Scholar] [CrossRef]
- Brochado, A.R.; Telzerow, A.; Bobonis, J.; Banzhaf, M.; Mateus, A.; Selkrig, J.; Huth, E.; Bassler, S.; Beas, J.Z.; Zietek, M. Species-specific activity of antibacterial drug combinations. Nature 2018, 559, 259–263. [Google Scholar] [CrossRef]
- Ni, W.; Cui, J.; Liang, B.; Cai, Y.; Bai, N.; Cai, X.; Wang, R. In vitro effects of tigecycline in combination with colistin (Polymyxin E) and sulbactam against multidrug-resistant Acinetobacter baumannii. J. Antibiot. 2013, 66, 705–708. [Google Scholar] [CrossRef] [PubMed]
- Zhanel, G.G.; Mayer, M.; Laing, N.; Adam, H.J. Mutant prevention concentrations of levofloxacin alone and in combination with azithromycin, ceftazidime, colistin (Polymyxin E), meropenem, piperacillin-tazobactam, and tobramycin against Pseudomonas aeruginosa. Antimicrob. Agents Chemother. 2006, 50, 2228–2230. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Tamma, P.D.; Cosgrove, S.E.; Maragakis, L.L. Combination therapy for treatment of infections with gram-negative bacteria. Clin. Microbiol. Rev. 2012, 25, 450–470. [Google Scholar] [CrossRef] [PubMed]
- Vestergaard, M.; Paulander, W.; Marvig, R.L.; Clasen, J.; Jochumsen, N.; Molin, S.; Jelsbak, L.; Ingmer, H.; Folkesson, A. Antibiotic combination therapy can select for broad-spectrum multidrug resistance in Pseudomonas aeruginosa. Int. J. Antimicrob. Agents 2016, 47, 48–55. [Google Scholar] [CrossRef]
- Deresinski, S. Vancomycin in combination with other antibiotics for the treatment of serious methicillin-resistant Staphylococcus aureus infections. Clin. Infect. Dis. 2009, 49, 1072–1079. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Gefen, O.; Ronin, I.; Bar-Meir, M.; Balaban, N.Q. Effect of tolerance on the evolution of antibiotic resistance under drug combinations. Science 2020, 367, 200–204. [Google Scholar] [CrossRef] [PubMed]
- Drlica, K.; Zhao, X. Mutant selection window hypothesis updated. Clin. Infect. Dis. 2007, 44, 681–688. [Google Scholar] [CrossRef]
- Golikova, M.V.; Strukova, E.N.; Portnoy, Y.A.; Dovzhenko, S.A.; Kobrin, M.B.; Zinner, S.H.; Firsov, A.A. A novel parameter to predict the effects of antibiotic combinations on the development of Staphylococcus aureus resistance, in vitro model studies at subtherapeutic daptomycin and rifampicin exposures. J. Chemother. 2019, 31, 320–328. [Google Scholar] [CrossRef]
- Firsov, A.A.; Golikova, M.V.; Strukova, E.N.; Portnoy, Y.A.; Dovzhenko, S.A.; Kobrin, M.B.; Zinner, S.H. Pharmacokinetically-based prediction of the effects of antibiotic combinations on resistant Staphylococcus aureus mutants, in vitro model studies with linezolid and rifampicin. J. Chemother. 2017, 29, 220–226. [Google Scholar] [CrossRef]
- Zinner, S.H.; Golikova, M.V.; Strukova, E.N.; Portnoy, Y.A.; Firsov, A.A. Predicting antibiotic combination effects on the selection of resistant Staphylococcus aureus, in vitro model studies with linezolid and gentamicin. Int. J. Antimicrob. Agents 2018, 52, 854–860. [Google Scholar] [CrossRef]
- Homma, T.; Hori, T.; Sugimori, G.; Yamano, Y. Pharmacodynamic assessment based on mutant prevention concentrations of fluoroquinolones to prevent the emergence of resistant mutants of Streptococcus pneumoniae. Antimicrob. Agents Chemother. 2007, 51, 3810–3815. [Google Scholar] [CrossRef] [PubMed]
- Alieva, K.N.; Strukova, E.N.; Golikova, M.V.; Portnoy, Y.A.; Zinner, S.H.; Firsov, A.A. Time inside the mutant selection window as a predictor of staphylococcal resistance to linezolid. J. Antibiot. 2018, 71, 514–521. [Google Scholar] [CrossRef] [PubMed]
- Zinner, S.H.; Gilbert, D.; Lubenko, I.Y.; Greer, K.; Firsov, A.A. Selection of linezolid-resistant Enterococcus faecium in an in vitro dynamic model, protective effect of doxycycline. J. Antimicrob. Chemother. 2008, 61, 629–635. [Google Scholar] [CrossRef]
- Xu, X.; Xu, L.; Yuan, G.; Wang, Y.; Qu, Y.; Zhou, M. Synergistic combination of two antimicrobial agents closing each other’s mutant selection windows to prevent antimicrobial resistance. Sci. Rep. 2018, 8, 7237. [Google Scholar] [CrossRef]
- Xu, X.; Xu, L.; Yuan, G.; Li, J. The correlations between fraction inhibitory concentration index and mutant selection index in an antimicrobial combination. Int. J. Antimicrob. Agents 2017, 50, S159–S160. [Google Scholar]
- Baym, M.; Stone, L.K.; Kishony, R. Multidrug evolutionary strategies to reverse antibiotic resistance. Science 2016, 351, aad3292. [Google Scholar] [CrossRef]
- Szybalski, W.; Bryson, V. Genetic studies on microbial cross resistance to toxic agents. I. Cross resistance of Escherichia coli to fifteen antibiotics. J. Bacteriol. 1952, 64, 489–499. [Google Scholar] [CrossRef]
- Yuan, G.; Li, P.; Qin, H.; Xu, X.; Song, X.; Cao, S.; He, S.; Lai, S. Opinions and regularity conclusions on drug combination to prevent resistance. J. Integr. Omics 2019, 9, 6. [Google Scholar]
- Sindelar, G.; Zhao, X.; Liew, A.; Dong, Y.; Lu, T.; Zhou, J.; Domagala, J.; Drlica, K. Mutant prevention concentration as a measure of fluoroquinolone potency against mycobacteria. Antimicrob. Agents Chemother. 2000, 44, 3337–3343. [Google Scholar] [CrossRef]
- Marcusson, L.; Olofsson, S.; Lindgren, P.; Cars, O.; Hughes, D. Mutant prevention concentration of ciprofloxacin for urinary tract infection isolates of Escherichia coli. J. Antimicrob. Chemother. 2005, 55, 938–943. [Google Scholar] [CrossRef]
- Drlica, K.; Zhao, X.; Blondeau, J.; Hesje, C. Low correlation between minimal inhibitory concentration (MIC) and mutant prevention concentration (MPC). Antimicrob. Agents Chemother. 2006, 50, 403–404. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Ni, W.; Li, G.; Zhao, J.; Cui, J.; Wang, R.; Gao, Z.; Liu, Y. In vitro activity of minocycline combined with aminoglycosides against Klebsiella pneumoniae carbapenemase-producing K. pneumoniae. J. Antibiot. 2018, 71, 506–513. [Google Scholar] [CrossRef]
- Liu, L.G.; Zhu, Y.; Hu, L.; Cheng, J.; Ye, Y.; Li, J. Comparative study of the mutant prevention concentrations of vancomycin alone and in combination with levofloxacin, rifampicin and fosfomycin against methicillin-resistant Staphylococcus epidermidis. J. Antibiot. 2013, 66, 709–712. [Google Scholar] [CrossRef]
- Wu, J.; Jiang, T.; Su, J.; Li, L. Antimicrobial activity of linezolid combined with minocycline against vancomycin-resistant Enterococci. Chin. Med. J. 2013, 126, 2670–2675. [Google Scholar]
- Abdullah, M.R.; Abdulkareem, M.S. Mutant prevention concentration of levofloxacin alone and in combination with ceftazidime against levofloxacin and ceftazidime sensitive and resistant isolates of Pseudomonas aeruginosa. Iraqi J. Sci. 2009, 50, 491–495. [Google Scholar]
- Hansen, G.T.; Metzler, K.; Drlica, K.; Blondeau, J.M. Mutant prevention concentration of gemifloxacin for clinical isolates of Streptococcus pneumoniae. Antimicrob. Agents Chemother. 2003, 47, 440–441. [Google Scholar] [CrossRef]
- Lu, T.; Zhao, X.; Li, X.; Hansen, G.; Blondeau, J.; Drlica, K. Effect of chloramphenicol, erythromycin, moxifloxacin, penicillin and tetracycline concentration on the recovery of resistant mutants of Mycobacterium smegmatis and Staphylococcus aureus. J. Antimicrob. Chemother. 2003, 52, 61–64. [Google Scholar] [CrossRef]
- Díez-Aguilar, M.; Morosini, M.I.; Tedim, A.P.; Rodríguez, I.; Aktaş, Z.; Cantón, R. Antimicrobial activity of fosfomycin-tobramycin combination against Pseudomonas aeruginosa isolates assessed by time-kill assays and mutant prevention concentrations. Antimicrob. Agents Chemother. 2015, 59, 6039–6045. [Google Scholar] [CrossRef]
- Firsov, A.A.; Vostrov, S.N.; Lubenko, I.Y.; Portnoy, Y.A.; Zinner, S.H. Prevention of the selection of resistant Staphylococcus aureus by moxifloxacin plus doxycycline in an in vitro dynamic model, an additive effect of the combination. Int. J. Antimicrob. Agents 2004, 23, 451–456. [Google Scholar] [CrossRef]
- Berghaus, L.J.; Giguère, S.; Guldbech, K. Mutant prevention concentration and mutant selection window for 10 antimicrobial agents against Rhodococcus equi. Vet. Microbiol. 2013, 166, 670–675. [Google Scholar] [CrossRef]
- Cai, X.; Yang, Z.; Dai, J.; Chen, K.; Zhang, L.; Ni, W.; Wei, C.; Cui, J. Pharmacodynamics of tigecycline alone and in combination with colistin against clinical isolates of multidrug-resistant Acinetobacter baumannii in an in vitro pharmacodynamic model. Int. J. Antimicrob. Agents 2017, 49, 609–616. [Google Scholar] [CrossRef]
- Mei, Q.; Yu, T.; Zhu, Y.; Cheng, J.; Ye, Y.; Li, J. Study on mutant prevention concentrations of vancomycin alone and in combination with rifampicin or fosfomycin against MRSA. Chin. Pharmacol. Bull. 2011, 27, 944–947. [Google Scholar]
- Allen, G.P.; Harris, K.A. In vitro resistance selection in Shigella flexneri by azithromycin, ceftriaxone, ciprofloxacin, levofloxacin, and moxifloxacin. Antimicrob. Agents Chemother. 2017, 61, e00086-17. [Google Scholar] [CrossRef]
- Blondeau, J.M.; Shebelski, S.D.; Hesje, C.K. Killing of Streptococcus pneumoniae by azithromycin, clarithromycin, erythromycin, telithromycin and gemifloxacin using drug minimum inhibitory concentrations and mutant prevention concentrations. Int. J. Antimicrob. Agents 2015, 45, 594–599. [Google Scholar] [CrossRef]
- Huang, Z.; Mao, C.; Wei, Y.; Gu, X.; Cai, Q.; Shen, X.; Ding, H. Analysis of the mutant selection window and killing of Mycoplasma hyopneumoniae for doxycycline, tylosin, danofloxacin, tiamulin, and valnemulin. PLoS ONE 2020, 15, e0220350. [Google Scholar] [CrossRef]
- Zhao, J.; Huang, Y.; Li, J.; Zhang, B.; Dong, Z.; Wang, D. In vitro antibacterial activity and resistance prevention of antimicrobial combinations for dihydropteroate synthase-carrying Stenotrophomonas maltophilia. Infect. Drug Resist. 2022, 15, 3039–3046. [Google Scholar] [CrossRef]
- Yuan, G.; Guan, Y.; Yi, H.; Lai, S.; Sun, Y.; Cao, S. Antibacterial activity and mechanism of plant flavonoids to gram-positive bacteria predicted from their lipophilicities. Sci. Rep. 2021, 11, 10471. [Google Scholar] [CrossRef]
- Imamovic, L.; Sommer, M.O. Use of collateral sensitivity networks to design drug cycling protocols that avoid resistance development. Sci. Transl. Med. 2013, 5, 204ra132. [Google Scholar] [CrossRef]
- Lázár, V.; Singh, G.P.; Spohn, R.; Nagy, I.; Horváth, B.; Hrtyan, M.; Busa-Fekete, R.; Bogos, B.; Méhi, O.; Csörgő, B.; et al. Bacterial evolution of antibiotic hypersensitivity. Mol. Syst. Biol. 2013, 9, 700. [Google Scholar] [CrossRef]
- Gonzales, P.R.; Gonzales, P.R.; Pesesky, M.W.; Bouley, R.; Ballard, A.; Biddy, B.A.; Suckow, M.A.; Wolter, W.R.; Schroeder, V.A.; Burnham, C.D.; et al. Synergistic, collaterally sensitive beta-lactam combinations suppress resistance in MRSA. Nat. Chem. Biol. 2015, 11, 855–861. [Google Scholar] [CrossRef]
- Barbosa, C.; Trebosc, V.; Kemmer, C.; Rosenstiel, P.; Beardmore, R.; Schulenburg, H.; Jansen, G. Alternative evolutionary paths to bacterial antibiotic resistance cause distinct collateral effects. Mol. Biol. Evol. 2017, 34, 2229–2244. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Lieberman, T.D.; Kishony, R. Alternating antibiotic treatments con-strain evolutionary paths to multidrug resistance. Proc. Natl. Acad. Sci. USA 2014, 111, 14494–14499. [Google Scholar] [CrossRef] [PubMed]
- Imamovic, L.; Ellabaan, M.M.H.; Machado, A.M.D.; Citterio, L.; Wulff, T.; Molin, S.; Johansen, H.K.; Sommer, M.O.A. Drug-driven phenotypic convergence supports rational treatment strategies of chronic infections. Cell 2018, 172, 121–134.e114. [Google Scholar] [CrossRef] [PubMed]
- Podnecky, N.L.; Fredheim, E.G.A.; Kloos, J.; Sørum, V.; Primicerio, R.; Roberts, A.P.; Rozen, D.E.; Samuelsen, Ø.; Johnsen, P.J. Conserved collateral antibiotic susceptibility networks in diverse clinical strains of Escherichia coli. Nat. Commun. 2018, 9, 3673. [Google Scholar] [CrossRef] [PubMed]
- Maisuria, V.B.; Okshevsky, M.; Déziel, E.; Tufenkji, N. Proanthocyanidin interferes with intrinsic antibiotic resistance mechanisms of gram-negative bacteria. Adv. Sci. 2019, 6, 1802333. [Google Scholar] [CrossRef] [PubMed]
- Liang, R.M.; Yong, X.L.; Duan, Y.Q.; Tan, Y.H.; Zeng, P.; Zhou, Z.Y.; Jiang, Y.; Wang, S.; Jiang, Y.; Huang, X.; et al. Potent in vitro synergism of fusidic acid (FA) and berberine chloride (BBR) against clinical isolates of methicillin-resistant Staphylococcus aureus (MRSA). World J. Microb. Biot. 2014, 30, 2861–2869. [Google Scholar] [CrossRef] [PubMed]
- Kristiansen, J.E.; Hendricks, O.; Delvin, T.; Butterworth, T.S.; Aagaard, L.; Christensen, J.B.; Flores, V.C.; Keyzer, H. Reversal of resistance in microorganisms by help of non-antibiotics. J. antimicrob. chemother. 2007, 59, 1271–1279. [Google Scholar] [CrossRef]
- Yuan, G.; Xia, X.; Guan, Y.; Yi, H.; Lai, S.; Sun, Y.; Cao, S. The antimicrobial quantitative relationship and mechanism of plant flavonoids to gram-positive bacteria. Res. Sq. 2022. [Google Scholar] [CrossRef]
- Vázquez, N.M.; Fiorilli, G.; Guido, P.A.C.; Moreno, S. Carnosic acid acts synergistically with gentamicin in killing methicillin-resistant Staphylococcus aureus clinical isolates. Phytomedicine 2016, 23, 1337–1343. [Google Scholar] [CrossRef]
- Johnson, D.E.; Thompson, B. Efficacy of single-agent therapy with azlocillin, ticarcillin, and amikacin and beta-lactam/amikacin combinations for treatment of Pseudomonas aeruginosa bacteremia in granulocytopenic rats. Am. J. Med. 1986, 80, 53–58. [Google Scholar]
- Sahuquillo Arce, J.M.; Colombo, G.E.; Gil, B.A.; Ortiz, E.R.; Cantón, E.; Gobernado, M. In vitro activity of linezolid in combination with doxycycline, fosfomycin, levofloxacin, rifampicin and vancomycin against methicillin-susceptible Staphylococcus aureus. Rev. Esp. Quimioterap. 2006, 19, 252–257. [Google Scholar]
- Robertson, G.T.; Bonventre, E.J.; Doyle, T.B.; Du, Q.; Duncan, L.; Morris, T.W.; Roche, E.D.; Yan, D.; Simon Lynch, A. In vitro Evaluation of CBR-2092, a novel rifamycin-quinolone hybrid antibiotic, Microbiology profiling studies with Staphylococci and Streptococci. Antimicrob. Agents Chemother. 2008, 52, 2324–2334. [Google Scholar] [CrossRef] [PubMed]
- Firsov, A.A.; Smirnova, M.V.; Strukova, E.N.; Vostrov, S.N.; Portnoy, Y.A.; Zinner, S.H. Enrichment of resistant Staphylococcus aureus at ciprofloxacin concentrations simulated within the mutant selection window, bolus versus continuous infusion. Int. J. Antimicrob. Agents 2008, 32, 488–493. [Google Scholar] [CrossRef]
- Liang, B.; Bai, N.; Cai, Y.; Wang, R.; Drlica, K.; Zhao, X. Mutant prevention concentration-based pharmacokinetic/pharmacodynamic indices as dosing targets for suppressing the enrichment of levofloxacin-resistant subpopulations of Staphylococcus aureus. Antimicrob. Agents Chemother. 2011, 55, 2409–2412. [Google Scholar] [CrossRef]
- Song, M.; Liu, Y.; Li, T.; Liu, X.; Hao, Z.; Ding, S.; Panichayupakaranant, P.; Zhu, K.; Shen, J. Plant natural flavonoids against multidrug resistant pathogens. Adv. Sci. 2021, 8, 2100749. [Google Scholar] [CrossRef]
- Yuan, G.; Li, P.; Yang, J.; Pang, H.; Pei, Y. Anti-methicillin-resistant Staphylococcus aureus assay of azalomycin F5a and its derivatives. Chin. J. Nat. Med. 2014, 12, 309–313. [Google Scholar] [CrossRef]
- Van der Horst, M.A.; Schuurmans, J.M.; Smid, M.C.; Koenders, B.B.; ter Kuile, B.H. De novo acquisition of resistance to three antibiotics by Escherichia coli. Microb. Drug Resist. 2011, 17, 141–147. [Google Scholar] [CrossRef]
- Hoeksema, M.; Jonker, M.J.; Brul, S.; ter Kuile, B.H. Effects of a previously selected antibiotic resistance on mutations acquired during development of a second resistance in Escherichia coli. BMC Genom. 2019, 20, 284. [Google Scholar] [CrossRef]
- Yuan, G.; Li, P.; Xu, X.; Li, P.; Zhong, Q.; He, S.; Yi, H.; Yi, W.; Guan, Y.; Wen, Z.T. Azalomycin F5a eradicates Staphylococcus aureus biofilm by rapidly penetrating and subsequently inducing cell lysis. Int. J. Mol. Sci. 2020, 21, 862. [Google Scholar] [CrossRef]
| Drug Combination a | MRSA Isolates | Regression Equation b | Correlation Coefficients (r) c | Coefficient of Determination (R2) | Goodness of Fit d | ||||
|---|---|---|---|---|---|---|---|---|---|
| Type I | Type II | Type I | Type II | Type I | Type II | Type I | Type II | ||
| RM/DC | 01 | y = 0.3613x−0.487 | y = −0.161ln(x) + 0.456 | 0.8292 * | 0.9070 | 0.6876 | 0.8226 | / | better |
| y = 0.1838x−0.618 | y = −0.126ln(x) + 0.2629 | 0.8472 | 0.8849 | 0.7177 | 0.7830 | / | better | ||
| 02 | y = 0.3392x−0.318 | y = −0.108ln(x) + 0.3729 | 0.9804 | 0.9825 | 0.9611 | 0.9654 | / | better | |
| y = 0.3669x−0.678 | y = −0.289ln(x) + 0.5385 | 0.9773 | 0.9707 | 0.9552 | 0.9422 | better | / | ||
| 03 | y = 0.0124x−0.925 | y = −0.018ln(x) + 0.0251 | 0.9982 | 0.8984 | 0.9964 | 0.8072 | better | / | |
| y = 3.0580x−0.071 | y = −0.203ln(x) + 3.0703 | 0.7740 | 0.7890 | 0.5990 | 0.6225 | / | better | ||
| VM/OX | 01 | y = 2.6565x−0.519 | y = −1.509ln(x) + 3.5271 | 0.7289 * | 0.8002 | 0.5313 | 0.6404 | — | better |
| y = 2.6561x−0.481 | y = −1.246ln(x) + 3.2771 | 0.9481 | 0.9608 | 0.8989 | 0.9232 | / | better | ||
| 02 | y = 1.7752x−0.463 | y = −0.929ln(x) + 2.1907 | 0.9778 | 0.9565 | 0.9561 | 0.9149 | better | / | |
| y = 1.7769x−0.537 | y = −1.217ln(x) + 2.3864 | 0.9541 | 0.8703 | 0.9103 | 0.7575 | better | / | ||
| 03 | y = 3.6279x−0.569 | y = −1.951ln(x) + 4.4196 | 0.9634 | 0.9132 | 0.9281 | 0.8340 | better | / | |
| y = 0.7627x−0.619 | y = −0.463ln(x) + 1.0457 | 0.9468 | 0.9794 | 0.8964 | 0.9592 | / | better | ||
| VM/FF | 01 | y = 4.5965x0.046 | y = 0.2592ln(x) + 4.8057 | 0.2128 * | 0.2191 * | 0.0453 | 0.0480 | — | — |
| y = 0.0716x−1.049 | y = −0.122ln(x) + 0.1719 | 0.9634 | 0.9046 | 0.9281 | 0.8183 | better | / | ||
| 02 | y = 2.5407x−0.278 | y = −0.747ln(x) + 2.8193 | 0.8573 | 0.8255 | 0.735 | 0.6814 | better | / | |
| y = 0.1587x−0.722 | y = −0.156ln(x) + 0.2629 | 0.8719 | 0.8680 | 0.7602 | 0.7535 | better | / | ||
| 03 | y = 10.24x−0.129 | y = −1.464ln(x) + 10.541 | 0.7463 * | 0.7187 * | 0.5569 | 0.5166 | — | — | |
| y = 0.1483x−0.93 | y = −0.212ln(x) + 0.3019 | 0.9993 | 0.8900 | 0.9987 | 0.7921 | better | / | ||
| No. | y = axb (a > 0, x > 0) | y = aln(x) + b (b > 0, x > 0) b | ||
|---|---|---|---|---|
| 1 | Most, b < 0 | Depended on the ratio of two agents in a drug combination, the MSWs of most agents can be generally closed whatever synergism or not. | Most, a < 0 | Same |
| Monotone decreasing function |
| Monotone decreasing function | Just replaces |b| with |a|. | |
| The curves must pass through the dot (1, a) | When the ratio of two agents is equal to 1 (x = 1), the SI is equal to a (y = a).
| The curves pass through the dot (1, b) | Just replaces a with b. | |
|
| Two functions y = a1ln(x)+b1 and y = a2ln(x) + b2 were established for two agents in a drug combination, and their MICs and MPCs alone were repsectively marked as MIC1 and MIC2, and MPC1 and MPC2. | (6) No relationship between b1/b2 = MIC2/MIC1 can be established, while one agent with larger MIC value also presents a smaller b value in a drug combination. | |
| (7) Just replaces a with b, and a linear equation y = 1.9721x (r = 0.9910) was established and detailed in Table S2. | |||
| (8) Just replaces a with b, and maybe both b1 and b2 ≤ 1.0 or (a1 + a2) ≤ 2. | |||
| (9) Just replaces a with b. | |||
| (10) No relationship for a1 + a2 can be established. | |||
| (11) No correlation between the MPC and the |b| value was observed. | |||
| (12) Just replaces a with b, while the lower correlation between the value (more than 1) of a1/a2 or a2/a1 and that of MPC1/MPC2 or MPC2/MPC1 in aloned presents a linear equation y = 29.956x − 28.956, with the r value of 0.9521, in Table S4. | |||
| ||||
| 2 | Occasionally, b > 0 | Generally, the MSW cannot be closed except that a ≤ 1 (rarely), whatever synergism or not. | Occasionally, a > 0 | Just replaces a with b |
| MRSA Isolates | Combinations b (A/B) | MIC Ratios c | MPC Ratios | SI Ratios | MPSIs | ||
|---|---|---|---|---|---|---|---|
| C1 | C2 | C1 | C2 | MPC/MIC | |||
| 01 | RM/DC | 0.520 | 0.276 | 0.082 | 0.044 | 0.158 | 0.082 |
| VM/OX | 1.000 | 0.249 | 0.602 | 0.150 | 0.602 | 0.470 | |
| VM/FF | 0.031 | 0.003 | 0.015 | 0.001 | 0.493 | 0.002 | |
| 02 | RM/DC | 1.000 | 0.531 | 0.080 | 0.042 | 0.080 | 0.040 |
| VM/OX | 1.000 | 0.249 | 0.833 | 0.208 | 0.833 | 0.554 | |
| VM/FF | 0.063 | 0.006 | 0.016 | 0.002 | 0.256 | 0.008 | |
| 03 | RM/DC | 246.154 | 130.678 | 656.410 | 348.475 | 2.667 | 3094.505 |
| VM/OX | 0.250 | 0.062 | 1.875 | 0.468 | 7.500 | 0.778 | |
| VM/FF | 0.016 | 0.001 | 0.059 | 0.006 | 3.750 | 0.008 | |
| Independent Variable (x) | Regression Equation (Equation Number) | r b | R2 | r0.995 (n-2) |
|---|---|---|---|---|
| MIC ratio | y = 12.2602x − 122.5719 (10.1 ≤ x ≤ 246.2) (1) | 0.9719 ** | 0.9445 | 0.798 |
| y = 0.0450x2 + 1.4972x (1.5 ≤ x ≤ 246.2) (2) | 0.9973 ** | 0.9945 | 0.798 | |
| MPC ratio | y = 4.7313x − 14.7324 (3.4 ≤ x ≤ 656.4) (3) | 0.9973 ** | 0.9946 | 0.798 |
| y = 0.0009x2 + 4.1115x (4.2 ≤ x ≤ 656.4) (4) | 0.9974 ** | 0.9948 | 0.798 | |
| y = 4.7352x − 16.8261 (3.8 ≤ x ≤ 656.4) (5) | 0.9973 ** | 0.9945 | 0.834 | |
| y = 0.0009x2 + 4.1116x (4.2 ≤ x ≤ 656.4) (6) | 0.9973 ** | 0.9946 | 0.834 |
| Concentration Range | Regression Equation (Equation Number) | r | r0.995 (179) | R2 |
|---|---|---|---|---|
| 0.0312~1024 (μg/mL) | y = 16.025x (7) | 0.980 ** | 0.20 | 0.9622 |
| y = 0.00006x3 − 0.0710x2 + 25.5154x (8) | 0.9837 ** | 0.9677 | ||
| y = 0.9351x + 1.2373 b (9) | 0.8414 ** | 0.7079 | ||
| 0.0414~1873 (μM/L) | y = 18.743x (10) | 0.9354 ** | 0.8750 | |
| y = 0.000004x3 − 0.0142x2 + 29.8848x (11) | 0.9528 ** | 0.9079 | ||
| y = 0.922x + 1.2588 b (12) | 0.8737 ** | 0.7633 |
| MRSA Isolates | FICI | Proportion Number | Ratio of Two Agents RM/DC | Antibiotic Concentration (μg/mL) RM/DC b | Dose Range RM/DC (μg/mL) | Susceptibility Changes (×MIC) RM/DC c | SI in Combination (RM/DC) d |
|---|---|---|---|---|---|---|---|
| 01 | 0.26~0.50 | 1 | 8:1 | 0.09/0.01 | <MIC/<MIC | R (1024×)/― | >1/<1 |
| 2 | 4:1 | 0.10/0.02 | <MIC/<MIC | R (1024×)/― | >1/<1 | ||
| 3 | 2:1 | 0.07/0.03 | <MIC/<MIC | R (16~32×)/― | >1/<1 | ||
| 4 | 1:1 | 0.08/0.08 | <MIC/<MIC | R (32~64×)/― | >1/<1 | ||
| 5 | 1:2 | 0.03/0.05 | <MIC/<MIC | ―/― | <1/<1 | ||
| 6 | 1:4 | 0.04/0.15 | <MIC/<MIC | R (256×)/― | 1≈/<1 | ||
| 7 | 1:8 | 0.01/0.12 | <MIC/<MIC | ―/― | <1/<1 | ||
| 03 | 0.53~0.75 | 1 | 8:1 | 2.64/0.33 | <MIC/MIC~MPC | ―/― | >1/>1 |
| 2 | 4:1 | 1.34/0.34 | <MIC/MIC~MPC | ―/― | >1/>1 | ||
| 3 | 2:1 | 0.86/0.43 | <MIC/>MPC | ―/― | >1/>1 | ||
| 4 | 1:1 | 0.41/0.41 | <MIC/>MPC | ―/― | >1/>1 | ||
| 5 | 1:2 | 0.20/0.41 | <MIC/>MPC | ―/― | <1/>1 | ||
| 6 | 1:4 | 0.11/0.42 | <MIC/>MPC | S (2×)/― | <1/>1 | ||
| 7 | 1:8 | 0.07/0.56 | <MIC/>MPC | S (4×)/― | <1/>1 |
| MRSA Isolates | FICI | Proportion Number | Ratio of Two Agents RM/DC | Antibiotic Concentration (μg/mL) RM/DC | Dose Range RM/DC (μg/mL) | Susceptibility Changes (×MIC) RM/DC b | SI in Combination (RM/DC) c |
|---|---|---|---|---|---|---|---|
| 01 | 0.26~0.50 | 8 | 1:4 | 0.13/0.52 | =MIC/MIC~MPC | R (4096×)/S (<1/4×) | 1≈/<1 |
| 9 | 1:8 | 0.13/1.04 | =MIC/MIC~MPC | R (2×)/S (<1/4×) | <1/<1 | ||
| 10 | 1:1 | 0.21/0.21 | MIC~MPC/<MIC | R (4096×)/S (<1/4×) | >1/<1 | ||
| 11 | 8:1 | 10.24/1.28 | >MPC/MIC~MPC | S (<1/2×)/S (<1/4×) | >1/<1 | ||
| 12 | 4:1 | 10.24/2.56 | >MPC/=MPC | S (<1/2×)/S (<1/4×) | >1/<1 | ||
| 13 | 16:1 | 10.24/0.64 | >MPC/MIC~MPC | S (<1/2×)/S (<1/4×) | >1/<1 | ||
| 14 | 1:16 | 0.16/2.56 | MIC~MPC/=MPC | S (<1/2×)/S(<1/4×) | <1/NS | ||
| 15 | 1:16 | 0.32/5.12 | =MPC/>MPC | S (<1/2×)/S (<1/4×) | <1/NS | ||
| 16 | 1:32 | 0.08/2.56 | < MIC/=MPC | S (<1/2×)/S (<1/4×) | <1/NS | ||
| 17 | 1:32 | 0.16/5.12 | MIC~MPC/>MPC | S (<1/2×)/S (1/2×) | <1/NS | ||
| 18 | 1:32 | 0.32/10.24 | =MPC/>MPC | S (<1/2×)/S (<1/4×) | <1/NS | ||
| 03 | 0.53~0.75 | 8 | 3200:1 | 128/0.04 | MIC~MPC/<MIC MIC~MPC/<MIC | R (>8×)/― | SIRM > SIDC |
| 9 | 1600:1 | 128/0.08 | R (>8×)/(1/2~1×) ― | SIRM > SIDC | |||
| 10 | 800:1 | 128/0.16 | MIC~MPC/MIC~MPC | R (>8×)/― | SIRM > SIDC | ||
| 11 | 400:1 | 128/0.32 | MIC~MPC/MIC~MPC | R (>8×)/― | SIRM > SIDC | ||
| 12 | 200:1 | 128/0.64 | MIC~MPC/>MPC | R (>8×)/― | SIRM > SIDC | ||
| 13 | 100:1 | 128/1.28 | MIC~MPC/>MPC | R (4×)/― | SIRM > SIDC | ||
| 14 | 3200:1 | 256/0.08 | =MPC/<MIC | ―(1~2×)/― | SIRM > SIDC | ||
| 15 | 1600:1 | 256/0.16 | =MPC/MIC~MPC | ―(1/2~1×)/― | SIRM > SIDC | ||
| 16 | 800:1 | 256/0.32 | =MPC/MIC~MPC | ―(1/2~1×)/― | SIRM > SIDC | ||
| 17 | 400:1 | 256/0.64 | =MPC/>MPC | ―/― | SIRM > SIDC | ||
| 18 | 200:1 | 256/1.28 | =MPC/>MPC | ―(1~2×)/― | SIRM > SIDC | ||
| 19 | 100:1 | 256/2.56 | =MPC/>MPC | ―(1/2~1×)/― | SIRM > SIDC | ||
| 20 | 3200:1 | 32/0.01 | =MIC/<MIC | R (2×)/― | SIRM > SIDC | ||
| 21 | 1600:1 | 32/0.02 | =MIC/<MIC | R (2×)/― | SIRM > SIDC | ||
| 22 | 800:1 | 32/0.04 | =MIC/<MIC | R (2~4×)/― | SIRM > SIDC | ||
| 23 | 400:1 | 32/0.08 | =MIC/<MIC | R (4×)/― | SIRM > SIDC | ||
| 24 | 200:1 | 32/0.16 | =MIC/MIC~MPC | R (4×)/― | SIRM > SIDC | ||
| 25 | 100:1 | 32/0.32 | =MIC/MIC~MPC | R (2~4×)/― | SIRM > SIDC |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, H.; Yuan, G.; Li, S.; Xu, X.; Guan, Y.; Zhang, L.; Yan, Y. Drug Combinations to Prevent Antimicrobial Resistance: Various Correlations and Laws, and Their Verifications, Thus Proposing Some Principles and a Preliminary Scheme. Antibiotics 2022, 11, 1279. https://doi.org/10.3390/antibiotics11101279
Yi H, Yuan G, Li S, Xu X, Guan Y, Zhang L, Yan Y. Drug Combinations to Prevent Antimicrobial Resistance: Various Correlations and Laws, and Their Verifications, Thus Proposing Some Principles and a Preliminary Scheme. Antibiotics. 2022; 11(10):1279. https://doi.org/10.3390/antibiotics11101279
Chicago/Turabian StyleYi, Houqin, Ganjun Yuan, Shimin Li, Xuejie Xu, Yingying Guan, Li Zhang, and Yu Yan. 2022. "Drug Combinations to Prevent Antimicrobial Resistance: Various Correlations and Laws, and Their Verifications, Thus Proposing Some Principles and a Preliminary Scheme" Antibiotics 11, no. 10: 1279. https://doi.org/10.3390/antibiotics11101279
APA StyleYi, H., Yuan, G., Li, S., Xu, X., Guan, Y., Zhang, L., & Yan, Y. (2022). Drug Combinations to Prevent Antimicrobial Resistance: Various Correlations and Laws, and Their Verifications, Thus Proposing Some Principles and a Preliminary Scheme. Antibiotics, 11(10), 1279. https://doi.org/10.3390/antibiotics11101279







