Novel Pharmacokinetic/Pharmacodynamic Parameters Quantify the Exposure–Effect Relationship of Levofloxacin against Fluoroquinolone-Resistant Escherichia coli
Abstract
1. Introduction
2. Results
2.1. Characterisation of Bacterial Strains
2.2. In Vitro Infection Model Experiments
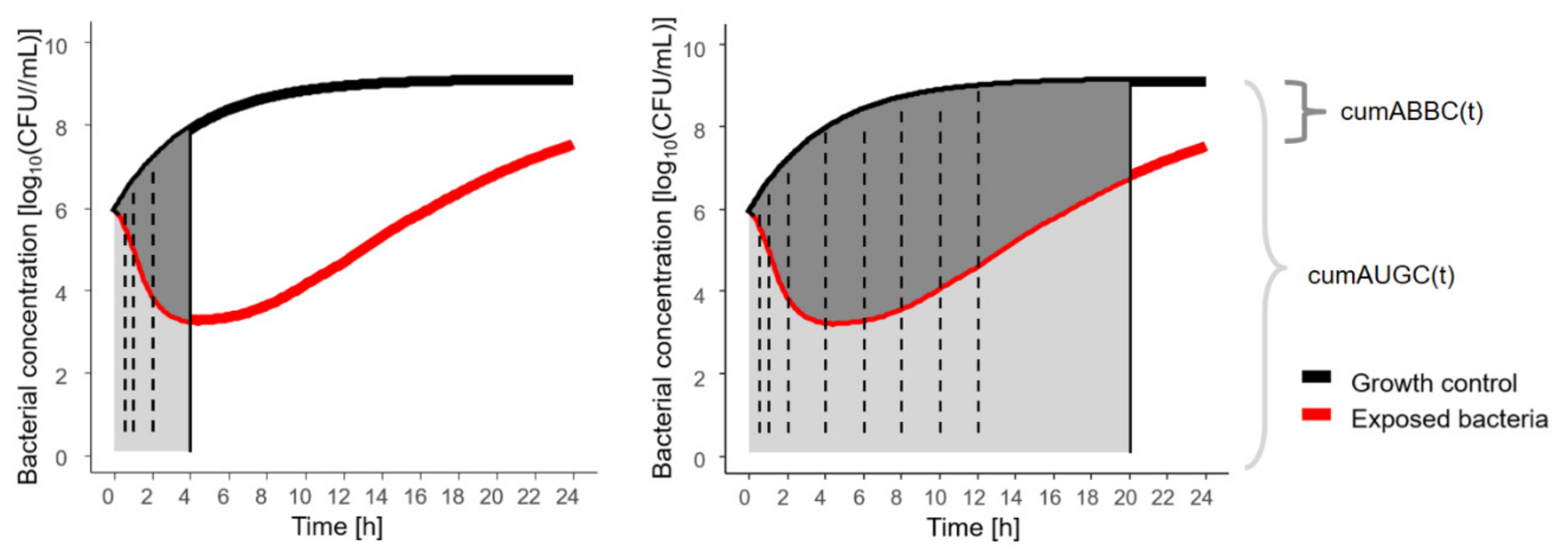
2.3. Pharmacokinetic/Pharmacodynamic Metrics
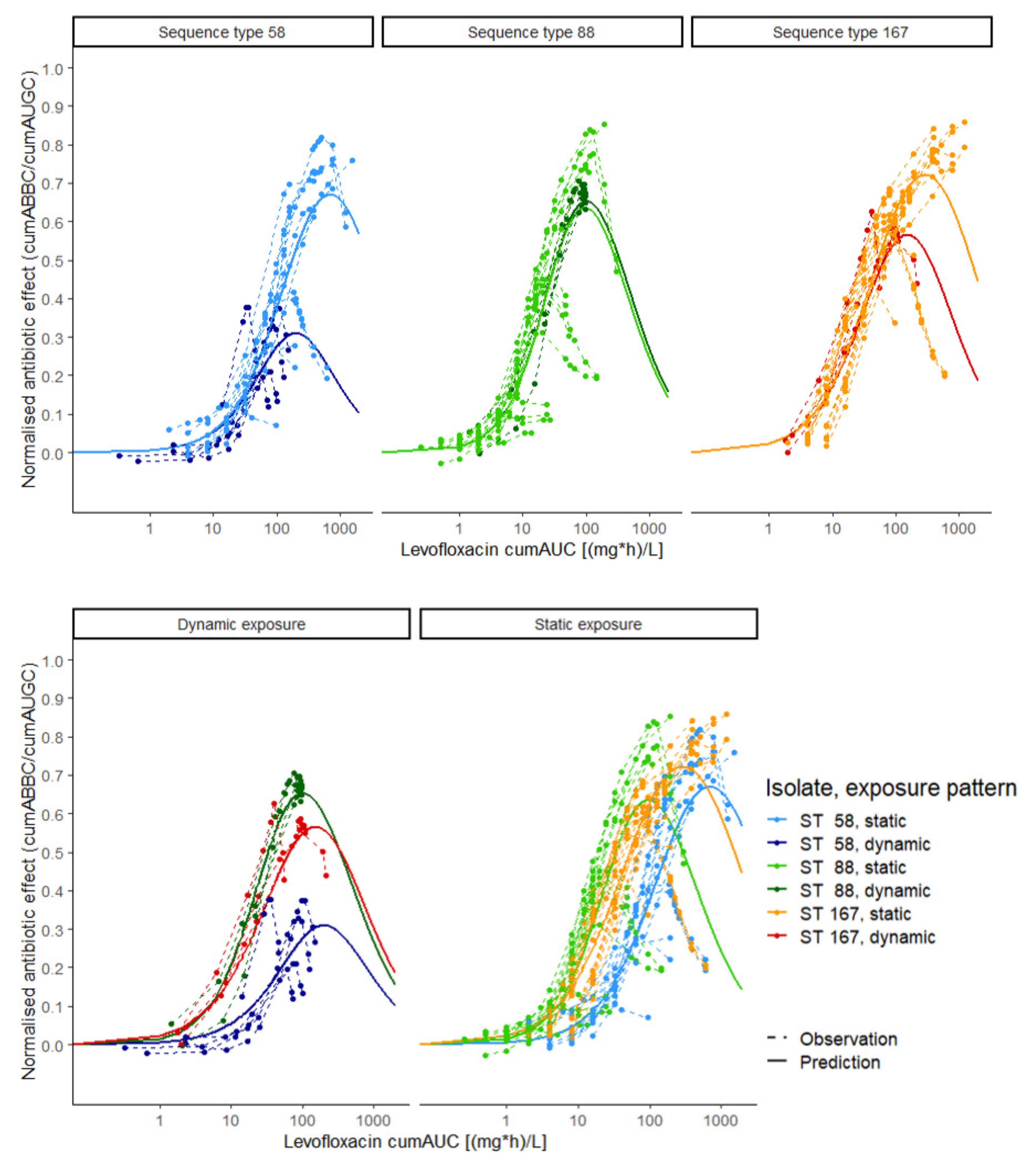
2.4. Exposure–Effect Relationship
2.4.1. Stratification per E.coli Strain
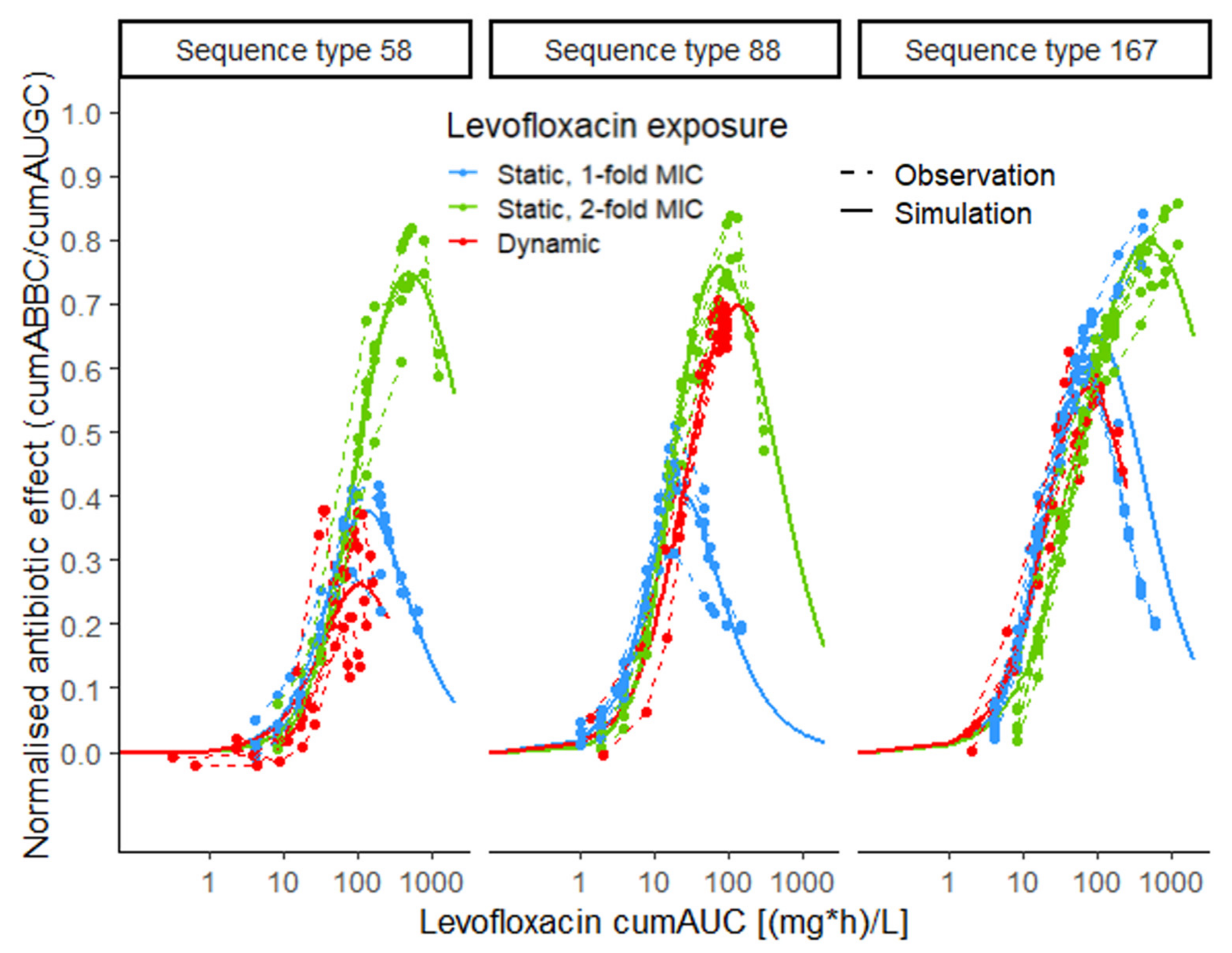
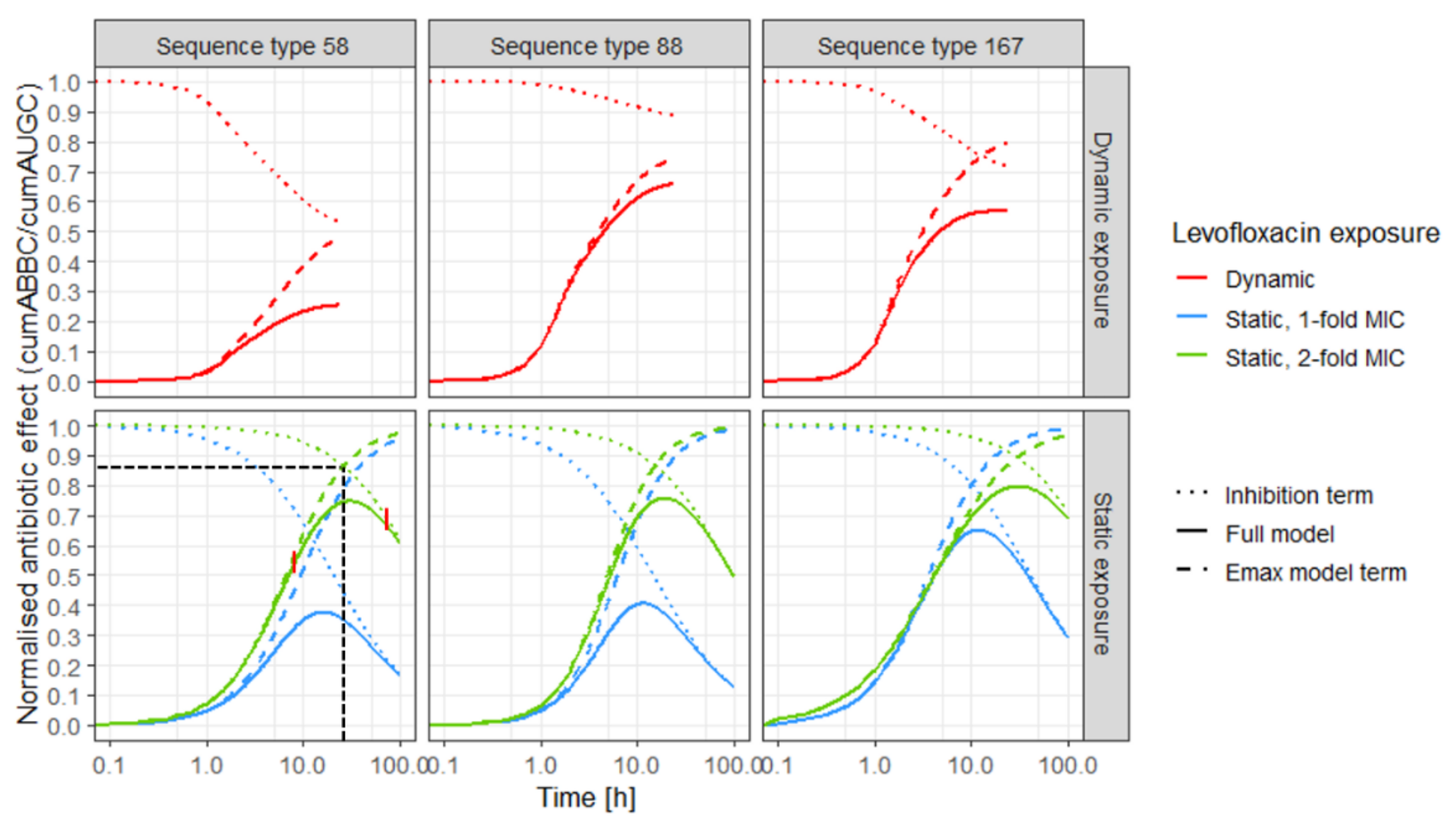
2.4.2. Stratification for Static and Dynamic Exposure
3. Discussion
4. Materials and Methods
4.1. Characterisation of Bacterial Strains
4.1.1. Genotypic Resistance
4.1.2. Antimicrobial Susceptibility Testing
4.2. In Vitro Infection Model Experiments
4.3. Pharmacokinetic/Pharmacodynamic Metrics
4.4. Exposure–effect Relationship
4.4.1. Stratification per E. coli Strain
4.4.2. Stratification for Static and Dynamic Exposure
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mouton, J.W.; Dudley, M.N.; Cars, O.; Derendorf, H.; Drusano, G.L. Standardization of pharmacokinetic/pharmacodynamic (PK/PD) terminology for anti-infective drugs: An update. J. Antimicrob. Chemother. 2005, 55, 601–607. [Google Scholar] [CrossRef]
- Drusano, G.L.; Preston, S.L.; Fowler, C.; Corrado, M.; Weisinger, B.; Kahn, J. Relationship between fluoroquinolone area under the curve: Minimum inhibitory concentration ratio and the probability of eradication of the infecting pathogen, in patients with nosocomial pneumonia. J. Infect. Dis. 2004, 189, 1590–1597. [Google Scholar] [CrossRef]
- Craig, W.A. Basic pharmacodynamics of antibacterials with clinical applications to the use of beta-lactams, glycopeptides, and linezolid. Infect. Dis. Clin. N. Am. 2003, 17, 479–501. [Google Scholar] [CrossRef]
- Weinstein, M.P. M07: Methods for Dilution Antimicrobial Susceptibility Tests for Bacteria that Grow Aerobically; National Committee for Clinical Laboratory Standards: Wayne, PA, USA, 2018. [Google Scholar]
- Hombach, M.; Ochoa, C.; Maurer, F.P.; Pfiffner, T.; Böttger, E.C.; Furrer, R. Relative contribution of biological variation and technical variables to zone diameter variations of disc diffusion susceptibility testing. J. Antimicrob. Chemother. 2016, 71, 141–151. [Google Scholar] [CrossRef] [PubMed]
- Mouton, J.W.; Muller, A.E.; Canton, R.; Giske, C.G.; Kahlmeter, G.; Turnidge, J. MIC-based dose adjustment: Facts and fables. J. Antimicrob. Chemother. 2018, 73, 564–568. [Google Scholar] [CrossRef] [PubMed]
- Ballestero-Téllez, M.; Jiménez-Morgades, E. Camachom Pilar Arjona Inter-technique variability between antimicrobial susceptibility testing methods affects clinical classification of cefuroxime in strains close to breakpoints. Clin. Microbiol. Infect. 2020, 26, 648.e1–648.e3. [Google Scholar] [CrossRef] [PubMed]
- EUCAST-European Committee on Antimicrobial Suscetibility Testing Standard Operating Procedure. MIC Distributions and the Setting of Epidemiological Cut-Off (ECOFF) Values; EUCAST-European Committee on Antimicrobial Suscetibility Testing Standard Operating Procedure: Växjö, Sweden, 2017; pp. 7–10. [Google Scholar]
- Müller, M.; Dela Peña, A.; Derendorf, H. Issues in pharmacokinetics and pharmacodynamics of anti-infective agents: Kill curves versus MIC. Antimicrob. Agents Chemother. 2004, 48, 369–377. [Google Scholar] [CrossRef]
- Ellington, M.J.; Ekelund, O.; Aarestrup, F.M.; Canton, R.; Doumith, M.; Giske, C.; Grundman, H.; Hasman, H.; Holden, M.T.G.; Hopkins, K.L.; et al. The role of whole genome sequencing in antimicrobial susceptibility testing of bacteria: Report from the EUCAST Subcommittee. Clin. Microbiol. Infect. 2017, 23, 2–22. [Google Scholar] [CrossRef]
- Lewis, K. Persister cells, dormancy and infectious disease. Nat. Rev. Microbiol. 2007, 5, 48–56. [Google Scholar] [CrossRef]
- Qin, T.; Kang, H.; Ma, P.; Li, P.; Huang, L.; Gu, B. SOS response and its regulation on the fluoroquinolone resistance. Ann. Transl. Med. 2015, 3, 358. [Google Scholar] [CrossRef]
- Balaban, N.Q.; Helaine, S.; Lewis, K.; Ackermann, M.; Aldridge, B.; Andersson, D.I.; Brynildsen, M.P.; Bumann, D.; Camilli, A.; Collins, J.J.; et al. Definitions and guidelines for research on antibiotic persistence. Nat. Rev. Microbiol. 2019, 17, 441–448. [Google Scholar] [CrossRef]
- Uelze, L.; Grützke, J.; Borowiak, M.; Hammerl, J.A.; Juraschek, K.; Deneke, C.; Tausch, S.H.; Malorny, B. Typing methods based on whole genome sequencing data. One Health Outlook 2020, 2, 3. [Google Scholar] [CrossRef]
- European Medicines Agency. Guideline on the Use of Pharmacokinetics and Pharmacodynamics in the Development of Antibacterial Medicinal Products; European Medicines Agency: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Wicha, S.G.; Kees, M.G.; Kuss, J.; Kloft, C. Pharmacodynamic and response surface analysis of linezolid or vancomycin combined with meropenem against Staphylococcus aureus. Pharm. Res. 2015, 32, 2410–2418. [Google Scholar] [CrossRef]
- Gloede, J.; Scheerans, C.; Derendorf, H.; Kloft, C. In vitro pharmakodynamic models to determine the effect of antibacterial drugs. J. Antimicrob. Chemother. 2010, 65, 186–201. [Google Scholar] [CrossRef] [PubMed]
- Firsov, A.A.; Chernykh, V.M.; Navashin, S.M. Quantitative analysis of antimicrobial effect kinetics in in vitro dynamic model. Microbiology 1990, 34, 1312–1317. [Google Scholar] [CrossRef]
- EUCAST—European Committee on Antimicrobial Suscetibility Testing. Levofloxacin: Rationale for EUCAST Clinical Breakpoints; EUCAST: Växjö, Sweden, 2021; pp. 1–13. [Google Scholar]
- European Centre for Disease Prevention and Control (ECDC). Antimicrobial Resistance in the EU in 2019. Available online: https://www.ecdc.europa.eu/sites/default/files/documents/surveillance-antimicrobial-resistance-Europe-2019.pdf (accessed on 6 April 2021).
- WHO Advisory Group on Integreted Surveillance of Antimicrobial Resistance (AGISAR). Critically Important Antimicrobials for Human Medicine. Available online: https://apps.who.int/iris/bitstream/handle/10665/312266/9789241515528-eng.pdf (accessed on 6 April 2021).
- U.S. Food and Drug Administration. Levaquin Prescribing Information; U.S. Food and Drug Administration: Silver Spring, Maryland, USA, 2018. [Google Scholar]
- Drusano, G.L. Antimicrobial pharmacodynamics: Critical interactions of “bug and drug”. Nat. Rev. Microbiol. 2004, 2, 289–300. [Google Scholar] [CrossRef]
- Preston, S.L.; Drusano, G.L.; Berman, A.L.; Fowler, C.L.; Chow, A.T.; Dornseif, B.; Reichl, V.; Natarajan, J.; Corrado, M. Pharmacodynamics of levofloxacin: A new paradigm for early clinical trials. JAMA 1998, 279, 125–129. [Google Scholar] [CrossRef]
- Ambrose, P.G.; Grasela, D.M.; Grasela, T.H.; Passarell, J.; Mayer, H.B.; Pierce, P.F. Pharmacodynamics of fluoroquinolones against Streptococcus pneumoniae in patients with community-acquired respiratory tract infections. Antimicrob. Agents Chemother. 2001, 45, 2793–2797. [Google Scholar] [CrossRef]
- Odenholt, I.; Cars, O. Pharmacodynamics of moxifloxacin and levofloxacin against Streptococcus pneumoniae, Staphylococcus aureus, Klebsiella pneumoniae and Escherichia coli: Simulation of human plasma concentrations after intravenous dosage in an in vitro kinetic model. J. Antimicrob. Chemother. 2006, 58, 960–965. [Google Scholar] [CrossRef] [PubMed]
- Roberts, J.A.; Cotta, M.O.; Cojutti, P.; Lugano, M.; Della Rocca, G.; Pea, F. Does critical illness change levofloxacin pharmacokinetics? Antimicrob. Agents Chemother. 2016, 60, 1459–1463. [Google Scholar] [CrossRef] [PubMed]
- McAleenan, A.; Ambrose, P.G.; Bhavnani, S.M.; Drusano, G.L.; Hope, W.W.; Mouton, J.W.; Higgins, J.P.T.; MacGowan, A.P. Methodological features of clinical pharmacokinetic–pharmacodynamic studies of antibacterials and antifungals: A systematic review. J. Antimicrob. Chemother. 2020, 75. [Google Scholar] [CrossRef] [PubMed]
- Redgrave, L.S.; Sutton, S.B.; Webber, M.A.; Piddock, L.J. Fluoroquinolone resistance: Mechanisms, impact on bacteria, and role in evolutionary success. Trends Microbiol. 2014, 22, 438–445. [Google Scholar] [CrossRef] [PubMed]
- Hooper, D.C.; Jacoby, G.A. Mechanisms of drug resistance: Quinolone resistance. Ann. N. Y. Acad. Sci. 2015, 1354, 12–31. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Martínez, J.M.; Machuca, J.; Cano, M.E.; Calvo, J.; Martínez-Martínez, L.; Pascual, A. Plasmid-mediated quinolone resistance: Two decades on. Drug Resist. Updates 2016, 29, 13–29. [Google Scholar] [CrossRef]
- Han, J.H.; Nachamkin, I.; Tolomeo, P.; Mao, X.; Bilker, W.B.; Lautenbach, E. Temporal changes in resistance mechanisms in colonizing Escherichia coli isolates with reduced susceptibility to fluoroquinolones. Diagn. Microbiol. Infect. Dis. 2013, 76, 491–496. [Google Scholar] [CrossRef]
- EUCAST—European Committee on Antimicrobial Suscetibility Testing. Breakpoint Tables for Interpretation of MICs and Zone Diameters; EUCAST: Växjö, Sweden, 2020. [Google Scholar]
- Seeger, J.; Michelet, R.; Kloft, C. Quantification of persister formation of Escherichia coli leveraging electronic cell counting and semi-mechanistic pharmacokinetic/pharmacodynamic modelling. J. Antimicrob. Chemother. 2021. [Google Scholar] [CrossRef]
- Busse, D.; Schaeftlein, A.; Solms, A.; Ilia, L.; Michelet, R.; Zeitlinger, M.; Huisinga, W.; Kloft, C. Which Analysis Approach Is Adequate to Leverage Clinical Microdialysis Data? A Quantitative Comparison to Investigate Exposure and Reponse Exemplified by Levofloxacin. Pharm. Res. 2021, 38, 381–395. [Google Scholar] [CrossRef]
- Firsov, A.A.; Vostrov, S.N.; Shevchenko, A.A.; Cornaglia, G. Parameters of bacterial killing and regrowth kinetics and antimicrobial effect examined in terms of area under the concentration-time curve relationships: Action of ciprofloxacin against Escherichia coli in an in vitro dynamic model. Antimicrob. Agents Chemother. 1997, 41, 1281–1287. [Google Scholar] [CrossRef][Green Version]
- Nielsen, E.I.; Viberg, A.; Löwdin, E.; Cars, O.; Karlsson, M.O.; Sandström, M. Semimechanistic pharmacokinetic/pharmacodynamic model for assessment of activity of antibacterial agents from time-kill curve experiments. Antimicrob. Agents Chemother. 2007, 51, 128–136. [Google Scholar] [CrossRef]
- Khan, D.D.; Lagerbaeck, P.; Cao, S.; Lustig, U.; Nielsen, E.I.; Cars, O.; Hughes, D.; Andersson, D.I.; Friberg, L.E. A mechanism-based pharmacokinetic/pharmacodynamic model allows prediction of antibiotic killing from MIC values for WT and mutants. J. Antimicrob. Chemother. 2015, 70, 3051–3060. [Google Scholar] [CrossRef]
- Ungphakorn, W.; Tängdén, T.; Sandegren, L.; Nielsen, E.I. A pharmacokinetic-pharmacodynamic model characterizing the emergence of resistant Escherichia coli subpopulations during ertapenem exposure. J. Antimicrob. Chemother. 2016, 71, 2521–2533. [Google Scholar] [CrossRef]
- Thorsted, A.; Tano, E.; Kaivonen, K.; Sjölin, J.; Friberg, L.E.; Nielsen, E.I. Extension of pharmacokinetic/pharmacodynamic (PK/PD) time-kill studies to include LPS/endotoxin release from E. coli exposed to cefuroxime. Antimicrob. Agents Chemother. 2020, 64, 1–12. [Google Scholar] [CrossRef]
- Jacobs, M.; Grégoire, N.; Couet, W.; Bulitta, J.B. Distinguishing antimicrobial models with different resistance mechanisms via population pharmacodynamic modeling. PLoS Comput. Biol. 2016, 12, e1004782. [Google Scholar] [CrossRef]
- Machuca, J.; Briales, A.; Díaz-de-Alba, P.; Martínez-Martínez, L.; Pascual, Á.; Rodríguez-Martínez, J.M. Effect of the efflux pump QepA2 combined with chromosomally mediated mechanisms on quinolone resistance and bacterial fitness in Escherichia coli. J. Antimicrob. Chemother. 2015, 70, 2524–2527. [Google Scholar] [CrossRef]
- Franck, S.; Michelet, R.; Casilag, F.; Sirard, J.; Wicha, S.G.; Kloft, C. A Model-Based Pharmacokinetic/Pharmacodynamic Analysis of the Combination of Amoxicillin and Monophosphoryl Lipid A Against S. pneumoniae in Mice. Pharmaceutics 2021, 13, 469. [Google Scholar] [CrossRef]
- Zankari, E.; Hasman, H.; Cosentino, S.; Vestergaard, M.; Rasmussen, S.; Lund, O.; Aarestrup, F.M.; Larsen, M.V. Identification of acquired antimicrobial resistance genes. J. Antimicrob. Chemother. 2012, 67, 2640–2644. [Google Scholar] [CrossRef]
- Larsen, M.V.; Cosentino, S.; Rasmussen, S.; Friis, C.; Hasman, H.; Marvig, R.L.; Jelsbak, L.; Sicheritz-Pontén, T.; Ussery, D.W.; Aarestrup, F.M.; et al. Multilocus sequence typing of total-genome-sequenced bacteria. J. Clin. Microbiol. 2012, 50, 1355–1361. [Google Scholar] [CrossRef]
- Löwdin, E.; Odenholt, I.; Bengtsson, S.; Cars, O. Pharmacodynamic effects of sub-MICs of benzylpenicillin against Streptococcus pyogenes in a newly developed in vitro kinetic model. Antimicrob. Agents Chemother. 1996, 40, 2478–2482. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Automat. Contr. 1974, 19, 716–723. [Google Scholar] [CrossRef]
| Sequence Type | Mutations in QRDR | Acquired Fluoroquinolone Resistance | Minimal Inhibitory Concentration (mg/L) | |
|---|---|---|---|---|
| gyrA | parC | |||
| 58 | Ser-83→Leu | WT | - | 8 |
| 88 | Ser-83→Leu | WT | qnrS1 | 2 |
| 167 | Ser-83→Leu Asp-87→Asn | Ser-80→Ile | - | 8 |
| Parameter (unit) | Estimate (RSE, %) | ||
|---|---|---|---|
| Sequence Type 58 | Sequence Type 88 | Sequence Type 167 | |
| cumAUC50 (mg·h·L−1) | 158 (9.45) | 28.6 (7.85) | 49.4 (7.54) |
| Hill | 1.02 (5.49) | 1.25 (5.37) | 0.961 (6.62) |
| cumAUCreg, static (mg·h·L−1) | 3132 (36.5) | 330 (22.9) | 1679 (20.3) |
| cumAUCreg, dynamic (mg·h·L−1) | 248 (34.6) | 373 (34.9) | 473 (39.2) |
| cumAUCreg,static/cumAUCreg,dynamic ratio | 12.6 | 0.885 | 3.55 |
| Proportional residual variability, % CV | 4.00 (11.8) | 4.33 (11.7) | 3.33 (11.3) |
| Sequence Type 58 | Sequence Type 88 | Sequence Type 167 | ||||
|---|---|---|---|---|---|---|
| CLVX = 1-fold MIC | Time (h) | Effect | Time (h) | Effect | Time (h) | Effect |
| Dominance of killing process (Higher impact of Emax term) | ≤1.10 | ≤0.0539 | ≤0.80 | ≤0.358 | ≤2.20 | ≤0.320 |
| Intersection of killing and regrowth trajectories | 13.3 | 0.610 | 8.7 | 0.630 | 10.1 | 0.803 |
| Dominance of regrowth process (Higher impact of inhibition term) | ≥90.0 | ≥0.179 | ≥41.0 | ≥0.252 | ≥31.4 | ≥0.541 |
| CLVX = 2-fold MIC | ||||||
| Dominance of killing process (Higher impact of Emax term) | ≤8.70 | ≤0.560 | ≤5.30 | ≤0.503 | ≤13.1 | ≤0.737 |
| Intersection of killing and regrowth trajectories | 26.2 | 0.863 | 15.3 | 0.866 | 29.9 | 0.892 |
| Dominance of regrowth process (Higher impact of inhibition term) | ≥60.0 | ≥0.697 | ≥29.5 | ≥0.732 | ≥66.0 | ≥0.750 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seeger, J.; Guenther, S.; Schaufler, K.; Heiden, S.E.; Michelet, R.; Kloft, C. Novel Pharmacokinetic/Pharmacodynamic Parameters Quantify the Exposure–Effect Relationship of Levofloxacin against Fluoroquinolone-Resistant Escherichia coli. Antibiotics 2021, 10, 615. https://doi.org/10.3390/antibiotics10060615
Seeger J, Guenther S, Schaufler K, Heiden SE, Michelet R, Kloft C. Novel Pharmacokinetic/Pharmacodynamic Parameters Quantify the Exposure–Effect Relationship of Levofloxacin against Fluoroquinolone-Resistant Escherichia coli. Antibiotics. 2021; 10(6):615. https://doi.org/10.3390/antibiotics10060615
Chicago/Turabian StyleSeeger, Johanna, Sebastian Guenther, Katharina Schaufler, Stefan E. Heiden, Robin Michelet, and Charlotte Kloft. 2021. "Novel Pharmacokinetic/Pharmacodynamic Parameters Quantify the Exposure–Effect Relationship of Levofloxacin against Fluoroquinolone-Resistant Escherichia coli" Antibiotics 10, no. 6: 615. https://doi.org/10.3390/antibiotics10060615
APA StyleSeeger, J., Guenther, S., Schaufler, K., Heiden, S. E., Michelet, R., & Kloft, C. (2021). Novel Pharmacokinetic/Pharmacodynamic Parameters Quantify the Exposure–Effect Relationship of Levofloxacin against Fluoroquinolone-Resistant Escherichia coli. Antibiotics, 10(6), 615. https://doi.org/10.3390/antibiotics10060615







