Enhanced Sensitivity of Binary/Ternary Locally Resonant Porous Phononic Crystal Sensors for Sulfuric Acid Detection: A New Class of Fluidic-Based Biosensors
Abstract
1. Introduction
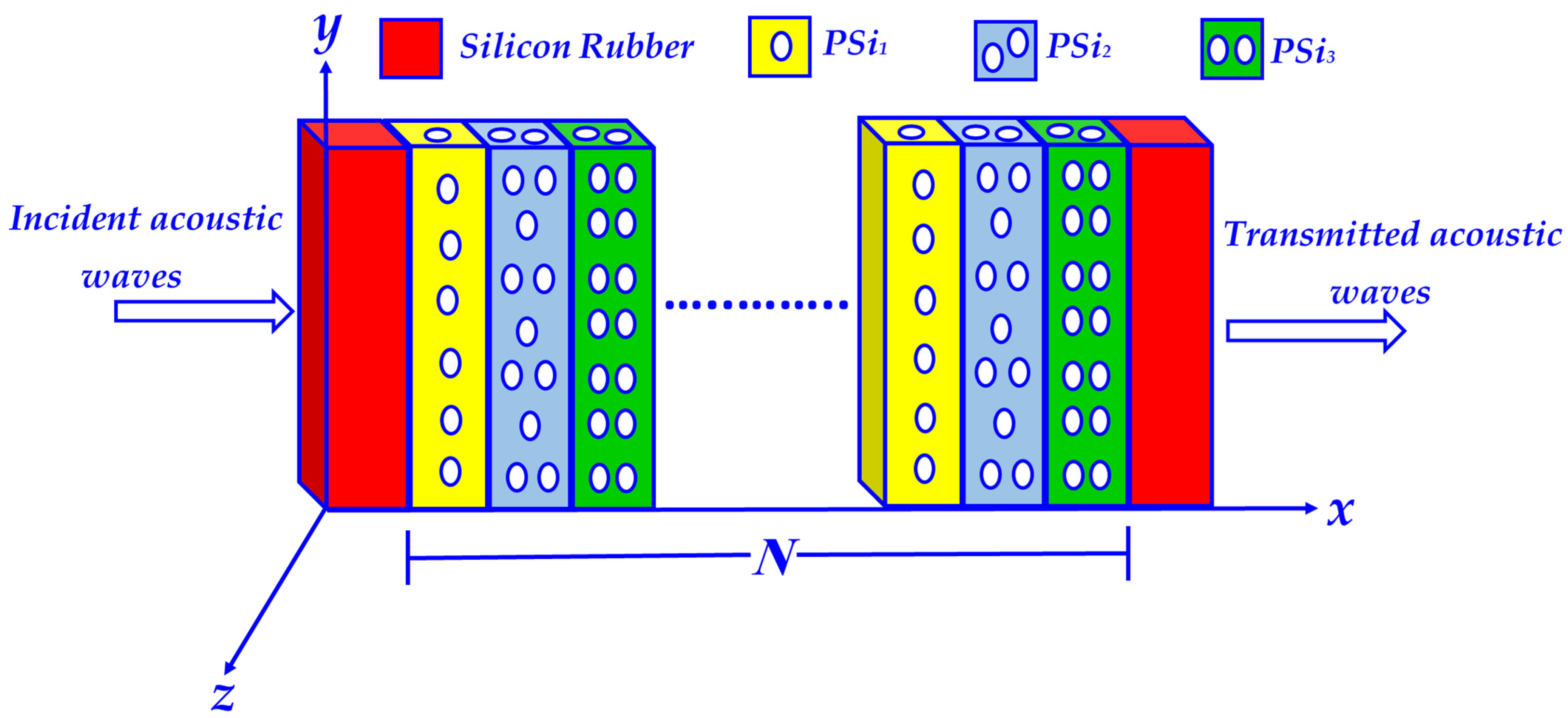
2. Sensor Design and Theoretical Background
2.1. The Candidate Sensing Tool
2.2. Theoretical Methodology
2.3. Porous Silicon Acoustic Velocity and Density
2.4. Acoustic Properties of H2SO4 Aqueous Solution
3. Numerical Verifications and Discussions
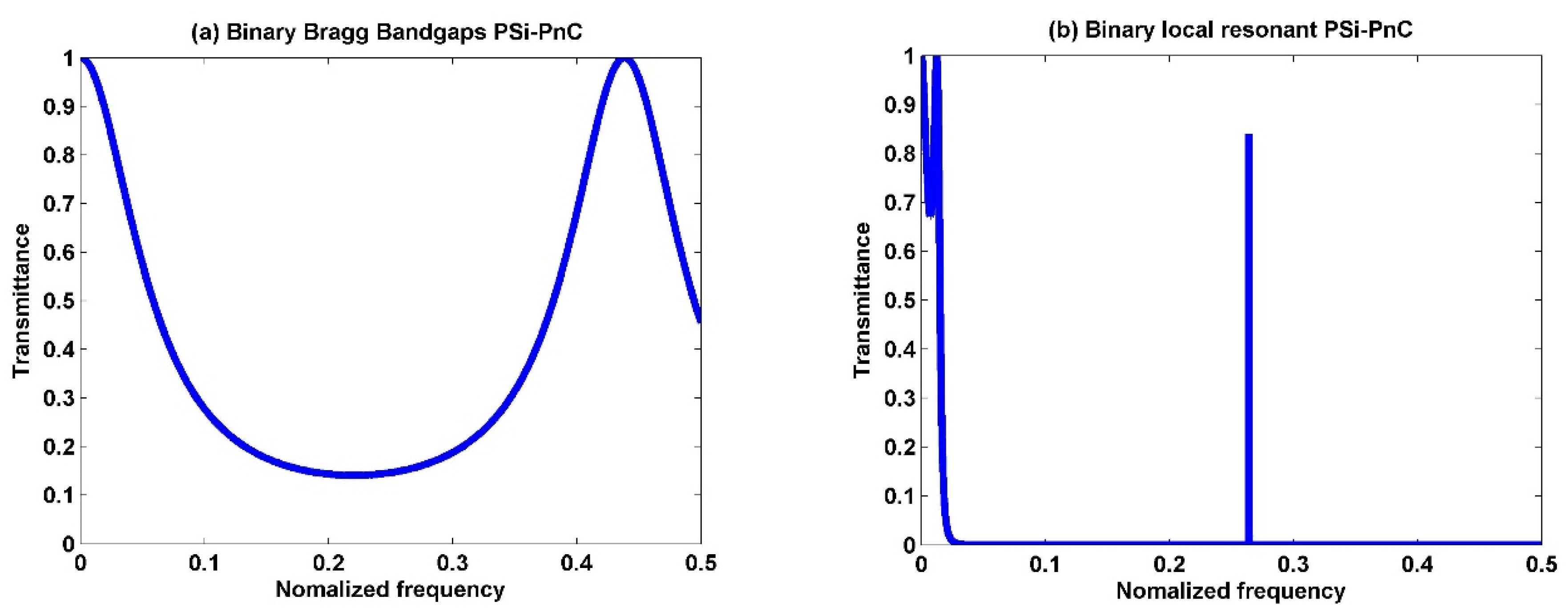
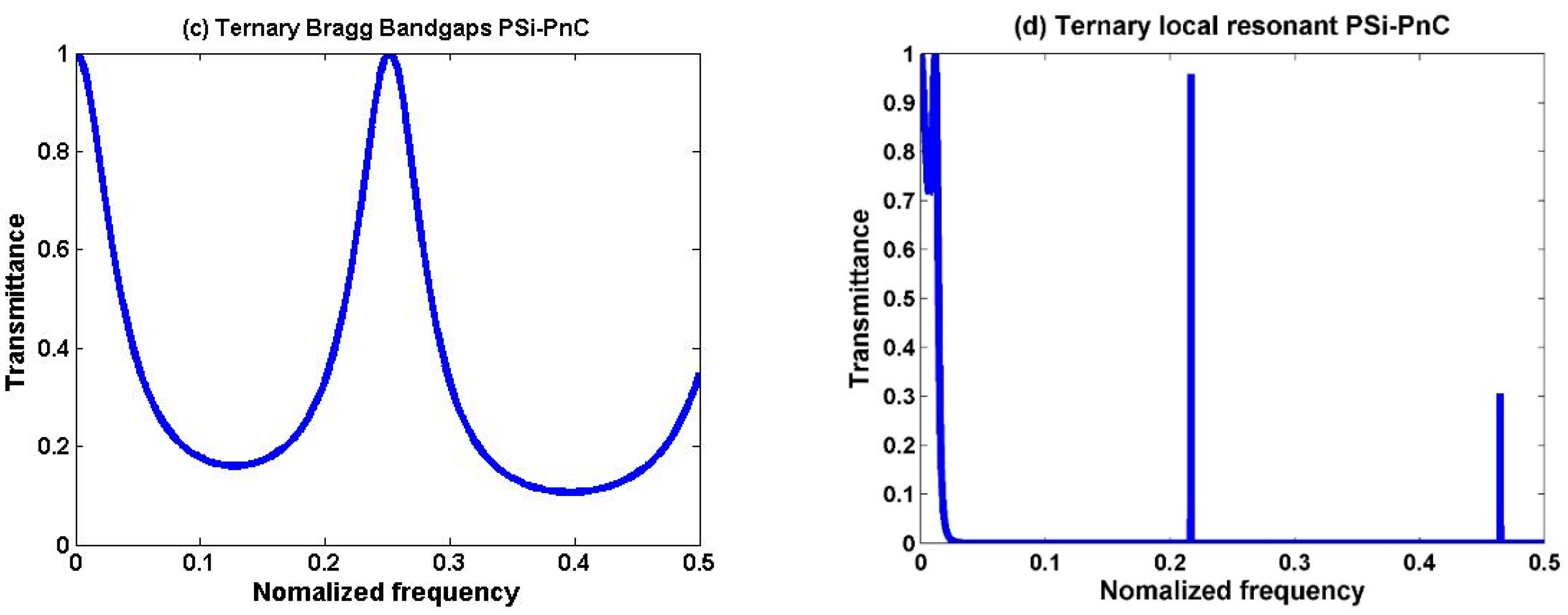
3.1. Transmission Spectra of the Proposed Sensor Design
3.2. Binary Structure
3.3. Ternary Structure
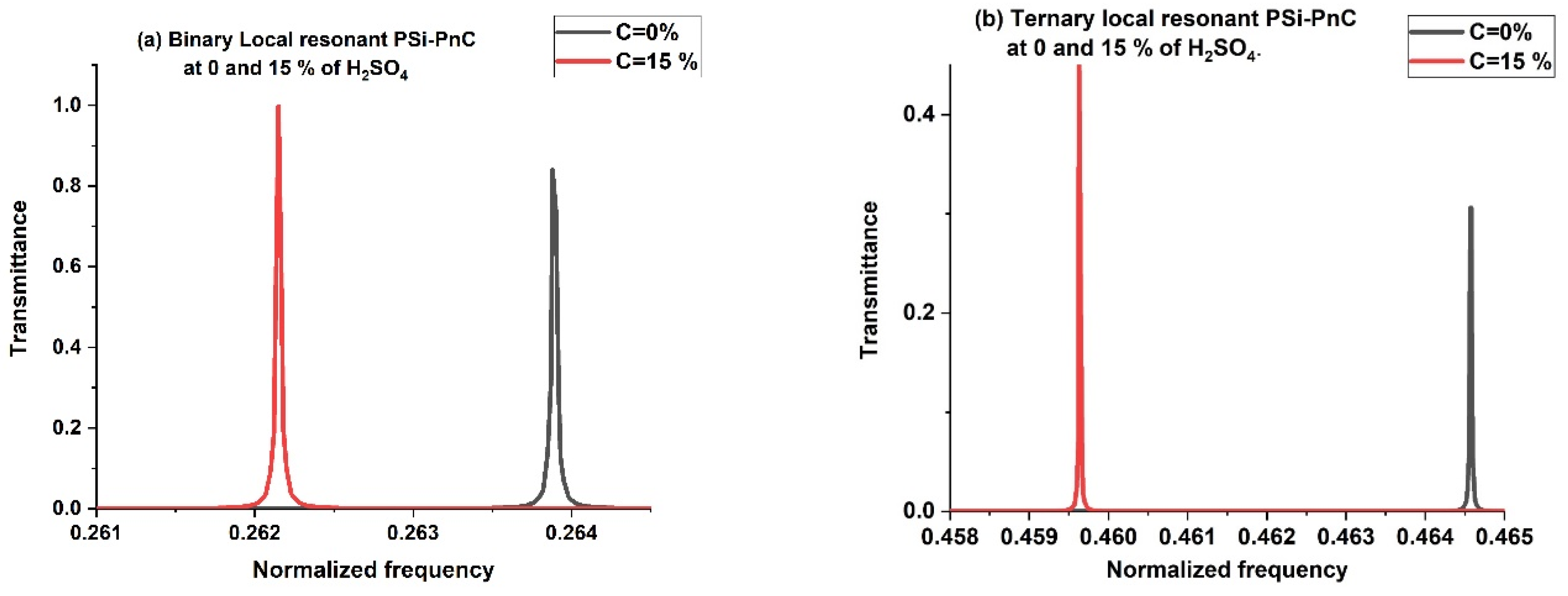
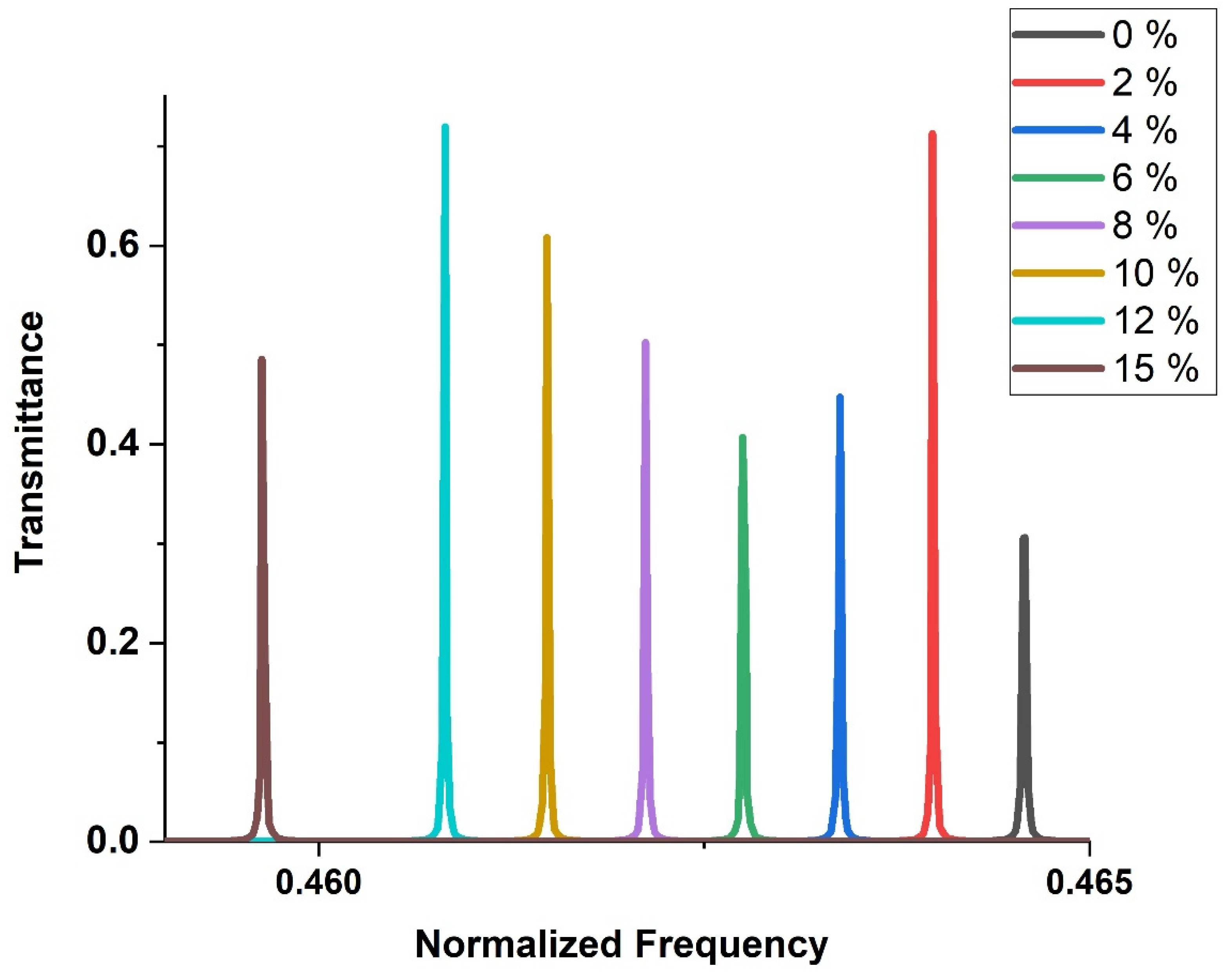
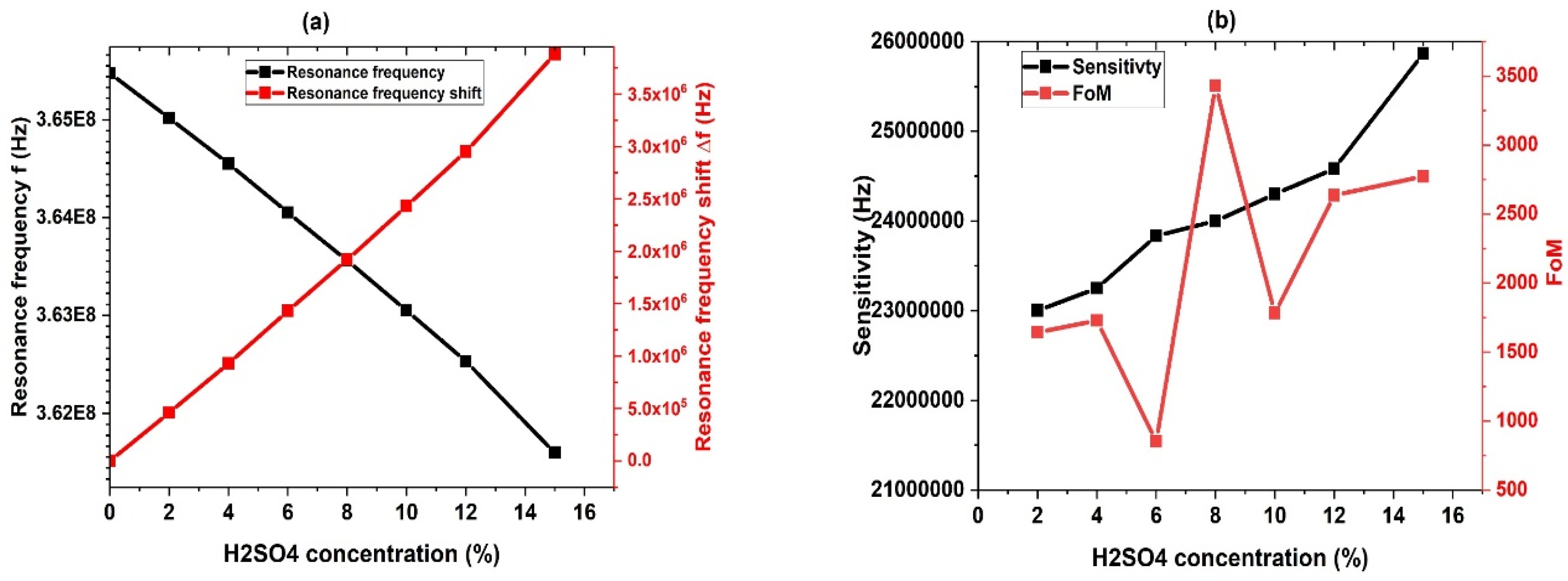
3.4. Effect of H2SO4 Concentration
3.5. Performance Study
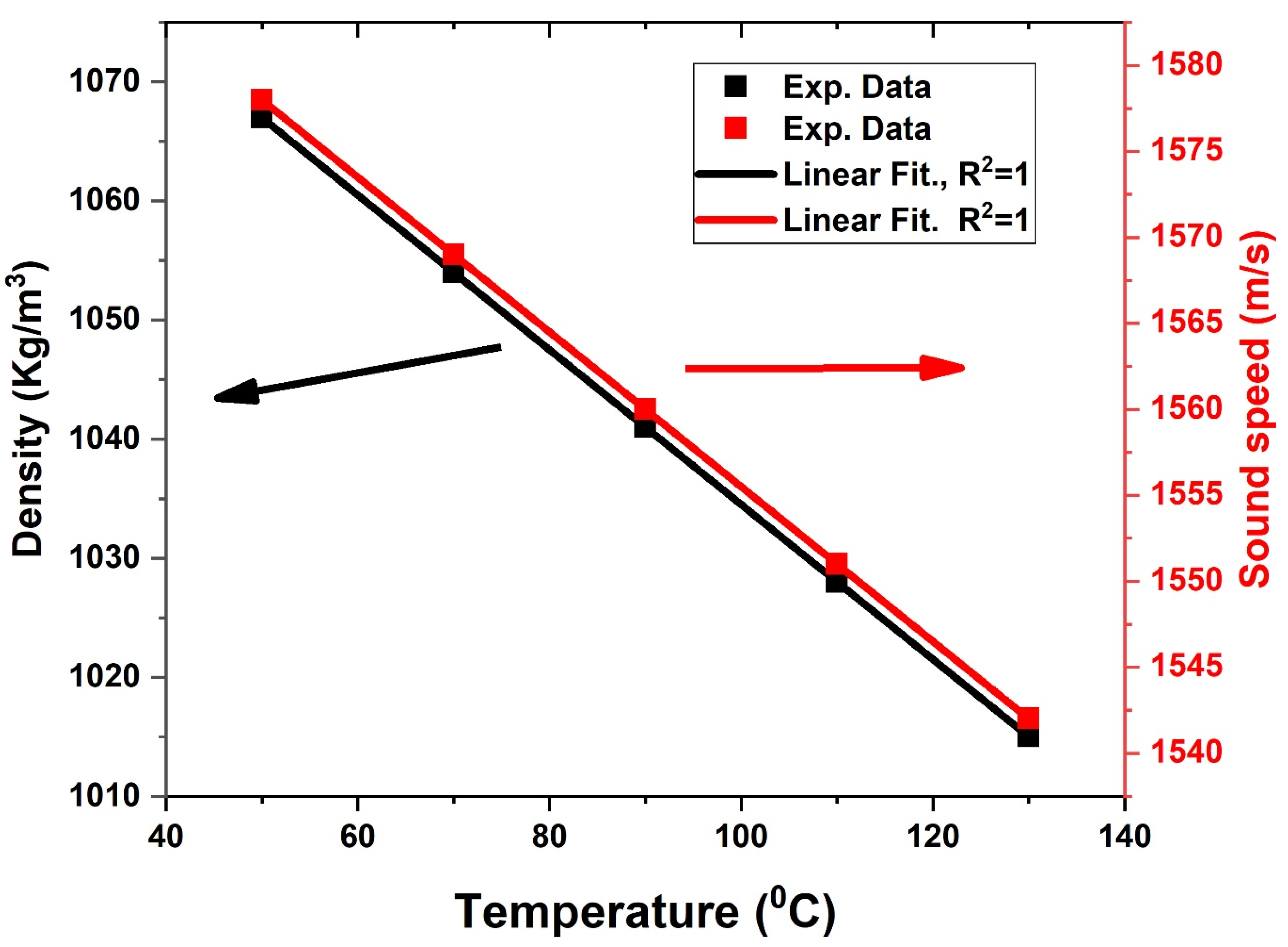
3.6. Effect of Temperature on the Performance of the Phononic Sensor
3.7. Effect of Temperature on Performance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Greenwood, N.N.; Earnshaw, A. Chemistry of the Elements, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 1997. [Google Scholar]
- Fraenkel, D. Structure and ionization of sulfuric acid in water. New J. Chem. 2015, 39, 5124–5136. [Google Scholar] [CrossRef]
- Maidi, A.M.; Kalam, A.; Begum, F. Photonic Crystal Fiber Sensor for Detecting Sulfuric Acid in Different Concentrations. Photonics 2022, 9, 958. [Google Scholar] [CrossRef]
- Zhou, X.; Hu, P.; Ma, C.; Huang, S.; Sun, J. SO3 and sulfuric acid (H2SO4) aerosol detection by UV absorption spectroscopy of liquid H2SO4 solution. Optik 2022, 265, 169522. [Google Scholar] [CrossRef]
- Biermann, U.M.; Luo, B.P.; Peter, T. Absorption spectra and optical constants of binary and ternary solutions of H2SO4, HNO3, and H2O in the Mid Infrared at Atmospheric Temperatures. J. Phys. Chem. A 2000, 104, 783–793. [Google Scholar] [CrossRef]
- Givan, A.; Larsen, L.; Loewenschuss, A.; Nielsen, C. Matrix isolation mid- and far-infrared spectra of sulfuric acid and deuterated sulfuric acid vapors. J. Mol. Struct. 1999, 509, 35–47. [Google Scholar] [CrossRef]
- Karagulian, F.; Clarisse, L.; Clerbaux, C.; Prata, A.J.; Hurtmans, D.; Coheur, P.F. Detection of volcanic SO2, ash, and H2SO4 using the infrared atmospheric sounding interferometer (IASI). J. Geophys. Res. 2010, 115, D00L02. [Google Scholar] [CrossRef]
- Heathfield, A.E.; Newnham, D.A.; Ballard, J.; Grainger, R.G.; Lambert, A. Infrared and visible fourier-transform spectra of sulfuric-acid-water aerosols at 230 and 294 K. Appl. Opt. 1999, 38, 6408–6420. [Google Scholar] [CrossRef]
- Altowyan, A.S.; Shaban, M.; Gamel, A.; Gamal, A.; Ali, M.; Rabia, M. High-Performance pH Sensor Electrodes Based on a Hexagonal Pt Nanoparticle Array-Coated Nanoporous Alumina Membrane. Materials 2022, 15, 6515. [Google Scholar] [CrossRef]
- Leon, M.J.B.M.; Kabir, M.A. Design of a liquid sensing photonic crystal fiber with high sensitivity, bireferingence & low confinement loss. Sens. Bio-Sens. Res. 2020, 28, 100335. [Google Scholar]
- Deng, W.-M.; Chen, Z.-M.; Li, M.-Y.; Guo, C.-H.; Tian, Z.-T.; Sun, K.-X.; Chen, X.-D.; Chen, W.-J.; Dong, J.-W. Ideal nodal rings of one-dimensional photonic crystals in the visible region. Light. Sci. Appl. 2022, 11, 134. [Google Scholar] [CrossRef]
- Vitiello, M.S.; Nobile, M.; Ronzani, A.; Tredicucci, A.; Castellano, F.; Talora, V.; Li, L.; Linfield, E.H.; Davies, A.G. Photonic quasi-crystal terahertz lasers. Nat. Commun. 2014, 5, 5884. [Google Scholar] [CrossRef]
- Rashwan, H.H.; Mostafa, S.I.; El-Khawas, E.H.; El-Naggar, S.A. Tunable filter based on one-dimensional photonic crystal including nanocomposite material. Eur. Phys. J. D 2022, 76, 50. [Google Scholar] [CrossRef]
- Akahane, Y.; Asano, T.; Song, B.-S.; Noda, S. High-Q photonic nanocavity in a two-dimensional photonic crystal. Nature 2003, 425, 944–947. [Google Scholar] [CrossRef]
- Sharifi, M.; Rezaei, B.; Adl, H.P.; Zakerhamidi, M.S. Tunable Fano resonance in coupled topological one-dimensional photonic crystal heterostructure and defective photonic crystal. J. Appl. Phys. 2023, 133, 83102. [Google Scholar] [CrossRef]
- Raja, S.J.; Jose, T.; Charlcedony, R.; Paul, M.S.; Chakravarthi, R. Design of hexagonal chalcogenide photonic crystal fiber with ultra-flattened dispersion in mid-infrared wavelength spectrum. Beni-Suef Univ. J. Basic Appl. Sci. 2022, 11, 103. [Google Scholar] [CrossRef]
- Juneau-Fecteau, A.; Fréchette, L.G. Tamm plasmon-polaritons in a metal coated porous silicon photonic crystal. Opt. Mater. Express 2018, 8, 2774–2781. [Google Scholar] [CrossRef]
- Patel, P.N.; Mishra, V. Modelling and analysis of Porous Silicon Photonic Crystals. In Proceedings of the 1st International Conference on Emerging Technology Trends in Electronics, Communication & Networking, Surat, India, 19–21 December 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Nozaki, K.; Matsuo, S.; Fujii, T.; Takeda, K.; Ono, M.; Shakoor, A.; Kuramochi, E.; Notomi, M. Photonic-crystal nano-photodetector with ultrasmall capacitance for on-chip light-to-voltage conversion without an amplifier. Optica 2016, 3, 483–492. [Google Scholar] [CrossRef]
- Uniyal, A.; Srivastava, G.; Pal, A.; Taya, S.; Muduli, A. Recent Advances in Optical Biosensors for Sensing Applications: A Review. Plasmonics 2023, 18, 735–750. [Google Scholar] [CrossRef]
- Sassi, I.A.; Rhouma, M.B.E.H.; Daher, M.G. Highly sensitive refractive index gas sensor using two-dimensional silicon carbide grating based on surface plasmon resonance. Opt. Quantum Electron. 2023, 55, 402. [Google Scholar] [CrossRef]
- Maldovan, M.; Thomas, E.L. Periodic Materials and Interference Lithography: For Photonics, Phononics and Mechanics, 1st ed.; Wiley-VCH: Hoboken, NJ, USA, 2008. [Google Scholar]
- Zhang, Q.; Lee, D.; Zheng, L.; Ma, X.; Meyer, S.I.; He, L.; Ye, H.; Gong, Z.; Zhen, B.; Lai, K.; et al. Gigahertz topological valley Hall effect in nanoelectromechanical phononic crystals. Nat. Electron. 2022, 5, 157–163. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022–2025. [Google Scholar] [CrossRef]
- Kuang, W.; Hou, Z.; Liu, Y.; Li, H. The bandgaps of cubic phononic crystals with different shapes of scatters. J. Phys. D Appl. Phys. 2006, 39, 2067. [Google Scholar] [CrossRef]
- Allein, F.; Tournat, V.; Gusev, V.E.; Theocharis, G. Tunable magneto-granular phononic crystals. Appl. Phys. Lett. 2016, 108, 161903. [Google Scholar] [CrossRef]
- Pennec, Y.; Djafari-Rouhani, B.; Larabi, H.; Vasseur, J.O.; Hladky-Hennion, A.C. Low-frequency gaps in a phononic crystal constituted of cylindrical dots deposited on a thin homogeneous plate. Phys. Rev. B 2008, 78, 104105. [Google Scholar] [CrossRef]
- Singh, M.R.; Guo, J.; Gumbs, G. Phonon transport in nanocomposties. Phys. Stat. Sol. B 2017, 254, 1700142. [Google Scholar] [CrossRef]
- Gao, F.; Bermak, A.; Benchabane, S.; Robert, L.; Khelif, A. Acoustic radiation-free surface phononic crystal resonator for in-liquid low-noise gravimetric detection. Microsyst. Nanoeng. 2021, 7, 8. [Google Scholar] [CrossRef]
- Biçer, A. Acoustic Add-Drop filter involving a ring resonator based on a One-Dimensional surface phononic crystal. Ultrasonics 2021, 117, 106551. [Google Scholar] [CrossRef] [PubMed]
- Bergamini, A.; Miniaci, M.; Delpero, T.; Tallarico, D.; Van Damme, B.; Hannema, G.; Leibacher, I.; Zemp, A. Tacticity in chiral phononic crystals. Nat. Commun. 2019, 10, 4525. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, B.; Zhang, X.; Wu, Q.; Wang, X. Zone folding induced tunable topological interface states in one-dimensional phononic crystal plates. Phys. Lett. A 2019, 383, 2797–2801. [Google Scholar] [CrossRef]
- Babaki, J.; Nazari, F. Heterostructure based demultiplexer using solid–solid phononic crystal ring resonators. J. Phys. D Appl. Phys. 2020, 53, 375301. [Google Scholar] [CrossRef]
- Babaki, J.; Nazari, F. Solid–liquid modulator via phononic crystal-based Mach–Zehnder interferometer. Eur. Phys. J. Plus 2022, 137, 172. [Google Scholar] [CrossRef]
- Fang, T.-Y.; Sun, X.-W.; Wen, X.-D.; Li, Y.-X.; Liu, X.-X.; Song, T.; Song, Y.-Z.; Liu, Z.-J. High-performance phononic crystal sensing structure for acetone solution concentration sensing. Sci. Rep. 2023, 13, 7057. [Google Scholar] [CrossRef] [PubMed]
- Mehaney, A.; Gharibi, H.; Bahrami, A. Phononic Eco-Sensor for Detection of Heavy Metals Pollutions in Water with Spectrum Analyzer. IEEE Sens. J. 2020, 21, 6733–6740. [Google Scholar] [CrossRef]
- Rostami-Dogolsara, B.; Moravvej-Farshi, M.K.; Nazari, F. Designing phononic crystal based tunable four-channel acoustic demultiplexer. J. Mol. Liq. 2019, 281, 100–107. [Google Scholar] [CrossRef]
- Lucklum, F. Phononic-fluidic cavity sensors for high-resolution measurement of concentration and speed of sound in liquid solutions and mixtures. Meas. Sci. Technol. 2021, 32, 85108. [Google Scholar] [CrossRef]
- Villa-Arango, S.; Betancur, D.; Torres, R.; Kyriacou, P. Use of Transient Time Response as a Measure to Characterize Phononic Crystal Sensors. Sensors 2018, 18, 3618. [Google Scholar] [CrossRef] [PubMed]
- Taha, T.A.; Elsayed, H.A.; Mehaney, A. One-dimensional symmetric phononic crystals sensor: Towards salinity detection and water treatment. Opt. Quantum Electron. 2022, 54, 313. [Google Scholar] [CrossRef]
- Banerjee, A. Enhanced refractometric optical sensing by using one-dimensional ternary photonic crystals. Prog. Electromagn. Res. 2009, 89, 11–22. [Google Scholar] [CrossRef]
- Ahmed, A.M.; Mehaney, A. Ultra-high sensitive 1D porous silicon photonic crystal sensor based on the coupling of Tamm/Fano resonances in the mid-infrared region. Sci. Rep. 2019, 9, 6973. [Google Scholar] [CrossRef]
- Alrowaili, Z.; Aouassa, M.; Mahmoud, M.; El-Nasser, K.S.; Elsayed, H.A.; Taha, T.; Ahmed, A.M.; Hajjiah, A.; Mehaney, A. Locally resonant porous phononic crystal sensor for heavy metals detection: A new approach of highly sensitive liquid sensors. J. Mol. Liq. 2023, 369, 120964. [Google Scholar] [CrossRef]
- Aliev, G.N.; Goller, B. Quasi-periodic Fibonacci and periodic one-dimensional hypersonic phononic crystals of porous silicon: Experiment and simulation. J. Appl. Phys. 2014, 116, 94903. [Google Scholar] [CrossRef]
- Thomas, L.; Aliev, G.N.; Snow, P.A. Hypersonic rugate filters based on porous silicon. Appl. Phys. Lett. 2010, 97, 173503. [Google Scholar] [CrossRef]
- Kharat, S. Density, viscosity, conductivity, ultrasonic velocity, and refractive index studies of aqueous solutions of citric acid at different temperatures. Int. J. Appl. Chem. 2008, 4, 223–235. [Google Scholar]
- Maciá, E. Exploiting aperiodic designs in nanophotonic devices. Rep. Prog. Phys. 2012, 75, 36502. [Google Scholar] [CrossRef]
- Yin, J.; Ruzzene, M.; Wen, J.; Yu, D.; Cai, L.; Yue, L. Band transition and topological interface modes in 1D elastic phononic crystals. Sci. Rep. 2018, 8, 6806. [Google Scholar] [CrossRef]
- King, P.D.C.; Cox, T.J. Acoustic band gaps in periodically and quasiperiodically modulated waveguides. J. Appl. Phys. 2007, 102, 14902. [Google Scholar] [CrossRef]
- Amoudache, S.; Moiseyenko, R.; Pennec, Y.; Rouhani, B.D.; Khater, A.; Lucklum, R.; Tigrine, R. Optical and acoustic sensing using Fano-like resonances in dual phononic and photonic crystal plate. J. Appl. Phys. 2016, 119, 114502. [Google Scholar] [CrossRef]
- Hussein, M.I.; Hulbert, G.M.; Scott, R.A. Dispersive elastodynamics of 1D banded materials and structures: Analysis. J. Sound Vib. 2006, 289, 779–806. [Google Scholar] [CrossRef]
- Li, S.; Gao, X.L. Phase field approach and micromechanics in ferroelectric crystals. In Handbook of Micromechanics Nanomechanics; Routledge: Abingdon, UK, 2013; pp. 73–140. [Google Scholar]
- Gomis-Bresco, J.; Navarro-Urrios, D.; Oudich, M.; El-Jallal, S.; Griol, A.; Puerto, D.; Chavez, E.; Pennec, Y.; Djafari-Rouhani, B.; Alzina, F.; et al. A one-dimensional optomechanical crystal with a complete phononic band gap. Nat. Commun. 2014, 5, 4452. [Google Scholar] [CrossRef]
- Sellami, K.; Ketata, H.; Ben Ghozlen, M.H. Locally resonant phononic crystals band-gap analysis on a two dimensional phononic crystal with a square and a triangular lattice. Opt. Quantum Electron. 2019, 51, 311. [Google Scholar] [CrossRef]
- Snow, P. Porous Silicon Phononic Crystals. In Handbook of Porous Silicon; Canham, L., Ed.; Springer: Cham, Switzerland, 2014. [Google Scholar] [CrossRef]
- Wang, G.; Yu, D.; Wen, J.; Liu, Y.; Wen, X. One-dimensional phononic crystals with locally resonant structures. Phys. Lett. A 2004, 327, 512–521. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally Resonant Sonic Materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef]
- Zhou, X.; Xu, Y.; Liu, Y.; Lv, L.; Peng, F.; Wang, L. Extending and lowering band gaps by multilayered locally resonant phononic crystals. Appl. Acoust. 2018, 133, 97–106. [Google Scholar] [CrossRef]
- Lu, M.-H.; Feng, L.; Chen, Y.-F. Phononic crystals and acoustic metamaterials. Mater. Today 2009, 12, 34–42. [Google Scholar] [CrossRef]
- Ma, J. Phonon Engineering of Micro- and Nanophononic Crystals and Acoustic Metamaterials: A Review. Small Sci. 2023, 3, 202200052. [Google Scholar] [CrossRef]
- Vasileiadis, T.; Varghese, J.; Babacic, V.; Gomis-Bresco, J.; Urrios, D.N.; Graczykowski, B. Progress and perspectives on phononic crystals. J. Appl. Phys. 2021, 129, 160901. [Google Scholar] [CrossRef]
- Paulauskas, A.; Tumenas, S.; Selskis, A.; Tolenis, T.; Valavicius, A.; Balevicius, Z. Hybrid Tamm-surface plasmon polaritons mode for detection of mercury adsorption on 1D photonic crystal/gold nanostructures by total internal reflection ellipsometry. Opt. Express 2018, 26, 30400–30408. [Google Scholar] [CrossRef]
- Mohammed, N.A.; Hamed, M.M.; Khalaf, A.A.; Alsayyari, A.; El-Rabaie, S. High-sensitivity ultra-quality factor and remarkable compact blood components biomedical sensor based on nanocavity coupled photonic crystal. Results Phys. 2019, 14, 102478. [Google Scholar] [CrossRef]
- Lu, X.; Ge, H.; Jiang, Y.; Zhang, Y. A Dual-Band High-Sensitivity THz Metamaterial Sensor Based on Split Metal Stacking Ring. Biosensors 2022, 12, 471. [Google Scholar] [CrossRef]
- Taya, S.A.; Alhamss, D.N.; Colak, I.; Patel, S.K. Sensitivity enhancement of an optical sensor based on a binary photonic crystal for the detection of Escherichia coli by controlling the central wavelength and the angle of incidence. Opt. Quantum Electron. 2022, 54, 127. [Google Scholar] [CrossRef]
- Ha, T.D. A wide band gap phononic crystal strip for quality factor improvement in a length extensional mode MEMS resonator. Arch. Appl. Mech. 2022, 92, 1493–1505. [Google Scholar] [CrossRef]
- Inomata, N.; Tonsho, Y.; Ono, T. Quality factor control of mechanical resonators using variable phononic bandgap on periodic microstructures. Sci. Rep. 2022, 12, 392. [Google Scholar] [CrossRef]
- Rumble, J.R. (Ed.) Section 14: Geophysics, Astronomy and Acoustics; CRC Press/Taylor & Francis: Boca Raton, FL, USA, 2022; Available online: https://www.routledge.com/CRC-Handbook-of-Chemistry-and-Physics/Rumble/p/book/9781032121710 (accessed on 17 May 2023).
- Kozhevnikov, V.F.; Viner, J.M.; Taylor, P.C. Power law in properties of sulfur near the polymerization transition. Phys. Rev. B 2001, 64, 214109. [Google Scholar] [CrossRef]
- Application Note: Measurement of Sulfuric Acid Concentration with the Rhosonics Model 8100 Using Ultrasound. 2002. Available online: http://www.southeastern-automation.com/PDF/Procon/2004_Ultrasonic_CD/7.04.pdf (accessed on 29 May 2023).
- Lucklum, R.; Mukhin, N.; Rouhani, B.D.; Pennec, Y. Phononic Crystal Sensors: A New Class of Resonant Sensors—Chances and Challenges for the Determination of Liquid Properties. Front. Mech. Eng. 2021, 7, 705194. [Google Scholar] [CrossRef]
- Bicer, A.; Durmuslar, A.S.; Korozlu, N.; Cicek, A. An Acoustic Add-Drop Filter in a Phononic Crystal for High-Sensitivity Detection of Methanol in Ethanol in the Liquid Phase. IEEE Sens. J. 2022, 22, 3185926. [Google Scholar] [CrossRef]
- Ameen, A.A.; Elsayed, H.A.; Mahmoud, M.A.; Aly, A.H. Optimizing photonic and phononic crystal parameters for sensing organic compounds. Appl. Nanosci. 2021, 11, 2703–2716. [Google Scholar] [CrossRef]
- Mukhin, N.V.; Oseev, A.; Kutia, M.M.; Borodacheva, E.S.; Korolev, P.G. Determination of Ethanol Content in Fuels with Phononic Crystal Sensor. J. Russ. Univ. Radioelectron. 2019, 22, 107–115. [Google Scholar] [CrossRef]
- Mukhin, N.; Kutia, M.; Oseev, A.; Steinmann, U.; Palis, S.; Lucklum, R. Narrow Band Solid-Liquid Composite Arrangements: Alternative Solutions for Phononic Crystal-Based Liquid Sensors. Sensors 2019, 19, 3743. [Google Scholar] [CrossRef] [PubMed]
- Zaremanesh, M.; Carpentier, L.; Gharibi, H.; Bahrami, A.; Mehaney, A.; Gueddida, A.; Lucklum, R.; Djafari-Rouhani, B.; Pennec, Y. Temperature biosensor based on triangular lattice phononic crystals. APL Mater. 2021, 9, 061114. [Google Scholar] [CrossRef]
- Lucklum, R.; Zubtsov, M.; Oseev, A.; Schmidt, M.-P.; Hirsch, S.; Hagemann, F. Ultrasonic Sensors. In Proceedings of the SENSOR 2013, AMA Conferences, Nurnberg, Germany, 14–16 May 2013. [Google Scholar] [CrossRef]
- Khateib, F.; Mehaney, A.; Aly, A.H. Glycine sensor based on 1D defective phononic crystal structure. Opt. Quantum Electron. 2020, 52, 489. [Google Scholar] [CrossRef]
- Chen, W.-H.; Uribe, M.C.; Kwon, E.E.; Lin, K.-Y.A.; Park, Y.-K.; Ding, L.; Saw, L.H. A comprehensive review of thermoelectric generation optimization by statistical approach: Taguchi method, analysis of variance (ANOVA), and response surface methodology (RSM). Renew. Sustain. Energy Rev. 2022, 169, 112917. [Google Scholar] [CrossRef]
- Hassani, S.; Dackermann, U. A Systematic Review of Optimization Algorithms for Structural Health Monitoring and Optimal Sensor Placement. Sensors 2023, 23, 3293. [Google Scholar] [CrossRef] [PubMed]
- Arano-Martinez, J.A.; Martínez-González, C.L.; Salazar, M.I.; Torres-Torres, C. A Framework for Biosensors Assisted by Multiphoton Effects and Machine Learning. Biosensors 2022, 12, 710. [Google Scholar] [CrossRef] [PubMed]




| Material | Density (kg/m3) | Acoustic Sound Speed (m/s) | |
|---|---|---|---|
| PSi1 (P = 20%) | 2063.6 | 7741.1 [45,46] | 6 |
| PSi2 (P = 40%) | 1797.4 | 7088.3 [45,46] | 3 |
| PSi3 (P = 60%) | 1530.9 | 6210.1 [45,46] | 1.5 |
| Silicon Rubber | 1.30 | 25 [46] | 0.01–0.20 |
| Water | 1001 | 1507 [47] | — |
| H2SO4 salt | 1830 | 1253 [47] | — |
| Structure | Liquid/Gas | Sensitivity | Ref |
|---|---|---|---|
| 2D-PnC with ring resonator cells | Methanol | 12.54 Hz/% | [72] |
| Multilayer periodic structure 1with a defect layer | Organic compounds | 0.1614 107 MHz/(ms−1) | [73] |
| Stainless steel plate with cylindrical holes and a resonant cavity | Ethanol | 0.91 103 Hz/(ms−1) | [74] |
| 2D periodic arrangement of cylindrical holes | Propanol | 0.4 103 Hz/(m s−1) | [75] |
| Triangular lattice PnC | Temperature | 4.4 103 Hz/K | [76] |
| 2D-PnC crystal slab with defect | Propanol | 0.39 107 Hz/m s−1 | [77] |
| 1D-PnCs with defect layer | Glycine | 969.9 103 Hz | [78] |
| Ternary locally resonant porous silicon 1D-PnC | Sulfuric acid | 2.5867 107 Hz | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aliqab, K.; Elsayed, H.A.; Alsharari, M.; Armghan, A.; Ahmed, A.M.; Mehaney, A. Enhanced Sensitivity of Binary/Ternary Locally Resonant Porous Phononic Crystal Sensors for Sulfuric Acid Detection: A New Class of Fluidic-Based Biosensors. Biosensors 2023, 13, 683. https://doi.org/10.3390/bios13070683
Aliqab K, Elsayed HA, Alsharari M, Armghan A, Ahmed AM, Mehaney A. Enhanced Sensitivity of Binary/Ternary Locally Resonant Porous Phononic Crystal Sensors for Sulfuric Acid Detection: A New Class of Fluidic-Based Biosensors. Biosensors. 2023; 13(7):683. https://doi.org/10.3390/bios13070683
Chicago/Turabian StyleAliqab, Khaled, Hussein A. Elsayed, Meshari Alsharari, Ammar Armghan, Ashour M. Ahmed, and Ahmed Mehaney. 2023. "Enhanced Sensitivity of Binary/Ternary Locally Resonant Porous Phononic Crystal Sensors for Sulfuric Acid Detection: A New Class of Fluidic-Based Biosensors" Biosensors 13, no. 7: 683. https://doi.org/10.3390/bios13070683
APA StyleAliqab, K., Elsayed, H. A., Alsharari, M., Armghan, A., Ahmed, A. M., & Mehaney, A. (2023). Enhanced Sensitivity of Binary/Ternary Locally Resonant Porous Phononic Crystal Sensors for Sulfuric Acid Detection: A New Class of Fluidic-Based Biosensors. Biosensors, 13(7), 683. https://doi.org/10.3390/bios13070683






