Biomechanical Sensing Using Gas Bubbles Oscillations in Liquids and Adjacent Technologies: Theory and Practical Applications
Abstract
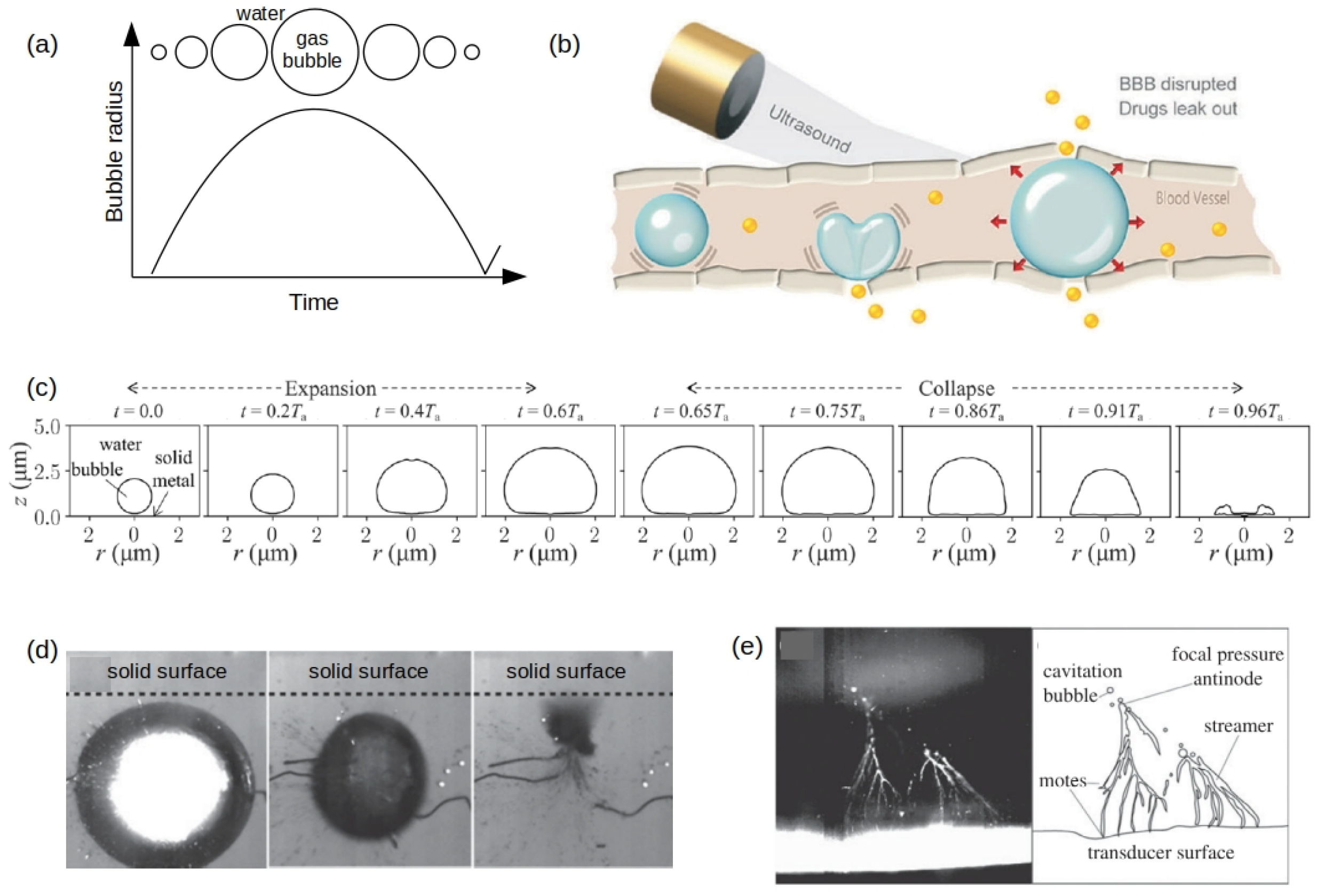
:1. Introduction and Motivation
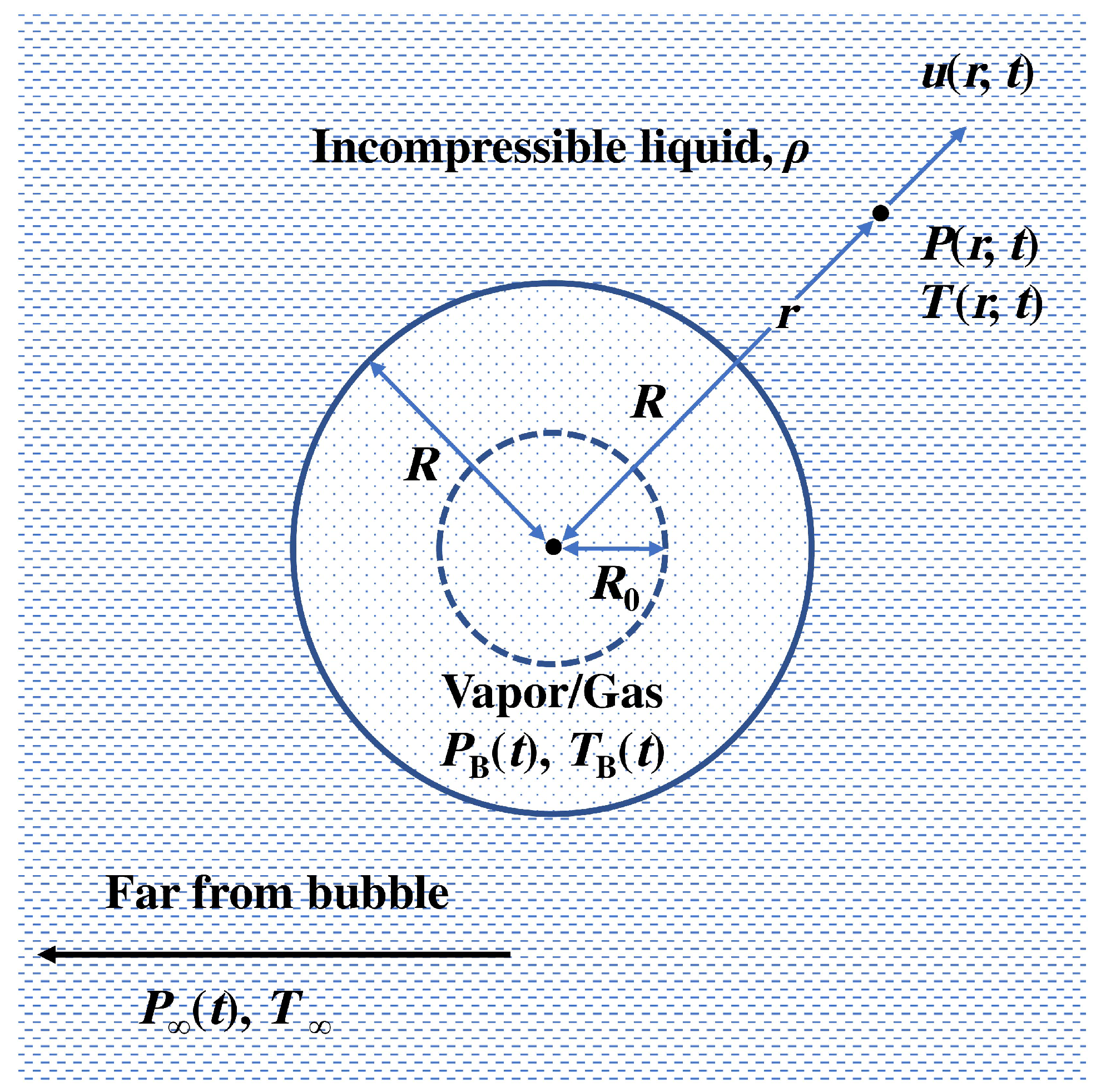
2. Physics of Acoustically Driven Bubble Oscillations
2.1. Acoustically Driven Oscillations of a Single Bubble in Unbounded Liquid
Extensions of Rayleigh-Plesset Equation
2.2. Single Bubble Oscillating near a Boundary
2.2.1. Bubble Oscillating near a Solid Wall
2.2.2. Bubble Oscillating near an Elastic Wall
2.3. Interaction of Oscillating Bubbles in a Bubble Cluster
3. Determining Mechanical Properties of Cells, Bacteria and Biological Yissues
3.1. Brillouin Light Scattering Spectroscopy
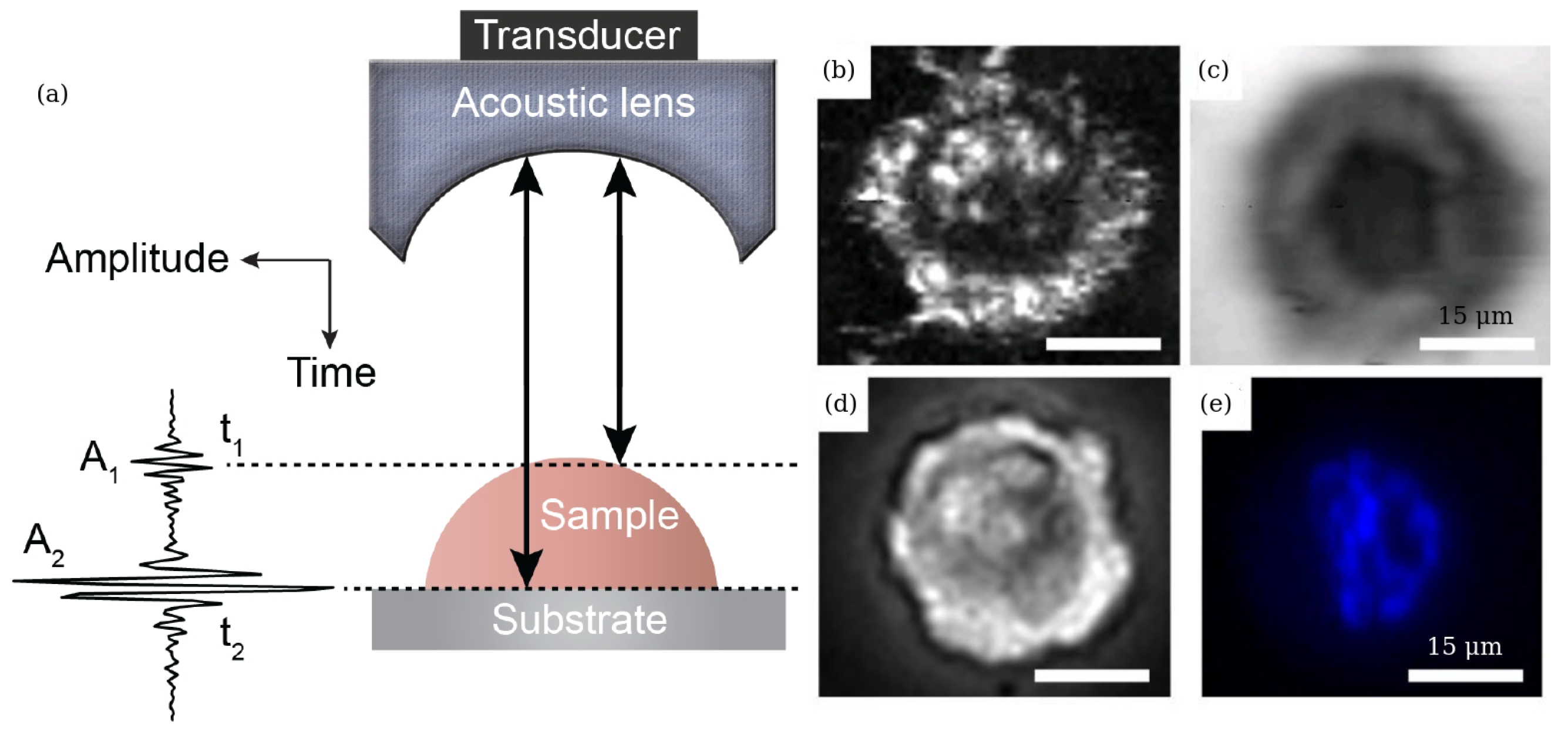
3.2. Scanning Acoustic Microscopy
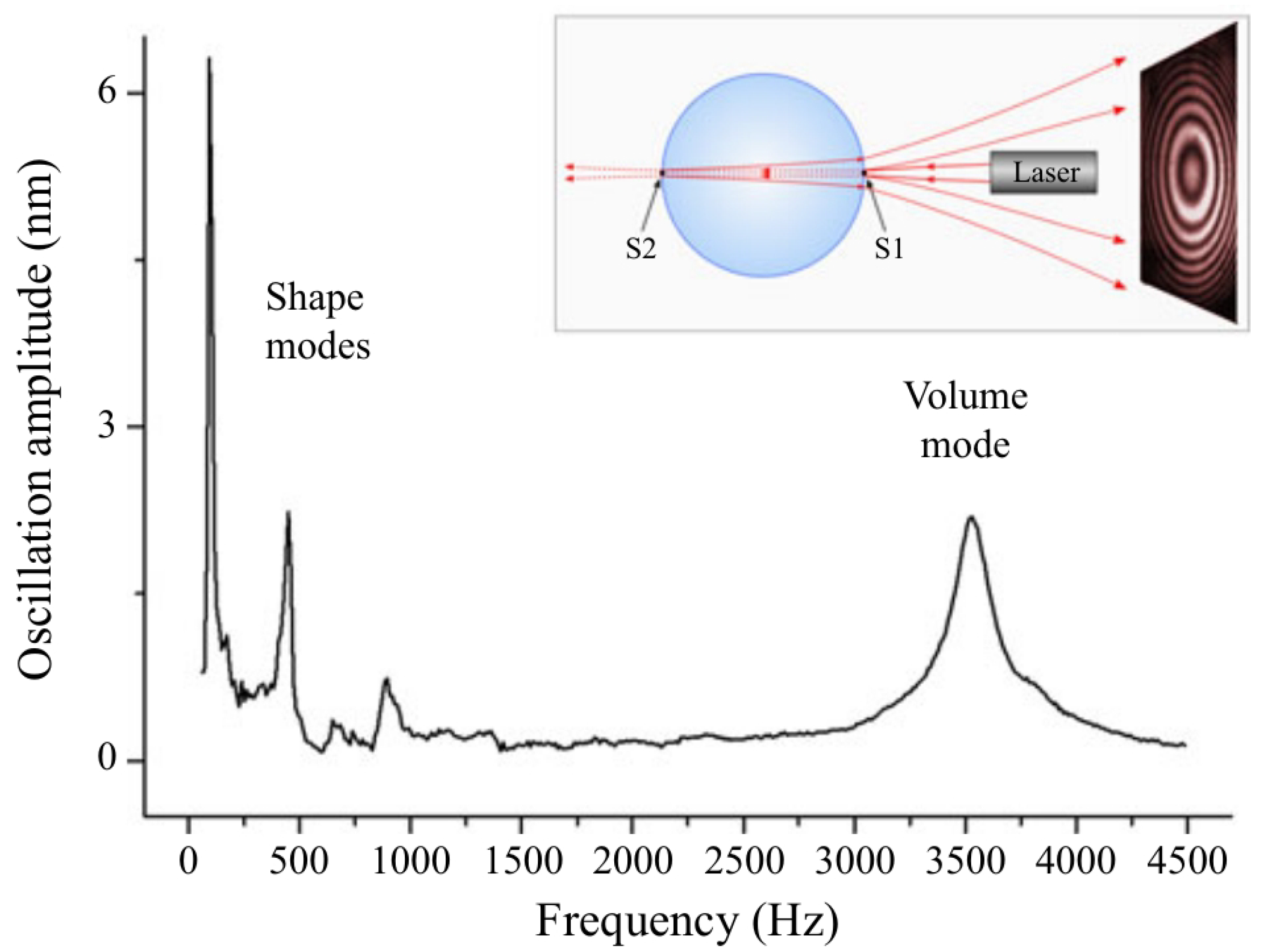
3.3. Deformation of Cells and Bacteria
3.3.1. Mechanical Resonance Properties of Cells And Bacteria
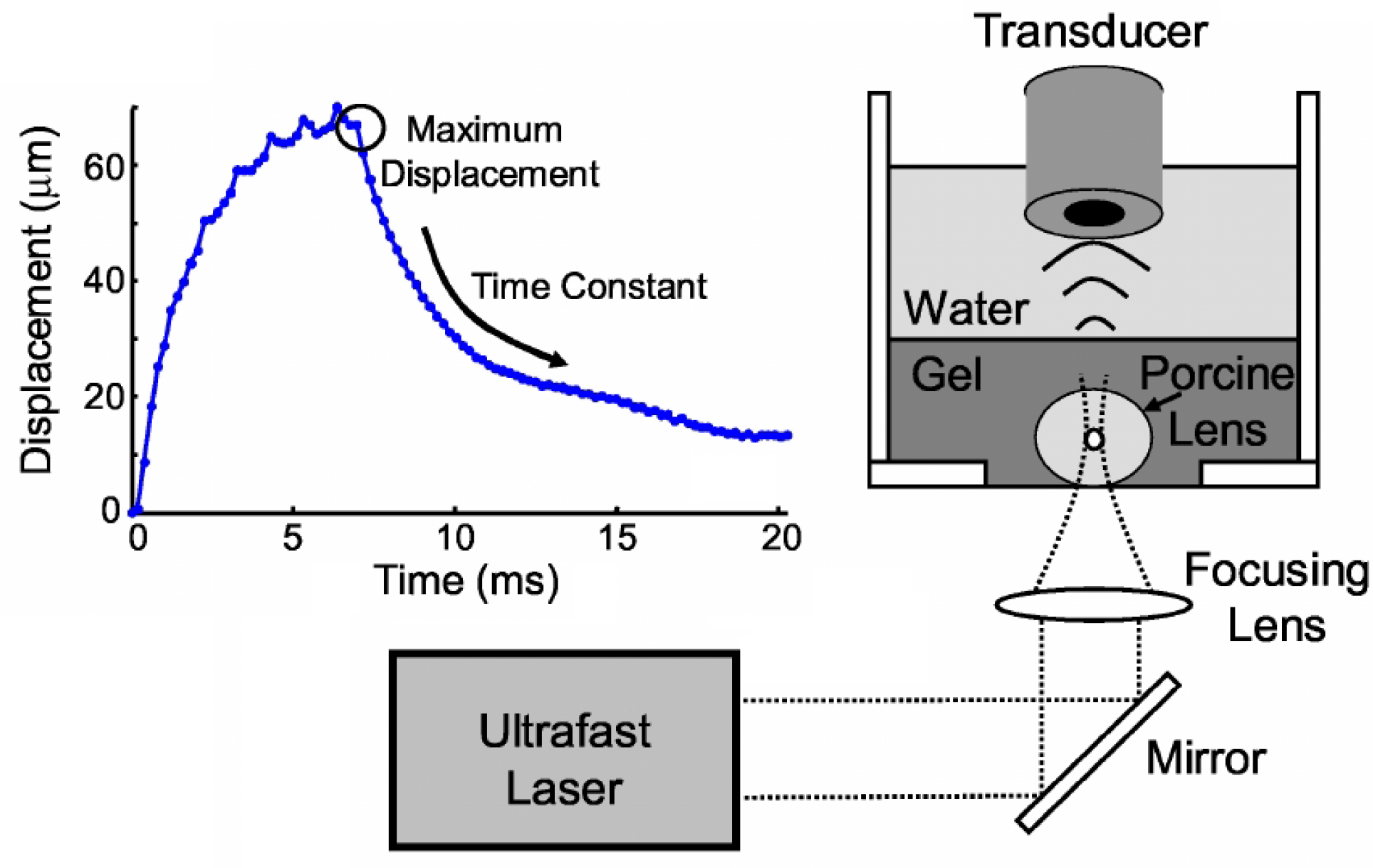
3.3.2. Deformation of Cells and Bacteria by Bubbles
4. Acoustic Frequency Combs
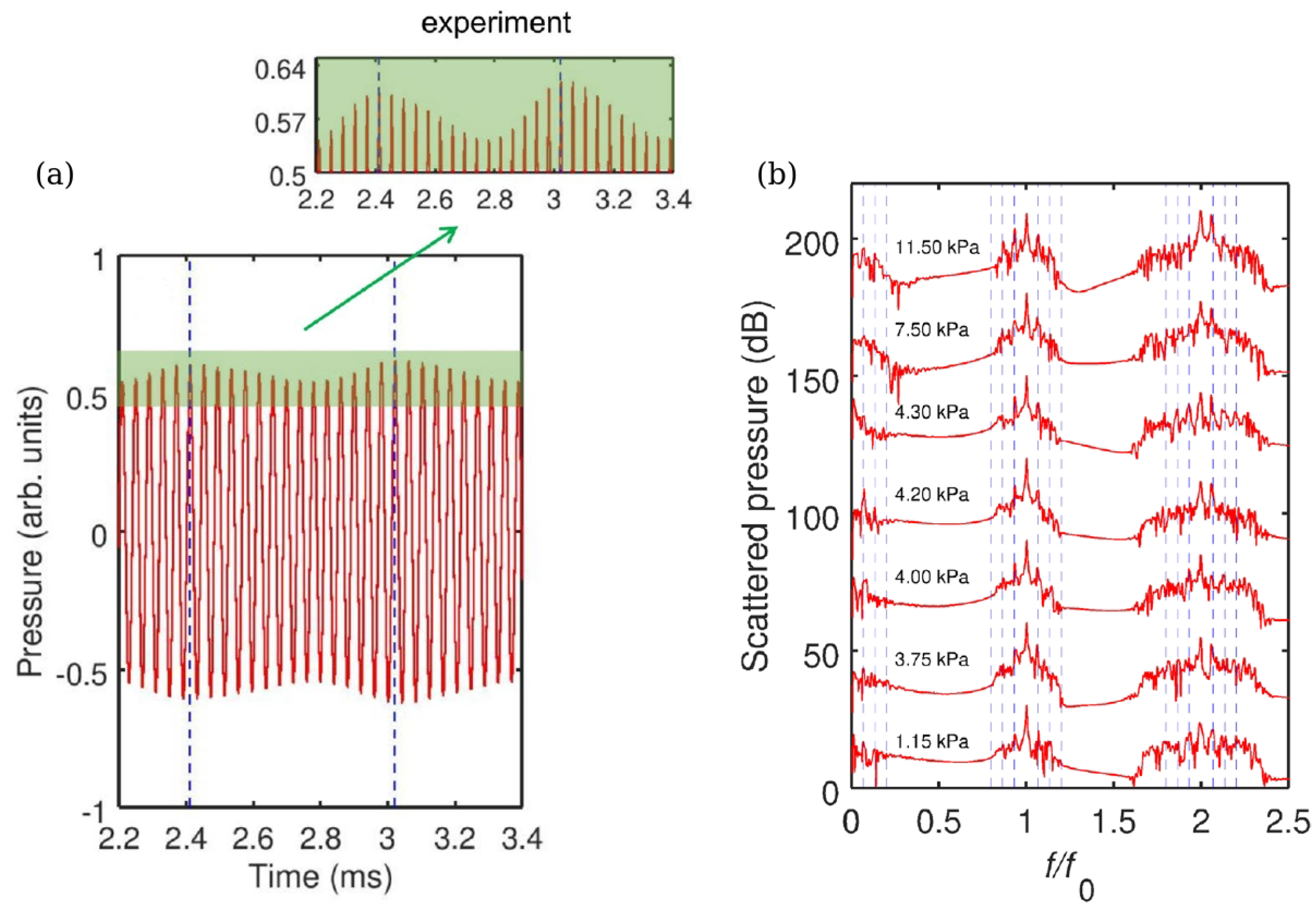
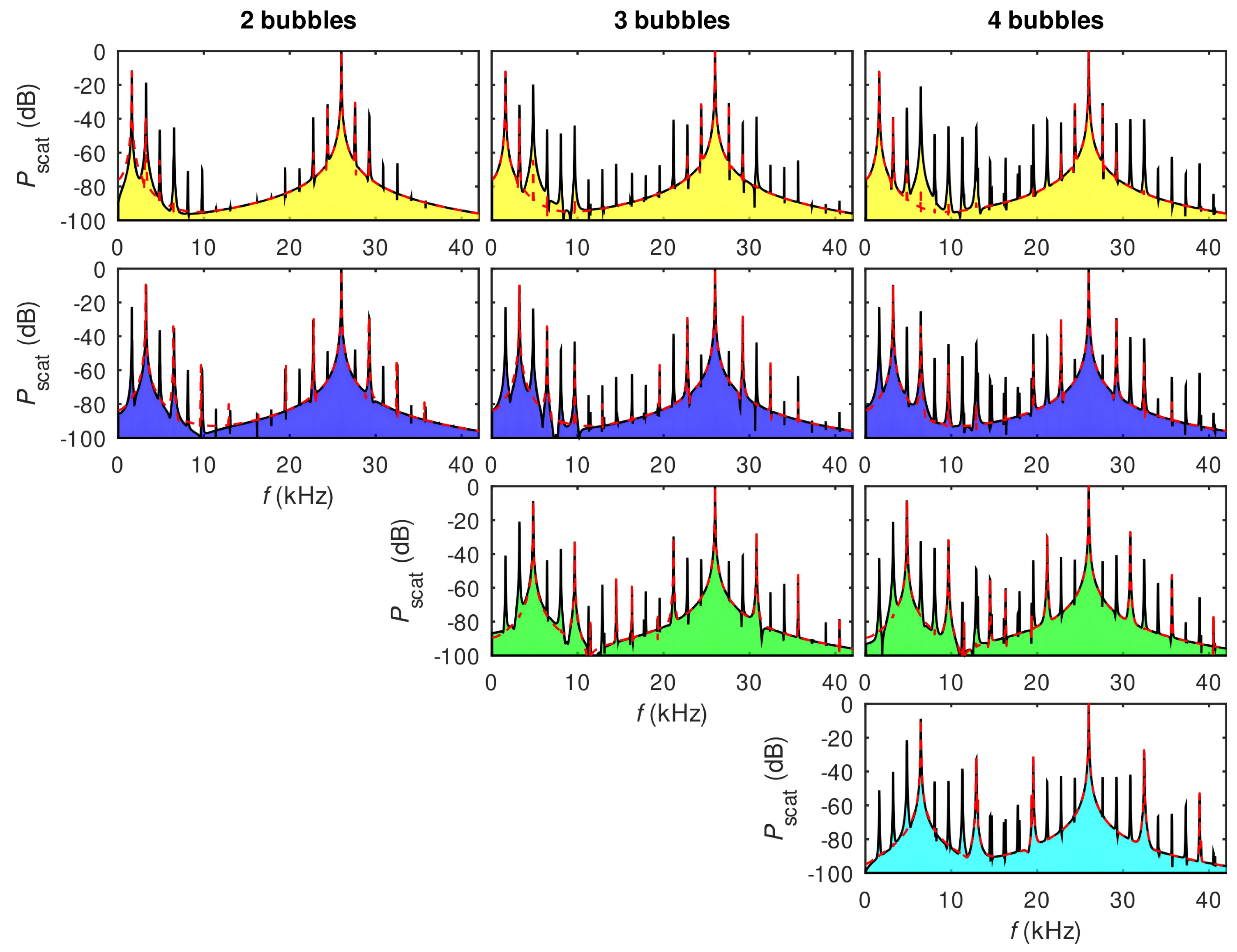
4.1. Physical Principles of Operation of Bubble-Based Acoustic Frequency Combs
4.2. Spectrally Wide Acoustic Frequency Combs
4.3. Application of Bubble-Based AFCs in Biosensing
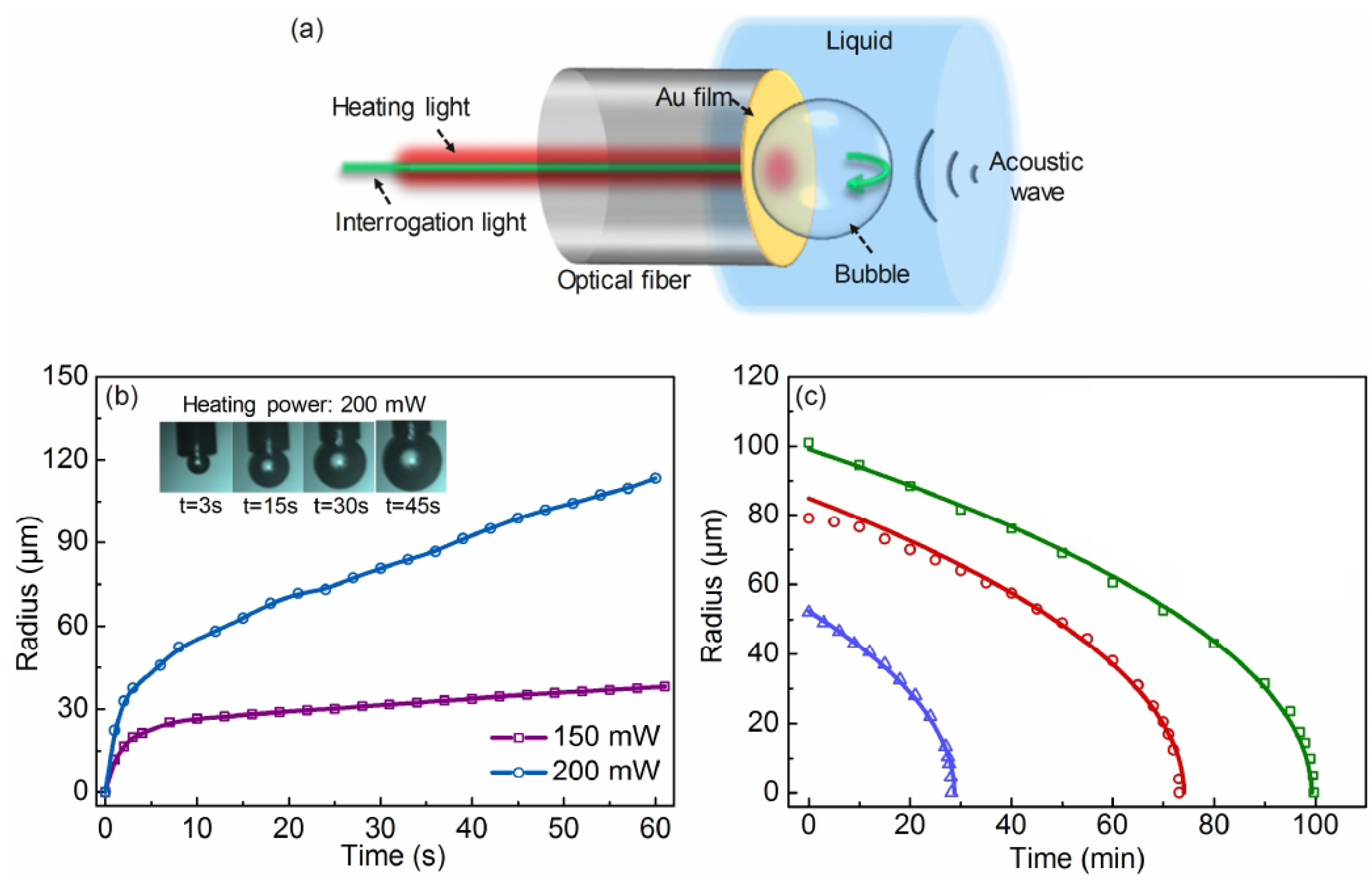
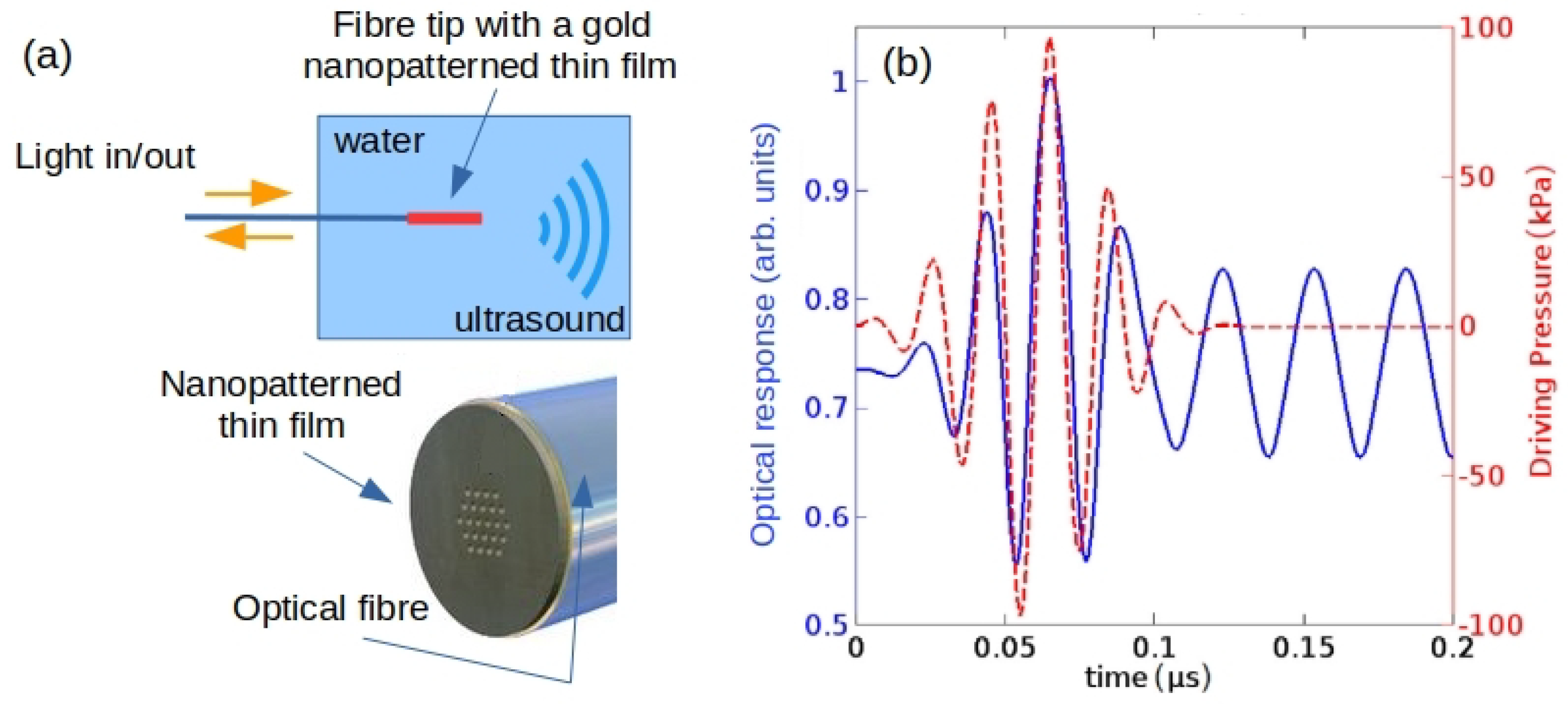
5. Applications of Gas Bubbles in Photoacoustic and Acousto-Optical Biosensors
Acousto-Optical Sensors Using Bubbles
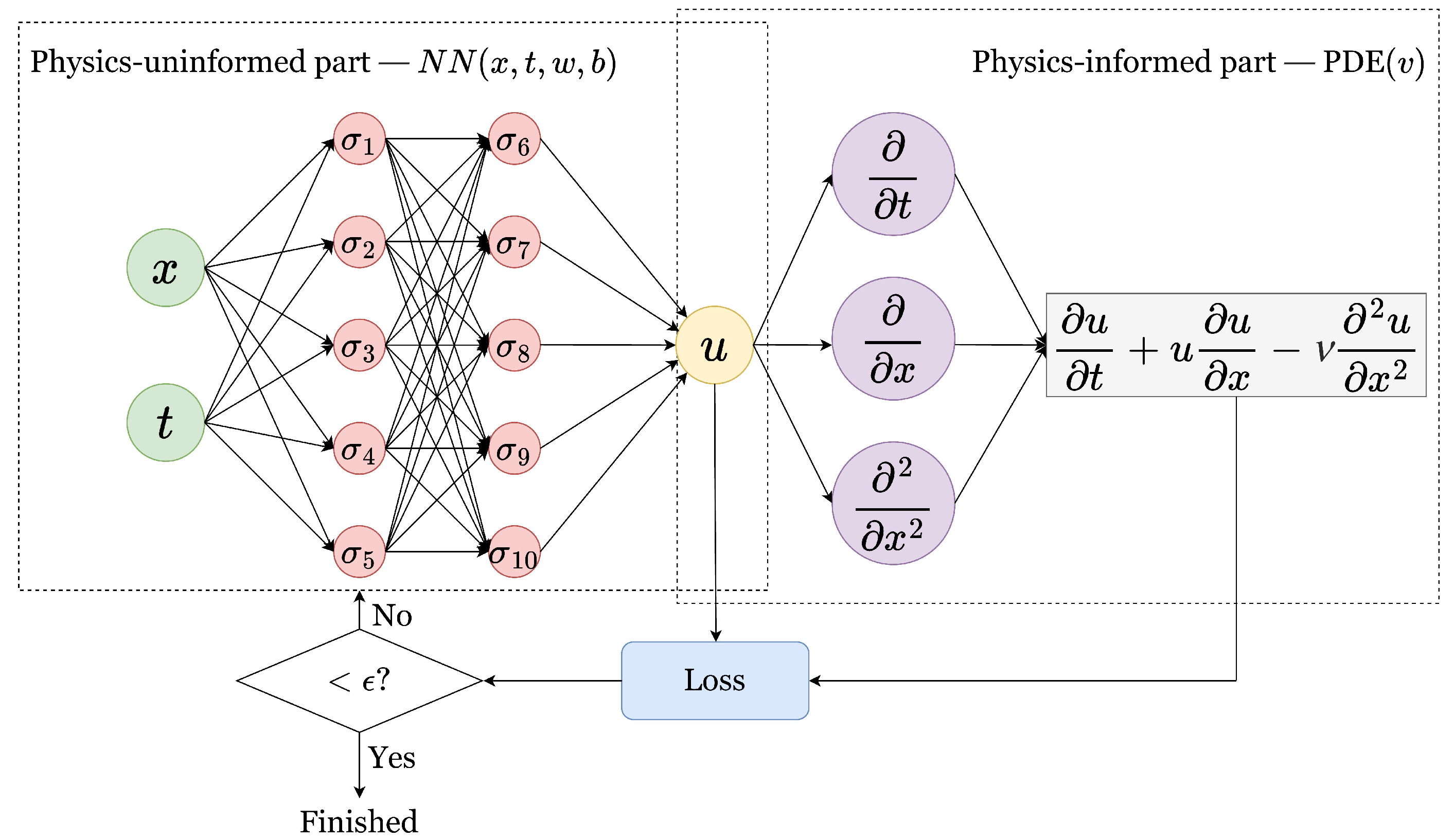
6. Gas Bubble Sensors and Artificial Intelligence Algorithms
7. Bubble Generation
8. Conclusions and Outlook
Funding
Conflicts of Interest
Abbreviations
| atomic force microscopy | AFM |
| acoustic frequency comb | AFC |
| artificial intelligence | AI |
| blood-brain barrier | BBB |
| Brillouin light scattering | BLS |
| in vitro fertilisation | IVF |
| Keller-Miksis | KM |
| mean squared error | MSE |
| machine learning | ML |
| optical frequency comb | OFC |
| partial differential equation | PDE |
| physics-informed neural network | PINN |
| Rayleigh-Plesset | RP |
| scanning acoustic microscopy | SAM |
| signal-to-noise | SNR |
References
- Brennen, C.E. Cavitation and Bubble Dynamics; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Lauterborn, W.; Kurz, T. Physics of bubble oscillations. Rep. Prog. Phys. 2010, 73, 106501. [Google Scholar] [CrossRef]
- Minnaert, M. On musical air-bubbles and the sound of running water. Phil. Mag. 1933, 16, 235–248. [Google Scholar] [CrossRef]
- Leighton, T.G.; Walton, A.J. An experimental study of the sound emitted from gas bubbles in a liquid. Eur. J. Phys. 1987, 8, 98–104. [Google Scholar] [CrossRef]
- Kalson, N.H.; Furman, D.; Zeiri, Y. Cavitation-induced synthesis of biogenic molecules on primordial Earth. ACS Cent. Sci. 2017, 3, 1041–1049. [Google Scholar] [CrossRef]
- Cernak, I. Understanding blast-induced neurotrauma: How far have we come? Concussion 2017, 2, CNC42. [Google Scholar] [CrossRef]
- Barney, C.W.; Dougan, C.E.; McLeod, K.R.; Kazemi-Moridani, A.; Zheng, Y.; Ye, Z.; Tiwari, S.; Sacligil, I.; Riggleman, R.A.; Cai, S.; et al. Cavitation in soft matter. Proc. Natl. Acad. Sci. USA 2020, 117, 9157–9165. [Google Scholar] [CrossRef]
- Denis, P.A. Alzheimer’s disease: A gas model. The NADPH oxidase-Nitric Oxide system as an antibubble biomachinery. Med. Hypotheses 2013, 81, 976–987. [Google Scholar] [CrossRef]
- Burgess, A.; Shah, K.; Hough, O.; Hynynen, K. Focused ultrasound-mediated drug delivery through the blood-brain barrier. Expert. Rev. Neurother. 2015, 15, 477–491. [Google Scholar] [CrossRef]
- Kang, S.T.; Yeh, C.K. Ultrasound microbubble contrast agents for diagnostic and therapeutic applications: Current status and future Design. Chang Gung Med. J. 2012, 35, 125–139. [Google Scholar]
- Deng, W.; Chen, W.; Clement, S.; Guller, A.; Zhao, Z.; Engel, A.; Goldys, E.M. Controlled gene and drug release from a liposomal delivery platform triggered by X-ray radiation. Nat. Commun. 2018, 9, 2713. [Google Scholar] [CrossRef]
- Lindner, J.R. Microbubbles in medical imaging: Current applications and future directions. Nat. Rev. Drug Discov. 2004, 3, 527–532. [Google Scholar] [CrossRef] [PubMed]
- Postema, M.; Gilja, O.H. Contrast-enhanced and targeted ultrasound. World J. Gastroenterol. 2011, 17, 28–41. [Google Scholar] [CrossRef] [PubMed]
- Dutta, A.; Chengara, A.; Nikolov, A.D.; Wasan, D.T.; Chen, K.; Campbell, B. Destabilization of aerated food products: Effects of Ostwald ripening and gas diffusion. J. Food Eng. 2004, 62, 177–184. [Google Scholar] [CrossRef]
- May, E.F.; Lim, V.W.; Metaxas, P.J.; Du, J.; Stanwix, P.L.; Rowland, D.; Johns, M.L.; Haandrikman, G.; Crosby, D.; Aman, Z.M. Gas Hydrate Formation Probability Distributions: The Effect of Shear and Comparisons with Nucleation Theory. Langmuir 2018, 34, 3186–3196. [Google Scholar] [CrossRef] [PubMed]
- Khan, S.A.; Duraiswamy, S. Controlling bubbles using bubbles-microfluidic synthesis of ultra-small gold nanocrystals with gas-evolving reducing agents. Lab Chip 2012, 12, 1807–1812. [Google Scholar] [CrossRef] [PubMed]
- Hashmi, A.; Yu, G.; Reilly-Collette, M.; Heiman, G.; Xu, J. Oscillating bubbles: A versatile tool for lab on a chip applications. Lab Chip 2012, 12, 4216. [Google Scholar] [CrossRef] [PubMed]
- Gogate, P. Treatment of wastewater streams containing phenolic compounds using hybrid techniques based on cavitation: A review of the current status and the way forward. Ultrason. Sonochem. 2008, 15, 1–15. [Google Scholar] [CrossRef]
- Mason, T.J. Sonochemistry and sonoprocessing: The link, the trends and (probably) the future. Ultrason. Sonochem. 2003, 10, 175–179. [Google Scholar] [CrossRef]
- Rubio, F.; Blandford, E.D.; Bond, L.J. Survey of advanced nuclear technologies for potential applications of sonoprocessing. Ultrasonics 2016, 71, 211–222. [Google Scholar] [CrossRef]
- Preisig, J. The impact of bubbles on underwater acoustic communications in shallow water environments. J. Acoust. Soc. Am. 2003, 114, 2370. [Google Scholar] [CrossRef]
- Cole, R.H. Underwater Explosions; Princeton University Press: New York, NY, USA, 1948. [Google Scholar]
- Troyanova-Wood, M.; Meng, Z.; Yakovlev, V.V. Differentiating melanoma and healthy tissues based on elasticity-specific Brillouin microspectroscopy. Biomed. Opt. Express 2019, 10, 1774–1781. [Google Scholar] [CrossRef] [PubMed]
- Runel, G.; Lopez-Ramirez, N.; Chlasta, J.; Masse, I. Biomechanical properties of cancer cells. Cells 2021, 10, 887. [Google Scholar] [CrossRef] [PubMed]
- Pelrine, R.; Kornbluh, R.; Pei, Q.; Joseph, J. High-speed electrically actuated elastomers with strain greater than 100%. Science 2000, 287, 836–839. [Google Scholar] [CrossRef] [PubMed]
- Chan, M.W.C.; Hinz, B.; McCulloch, C.A. Mechanical induction of gene expression in connective tissue cells. Methods Cell. Biol. 2010, 98, 178–205. [Google Scholar]
- Becerra, N.; Salis, B.; Tedesco, M.; Flores, S.M.; Vena, P.; Raiteri, R. AFM and fluorescence microscopy of single cells with simultaneous mechanical stimulation via electrically stretchable substrates. Materials 2021, 14, 4131. [Google Scholar] [CrossRef]
- Tang, D.D.; Gerlach, B.D. The roles and regulation of the actin cytoskeleton, intermediate filaments and microtubules in smooth muscle cell migration. Respir. Res. 2017, 18, 54. [Google Scholar] [CrossRef]
- Lucci, G.; Preziosi, L. A nonlinear elastic description of cell preferential orientations over a stretched substrate. Biomech. Model. Mechanobiol. 2021, 20, 631–649. [Google Scholar] [CrossRef]
- Doinikov, A.A.; Aired, L.; Bouakaz, A. Acoustic scattering from a contrast agent microbubble near an elastic wall of finite thickness. Phys. Med. Biol. 2011, 56, 6951–6967. [Google Scholar] [CrossRef]
- Doinikov, A.A.; Aired, L.; Bouakaz, A. Dynamics of a contrast agent microbubble attached to an elastic wall. IEEE Trans. Med. Imaging 2012, 31, 654–662. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Q.; Guo, X.; Tu, J.; Zhang, D. Mechanisms underlying sonoporation: Interaction between microbubbles and cells. Ultrason. Sonochem. 2020, 67, 105096. [Google Scholar] [CrossRef]
- Boyd, B.; Suslov, S.A.; Becker, S.; Greentree, A.D.; Maksymov, I.S. Beamed UV sonoluminescence by aspherical air bubble collapse near liquid-metal microparticles. Sci. Rep. 2020, 10, 1501. [Google Scholar] [CrossRef]
- Ohl, S.W.; Klaseboer, E.; Khoo, B.C. Bubbles with shock waves and ultrasound: A review. Interface Focus 2015, 5, 20150019. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Su, J.L.; Karpiouk, A.B.; Sokolov, K.V.; Smalling, R.W.; Emelianov, S.Y. Intravascular photoacoustic imaging. IEEE J. Sel. Top. Quantum Electron. 2010, 16, 588–599. [Google Scholar] [CrossRef] [PubMed]
- Maksymov, I.S. Magneto-plasmonic nanoantennas: Basics and applications. Rev. Phys. 2016, 1, 36–51. [Google Scholar] [CrossRef]
- Orth, A.; Ploschner, M.; Wilson, E.R.; Maksymov, I.S.; Gibson, B.C. Optical fiber bundles: Ultra-slim light field imaging probes. Sci. Adv. 2019, 5, eaav1555. [Google Scholar] [CrossRef]
- Sanderson, M.J.; Smith, I.; Parker, I.; Bootman, M.D. Fluorescence microscopy. Cold Spring Harb. Protoc. 2014, 2014, pdb.top071795. [Google Scholar] [CrossRef]
- Reineck, P.; Gibson, B.C. Near-infrared fluorescent nanomaterials for bioimaging and sensing. Adv. Opt. Mater. 2017, 5, 1600446. [Google Scholar] [CrossRef]
- Zabolocki, M.; McCormack, K.; van den Hurk, M.; Milky, B.; Shoubridge, A.P.; Adams, R.; Tran, J.; Mahadevan-Jansen, A.; Reineck, P.; Thomas, J.; et al. BrainPhys neuronal medium optimized for imaging and optogenetics in vitro. Nat. Commun. 2020, 11, 5550. [Google Scholar] [CrossRef]
- Purdey, M.S.; Thompson, J.G.; Monro, T.M.; Abell, A.D.; Schartner, E.P. A dual sensor for pH and hydrogen peroxide using polymer-coated optical fibre tips. Sensors 2015, 15, 31904–31913. [Google Scholar] [CrossRef]
- Whitworth, M.; Bricker, L.; Mullan, C. Ultrasound for fetal assessment in early pregnancy. Cochrane Database Syst. Rev. 2015, 2015, CD007058. [Google Scholar] [CrossRef]
- Yusefi, H.; Helfield, B. Ultrasound contrast imaging: Fundamentals and emerging technology. Front. Phys. 2022, 10, 791145. [Google Scholar] [CrossRef]
- Zhou, Y.; Seshia, A.A.; Hall, E.A.H. Microfluidics-based acoustic microbubble biosensor. In Proceedings of the IEEE SENSORS 2013, Baltimore, MD, USA, 3–6 November 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Miele, I. Acoustic Biosensing Using Functionalised Microbubbles. Ph.D. Thesis, The University of Cambridge, Cambridge, UK, 2019. [Google Scholar]
- Doinikov, A.A. Bubble and Particle Dynamics in Acoustic Fields: Modern Trends and Applications; Research Signpost: Kerala, India, 2005. [Google Scholar]
- Marston, P.L.; Trinh, E.H.; Depew, J.; Asaki, J. Response of bubbles to ultrasonic radiation pressure: Dynamics in low gravity and shape oscillations. In Bubble Dynamics and Interface Phenomena; Blake, J.R., Boulton-Stone, J.M., Thomas, N.H., Eds.; Kluwer Academic: Dordrecht, The Netherlands, 1994; pp. 343–353. [Google Scholar]
- Manasseh, R. Acoustic Bubbles, Acoustic Streaming, and Cavitation Microstreaming. In Handbook of Ultrasonics and Sonochemistry; Springer: Singapore, 2016; pp. 33–68. [Google Scholar] [CrossRef]
- Fong, S.W.; Klaseboer, E.; Turangan, C.K.; Khoo, B.C.; Hung, K.C. Numerical analysis of a gas bubble near bio-materials in an ultrasound field. Ultrasound Med. Biol. 2006, 32, 925–942. [Google Scholar] [CrossRef] [PubMed]
- Curtiss, G.A.; Leppinen, D.M.; Wang, Q.X.; Blake, J.R. Ultrasonic cavitation near a tissue layer. J. Fluid Mech. 2013, 730, 245–272. [Google Scholar] [CrossRef]
- Boyd, B.; Becker, S. Numerical modelling of an acoustically-driven bubble collapse near a solid boundary. Fluid Dyn. Res. 2018, 50, 065506. [Google Scholar] [CrossRef]
- Boyd, B.; Becker, S. Numerical modeling of the acoustically driven growth and collapse of a cavitation bubble near a wall. Phys. Fluids 2019, 31, 032102. [Google Scholar] [CrossRef]
- Daneman, R.; Prat, A. The blood-brain barrier. Cold Spring Harb. Perspect. Biol. 2015, 7, a020412. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.; Gao, Y.; Song, Y. Gas-propelled biosensors for quantitative analysis. Analyst 2021, 146, 1115–1126. [Google Scholar] [CrossRef] [PubMed]
- Beranek, L.L. Acoustics; The Acoustical Society of America: New York, NY, USA, 1996. [Google Scholar]
- Länge, K.; Rapp, B.E.; Rapp, M. Surface acoustic wave biosensors: A review. Anal. Bioanal. Chem. 2008, 391, 1509–1519. [Google Scholar] [CrossRef]
- Fogel, R.; Limson, J.; Seshia, A.A. Acoustic biosensors. Essays Biochem. 2016, 60, 101–110. [Google Scholar]
- Lakshmanan, A.; Jin, Z.; Nety, S.P.; Sawyer, D.P.; Lee-Gosselin, A.; Malounda, D.; Swift, M.B.; Maresca, D.; Shapiro, M.G. Acoustic biosensors for ultrasound imaging of enzyme activity. Nat. Chem. Biol. 2020, 16, 988–996. [Google Scholar] [CrossRef]
- Damiati, S. Acoustic Biosensors for Cell Research. In Handbook of Cell Biosensors; Thouand, G., Ed.; Springer International Publishing: New York, NY, USA, 2020; pp. 1–32. [Google Scholar]
- Zida, S.I.; Lin, Y.D.; Khung, Y.L. Current trends on surface acoustic wave biosensors. Adv. Mater. Technol. 2021, 6, 2001018. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X.; Wei, X.; Xue, Y.; Wan, H.; Wang, P. Recent advances in acoustic wave biosensors for the detection of disease-related biomarkers: A review. Anal. Chim. Acta 2021, 1164, 338321. [Google Scholar] [CrossRef] [PubMed]
- Rayleigh, L. On the pressure developed in a liquid during the collapse of a spherical cavity. Phyl. Mag. 1917, 34, 94–98. [Google Scholar] [CrossRef]
- Plesset, M.S. The dynamics of cavitation bubbles. J. Appl. Mech. 1949, 16, 228–231. [Google Scholar] [CrossRef]
- Prosperetti, A. Nonlinear oscillations of gas bubbles in liquids: Steady-state solutions. J. Acoust. Soc. Am. 1974, 56, 878–885. [Google Scholar] [CrossRef]
- Parlitz, U.; Englisch, V.; Scheffczyk, C.; Lauterborn, W. Bifurcation structure of bubble oscillators. J. Acoust. Soc. Am. 1990, 88, 1061–1077. [Google Scholar] [CrossRef]
- Oguz, H.N.; Prosperetti, A. A generalization of the impulse and virial theorems with an application to bubble oscillations. J. Fluid Mech. 1990, 218, 143–162. [Google Scholar] [CrossRef]
- Mettin, R.; Akhatov, I.; Parlitz, U.; Ohl, C.D.; Lauterborn, W. Bjerknes forces between small cavitation bubbles in a strong acoustic field. Phys. Rev. E 1997, 56, 2924–2931. [Google Scholar] [CrossRef]
- Plesset, M.S.; Prosperetti, A. Bubble dynamics and cavitation. Annu. Rev. Fluid Mech. 1977, 9, 145–185. [Google Scholar] [CrossRef]
- Prosperetti, A. A new mechanism for sonoluminescence. J. Acoust. Soc. Am. 1997, 101, 2003–2007. [Google Scholar] [CrossRef]
- Brenner, M.P.; Hilgenfeldt, S.; Lohse, D. Single-bubble sonoluminescence. Rev. Mod. Phys. 2002, 74, 425–484. [Google Scholar] [CrossRef]
- Manasseh, R.; Ooi, A. Frequencies of acoustically interacting bubbles. Bubble Sci. Eng. Technol. 2009, 1, 58–74. [Google Scholar] [CrossRef]
- Stride, E.; Saffari, N. Microbubble ultrasound contrast agents: A review. Proc. Inst. Mech. Eng. H 2003, 217, 429–447. [Google Scholar] [CrossRef] [PubMed]
- Doinikov, A.A.; Bouakaz, A. Review of shell models for contrast agent microbubbles. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 981–993. [Google Scholar] [CrossRef]
- Jeong, J.; Jang, D.; Kim, D.; Lee, D.; Chung, S.K. Acoustic bubble-based drug manipulation: Carrying, releasing and penetrating for targeted drug delivery using an electromagnetically actuated microrobot. Sens. Actuators A 2020, 306, 111973. [Google Scholar] [CrossRef]
- Ainslie, M.A.; Leighton, T.G. Review of scattering and extinction cross-sections, damping factors, and resonance frequencies of a spherical gas bubble. J. Acoust. Soc. Am. 2011, 130, 3184–3208. [Google Scholar] [CrossRef]
- Devin, C. Survey of Thermal, Radiation, and Viscous Damping of Pulsating Air Bubbles in Water. J. Acoust. Soc. Am. 1959, 31, 1654–1667. [Google Scholar] [CrossRef]
- Qin, Z.; Bremhorst, K.; Alehossein, H.; Meyer, T. Simulation of cavitation bubbles in a convergent-divergent nozzle water jet. J. Fluid Mech. 2007, 573, 1–25. [Google Scholar] [CrossRef]
- Prosperetti, A.; Lezzi, A. Bubble dynamics incompressible liquid. I. First-order theory. J. Fluid Mech. 1986, 168, 457–748. [Google Scholar] [CrossRef]
- Lezzi, A.; Prosperetti, A. Bubble dynamics in a compressible liquid. 2. Second-order theory. J. Fluid Mech. 1987, 185, 289–321. [Google Scholar] [CrossRef]
- Prosperetti, A.; Hao, Y. Modelling of spherical gas bubble oscillations and sonoluminescence. Philos. Trans. R. Soc. London Ser. A 1999, 357, 203–223. [Google Scholar] [CrossRef]
- Gilmore, F.R. The Growth or Collapse of a Spherical Bubble in a Viscous Compressible Liquid; report 26-4; Hydrodynamics Laboratory, California Institute Technology: Pasadena, CA, USA, 1952. [Google Scholar]
- Keller, J.B.; Miksis, M. Bubble oscillations of large amplitude. J. Acoust. Soc. Am. 1980, 68, 628–633. [Google Scholar] [CrossRef]
- Suslov, S.A.; Ooi, A.; Manasseh, R. Nonlinear dynamic behavior of microscopic bubbles near a rigid wall. Phys. Rev. E 2012, 85, 066309. [Google Scholar] [CrossRef] [PubMed]
- Shima, A.; Tomita, Y. The behavior of a spherical bubble near a solid wall in a compressible liquid. Ing. Arch. 1981, 51, 243. [Google Scholar] [CrossRef]
- Vos, H.J.; Dollet, B.; Bosch, J.G.; Versluis, M.; de Jong, N. Nonspherical Vibrations of Microbubbles in Contact with a Wall-A Pilot Study at Low Mechanical Index. Ultrasound Med. Bio. 2008, 34, 685. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, B.Q.H.; Maksymov, I.S.; Suslov, S.A. Spectrally wide acoustic frequency combs generated using oscillations of polydisperse gas bubble clusters in liquids. Phys. Rev. E 2021, 104, 035104. [Google Scholar] [CrossRef]
- Maksymov, I.S.; Nguyen, B.Q.H.; Pototsky, A.; Suslov, S.A. Acoustic, phononic, Brillouin light scattering and Faraday wave-based frequency combs: Physical foundations and applications. Sensors 2022, 22, 3921. [Google Scholar] [CrossRef]
- Zabolotskaya, A.E. Interaction of gas bubbles in a sound field. Sov. Phys. Acoust. 1984, 30, 365–368. [Google Scholar]
- Watanabe, T.; Kukita, Y. Translational and radial motions of a bubble in an acoustic standing wave field. Phys. Fluids A 1993, 5, 2682–2688. [Google Scholar] [CrossRef]
- Pelekasis, N.A.; Tsamopuolos, J.A. Bjerknes forces between two bubbles. Part 2. Response to an oscillatory pressure field. J. Fluid Mech. 1993, 254, 501–527. [Google Scholar] [CrossRef]
- Doinikov, A.A.; Zavtrak, S.T. On the mutual interaction of two gas bubbles in a sound field. Phys. Fluids 1995, 7, 1923–1930. [Google Scholar] [CrossRef]
- Barbat, T.; Ashgriz, N.; Liu, C.S. Dynamics of two interacting bubbles in an acoustic field. J. Fluid Mech. 1999, 389, 137–168. [Google Scholar] [CrossRef]
- Harkin, A.; Kaper, T.J.; Nadim, A. Coupled pulsation and translation of two gas bubbles in a liquid. J. Fluid. Mech. 2001, 445, 377–411. [Google Scholar] [CrossRef]
- Doinikov, A.A. Translational motion of two interacting bubbles in a strong acoustic field. Phys. Rev. E 2001, 64, 026301. [Google Scholar] [CrossRef] [PubMed]
- Macdonald, C.A.; Gomatam, J. Chaotic dynamics of microbubbles in ultrasonic fields. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2006, 220, 333–343. [Google Scholar] [CrossRef]
- Mettin, R.; Doinikov, A.A. Translational instability of a spherical bubble in a standing ultrasound wave. Appl. Acoust. 2009, 70, 1330–1339. [Google Scholar] [CrossRef]
- Dzaharudin, F.; Suslov, S.A.; Manasseh, R.; Ooi, A. Effects of coupling, bubble size, and spatial arrangement on chaotic dynamics of microbubble cluster in ultrasonic fields. J. Acoust. Soc. Am. 2013, 134, 3425–3434. [Google Scholar] [CrossRef]
- Lanoy, M.; Derec, C.; Tourin, A.; Leroy, V. Manipulating bubbles with secondary Bjerknes forces. Appl. Phys. Lett. 2015, 107, 214101. [Google Scholar] [CrossRef]
- Bjerknes, V. Fields of Force; The Columbia University Press: New York, NY, USA, 1906. [Google Scholar]
- Leighton, T.G.; Walton, A.J.; Pickworth, M.J.W. Primary Bjerknes forces. Eur. J. Phys. 1990, 11, 47–50. [Google Scholar] [CrossRef]
- Kazantsev, G.N. The motion of gaseous bubbles in a liquid under the influence of Bjerknes forces arising in an acoustic field. Sov. Phys. Dokl. 1960, 4, 1250. [Google Scholar]
- Crum, L.A. Bjerknes forces on bubbles in a stationary sound field. J. Acoust. Soc. Am. 1975, 57, 1363–1370. [Google Scholar] [CrossRef]
- Doinikov, A.A. Mathematical model for collective bubble dynamics in strong ultrasound fields. J. Acoust. Soc. Am. 2004, 116, 821–827. [Google Scholar] [CrossRef]
- Levich, B.V. Physicochemical Hydrodynamics; Prentice-Hall: Englewood Cliffs, NJ, USA, 1962. [Google Scholar]
- Evans, E.A.; Skalak, R. Mechanics and Thermodynamics of Biomembranes; CRC Press: Boca Raton, FL, USA, 1980. [Google Scholar]
- Fung, Y.C. Biomechanics. Mechanical Properties of Living Tissues; Springer-Verlag: New York, NY, USA, 1993. [Google Scholar]
- Boal, D. Mechanics of the Cell; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Bao, G.; Suresh, S. Cell and molecular mechanics of biological materials. Nat. Mater. 2003, 2, 715–725. [Google Scholar] [CrossRef]
- Pearson, C.G.; Maddox, P.S.; Salmon, E.D.; Bloom, K. Budding yeast chromosome structure and dynamics during mitosis. J. Cell Biol. 2001, 152, 1255–1266. [Google Scholar] [CrossRef]
- Weiss, E.C.; Anastasiadis, P.; Pilarczyk, G.; Lemor, R.M.; Zinin, P.V. Mechanical properties of single cells by high-frequency time-resolved acoustic microscopy. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2007, 54, 2257–2271. [Google Scholar] [CrossRef]
- Nematbakhsh, Y.; Pang, K.T.; Lim, C.T. Correlating the viscoelasticity of breast cancer cells with their malignancy. Converg. Sci. Phys. Oncol. 2017, 3, 034003. [Google Scholar] [CrossRef]
- Mierke, C.T. Viscoelasticity acts as a marker for tumor extracellular matrix characteristics. Front. Cell Dev. Biol. 2021, 9, 785138. [Google Scholar] [CrossRef]
- Abidine, Y.; Giannetti, A.; Revilloud, J.; Laurent, V.M.; Verdier, C. Viscoelastic properties in cancer: From cells to spheroids. Cells 2021, 10, 1704. [Google Scholar] [CrossRef]
- Zhang, G.; Long, M.; Wu, Z.Z.; Yu, W.Q. Mechanical properties of hepatocellular carcinoma cells. World J. Gastroenterol. 2002, 8, 243–246. [Google Scholar] [CrossRef]
- Beil, M.; Micoulet, A.; von Wichert, G.; Paschke, S.; Walther, P.; Omary, M.B.; Veldhoven, P.P.V.; Gern, U.; Wolff-Hieber, E.; Eggermann, J.; et al. Sphingosylphosphorylcholine regulates keratin network architecture and visco-elastic properties of human cancer cells. Nat. Cell Biol. 2003, 5, 803–811. [Google Scholar] [CrossRef]
- Suresh, S.; Spatz, J.; Mills, J.P.; Micoulet, A.; Dao, M.; Lim, C.T.; Beil, M.; Seufferlein, T. Connections between single-cell biomechanics and human disease states: Gastrointestinal cancer and malaria. Acta Biomater. 2005, 1, 15–30. [Google Scholar] [CrossRef] [PubMed]
- Guck, J.; Schinkinger, S.; Lincoln, B.; Wottawah, F.; Ebert, S.; Romeyke, M.; Lenz, D.; Erickson, H.M.; Ananthakrishnan, R.; Mitchell, D.; et al. Optical deformability as an inherent cell marker for testing malignant transformation and metastatic competence. Biophys. J. 2005, 88, 3689–3698. [Google Scholar] [CrossRef] [PubMed]
- Ford, L.H. Estimate of the vibrational frequencies of spherical virus particles. Phys. Rev. E 2003, 67, 051924. [Google Scholar] [CrossRef] [PubMed]
- Fonoberov, V.A.; Balandin, A.A. Low-frequency vibrational modes of viruses used for nanoelectronic self-assemblies. Phys. Status Solidi B 2004, 241, R67–R69. [Google Scholar] [CrossRef]
- van Vlijmen, H.W.T.; Karplus, M. Normal mode calculations of icosahedral viruses with full dihedral flexibility by use of molecular symmetry. J. Molec. Biol. 2005, 350, 528–542. [Google Scholar] [CrossRef]
- Talati, M.; Jha, P.K. Acoustic phonon quantization and low-frequency Raman spectra of spherical viruses. Phys. Rev. E 2006, 73, 011901. [Google Scholar] [CrossRef]
- Zinin, P.V.; Allen, J.S., III; Levin, V.M. Mechanical resonances of bacteria cells. Phys. Rev. E 2005, 72, 061907. [Google Scholar] [CrossRef]
- Backholm, M.; Ryu, W.S.; Dalnoki-Veress, K. Viscoelastic properties of the nematode Caenorhabditis Elegans, A Self-Similar, Shear-Thinning Worm. Proc. Natl. Acad. Sci. USA 2013, 110, 4528–4533. [Google Scholar] [CrossRef]
- Maksymov, I.S.; Pototsky, A. Excitation of Faraday-like body waves in vibrated living earthworms. Sci. Reps. 2020, 10, 8564. [Google Scholar] [CrossRef]
- Fabelinskii, I.L. Molecular Scattering of Light; Springer: Berlin, Germany, 1969. [Google Scholar]
- Miller, D.L. Effects of a high-amplitude 1-MHz standing ultrasonic field on the algae hydrodictyon. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1986, 33, 165–170. [Google Scholar] [CrossRef]
- Watmough, D.J.; Dendy, P.P.; Eastwood, L.M.; Gregory, D.W.; Gordon, F.C.A.; Wheatley, D.N. The biophysical effects of therapeutic ultrasound on HeLa cells. Ultrasound Med. Biol. 1977, 3, 217–219. [Google Scholar] [CrossRef]
- Church, C.C.; Miller, M.W. The kinetics and mechanics of ultrasonically-induced cell lysis produced by non-trapped bubbles in a rotating culture tube. Ultrasound Med. Biol. 1983, 9, 385–393. [Google Scholar] [CrossRef]
- Meng, Z.; Traverso, A.J.; Ballmann, C.W.; Troyanova-Wood, M.A.; Yakovlev, V.V. Seeing cells in a new light: A renaissance of Brillouin spectroscopy. Adv. Opt. Photon. 2016, 8, 300–327. [Google Scholar] [CrossRef]
- McKenzie, B.M.; Dexter, A.R. Physical properties of casts of the earthworm Aporrectodea Rosea. Biol. Fertil. Soils 1987, 5, 152–157. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M. Optical trapping and manipulation of viruses and bacteria. Science 1987, 235, 1517–1520. [Google Scholar] [CrossRef]
- Puig-De-Morales, M.; Grabulosa, M.; Alcaraz, J.; Mullol, J.; Maksym, G.N.; Fredberg, J.J.; Navajas, D. Measurement of cell microrheology by magnetic twisting cytometry with frequency domain demodulation. J. Appl. Phys. 2001, 91, 1152–1159. [Google Scholar] [CrossRef]
- Vliet, K.J.V.; Bao, G.; Suresh, S. The biomechanics toolbox: Experimental approaches for living cells and biomolecules. Acta Mater. 2003, 51, 5881–5905. [Google Scholar] [CrossRef]
- Traverso, A.J.; Thompson, J.V.; Steelman, Z.A.; Meng, Z.; Scully, M.O.; Yakovlev, V.V. Dual Raman-Brillouin microscope for chemical and mechanical characterization and imaging. Laser Photon. Rev. 2013, 8, 368–393. [Google Scholar] [CrossRef]
- Akilbekova, D.; Ogay, V.; Yakupov, T.; Sarsenova, M.; Umbayev, B.; Nurakhmetov, A.; Tazhin, K.; Yakovlev, V.V.; Utegulov, Z.N. Brillouin spectroscopy and radiography for assessment of viscoelastic and regenerative properties of mammalian bones. J. Biomed. Opt. 2018, 23, 097004. [Google Scholar] [CrossRef]
- Bu, Y.; Li, L.; Yang, C.; Li, R.; Wang, J. Measuring viscoelastic properties of living cells. Acta Mech. Solida Sin. 2019, 32, 599–610. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Y.; Cui, M.; Zhao, X.; Sun, M.; Zhao, X. A cell’s viscoelasticity measurement method based on the spheroidization process of non-spherical shaped cell. Sensors 2021, 21, 5561. [Google Scholar] [CrossRef] [PubMed]
- Kojima, S. 100th anniversary of Brillouin scattering: Impact on materials science. Materials 2022, 15, 3518. [Google Scholar] [CrossRef] [PubMed]
- Palombo, F.; Fioretto, D. Brillouin light scattering: Applications in biomedical sciences. Chem. Rev. 2019, 119, 7833–7847. [Google Scholar] [CrossRef] [PubMed]
- Poon, C.; Chou, J.; Cortie, M.; Kabakova, I. Brillouin imaging for studies of micromechanics in biology and biomedicine: From current state-of-the-art to future clinical translation. J. Phys. Photonics 2021, 3, 012002. [Google Scholar] [CrossRef]
- Baltuška, A.; Udem, T.; Uiberacker, M.; Hentschel, M.; Goulielmakis, E.; Gohle, C.; Holzwarth, R.; Yakovlev, V.S.; Scrinzi, A.; Hänsch, T.W.; et al. Attosecond control of electronic processes by intense light fields. Nature 2003, 421, 611–615. [Google Scholar] [CrossRef] [PubMed]
- Anastasiadis, P.; Zinin, P.V. High-frequency time-resolved scanning acoustic microscopy for biomedical applications. Open Neuroimaging J. 2018, 12, 69–85. [Google Scholar] [CrossRef]
- Weiss, E.C.; Lemor, R.M.; Pilarczyk, G.; Anastasiadis, P.; Zinin, P.V. Imaging of focal contacts of chicken heart muscle cells by high-frequency acoustic microscopy. Ultrasound Med. Biol. 2007, 33, 1320–1326. [Google Scholar] [CrossRef] [PubMed]
- Titov, S.A.; Burlakov, A.B.; Zinin, P.V.; Bogachenkov, A.N. Measuring the speed of sound in tissues of teleost fish embryos. Bull. Russ. Acad. Sci. Phys. 2021, 85, 103–107. [Google Scholar] [CrossRef]
- Strohm, E.M.; Czarnota, G.J.; Kolios, M.C. Quantitative measurements of apoptotic cell properties using acoustic microscopy. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 2293–2304. [Google Scholar] [CrossRef]
- Pérez-Cota, F.; Smith, R.J.; Moradi, E.; Webb, K.; Clark, M. Thin-film transducers for the detection and imaging of Brillouin oscillations in transmission on cultured cells. J. Phys. Conf. Ser. 2016, 684, 012003. [Google Scholar] [CrossRef]
- Pérez-Cota, F.; Smith, R.J.; Moradi, E.; Marques, L.; Webb, K.; Clark, M. High resolution 3D imaging of living cells with sub-optical wavelength phonons. Sci. Reps. 2016, 6, 39326. [Google Scholar] [CrossRef] [PubMed]
- Yu, K.; Devkota, T.; Beane, G.; Wang, G.P.; Hartland, G.V. Brillouin oscillations from single Au nanoplate opto-acoustic transducers. ACS Nano 2017, 11, 8064–8071. [Google Scholar] [CrossRef] [PubMed]
- Gusev, V.E. Contra-intuitive features of time-domain Brillouin scattering in collinear paraxial sound and light beams. Photoacoustics 2020, 20, 100205. [Google Scholar] [CrossRef] [PubMed]
- Ackerman, E. Resonances of biological cells at audible frequencies. Bull. Math. Biophys. 1951, 13, 93–106. [Google Scholar] [CrossRef]
- Ackerman, E. An extension of the theory of resonances of biological cells: III. Relationship of breakdown curves and mechanical Q. Bull. Math. Biophys. 1957, 19, 1–7. [Google Scholar] [CrossRef]
- Zinin, P.V.; Levin, V.M.; Maev, R.G. Natural oscillation of biological microspecimens. Biophysics 1987, 32, 202–210. [Google Scholar]
- Zinin, P.V. Theoretical analysis of sound attenuation mechanisms in blood and in erythrocyte suspensions. Ultrasonics 1992, 30, 26–34. [Google Scholar] [CrossRef]
- Marston, P.L. Shape oscillation and static deformation of drops and bubbles driven by modulated radiation stresses–theory. J. Acoust. Soc. Am. 1980, 67, 15–26. [Google Scholar] [CrossRef]
- Rayleigh, L. On the capillary phenomena of jets. Proc. R. Soc. Lond. 1879, 29, 71–97. [Google Scholar]
- Oh, J.M.; Ko, S.H.; Kang, K.H. Shape oscillation of a drop in ac electrowetting. Langmuir 2008, 24, 8379–8386. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; Oxford University Press: New York, NY, USA, 1961. [Google Scholar]
- Miller, C.; Scriven, L. The oscillations of a fluid droplet immersed in another fluid. J. Fluid Mech. 1968, 32, 417–435. [Google Scholar] [CrossRef]
- Maksymov, I.S.; Greentree, A.D. Dynamically reconfigurable plasmon resonances enabled by capillary oscillations of liquid-metal nanodroplets. Phys. Rev. A 2017, 96, 043829. [Google Scholar] [CrossRef]
- Marston, P.L.; Apfel, R.E. Quadrupole resonance of drops driven by modulated acoustic radiation pressure–experimental properties. J. Acoust. Soc. Am. 1980, 67, 27–37. [Google Scholar] [CrossRef]
- Maksymov, I.S.; Greentree, A.D. Plasmonic nanoantenna hydrophones. Sci. Rep. 2016, 6, 32892. [Google Scholar] [CrossRef] [PubMed]
- Maksymov, I.S.; Greentree, A.D. Coupling light and sound: Giant nonlinearities from oscillating bubbles and droplets. Nanophotonics 2019, 8, 367–390. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Enoch, S.; Bonod, N. Plasmonics: From Basic to Advanced Topics; Springer: Berlin, Germany, 2012. [Google Scholar]
- Han, L.; Chen, S.; Chen, H. Water wave polaritons. Phys. Rev. Lett. 2022, 128, 204501. [Google Scholar] [CrossRef]
- Zinin, P.V.; Allen, J.S., III. Deformation of biological cells in the acoustic field of an oscillating bubble. Phys. Rev. E 2009, 79, 021910. [Google Scholar] [CrossRef]
- Erpelding, T.N.; Hollman, K.W.; O’Donnell, M. Mapping age-related elasticity changes in porcine lenses using bubble-based acoustic radiation force. Exp. Eye Res. 2007, 84, 332–341. [Google Scholar] [CrossRef]
- Chisti, Y. Sonobioreactors: Using ultrasound for enhanced microbial productivity. Trends Biotechnol. 2003, 21, 89–93. [Google Scholar] [CrossRef]
- Yasui, K.; Tuziuti, T.; Lee, J.; Kozuka, T.; Towata, A.; Iida, Y. Numerical simulations of acoustic cavitation noise with the temporal fluctuation in the number of bubbles. Ultrason. Sonochem. 2010, 17, 460–472. [Google Scholar] [CrossRef]
- Helfield, B.; Chen, X.; Watkins, S.C.; Villanueva, F.S. Biophysical insight into mechanisms of sonoporation. Proc. Natl. Acad. Sci. USA 2016, 113, 9983–9988. [Google Scholar] [CrossRef] [PubMed]
- Robertson, J.; Becker, S. Influence of acoustic reflection on the intertial cavittaion dose in Franz diffusion cell. Ultrasound Med. Biol. 2018, 44, 1100–1109. [Google Scholar] [CrossRef] [PubMed]
- Robertson, J.; Squire, M.; Becker, S. A thermoelectric device for coupling fluid temperature regulation during continuous skin sonoporation or sonophoresis. AAPS PharmSciTech. 2019, 20, 147. [Google Scholar] [CrossRef] [PubMed]
- Joersbo, M.; Brunstedt, J. Sonication: A new method for gene transfer to plants. Physiol. Plant. 1992, 85, 230–234. [Google Scholar] [CrossRef]
- Kim, H.; Hwang, J.K.; Jung, M.; Choi, J.; Kang, H.W. Laser-induced optical breakdown effects of micro-lens arrays and diffractive optical elements on ex vivo porcine skin after 1064 nm picosecond laser irradiation. Biomed. Opt. Express. 2020, 11, 7286–7298. [Google Scholar] [CrossRef]
- Picqué, N.; Hänsch, T.W. Frequency comb spectroscopy. Nat. Photon. 2019, 13, 146–157. [Google Scholar] [CrossRef]
- Urick, R.J. Principles of Underwater Sound; McGraw-Hill: New York, NY, USA, 1983. [Google Scholar]
- Wu, H.; Qian, Z.; Zhang, H.; Xu, X.; Xue, B.; Zhai, J. Precise underwater distance measurement by dual acoustic frequency combs. Ann. Phys. 2019, 531, 1900283. [Google Scholar] [CrossRef]
- Qian, Z.; Sun, W.; Ma, X.; Han, G.; Fu, X.; Zhai, J. Quadrature acoustic frequency combs multiplexing for massive parallel underwater acoustic communications. Ann. Phys. 2022, 534, 2100426. [Google Scholar] [CrossRef]
- Boyd, R.W. Nonlinear Optics; Academic Press: Cambridge, UK, 2008. [Google Scholar]
- Chembo, Y.K. Kerr optical frequency combs: Theory, applications and perspectives. Nanophotonics 2016, 5, 214–230. [Google Scholar] [CrossRef]
- Rudenko, O.V. Giant nonlinearities in structurally inhomogeneous media and the fundamentals of nonlinear acoustic diagnostic technique. Phys-Usp. 2006, 49, 69–87. [Google Scholar] [CrossRef]
- Francescutto, A.; Nabergoj, R. Steady-state oscillations of gas bubbles in liquids: Explicit formulas for frequency response curves. J. Acoust. Soc. Am. 1983, 73, 457–460. [Google Scholar] [CrossRef]
- Francescutto, A.; Nabergoj, R. A multiscale analysis of gas bubble oscillations: Transient and steady-state solutions. Acoustica 1984, 56, 12–22. [Google Scholar]
- Nguyen, B.Q.H.; Maksymov, I.S.; Suslov, S.A. Acoustic frequency combs using gas bubble cluster oscillations in liquids: A proof of concept. Sci. Reps. 2021, 11, 38. [Google Scholar] [CrossRef] [PubMed]
- Hwang, P.A.; Teague, W.J. Low-frequency resonant scattering of bubble clouds. J. Atmos. Ocean. Technol. 2000, 17, 847–853. [Google Scholar] [CrossRef]
- Zhang, M.; Buscaino, B.; Wang, C.; Shams-Ansari, A.; Reimer, C.; Zhu, R.; Kahn, J.M.; Lončar, M. Broadband electro-optic frequency comb generation in a lithium niobate microring resonator. Nature 2019, 568, 373–377. [Google Scholar] [CrossRef]
- Ye, J.; Cundiff, S.T. Femtosecond Optical Frequency Comb: Principle, Operation and Applications; Springer Science + Business Media: Boston, MA, USA, 2005. [Google Scholar]
- Maddaloni, P.; Bellini, M.; de Natale, P. Laser-Based Measurements for Time and Frequency Domain Applications: A Handbook; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Maehara, A.; Mintz, G.S.; Weissman, N.J. Advances in intravascular imaging. Circ. Cardiovasc. Intervent. 2009, 2, 482–490. [Google Scholar] [CrossRef]
- Weissleder, R.; Nahrendorf, M.; Pittet, M.J. Imaging macrophages with nanoparticles. Nat. Mater. 2014, 13, 125–138. [Google Scholar] [CrossRef]
- Wang, C.; Guo, L.; Wang, G.; Ye, T.; Wang, B.; Xiao, J.; Liu, X. In-vivo Imaging Melanoma Simultaneous Dual-Wavel. Acoust.-Resolut. Photoacoustic/ultrasound Microsc. Appl. Opt. 2021, 60, 3772–3778. [Google Scholar] [CrossRef]
- Duocastella, M.; Surdo, S.; Zunino, A.; Diaspro, A.; Saggau, P. Acousto-optic systems for advanced microscopy. J. Phys. Photonics 2021, 3, 012004. [Google Scholar] [CrossRef]
- Wang, B.; Yantsen, E.; Larson, T.; Karpiouk, A.B.; Sethuraman, S.; Su, J.L.; Sokolov, K.; Emelianov, S.Y. Plasmonic intravascular photoacoustic imaging for detection of macrophages in atherosclerotic plaques. Nano Lett. 2009, 9, 2212–2217. [Google Scholar] [CrossRef]
- Wilson, K.; Homan, K.; Emelianov, S. Biomedical photoacoustics beyond thermal expansion using triggered nanodroplet vaporization for contrast-enhanced imaging. Nat. Commun. 2011, 3, 618. [Google Scholar] [CrossRef] [PubMed]
- Dove, J.D.; Murray, T.W.; Borden, M.A. Enhanced photoacoustic response with plasmonic nanoparticle-templated microbubbles. Soft Matter 2013, 9, 7743–7750. [Google Scholar] [CrossRef]
- Mie, G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Ann. Der Phys. 1908, 330, 377–445. [Google Scholar] [CrossRef]
- Stratton, J.A. Electromagnetic Theory; McGraw-Hill: New York, NY, USA, 1941. [Google Scholar]
- Shifrin, K.S. Scattering of Light in a Turbid Medium; National Aeronautics and Space Administration: Washington, DC, USA, 1959.
- Bohren, C.F.; Huffmann, D.R. Absorption and Scattering of Light by Small Particles; Wiley-Interscience: New York, NY, USA, 2010. [Google Scholar]
- Hansen, G.M. Mie scattering as a technique for the sizing of air bubbles. Appl. Opt. 1985, 24, 3214–3220. [Google Scholar] [CrossRef] [PubMed]
- Lentz, W.J.; Atchley, A.A.; Gaitan, D.F. Mie scattering from a sonoluminescing air bubble in water. Appl. Opt. 1995, 34, 2648–2654. [Google Scholar] [CrossRef]
- Wells, J.D.; Thomsen, S.; Whitaker, P.; Jansen, E.D.; Kao, C.C.; Konrad, P.E.; Mahadevan-Jansen, A. Optically mediated nerve stimulation: Identification of injury thresholds. Lasers Surg. Med. 2007, 39, 513–526. [Google Scholar] [CrossRef]
- Errico, C.; Pierre, J.; Pezet, S.; Desailly, Y.; Lenkei, Z.; Couture, O.; Tanter, M. Ultrafast ultrasound localization microscopy for deep super-resolution vascular imaging. Nature 2015, 527, 499–502. [Google Scholar] [CrossRef]
- François, A.; Reynolds, T.; Monro, T.M. A fiber-tip label-free biological sensing platform: A practical approach toward in-vivo sensing. Sensors 2015, 15, 1168–1181. [Google Scholar] [CrossRef]
- Nguyen, L.V.; Hill, K.; Warren-Smith, S.; Monro, T. Interferometric-type optical biosensor based on exposed core microstructured optical fiber. Sens. Actuators B Chem. 2015, 221, 320–327. [Google Scholar] [CrossRef]
- Wang, X.; Wolfbeis, O.S. Fiber-optic chemical sensors and biosensors (2015–2019). Anal. Chem. 2020, 92, 397–430. [Google Scholar] [CrossRef]
- Lu, C.; Froriep, U.P.; Koppes, R.A.; Canales, A.; Caggiano, V.; Selvidge, J.; Bizzi, E.; Anikeeva, P. Polymer fiber probes enable optical control of spinal cord and muscle function in vivo. Adv. Mater. 2014, 24, 6594–6600. [Google Scholar] [CrossRef]
- Ung, K.; Arenkiel, B.R. Fiber-optic implantation for chronic optogenetic stimulation of brain tissue. J. Vis. Exp. 2012, 68, 50004. [Google Scholar] [CrossRef] [PubMed]
- Tsakas, A.; Tselios, C.; Ampeliotis, D.; Politi, C.T.; Alexandropoulos, D. Review of optical fiber technologies for optogenetics. Res. Opt. 2021, 5, 100168. [Google Scholar] [CrossRef]
- Zhang, Y.; Shibru, H.; Cooper, K.L.; Wang, A. Miniature fiber-optic multicavity Fabry–Perot interferometric biosensor. Opt. Lett. 2005, 30, 1021–1023. [Google Scholar] [CrossRef] [PubMed]
- Klantsataya, E.; Jia, P.; Ebendorff-Heidepriem, H.; Monro, T.M.; François, A. Plasmonic fiber optic refractometric sensors: From conventional architectures to recent design trends. Sensors 2017, 17, 12. [Google Scholar] [CrossRef]
- Xu, H.; Wang, G.; Ma, J.; Jin, L.; Oh, K.; Guan, B. Bubble-on-fiber (BoF): A built-in tunable broadband acousto-optic sensor for liquid-immersible in situ measurements. Opt. Express 2018, 26, 11976–11983. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Y.; Li, S.; Sun, W.; Lewis, E. Influence of bubble deformation on the signal characteristics denerated using an optical fiber gas-liquid two-phase flow sensor. Sensors 2021, 21, 7338. [Google Scholar] [CrossRef]
- Maksymov, I.S.; Greentree, A.D. Synthesis of discrete phase-coherent optical spectra from nonlinear ultrasound. Opt. Express 2017, 25, 7496–7506. [Google Scholar] [CrossRef]
- Genet, C.; Ebbesen, T.W. Light in tiny holes. Nature 2007, 445, 39–46. [Google Scholar] [CrossRef]
- de Abajo, F.J.G. Colloquium: Light scattering by particle and hole arrays. Rev. Mod. Phys. 2007, 79, 1267–1290. [Google Scholar] [CrossRef]
- Christensen, J.; Fernandez-Dominguez, A.I.; de Leon-Perez, F.; Martin-Moreno, L.; Garcia-Vidal, F.J. Collimation of sound assisted by acoustic surface waves. Nat. Phys. 2007, 3, 851–852. [Google Scholar] [CrossRef]
- Maksymov, I.S.; Greentree, A.D. Acoustically tunable optical transmission through a subwavelength hole with a bubble. Phys. Rev. A 2017, 95, 033811. [Google Scholar] [CrossRef]
- Oguz, H.N.; Prosperetti, A. The natural frequency of oscillation of gas bubbles in tubes. J. Acoust. Soc. Am. 1998, 103, 3301–3308. [Google Scholar] [CrossRef]
- Morse, P.M.; Ingard, K.U. Theoretical Acoustics; McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]
- Raciti, D.; Brocca, P.; Raudino, A.; Corti, M. Interferometric detection of hydrodynamic bubble-bubble interactions. J. Fluid Mech. 2022, 942, R1. [Google Scholar] [CrossRef]
- Corti, M.; Bonomo, M.; Raudino, A. New interferometric technique to evaluate the electric charge of gas bubbles in liquids. Langmuir 2012, 28, 6060–6066. [Google Scholar] [CrossRef]
- Tsamopoulos, J.A.; Brown, R.A. Nonlinear oscillations of inviscid drops and bubbles. J. Fluid Mech. 1983, 127, 519–537. [Google Scholar] [CrossRef]
- Ma, X.; Wang, C.; Huang, B.; Wang, G. Application of two-branch deep neural network to predict bubble migration near elastic boundaries. Phys. Fluids 2019, 31, 102003. [Google Scholar] [CrossRef]
- Zhai, H.; Zhou, Q.; Hu, G. Predicting micro-bubble dynamics with semi-physics-informed deep learning. AIP Adv. 2022, 12, 035153. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Pearson-Prentice Hall: Singapore, 1998. [Google Scholar]
- Small, M. Applied Nonlinear Time Series Analysis: Applications in Physics, Physiology and Finance; World Scientific: Singapore, 2005. [Google Scholar]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Maksymov, I.S.; Pototsky, A.; Suslov, S.A. Neural echo state network using oscillations of gas bubbles in water. Phys. Rev. E 2022, 105, 044206. [Google Scholar] [CrossRef] [PubMed]
- Baydin, A.G.; Pearlmutter, B.A.; Radul, A.A.; Siskind, J.M. Automatic differentiation in machine learning: A survey. J. Mach. Learn. Res. 2018, 18, 1–43. [Google Scholar]
- Burgers, J.M. A mathematical model illustrating the theory of turbulence. Adv. Appl. Mech. 1948, 1, 171–199. [Google Scholar]
- Lin, C.; Maxey, M.; Li, Z.; Karniadakis, G.E. A seamless multiscale operator neural network for inferring bubble dynamics. J. Fluid Mech. 2021, 929, A18. [Google Scholar] [CrossRef]
- Lin, C.; Li, Z.; Lu, L.; Cai, S.; Maxey, M.R.; Karniadakis, G.E. Operator learning for predicting multiscale bubble growth dynamics. J. Chem. Phys. 2021, 154, 104118. [Google Scholar] [CrossRef]
- Blake, J.R. The Kelvin impulse: Applications to cavitation bubble dynamics. J. Austral. Math. Soc. Ser. B 1988, 30, 127–146. [Google Scholar] [CrossRef]
- Blake, J.R.; Leppinen, D.M.; Wang, Q. Cavitation and bubble dynamics: The Kelvin impulse and its applications. Interface Focus 2015, 5, 20150017. [Google Scholar] [CrossRef]
- Yasui, K. Multibubble sonoluminescence from a theoretical perspective. Molecules 2021, 26, 4624. [Google Scholar] [CrossRef]
- Tandiono; Ohl, S.W.; Ow, D.S.W.; Klaseboer, E.; Wong, V.V.; Dumke, R.; Ohl, C.D. Sonochemistry and sonoluminescence in microfluidics. Proc. Natl. Acad. Sci. USA 2011, 108, 5996–5998. [Google Scholar] [CrossRef]
- Beguin, E.; Shrivastava, S.; Dezhkunov, N.V.; McHale, A.P.; Callan, J.F.; Stride, E. Direct evidence of multibubble sonoluminescence using therapeutic ultrasound and microbubbles. ACS Appl. Mater. Interfaces 2019, 11, 19913–19919. [Google Scholar] [CrossRef]
- Vighetto, V.; Troia, A.; Laurenti, M.; Carofiglio, M.; Marcucci, N.; Canavese, G.; Cauda, V. Insight into sonoluminescence augmented by ZnO-functionalized nanoparticles. ACS Omega 2020, 7, 6591–6600. [Google Scholar] [CrossRef] [PubMed]
- Song, D.; Xu, W.; Luo, M.; You, K.; Tang, J.; Wen, H.; Cheng, X.; Luo, X.; Wang, Z. Turning single bubble sonoluminescence from blue in pure water to green by adding trace amount of carbon nanodots. Ultrason. Sonochem. 2021, 78, 105727. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Joh, H.; Fan, D.E.; Fischer, P. Dynamic ultrasound projector controlled by light. Adv. Sci. 2022, 9, 2104401. [Google Scholar] [CrossRef]
- Goyal, R.; Athanassiadis, A.G.; Ma, Z.; Fischer, P. Amplification of acoustic forces using microbubble arrays enables manipulation of centimeter-scale objects. Phys. Rev. Lett. 2022, 128, 254502. [Google Scholar] [CrossRef] [PubMed]
- Birkin, P.R.; Watson, Y.E.; Leighton, T.G.; Smith, K.L. Electrochemical detection of Faraday waves on the surface of a gas bubble. Langmuir 2002, 18, 2135–2140. [Google Scholar] [CrossRef]
- Blamey, J.; Yeo, L.Y.; Friend, J.R. Microscale capillary wave turbulence excited by high frequency vibration. Langmuir 2013, 29, 3835–3845. [Google Scholar] [CrossRef] [PubMed]
- Faraday, M. On a peculiar class of acoustical figures; and on certain forms assumed by groups of particles upon vibrating elastic surfaces. Philos. Trans. R. Soc. Lond. 1831, 121, 299–340. [Google Scholar]
- Matafonova, G.; Batoev, V. Review on low- and high-frequency sonolytic, sonophotolytic and sonophotochemical processes for inactivating pathogenic microorganisms in aqueous media. Water Res. 2019, 166, 115085. [Google Scholar] [CrossRef]
- Phillips, N.; Draper, T.C.; Mayne, R.; Adamatzky, A. Marimo machines: Oscillators, biosensors and actuators. J. Biol. Eng. 2019, 13, 72. [Google Scholar] [CrossRef]










Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maksymov, I.S.; Huy Nguyen, B.Q.; Suslov, S.A. Biomechanical Sensing Using Gas Bubbles Oscillations in Liquids and Adjacent Technologies: Theory and Practical Applications. Biosensors 2022, 12, 624. https://doi.org/10.3390/bios12080624
Maksymov IS, Huy Nguyen BQ, Suslov SA. Biomechanical Sensing Using Gas Bubbles Oscillations in Liquids and Adjacent Technologies: Theory and Practical Applications. Biosensors. 2022; 12(8):624. https://doi.org/10.3390/bios12080624
Chicago/Turabian StyleMaksymov, Ivan S., Bui Quoc Huy Nguyen, and Sergey A. Suslov. 2022. "Biomechanical Sensing Using Gas Bubbles Oscillations in Liquids and Adjacent Technologies: Theory and Practical Applications" Biosensors 12, no. 8: 624. https://doi.org/10.3390/bios12080624
APA StyleMaksymov, I. S., Huy Nguyen, B. Q., & Suslov, S. A. (2022). Biomechanical Sensing Using Gas Bubbles Oscillations in Liquids and Adjacent Technologies: Theory and Practical Applications. Biosensors, 12(8), 624. https://doi.org/10.3390/bios12080624





