Abstract
In this work, we designed structures based on copper nanosubstrate with graphene and two-dimensional transition metal dichalcogenides (TMDC) in order to achieve an ultrasensitive surface plasmon resonance biosensor. This system contains seven components: SF11 triangular prism, BK-7 glass, Chromium (Cr) adhesion layer, thin copper film, layers of one of the types of transition metal dichalcogenides: MoS2, MoSe2, WS2 or WSe2 (defined as MX2), graphene, sensing layer with biomolecular analyte. Copper was chosen as a plasmonic material because it has a higher conductivity than gold which is commonly used in plasmonic sensors. Moreover, copper is a cheap and widespread material that is easy to produce on a large scale. We have carried out both theoretical and numerical sensitivity calculations of these kinds of structures using the Goos–Hänchen (GH) shift method. GH shift is lateral position displacement of the p-polarized reflected beam from a boundary of two media having different indices of refraction under total internal reflection condition and its value can be retrieved from the phase change of the beam. The SPR signal based on the GH shift is much more sensitive compared to other methods, including angular and wavelength scanning, due to much more abrupt phase change of the SPR reflected light than its intensity ones. By optimizing the parameters of the SPR sensing substrate, such as thickness of copper, number of layers of 2D materials and excitation wavelength, we theoretically showed an enhanced sensitivity with a detection limit 10−9 refractive index unit (RIU).
1. Introduction
The surface plasmon resonance (SPR) technique is considered as the most successful plasmonic application so far [1]. Among all biosensors, surface plasmon resonance (SPR) sensor exhibited several key advantages that cannot be achieved by other sensing techniques such as real-time detection, high signal-to-noise ratio and wide dynamic range with ultra-high sensitivity for small chemical and biological markers [2,3]. The path of the laser beam used in the technique does not pass the sample, making it available for the detection in complex samples like blood or plasma. Detection time is also better: around 10 min compared to 72 h for polymerase chain reaction (PCR) tests, and it has less preparation time. Another cost-effective advantage of SPR is the possibility to use sensor chips more than once. Sensor chips directly influence the quality of the result and serve as an essential component of biosensing.
The major barrier to broad application of plasmonic devices is the absence of available and inexpensive materials which can be easily manufactured. Most of the current SPR biosensors are based on gold thin film. However, the sensitivity for the continuous gold with thickness around 45–50 nm is not sufficient for low concentration (1 fM to 1 nM) of biomarkers detection. Recently, many research groups have investigated novel nanomaterials capable of flexible tuning the optical properties of the plasmon resonance at the sensing interface [4,5].
The stability of plasmonic materials was reached by investigating new methods of protection from oxidation. Copper (Cu) exhibits better electrical conductivity compared to gold and SPR systems can be made by using copper substrate [6]. This can be explained as follows: when atoms get larger, with a high number of electrons the influence of the positively charged core of the atom on the furthest electrons is weak. However, for atoms ending with d-orbitals, including copper which has only 29 electrons, the electrical conductivity is higher than some metals containing more electrons, such as gold with 79 outer electrons.
Graphene (~0.34 nm), which is a single carbon atomic layer that can exist at room temperature, was firstly obtained in 2004. The semi-metal properties of graphene allow the tuning of the sensitivity properties of sensing devices. When graphene layers are deposited on a metal substrate, the electron charge transfer between the graphene and gold substrate results in a large near field amplification, thus a strong plasmonic coupling will happen at the sensing areas. [7]. Work done by Geim and Novoselov made it possible to produce graphene in comparingly large scale for practical use and was awarded the Noble prize in physics in 2010 [8]. A large area of graphene layers ranging from 1 cm to 90 cm can be grown with chemical vapor deposition (CVD) method [9]. According to CVD method, graphene is first deposited on the copper substrate. In addition, copper (Cu) exhibits a higher conductivity than gold and can be used as plasmonic material. Graphene layers can also protect the Cu surface from oxidation. Cu was covered by graphene and proved by the experiment that it can retain plasmonic properties even after half of a year [10].
We have designed a hybrid SPR sensing nanostructures based on graphene and other types of 2D materials—transition metal dichalcogenides (TMDCs). TMDCs can enhance the performance of biosensors by precisely tuning the optical absorption of the sensing substrate. 2D materials used here are intended to improve the sensitivity of the system, as well as protect the metal surface from deterioration. For graphene layers, it can enhance the attachment of molecules due to the pi stacking forces. Maurya, J. B., and Prajapati Y. K. first described the reflectivity of Cu film with monolayers of MoS2 and graphene [11]. They provided the angular sensitivity of this configuration, i.e., SPR angle shift corresponding to refractive index change of the sensing media. In addition to Cu film, the reflectivity and angular sensitivity of Au, Ag and Al films with MoS2 and graphene monolayers were discussed in this work as well. Rather than interrogating the change of SPR angle, our work mostly focuses on the phase and phase-singularity enhanced GH shift. Moreover, we explored different MX2 materials more than only MoS2, such as MoSe2, WS2 and WSe2 in combination with graphene. Here, we have proposed a graphene-TMDC hybrid nanostructures for the SPR sensitivity improvement. Theoretic work was done using TMDC materials in SPR biosensors with Au-Ag bimetallic film [12] and it showed that graphene with 2 layers WS2 can improve the optical absorption, resulting lower dip in the reflectance curve under resonance condition. Additionally, the improved sensors are of great importance in the emerging field of edge sensing and computing, as described by Passian A. and Imam N. [13].
The SPR reflection spectra of this configuration were theoretically modelled by using the Transfer Matrix Method (TMM) and Fresnel equations. These equations and TMM are known to be used to study multi-layered SPR structures under excitation condition [14]. In this project, another key novelty is based on the SPR phase singularity-enhanced lateral position shift (Goos-Hänchen (GH) shift) [15]. Under the resonance condition, the large position shift due to the strong plasmon resonance coupling is only generated by the p-polarized light corresponding to the TM waves, where s polarization is taken as a reference signal. It will also significantly improve the sensing configuration’s signal-to-noise ratio. Surface plasmon resonance phenomenon can produce a GH shift larger than 50 times of the incident wavelength [16]. Moreover, it is possible to measure this position shift by a quadrant position sensor. Thus, if one can achieve an ultra-low reflection in the SPR dip, a steep optical phase jump can be obtained [17]. In general, the phase in electromagnetic mechanisms is determined by oscillation cycle of the signal. Optical phase signal can be extremely large and sharp when the light intensity is reaching zero, which means the lower the intensity at the sensing interface, the higher the phase signal change. Thus, by tuning the plasmonic nanostructures, we can achieve the darkness and enhance the phase singularity [18]. This steep phase signal change will result in a large position shift in the x-direction. An ultra-high sensitivity by 2–3 orders of magnitudes can be achieved compared to current SPR sensors based on angular or wavelength scanning [15,17]. Because of advantages of GH shift in optical sensing and precision measurement, it has been widely discussed in the chemistry and sensors area [19,20].
Here we have reported new SPR sensing substrate based on copper enhanced by TMDC materials and graphene layers. In this system, 2D materials are used to improve light absorption giving sufficient energy to electrons. Graphene is also used for enhancing the adsorption of target biomolecules through the force of pi-stacking.
The highest sensitivity value observed equals to 2.26 × 106 µm/RIU and it was obtained with TMDC material—WSe2 in combination with 2 layers of graphene under the excitation wavelength of 1024 nm in the near infrared region. The 1024 nm excitation wavelength results the highest sensitivity value for WSe2. The use of higher excitation wavelengths has an appreciable effect on the width of the resonance curve. This is one of the reasons why (near-) infrared SPR experiments are attracting attention. The width of the resonance curve is mainly determined by the complex value of the metal’s dielectric constant [21]. For the copper substrate, the 1024 nm excitation wavelength results a large imaginary part. Moreover, for graphene, the imaginary part of its refractive index gets larger with increasing the wavelength.
2. Methods
The proposed sensing configuration is consisted of the following components: SF11 triangular prism, BK-7 substrate, a chromium layer, a thin copper film, layers of one of the types of transition metal dichalcogenides: MoS2/MoSe2/WS2/WSe2 (defined as MX2), a graphene layer for capturing the targeted sample molecule, and a sensing layer with biomolecular analyte. Kretschmann’s attenuated total reflection (ATR) structure is chosen for this surface plasmon resonance sensor model. An illustration of the configuration is in Figure 1 [22].
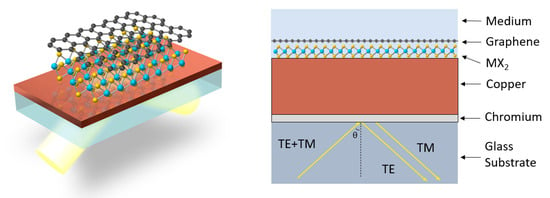
Figure 1.
Schematic picture of Cu—TMDCs—graphene enhanced SPR biosensor system. The difference of GH shift for TM and TE waves are measured in order to improve the signal to noise ratio since the signals for TE waves can be used as a reference.
In surface plasmon detection systems there are three main methods of detections:
- Angle interrogation;
- Wavelength interrogation;
- Phase change measurements;
The GH shift is in a higher order function of the optical phase, as shown in Equation (8). The lateral position shift was theoretically retrieved from the phase modulation. The reflectivity of the configuration was found from the Fresnel equations, describing the multi-layered plasmonic structures under excitation condition. Chromium adhesion layer’s thickness was chosen as 1.5 nm. The results were obtained using several incident wavelengths both in visible and near-infrared regions: 600 nm, 633 nm, 660 nm, 785 nm, and 1024 nm. Structures with varying numbers of TMDC layers were covered with 0, 1 and 2 layers of graphene.
2.1. Reflectivity (Rp) and Phase (ϕp) Calculations
Recently, phase shift detection method was implemented to significantly improve the sensitivity of SPR biosensors. Many experimental schemes for phase shift detection from the reflected light have been demonstrated [23].
To study the phase (ϕp) and reflectivity (Rp), the transfer matrix method (TMM) and the Fresnel equation for multilayer systems are taken. The system consists of coatings situated parallel to each other. Transmission matrix’s structure is defined as M in equations. Calculations for the light with p-polarization are made as follows [24]:
with
where
and
Here, nk corresponds to refractive index of k layer (Appendix A). εk corresponds to the dielectric constant. dk is the thickness of a particular layer. ϴ1 is the incident angle of the light and λ is the excitation wavelength. The reflection coefficient is indicated as rp, index “p” means belonging to the p-polarization and has a relation:
where q1 is the value for the layer number 1, qN is—the value for the last layer in Equation (3). Finally, the phase (ϕp) and reflectance (Rp) for the p-polarized light calculated:
and
The graph of reflectance (Rp) depending on the incident angle is so called SPR curve. The angle of the dip in SPR curve is known as the resonant angle of SPR (ϴSPR). This angle changes with variation of refractive index related to a surface medium that is induced from binding of target molecules.
2.2. Goos-Hanchen (GH) Shift Calculations
The phase signal (ϕp) undergoes a much sharper change compared to the change in angle of reflection or change of wavelength. GH shift (Lshift) can be determined as a higher order phase variation. Because GH shift can be calculated from the phase change as shown in Equation (8). GH shift value is directly proportional to the phase derivative of the angle of incidence. It corresponds to the displacement of reflected light from the metal surface.
Quantitative measurement of the GH shift is challenging for total internal reflection (also called weak measurement), because of its low magnitude. However, when the incident angle at the surface plasmon resonance angle, this shift could be improved by 2–3 orders.
Upon excitation of surface plasmon resonance, the reflected light intensity for p-polarization of light is close to zero, and a phase jump was detected at the resonant angle. The phase jump is a sharp, quasi-vertical phase change corresponding to different angles of incidence under the SPR excitation condition. Phase delay at this exact point results in a large GH shift. Phase (ϕp) and GH shift (Lshift) are extremely sensitive to variations of ∆ntarget from analyte in the media. In general, GH shift value is derived from the phase and angle of incidence ϴinc [25]:
The sensitivity based on GH shift method is defined as follows [15]:
According to Equation (9), the unit of sensitivity will be µm/RIU. The limit of detection of GH shift is better than values of refractive index measurements by other methods. RIU/nm is another unit of measure for the sensitivity.
GH shift values for 2 cases were calculated: with normal refractive index n, usually water, then with adding RI difference: n + ∆n. The value of ∆n was taken as 5 × 10−5 RIU. Then divide by ∆n the difference between these two GH shift values.
3. Results
3.1. Reflectance, Phase Change and GH Shift of WSe2 Structure
The sensitivity has been optimized considering three substrate parameters: the thickness of Cu, 2D materials type, and number of 2D layers.
Different excitation wavelengths were studied to obtain the optimal performance. Among the five visible and near-infrared wavelengths, it was found that 1024 nm excitation wavelength shows the highest value which equals to 2.26 × 106 µm/RIU or 4.43 × 10−10 RIU/nm. This structure consists of 35 nm Cu, 5 layers of WSe2 and 2 layers of graphene. In Figure 2, the reflectance curves are shown.
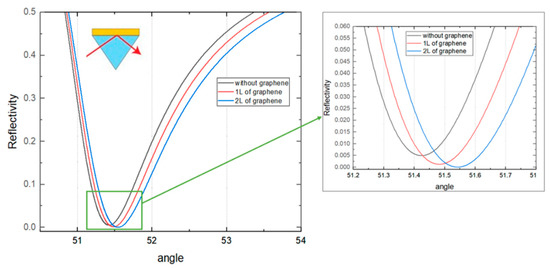
Figure 2.
Reflectivity of the structure with 5 layers of WSe2 and 35 nm of Cu depending on the angle of incidence (degrees).
In Figure 3a the phase change is shown corresponding to the structures with different number of graphene layers. The quasi-vertical phase change in SPR angle is obtained for 2 layers of graphene, therefore it has a higher value for GH shift, as shown in Figure 3b.
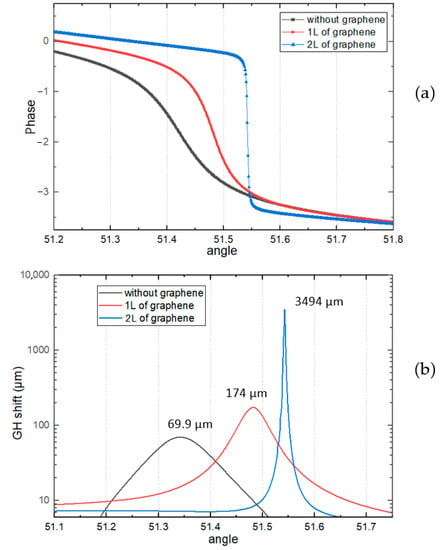
Figure 3.
Phase calculations (a) and GH shift values (b) of the structure with 5 layers of WSe2 and 35 nm of Cu depending on the angle of incidence (degrees).
The dip of the curve was shifted to the larger angle of incidence by increasing the number of graphene layers and having a lower value. The curve with the lowest reflectivity corresponds to the substrate with 2 layers of graphene. This dip in reflectance indicates the resonance angle for a given configuration and excitation wavelength. Most of the p-polarized light intensity was absorbed and thus leading to a strong resonance at the SPR angle when resonance occurred. Due to strong surface plasmon polariton coupling, minimum intensity reflected light was then detected.
3.2. Sensitivity with Graphene Layers
Firstly, structure with a copper covered by graphene was calculated. Number of layers of graphene was chosen as 2, because 1 layer will not be sufficient to protect the surface of copper from degradation, as some defects appear during the deposition process such a comparingly big surface.
As shown in the Table 1, the values for sensitivity vary from thickness of copper and wavelengths. For 30 and 50 nm of copper, the high values of sensitivity obtained mostly from the structure without graphene; for 35, 40 and 45 nm highest values are from 2 layers of graphene. Therefore, 35, 40 and 45 nm of thin copper film thicknesses were selected to achieve better performances. These calculations demonstrated the sensitivity enhancement by graphene. Moreover, copper surface oxidizes without a protective coating, resulting in much lower performance.

Table 1.
Theoretical sensitivity (µm/RIU) calculation results for SPR biosensor with different thicknesses of copper without graphene and covered with 2 layers of graphene. The best values are marked in bold.
3.3. Sensitivity with TMDC Enhanced Model
The sensing performance with different TMDC layers were further investigated in addition to the configurations with graphene only. Configurations giving best improvement to the sensitivity were shown in the Figure 4, Figure 5 and Figure 6. First, the substrate only covered by four different TMDCs, without any graphene, was simulated. Because MX2 materials itself can protect copper surface from oxidation. In Figure 4, 3 configurations of 40 nm-thick copper covered by different 2D materials are shown.
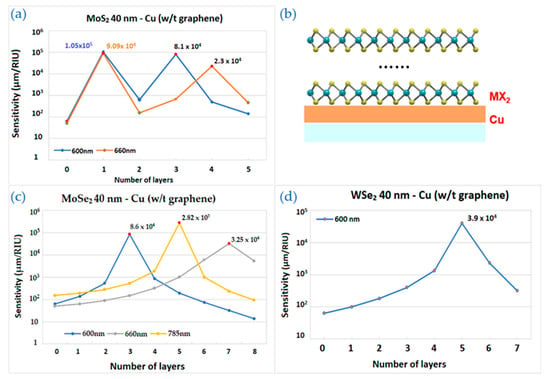
Figure 4.
The sensitivity values of the enhanced model by number of TMDC layers with 40 nm of copper: (a) The wavelengths are 600 nm and 660 nm for MoS2 layers; (b) the schematic structure; (c) The wavelengths are 600 nm, 660 nm, and 785 nm for MoSe2 layers; (d) The wavelength is 600 nm for WSe2 layers and 40 nm of Cu.
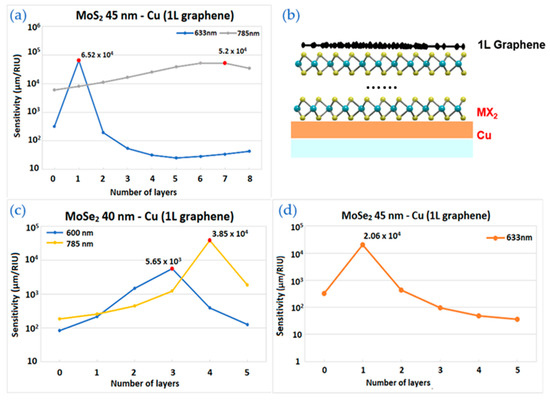
Figure 5.
The sensitivity values of the enhanced model with 1 layer of graphene by TMDC layers and thickness of copper: (a) The wavelengths are 633 nm and 785 nm for MoS2 layers with 45 nm of copper; (b) the schematic structure; (c) The wavelengths are 600 nm and 785 nm for MoSe2 layers with 40 nm of copper; (d) The wavelength is 633 nm for MoSe2 layers with 45 nm of copper.
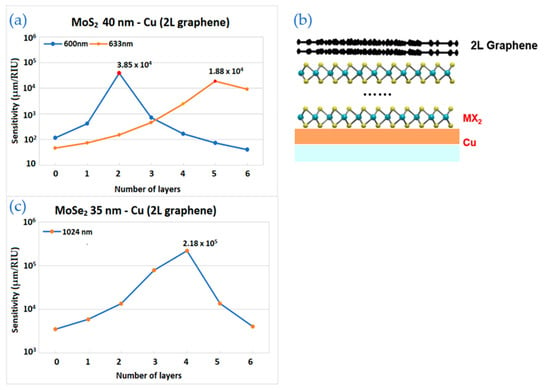
Figure 6.
The sensitivity values of the enhanced model with 2 layers of graphene by TMDC layers and thickness of copper: (a) The wavelengths are 600 nm and 633 nm for MoS2 layers with 40 nm of copper; (b) the schematic structure; (c) The wavelength is 1024 nm for MoSe2 layers with 35 nm of copper.
Values for sensitivity has been calculated for all 4 TMDC materials for different thicknesses of copper and wavelengths. In Figure 4a, for the structure with MoS2, results for the excitation wavelengths 600 nm and 660 nm are shown. Number of layers are taken up to 5 layers. The 0 layer in the graph corresponds to structure without MoS2 layers on the surface and its value is indicated for comparison. The highest values of sensitivities for both incident wavelengths are around 9 × 104 µm/RIU and correspond for 1 layer of MoS2. Another peak of sensitivity for 600 nm corresponds to 3 layers, and for 660 nm to 4 layers of MoS2. In Figure 4c, 40 nm Cu covered by different number of layers MoSe2 are shown. One can see from Figure 4 that for different excitation wavelengths, the highest SPR sensitivities are achieved with different optimum 2D material layers (600 nm with 3 layers of MoSe2, 600 nm with 7 layers and 785 nm with 5 layers). The highest sensitivity for this TMDC corresponds to 5 layers of MoSe2 and 785 nm as the incident wavelength.
In Figure 4d, thickness of copper film is 40 nm and coated by WSe2 up to 7 layers. There is only 1 excitation wavelength of 600 nm for sensitivity, because the results from other incident wavelengths are small compared to the result shown. For the excitation wavelength 600 nm and 5 layers of WSe2, the highest sensitivity for this structure was observed that equals to 3.98 × 104 µm/RIU.
The best sensitivity value from the non-graphene results was 2.82 × 105 µm/RIU shown in Figure 4c, which belongs to 5 layers of MoSe2 with 785 nm of excitation wavelength.
3.4. Sensitivity for TMDC and Graphene Enhanced Model
Previous configurations consisted of only thin film of copper covered by MX2 materials were studied. Combination of TMDC materials with graphene was taken to further enhance the sensitivity. Here we optimized the number of TDMC layers and incident wavelength. The number of graphene layers was fixed at 1.
Figure 5a illustrates the sensitivity calculations at 633 nm and 785 nm. For 1 layer of MoS2, the structure has an excellent result at 633 nm. Sensitivity value of 6.5 × 103 µm/RIU is more than 100 times higher than without MoS2 layer. A gradual increase of sensitivity was observed with 785 nm incident wavelength, having its highest value for 7 layers.
In Figure 5c, the highest sensitivity quantity received is 3.85 × 104 µm/RIU for 4 layers of MoSe2 on 40 nm Cu substrate at 785 nm. The sensitivities at 600 nm are also shown for comparison and its peak corresponding to 3 layers equals to 5.65 × 103 µm/RIU.
Figure 5d shows the sensitivities of MoSe2 layers on 45 nm thick copper film with 633 nm excitation. The best sensitivity value corresponds to 1 layer of MoSe2. For other wavelengths, particularly for 660 nm, the curve has almost 4 times lower maximum sensitivity value.
Figure 6 shows the sensitivity results for MX2-graphene enhanced structure. The main difference from the structures above is 2 layers of graphene on top of thin layer of copper covered by TMDC layers. As shown in Figure 6, the optimal results do not always have the same wavelength and copper thickness.
Figure 6a shows the calculation by varying MoS2 layers with fixed 2 layers of graphene. The structure working at 600 nm and 633 nm has maximum sensitivities with 2 and 5 layers of TMDC, respectively. In Figure 6b, the schematic image of the structure is drawn.
In Figure 6c, there is a curve corresponding for 35 nm of Cu in near infrared wavelength range—1024 nm and with 2 layers of graphene. Sensitivity increases gradually starting from 0 up to 4 layers of MoSe2, where reaches its highest value—2.18 × 105 µm/RIU and decreases with a further addition in the number of layers.
Figure 7a shows the result for the configuration with 35 nm of copper film and 1024 nm near-infrared excitation wavelength. This SPR substrate exhibits the highest sensitivity observed so far, containing 5 layers of WSe2 and 2 layers of graphene. Its value equals to 2.26 × 106 µm/RIU or 4.43 × 10−10 RIU/nm in another form.
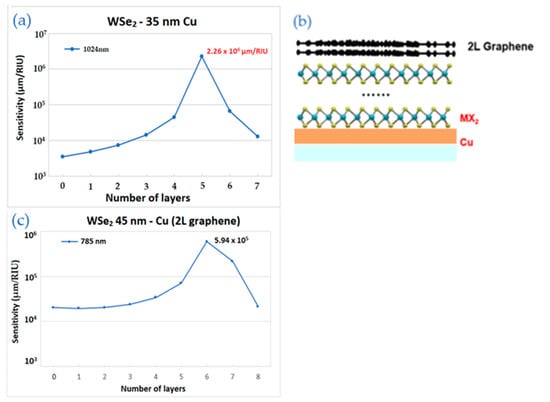
Figure 7.
The sensitivity values of the enhanced model with 2 layers of graphene by TMDC layers and thickness copper: (a) The wavelength is 1024 nm for WSe2 layers with 35 nm of copper; (b) the schematic structure; (c) The wavelength is 1024 nm for WSe2 layers with 45 nm of copper.
4. Discussion
4.1. Comparison of Structures without and 1, 2 Layers of Graphene
By using different incident wavelengths from 600 nm up to near-infrared 1024 nm, variation of the complex refractive index was observed. Especially the ratio between the real and imaginary part has a big influence on optical properties of the material.
In Table 2, the maximum sensitivity values for structures of different number of graphene layers with 4 different TMDC materials with varying thickness of copper are shown. Here, sensitivity values for some structures are skipped, due to their low value even when compared to the structure without TMDC material.

Table 2.
Sensitivity values (µm/RIU) by graphene layers with MX2 materials. In the brackets number of MX2 layers and excitation wavelength are indicated.
The highest values of sensitivity are highlighted. First, comparing the results from the different thicknesses of thin copper film, it was found that only 35, 40 and 45 nm of Cu gives the best results. When the thickness of copper is too big, light cannot penetrate deep enough to excite surface plasmon polaritons on the other side of the metal. In addition, in the opposite case, when the thickness of copper is too small, there are not enough free electrons to create strong oscillations. Therefore, it was confirmed that the optimal thickness of thin copper film is from 35 up to 45 nm.
4.2. Best Results for Each Wavelength
These hybrid systems are highly dependent from excitation wavelength and incident angle of the beam. It is important to determine the best performance for every excitation wavelength used. Using different excitation wavelengths from visible and infrared regions causes a change in the complex refractive index. The ratio between real and imaginary part changes resulting in different optical properties of a plasmonic substrate.
Table 3 shows the best results for each wavelength. The maximum sensitivity values grow by applying bigger excitation wavelengths. It is caused by transmittance of graphene [26] and TMDC materials [27]. The highest sensitivities for 600 nm, 633 nm and 660 nm incident light corresponds to the structure with 1 layer of graphene or without any graphene. This indicates that for these relatively short wavelengths graphene transmits electromagnetic waves inefficiently. For wavelengths in the red or infrared region, the best values correspond to 5–6 layers of TMDC with 2 layers of graphene. These configurations still transmit light and show even better performances. The imaginary part in a refractive index related to absorption coefficient and can change the materials absorption properties with varying incident wavelength.

Table 3.
Highest sensitivity values (µm/RIU) for wavelengths: 600 nm, 633 nm, 660 nm, 785 nm, and 1024 nm.
The best sensitivity observed corresponds to near infrared—1024 nm incident wavelength and its value equals to 2.26 × 106 µm/RIU. This result is almost 4 times higher than for 785 nm excitation wavelength. The structure consists of 35 nm Cu, 5 layers of WSe2 and 2 layers of graphene. While 10 layers of graphene applied on Au surface, the performance of the plasmonic biosensor was improved by 25% [28].
In Table 3, only 3 TMDC materials from 4 used during simulations are included, which means that WS2 has poor plasmonic performance than other materials used. WS2 has relatively low maximum of sensitivity—5788 µm/RIU and it is almost 390 times lower than the best result observed.
5. Conclusions
We have demonstrated sensitivity calculations of the SPR system consisting of graphene with two dimensional TMDCs on Kretschmann configuration. The wavelength of incident light affects sensor’s performance. Five different wavelengths were chosen, both in visible and near-infrared region: 600 nm, 633 nm, 660 nm, 785 nm, and 1024 nm. TMM and Fresnel equations applied for phase change calculations.
To investigate the enhancement in sensitivity of such biosensors, we designed different models, such as graphene-MoS2, graphene-MoSe2, graphene-WS2 and graphene-WSe2. Moreover, we calculated systems only with graphene layers and then only with TMDC layers, to explore all the possible options. Even 2 layers of graphene, on top of thin copper film with a thickness from 35 up to 45 nm, can enhance the SPR resonance resulting better performance. TMDC materials can be used as a protection for copper surface from oxidation as graphene, so it can be used without graphene layers. We still observe some enhancement with only TMDC materials, and its highest value corresponds to 2.82 × 105 µm/RIU. This value is from using 5 layers of MoSe2 with 40 nm of copper with 785 nm incident wavelength.
TMDC materials in combination with graphene gives even higher sensitivity results. The best value for sensitivity was 2.26 × 106 µm/RIU, which is 1 order higher than the configuration without graphene.
With our system, we observed excellent sensitivity, and its detection limit equals to 8.8 × 10−9 RIU—lower than measurements with angle or wavelength interrogation [29]. This result corresponds to 5 layers of WSe2 and 2 layers of graphene, showing that combination of graphene with TMDC can enhance the sensitivity significantly.
These findings show that the thin copper film together with each of four TMDC materials could enhance the SPR effect and notably improve the sensitivity of the biosensors. Moreover, by varying the thickness of copper film and combining TMDC materials with graphene layers, it is possible to reach even higher values of detection sensitivity. These results are important for biosensors development, where sensitivity and stability are crucial for the effective use of final product.
Author Contributions
Conceptualization, S.Z. (Shuwen Zeng) and N.Z.; methodology, S.Z. (Shuwen Zeng); software, N.Z.; formal analysis, N.Z., S.Z. (Shaodi Zhu), A.B., G.L. and R.B.; investigation, N.Z. and S.Z. (Shaodi Zhu); writing—original draft preparation, N.Z.; writing—review and editing, S.Z. (Shuwen Zeng), S.Z. (Shaodi Zhu), A.B. and R.B.; visualization, S.Z. (Shaodi Zhu); supervision, S.Z. (Shuwen Zeng); funding acquisition, S.Z. (Shuwen Zeng). All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported under the UTT Project Stratégique NanoSPR (OPE-2022-0293), the Graduate School (Ecole Universitaire de Recherche) “NANOPHOT” (ANR-18-EURE-0013), ANR Région Grand Est with project number DRD-19, PHC PROCORE-Campus France/Hong Kong Joint Research Scheme (No. 44683Q) and AAP1-LABEX SigmaPIX 2021.
Data Availability Statement
Data and MATLAB software underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Refractive Indices of Layers
Refractive index is one of the most important values for our calculations. The refractive index values for each layer were taken from reliable sources [30,31,32,33,34,35]. Refractive index values of Transition metal dichalcogenide (TMDC) were taken from the open database [30]. SF11 prism’s dispersion formula n1 as follows:
where λ refers to wavelength in micrometers and in range of 0.37–2.50 microns.
The second layer is the BK7′s refractive index n2 can be found as follows [30]:
The complex refractive index of Chromium and copper thin film are from experimental data [31,32]. For graphene [33] the refractive index can be calculated as:
where C1 = 5.446 µm−1. 1 layer of graphene has a thickness around 0.34 nm.
Fifth layer of the proposed SPR substrate is TMDC material and its complex refractive index and thickness are taken from experimental works as shown in Table A1 [34,35].

Table A1.
The complex refractive indices of MoS2, MoSe2, WS2, and WSe2 with different excitation wavelengths from 600 nm to 1024 nm.
Table A1.
The complex refractive indices of MoS2, MoSe2, WS2, and WSe2 with different excitation wavelengths from 600 nm to 1024 nm.
| Type of TMDC | Thickness of Monolayer TMDC (nm) | λ = 600 nm | λ = 633 nm | λ = 660 nm | λ = 785 nm | λ = 1024 nm |
|---|---|---|---|---|---|---|
| MoS2 | 0.65 | n = 4.3934 | n = 5.0805 | n = 4.9991 | n = 4.6348 | n = 4.5660 |
| κ = 1.2269 | κ = 1.1723 | κ = 1.2563 | κ = 0.1163 | κ = 0.1058 | ||
| MoSe2 | 0.7 | n = 4.7586 | n = 4.6226 | n = 4.4963 | n = 4.2984 | n = 3.8768 |
| κ = 1.1504 | κ = 1.0063 | κ = 0.9382 | κ = 0.8225 | κ = 0.3561 | ||
| WS2 | 0.8 | n = 3.5202 | n = 4.8937 | n = 4.4735 | n = 4.0123 | n = 5.0110 |
| κ = 0.6048 | κ = 0.3124 | κ = 0.2059 | κ = 0.0399 | κ = 0.2562 | ||
| WSe2 | 0.7 | n = 4.5039 | n = 4.5501 | n = 4.3357 | n = 4.3655 | n = 4.8690 |
| κ = 0.9340 | κ = 0.4332 | κ = 0.2532 | κ = 0.0367 | κ = 0.2444 |
The formula of complex dielectric constant is as follows:
ε = ε′ + ε″i
In the formula above, ε′ corresponds to energy inside of the material. And ε″ corresponds to the energy dissipation. It is possible to retrieve the refractive index with following relation:
where the real part n corresponds to the phase velocity and the imaginary part κ known as the extinction coefficient and refers to the mass attenuation coefficient [36].
ñ = √ε = n + κi
References
- Liedberg, B.; Nylander, C.; Lundström, I. Biosensing with surface plasmon resonance—How it all started. Biosens. Bioelectron. 1995, 10, 1–9. [Google Scholar] [CrossRef]
- Zheng, G.; Chen, Y.; Bu, L.; Xu, L.; Su, W. Waveguide-coupled surface phonon resonance sensors with super-resolution in the mid-infrared region. Opt. Lett. 2016, 41, 1582–1585. [Google Scholar] [CrossRef] [PubMed]
- Gupta, G.; Kondoh, J. Tuning and sensitivity enhancement of surface plasmon resonance sensor. Sens. Actuators B Chem. 2007, 122, 381–388. [Google Scholar] [CrossRef]
- Jia, B.; Chen, J.; Zhou, J.; Zeng, Y.; Ho, H.-P.; Shao, Y. Passively and actively enhanced surface plasmon resonance sensing strategies towards single molecular detection. Nano Res. 2022, 15, 8367–8388. [Google Scholar] [CrossRef]
- Naik, G.V.; Shalaev, V.M.; Boltasseva, A. Alternative Plasmonic Materials: Beyond Gold and Silver. Adv. Mater. 2013, 25, 3264–3294. [Google Scholar] [CrossRef] [PubMed]
- Futamata, M. Application of attenuated total reflection surface-plasmon-polariton Raman spectroscopy to gold and copper. Appl. Opt. 1997, 36, 364–375. [Google Scholar] [CrossRef] [PubMed]
- Kang, L.; Chu, J.; Zhao, H.; Xu, P.; Sun, M. Recent progress in the applications of graphene in surface-enhanced Raman scattering and plas-mon-induced catalytic reactions. J. Mater. Chem. C 2015, 3, 9024–9037. [Google Scholar] [CrossRef]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nanosci. Technol. 2010, 1, 11–19. [Google Scholar]
- Xue, Y.; Wu, B.; Guo, Y.; Huang, L.; Jiang, L.; Chen, J.; Geng, D.; Liu, Y.; Hu, W.; Yu, G. Synthesis of large-area, few-layer graphene on iron foil by chemical vapor deposition. Nano Res. 2011, 4, 1208–1214. [Google Scholar] [CrossRef]
- Kravets, V.G.; Jalil, R.; Kim, Y.-J.; Ansell, D.; Aznakayeva, D.E.; Thackray, B.; Britnell, L.; Belle, B.D.; Withers, F.; Radko, I.; et al. Graphene-protected copper and silver plasmonics. Sci. Rep. 2014, 4, 5517. [Google Scholar] [CrossRef]
- Maurya, J.B.; Prajapati, Y.K. A comparative study of different metal and prism in the surface plasmon resonance bio-sensor having MoS2-graphene. Opt. Quantum Electron. 2016, 48, 1–12. [Google Scholar] [CrossRef]
- Wang, M.; Huo, Y.; Jiang, S.; Zhang, C.; Yang, C.; Ning, T.; Liu, X.; Li, C.; Zhang, W.; Man, B. Theoretical design of a surface plasmon resonance sensor with high sensitivity and high resolution based on graphene–WS2 hybrid nanostructures and Au–Ag bimetallic film. RSC Adv. 2017, 7, 47177–47182. [Google Scholar] [CrossRef]
- Passian, A.; Imam, N. Nanosystems, Edge Computing, and the Next Generation Computing Systems. Sensors 2019, 19, 4048. [Google Scholar] [CrossRef]
- Huamán, A.; Usaj, G. Anomalous Goos-Hänchen shift in the Floquet scattering of Dirac fermions. Phys. Rev. A 2019, 100, 033409. [Google Scholar] [CrossRef]
- Shaaban, A.; Hameed, M.F.O.; Gomaa, L.; Obayya, S. Accurate calculation of Goos-Hänchen shift at critical angle for complex laser beam profiles using beam propagation method. Optik 2018, 157, 1106–1114. [Google Scholar] [CrossRef]
- Yin, X.; Hesselink, L.; Liu, Z.; Fang, N.; Zhang, X. Large positive and negative lateral optical beam displacements due to surface plasmon resonance. Appl. Phys. Lett. 2004, 85, 372–374. [Google Scholar] [CrossRef]
- A Carvalho, S.; De Leo, S.; Huguenin, J.A.O.; Martino, M.; Da Silva, L. Experimental evidence of laser power oscillations induced by the relative Fresnel (Goos–Hänchen) phase. Laser Phys. Lett. 2019, 16, 065001. [Google Scholar] [CrossRef]
- Kravets, V.G.; Schedin, F.; Jalil, R.; Britnell, L.; Gorbachev, R.; Ansell, D.; Thackray, B.; Novoselov, K.; Geim, A.K.; Kabashin, A.; et al. Singular phase nano-optics in plasmonic metamaterials for label-free single-molecule detection. Nat. Mater. 2013, 12, 304–309. [Google Scholar] [CrossRef]
- Saito, H.; Neo, Y.; Matsumoto, T.; Tomita, M. Giant and highly reflective Goos-Hänchen shift in a metal-dielectric multilayer Fano structure. Opt. Express 2019, 27, 28629–28639. [Google Scholar] [CrossRef]
- Malik, A.; You-Lin, C.; Muqadder, A. Giant negative and positive Goos–Hänchen shifts via Doppler broadening effect. Laser Phys. 2019, 29, 075201. [Google Scholar] [CrossRef]
- Kooyman, R.P.H. Physics of Surface Plasmon Resonance. In Handbook of Surface Plasmon Resonance; Royal Society of Chemistry: London, UK, 2008. [Google Scholar]
- Kretschmann, E.; Raether, H. Notizen: Radiative Decay of Non Radiative Surface Plasmons Excited by Light. Z. Nat. A 1968, 23, 2135–2136. [Google Scholar] [CrossRef]
- Sreekanth, K.V.; Das, C.M.; Medwal, R.; Mishra, M.; Oyang, Q.; Rawat, R.S.; Yong, K.-T.; Sing, R. Electrically Tunable Singular Phase and Goos–Hänchen Shifts in Phase-Change-Material-Based Thin-Film Coatings as Optical Absorbers. Adv. Mater. 2021, 33, 2006926. [Google Scholar] [CrossRef] [PubMed]
- Zeng, S.; Hu, S.; Xia, J.; Anderson, T.; Dinh, X.-Q.; Meng, X.-M.; Coquet, P.; Yong, K.-T. Graphene–MoS2 hybrid nanostructures enhanced surface plasmon resonance biosensors. Sens. Actuators B Chem. 2015, 207, 801–810. [Google Scholar] [CrossRef]
- Zeng, S.; Baillargeat, D.; Ho, H.-P.; Yong, K.-T. Nanomaterials enhanced surface plasmon resonance for biological and chemical sensing applications. Chem. Soc. Rev. 2014, 43, 3426–3452. [Google Scholar] [CrossRef]
- Xiong, X.; Jiang, C.; Xie, Q. Broadband transmission properties of graphene-dielectric interfaces. Results Phys. 2019, 14, 102521. [Google Scholar] [CrossRef]
- Chaves, A.; Azadani, J.G.; Alsalman, H.; Da Costa, D.R.; Frisenda, R.; Chaves, A.J.; Song, S.H.; Kim, Y.D.; He, D.; Zhou, J.; et al. Bandgap engineering of two-dimensional semiconductor materials. NPJ 2D Mater. Appl. 2020, 4, 1–21. [Google Scholar] [CrossRef]
- Wu, L.; Chu, H.S.; Koh, W.S.; Li, E.P. Highly sensitive graphene biosensors based on surface plasmon resonance. Opt. Express 2010, 18, 14395–14400. [Google Scholar] [CrossRef]
- Zeng, Y.; Hu, R.; Wang, L.; Gu, D.; He, J.; Wu, S.-Y.; Ho, H.-P.; Li, X.; Qu, J.; Gao, B.Z.; et al. Recent advances in surface plasmon resonance imaging: Detection speed, sensitivity, and portability. Nanophotonics 2017, 6, 1017–1030. [Google Scholar] [CrossRef]
- Polyanskiy, M.N. Refractive Index Database. Available online: https://refractiveindex.info (accessed on 25 April 2022).
- Johnson, P.B.; Christy, R.W. Optical constants of transition metals: Ti, V, Cr, Mn, Fe, Co, Ni, and Pd. Phys. Rev. B 1974, 9, 5056. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical Constants of the Noble Metals. Phys. Rev. B 1972, 6, 4370. [Google Scholar] [CrossRef]
- Bruna, M.; Borini, S.M. Optical constants of graphene layers in the visible range. Appl. Phys. Lett. 2009, 94, 031901. [Google Scholar] [CrossRef]
- Li, Y.; Chernikov, A.; Zhang, X.; Rigosi, A.; Hill, H.M.; van der Zande, A.M.; Chenet, D.A.; Shih, E.-M.; Hone, J.; Heinz, T.F. Measurement of the optical dielectric function of monolayer transition-metal dichalcogenides: MoS2, MoSe2, WS2, and WSe2. Phys. Rev. B 2014, 90, 205422. [Google Scholar] [CrossRef]
- Liu, H.-L.; Shen, C.-C.; Su, S.-H.; Hsu, C.-L.; Li, M.-Y.; Li, L.-J. Optical properties of monolayer transition metal dichalcogenides probed by spectroscopic ellipsometry. Appl. Phys. Lett. 2014, 105, 201905. [Google Scholar] [CrossRef]
- Ouyang, Q.; Zeng, S.; Jiang, L.; Hong, L.; Xu, G.; Dinh, X.Q.; Qian, J.; He, S.; Qu, J.; Coquet, P.; et al. Sensitivity Enhancement of Transition Metal Dichalcogenides/Silicon Nanostructure-based Surface Plasmon Resonance Biosensor. Sci. Rep. 2016, 6, 28190. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).