Dissociation Constant of Integrin-RGD Binding in Live Cells from Automated Micropipette and Label-Free Optical Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Cell Culture and Seeding
2.2. Surface Coating
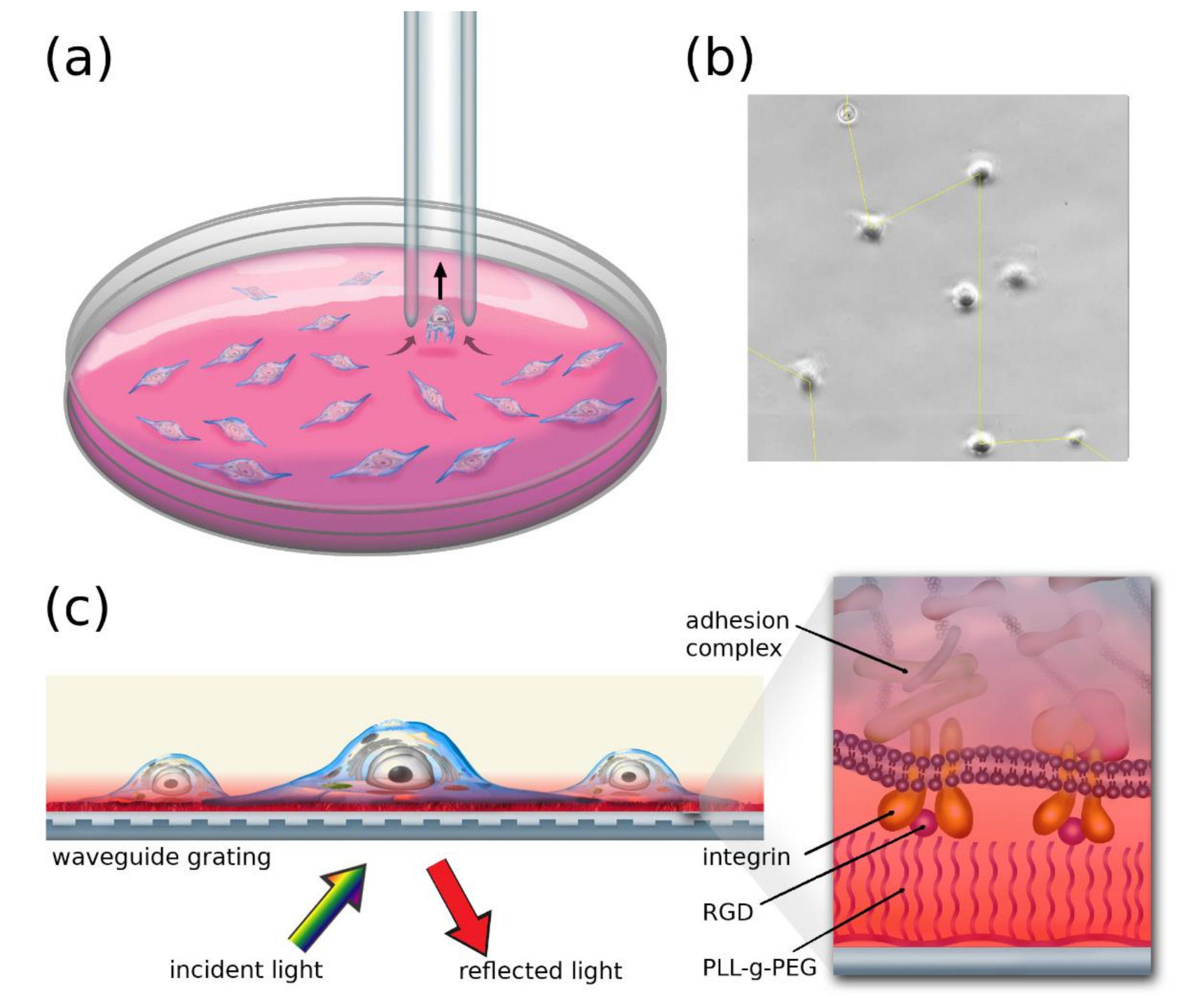
2.3. Micropipette Measurements
2.4. The Resonant Waveguide Grating (RWG) Imager Biosensor
3. Results
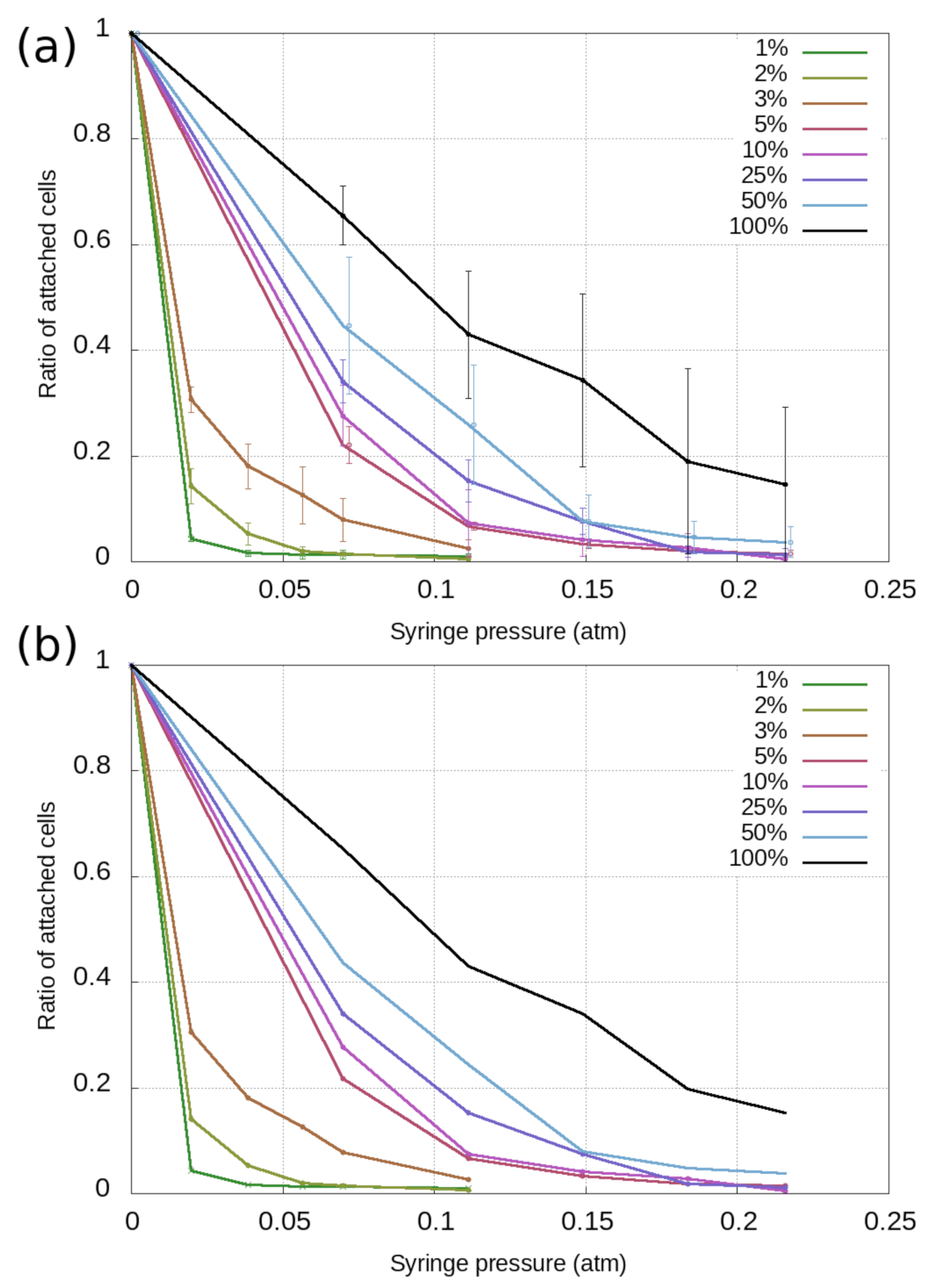
3.1. Cell-Based Dissociation Assay
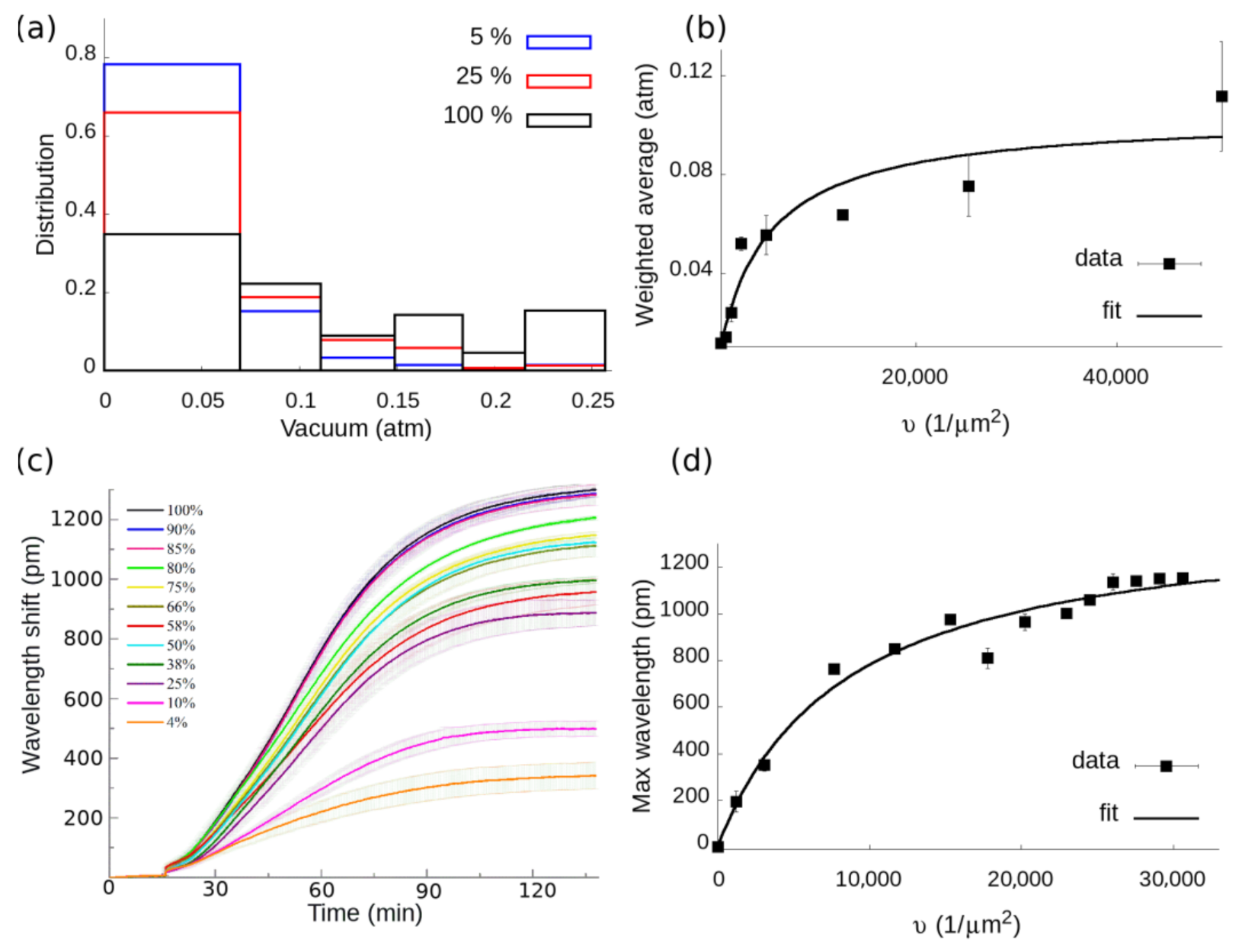
3.2. Cell Adhesion on RGD-Tuned Surfaces with RWG Biosensor
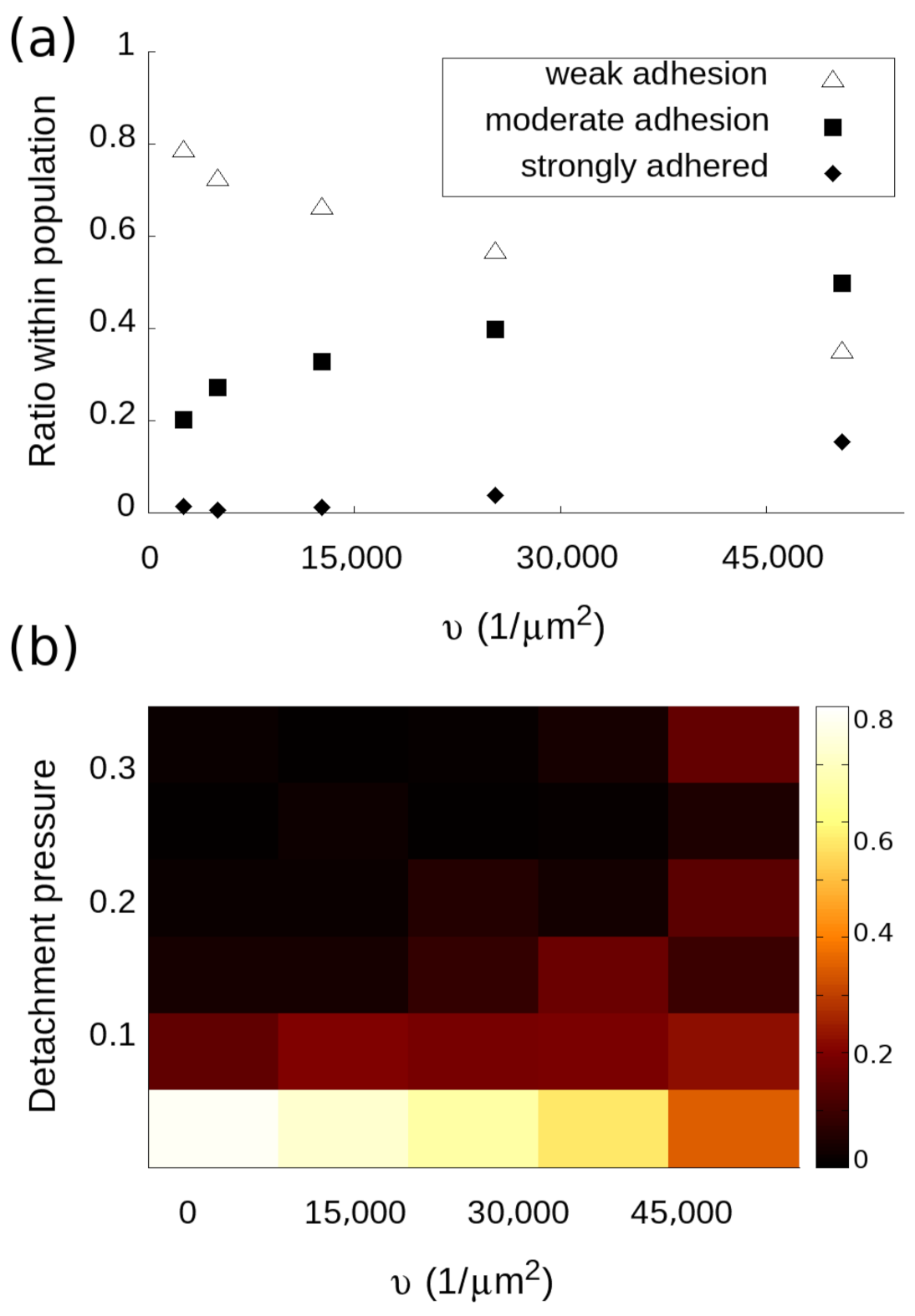
3.3. Analysis of Subpopulations
4. Discussion and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Beckerle, M.C. Cell Adhesion; Oxford University Press Inc.: New York, NY, USA, 2001. [Google Scholar]
- Slack, J.M.W. Molecular Biology of the Cell. In Principles of Tissue Engineering, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar] [CrossRef]
- Galbraith, C.G.; Yamada, K.M.; Sheetz, M.P. The relationship between force and focal complex development. J. Cell Biol. 2002, 159, 695–705. [Google Scholar] [CrossRef] [PubMed]
- Dermutz, H.; Gruter, R.R.; Truong, A.M.; Demkó, L.; Voros, J.; Zambelli, T. Local polymer replacement for neuron patterning and in situ neurite guidance. Langmuir 2014, 30, 7037–7046. [Google Scholar] [CrossRef]
- Saftics, A.; Turk, B.; Sulyok, A.; Nagy, N.; Gerecsei, T.; Szekacs, I.; Kurunczi, S.; Horvath, R. Biomimetic Dextran-Based Hydrogel Layers for Cell Micropatterning over Large Areas Using the FluidFM BOT Technology. Langmuir 2019, 35, 2412–2421. [Google Scholar] [CrossRef]
- Irvine, D.J.; Mayes, A.M.; Griffith, L.G. Nanoscale clustering of RGD peptides at surfaces using comb polymers. 1. Synthesis and characterization of comb thin films. Biomacromolecules 2001, 2, 85–94. [Google Scholar] [CrossRef]
- Cavalcanti-Adam, E.A.; Micoulet, A.; Blümmel, J.; Auernheimer, J.; Kessler, H.; Spatz, J.P. Lateral spacing of integrin ligands influences cell spreading and focal adhesion assembly. Eur. J. Cell Biol. 2006, 85, 219–224. [Google Scholar] [CrossRef]
- Huang, J.; Grater, S.V.; Corbellini, F.; Rinck, S.; Bock, E.; Kemkemer, R.; Kessler, H.; Ding, J.; Spatz, J.P. Impact of order and disorder in RGD nanopatterns on cell adhesion. Nano Lett. 2009, 9, 1111–1116. [Google Scholar] [CrossRef]
- VandeVondele, S.; Vörös, J.; Hubbell, J.A. RGD-grafted poly-L-lysine-graft-(polyethylene glycol) copolymers block non-specific protein adsorption while promoting cell adhesion. Biotechnol. Bioeng. 2003, 82, 784–790. [Google Scholar] [CrossRef]
- Schlapak, R.; Armitage, D.; Saucedo-Zeni, N.; Chrzanowski, W.; Hohage, M.; Caruana, D.; Howorka, S. Selective protein and DNA adsorption on PLL-PEG films modulated by ionic strength. Soft Matter 2009, 5, 613–625. [Google Scholar] [CrossRef]
- Kanyo, N.; Kovacs, K.D.; Saftics, A.; Szekacs, I.; Peter, B.; Santa-Maria, A.R.; Walter, F.R.; Dér, A.; Deli, M.A.; Horvath, R. Glycocalyx regulates the strength and kinetics of cancer cell adhesion revealed by biophysical models based on high resolution label-free optical data. Sci. Rep. 2020, 10, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Guo, L.; Chen, B.; Liu, R.; Liu, P.; Xia, G.; Wang, Y.; Li, X.; Chen, W.; Wang, X.; Jiang, H. Biocompatibility assessment of polyethylene glycol-poly l-lysine-poly lactic-co-glycolic acid nanoparticles in vitro and in vivo. J. Nanosci. Nanotechnol. 2015, 15, 3710–3719. [Google Scholar] [CrossRef] [PubMed]
- Orgovan, N.; Peter, B.; Bősze, S.; Ramsden, J.J.; Szabó, B.; Horvath, R. Dependence of cancer cell adhesion kinetics on integrin ligand surface density measured by a high-throughput label-free resonant waveguide grating biosensor. Sci. Rep. 2015, 4, 4034. [Google Scholar] [CrossRef] [PubMed]
- Chandra, P.; Prakash, R.; Applications, T. Nanobiomaterial Engineering; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar] [CrossRef]
- Ungai-Salánki, R.; Peter, B.; Gerecsei, T.; Orgovan, N.; Horvath, R.; Szabó, B. A practical review on the measurement tools for cellular adhesion force. Adv. Colloid Interface Sci. 2019, 269, 309–333. [Google Scholar] [CrossRef] [PubMed]
- Salánki, R.; Hős, C.; Orgovan, N.; Peter, B.; Sándor, N.; Bajtay, Z.; Erdei, A.; Horvath, R.; Szabó, B. Single cell adhesion assay using computer controlled micropipette. PLoS ONE 2014, 9, e111450. [Google Scholar] [CrossRef] [PubMed]
- Gerecsei, T.; Erdődi, I.; Peter, B.; Hős, C.; Kurunczi, S.; Derényi, I.; Szabó, B.; Horvath, R. Adhesion force measurements on functionalized microbeads: An in-depth comparison of computer controlled micropipette and fluidic force microscopy. J. Colloid Interface Sci. 2019, 555, 245–253. [Google Scholar] [CrossRef]
- Zhu, D.M.; Dustin, M.L.; Cairo, C.W.; Golan, D.E. Analysis of two-dimensional dissociation constant of laterally mobile cell adhesion molecules. Biophys. J. 2007, 92, 1022–1034. [Google Scholar] [CrossRef]
- Yu, L.; Hou, Y.; Xie, W.; Camacho, J.L.C.; Cheng, C.; Holle, A.; Young, J.; Trappmann, B.; Zhao, W.; Melzig, M.F.; et al. Ligand Diffusion Enables Force-Independent Cell Adhesion via Activating α5β1 Integrin and Initiating Rac and RhoA Signaling. Adv. Mater. 2020, 32, 1–12. [Google Scholar] [CrossRef]
- Bell, G.I.; Dembo, M.; Bongrand, P. Cell adhesion. Competition between nonspecific repulsion and specific bonding. Biophys. J. 1984, 45, 1051–1064. [Google Scholar] [CrossRef]
- Goodman, S.L.; Holzemann, G.; Sulyok, G.A.; Kessler, H. Nanomolar small molecule inhibitors for alphav(beta)6, alphav(beta)5, and alphav(beta)3 integrins. J. Med. Chem. 2002, 45, 1045–1051. [Google Scholar] [CrossRef]
- Frank, A.O.; Otto, E.; Mas-Moruno, C.; Schiller, H.B.; Marinelli, L.; Cosconati, S.; Bochen, A.; Vossmeyer, D.; Zahn, G.; Stragies, R.; et al. Conformational control of integrin-subtype selectivity in isodgr peptide motifs: A biological switch. Angew. Chem. Int. Ed. 2010, 49, 9278–9281. [Google Scholar] [CrossRef]
- Kapp, T.G.; Rechenmacher, F.; Neubauer, S.; Maltsev, O.V.; Cavalcanti-Adam, E.A.; Zarka, R.; Reuning, U.; Notni, J.; Wester, H.J.; Mas-Moruno, C.; et al. A comprehensive evaluation of the activity and selectivity profile of ligands for RGD-binding integrins. Sci. Rep. 2017, 7, 1–13. [Google Scholar] [CrossRef]
- Van der Flier, A.; Badu-Nkansah, K.; Whittaker, C.A.; Crowley, D.; Bronson, R.T.; Lacy-Hulbert, A.; Hynes, R.O. Endothelial α5 and αv integrins cooperate in remodeling of the vasculature during development. Development 2010, 137, 2439–2449. [Google Scholar] [CrossRef] [PubMed]
- Koo, L.Y.; Irvine, D.J.; Mayes, A.M.; Lauffenburger, D.A.; Griffith, L.G. Co-regulation of cell adhesion by nanoscale RGD organization and mechanical stimulus. J. Cell Sci. 2002, 115, 1423–1433. [Google Scholar] [PubMed]
- Assa-Munt, N.; Jia, X.; Laakkonen, P.; Ruoslahti, E. Solution structures and integrin binding activities of an RGD peptide with two isomers. Biochemistry 2001, 40, 2373–2378. [Google Scholar] [CrossRef] [PubMed]
- Bochen, A.; Marelli, U.K.; Otto, E.; Pallarola, D.; Mas-Moruno, C.; Di Leva, F.S.; Boehm, H.; Spatz, J.P.; Novellino, E.; Kessler, H.; et al. Biselectivity of isoDGR peptides for fibronectin binding integrin subtypes α5β1 and αvβ6: Conformational control through flanking amino acids. J. Med. Chem. 2013, 56, 1509–1519. [Google Scholar] [CrossRef] [PubMed]
- Sztilkovics, M.; Gerecsei, T.; Peter, B.; Saftics, A.; Kurunczi, S.; Szekacs, I.; Szabo, B.; Horvath, R. Single-cell adhesion force kinetics of cell populations from combined label-free optical biosensor and robotic fluidic force microscopy. Sci. Rep. 2020, 10, 1–13. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gerecsei, T.; Chrenkó, P.; Kanyo, N.; Péter, B.; Bonyár, A.; Székács, I.; Szabo, B.; Horvath, R. Dissociation Constant of Integrin-RGD Binding in Live Cells from Automated Micropipette and Label-Free Optical Data. Biosensors 2021, 11, 32. https://doi.org/10.3390/bios11020032
Gerecsei T, Chrenkó P, Kanyo N, Péter B, Bonyár A, Székács I, Szabo B, Horvath R. Dissociation Constant of Integrin-RGD Binding in Live Cells from Automated Micropipette and Label-Free Optical Data. Biosensors. 2021; 11(2):32. https://doi.org/10.3390/bios11020032
Chicago/Turabian StyleGerecsei, Tamás, Péter Chrenkó, Nicolett Kanyo, Beatrix Péter, Attila Bonyár, Inna Székács, Balint Szabo, and Robert Horvath. 2021. "Dissociation Constant of Integrin-RGD Binding in Live Cells from Automated Micropipette and Label-Free Optical Data" Biosensors 11, no. 2: 32. https://doi.org/10.3390/bios11020032
APA StyleGerecsei, T., Chrenkó, P., Kanyo, N., Péter, B., Bonyár, A., Székács, I., Szabo, B., & Horvath, R. (2021). Dissociation Constant of Integrin-RGD Binding in Live Cells from Automated Micropipette and Label-Free Optical Data. Biosensors, 11(2), 32. https://doi.org/10.3390/bios11020032






