A Novel Efficient FEM Thin Shell Model for Bio-Impedance Analysis
Abstract
1. Introduction
2. Materials and Methods
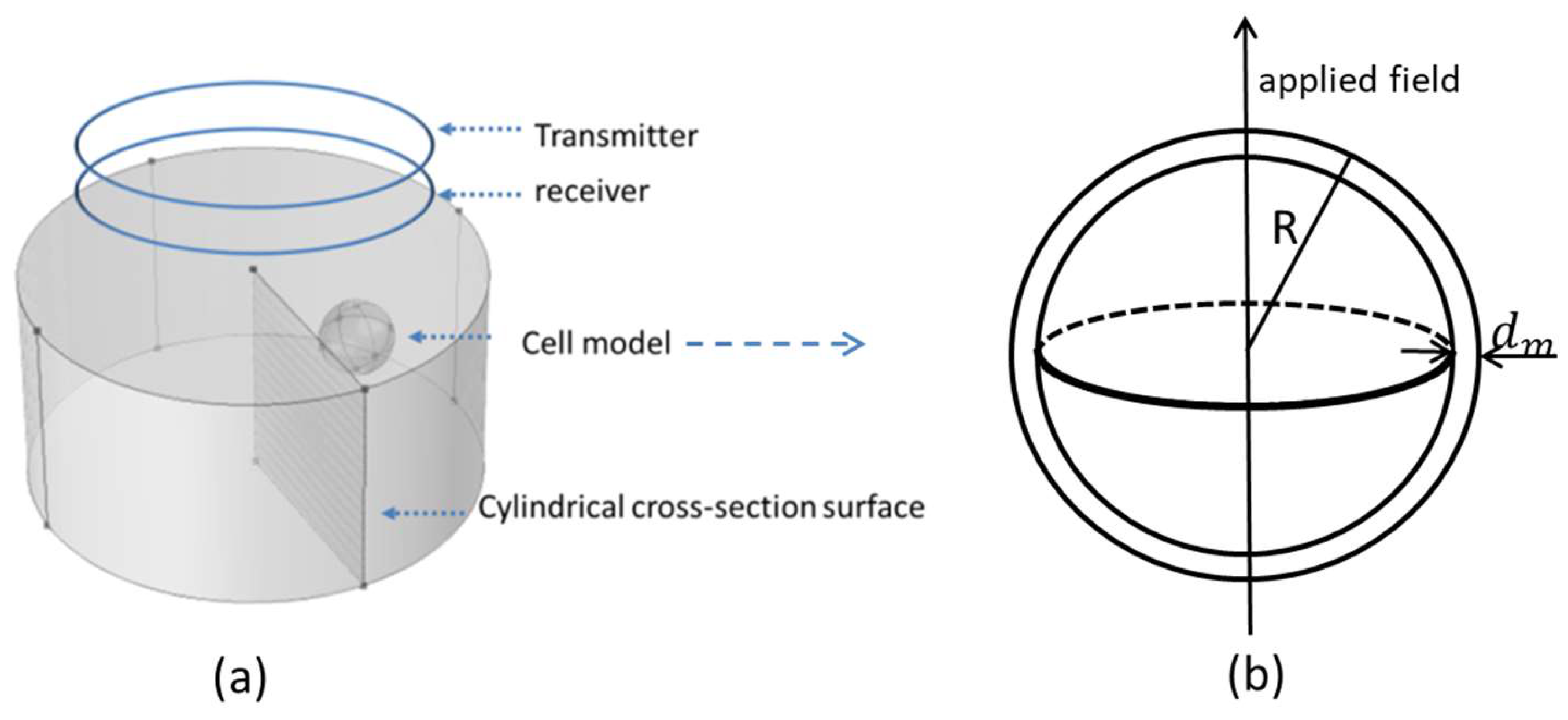
2.1. Single Spherical Cell Model
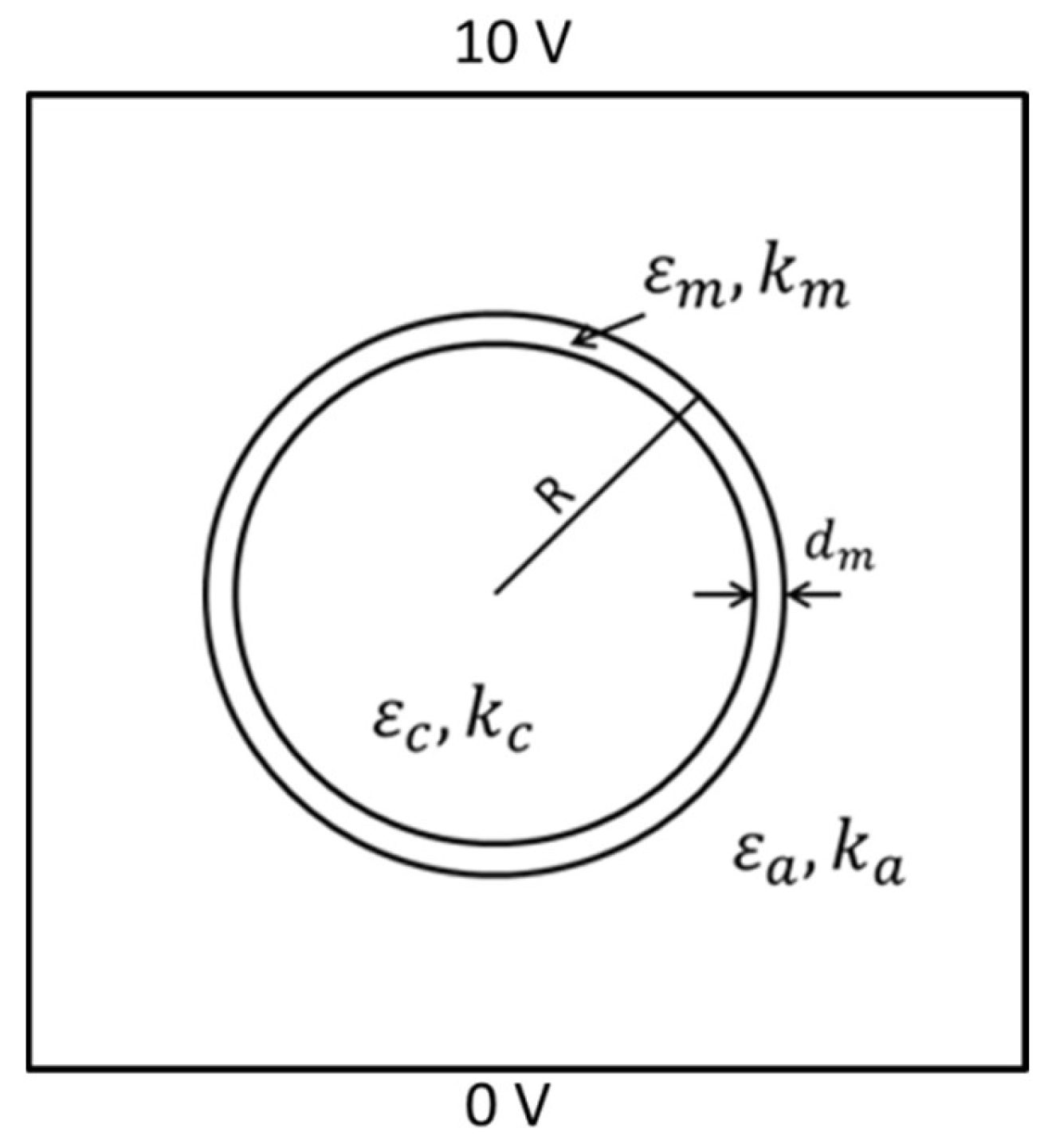
2.2. D FEM Simulation
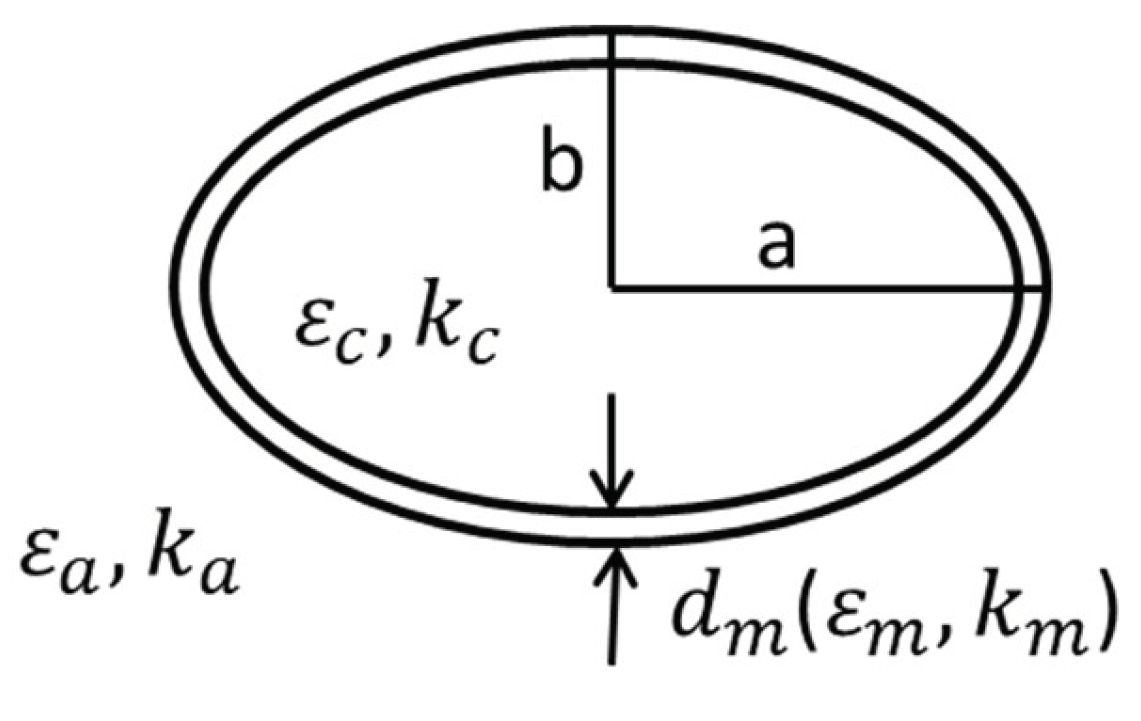
2.3. D FEM Simulation
2.4. Acceleration Method
2.5. Meshing Details
3. Results and Discussion
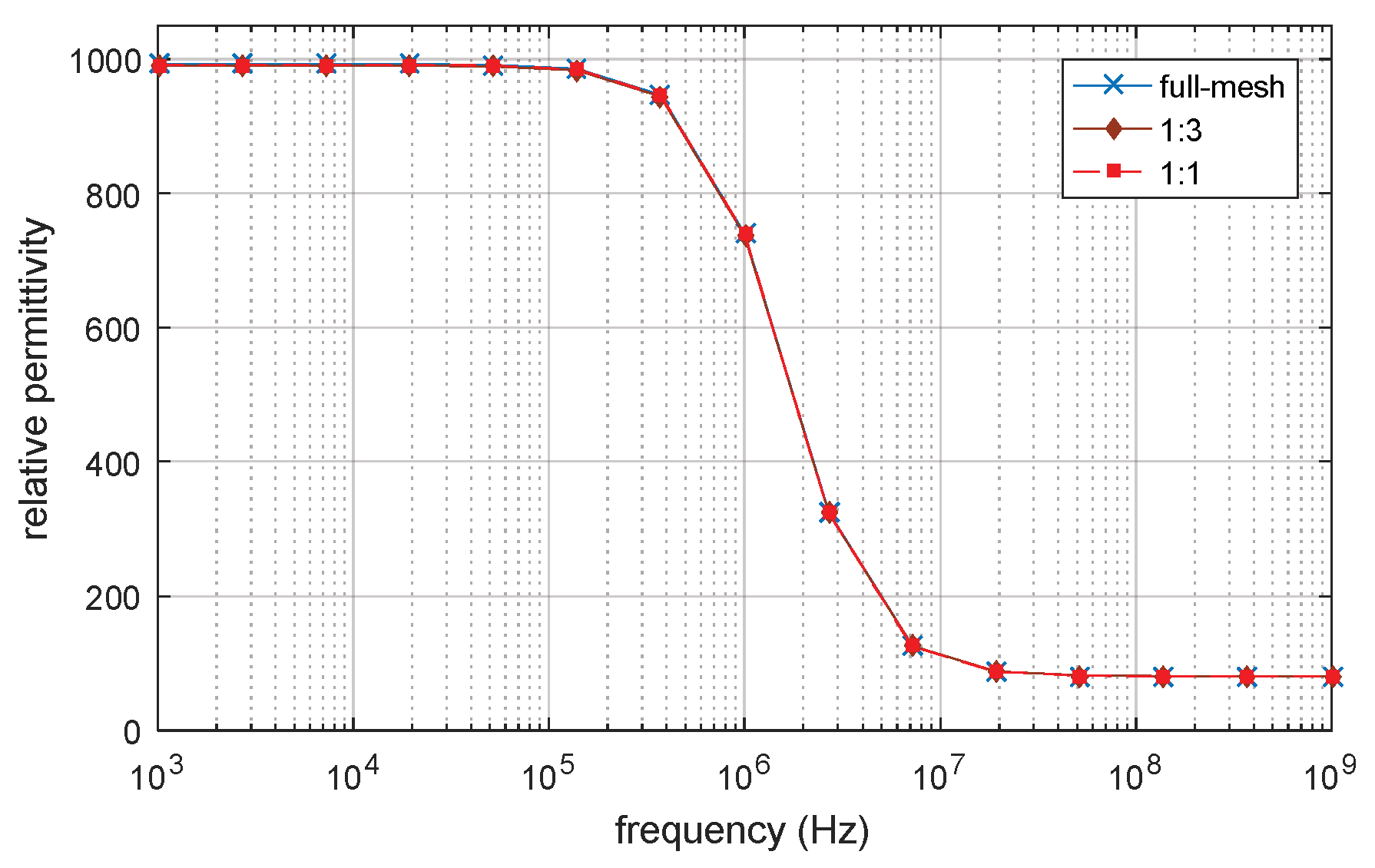
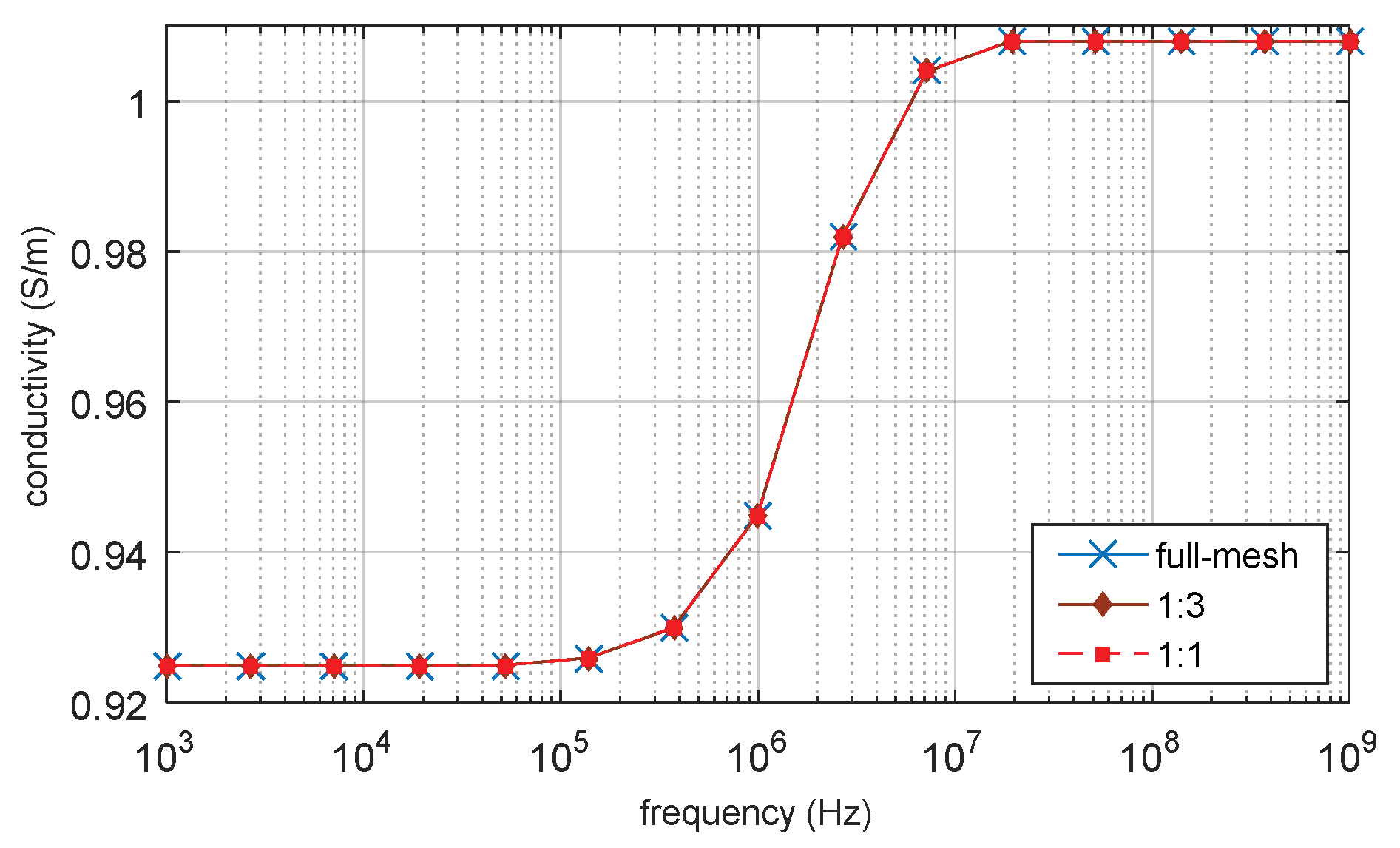
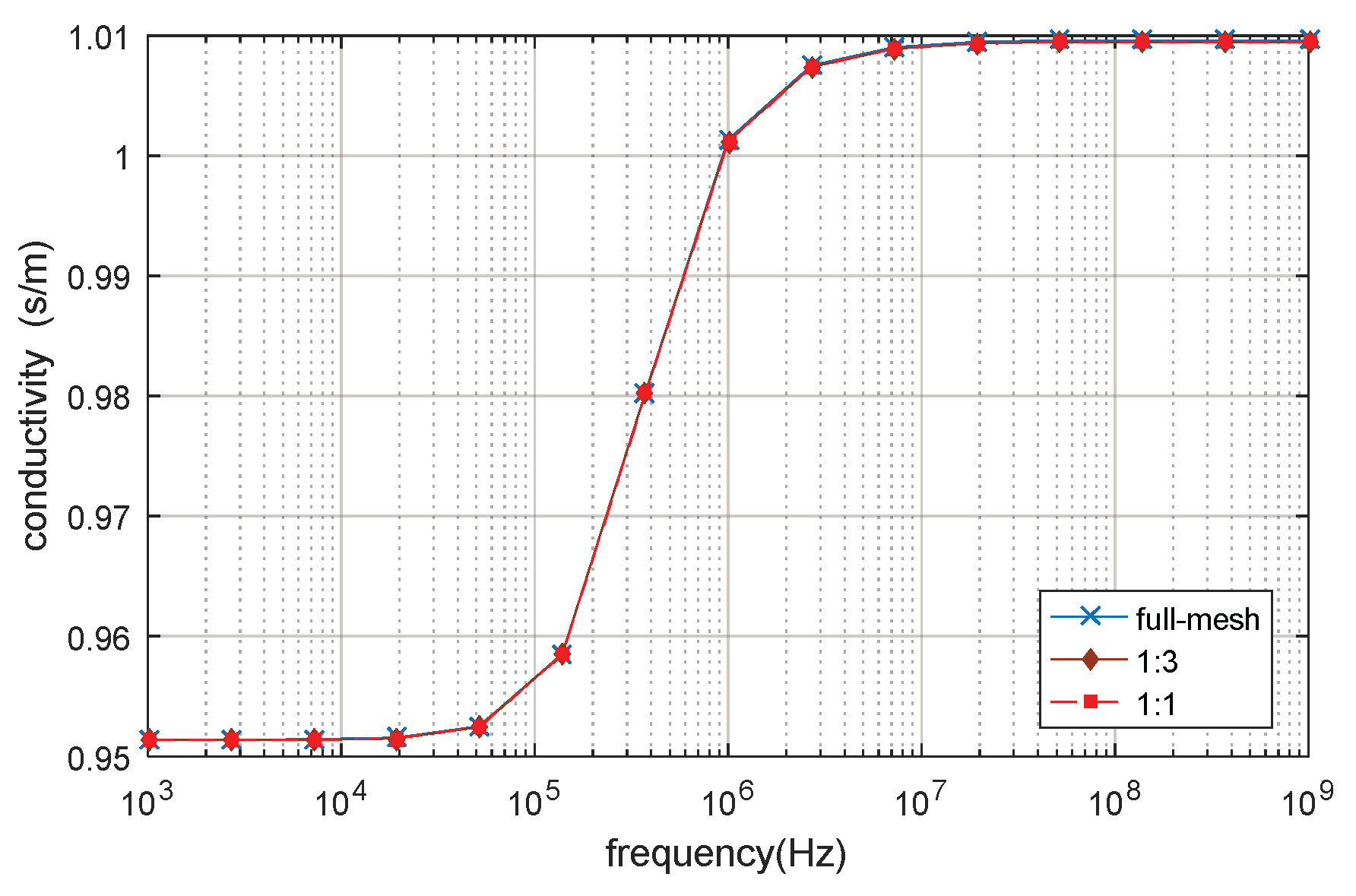
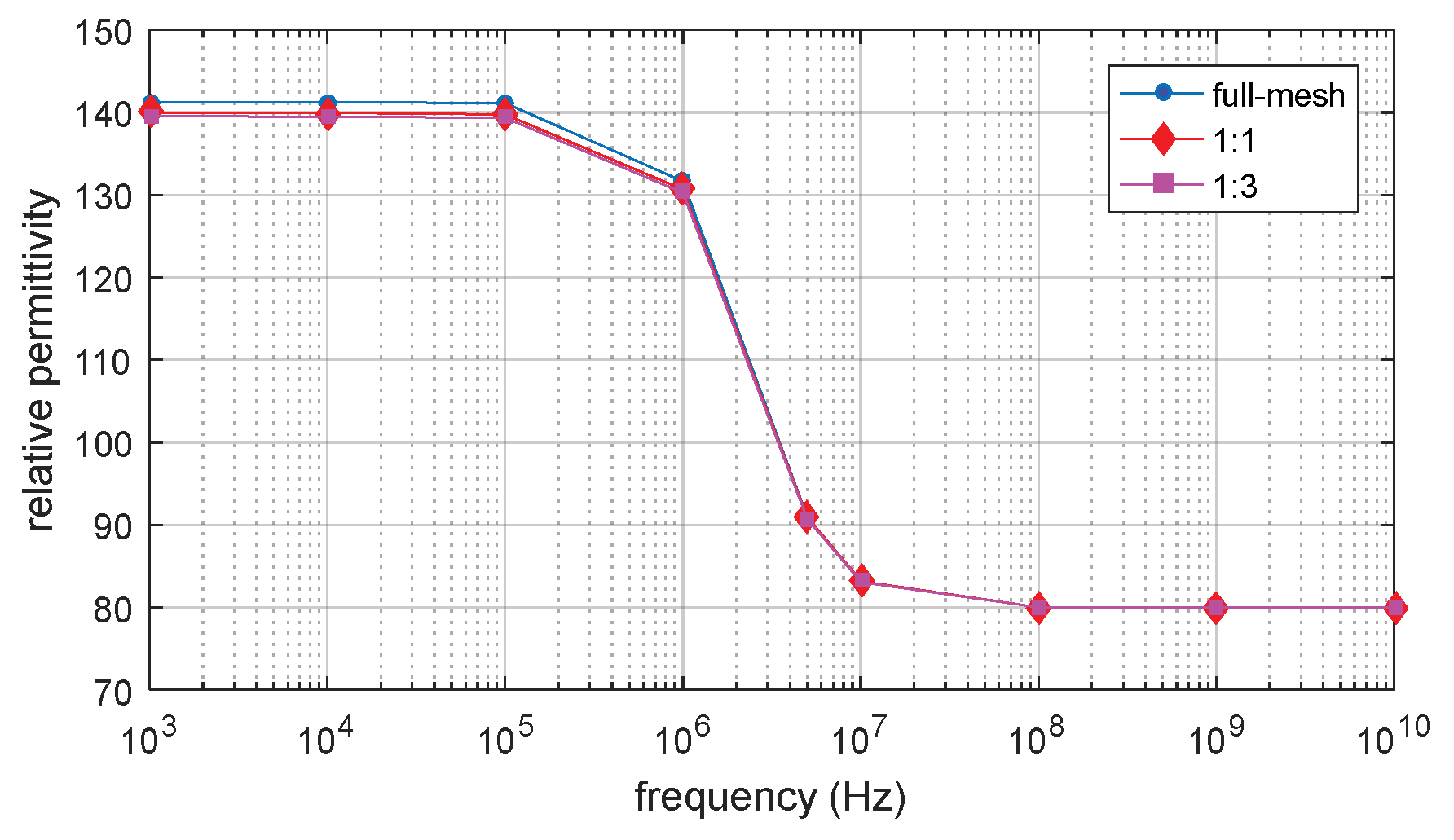
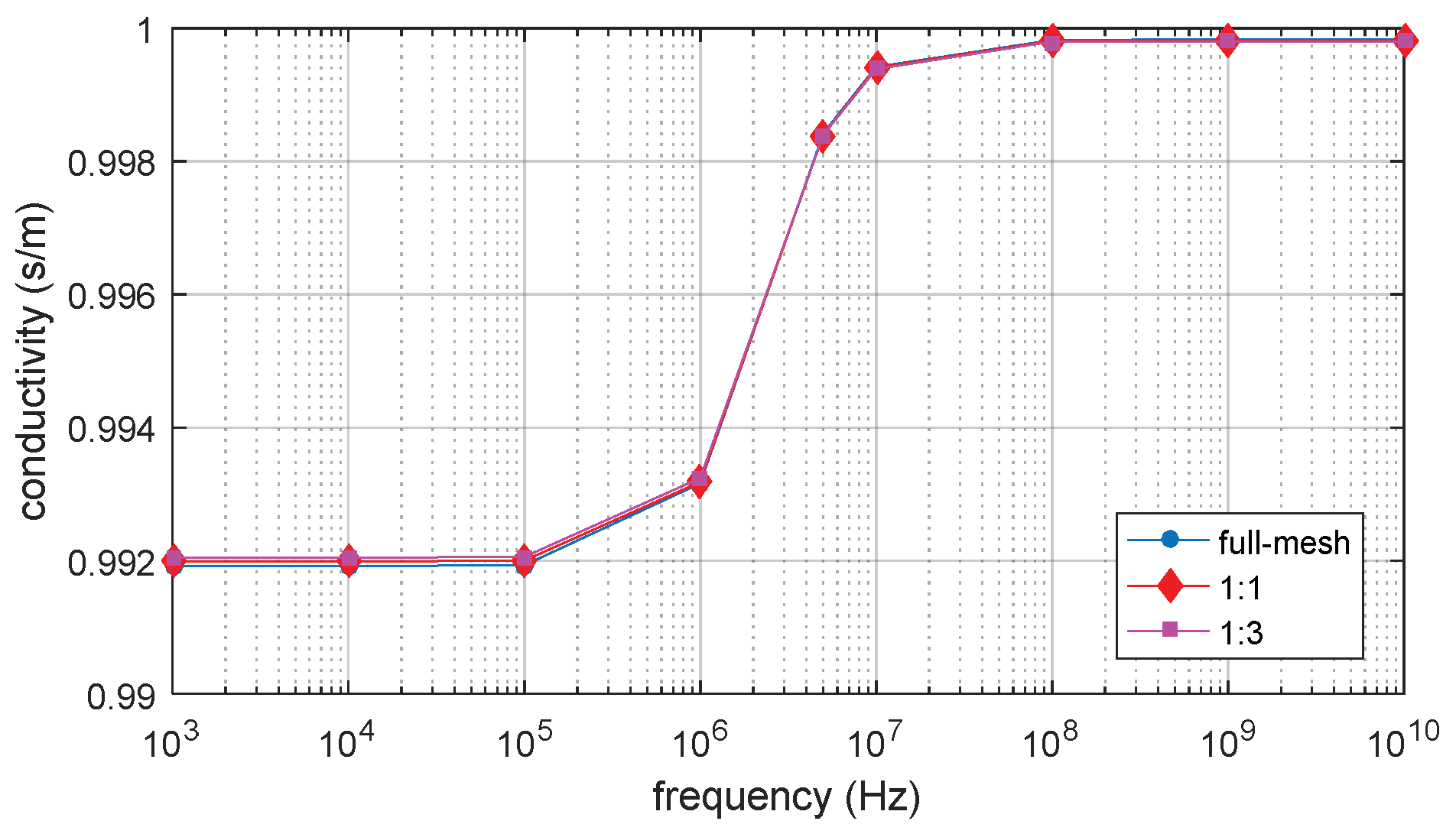
3.1. D Single Spherical Cell Model
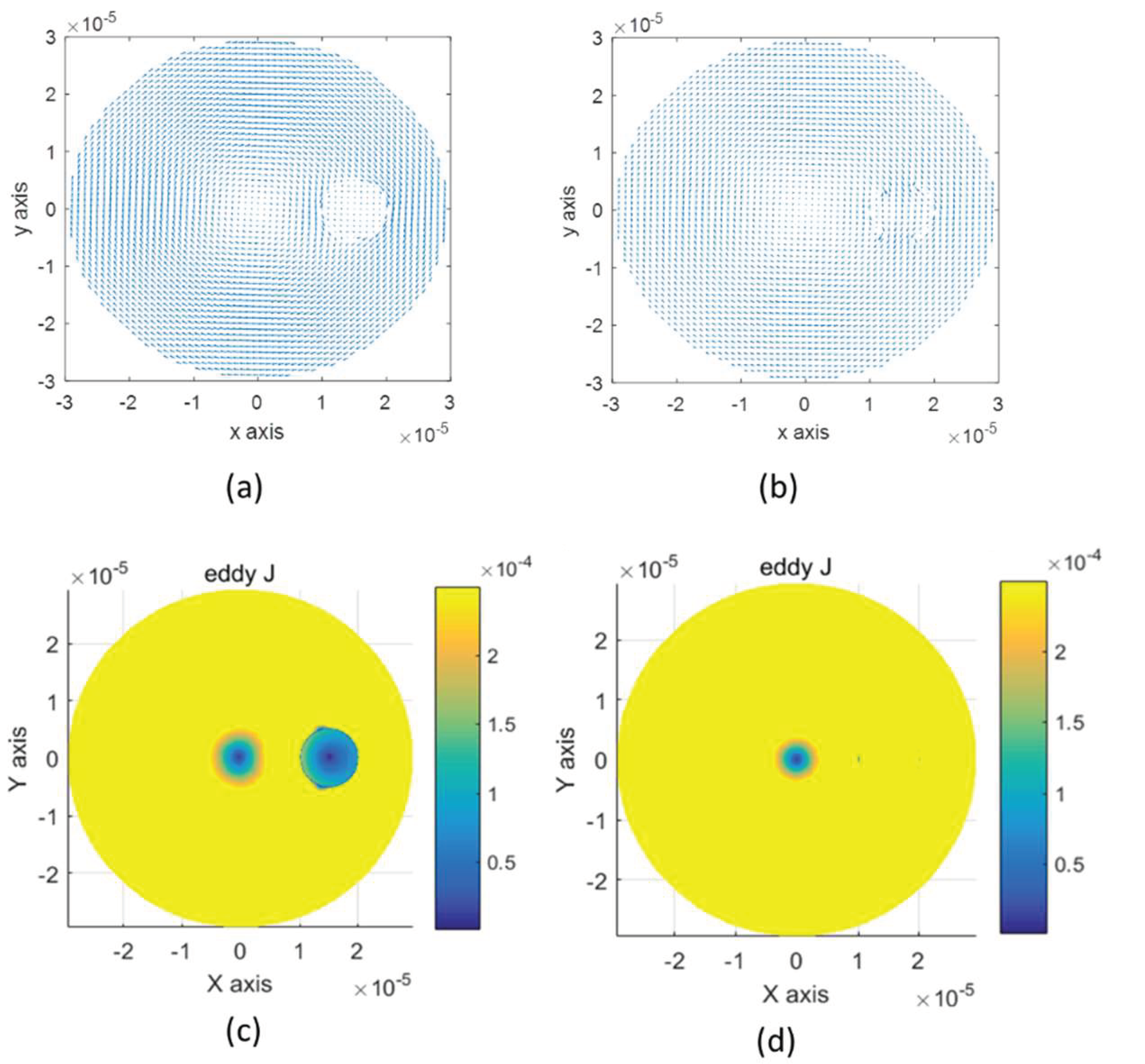
3.2. D Cell Deformation Model
3.3. D Spherical Cell Model
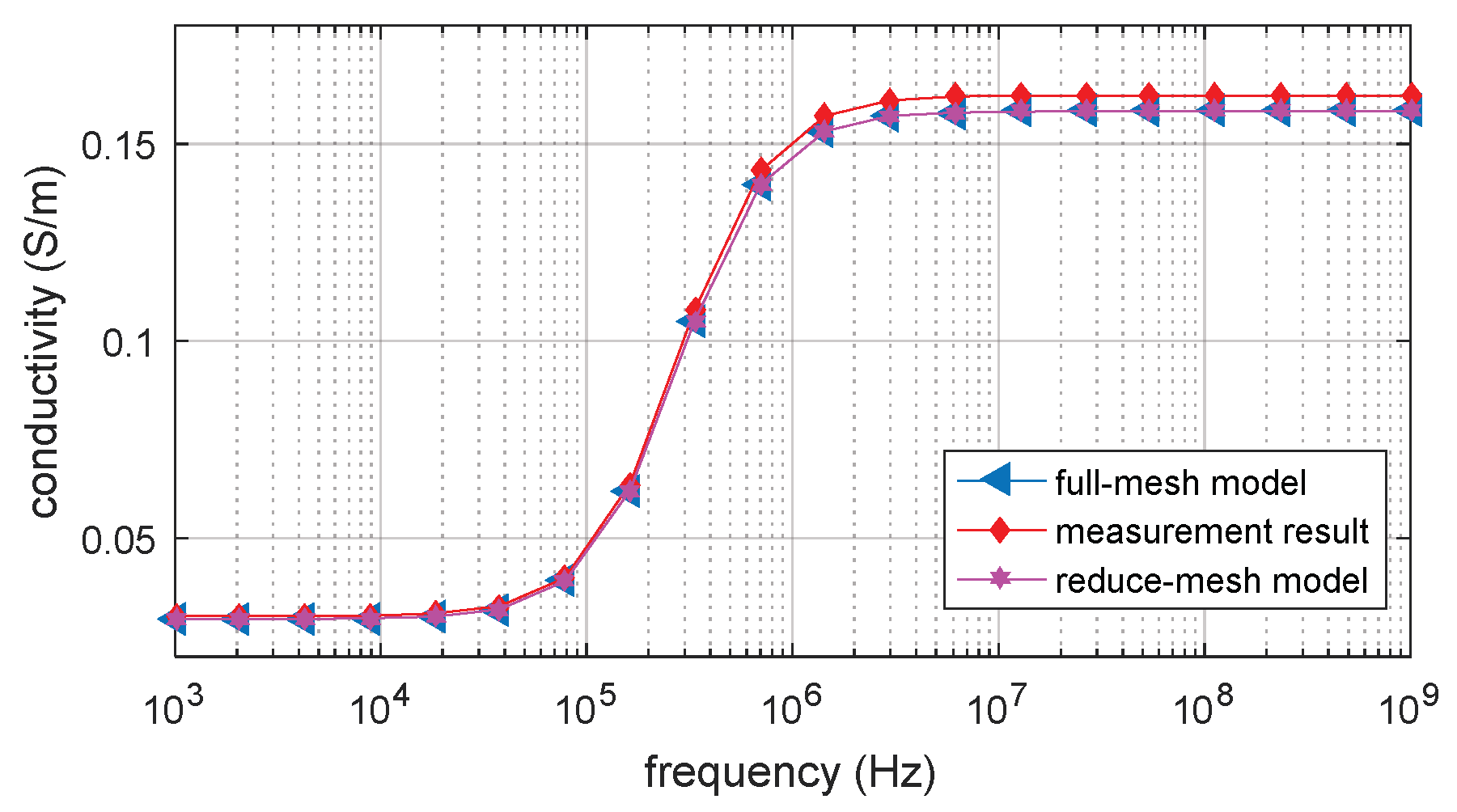
3.4. Experimental Validation by Contact-Electrode Measurement
3.5. Verification by Analytical Result
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gimsa, J.; Schnelle, T.; Zechel, G.; Glaser, R. Dielectric spectroscopy of human erythrocytes: Investigations under the influence of nystatin. Biophys. J. 1994, 66, 1244–1253. [Google Scholar] [CrossRef][Green Version]
- Awayda, M.S.; Driessche, W.; Helman, S.I. Frequency-dependent capacitance of the apical membrane of frog skin: Dielectric relaxation processes. Biophys. J. 1999, 76, 219–232. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.C.; Gooneratne, C.P. A novel planar-type biosensor for noninvasive meat inspection. IEEE Sens. J. 2007, 7, 1340–1346. [Google Scholar] [CrossRef]
- Jaffrin, M.Y.; Morel, H. Body fluid volumes measurements by impedance: A review of bioimpedance spectroscopy (BIS) and bioimpedance analysis (BIA) methods. Med. Eng. Phys. 2008, 30, 1257–1269. [Google Scholar] [CrossRef] [PubMed]
- Morimoto, T.; Kimura, S.; Konishi, Y.; Komaki, K.; Uyama, T.; Monden, Y.; Kinouchi, D.Y.; Iritani, D.T. A study of the electrical bio-impedance of tumors. J. Investig. Surg. 1993, 6, 25–32. [Google Scholar] [CrossRef] [PubMed]
- Kerner, T.E.; Paulsen, K.D.; Hartov, A.; Soho, S.K.; Poplack, S.P. Electrical impedance spectroscopy of the breast: Clinical imaging results in 26 subjects. IEEE Trans. Med. Imaging 2002, 21, 638–645. [Google Scholar] [CrossRef] [PubMed]
- Romsauerova, A.; McEwan, A.; Horesh, L.; Yerworth, R.; Bayford, R.H.; Holder, D.S. Multi-frequency electrical impedance tomography (EIT) of the adult human head: Initial findings in brain tumours, arteriovenous malformations and chronic stroke, development of an analysis method and calibration. Physiol. Meas. 2006, 27, S147. [Google Scholar] [CrossRef]
- Schwan, A.; Herman, P. Electrical properties of tissue and cell suspensions. Adv. Biol. Med. Phys. 1957, 5, 147–209. [Google Scholar]
- Schwan, A.; Herman, P. Electrical properties of tissues and cell suspensions: Mechanisms and models. In Proceedings of the 16th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Baltimore, MD, USA, 3–6 November 1994. [Google Scholar]
- Damez, J.L.; Clerjon, S.; Abouelkaram, S.; Lepetit, J. Dielectric behavior of beef meat in the 1–1500 kHz range: Simulation with the Fricke/Cole–Cole model. Meat Sci. 2007, 77, 512–519. [Google Scholar] [CrossRef]
- Stubbe, M.; Gimsa, J. Maxwell’s Mixing Equation Revisited: Characteristic Impedance Equations for Ellipsoidal Cells. Biophys. J. 2015, 109, 194–208. [Google Scholar] [CrossRef]
- Asami, K.; Tetsuya, H.; Naokazu, K. Dielectric approach to suspensions of ellipsoidal particles covered with a shell in particular reference to biological cells. Jpn. J. Appl. Phys. 1980, 19, 359. [Google Scholar] [CrossRef]
- Pauly, H.; Schwan, H.P. Impedance of a suspension of ball-shaped particles with a shell; a model for the dielectric behavior of cell suspensions and protein solutions. Z. Naturforsch. 1959, 14, 125. [Google Scholar] [CrossRef]
- Tuncer, E.; Stanisław, M.; Gubański, C.; Nettelblad, B. Dielectric relaxation in dielectric mixtures: Application of the finite element method and its comparison with dielectric mixture formulas. J. Appl. Phys. 2001, 89, 8092–8100. [Google Scholar] [CrossRef]
- Asami, K. Dielectric dispersion in biological cells of complex geometry simulated by the three-dimensional finite difference method. J. Phys. D Appl. Phys. 2006, 39, 492. [Google Scholar] [CrossRef]
- Mejdoubi, A.; Brosseau, C. Finite-element simulation of the depolarization factor of arbitrarily shaped inclusions. Phys. Rev. E 2006, 74, 031405. [Google Scholar] [CrossRef]
- Takashima, S.; Asami, K.; Takahashi, Y. Frequency domain studies of impedance characteristics of biological cells using micropipet technique. Biophys. J. 1988, 54, 995. [Google Scholar] [CrossRef]
- Fricke, H. The Maxwell-Wagner dispersion in a suspension of ellipsoids. J. Phys. Chem. 1953, 57, 934–937. [Google Scholar] [CrossRef]
- Jin, J.M. The Finite Element Method in Electromagnetics; Wiley-IEEE Press; John Wiley & Sons: Hoboken, NJ, USA, 2015; pp. 1–876. [Google Scholar]
- Bíró, O. Edge element formulations of eddy current problems. Comput. Methods Appl. Mech. Eng. 1999, 169, 391–405. [Google Scholar] [CrossRef]
- O’Toole, M.D.; Marsh, L.A.; Davidson, J.L.; Tan, Y.M.; Armitage, D.W.; Peyton, A.J. Non-contact multi-frequency magnetic induction spectroscopy system for industrial-scale bio-impedance measurement. Meas. Sci. Tech. 2015, 26, 035102. [Google Scholar] [CrossRef]
- Georgii, J.; Rudiger, W. A streaming approach for sparse matrix products and its application in Galerkin multigrid methods. Electron. Trans. Numer. Anal. 2010, 37, 263–275. [Google Scholar]
- Fritschy, J.; Horesh, L.; Holder, D.S.; Bayford, R.H. Using the GRID to improve the computation speed of electrical impedance tomography (EIT) reconstruction algorithms. Physiol. Meas. 2005, 26, S209. [Google Scholar] [CrossRef][Green Version]
- Lu, M.Y.; Anthony, P.; Yin, W.L. Acceleration of Frequency Sweeping in Eddy-Current Computation. IEEE Trans. Magn. 2017, 53, 1–8. [Google Scholar] [CrossRef]
- Gheorghiu, E. Measuring living cells using dielectric spectroscopy. Bioelectrochem. Bioenerg. 1996, 40, 133–139. [Google Scholar] [CrossRef]
- Sekine, K. Application of boundary element method to calculation of the complex permittivity of suspensions of cells in shape of D∞ h symmetry. Bioelectrochemistry 2000, 52, 1–7. [Google Scholar] [CrossRef]
- Beving, H.; Eriksson, L.E.G.; Davey, C.L.; Kell, D.B. Dielectric properties of human blood and erythrocytes at radio frequencies (0.2–10 MHz); dependence on cell volume fraction and medium composition. Eur. Biophys. J. 1994, 23, 207–215. [Google Scholar] [CrossRef] [PubMed]
- Di Biasio, A.; Cametti, C. Effect of shape on the dielectric properties of biological cell suspensions. Bioelectrochemistry 2007, 71, 149–156. [Google Scholar] [CrossRef]
- Saville, D.A.; Bellini, T.; Degiorgio, V.; Mantegazza, F. An extended Maxwell–Wagner theory for the electric birefringence of charged colloids. J. Chem. Phys. 2000, 113, 6974–6983. [Google Scholar] [CrossRef]
- Davis, L.C. Polarization forces and conductivity effects in electrorheological fluids. J. Appl. Phys. 1992, 72, 1334–1340. [Google Scholar] [CrossRef]
- Zhou, Y.Y.; Wang, A.P.; Zhou, P.; Wang, H.; Chai, T.Y. Dynamic performance enhancement for nonlinear stochastic systems using RBF driven nonlinear compensation with extended Kalman filter. Automatica 2020, 112, 108693. [Google Scholar] [CrossRef]
- Tang, J.W.; Yin, W.L.; Lu, M.Y. Bio-impedance spectroscopy for frozen-thaw of bio-samples: Non-contact inductive measurement and finite element (FE) based cell modelling. J. Food Eng. 2020, 272, 109784. [Google Scholar] [CrossRef]




| Original Model Meshing Information | Acceleration Model Meshing Information | |
|---|---|---|
| Maximum element size | 0.1 | 0.1 |
| Minimum element size | 0.01 | 0.01 |
| Maximum element growth rate | 1.20 | 1.20 |
| Narrow factor | 1 | 1 |
| Regions | Original Model | Acceleration Model |
|---|---|---|
| Extracellular fluid | 32,814 | 15,668 |
| Intracellular fluid | 30,566 | 14,748 |
| Cell membrane | 9712 | 4856 |
| Region around cell membrane | 70,528 | 33,620 |
| Total suspension | 73,092 | 35,272 |
| Thickness Ratio | Number of Elements | Error | Computing Time (Minutes) |
|---|---|---|---|
| Original model | 73,092 | N/A | 73 |
| 1:1 | 35,272 | 0.07% | 28 |
| 1:3 | 17,342 | 0.2% | 13 |
| Thickness Ratio | Number of Elements | Error | Computing Time |
|---|---|---|---|
| Original (a = 12, b = 2) | 133,184 | N/A | 2 h 24 min |
| 1:1 | 64,600 | 0.04% | 62 min |
| 1:3 | 32,097 | 0.11% | 25 min |
| Thickness Ratio | Number of Elements | Error | Computing Time |
|---|---|---|---|
| Original model | 205,604 | N/A | 4 h 37 min |
| 1:1 | 141,870 | 0.4% | 3 h 5 min |
| 1:3 | 57,934 | 2% | 1 h 11 min |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, J.; Lu, M.; Xie, Y.; Yin, W. A Novel Efficient FEM Thin Shell Model for Bio-Impedance Analysis. Biosensors 2020, 10, 69. https://doi.org/10.3390/bios10060069
Tang J, Lu M, Xie Y, Yin W. A Novel Efficient FEM Thin Shell Model for Bio-Impedance Analysis. Biosensors. 2020; 10(6):69. https://doi.org/10.3390/bios10060069
Chicago/Turabian StyleTang, Jiawei, Mingyang Lu, Yuedong Xie, and Wuliang Yin. 2020. "A Novel Efficient FEM Thin Shell Model for Bio-Impedance Analysis" Biosensors 10, no. 6: 69. https://doi.org/10.3390/bios10060069
APA StyleTang, J., Lu, M., Xie, Y., & Yin, W. (2020). A Novel Efficient FEM Thin Shell Model for Bio-Impedance Analysis. Biosensors, 10(6), 69. https://doi.org/10.3390/bios10060069








