Bioinspired Cilia Sensors with Graphene Sensing Elements Fabricated Using 3D Printing and Casting
Abstract
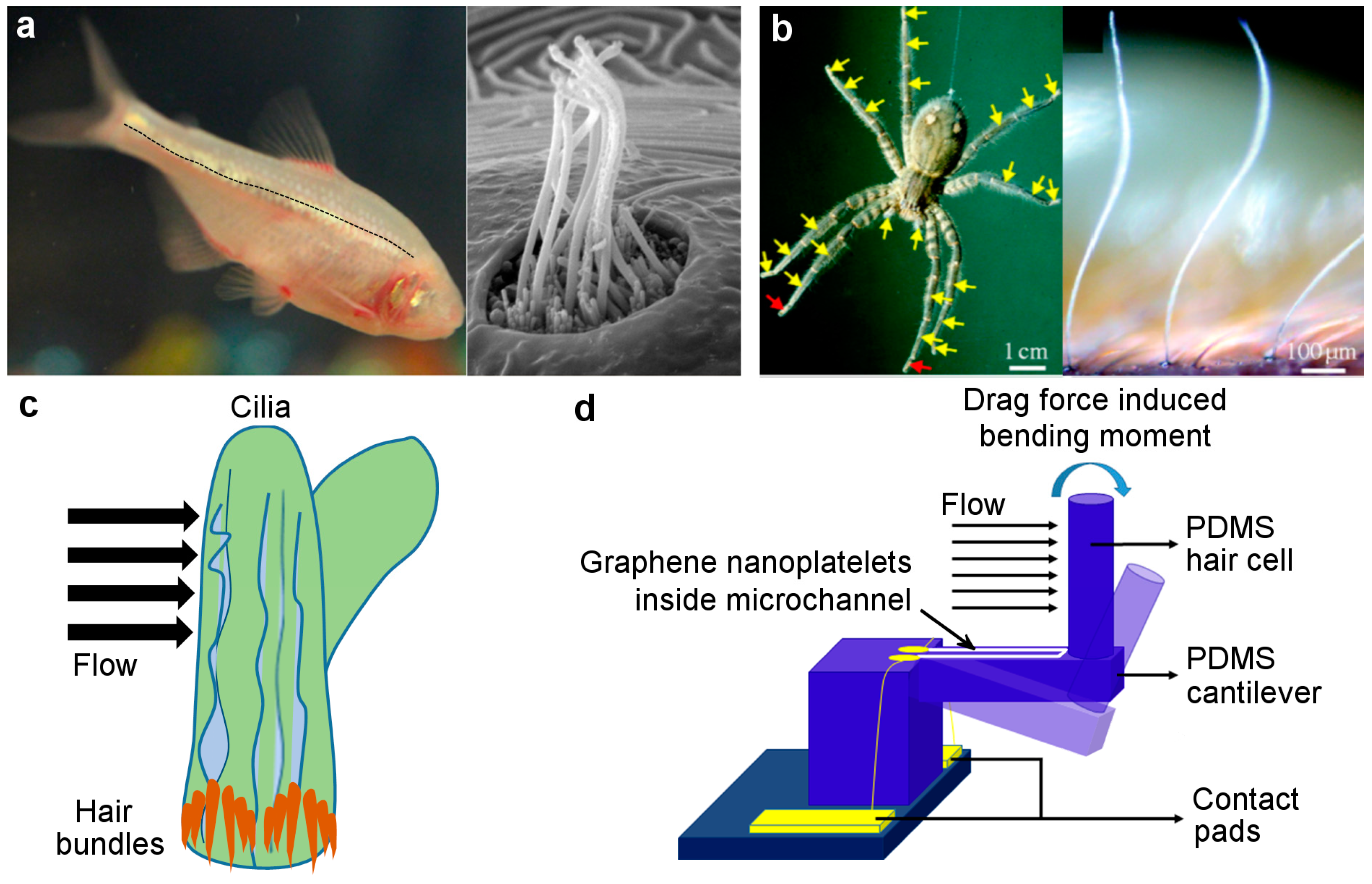
1. Introduction
2. Materials and Methods
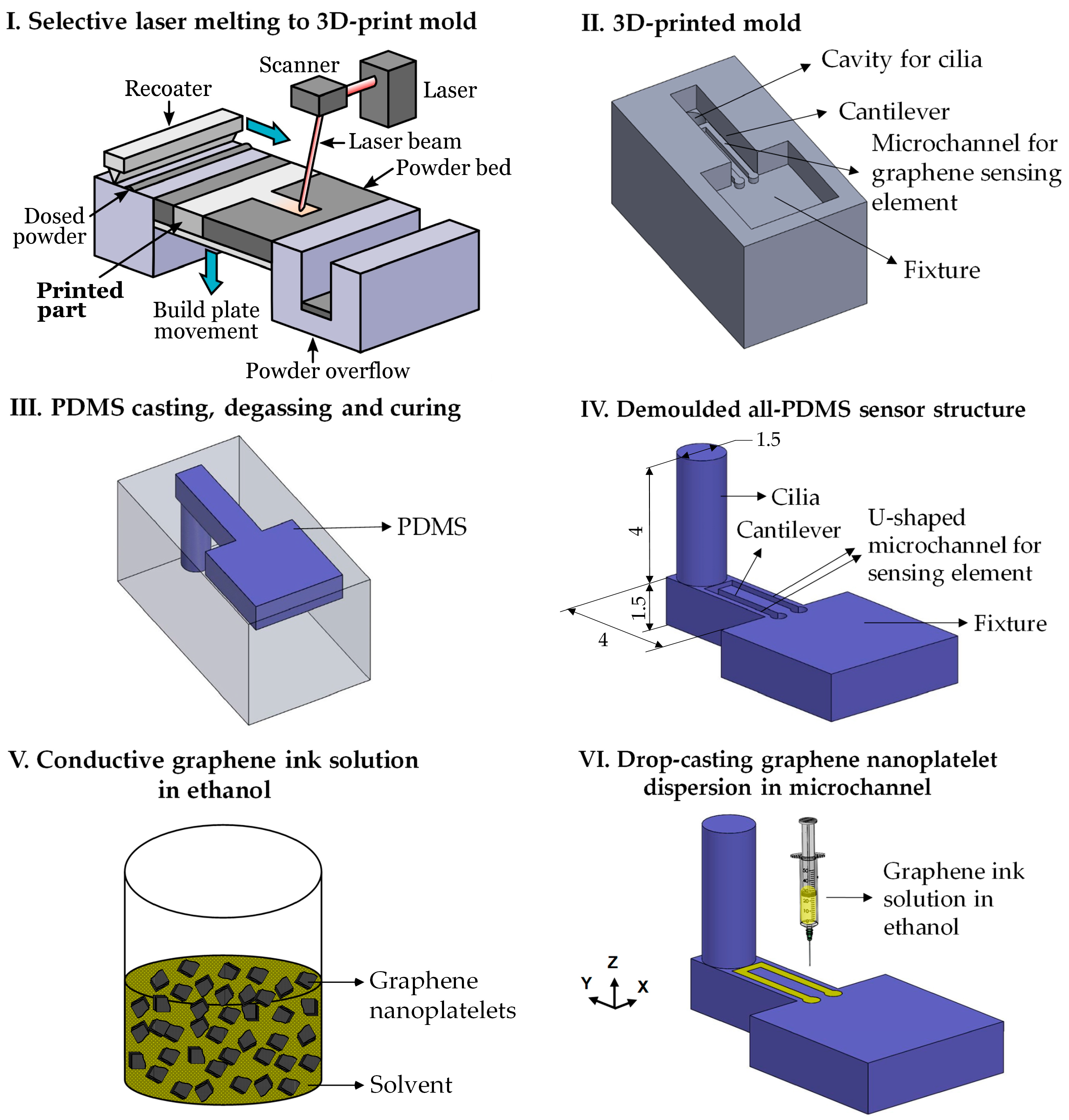
2.1. Sensor Fabrication
2.1.1. 3D Printing of the Metallic Mold
2.1.2. PDMS Casting and GN Infusion
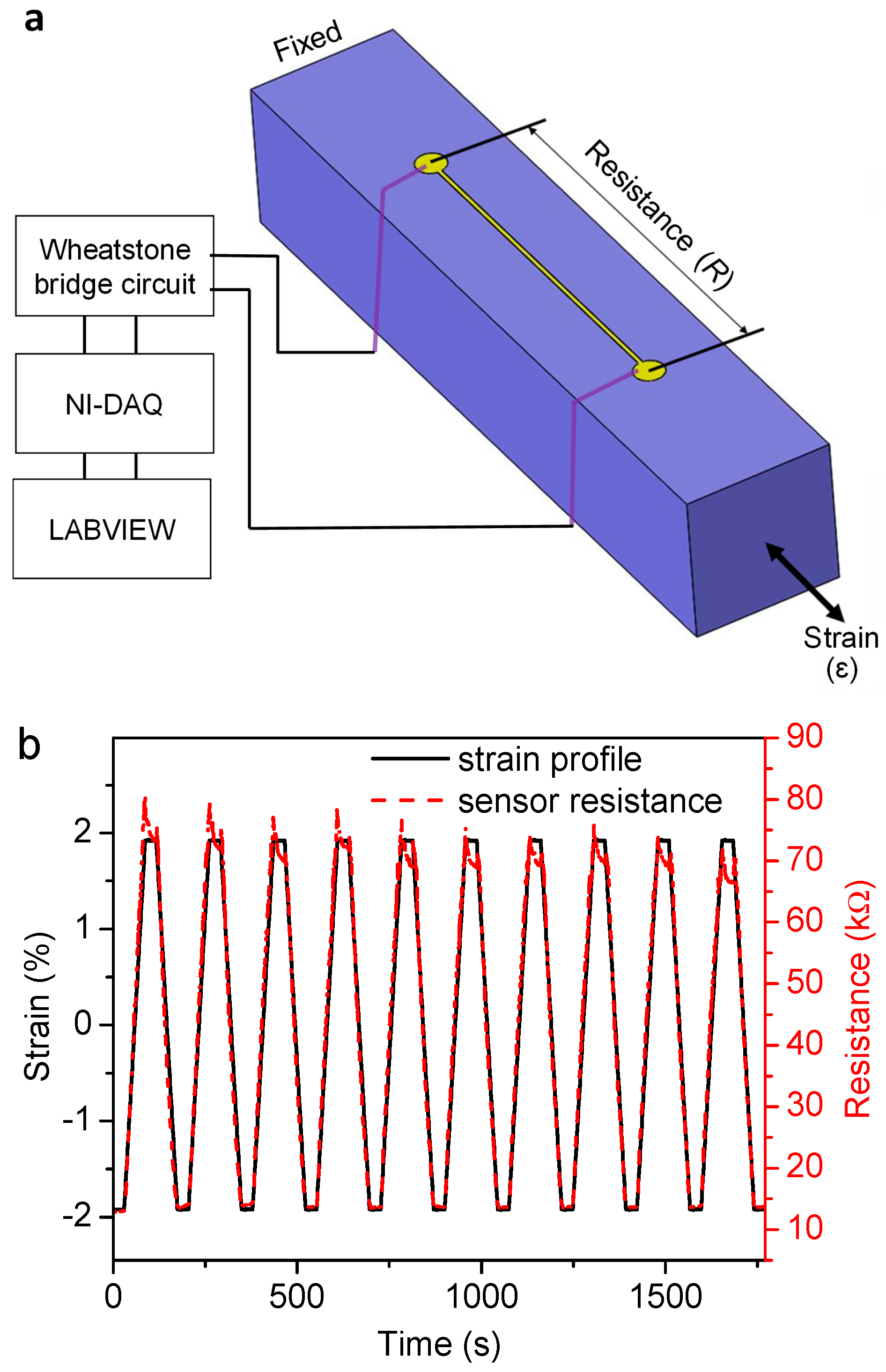
2.2. Gauge Factor Characterization
2.3. Sensor Testing
2.3.1. Data Acquisition
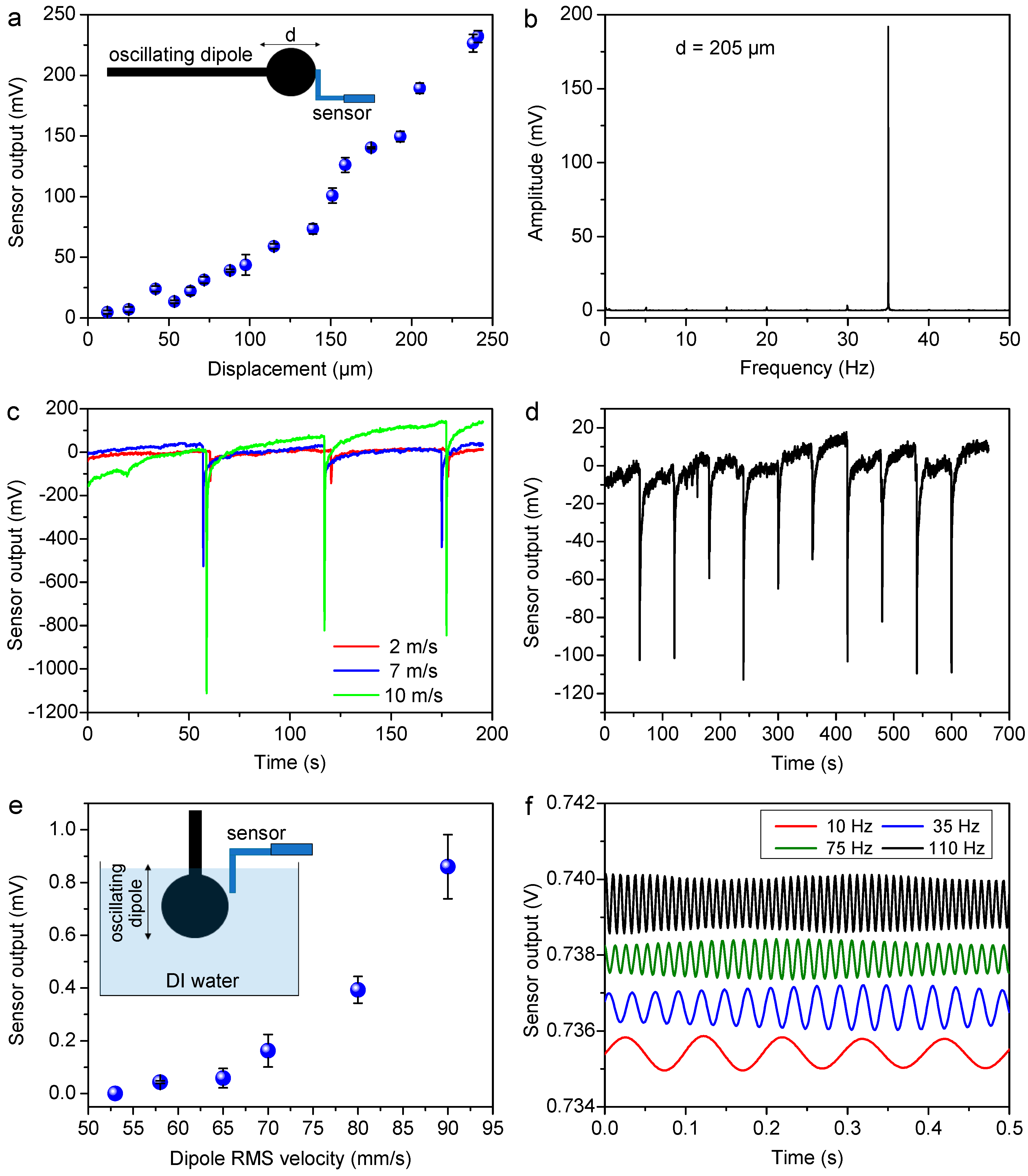
2.3.2. Experimental Setup for Oscillatory Stimuli
3. Results
3.1. Gauge Factor of Graphene-on-PDMS Strain Gauge
3.2. Characterization of the Biomimetic Cilium Sensor
4. Conclusions and Future Research
Author Contributions
Funding
Conflicts of Interest
References
- Barth, F.G.; Humphrey, J.A.C.; Secomb, T.W. Sensors and Sensing in Biology and Engineering; Springer: Wien, Austria, 2003. [Google Scholar]
- Valle, M. Bioinspired sensor systems. Sensors 2011, 11, 10180–10186. [Google Scholar] [CrossRef] [PubMed]
- Wasilewski, T.; Gębicki, J.; Kamysz, W. Advances in olfaction-inspired biomaterials applied to bioelectronic noses. Sens. Actuatorsb. Chem. 2018, 257, 511–537. [Google Scholar] [CrossRef]
- Johnson, E.A.C.; Bonser, R.H.C.; Jeronimidis, G. Recent advances in biomimetic sensing technologies. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2009, 367, 1559–1569. [Google Scholar] [CrossRef] [PubMed]
- Bleckmann, H.; Klein, A.; Meyer, G. Nature as a model for technical sensors. In Frontiers in Sensing: From Biology to Engineering; Springer: Vienna, Austria, 2012; pp. 3–18. [Google Scholar]
- Kottapalli, A.G.P.; Asadnia, M.; Miao, J.; Triantafyllou, M.S. Biomimetic Microsensors Inspired by Marine Life; Springer International Publishing: Cham, Switzerland, 2017; ISBN 978-3-319-47499-1. [Google Scholar]
- Ejeian, F.; Azadi, S.; Razmjou, A.; Orooji, Y.; Kottapalli, A.; Warkiani, M.E.; Asadnia, M. Design and applications of MEMS flow sensors: A review. Sens. Actuators A Phys. 2019, 295, 483–502. [Google Scholar] [CrossRef]
- Ha, M.; Lim, S.; Park, J.; Um, D.S.; Lee, Y.; Ko, H. Bioinspired interlocked and hierarchical design of zno nanowire arrays for static and dynamic pressure-sensitive electronic skins. Adv. Funct. Mater. 2015, 25, 2841–2849. [Google Scholar] [CrossRef]
- Ha, M.; Lim, S.; Cho, S.; Lee, Y.; Na, S.; Baig, C.; Ko, H. Skin-Inspired Hierarchical Polymer Architectures with Gradient Stiffness for Spacer-Free, Ultrathin, and Highly Sensitive Triboelectric Sensors. ACS Nano 2018, 12, 3964–3974. [Google Scholar] [CrossRef] [PubMed]
- Shimozawa, T.; Murakami, J.; Kumagai, T. Cricket Wind Receptors: Thermal Noise for the Highest Sensitivity Known. In Sensors and Sensing in Biology and Engineering; Barth, F.G., Humphrey, J.A.C., Secomb, T.W., Eds.; Springer: Vienna, Austria, 2003; pp. 145–157. [Google Scholar]
- Montgomery, J.C.; Baker, C.F.; Carton, A.G. The lateral line can mediate rheotaxis in fish. Nature 1997, 389, 960–963. [Google Scholar] [CrossRef]
- Kroese, A.B.A.; der Zalm, J.M.; den Bercken, J. Frequency response of the lateral-line organ of xenopus laevis. Pflügers Arch. 1978, 375, 167–175. [Google Scholar] [CrossRef]
- Coombs, S.; Jansse, J. Peripheral Processing by the Lateral Line System of the Mottled Sculpin (Cottus bairdi). In Proceedings of the The Mechanosensory Lateral Line; Coombs, S., Görner, P., Münz, H., Eds.; Springer: New York, NY, USA, 1989; pp. 299–319. [Google Scholar]
- McConney, M.E.; Schaber, C.F.; Julian, M.D.; Eberhardt, W.C.; Humphrey, J.A.C.; Barth, F.G.; Tsukruk, V.V. Surface force spectroscopic point load measurements and viscoelastic modelling of the micromechanical properties of air flow sensitive hairs of a spider (Cupiennius salei). J. R. Soc. Interface 2009, 6, 681–694. [Google Scholar] [CrossRef]
- Corey, D.P.; Hudspeth, A.J. Response latency of vertebrate hair cells. Biophys. J. 1979, 26, 499–506. [Google Scholar] [CrossRef]
- Dehnhardt, G.; Mauck, B.; Hanke, W.; Bleckmann, H. Hydrodynamic Trail-Following in Harbor Seals (Phoca vitulina). Science. 2001, 293, 102–104. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Liu, Z. Biomimetic Cilia Based on MEMS Technology. J. Bionic Eng. 2008, 5, 358–365. [Google Scholar] [CrossRef]
- Kottapalli, A.G.P.; Asadnia, M.; Miao, J.; Triantafyllou, M. Touch at a distance sensing: Lateral-line inspired MEMS flow sensors. Bioinspiration Biomim. 2014, 9. [Google Scholar]
- Kottapalli, A.G.P.; Bora, M.; Asadnia, M.; Miao, J.; Venkatraman, S.S.; Triantafyllou, M. Nanofibril scaffold assisted MEMS artificial hydrogel neuromasts for enhanced sensitivity flow sensing. Sci. Rep. 2016, 6, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Forge, A. Fish neuromast organ. Available online: https://wellcomecollection.org/works/hy7hpafr (accessed on 28 May 2019).
- Yang, Y.; Chen, J.; Engel, J.; Pandya, S.; Chen, N.; Tucker, C.; Coombs, S.; Jones, D.L.; Liu, C. Distant touch hydrodynamic imaging with an artificial lateral line. Proc. Natl. Acad. Sci. 2006, 103, 18891–18895. [Google Scholar] [CrossRef] [PubMed]
- Dijkstra, M.; van Baar, J.J.; Wiegerink, R.J.; Lammerink, T.S.J.; de Boer, J.H.; Krijnen, G.J.M. Artificial sensory hairs based on the flow sensitive receptor hairs of crickets. J. Micromechanics Microengineering 2005, 15, S132–S138. [Google Scholar] [CrossRef]
- Wolf, B.J.; Morton, J.A.S.; Macpherson, W.N.; Van Netten, S.M. Bio-inspired all-optical artificial neuromast for 2D flow sensing. Bioinspiration Biomim. 2018, 13. [Google Scholar] [CrossRef]
- Asadnia, M.; Kottapalli, A.G.P.; Miao, J.; Warkiani, M.E.; Triantafyllou, M.S. Artificial fish skin of self-powered micro-electromechanical systems hair cells for sensing hydrodynamic flow phenomena. J. R. Soc. Interface 2015, 12. [Google Scholar] [CrossRef]
- Kottapalli, A.G.P.; Asadnia, M.; Miao, J.M.; Barbastathis, G.; Triantafyllou, M.S. A flexible liquid crystal polymer MEMS pressure sensor array for fish-like underwater sensing. Smart Mater. Struct. 2012, 21. [Google Scholar] [CrossRef]
- Peleshanko, S.; Julian, M.D.; Ornatska, M.; McConney, M.E.; LeMieux, M.C.; Chen, N.; Tucker, C.; Yang, Y.; Liu, C.; Humphrey, J.A.C.; et al. Hydrogel-encapsulated microfabricated haircells mimicking fish cupula neuromast. Adv. Mater. 2007, 19, 2903–2909. [Google Scholar] [CrossRef]
- Chen, N.; Tucker, C.; Engel, J.M.; Yang, Y.; Pandya, S.; Liu, C. Design and characterization of artificial haircell sensor for flow sensing with ultrahigh velocity and angular sensitivity. J. Microelectromechanical Syst. 2007, 16, 999–1014. [Google Scholar] [CrossRef]
- Casas, J.; Steinmann, T.; Krijnen, G. Why do insects have such a high density of flow-sensing hairs? Insights from the hydromechanics of biomimetic MEMS sensors. J. R. Soc. Interface 2010, 7, 1487–1495. [Google Scholar] [CrossRef] [PubMed]
- Alfadhel, A.; Kosel, J. Magnetic Nanocomposite Cilia Tactile Sensor. Adv. Mater. 2015, 27, 7888–7892. [Google Scholar] [CrossRef] [PubMed]
- Amjadi, M.; Pichitpajongkit, A.; Lee, S.; Ryu, S.; Park, I. Highly stretchable and sensitive strain sensor based on silver nanowire-elastomer nanocomposite. ACS Nano 2014, 8, 5154–5163. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Zhang, H.; Yao, G.; Liao, F.; Gao, M.; Huang, Z.; Li, K.; Lin, Y. Highly stretchable, sensitive, and flexible strain sensors based on silver nanoparticles/carbon nanotubes composites. J. Alloy. Compd. 2015, 652, 48–54. [Google Scholar] [CrossRef]
- Zhang, S.; Cai, L.; Li, W.; Miao, J.; Wang, T.; Yeom, J.; Sepúlveda, N.; Wang, C. Fully Printed Silver-Nanoparticle-Based Strain Gauges with Record High Sensitivity. Adv. Electron. Mater. 2017, 3, 1–6. [Google Scholar] [CrossRef]
- Xiao, X.; Yuan, L.; Zhong, J.; Ding, T.; Liu, Y.; Cai, Z.; Rong, Y.; Han, H.; Zhou, J.; Wang, Z.L. High-strain sensors based on ZnO nanowire/polystyrene hybridized flexible films. Adv. Mater. 2011, 23, 5440–5444. [Google Scholar] [CrossRef]
- Kong, J.H.; Jang, N.S.; Kim, S.H.; Kim, J.M. Simple and rapid micropatterning of conductive carbon composites and its application to elastic strain sensors. Carbonn. Y. 2014, 77, 199–207. [Google Scholar] [CrossRef]
- Yamada, T.; Hayamizu, Y.; Yamamoto, Y.; Yomogida, Y.; Izadi-Najafabadi, A.; Futaba, D.N.; Hata, K. A stretchable carbon nanotube strain sensor for human-motion detection. Nat. Nanotechnol. 2011, 6, 296–301. [Google Scholar] [CrossRef]
- Bulut Coskun, M.; Akbari, A.; Lai, D.T.H.; Neild, A.; Majumder, M.; Alan, T. Ultrasensitive Strain Sensor Produced by Direct Patterning of Liquid Crystals of Graphene Oxide on a Flexible Substrate. Acs Appl. Mater. Interfaces 2016, 8, 22501–22505. [Google Scholar] [CrossRef]
- Wang, D.Y.; Tao, L.Q.; Liu, Y.; Zhang, T.Y.; Pang, Y.; Wang, Q.; Jiang, S.; Yang, Y.; Ren, T.L. High performance flexible strain sensor based on self-locked overlapping graphene sheets. Nanoscale 2016, 8, 20090–20095. [Google Scholar] [CrossRef] [PubMed]
- Bae, S.H.; Lee, Y.; Sharma, B.K.; Lee, H.J.; Kim, J.H.; Ahn, J.H. Graphene-based transparent strain sensor. Carbonn. Y. 2013, 51, 236–242. [Google Scholar] [CrossRef]
- Choi, Y.S.; Gwak, M.J.; Lee, D.W. Polymeric cantilever integrated with PDMS/graphene composite strain sensor. Rev. Sci. Instrum. 2016, 87. [Google Scholar] [CrossRef] [PubMed]
- Chun, S.; Choi, Y.; Park, W. All-graphene strain sensor on soft substrate. Carbonn. Y. 2017, 116, 753–759. [Google Scholar] [CrossRef]
- Filippidou, M.K.; Tegou, E.; Tsouti, V.; Chatzandroulis, S. A flexible strain sensor made of graphene nanoplatelets/polydimethylsiloxane nanocomposite. Microelectron. Eng. 2015, 142, 7–11. [Google Scholar] [CrossRef]
- Wang, B.; Lee, B.K.; Kwak, M.J.; Lee, D.W. Graphene/polydimethylsiloxane nanocomposite strain sensor. Rev. Sci. Instrum. 2013, 84. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, D.; Wang, K.; Liu, Y.; Shang, Y. A novel strain sensor based on graphene composite films with layered structure. Compos. Part. A Appl. Sci. Manuf. 2016, 80, 95–103. [Google Scholar] [CrossRef]
- Hempel, M.; Nezich, D.; Kong, J.; Hofmann, M. A novel class of strain gauges based on layered percolative films of 2D materials. Nano Lett. 2012, 12, 5714–5718. [Google Scholar] [CrossRef]
- Amjadi, M.; Kyung, K.U.; Park, I.; Sitti, M. Stretchable, Skin-Mountable, and Wearable Strain Sensors and Their Potential Applications: A Review. Adv. Funct. Mater. 2016, 26, 1678–1698. [Google Scholar] [CrossRef]
- Chen, J.; Zheng, J.; Gao, Q.; Zhang, J.; Zhang, J.; Omisore, O.; Wang, L.; Li, H. Polydimethylsiloxane (PDMS)-Based Flexible Resistive Strain Sensors for Wearable Applications. Appl. Sci. 2018, 8, 345. [Google Scholar] [CrossRef]
- Yan, T.; Wang, Z.; Pan, Z.J. Flexible strain sensors fabricated using carbon-based nanomaterials: A review. Curr. Opin. Solid State Mater. Sci. 2018, 22, 213–228. [Google Scholar] [CrossRef]
- Kim, Y.J.; Cha, J.Y.; Ham, H.; Huh, H.; So, D.S.; Kang, I. Preparation of piezoresistive nano smart hybrid material based on graphene. Curr. Appl. Phys. 2011, 11, S350–S352. [Google Scholar] [CrossRef]
- Ni, Y.; Ji, R.; Long, K.; Bu, T.; Chen, K.; Zhuang, S. A review of 3D-printed sensors. Appl. Spectrosc. Rev. 2017, 52, 623–652. [Google Scholar] [CrossRef]
- Liu, C.; Huang, N.; Xu, F.; Tong, J.; Chen, Z.; Gui, X.; Fu, Y.; Lao, C. 3D printing technologies for flexible tactile sensors toward wearable electronics and electronic skin. Polym. (Basel). 2018, 10, 629. [Google Scholar] [CrossRef] [PubMed]
- Dijkshoorn, A.; Werkman, P.; Welleweerd, M.; Wolterink, G.; Eijking, B.; Delamare, J.; Sanders, R.; Krijnen, G.J.M. Embedded sensing: Integrating sensors in 3-D printed structures. J. Sens. Sens. Syst. 2018, 7, 169–181. [Google Scholar] [CrossRef]
- Delamare, J.; Sanders, R.; Krijnen, G. 3D printed biomimetic whisker-based sensor with co-planar capacitive sensing. In Proceedings of the 2016 IEEE SENSORS; 2016; pp. 1–3. [Google Scholar]
- Yap, C.Y.; Chua, C.K.; Dong, Z.L.; Liu, Z.H.; Zhang, D.Q.; Loh, L.E.; Sing, S.L. Review of selective laser melting: Materials and applications. Appl. Phys. Rev. 2015, 2. [Google Scholar] [CrossRef]
- Lowther, M.; Louth, S.; Davey, A.; Hussain, A.; Ginestra, P.; Carter, L.; Eisenstein, N.; Grover, L.; Cox, S. Clinical, industrial, and research perspectives on powder bed fusion additively manufactured metal implants. Addit. Manuf. 2019, 28, 565–584. [Google Scholar] [CrossRef]
- Keil, S. The Wheatstone bridge circuit; Wiley Online Library: Hoboken, NJ, USA, 2017. [Google Scholar]
- Lu, N.; Wang, X.; Suo, Z.; Vlassak, J. Metal films on polymer substrates stretched beyond 50%. Appl. Phys. Lett. 2007, 91, 1–4. [Google Scholar] [CrossRef]
- Asadnia, M.; Kottapalli, A.G.P.; Karavitaki, K.D.; Warkiani, M.E.; Miao, J.; Corey, D.P.; Triantafyllou, M. From Biological Cilia to Artificial Flow Sensors: Biomimetic Soft Polymer Nanosensors with High Sensing Performance. Sci. Rep. 2016, 6, 1–13. [Google Scholar] [CrossRef]
- DMP60 series Microprint GmBH. Available online: https://www.3dmicroprint.com/products/machines/dmp60-series/ (accessed on 16 May 2019).
- Nanofabrica. Available online: https://www.nano-fabrica.com/media/attachments/2019/05/04/td_280419_mail.pdf (accessed on 16 May 2019).

| Materials | Methods | Strain (%) | Gauge Factor | Reference |
|---|---|---|---|---|
| Graphene film on rubber | Spray coating | 5 | 6–35 | [43] |
| Graphene rosette strain gauge on PDMS film | Reactive ion etching, stamping | 7.1 | 14 | [38] |
| Graphene serpentine strain sensor on PDMS | Chemical vapor deposition, photolithography, spray coating | 20 | 42.2 | [40] |
| Graphene thin film on polyethylene terephthalate (PET) substrate | Spray deposition | 1.5 | 10–100 (depending on graphene concentration) | [44] |
| Graphene nanoplatelets in microchannel on PDMS | PDMS casting inside 3D-printed mold, graphene ink drop-casting | ±1.92 | 37 | This work |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamat, A.M.; Pei, Y.; Kottapalli, A.G.P. Bioinspired Cilia Sensors with Graphene Sensing Elements Fabricated Using 3D Printing and Casting. Nanomaterials 2019, 9, 954. https://doi.org/10.3390/nano9070954
Kamat AM, Pei Y, Kottapalli AGP. Bioinspired Cilia Sensors with Graphene Sensing Elements Fabricated Using 3D Printing and Casting. Nanomaterials. 2019; 9(7):954. https://doi.org/10.3390/nano9070954
Chicago/Turabian StyleKamat, Amar M., Yutao Pei, and Ajay G.P. Kottapalli. 2019. "Bioinspired Cilia Sensors with Graphene Sensing Elements Fabricated Using 3D Printing and Casting" Nanomaterials 9, no. 7: 954. https://doi.org/10.3390/nano9070954
APA StyleKamat, A. M., Pei, Y., & Kottapalli, A. G. P. (2019). Bioinspired Cilia Sensors with Graphene Sensing Elements Fabricated Using 3D Printing and Casting. Nanomaterials, 9(7), 954. https://doi.org/10.3390/nano9070954







