Studies on Possible Ion-Confinement in Nanopore for Enhanced Supercapacitor Performance in 4V EMIBF4 Ionic Liquids
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Materials Synthesis and Characterization
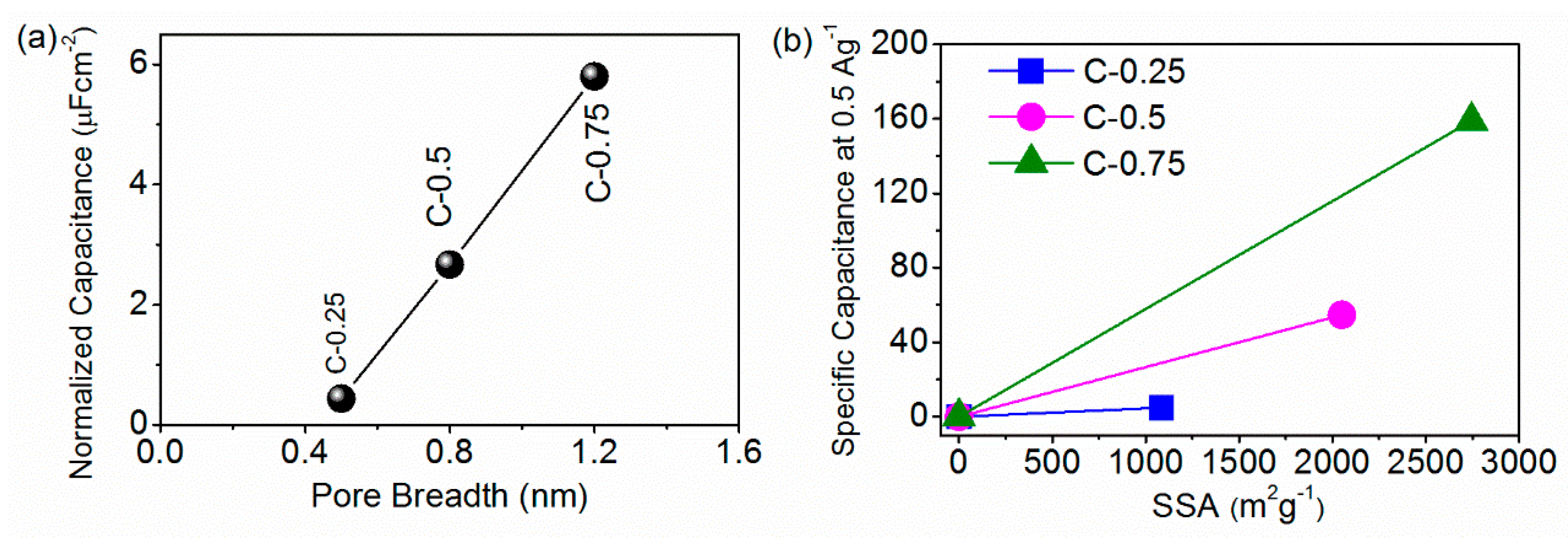
3.2. The Electrochemical Test
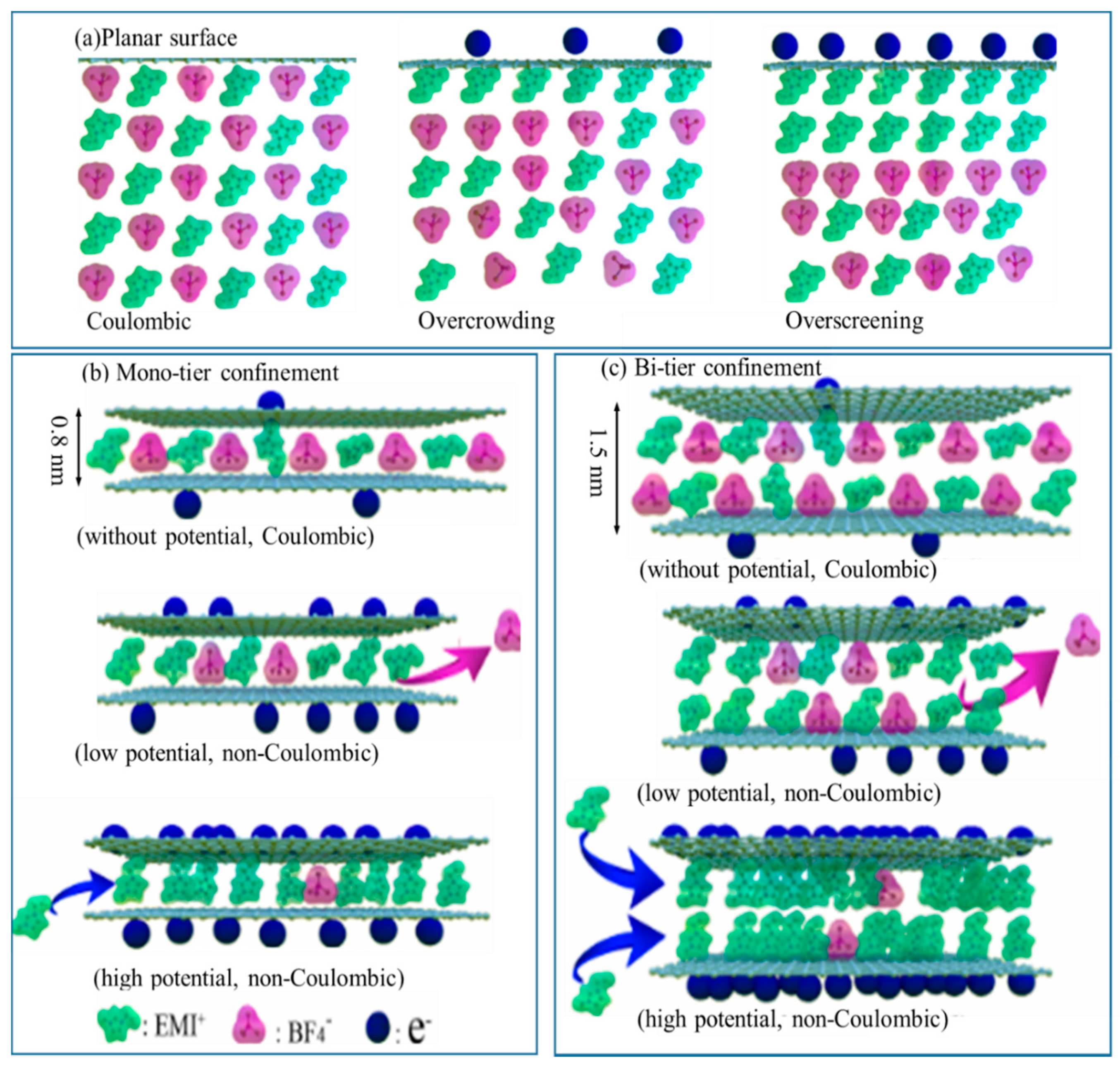
4. Discussion
4.1. The Ion Partitioning on C-0.25
4.2. The Ion Partitioning on C-0.5
4.3. The Ion Partitioning on C-0.75
4.4. Reasons for the Distince Ion Partitioning on C-0.75
4.4.1. DoC of Ions Inside all Electrodes
4.4.2. The EDL Overlapping Behavior
4.4.3. The Spatial Connectivity Influence
4.4.4. The Supports from the CV Data
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Simon, P.; Gogotsi, Y. Materials for electrochemical capacitors. Nat. Mater. 2008, 7, 845–854. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.G.; Song, Y.F.; Xia, Y.Y. Electrochemical capacitors: Mechanism, materials, systems, characterization and applications. Chem. Soc. Rev. 2016, 45, 5925–5950. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.L.; Zhao, X.S. Carbon-based materials as supercapacitor electrodes. Chem. Soc. Rev. 2009, 38, 2520–2531. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.B.; Ren, J.; Zhang, Z.T.; Chen, X.L.; Guan, G.Z.; Qiu, L.B.; Zhang, Y.; Peng, H.S. Recent advancement of nanostructured carbon for energy applications. Chem. Rev. 2015, 115, 5159–5223. [Google Scholar] [CrossRef] [PubMed]
- Dong, K.; Liu, X.M.; Dong, H.F.; Zhang, X.P.; Zhang, S.J. Multiscale studies on ionic liquids. Chem. Rev. 2017, 117, 6636–6695. [Google Scholar] [CrossRef] [PubMed]
- Robert, H.; Gregory, G.W.; Rob, A. Structure and nanostructure in ionic liquids. Chem. Rev. 2015, 115, 6357–6426. [Google Scholar]
- Zhong, C.; Deng, Y.D.; Hu, W.B.; Qiao, J.L.; Zhang, L.; Zhang, J.J. A review of electrolyte materials and compositions for electrochemical supercapacitors. Chem. Soc. Rev. 2015, 4, 7484–7539. [Google Scholar] [CrossRef]
- Merlet, C.; Pe’an, C.; Rotenberg, B.; Madden, P.A.; Daffos, B.; Taberna, P.L.; Simon, P.; Salanne, M. Highly confined ions store charge more efficiently in supercapacitors. Nat. Commun. 2013, 4, 2701. [Google Scholar] [CrossRef]
- Zhang, S.G.; Zhang, J.H.; Zhang, Y.; Deng, Y.Q. Nanoconfined ionic liquids. Chem. Rev. 2017, 117, 6755–6833. [Google Scholar] [CrossRef]
- Maxim, V.F.; Alexei, A.K. Ionic liquids at electrified interfaces. Chem. Rev. 2014, 114, 2978–3036. [Google Scholar]
- Alexander, C.F.; John, M.G.; Céline, M.; Javier, C.G.; Abdul, R.O.R.; Nicole, M.T.; Clare, P.G. Direct observation of ion dynamics in supercapacitor electrodes using in situ diffusion NMR spectroscopy. Nat. Energy 2017, 2, 16216. [Google Scholar] [CrossRef]
- Mercy, R.B.; Siddulu, N.T.; Stalin, J.; Kavitha, R.; Gurwinder, S.; Jessica, S.; Ugo, R.; Khalid, A.B.; Ajayan, V. Recent advances in functionalized micro and mesoporous carbon materials: Synthesis and applications. Chem. Soc. Rev. 2018, 47, 2680–2721. [Google Scholar]
- Wu, P.; Huang, J.S.; Vincent, M.; Bobby, G.S.; Qiao, R. Complex capacitance scaling in ionic liquids-filled nanopores. ACS Nano. 2011, 5, 9044–9051. [Google Scholar] [CrossRef] [PubMed]
- Ryan, S.; Clifford, E.W.; Jan, F. Capillary condensation of ionic liquid solutions in porous electrodes. J. Phys. Chem. C 2013, 117, 1728–1734. [Google Scholar]
- Xiong, R.; Anise, M.G.; Ma, R.L.; Zhang, S.; Vladimir, V.T. Naturally-derived biopolymer nanocomposites: Interfacial design, properties and emerging applications. Mater. Sci. Eng. Rep. 2018, 125, 1–41. [Google Scholar] [CrossRef]
- Li, J.; Wang, N.; Tian, J.R.; Qian, W.Z.; Chu, W. Cross-coupled macro-mesoporous carbon network toward record high energy-power eensity supercapacitor at 4 V. Adv. Funct. Mater. 2018, 28, 1806153. [Google Scholar] [CrossRef]
- Wang, H.L.; Gao, Q.M.; Hu, J. High hydrogen storage capacity of porous carbons prepared by using activated carbon. J. Am. Chem. Soc. 2009, 131, 7016–7022. [Google Scholar] [CrossRef]
- Nobuhiro, O.; Yuichi, I.; Tsuyoshi, S.; Yoji, T. Impedance spectroscopy characterization of porous electrodes under different electrode thickness using a symmetric cell for high-performance lithium-ion batteries. J. Phys. Chem. C 2015, 119, 4612–4619. [Google Scholar]
- Oleg, N.K.; Vitaly, V.C.; Valentin, V.L.; Oleg, V.P. Uniform diffusion of acetonitrile inside carbon nanotubes favors supercapacitor performance. Nano Lett. 2008, 8, 2126–2130. [Google Scholar]
- Alexander, C.F.; Céline, M.; Phoebe, K.A.; Elizabeth, K.H.; John, M.G.; Mesut, A.; Marco, Z.; Volker, P.; Yury, G.; Clare, P.G. New insights into the structure of nanoporous carbons from NMR, Raman, and Pair Distribution Function Analysis. Chem. Mater. 2015, 27, 6848–6857. [Google Scholar]
- Hao, L.; Ning, J.; Luo, Bi.; Wang, B.; Zhang, Y.B.; Tang, Z.H.; Yang, J.H.; Arne, T.; Zhi, L.J. Structural evolution of 2D microporous covalent triazine-based framework toward the study of high-performance supercapacitors. J. Am. Chem. Soc. 2015, 137, 219–225. [Google Scholar] [CrossRef] [PubMed]
- Sha, M.L.; Wu, G.Z.; Liu, Y.S.; Tang, Z.F.; Fang, H.P. Drastic phase transition in ionic liquid [Dmim][Cl] confined between graphite walls: New phase formation. J. Phys. Chem. C 2009, 113, 4618–4622. [Google Scholar] [CrossRef]
- Nav, N.R.; Joshua, M.; Ramesh, S.; Francisco, R.H. On the influence of pore size and pore loading on structural and dynamical heterogeneities of an ionic liquid confined in a slit nanopore. J. Phys. Chem. C 2012, 116, 5169–5181. [Google Scholar]
- Ramesh, S.; Nav, N.R.; He, X.X.; Joshua, M.; Francisco, R.H. Molecular dynamics simulations of the ionic liquid [EMIM+][TFMSI-] confined inside rutile (110) slit nanopores. Phys. Chem. Chem. Phys. 2013, 15, 16090–16103. [Google Scholar]
- Ramesh, S.; Joshua, M.; Francisco, R.H. Heterogeneity in the dynamics of the ionic liquid [BMIM+][PF6–] confined in a slit nanopore. J. Phys. Chem. C 2011, 115, 16544–16554. [Google Scholar]
- Gao, J.; Wang, X.; Zhang, Y.; Liu, J.; Lu, Q.; Liu, M. Boron-doped ordered mesoporous carbons for the application of supercapacitors. Electrochim. Acta 2016, 207, 266–274. [Google Scholar] [CrossRef]
- Li, J.; Wang, N.; Deng, J.; Qian, W.Z.; Chu, W. Flexible metal-templated fabrication of mesoporous onion-like crbon and Fe2O3@N-doped carbon foam for electrochemical energy storage. J. Mater. Chem. A 2018, 6, 13012–13020. [Google Scholar] [CrossRef]
- Na, W.; Jun, J.; Park, J.W.; Lee, G.; Jang, J. Highly porous carbon nanofibers co-doped with fluorine and nitrogen for outstanding supercapacitor performance. J. Mater. Chem. A 2017, 5, 17379–17387. [Google Scholar] [CrossRef]
- Zhao, J.; Lai, H.; Lyu, Z.; Jiang, Y.; Xie, K.; Wang, Z.; Wu, Q.; Yang, L.; Jin, Z.; Ma, Y.; et al. Hydrophilic hierarchical nitrogen-doped carbon nanocages for ultrahigh supercapacitive performance. Adv. Mater. 2015, 27, 3541–3545. [Google Scholar] [CrossRef]
- Wang, D.W.; Liu, S.J.; Jiao, L.; Fang, G.L. A smart bottom-up strategy for the fabrication of porous carbon nanosheets containing rGO for high-rate supercapacitors in organic electrolyte. Electrochim. Acta 2017, 252, 109–118. [Google Scholar] [CrossRef]
- Li, J.; Wei, M.; Chu, W.; Wang, N. High-stable α-phase NiCo double hydroxide microspheres via microwave synthesis for supercapacitor electrode materials. Chem. Eng. J. 2017, 316, 277–287. [Google Scholar] [CrossRef]
- Prehal, C.; Weingarth, D.; Perre, E.; Lechner, R.T.; Amenitsch, H.; Paris, O.; Presser, V. Tracking the structural arrangement of ions in carbon supercapacitor nanopores using in situ small-angle X-ray scattering. Energy Environ. Sci. 2015, 8, 1725–1735. [Google Scholar] [CrossRef]
- Nicolas, J.; Patrice, S.; Yury, G.; Volker, P. Increase in capacitance by subnanometer pores in carbon. ACS Energy Lett. 2016, 1, 1262–1265. [Google Scholar]
- Kevin, G.G.; Stephen, E.T.; Christoph, B.; Thomas, W.; Simon, F.L.; Matthias, T.; Peter, L.; Bryant, J.P.; Seungbum, H.; Brandon, L.; et al. Optimizing areal capacities through understanding the limitations of lithium-ion electrodes. J. Electrochem. Soc. 2016, 163, A138–A149. [Google Scholar]
- Martin, Z.B.; Brian, D.S.; Alexei, A.K. Double layer in ionic liquids: Overscreening versus crowding. Phys. Rev. Lett. 2012, 109, 149903–149906. [Google Scholar]
- Maxim, V.F.; Alexei, A.K. Towards understanding the structure and capacitance of electrical double layer in ionic liquids. Electrochim. Acta 2008, 53, 6835–6840. [Google Scholar]
- Christopher, C.R.; Alpha, A.L.; Gunnar, P.; Alexei, A.K. Interionic interactions in conducting nanoconfinement. ChemPhysChem 2013, 14, 4121–4125. [Google Scholar]
- Jenel, V.; Oleg, B.; Grant, D.S. Molecular insights into the potential and temperature dependences of the differential capacitance of a room-temperature ionic liquid at graphite electrodes. J. Am. Chem. Soc. 2010, 132, 14825–14833. [Google Scholar]
- Yang, L.; Brian, H.F.; Albert, Mi.; Lawrence, R.P. Molecular simulation of electric double-layer capacitors based on carbon nanotube forests. J. Am. Chem. Soc. 2009, 131, 12373–12376. [Google Scholar] [CrossRef]
- Feng, G.; Li, S.; Volker, P.; Peter, T.C. Molecular insights into carbon supercapacitors based on room-temperature ionic liquids. J. Phys. Chem. Lett. 2013, 4, 3367–3376. [Google Scholar] [CrossRef]
- Clarisse, P.; Barbara, D.; Benjamin, R.; Pierre, L.; Matthieu, H.; Pierre, L.T.; Patrice, S.; Mathieu, S. Confinement, desolvation and electrosorption effects on the diffusion of ions in nanoporous carbon electrodes. J. Am. Chem. Soc. 2015, 137, 12627–12632. [Google Scholar]
- Nicolas, J.; Steffen, P.E.; Benjamin, K.; Bernhard, R.; Volker, P. Quantitative information about electrosorption of ionic liquids in carbon nanopores from electrochemical eilatometry and quartz crystal microbalance measurements. J. Phys. Chem. C 2017, 121, 19120–19128. [Google Scholar]
- Shim, Y.; Kim, H.J. Nanoporous carbon supercapacitors in an ionic liquid: A computer simulation study. ACS Nano 2010, 4, 2345–2355. [Google Scholar] [CrossRef] [PubMed]
- Justin, N.N.; Aken, K.L.V.; Gogotsi, Y.; Wesolowski, D.J.; Wu, J.Z. Self-amplified surface charging and partitioning of ionic liquids in nanopores. Phys. Rev. Appl. 2017, 8, 034018. [Google Scholar]
- Xing, L.D.; Jenel, V.; Oleg, B.; Dmitry, B. On the atomistic nature of capacitance enhancement generated by ionic liquid electrolyte confined in subnanometer pores. J. Phys. Chem. Lett. 2013, 4, 132–140. [Google Scholar] [CrossRef]
- Monk, J.; Singh, R.; Hung, F.R. Effects of pore size and pore loading on the properties of ionic liquids confined inside nanoporous CMK-3 carbon materials. J. Phys. Chem. C 2011, 115, 3034–3042. [Google Scholar] [CrossRef]
- Joseé, L.B.; Feng, G.; Pasquale, F.F.; Li, S.; Gernot, D.S.; Peter, T.C.; David, J.W. Densification of ionic liquid molecules within a hierarchical nanoporous carbon structure revealed by small-angle scattering and molecular dynamics simulation. Chem. Mater. 2014, 26, 1144–1153. [Google Scholar]
- Zhou, H.; Michael, R.; Feng, G.; Lee, S.S.; Docherty, H.; Paul, F.; Peter, T.C.; Pasquale, F.F.; Dai, S.; John, M.D.; et al. Nanoscale perturbations of room temperature ionic liquid structure at charged and uncharged interfaces. ACS Nano 2012, 6, 9818–9827. [Google Scholar] [CrossRef]
- Yan, Z.F.; Meng, D.W.; Wu, X.L.; Zhang, X.L.; Liu, W.P.; He, K.H. Two-dimensional ordering of ionic liquids confined by layered silicate plates via molecular dynamics simulation. J. Phys. Chem. C 2015, 119, 19244–19252. [Google Scholar] [CrossRef]
- Fen, G.; Qiao, R.; Huang, J.S.; Sumpter, B.G.; Meunier, V. Atomistic insight on the charging energetics in subnanometer pore supercapacitors. J. Phys. Chem. C 2010, 114, 18012–18016. [Google Scholar]
- Chmiola, J.; Yushin, G.; Gogotsi, Y.; Portet, C.; Simon, P.; Taberna, P.L. Anomalous increase in carbon capacitance at pore sizes less than 1 nanometer. Science 2006, 313, 1760–1763. [Google Scholar] [CrossRef] [PubMed]
- Merlet, C.; Rotenberg, B.; Madden, P.A.; Taberna, P.L.; Simon, P.; Gogotsi, Y.; Salanne, M. On the molecular origin of supercapacitance in nanoporous carbon electrodes. Nat. Mater. 2012, 11, 306–310. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.G. Fluctuation in electrolyte solutions: The self-energy. Phys. Rev. E 2010, 81, 021501. [Google Scholar] [CrossRef] [PubMed]
- Lauw, Y.; Horne, M.D.; Rodopoulos, T.; Leermakers, F.A.M. Room-temperature ionic liquids: Excluded volume and ion polarizability effects in the electrical double-layer structure and capacitance. Phys. Rev. Lett. 2009, 103, 117801. [Google Scholar] [CrossRef]
- Ohba, T.; Hata, K.; Chaban, V.V. Nanocrystallization of imidazolium ionic liquid in carbon nanotubes. J. Phys. Chem. C 2015, 119, 28424–28429. [Google Scholar] [CrossRef]
- Gupta, A.K.; Singh, R.K.; Chandra, S. Crystallization kinetics behavior of ionic liquid [EMIM][BF4] confined in mesoporous silica matrices. RSC Adv. 2014, 4, 22277–22287. [Google Scholar] [CrossRef]
- Chen, S.; Kobayashi, K.; Miyata, Y.; Imazu, N.; Saito, T.; Kitaura, R.; Shinohara, H. Morphology and melting behavior of ionic liquids inside single-wall carbon nanotubes. J. Am. Chem. Soc. 2009, 131, 14850–14856. [Google Scholar] [CrossRef]
- Mei, L.; Yeh, L.H.; Qian, S. Buffer anions can enormously enhance the electrokinetic energy conversion in nanofluidics with highly overlapped double layers. Nano Energy 2017, 32, 374–381. [Google Scholar] [CrossRef]
- Baldessari, F. Electrokinetics in nanochannels part I. electric double layer overlap and channel-to-well equilibrium. J. Colloid Interface Sci. 2008, 325, 526–538. [Google Scholar] [CrossRef]
- Das, S.; Guha, A.; Mitra, S.K. Exploring new scaling regimes for streaming potential and electroviscous effects in a nanocapillary with overlapping electric double layers. Anal. Chim. Acta 2013, 804, 159–166. [Google Scholar] [CrossRef]
- Sprague, I.B.; Dutta, P. Improved kinetics from ion advection through overlapping electric double layers in nano-porous electrodes. Electrochim. Acta 2013, 91, 20–29. [Google Scholar] [CrossRef]
- Jiang, D.; Jin, Z.; Wu, J. Oscillation of capacitance inside nanopores. Nano Lett. 2011, 11, 5373–5377. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Liu, Z.; Huang, Q.; Gao, Y.; Regula, M.; Wang, D.; Chen, L.Q.; Wang, D. Stable metal battery anodes enabled by polyethylenimine sponge hosts by way of electrokinetic effects. Nat. Energy 2018, 3, 1076–1083. [Google Scholar] [CrossRef]
- Kondrat, S.; Wu, P.; Qiao, R.; Kornyshev, A.A. Accelerating charging dynamics in subnanometre pores. Nat. Mater. 2014, 13, 387–393. [Google Scholar] [CrossRef]

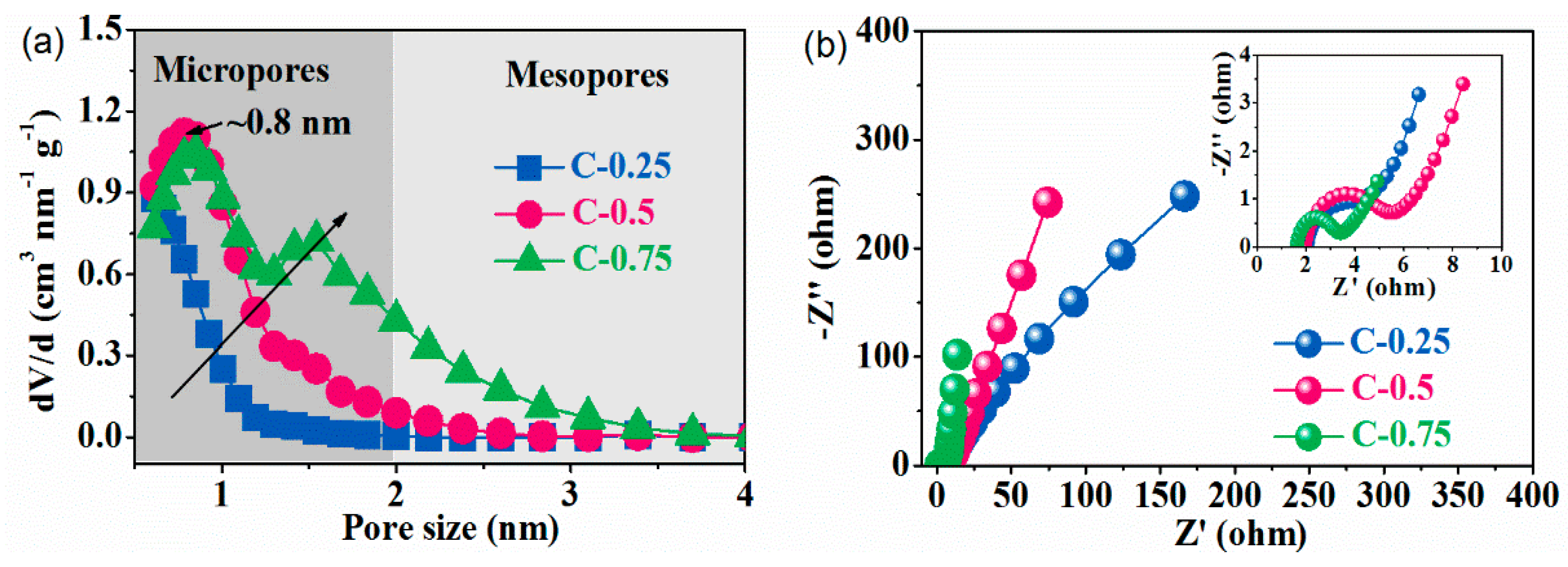
| Samples | Stotal (m2g−1) a | Smeso (cm2 g−1) | Smicro (cm2 g−1) b | Vtotal (cm3 g−1) c | Vmeso (cm3 g−1) | Vmicro (cm3 g−1) b | Nitrogen Contents (at. %) d |
|---|---|---|---|---|---|---|---|
| C-0.25 | 1084.3 | 45.5 | 1038.8 | 0.403 | 0.001 | 0.402 | 9.45 |
| C-0.5 | 2050.3 | 280.2 | 1770.1 | 0.825 | 0.107 | 0.718 | 5.52 |
| C-0.75 | 2744.6 | 880.5 | 1864.1 | 1.304 | 0.478 | 0.826 | 1.68 |
| Samples | Specific Capacitance (F g−1) at 0.5 A g−1 | Specific Capacitance (F g−1) at 10 A g−1 | Rate Capacity from 0.5 to 10 A g−1 | Energy Density (Wh kg−1) at 1 kW kg−1 | Energy Density (Wh kg−1) at 20 kW kg−1 | Capacity Retention at 10 A g−1 over 5000 Cycles |
|---|---|---|---|---|---|---|
| C-0.25 | 4.8 | 1.7 | 35.0% | 2.7 | 0.94 | 100% |
| C-0.5 | 54.7 | 22.4 | 41.0% | 30.4 | 12.4 | 87.0% |
| C-0.75 | 158.9 | 85.9 | 54.0% | 88.3 | 47.7 | 83.3% |
| Samples | Csur at 0.5 A g−1 | Csur at 10 A g−1 | Cvol at 0.5 A g−1 | Cvol at 10 A g−1 |
|---|---|---|---|---|
| C-0.25 | 0.44 µF cm−2 | 0.16 µF cm−2 | 11.9 F cm−3 | 4.2 F cm−3 |
| C-0.5 | 2.67 µF cm−2 | 1.09 µF cm−2 | 66.5 F cm−3 | 27.2 F cm−3 |
| C-0.75 | 5.80 µF cm−2 | 3.20 µF cm−2 | 122.0 F cm−3 | 65.9 F cm−3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, J.; Li, J.; Xiao, Z.; Song, S.; Li, L. Studies on Possible Ion-Confinement in Nanopore for Enhanced Supercapacitor Performance in 4V EMIBF4 Ionic Liquids. Nanomaterials 2019, 9, 1664. https://doi.org/10.3390/nano9121664
Deng J, Li J, Xiao Z, Song S, Li L. Studies on Possible Ion-Confinement in Nanopore for Enhanced Supercapacitor Performance in 4V EMIBF4 Ionic Liquids. Nanomaterials. 2019; 9(12):1664. https://doi.org/10.3390/nano9121664
Chicago/Turabian StyleDeng, Jie, Jing Li, Zhe Xiao, Shuang Song, and Luming Li. 2019. "Studies on Possible Ion-Confinement in Nanopore for Enhanced Supercapacitor Performance in 4V EMIBF4 Ionic Liquids" Nanomaterials 9, no. 12: 1664. https://doi.org/10.3390/nano9121664
APA StyleDeng, J., Li, J., Xiao, Z., Song, S., & Li, L. (2019). Studies on Possible Ion-Confinement in Nanopore for Enhanced Supercapacitor Performance in 4V EMIBF4 Ionic Liquids. Nanomaterials, 9(12), 1664. https://doi.org/10.3390/nano9121664




