External Field-Controlled Ablation: Magnetic Field
Abstract
1. Introduction
2. Results
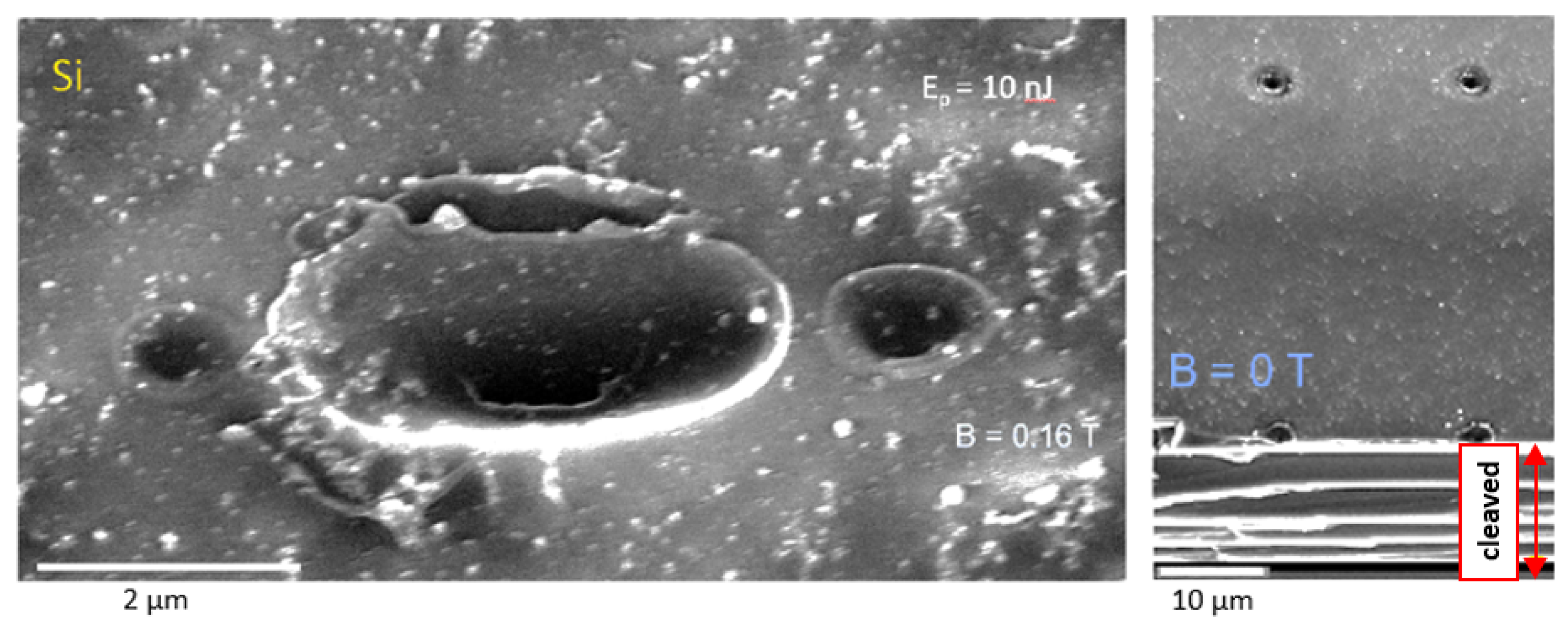
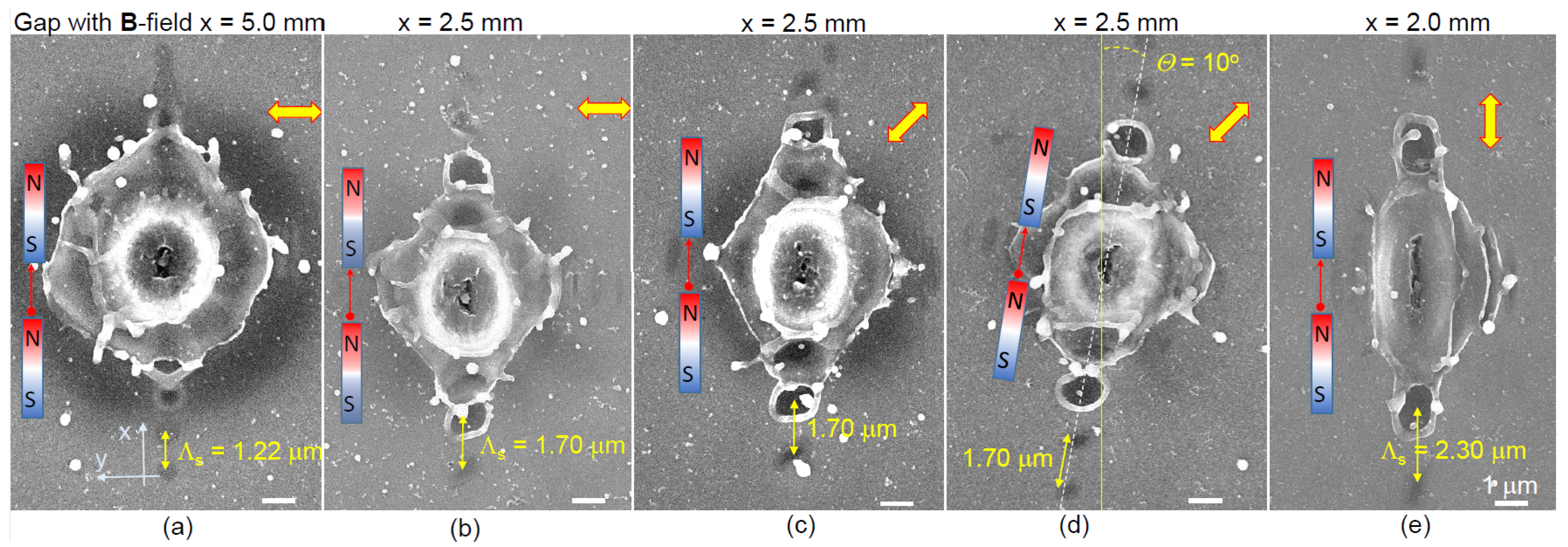
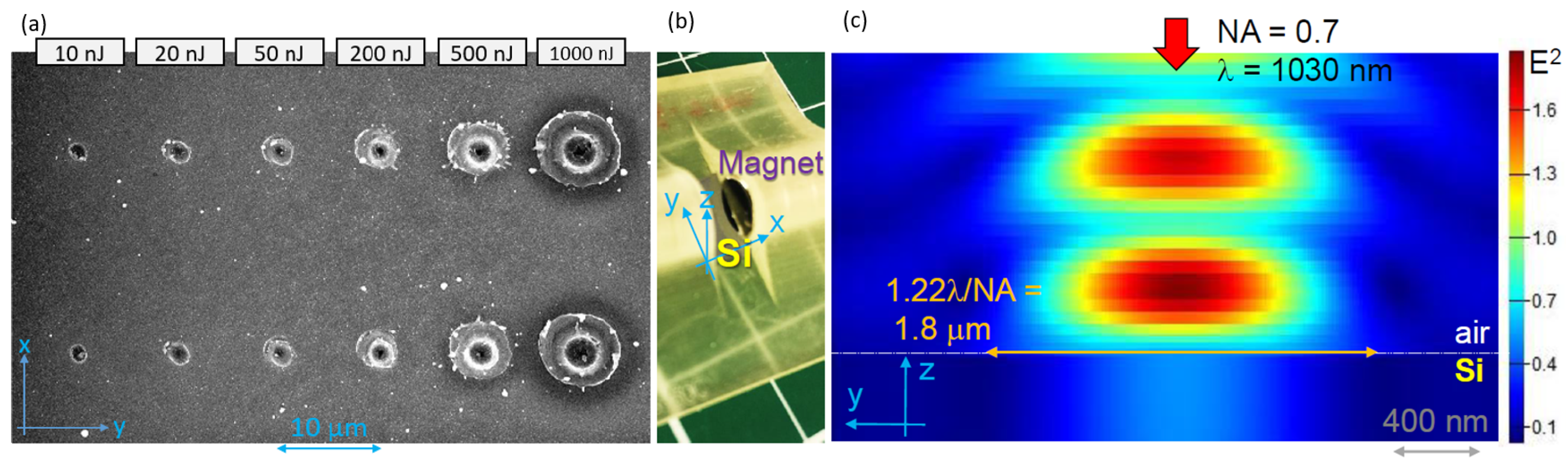
2.1. Peculiarities of Ablation Patterns in the External B-Field
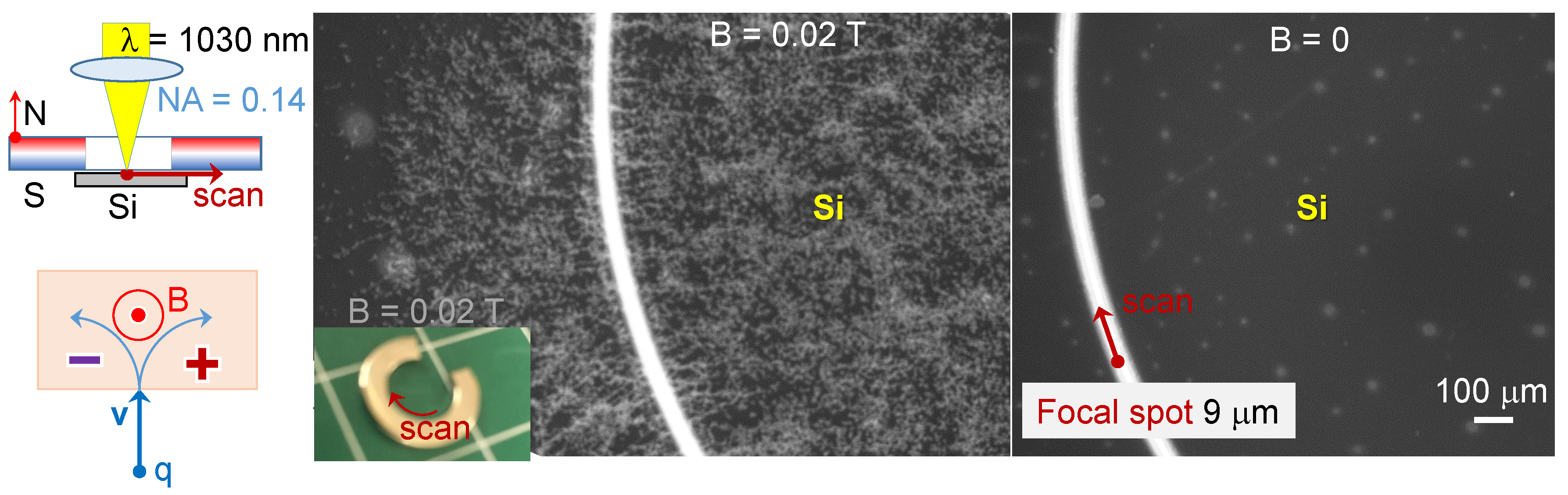
2.2. Debris Dispersion
3. Discussion
3.1. Surface Plasmon Polariton
3.2. B-Field Generation
4. Materials and Methods
5. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

References
- Davis, K.M.; Miura, K.; Sugimoto, N.; Hirao, K. Writing waveguides in glass with a femtosecond laser. Opt. Lett. 1996, 21, 1729–1731. [Google Scholar] [CrossRef] [PubMed]
- Ródenas, A.; Gu, M.; Corrielli, G.; Paiè, P.; John, S.; Kar, A.; Osellame, R. Three-dimensional femtosecond laser nanolithography of crystals. Nat. Photonics 2019, 13, 105–109. [Google Scholar] [CrossRef]
- Watanabe, M.; Juodkazis, S.; Matsuo, S.; Nishii, J.; Misawa, H. Cross-Talk in Photoluminescence Readout of Three-Dimensional Memory in vitreous Silica by One- and Two-Photon Excitation. Jpn. J. Appl. Phys. 2000, 39, 6763–6767. [Google Scholar] [CrossRef]
- Juodkazis, S.; Matsuo, S.; Misawa, H.; Mizeikis, V.; Marcinkevicius, A.; Sun, H.B.; Tokuda, Y.; Takahashi, M.; Yoko, T.; Nishii, J. Application of femtosecond laser pulses for microfabrication of transparent media. Appl. Surf. Sci. 2002, 197–198, 705–709. [Google Scholar] [CrossRef]
- Shimotsuma, Y.; Kazansky, P.; Qiu, J.; Hirao, K. Self-organized nanogratings in glass irradiated by ultrashort light pulses. Phys. Rev. Lett. 2003, 91, 247405. [Google Scholar] [CrossRef]
- Umran, F.A.; Liao, Y.; Elias, M.M.; Sugioka, K.; Stoian, R.; Cheng, G.; Cheng, Y. Formation of nanogratings in a transparent material with tunable ionization property by femtosecond laser irradiation. Opt. Express 2013, 21, 15259–15267. [Google Scholar] [CrossRef]
- Ozkan, A.; Malshe, A.; Railkar, T.; Brown, W.; Shirk, M.; Molian, P. Femtosecond laser-induced periodic structure writing on diamond crystals and microclusters. Appl. Phys. Lett. 1999, 75, 3716. [Google Scholar] [CrossRef]
- Das, S.K.; Messaoudi, H.; Debroy, A.; McGlynn, E.; Grunwald, R. Multiphoton excitation of surface plasmon-polaritons and scaling of nanoripple formation in large bandgap materials. Opt. Mat. Express 2013, 3, 1705–1715. [Google Scholar] [CrossRef]
- Juodkazis, S.; Nishimura, K.; Misawa, H.; Ebisui, T.; Waki, R.; Matsuo, S.; Okada, T. Control over the State of Crystallinity: Sapphire. Adv. Mat. 2006, 18, 1361–1364. [Google Scholar] [CrossRef]
- Gamaly, E.E.; Juodkazis, S.; Nishimura, K.; Misawa, H.; Luther-Davies, B.; Hallo, L.; Nicolai, P.; Tikhonchuk, V. Laser-matter interaction in a bulk of a transparent solid: confined micro-explosion and void formation. Phys. Rev. B 2006, 73, 214101. [Google Scholar] [CrossRef]
- Yamaguchi, M.; Ueno, S.; Kumai, R.; Kinoshita, K.; Murai, T.; Tomita, T.; Matsuo, S.; Hashimoto, S. Raman spectroscopic study of femtosecond laser-induced phase transformation associated with ripple formation on single-crystal SiC. Appl. Phys. A 2010, 99, 23–27. [Google Scholar] [CrossRef]
- Drs, J.; Kishi, T.; Bellouard, Y. Laser-assisted morphing of complex three dimensional objects. Opt. Express 2015, 23, 17355–17366. [Google Scholar] [CrossRef] [PubMed]
- Marcinkevicius, A.; Juodkazis, S.; Watanabe, M.; Miwa, M.; Matsuo, S.; Misawa, H.; Nishii, J. Femtosecond Laser-Assisted Three-Dimensional Microfabrication in Silica. Opt. Lett. 2001, 26, 277–279. [Google Scholar] [CrossRef] [PubMed]
- Yamasaki, K.; Juodkazis, S.; Matsuo, S.; Misawa, H. Three-dimensional microchannels in polymers: One step fabrication. Appl. Phys. A 2003, 77, 371–373. [Google Scholar] [CrossRef]
- Juodkazis, S.; Yamasaki, K.; Mizeikis, V.; Matsuo, S.; Misawa, H. Formation of Embedded Patterns in Glasses Using Femtosecond Irradiation. Appl. Phys. A 2004, 79, 1549–1553. [Google Scholar] [CrossRef]
- Zhang, D.; Gökce, B.; Barcikowski, S. Laser synthesis and processing of colloids: fundamentals and applications. Chem. Rev. 2017, 117, 3990–4103. [Google Scholar] [CrossRef]
- Oktem, B.; Pavlov, I.; Ilday, S.; Kalaycioglu, H.; Rybak, A.; Yavas, S.; Erdogan, M.; Ilday, F.O. Nonlinear laser lithography for indefinitely large-area nanostructuring with femtosecond pulses. Nat. Photonics 2013, 7, 897–901. [Google Scholar] [CrossRef]
- Bhuyan, M.K.; Courvoisier, F.; Lacourt, P.A.; Jacquot, M.; Salut, R.; Furfaro, L.; Dudley, J.M. High aspect ratio nanochannel machining using single shot femtosecond Bessel beams. Appl. Phys. Lett. 2010, 97, 081102. [Google Scholar] [CrossRef]
- Wang, G.; Yu, Y.; Jiang, L.; Li, X.; Xie, Q.; Lu, Y. Cylindrical shockwave-induced compression mechanism in femtosecond laser Bessel pulse micro-drilling of PMMA. Appl. Phys. Lett. 2017, 110, 161907. [Google Scholar] [CrossRef]
- Osellame, R.; Hoekstra, H.; Cerullo, G.; Pollnau, M. Femtosecond laser microstructuring: an enabling tool for optofluidic lab-on-chips. Laser Photonics Rev. 2011, 5, 442–463. [Google Scholar] [CrossRef]
- Farrokhi, H.; Gruzdev, V.; Zheng, H.; Zhoui, W. Fundamental mechanisms of nanosecond-laser-ablation enhancement by an axial magnetic field. J. Opt. Soc. Am 2019, 36, 1091–1100. [Google Scholar] [CrossRef]
- Tang, H.W.; Qiu, P.; Cao, R.X.; Zhuang, J.L.; Xu, S. Repulsive magnetic field-assisted laser-induced plasma micromachining for high-quality microfabrication. Int. J. Adv. Manuf. Tech. 2019, 102, 2223–2229. [Google Scholar] [CrossRef]
- Kuznetsov, A.I.; Miroshnichenko, A.E.; Fu, Y.H.; Zhang, J.; Luk’yanchuk, B. Magnetic light. Sci. Rep. 2012, 2, 492. [Google Scholar] [CrossRef] [PubMed]
- Iwase, H.; Kokubo, S.; Juodkazis, S.; Misawa, H. Suppression of ripples on Ni surface via a polarization grating. Opt. Express 2009, 17, 4388–4396. [Google Scholar] [CrossRef] [PubMed]
- Buividas, R.; Gervinskas, G.; Tadich, A.; Cowie, B.C.C.; Mizeikis, V.; Vailionis, A.; de Ligny, D.; Gamaly, E.G.; Rode, A.V.; Juodkazis, S. Phase Transformation in Laser-Induced Micro-Explosion in Olivine (Fe,Mg)2SiO4. Adv. Eng. Mat. 2014, 16, 767–773. [Google Scholar] [CrossRef]
- Schinke, C.; Peest, P.C.; Schmidt, J.; Brendel, R.; Bothe, K.; Vogt, M.R.; Kröger, I.; Winter, S.; Schirmacher, A.; Lim, S.; et al. Uncertainty analysis for the coefficient of band-to-band absorption of crystalline silicon. AIP Adv. 2015, 5, 67168. [Google Scholar] [CrossRef]
- Sokolowski-Tinten, K.; von der Linden, D. Generation of dense electron-hole plasmas in silicon. Phys. Rev. B 2000, 61, 2643–2650. [Google Scholar] [CrossRef]
- Gamaly, E.G.; Rode, A.V. Physics of ultra-short laser interaction with matter: From phonon excitation to ultimate transformations. J. Progr. Quant. Electron. 2013, 37, 215–323. [Google Scholar] [CrossRef]
- Gamaly, E.G.; Rode, A.V.; Luther-Davies, B. Ablation of solids by femtosecond lasers: Ablation mechanism and ablation thresholds for metals and dielectrics. Phys. Plasmas 2002, 18, 949–957. [Google Scholar] [CrossRef]
- Haines, M.G. Saturation Mechanisms for the Generated Magnetic Field in Nonuniform Laser-Matter Irradiation. Phys. Rev. Lett. 1997, 78, 254–257. [Google Scholar] [CrossRef]
- Wang, C.; Huo, H.; Johnson, M.; Shen, M.; Mazur, E. The thresholds of surface nano-/micro-morphology modifications with femtosecond laser pulse irradiations. Nanotechnology 2010, 21, 75304. [Google Scholar] [CrossRef] [PubMed]
- Gamaly, E.G.; Rode, A.V. Ultrafast re-structuring of the electronic landscape of transparent dielectrics: new material states (Die-Met). Appl. Phys. A 2018, 124, 278. [Google Scholar] [CrossRef]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maksimovic, J.; Ng, S.H.; Katkus, T.; Cowie, B.C.C.; Juodkazis, S. External Field-Controlled Ablation: Magnetic Field. Nanomaterials 2019, 9, 1662. https://doi.org/10.3390/nano9121662
Maksimovic J, Ng SH, Katkus T, Cowie BCC, Juodkazis S. External Field-Controlled Ablation: Magnetic Field. Nanomaterials. 2019; 9(12):1662. https://doi.org/10.3390/nano9121662
Chicago/Turabian StyleMaksimovic, Jovan, Soon Hock Ng, Tomas Katkus, Bruce C. C. Cowie, and Saulius Juodkazis. 2019. "External Field-Controlled Ablation: Magnetic Field" Nanomaterials 9, no. 12: 1662. https://doi.org/10.3390/nano9121662
APA StyleMaksimovic, J., Ng, S. H., Katkus, T., Cowie, B. C. C., & Juodkazis, S. (2019). External Field-Controlled Ablation: Magnetic Field. Nanomaterials, 9(12), 1662. https://doi.org/10.3390/nano9121662






