Interfacial Model and Characterization for Nanoscale ReB2/TaN Multilayers at Desired Modulation Period and Ratios: First-Principles Calculations and Experimental Investigations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Methods
2.2. Theoretical
3. Results and Discussion
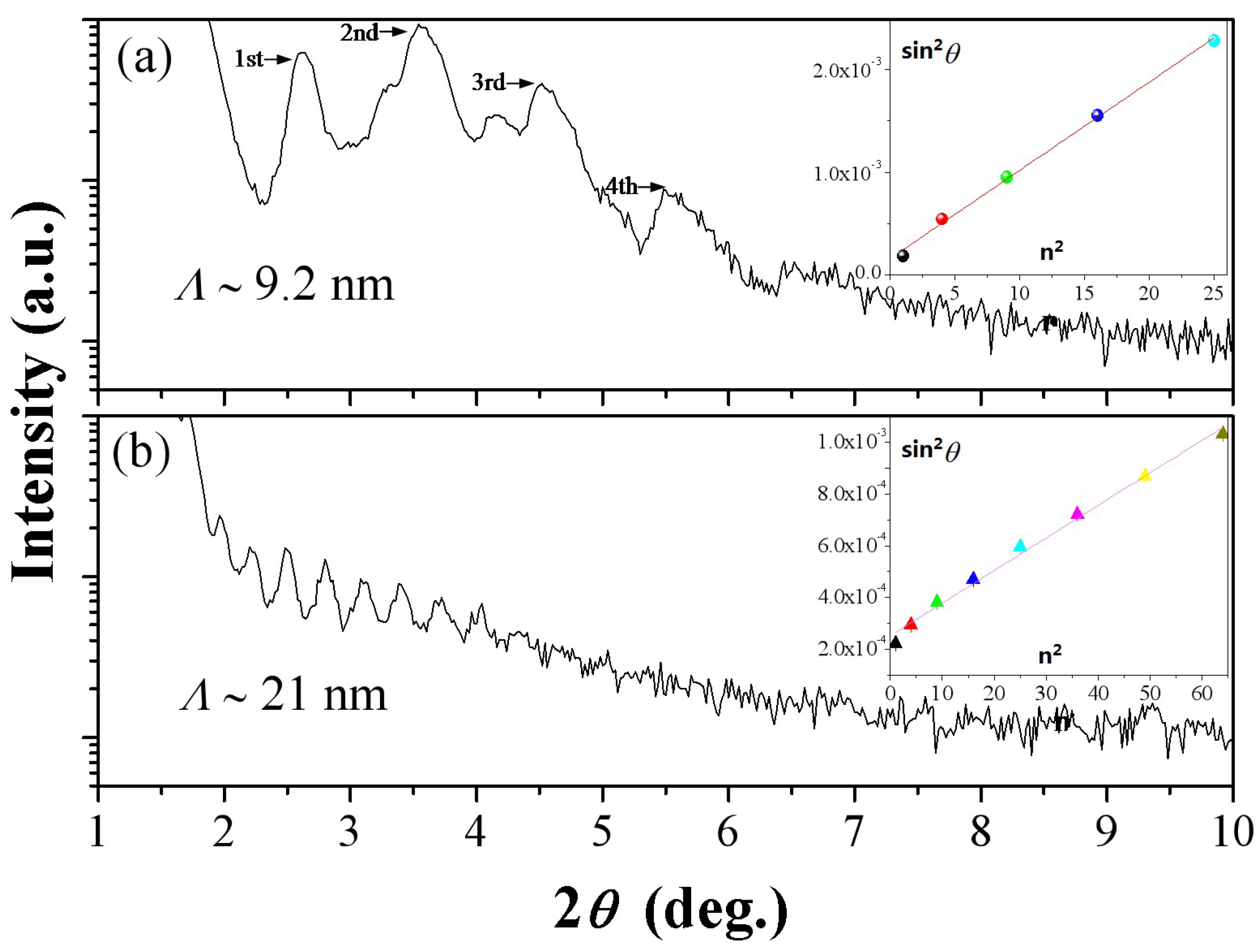
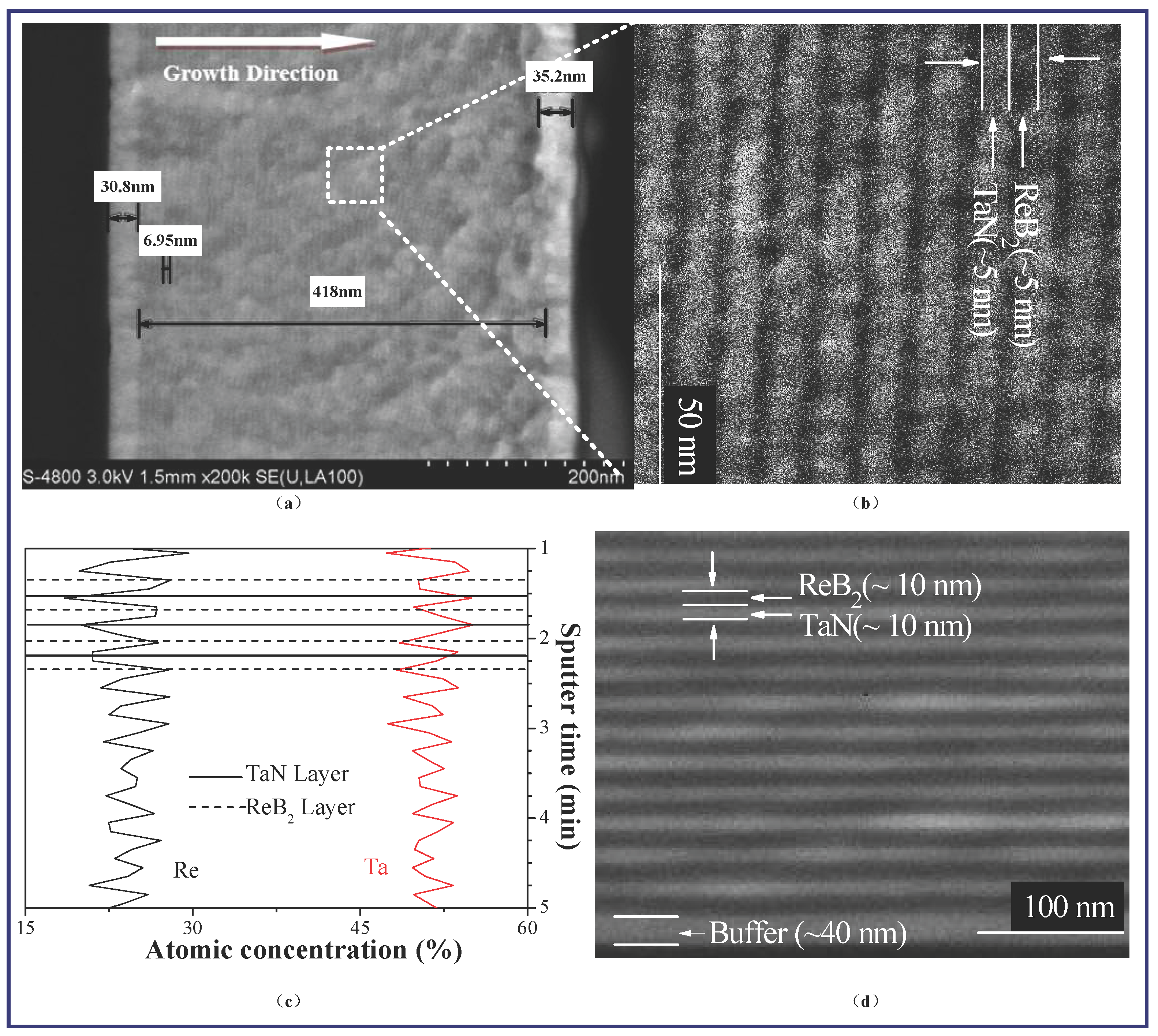
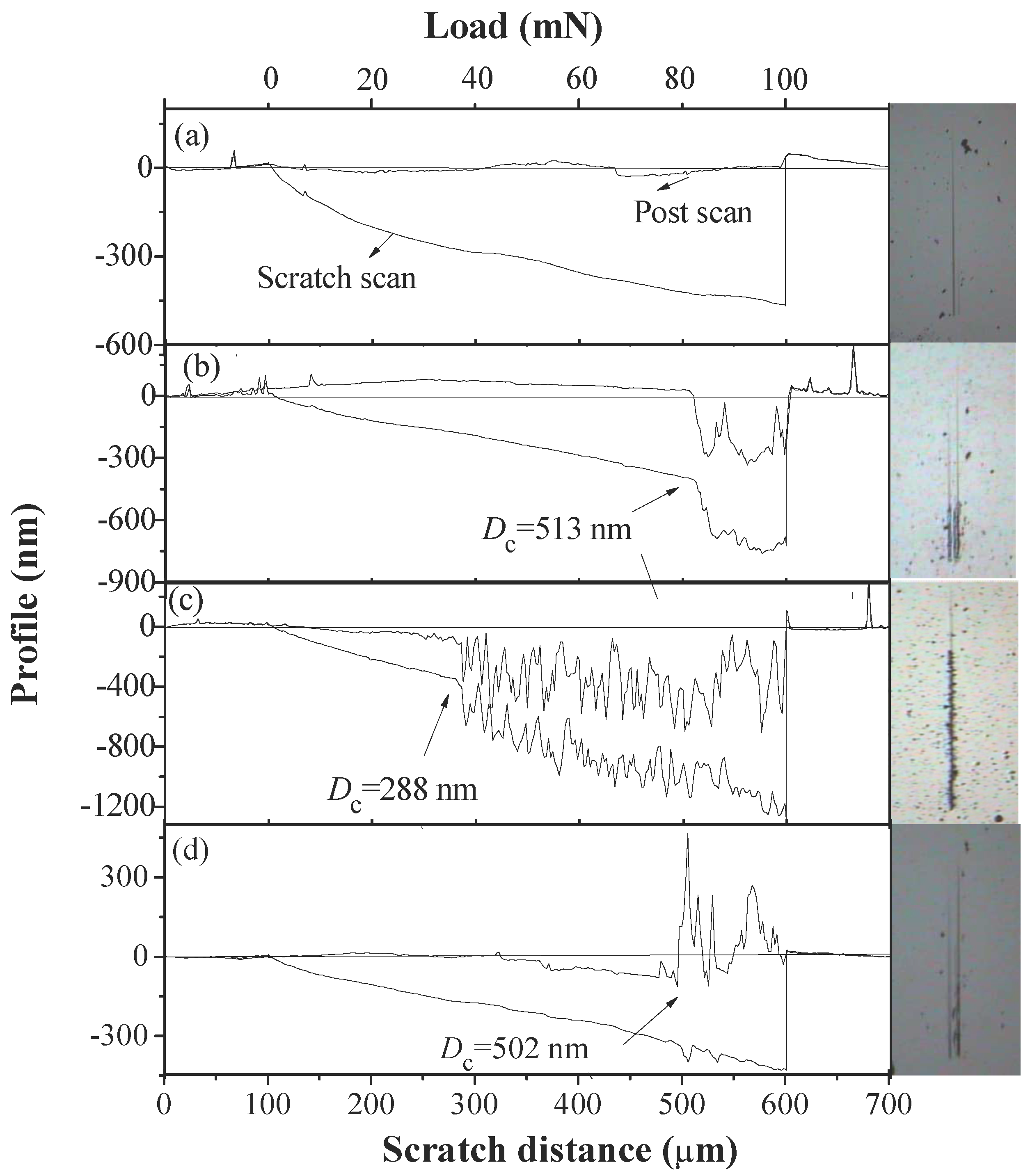
3.1. Microstructure Characterizations
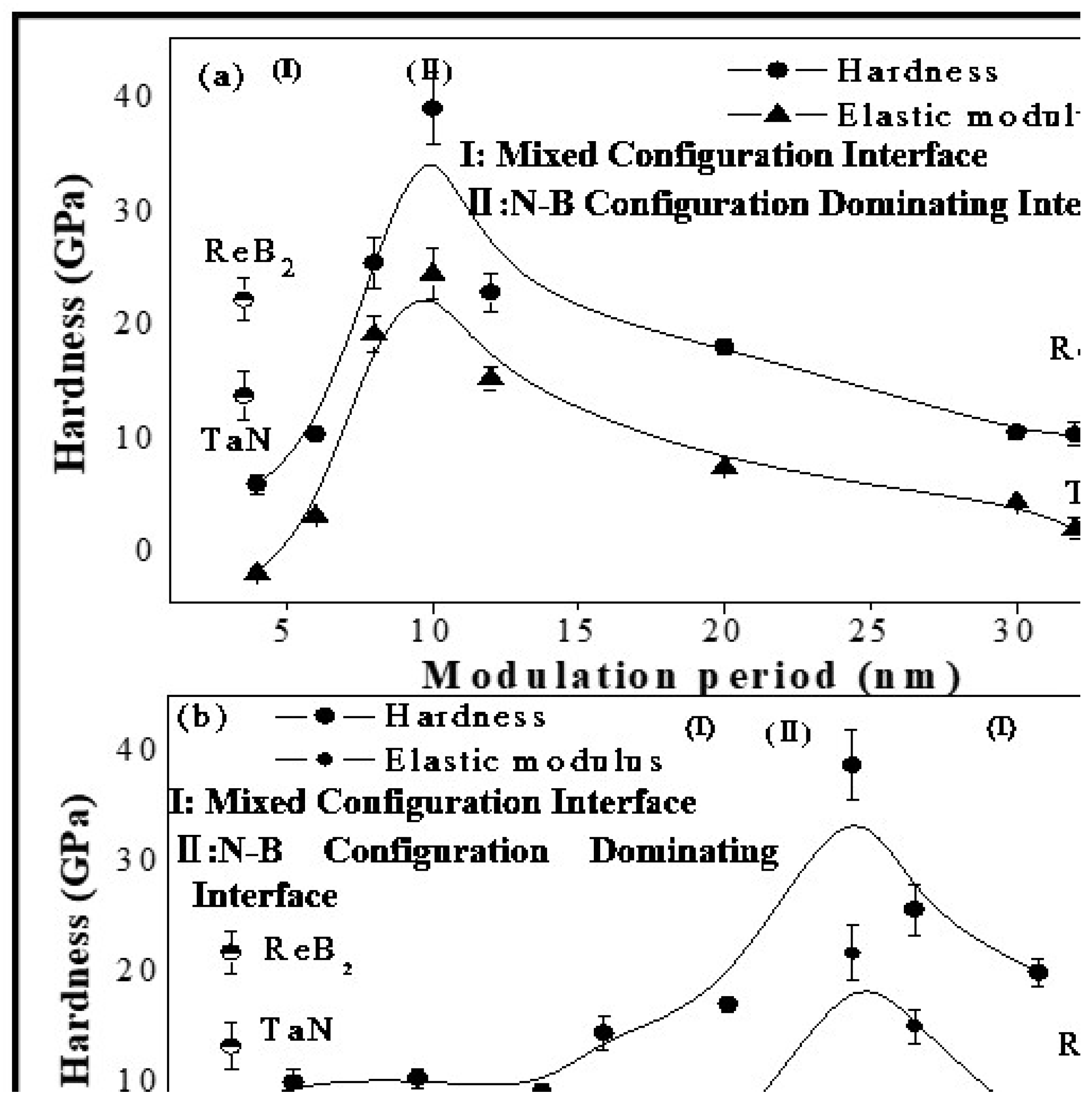
3.2. Mechanical Properties
3.3. Hard Mechanism
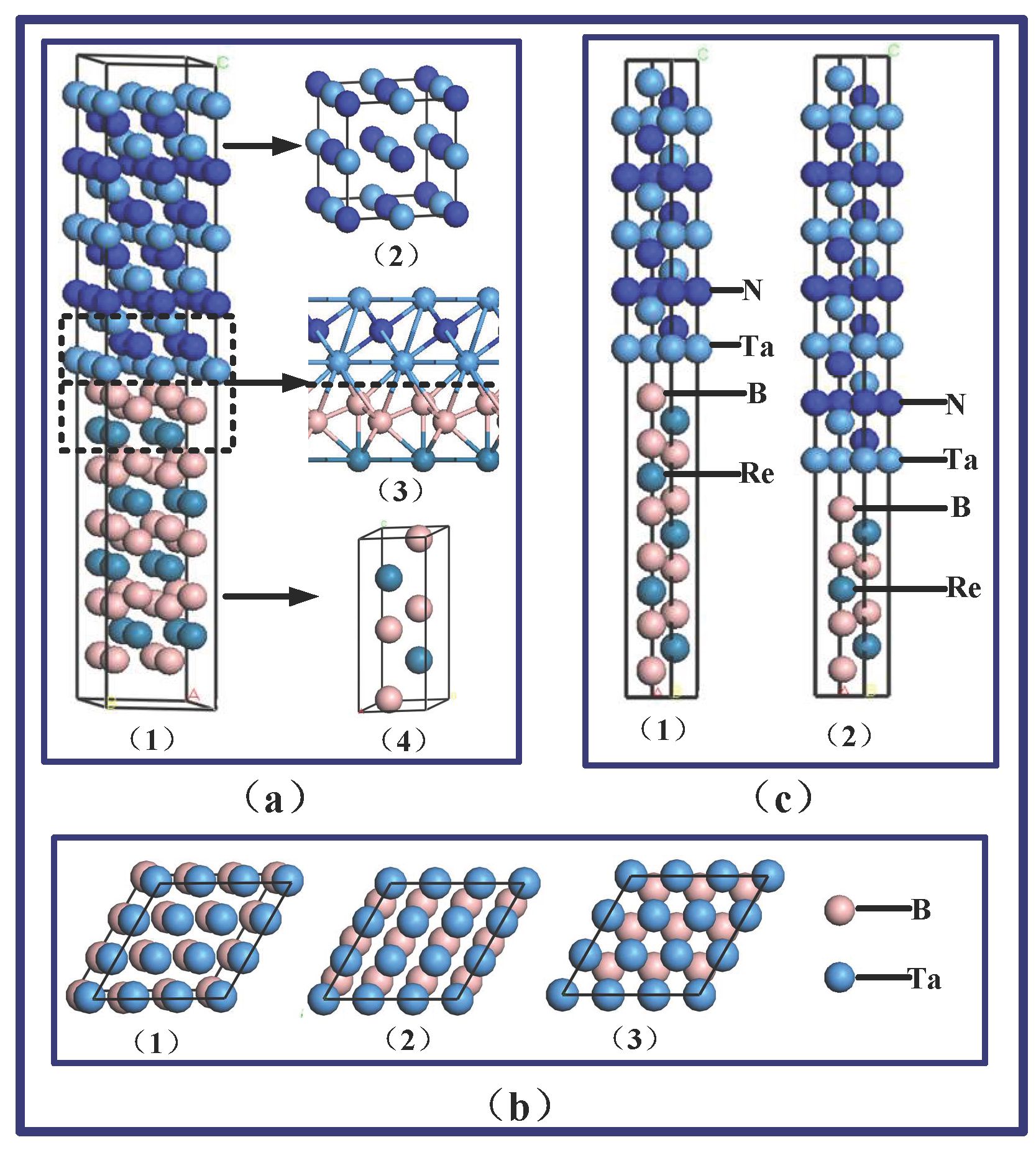
3.4. Theoretical Model, Calculation, and Discussion
4. Conclusions
- (1)
- The microstructure evolutions in the ReB2/TaN multilayers are carefully investigated by varying the modulation periods and modulation ratios. Clear coherent interfacial structures form between epitaxial layers at the optimal modulation period of 10 nm and the modulation ratio of 1:1. The fine nanocrystallites with small grain sizes are kept stable in individual layers at the optimal modulation condition.
- (2)
- A maximum hardness of 38.7 GPa occurs at Λ = 10 nm and tReB2:tTaN = 1:1. The highest multilayer also displays the highest fracture resistance and the highest resistance to plastic deformation.
- (3)
- The shallow indentations show little difference in hardness between the monolithic coatings and the multilayers. However, variations in the load versus displacement curves are observed at deeper indentation depths, indicating an enhancement of the hardness. One can deduce that the interface has a strong influence on the increase in the hardness.
- (4)
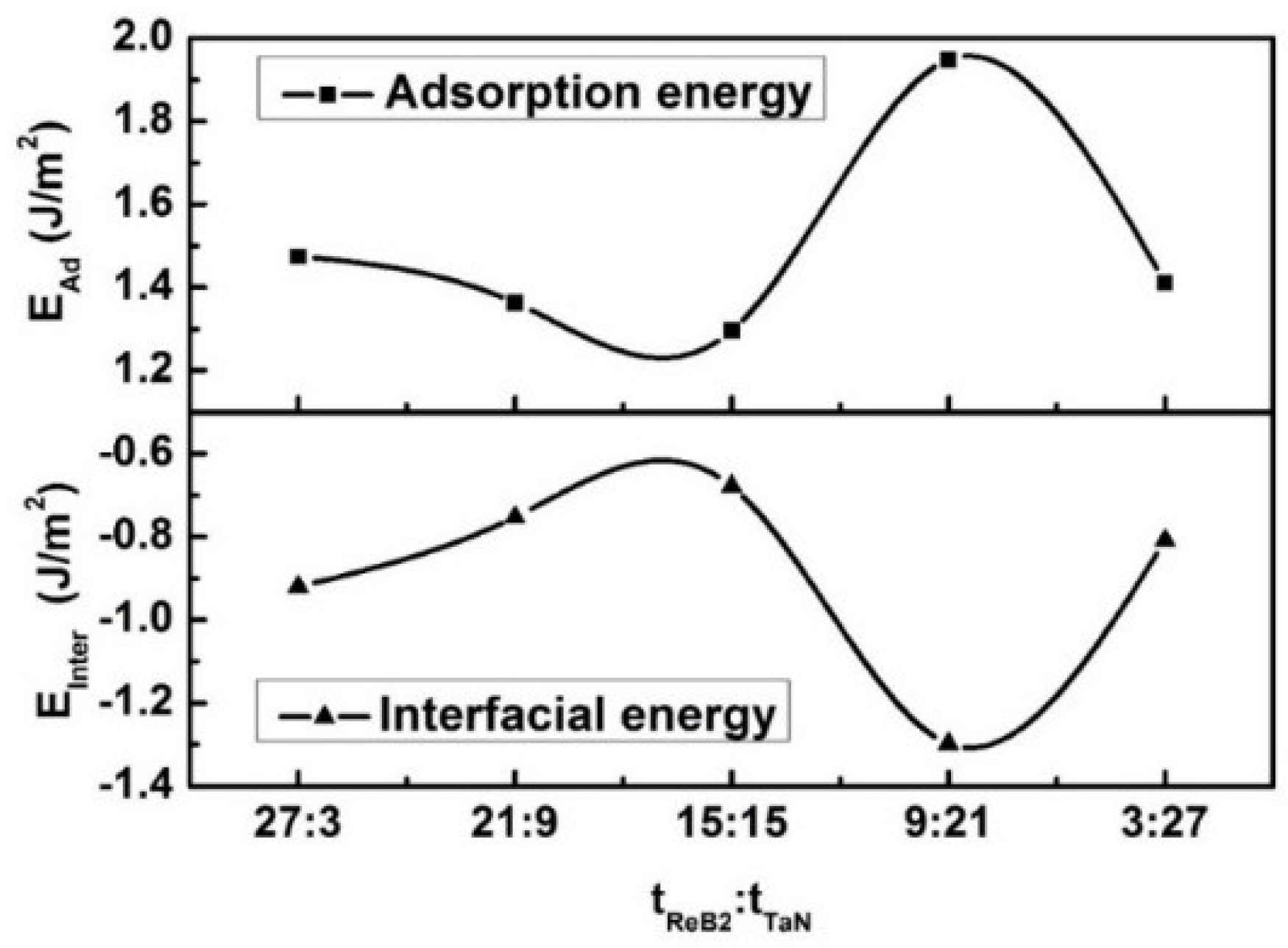
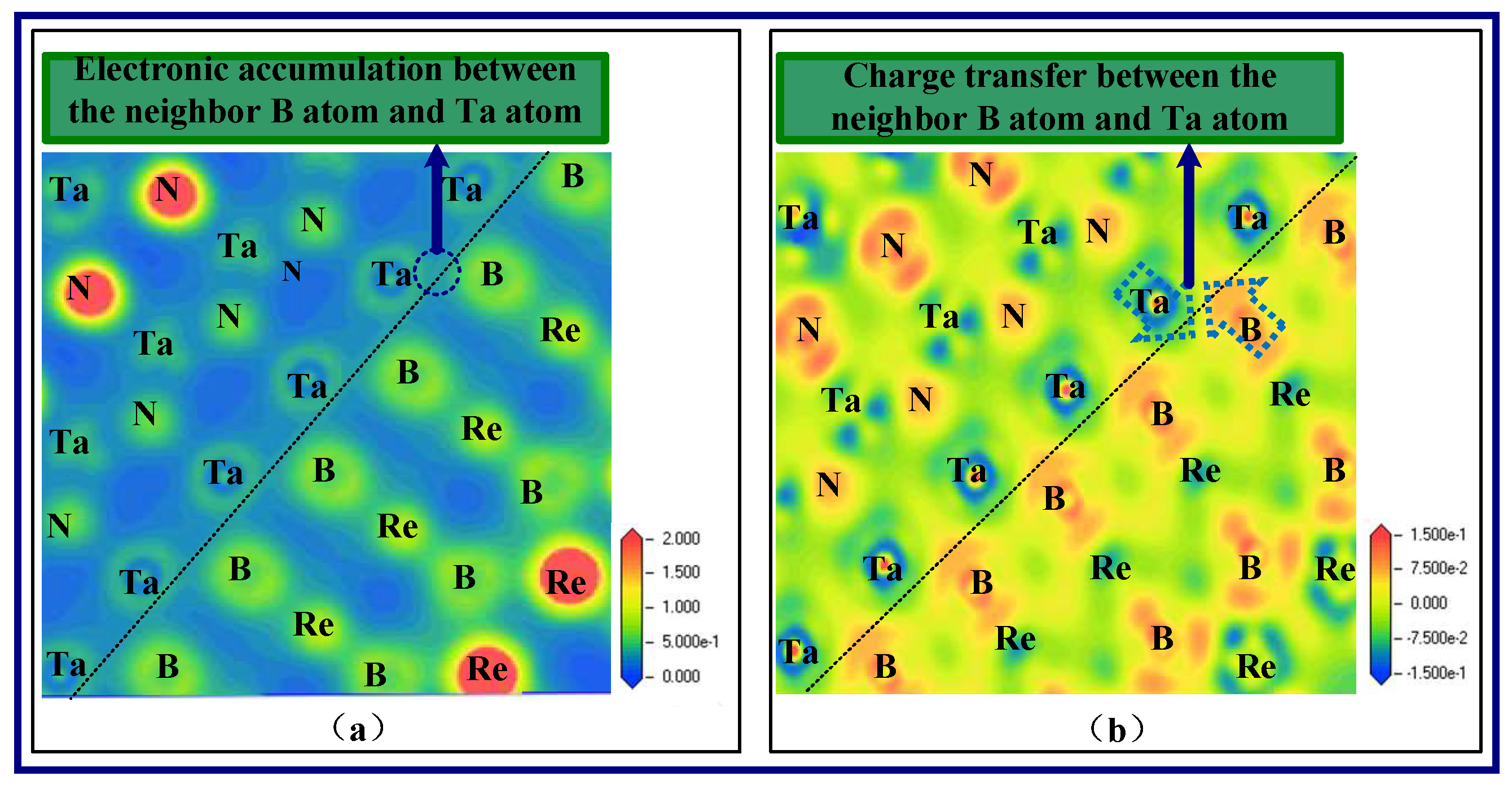
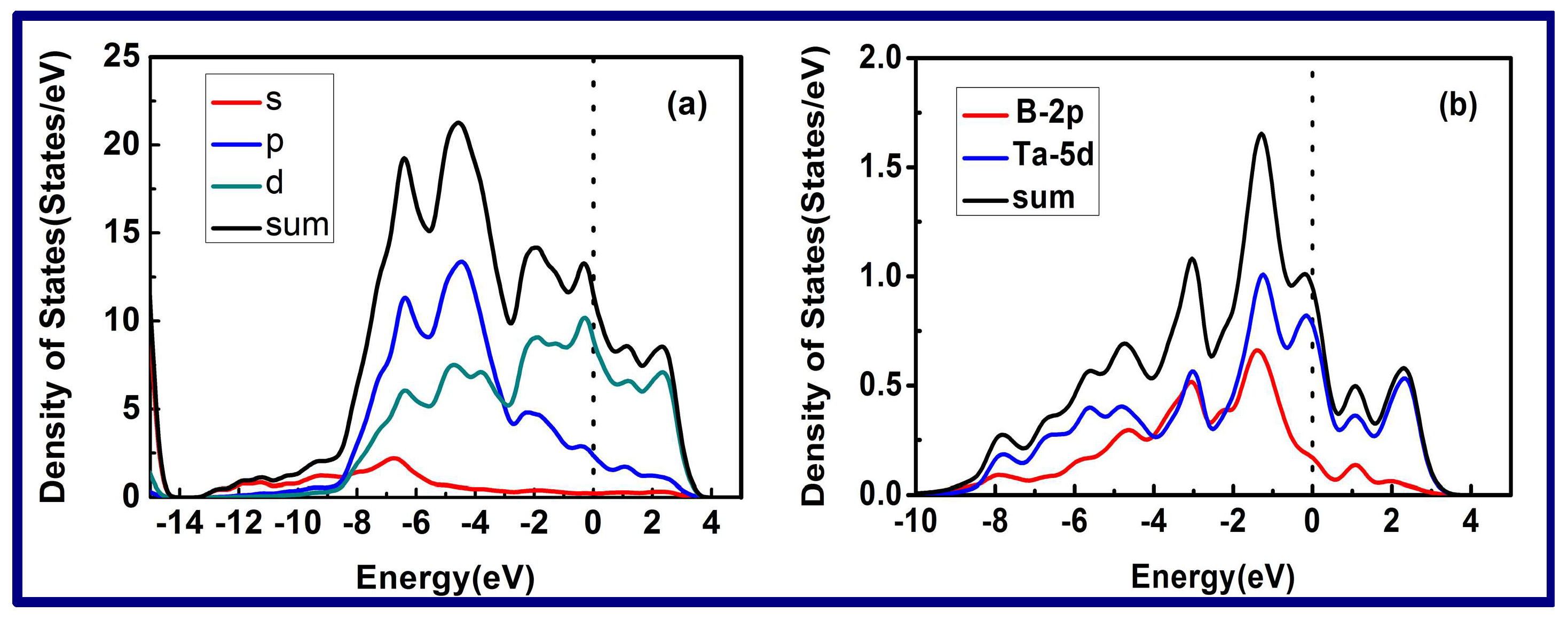
- Six possible multilayered interfaces, B-N, BB-N, Re-N, B-Ta, BB-Ta, and Re-Ta, including eighteen interface configurations of top, hcp, and bridge, are established. The highest adsorption energy, hence the best interface stability, occurs in the B-Ta interface configuration. The strengthening mechanisms of the multilayered structure are elucidated using the calculation results of the interfacial energies to advance the understanding of the relationship between the superior mechanical properties and the interfacial structure.
- (5)
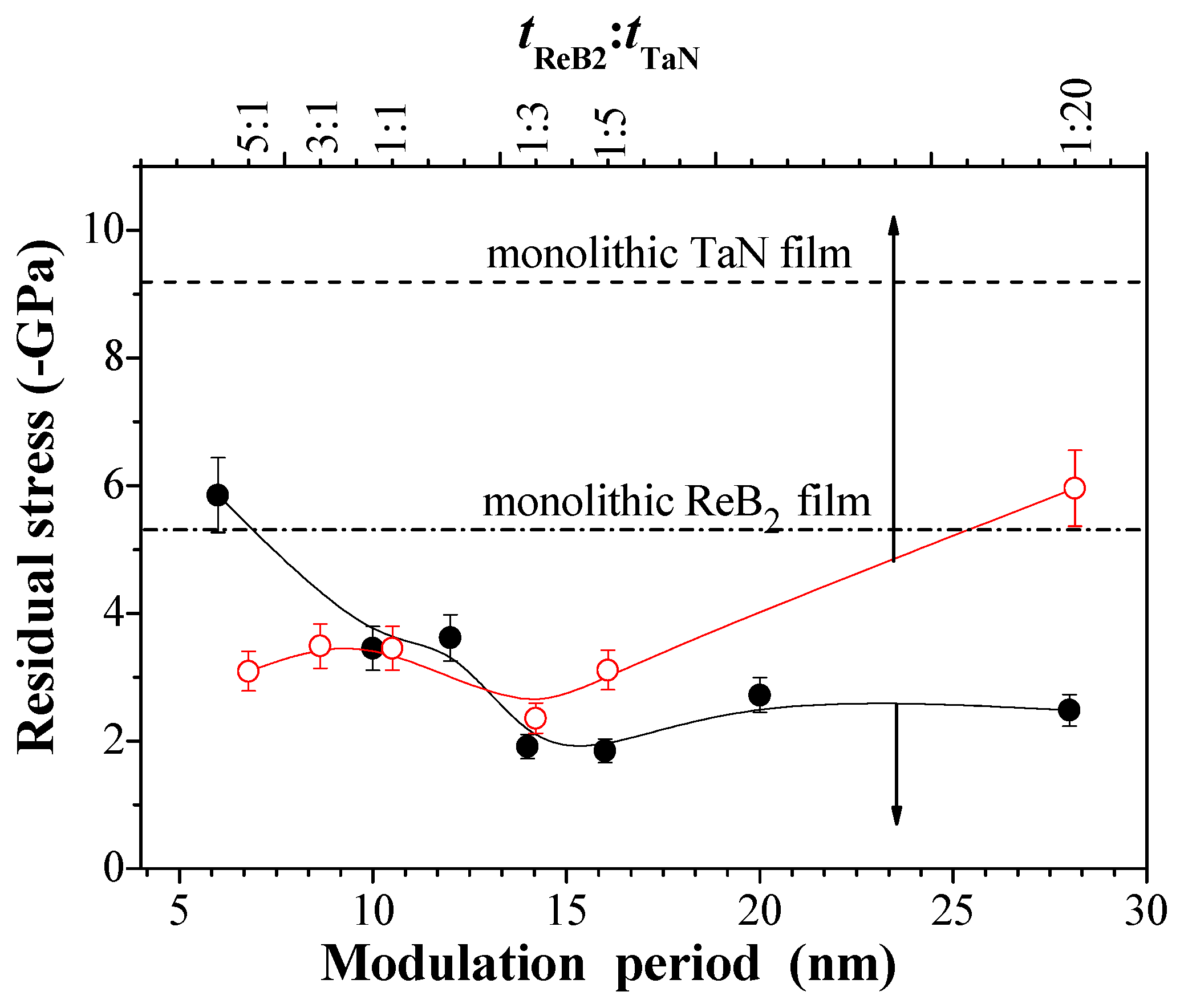
- The 3ReB2/27TaN, 9ReB2/21TaN, 15ReB2/15TaN, 21ReB2/3TaN, and 27ReB2/3TaN interfacial models are established to further explain the underlying mechanism for why the residual stress depends on the interfacial stability. The multilayers at a tReB2:tTaN of 1:3 exhibits the lowest residual stress, which agrees with the lowest interfacial energy and the highest adsorption energy of the 9ReB2/21TaN interfacial structure. Therefore, the 9ReB2/21TaN interfacial configuration is found to be the most stable interface, which is a main contribution to the residual stress release.
Author Contributions
Funding
Conflicts of Interest
References
- Gachon, J.; Rogachev, A.; Grigoryan, H.; Illarionova, E.; Kuntz, J.; Kovalev, D.; Nosyrev, A.; Sachova, N.; Tsygankov, P. On the mechanism of heterogeneous reaction and phase formation in Ti/Al multilayer nanofilms. Acta Metall. 2005, 53, 1225–1231. [Google Scholar] [CrossRef]
- Chung, H.; Weinberger, M.; Levine, J.; Kavner, A.; Yang, J.; Tolbert, S.; Kaner, R. Synthesis of Ultra-Incompressible Superhard Rhenium Diboride at Ambient Pressure. Science 2017, 316, 436. [Google Scholar] [CrossRef] [PubMed]
- Latini, A.; Rau, J.; Ferro, D.; Teghil, R.; Albertini, V.; Barinov, S. Superhard Rhenium Diboride Films: Preparation and Characterization. Chem. Mater. 2008, 20, 4507–4511. [Google Scholar] [CrossRef]
- Berger, M.; Karlsson, L.; Larsson, M.; Hogmark, S. Low stress TiB2 coatings with improved tribological properties. Thin Solid Films 2001, 401, 179–186. [Google Scholar] [CrossRef]
- Losbichler, P.; Mitterer, C. Stoichiometry of unbalanced magnetron sputtered Al–Mg alloy coatings. Surf. Coat. Technol. 1997, 97, 567–573. [Google Scholar] [CrossRef]
- Kwon, K.; Ryu, C.; Sinclair, R.; Simon, S. Evidence of heteroepitaxial growth of copper on beta-tantalum. Appl. Phys. Lett. 1997, 71, 3069–3071. [Google Scholar] [CrossRef]
- Dupraz, M.; Poloni, R.; Ratter, K.; Rodney, D.; DeSantis, M.; Gilles, B.; Beutier, G.; Verdier, M. Wetting layer of copper on the tantalum (001) surface. Phys. Rev. B 2016, 94, 235427. [Google Scholar] [CrossRef]
- Lee, W.; Lin, J.; Lee, C. Characterization of tantalum nitride films deposited by reactive sputtering of Ta in N2/Ar gas mixtures. Mater. Chem. Phys. 2001, 68, 266–271. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, D.; Li, C.; Foo, P. Comparative study of Ta, TaN and Ta/TaN bi-layer barriers for Cu-ultra low-k porous polymer integration. Thin Solid Films 2004, 462, 176–181. [Google Scholar] [CrossRef]
- Muller, C.M.; Sologubenko, A.S.; Gerstl, S.; Suess, M.J.; Courty, D.; Spolenak, R.; Nanoscale, R. Cu/Ta multilayer deposition by co-sputtering on a rotating substrate. Empirical model and experiment. Surf. Coat. Technol. 2016, 302, 284–292. [Google Scholar] [CrossRef]
- Hecker, M.; Fischer, D.; Hoffmann, V.; Engelmann, H.; Voss, A.; Mattern, N.; Wenzel, C.; Vogt, C.; Zschech, E. Influence of N content on microstructure and thermal stability of Ta–N thin films for Cu interconnection. Thin Solid Films 2002, 414, 184–191. [Google Scholar] [CrossRef]
- Zhou, Y.M.; He, M.Z.; Xie, Z. Diffusion barrier performance of novel Ti/TaN double layers for Cu metallization. Appl. Surf. Sci. 2014, 315, 353–359. [Google Scholar] [CrossRef]
- Yang, Y.H.; Wu, F.B. Microstructure evolution and protective properties of TaN multilayer coatings. Surf. Coat. Technol. 2016, 308, 108–114. [Google Scholar] [CrossRef]
- Xu, J.; Li, G.; Gu, M. The microstructure and mechanical properties of TaN/TiN and TaWN/TiN superlattice films. Thin Solid Films 2000, 370, 45–49. [Google Scholar]
- Baran, O.; Sukuroglu, E.; Efeoglu, I.; Totik, Y. The investigation of adhesion and fatigue properties of TiN/TaN multilayer coatings. J. Adhes. Sci. Technol. 2016, 30, 2188–2200. [Google Scholar] [CrossRef]
- An, J.; Zhang, Q. Structure, Hardness and Tribological Properties of Nanolayered TiN/TaN Multilayer Coatings. Mater. Charact. 2007, 58, 439–446. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, S.; Liu, M.; Li, D. Effect of Modulation Period on Structure and Mechanical Properties of ReB2/TaN Nanoscale Nanomultilayers. J. Mater. Eng. 2011, 10, 58–65. [Google Scholar]
- Barnett, S. Physics of Thin Films; Academic Press: New York, NY, USA, 1993; Volume 1. [Google Scholar]
- Anderson, P.; Li, C. Hall-Petch relations for multilayered materials. Nanostruct. Mater. 1955, 5, 349–362. [Google Scholar] [CrossRef]
- Friedman, L.; Chrzan, D. Scaling Theory of the Hall-Petch Relation for Multilayers. Phys. Rev. Lett. 1998, 81, 2715–2718. [Google Scholar] [CrossRef]
- Wang, P.; Wang, X.; Du, J.; Ren, F.; Zhang, Y.; Zhang, X.; Fu, E. The temperature and size effect on the electrical resistivity of Cu/V multilayer films. Acta Mater. 2017, 126, 294–301. [Google Scholar] [CrossRef]
- Huang, H.; Spaepen, F. Tensile testing of free-standing Cu, Ag and Al thin films and Ag/Cu multilayers. Acta Mater. 2000, 48, 3261–3269. [Google Scholar] [CrossRef]
- Misra, A.; Hirth, J.; Hoagland, R. Length-scale-dependent deformation mechanisms in incoherent metallic multilayered composites. Acta Mater. 2005, 53, 4817–4824. [Google Scholar] [CrossRef]
- Philips, M.; Clemens, B.; Nix, W. A model for dislocation behavior during deformation of Al/Al3Sc (fcc/L12) metallic multilayers. Acta Mater. 2003, 51, 3157. [Google Scholar] [CrossRef]
- Misra, A.; Hirth, J.; Kung, H. Single-dislocation-based strengthening mechanisms in nanoscale metallic multilayers. Philos. Mag. 2002, 82, 2935–2951. [Google Scholar] [CrossRef]
- Torabinejad, V.; Aliofkhazraei, M.; Assareh, S.; Allahyarzadeh, M.; Rouhaghdam, A. Electrodeposition of Ni-Fe alloys, composites, and nano coatings-A review. J. Alloys. Compd. 2017, 691, 841–859. [Google Scholar] [CrossRef]
- Jin, S.; Liu, N.; Zhang, S.; Li, D. The simulation of interface structure, energy and electronic properties of TaN/ReB2, multilayers using first-principles. Surf. Coat. Technol. 2017, 326, 417–423. [Google Scholar] [CrossRef]
- Chu, X.; Barnett, S. Model of superlattice yield stress and hardness enhancements. J. Appl. Phys. 1995, 77, 4403–4411. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, J.; Yang, J.; Li, D. Influence of Ar/N2 flow ratio on structure and properties of nanoscale ZrN/WN multilayered coatings. Surf. Coat. Technol. 2007, 201, 5472–5476. [Google Scholar] [CrossRef]
- Cullity, B. Elements of X-ray Diffraction; Addison Wesley: Reading, MA, USA, 1978; p. 512. [Google Scholar]
- Lattemann, M.; Ulrich, S. Investigation of structure and mechanical properties of magnetron sputtered monolayer and multilayer coatings in the ternary system Si–B–C. Surf. Coat. Technol. 2007, 201, 5564–5569. [Google Scholar] [CrossRef]
- Hamann, D.; Schluter, M.; Chiang, C. Norm-conserving pseudopotentials. Phys. Rev. Lett. 1979, 43, 1494–1497. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Perdew, J.; Wang, Y. Accurate and Simple Analytic Representation of the Electron-Gas Correlation Energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892–7895. [Google Scholar] [CrossRef]
- Kong, M.; Shao, N.; Dong, Y.; Yue, J.; Li, G. Growth, microstructure and mechanical properties of (Ti, Al)N/VN nanomultilayers. Mater. Lett. 2006, 60, 874–877. [Google Scholar] [CrossRef]
- Ohring, M. The Materials Science of Thin Films; Academic Press: New York, NY, USA, 1992; p. 416. [Google Scholar]
- Shtanski, D.; Kulinich, S.; Levashov, E.; Moore, J. Structure and physical-mechanical properties of nanostructured thin films. Phys. Solid. State 2003, 45, 1177–1184. [Google Scholar] [CrossRef]
- Chen, Y.; Polonsky, I.; Chung, Y.; Keer, L. Tribological properties and rolling-contact-fatigue lives of TiN/SiNx multilayer coatings. Surf. Coat. Technol. 2002, 154, 152–161. [Google Scholar] [CrossRef]
- Finnis, M. The theory of metal-ceramic interfaces. J. Phys. Condens. Matter. 1996, 8, 5811–5836. [Google Scholar] [CrossRef]
- Lin, Z.; Bristowe, Z. Microscopic characteristics of the Ag(111)/ZnO(0001) interface present in optical coatings. Phys. Rev. B 2007, 75, 205423. [Google Scholar] [CrossRef]
- Yin, D.; Peng, X.; Qin, Y.; Wang, Z. Electronic property and bonding configuration at the TiN(111)/VN(111) interface. J. Appl. Phys. 2010, 108, 033714. [Google Scholar] [CrossRef]
- Li, K.; Sun, Z.; Wang, F.; Zhou, N.; Hu, X. First-principles calculations on Mg/Al4C3 interfaces. Appl. Surf. Sci. 2013, 270, 584–589. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, L.; Pei, F.; Chang, K.; Du, Y. Effect of the Modulation Ratio on the Interface Structure of TiAlN/TiN and TiAlN/ZrN Multilayers: First-principles and Experimental Investigations. Acta Mater. 2017, 130, 281–288. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. A 1965, 140, 1133–1138. [Google Scholar] [CrossRef]
- Arya, A.; Carter, E. Structure, bonding, and adhesion at the TiC(100)/Fe(110) interface from first principles. J. Chem. Phys. 2003, 118, 8982–8996. [Google Scholar] [CrossRef]
- Kim, H.; Yoo, S. Enhanced low field magnetoresistance in La0.7Sr0.3MnO3-La2O3 composites. J. Alloys Compd. 2012, 521, 30–34. [Google Scholar] [CrossRef]
- Wang, C.; Gao, H.; Dai, Y.; Ruan, X.; Shen, J.; Jun, W.; Sun, B. In-situ technique for synthesizing Fe–TiN composites. J. Alloys Compd. 2010, 490, 9–11. [Google Scholar] [CrossRef]
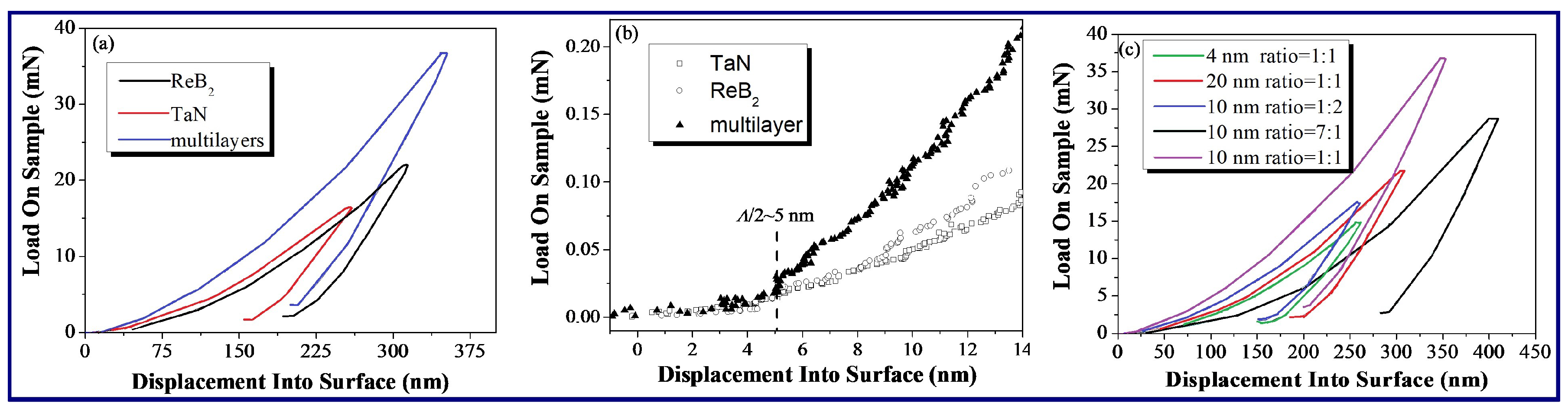
| Λ (nm) | tReB2:tTaN | H3/E2 (%) |
|---|---|---|
| 4 | 1:1 | 4.35 |
| 10 | 1:1 | 25.8 |
| 30 | 1:1 | 4.09 |
| 10 | 5:1 | 4.89 |
| 10 | 1:2 | 11.5 |
| Stacking | Ead (J/m2) | Stacking | Ead (J/m2) | Stacking | Ead (J/m2) |
|---|---|---|---|---|---|
| B1-N hcp | −2.668 | B1-N top | −3.244 | B1-N bridge | −3.301 |
| B2-N hcp | −2.668 | B2-N top | −2.653 | B2-N bridge | −2.665 |
| Re-N hcp | 0.145 | Re-N top | 0.063 | Re-N bridge | 1.110 |
| B1-Ta hcp | 6.341 | B1-Ta top | 6.028 | B1-Ta bridge | 7.046 |
| B2-Ta hcp | 6.316 | B2-Ta top | 6.296 | B2-Ta bridge | 7.213 |
| Re-Ta hcp | 4.814 | Re-Ta top | 4.090 | Re-Ta bridge | 5.142 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, S.; Li, D. Interfacial Model and Characterization for Nanoscale ReB2/TaN Multilayers at Desired Modulation Period and Ratios: First-Principles Calculations and Experimental Investigations. Nanomaterials 2018, 8, 421. https://doi.org/10.3390/nano8060421
Jin S, Li D. Interfacial Model and Characterization for Nanoscale ReB2/TaN Multilayers at Desired Modulation Period and Ratios: First-Principles Calculations and Experimental Investigations. Nanomaterials. 2018; 8(6):421. https://doi.org/10.3390/nano8060421
Chicago/Turabian StyleJin, Shangxiao, and Dejun Li. 2018. "Interfacial Model and Characterization for Nanoscale ReB2/TaN Multilayers at Desired Modulation Period and Ratios: First-Principles Calculations and Experimental Investigations" Nanomaterials 8, no. 6: 421. https://doi.org/10.3390/nano8060421
APA StyleJin, S., & Li, D. (2018). Interfacial Model and Characterization for Nanoscale ReB2/TaN Multilayers at Desired Modulation Period and Ratios: First-Principles Calculations and Experimental Investigations. Nanomaterials, 8(6), 421. https://doi.org/10.3390/nano8060421





