A Perspective on the Application of Spatially Resolved ARPES for 2D Materials
Abstract
1. Introduction
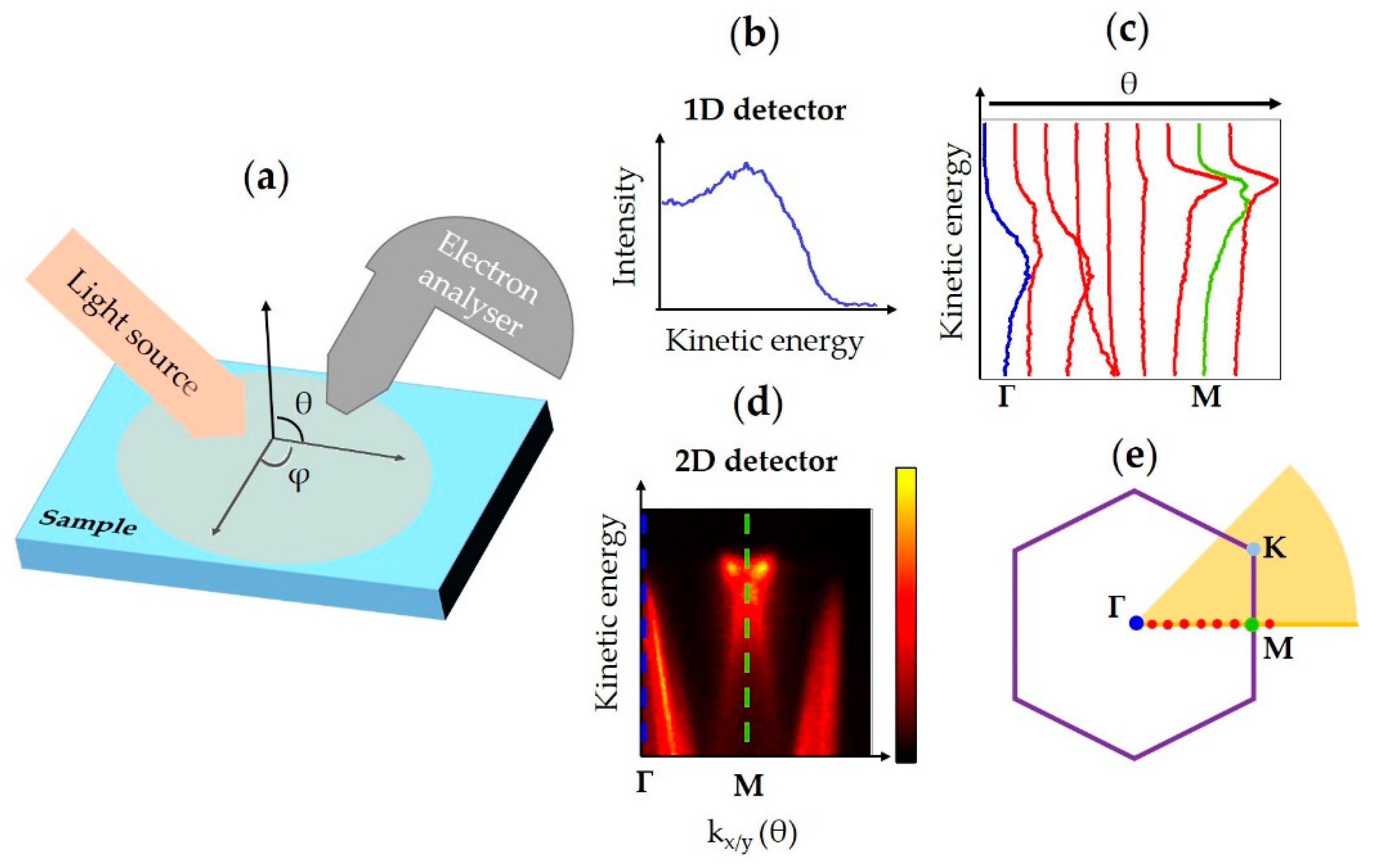
2. ARPES Setups: Technical Considerations
2.1. ARPES Technical Considerations
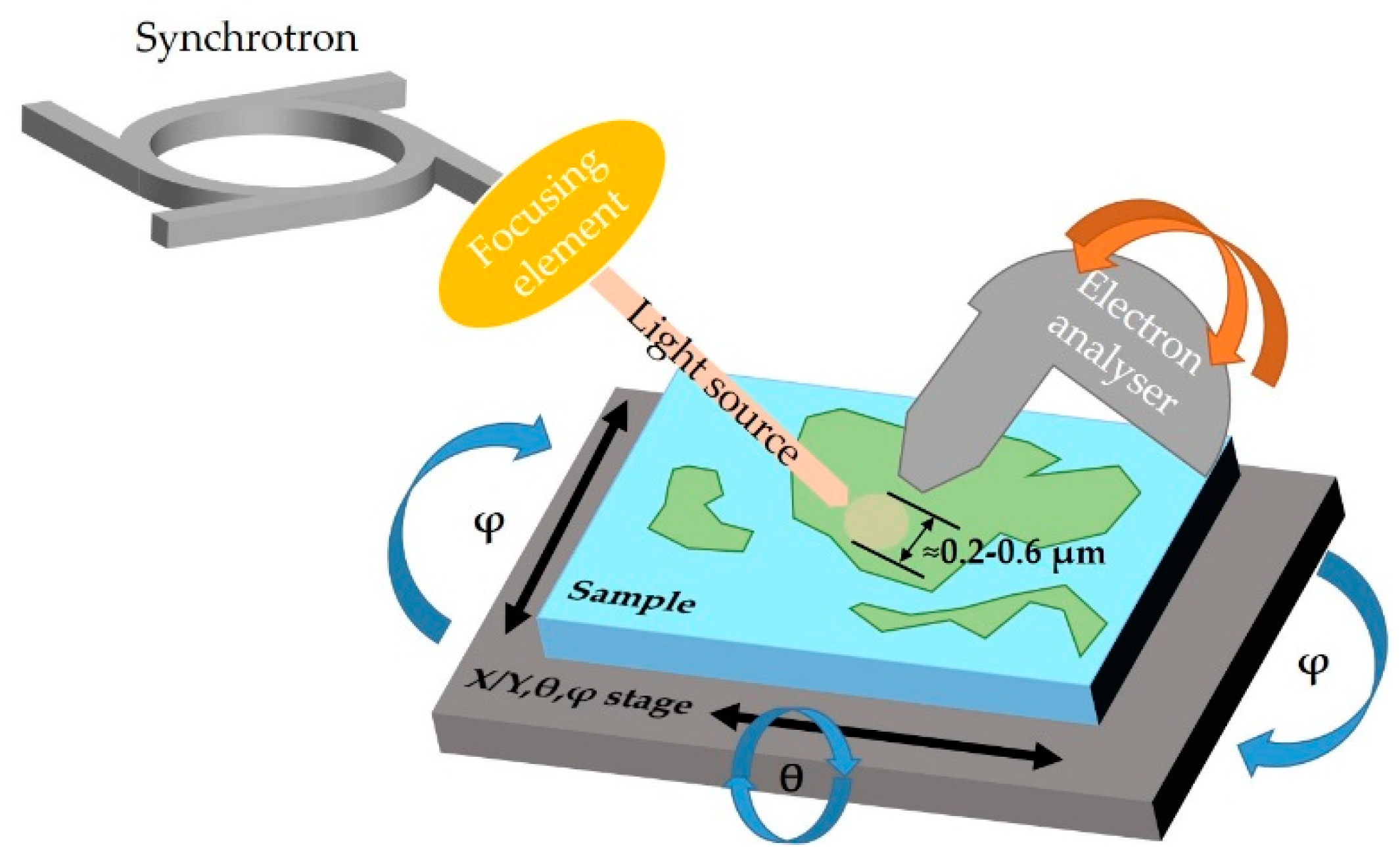
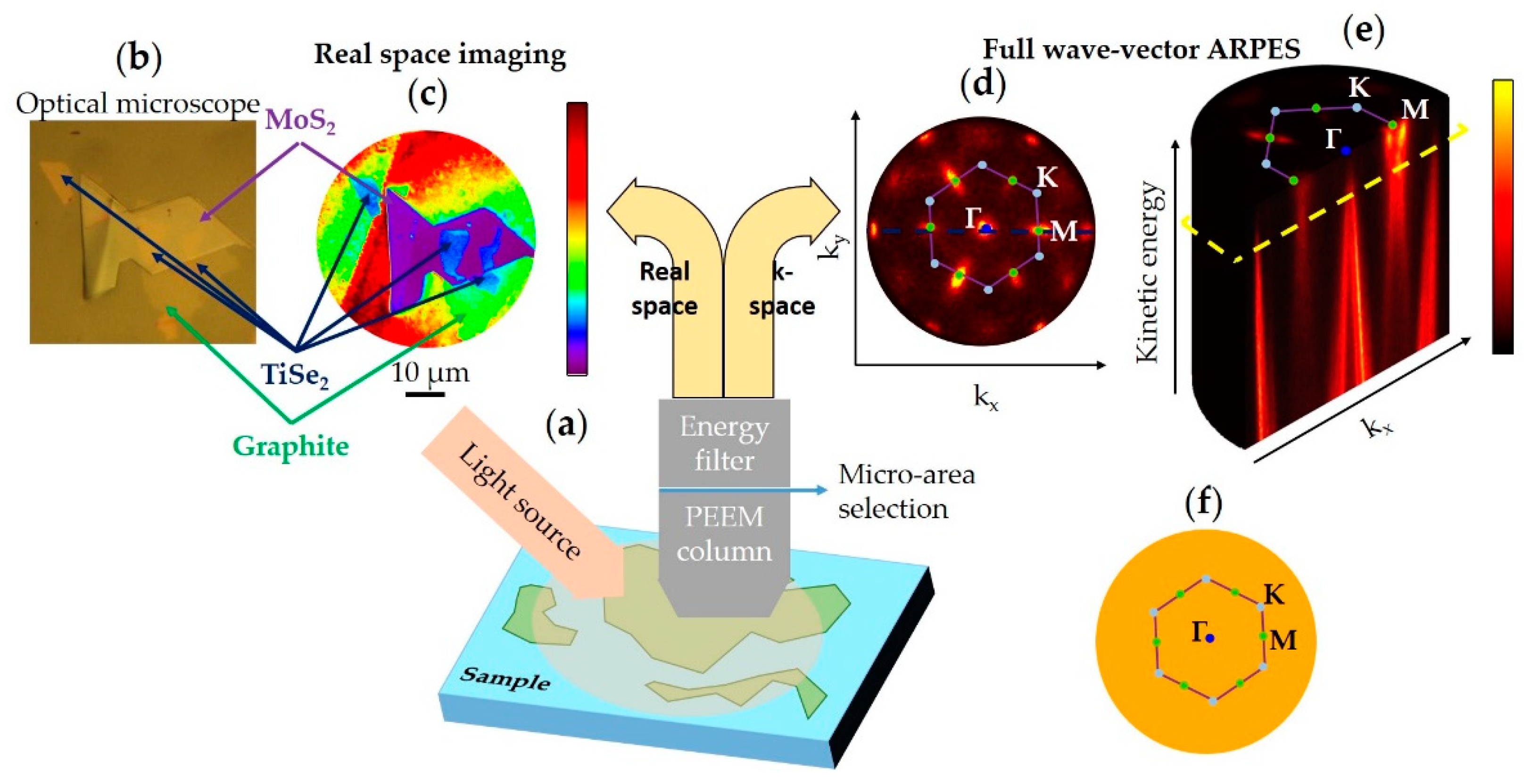
2.2. Spatially Localized ARPES
- setups that present extremely small light spots, and where surface mapping is done by moving the sample with respect to the light;
- setups that allow visualization of the real and k-space by extracting electrons using strong electric fields.
2.3. ARPES Setups Comparison
3. Spatially Resolved ARPES for 2D Materials
- Epitaxial growth by CVD or PVD. This method allows flat and azimuthally oriented layers to be deposited on large single crystal substrates. It is easy to control the number of layers by changing the deposition time, growth chambers can be directly mounted onto ARPES equipment so that samples can be transferred for analysis under UHV conditions. With epitaxial films it is not necessary to employ spatially-resolved ARPES to limit the analyses region on single material grains because the grains are azimuthally oriented with the substrate and form a macroscopic continuous ordered crystalline lattice. Because of the large amount of signal available for ARPES, advanced analyses such as spin-resolved or time-resolved ARPES are feasible on such samples (see in Table 1). There are two main disadvantages of this method: it is time consuming, because evaporators and setups must be carefully optimized for each different material; secondly, the interaction between the substrate and 2D materials is so strong that usually it is not feasible to transfer the 2D layers onto other substrates.
- Conventional CVD produces large micron-scale grains azimuthally misaligned. In respect to the epitaxial growth, the control of the number of layers it is more difficult and occasionally multi-layers are produced. Furthermore, this method is more prone to contamination because it is usually performed under non-UHV conditions. The advantage of conventional CVD with respect to epitaxial growth is that it is possible to use single crystal and polycrystalline substrates with weaker bonds to the 2D material, allowing their detachment and transfer.
- Mechanical exfoliation, also called “adhesive tape technique”, produces extremely high-quality layers because they are peeled from ultra-pure single crystals. The main drawbacks are the micron-sized areas of the layers and that the thickness is not easily controllable. This technique is the main method used for studying promising new 2D materials because it is fast and easily achievable, exploiting the ease of exfoliation along the weak van der Waals inter-layer bonds. Importantly, it is the main technique to form 2D heterostructures.
- characterization of the bulk material band structure;
- analysis of 2D exfoliated layers to observe quantum confinements effects and any difference with respect to the bulk;
- finding a method to produce large 2D layers and perform advanced characterizations such as spin-resolved, or time-resolved ARPES studies.
3.1. Graphene and Its Analogues
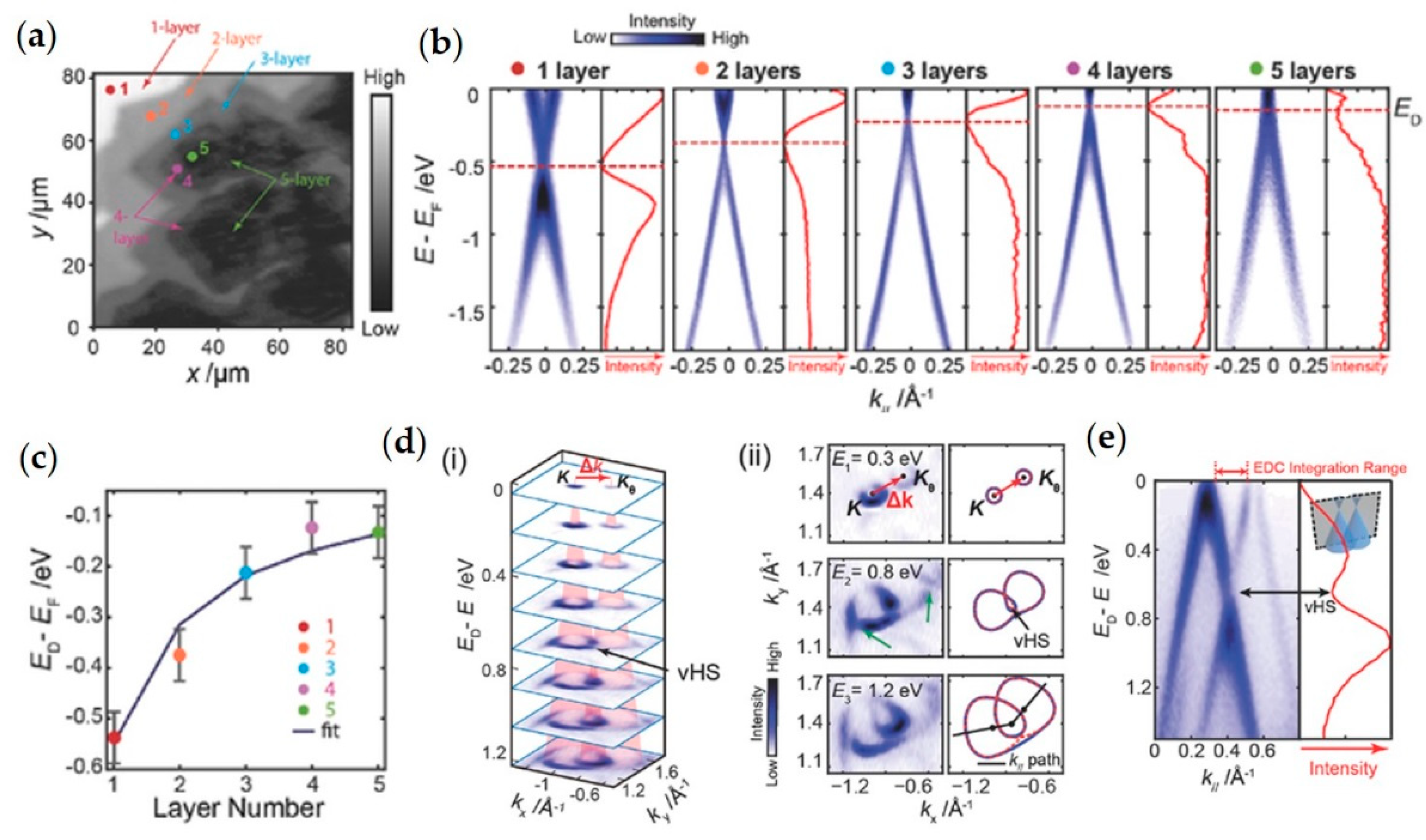
3.2. Transition Metal Dichalcogenides
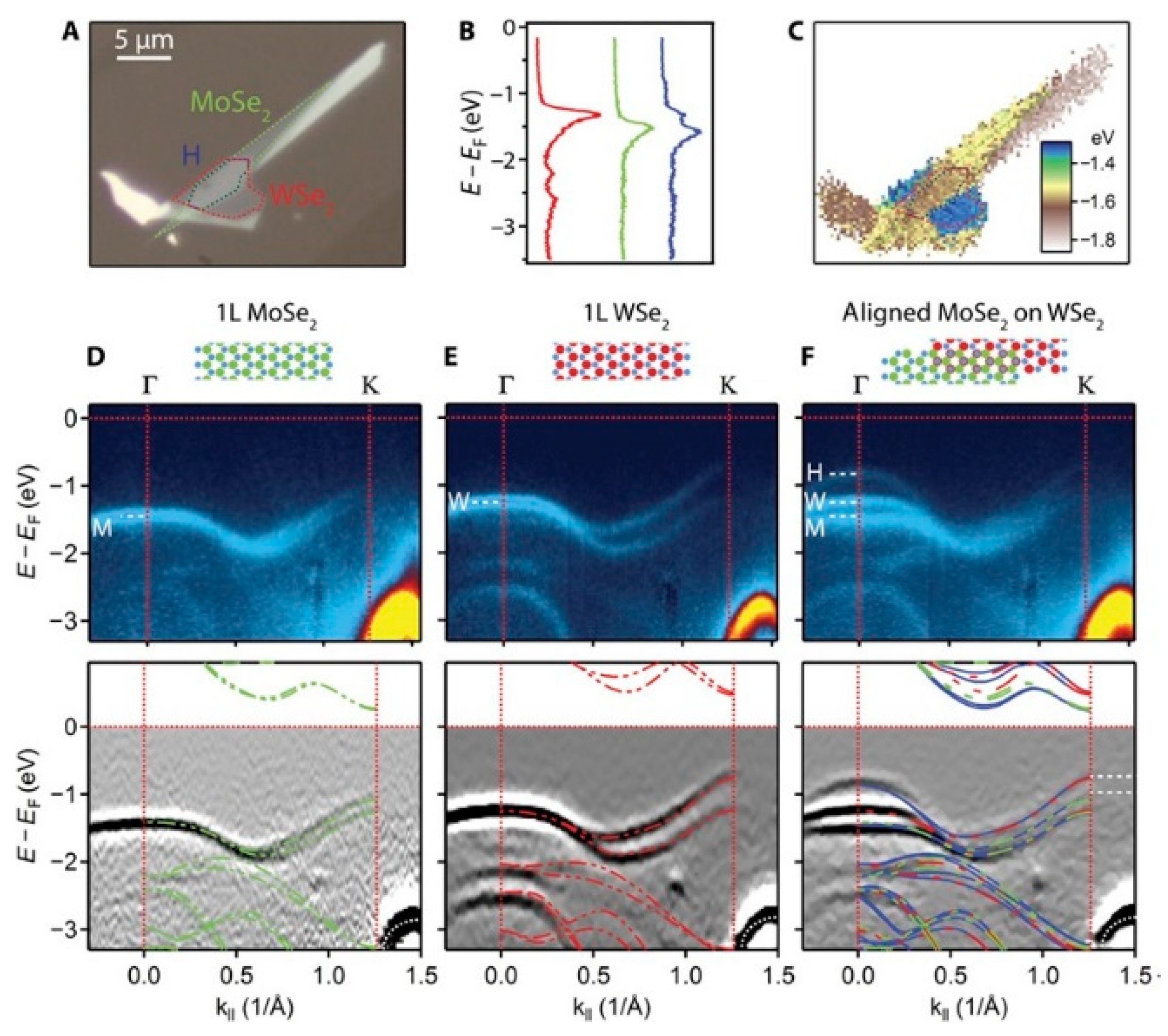
3.3. Two-Dimensional Heterostructures
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Geim, A.K. Nobel Lecture: Random walk to graphene. Rev. Mod. Phys. 2011, 83, 851–862. [Google Scholar] [CrossRef]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K.; Grigorieva, I.V. Van der Waals heterostructures. Nature 2013, 499, 419–425. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Ma, F.; Liang, W.; Sun, M. Electrical properties and applications of graphene, hexagonal boron nitride (h-BN), and graphene/h-BN heterostructures. Mater. Today Phys. 2017, 2, 6–34. [Google Scholar] [CrossRef]
- Ye, M.; Zhang, D.; Yap, Y.K. Recent Advances in Electronic and Optoelectronic Devices Based on Two-Dimensional Transition Metal Dichalcogenides. Electronics 2017, 6. [Google Scholar] [CrossRef]
- Nakamura, Y.; Yanase, Y. Odd-parity superconductivity in bilayer transition metal dichalcogenides. Phys. Rev. B 2017, 96, 054501. [Google Scholar] [CrossRef]
- Peng, H.; Schroter, N.B.M.; Yin, J.; Wang, H.; Chung, T.F.; Yang, H.; Ekahana, S.; Liu, Z.; Jiang, J.; Yang, L.; et al. Substrate Doping Effect and Unusually Large Angle van Hove Singularity Evolution in Twisted Bi- and Multilayer Graphene. Adv. Mater. 2017, 29, 1606741. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Chang, T.-R.; Zhou, B.; Cui, Y.-T.; Yan, H.; Liu, Z.; Schmitt, F.; Lee, J.; Moore, R.; Chen, Y.; et al. Direct observation of the transition from indirect to direct bandgap in atomically thin epitaxial MoSe2. Nat. Nanotechnol. 2013, 9, 111–115. [Google Scholar] [CrossRef] [PubMed]
- Yuan, H.; Liu, Z.; Xu, G.; Zhou, B.; Wu, S.; Dumcenco, D.; Yan, K.; Zhang, Y.; Mo, S.-K.; Dudin, P.; et al. Evolution of the Valley Position in Bulk Transition-Metal Chalcogenides and Their Monolayer Limit. Nano Lett. 2016, 16, 4738–4745. [Google Scholar] [CrossRef] [PubMed]
- Jones, A.; Sayers, C.J.; Cattelan, M.; Fox, N.A.; da Como, E.; Laverock, J. Role of Fermi surface nesting in the charge density wave of VSe2. unpublished.
- Gehlmann, M.; Aguilera, I.; Bihlmayer, G.; Nemšák, S.; Nagler, P.; Gospodarič, P.; Zamborlini, G.; Eschbach, M.; Feyer, V.; Kronast, F.; et al. Direct Observation of the Band Gap Transition in Atomically Thin ReS2. Nano Lett. 2017, 17, 5187–5192. [Google Scholar] [CrossRef] [PubMed]
- Hart, L.S.; Webb, J.L.; Dale, S.; Bending, S.J.; Mucha-Kruczynski, M.; Wolverson, D.; Chen, C.; Avila, J.; Asensio, M.C. Electronic bandstructure and van der Waals coupling of ReSe2 revealed by high-resolution angle-resolved photoemission spectroscopy. Sci. Rep. 2017, 7, 5145. [Google Scholar] [CrossRef] [PubMed]
- Diaz, H.C.; Avila, J.; Chen, C.; Addou, R.; Asensio, M.C.; Batzill, M. Direct observation of interlayer hybridization and Dirac relativistic carriers in graphene/MoS(2) van der Waals heterostructures. Nano Lett. 2015, 15, 1135–1140. [Google Scholar] [CrossRef] [PubMed]
- Avsar, A.; Vera-Marun, I.J.; Tan, J.Y.; Watanabe, K.; Taniguchi, T.; Neto, A.H.C.; Özyilmaz, B. Air-Stable Transport in Graphene-Contacted, Fully Encapsulated Ultrathin Black Phosphorus-Based Field-Effect Transistors. ACS Nano 2015, 9, 4138–4145. [Google Scholar] [CrossRef] [PubMed]
- Wilson, N.R.; Nguyen, P.V.; Seyler, K.; Rivera, P.; Marsden, A.J.; Laker, Z.P.L.; Constantinescu, G.C.; Kandyba, V.; Barinov, A.; Hine, N.D.M.; et al. Determination of band offsets, hybridization, and exciton binding in 2D semiconductor heterostructures. Sci. Adv. 2017, 3, e1601832. [Google Scholar] [CrossRef] [PubMed]
- Damascelli, A. Probing the electronic structure of complex systems by ARPES. Phys. Scr. 2004, T109, 61–74. [Google Scholar] [CrossRef]
- Dudin, P.; Lacovig, P.; Fava, C.; Nicolini, E.; Bianco, A.; Cautero, G.; Barinov, A. Angle-resolved photoemission spectroscopy and imaging with a submicrometre probe at the SPECTROMICROSCOPY-3.2 L beamline of Elettra. J. Synchrotron Radiat. 2010, 17, 445–450. [Google Scholar] [CrossRef] [PubMed]
- Avila, J.; Asensio, M.C. First NanoARPES User Facility Available at SOLEIL: An Innovative and Powerful Tool for Studying Advanced Materials. Synchrotron Radiat. News 2014, 27, 24–30. [Google Scholar] [CrossRef]
- Avila, J.; Boury, A.; Caja-Muñoz, B.; Chen, C.; Lorcy, S.; Asensio, M.C. Optimal focusing system of the Fresnel zone plates at the Synchrotron SOLEIL NanoARPES beamline. J. Phys. Conf. Ser. 2017, 849. [Google Scholar] [CrossRef]
- Escher, M.; Weber, N.; Merkel, M.; Ziethen, C.; Bernhard, P.; Schönhense, G.; Schmidt, S.; Forster, F.; Reinert, F.; Krömker, B.; et al. Nanoelectron spectroscopy for chemical analysis: A novel energy filter for imaging X-ray photoemission spectroscopy. J. Phys. Condens. Matter 2005, 17, S1329–S1338. [Google Scholar] [CrossRef]
- Tromp, R.M.; Reuter, M.C. Imaging with a low-energy electron microscope. Ultramicroscopy 1993, 50, 171–178. [Google Scholar] [CrossRef]
- Schneider, C.M.; Wiemann, C.; Patt, M.; Feyer, V.; Plucinski, L.; Krug, I.P.; Escher, M.; Weber, N.; Merkel, M.; Renault, O.; et al. Expanding the view into complex material systems: From micro-ARPES to nanoscale HAXPES. J. Electron. Spectrosc. Relat. Phenom. 2012, 185, 330–339. [Google Scholar] [CrossRef]
- Barrett, N.; Conrad, E.; Winkler, K.; Kromker, B. Dark field photoelectron emission microscopy of micron scale few layer graphene. Rev. Sci. Instrum. 2012, 83, 083706. [Google Scholar] [CrossRef] [PubMed]
- Usachov, D.; Vilkov, O.; Grüneis, A.; Haberer, D.; Fedorov, A.; Adamchuk, V.K.; Preobrajenski, A.B.; Dudin, P.; Barinov, A.; Oehzelt, M.; et al. Nitrogen-Doped Graphene: Efficient Growth, Structure, and Electronic Properties. Nano Lett. 2011, 11, 5401–5407. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Liu, H.; Yu, Z.; Quhe, R.; Zhou, S.; Wang, Y.; Liu, C.C.; Zhong, H.; Han, N.; Lu, J.; et al. Rise of silicene: A competitive 2D material. Prog. Mater. Sci. 2016, 83, 24–151. [Google Scholar] [CrossRef]
- Dávila, M.E.; Le Lay, G. Few layer epitaxial germanene: A novel two-dimensional Dirac material. Sci. Rep. 2016, 6, 20714. [Google Scholar] [CrossRef] [PubMed]
- Yao, W.; Wang, E.; Huang, H.; Deng, K.; Yan, M.; Zhang, K.; Miyamoto, K.; Okuda, T.; Li, L.; Wang, Y.; et al. Direct observation of spin-layer locking by local Rashba effect in monolayer semiconducting PtSe2 film. Nat. Commun. 2017, 8, 14216. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Joucken, F.; Tison, Y.; le Fèvre, P.; Tejeda, A.; Taleb-Ibrahimi, A.; Conrad, E.; Repain, V.; Chacon, C.; Bellec, A.; Girard, Y.; et al. Charge transfer and electronic doping in nitrogen-doped graphene. Sci. Rep. 2015, 5, 14564. [Google Scholar] [CrossRef] [PubMed]
- Hwang, C.; Siegel, D.A.; Mo, S.-K.; Regan, W.; Ismach, A.; Zhang, Y.; Zettl, A.; Lanzara, A. Fermi velocity engineering in graphene by substrate modification. Sci. Rep. 2012, 2, 590. [Google Scholar] [CrossRef]
- Fedorov, A.V.; Verbitskiy, N.I.; Haberer, D.; Struzzi, C.; Petaccia, L.; Usachov, D.; Vilkov, O.Y.; Vyalikh, D.V.; Fink, J.; Knupfer, M.; et al. Observation of a universal donor-dependent vibrational mode in graphene. Nat. Commun. 2014, 5, 3257. [Google Scholar] [CrossRef] [PubMed]
- Varykhalov, A.; Sanchez-Barriga, J.; Shikin, A.M.; Biswas, C.; Vescovo, E.; Rybkin, A.; Marchenko, D.; Rader, O. Electronic and magnetic properties of quasifreestanding graphene on Ni. Phys. Rev. Lett. 2008, 101, 157601. [Google Scholar] [CrossRef] [PubMed]
- Batzill, M. The surface science of graphene: Metal interfaces, CVD synthesis, nanoribbons, chemical modifications, and defects. Surf. Sci. Rep. 2012, 67, 83–115. [Google Scholar] [CrossRef]
- Sutter, P.W.; Flege, J.I.; Sutter, E.A. Epitaxial graphene on ruthenium. Nat. Mater. 2008, 7, 406–411. [Google Scholar] [CrossRef] [PubMed]
- Varykhalov, A.; Marchenko, D.; Sánchez-Barriga, J.; Scholz, M.R.; Verberck, B.; Trauzettel, B.; Wehling, T.O.; Carbone, C.; Rader, O. Intact Dirac Cones at Broken Sublattice Symmetry: Photoemission Study of Graphene on Ni and Co. Phys. Rev. X 2012, 2, 041017. [Google Scholar] [CrossRef]
- Varykhalov, A.; Sánchez-Barriga, J.; Marchenko, D.; Hlawenka, P.; Mandal, P.S.; Rader, O. Tunable Fermi level and hedgehog spin texture in gapped graphene. Nat. Commun. 2015, 6, 7610. [Google Scholar] [CrossRef] [PubMed]
- Usachov, D.Y.; Fedorov, A.V.; Petukhov, A.E.; Vilkov, O.Y.; Rybkin, A.G.; Otrokov, M.M.; Arnau, A.; Chulkov, E.V.; Yashina, L.V.; Farjam, M.; et al. Epitaxial B-Graphene: Large-Scale Growth and Atomic Structure. ACS Nano 2015, 9, 7314–7322. [Google Scholar] [CrossRef] [PubMed]
- Voloshina, E.N.; Generalov, A.; Weser, M.; Böttcher, S.; Horn, K.; Dedkov, Y.S. Structural and electronic properties of the graphene/Al/Ni(111) intercalation system. New J. Phys. 2011, 13, 113028. [Google Scholar] [CrossRef]
- Siegel, D.A.; Park, C.-H.; Hwang, C.; Deslippe, J.; Fedorov, A.V.; Louie, S.G.; Lanzara, A. Many-body interactions in quasi-freestanding graphene. Proc. Natl. Acad. Sci. USA 2011, 108, 11365–11369. [Google Scholar] [CrossRef] [PubMed]
- Jeon, C.; Shin, H.-C.; Song, I.; Kim, M.; Park, J.-H.; Nam, J.; Oh, D.-H.; Woo, S.; Hwang, C.-C.; Park, C.-Y.; et al. Opening and reversible control of a wide energy gap in uniform monolayer graphene. Sci. Rep. 2013, 3, 2725. [Google Scholar] [CrossRef] [PubMed]
- Larciprete, R.; Ulstrup, S.; Lacovig, P.; Dalmiglio, M.; Bianchi, M.; Mazzola, F.; Hornekær, L.; Orlando, F.; Baraldi, A.; Hofmann, P.; et al. Oxygen Switching of the Epitaxial Graphene–Metal Interaction. ACS Nano 2012, 6, 9551–9558. [Google Scholar] [CrossRef] [PubMed]
- Cattelan, M.; Peng, G.W.; Cavaliere, E.; Artiglia, L.; Barinov, A.; Roling, L.T.; Favaro, M.; Pis, I.; Nappini, S.; Magnano, E.; et al. The nature of the Fe-graphene interface at the nanometer level. Nanoscale 2015, 7, 2450–2460. [Google Scholar] [CrossRef] [PubMed]
- Klimovskikh, I.I.; Otrokov, M.M.; Voroshnin, V.Y.; Sostina, D.; Petaccia, L.; di Santo, G.; Thakur, S.; Chulkov, E.V.; Shikin, A.M. Spin–Orbit Coupling Induced Gap in Graphene on Pt(111) with Intercalated Pb Monolayer. ACS Nano 2017, 11, 368–374. [Google Scholar] [CrossRef] [PubMed]
- Kapitanova, O.O.; Kataev, E.Y.; Usachov, D.Y.; Sirotina, A.P.; Belova, A.I.; Sezen, H.; Amati, M.; Al-Hada, M.; Gregoratti, L.; Barinov, A.; et al. Laterally Selective Oxidation of Large-Scale Graphene with Atomic Oxygen. J. Phys. Chem. C 2017, 121, 27915–27922. [Google Scholar] [CrossRef]
- Yin, J.; Wang, H.; Peng, H.; Tan, Z.; Liao, L.; Lin, L.; Sun, X.; Koh, A.L.; Chen, Y.; Peng, H.; et al. Selectively enhanced photocurrent generation in twisted bilayer graphene with van Hove singularity. Nat. Commun. 2016, 7, 10699. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Xu, X.; Li, J.; Lin, L.; Sun, L.; Sun, X.; Zhao, S.; Tan, C.; Chen, C.; Dang, W.; et al. Surface Monocrystallization of Copper Foil for Fast Growth of Large Single-Crystal Graphene under Free Molecular Flow. Adv. Mater. 2016, 28, 8968–8974. [Google Scholar] [CrossRef] [PubMed]
- Lin, L.; Xu, X.; Yin, J.; Sun, J.; Tan, Z.; Koh, A.L.; Wang, H.; Peng, H.; Chen, Y.; Liu, Z. Tuning Chemical Potential Difference across Alternately Doped Graphene p-n Junctions for High-Efficiency Photodetection. Nano Lett. 2016, 16, 4094–4101. [Google Scholar] [CrossRef] [PubMed]
- Avila, J.; Razado, I.; Lorcy, S.; Fleurier, R.; Pichonat, E.; Vignaud, D.; Wallart, X.; Asensio, M.C. Exploring electronic structure of one-atom thick polycrystalline graphene films: A nano angle resolved photoemission study. Sci. Rep. 2013, 3, 2439. [Google Scholar] [CrossRef] [PubMed]
- Wilson, N.R.; Marsden, A.J.; Saghir, M.; Bromley, C.J.; Schaub, R.; Costantini, G.; White, T.W.; Partridge, C.; Barinov, A.; Dudin, P.; et al. Weak mismatch epitaxy and structural Feedback in graphene growth on copper foil. Nano Res. 2013, 6, 99–112. [Google Scholar] [CrossRef]
- Cattelan, M.; Agnoli, S.; Favaro, M.; Garoli, D.; Romanato, F.; Meneghetti, M.; Barinov, A.; Dudin, P.; Granozzi, G. Microscopic View on a Chemical Vapor Deposition Route to Boron-Doped Graphene Nanostructures. Chem. Mater. 2013, 25, 1490–1495. [Google Scholar] [CrossRef]
- Wu, Y.A.; Fan, Y.; Speller, S.; Creeth, G.L.; Sadowski, J.T.; He, K.; Robertson, A.W.; Allen, C.S.; Warner, J.H. Large Single Crystals of Graphene on Melted Copper Using Chemical Vapor Deposition. ACS Nano 2012, 6, 5010–5017. [Google Scholar] [CrossRef] [PubMed]
- Brown, L.; Lochocki, E.B.; Avila, J.; Kim, C.J.; Ogawa, Y.; Havener, R.W.; Kim, D.K.; Monkman, E.J.; Shai, D.E.; Wei, H.I.; et al. Polycrystalline graphene with single crystalline electronic structure. Nano Lett. 2014, 14, 5706–5711. [Google Scholar] [CrossRef] [PubMed]
- Sutter, P.; Sadowski, J.T.; Sutter, E. Graphene on Pt(111): Growth and substrate interaction. Phys. Rev. B 2009, 80, 245411. [Google Scholar] [CrossRef]
- Bao, C.; Yao, W.; Wang, E.; Chen, C.; Avila, J.; Asensio, M.C.; Zhou, S. Stacking-Dependent Electronic Structure of Trilayer Graphene Resolved by Nanospot Angle-Resolved Photoemission Spectroscopy. Nano Lett. 2017, 17, 1564–1568. [Google Scholar] [CrossRef] [PubMed]
- Kandyba, V.; Yablonskikh, M.; Barinov, A. Spectroscopic characterization of charge carrier anisotropic motion in twisted few-layer graphene. Sci. Rep. 2015, 5, 16388. [Google Scholar] [CrossRef] [PubMed]
- Johansson, L.I.; Armiento, R.; Avila, J.; Xia, C.; Lorcy, S.; Abrikosov, I.A.; Asensio, M.C.; Virojanadara, C. Multiple π-bands and Bernal stacking of multilayer graphene on C-face SiC, revealed by nano-Angle Resolved Photoemission. Sci. Rep. 2014, 4, 4157. [Google Scholar] [CrossRef] [PubMed]
- Sutter, P.; Hybertsen, M.S.; Sadowski, J.T.; Sutter, E. Electronic Structure of Few-Layer Epitaxial Graphene on Ru(0001). Nano Lett. 2009, 9, 2654–2660. [Google Scholar] [CrossRef] [PubMed]
- Sutter, P.; Sutter, E. Microscopy of Graphene Growth, Processing, and Properties. Adv. Funct. Mater. 2013, 23, 2617–2634. [Google Scholar] [CrossRef]
- Knox, K.R.; Wang, S.; Morgante, A.; Cvetko, D.; Locatelli, A.; Mentes, T.O.; Niño, M.A.; Kim, P.; Osgood, R.M. Spectromicroscopy of single and multilayer graphene supported by a weakly interacting substrate. Phys. Rev. B 2008, 78, 201408. [Google Scholar] [CrossRef]
- Tan, Z.; Yin, J.; Chen, C.; Wang, H.; Lin, L.; Sun, L.; Wu, J.; Sun, X.; Yang, H.; Chen, Y.; et al. Building Large-Domain Twisted Bilayer Graphene with van Hove Singularity. ACS Nano 2016, 10, 6725–6730. [Google Scholar] [CrossRef] [PubMed]
- Sutter, P.; Sadowski, J.T.; Sutter, E.A. Chemistry under Cover: Tuning Metal–Graphene Interaction by Reactive Intercalation. J. Am. Chem. Soc. 2010, 132, 8175–8179. [Google Scholar] [CrossRef] [PubMed]
- Petrović, M.; Rakić, I.Š.; Runte, S.; Busse, C.; Sadowski, J.T.; Lazić, P.; Pletikosić, I.; Pan, Z.H.; Milun, M.; Pervan, P.; et al. The mechanism of caesium intercalation of graphene. Nat. Commun. 2013, 4, 2772. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, K.; Taniguchi, T.; Kanda, H. Direct-bandgap properties and evidence for ultraviolet lasing of hexagonal boron nitride single crystal. Nat. Mater. 2004, 3, 404. [Google Scholar] [CrossRef] [PubMed]
- Cattelan, M.; Markman, B.; Lucchini, G.; Das, P.K.; Vobornik, I.; Robinson, J.A.; Agnoli, S.; Granozzi, G. New Strategy for the Growth of Complex Heterostructures Based on Different 2D Materials. Chem. Mater. 2015, 27, 4105–4113. [Google Scholar] [CrossRef]
- Usachov, D.; Adamchuk, V.K.; Haberer, D.; Grüneis, A.; Sachdev, H.; Preobrajenski, A.B.; Laubschat, C.; Vyalikh, D.V. Quasifreestanding single-layer hexagonal boron nitride as a substrate for graphene synthesis. Phys. Rev. B 2010, 82, 075415. [Google Scholar] [CrossRef]
- Henck, H.; Pierucci, D.; Fugallo, G.; Avila, J.; Cassabois, G.; Dappe, Y.J.; Silly, M.G.; Chen, C.; Gil, B.; Gatti, M.; et al. Direct observation of the band structure in bulk hexagonal boron nitride. Phys. Rev. B 2017, 95, 085410. [Google Scholar] [CrossRef]
- Liu, H.; Du, Y.; Deng, Y.; Ye, P.D. Semiconducting black phosphorus: Synthesis, transport properties and electronic applications. Chem. Soc. Rev. 2015, 44, 2732–2743. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Yu, Y.; Ye, G.J.; Ge, Q.; Ou, X.; Wu, H.; Feng, D.; Chen, X.H.; Zhang, Y. Black phosphorus field-effect transistors. Nat. Nanotechnol. 2014, 9, 372. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Baik, S.S.; Jung, S.W.; Sohn, Y.; Ryu, S.H.; Choi, H.J.; Yang, B.J.; Kim, K.S. Two-Dimensional Dirac Fermions Protected by Space-Time Inversion Symmetry in Black Phosphorus. Phys. Rev. Lett. 2017, 119, 226801. [Google Scholar] [CrossRef] [PubMed]
- Ehlen, N.; Sanna, A.; Senkovskiy, B.V.; Petaccia, L.; Fedorov, A.V.; Profeta, G.; Grüneis, A. Direct observation of a surface resonance state and surface band inversion control in black phosphorus. Phys. Rev. B 2018, 97. [Google Scholar] [CrossRef]
- Kim, J.; Baik, S.S.; Ryu, S.H.; Sohn, Y.; Park, S.; Park, B.; Denlinger, J.; Yi, Y.; Choi, H.J.; Kim, K.S. Observation of tunable band gap and anisotropic Dirac semimetal state in black phosphorus. Science 2015, 349, 723–726. [Google Scholar] [CrossRef] [PubMed]
- Golias, E.; Krivenkov, M.; Sánchez-Barriga, J. Disentangling bulk from surface contributions in the electronic structure of black phosphorus. Phys. Rev. B 2016, 93, 075207. [Google Scholar] [CrossRef]
- Han, C.Q.; Yao, M.Y.; Bai, X.X.; Miao, L.; Zhu, F.; Guan, D.D.; Wang, S.; Gao, C.L.; Liu, C.; Qian, D.; et al. Electronic structure of black phosphorus studied by angle-resolved photoemission spectroscopy. Phys. Rev. B 2014, 90. [Google Scholar] [CrossRef]
- Ehlen, N.; Senkovskiy, B.V.; Fedorov, A.V.; Perucchi, A.; di Pietro, P.; Sanna, A.; Profeta, G.; Petaccia, L.; Grüneis, A. Evolution of electronic structure of few-layer phosphorene from angle-resolved photoemission spectroscopy of black phosphorous. Phys. Rev. B 2016, 94. [Google Scholar] [CrossRef]
- Island, J.O.; Steele, G.A.; van der Zant, H.S.; Castellanos-Gomez, A. Environmental instability of few-layer black phosphorus. 2D Mater. 2015, 2. [Google Scholar] [CrossRef]
- Chhowalla, M.; Shin, H.S.; Eda, G.; Li, L.-J.; Loh, K.P.; Zhang, H. The chemistry of two-dimensional layered transition metal dichalcogenide nanosheets. Nat. Chem. 2013, 5, 263. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.H.; Kalantar-Zadeh, K.; Kis, A.; Coleman, J.N.; Strano, M.S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 2012, 7, 699–712. [Google Scholar] [CrossRef] [PubMed]
- Jin, W.; Yeh, P.C.; Zaki, N.; Zhang, D.; Sadowski, J.T.; Al-Mahboob, A.; van der Zande, A.M.; Chenet, D.A.; Dadap, J.I.; Herman, I.P.; et al. Direct measurement of the thickness-dependent electronic band structure of MoS2 using angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 2013, 111, 106801. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Yao, W.; Xiao, D.; Heinz, T.F. Spin and pseudospins in layered transition metal dichalcogenides. Nat. Phys. 2014, 10, 343–350. [Google Scholar] [CrossRef]
- Mo, S.K.; Hwang, C.; Zhang, Y.; Fanciulli, M.; Muff, S.; Dil, J.H.; Shen, Z.X.; Hussain, Z. Spin-resolved photoemssion study of epitaxially grown MoSe2 and WSe2 thin films. J. Phys. Condens. Matter 2016, 28, 454001. [Google Scholar] [CrossRef] [PubMed]
- Agnoli, S.; Ambrosetti, A.; Menteş, T.O.; Sala, A.; Locatelli, A.; Silvestrelli, P.L.; Cattelan, M.; Eichfeld, S.M.; Deng, D.D.; Robinson, J.A.; et al. Unravelling the Structural and Electronic Properties at the WSe2-Graphene Interface for a Rational Design of Van der Waals Heterostructures. ACS Appl. Mater. Interfaces 2018. [Google Scholar] [CrossRef]
- Xiao, D.; Liu, G.-B.; Feng, W.; Xu, X.; Yao, W. Coupled Spin and Valley Physics in Monolayers of MoS2 and Other Group-VI Dichalcogenides. Phys. Rev. Lett. 2012, 108, 196802. [Google Scholar] [CrossRef] [PubMed]
- Ye, Y.; Xiao, J.; Wang, H.; Ye, Z.; Zhu, H.; Zhao, M.; Wang, Y.; Zhao, J.; Yin, X.; Zhang, X. Electrical generation and control of the valley carriers in a monolayer transition metal dichalcogenide. Nat. Nanotechnol. 2016, 11, 598–602. [Google Scholar] [CrossRef] [PubMed]
- Schaibley, J.R.; Yu, H.; Clark, G.; Rivera, P.; Ross, J.S.; Seyler, K.L.; Yao, W.; Xu, X. Valleytronics in 2D materials. Nat. Rev. Mater. 2016, 1, 16055. [Google Scholar] [CrossRef]
- Riley, J.M.; Mazzola, F.; Dendzik, M.; Michiardi, M.; Takayama, T.; Bawden, L.; Granerød, C.; Leandersson, M.; Balasubramanian, T.; Hoesch, M.; et al. Direct observation of spin-polarized bulk bands in an inversion-symmetric semiconductor. Nat. Phys. 2014, 10, 835–839. [Google Scholar] [CrossRef]
- Suzuki, R.; Sakano, M.; Zhang, Y.J.; Akashi, R.; Morikawa, D.; Harasawa, A.; Yaji, K.; Kuroda, K.; Miyamoto, K.; Okuda, T.; et al. Valley-dependent spin polarization in bulk MoS2 with broken inversion symmetry. Nat. Nanotechnol. 2014, 9, 611–617. [Google Scholar] [CrossRef] [PubMed]
- Das, P.K.; di Sante, D.; Vobornik, I.; Fujii, J.; Okuda, T.; Bruyer, E.; Gyenis, A.; Feldman, B.E.; Tao, J.; Ciancio, R.; et al. Layer-dependent quantum cooperation of electron and hole states in the anomalous semimetal WTe2. Nat. Commun. 2016, 7, 10847. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.J.; Yoshida, M.; Suzuki, R.; Iwasa, Y. 2D crystals of transition metal dichalcogenide and their iontronic functionalities. 2D Mater. 2015, 2, 044004. [Google Scholar] [CrossRef]
- Tusche, C.; Ellguth, M.; Ünal, A.A.; Chiang, C.T.; Winkelmann, A.; Krasyuk, A.; Hahn, M.; Schönhense, G.; Kirschner, J. Spin resolved photoelectron microscopy using a two-dimensional spin-polarizing electron mirror. Appl. Phys. Lett. 2011, 99. [Google Scholar] [CrossRef]
- Amati, M.; Barinov, A.; Feyer, V.; Gregoratti, L.; Al-Hada, M.; Locatelli, A.; Mentes, T.O.; Sezen, H.; Schneider, C.M.; Kiskinova, M. Photoelectron microscopy at Elettra: Recent advances and perspectives. J. Electron. Spectrosc. Relat. Phenom. 2017. [Google Scholar] [CrossRef]
- Alidoust, N.; Bian, G.; Xu, S.-Y.; Sankar, R.; Neupane, M.; Liu, C.; Belopolski, I.; Qu, D.-X.; Denlinger, J.D.; Chou, F.-C.; et al. Observation of monolayer valence band spin-orbit effect and induced quantum well states in MoX2. Nat. Commun. 2014, 5, 4673. [Google Scholar] [CrossRef] [PubMed]
- Kim, B.S.; Kyung, W.S.; Seo, J.J.; Kwon, J.Y.; Denlinger, J.D.; Kim, C.; Park, S.R. Possible electric field induced indirect to direct band gap transition in MoSe2. Sci. Rep. 2017, 7, 5206. [Google Scholar] [CrossRef] [PubMed]
- Nikonov, K.; Ehlen, N.; Senkovskiy, B.; Saigal, N.; Fedorov, A.; Nefedov, A.; Woll, C.; di Santo, G.; Petaccia, L.; Gruneis, A. Synthesis and spectroscopic characterization of alkali-metal intercalated ZrSe2. Dalton Trans. 2017. [Google Scholar] [CrossRef] [PubMed]
- Riley, J.M.; Meevasana, W.; Bawden, L.; Asakawa, M.; Takayama, T.; Eknapakul, T.; Kim, T.K.; Hoesch, M.; Mo, S.K.; Takagi, H.; et al. Negative electronic compressibility and tunable spin splitting in WSe2. Nat. Nanotechnol. 2015, 10, 1043–1047. [Google Scholar] [CrossRef] [PubMed]
- Kang, M.; Kim, B.; Ryu, S.H.; Jung, S.W.; Kim, J.; Moreschini, L.; Jozwiak, C.; Rotenberg, E.; Bostwick, A.; Kim, K.S. Universal Mechanism of Band-Gap Engineering in Transition-Metal Dichalcogenides. Nano Lett. 2017, 17, 1610–1615. [Google Scholar] [CrossRef] [PubMed]
- Katoch, J.; Ulstrup, S.; Koch, R.J.; Moser, S.; McCreary, K.M.; Singh, S.; Xu, J.; Jonker, B.T.; Kawakami, R.K.; Bostwick, A.; et al. Giant spin-splitting and gap renormalization driven by trions in single-layer WS2/h-BN heterostructures. Nat. Phys. 2018. [Google Scholar] [CrossRef]
- Wallauer, R.; Reimann, J.; Armbrust, N.; Güdde, J.; Höfer, U. Intervalley scattering in MoS2 imaged by two-photon photoemission with a high-harmonic probe. Appl. Phys. Lett. 2016, 109. [Google Scholar] [CrossRef]
- Grubišić Čabo, A.; Miwa, J.A.; Grønborg, S.S.; Riley, J.M.; Johannsen, J.C.; Cacho, C.; Alexander, O.; Chapman, R.T.; Springate, E.; Grioni, M.; et al. Observation of Ultrafast Free Carrier Dynamics in Single Layer MoS2. Nano Lett. 2015, 15, 5883–5887. [Google Scholar] [CrossRef] [PubMed]
- Ulstrup, S.; Čabo, A.G.; Miwa, J.A.; Riley, J.M.; Grønborg, S.S.; Johannsen, J.C.; Cacho, C.; Alexander, O.; Chapman, R.T.; Springate, E.; et al. Ultrafast Band Structure Control of a Two-Dimensional Heterostructure. ACS Nano 2016, 10, 6315–6322. [Google Scholar] [CrossRef] [PubMed]
- Mikkelsen, A.; Schwenke, J.; Fordell, T.; Luo, G.; Klunder, K.; Hilner, E.; Anttu, N.; Zakharov, A.A.; Lundgren, E.; Mauritsson, J.; et al. Photoemission electron microscopy using extreme ultraviolet attosecond pulse trains. Rev. Sci. Instrum. 2009, 80, 123703. [Google Scholar] [CrossRef] [PubMed]
- Spiecker, H.; Schmidt, O.; Ziethen, C.; Menke, D.; Kleineberg, U.; Ahuja, R.C.; Merkel, M.; Heinzmann, U.; Schönhense, G. Time-of-flight photoelectron emission microscopy TOF-PEEM: First results. Nucl. Instrum. Methods Phys. Res. 1998, 406, 499–506. [Google Scholar] [CrossRef]
- Chernov, S.V.; Medjanik, K.; Tusche, C.; Kutnyakhov, D.; Nepijko, S.A.; Oelsner, A.; Braun, J.; Minár, J.; Borek, S.; Ebert, H.; et al. Anomalous d-like surface resonances on Mo(110) analyzed by time-of-flight momentum microscopy. Ultramicroscopy 2015, 159, 453–463. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.; Chan, Y.H.; Fang, X.Y.; Zhang, Y.; Chou, M.Y.; Mo, S.K.; Hussain, Z.; Fedorov, A.V.; Chiang, T.C. Charge density wave transition in single-layer titanium diselenide. Nat. Commun. 2015, 6, 8943. [Google Scholar] [CrossRef] [PubMed]
- Strocov, V.N.; Shi, M.; Kobayashi, M.; Monney, C.; Wang, X.; Krempasky, J.; Schmitt, T.; Patthey, L.; Berger, H.; Blaha, P. Three-dimensional electron realm in VSe2 by soft-X-ray photoelectron spectroscopy: Origin of charge-density waves. Phys. Rev. Lett. 2012, 109, 086401. [Google Scholar] [CrossRef] [PubMed]
- Sugawara, K.; Nakata, Y.; Shimizu, R.; Han, P.; Hitosugi, T.; Sato, T.; Takahashi, T. Unconventional Charge-Density-Wave Transition in Monolayer 1T-TiSe2. ACS Nano 2016, 10, 1341–1345. [Google Scholar] [CrossRef] [PubMed]
- Webb, J.L.; Hart, L.S.; Wolverson, D.; Chen, C.; Avila, J.; Asensio, M.C. Electronic band structure of ReS2 by high-resolution angle-resolved photoemission spectroscopy. Phys. Rev. B 2017, 96, 115205. [Google Scholar] [CrossRef]
- Le, D.; Barinov, A.; Preciado, E.; Isarraraz, M.; Tanabe, I.; Komesu, T.; Troha, C.; Bartels, L.; Rahman, T.S.; Dowben, P.A. Spin-orbit coupling in the band structure of monolayer WSe2. J. Phys. Condens. Matter 2015, 27, 182201. [Google Scholar] [CrossRef] [PubMed]
- Yeh, P.-C.; Jin, W.; Zaki, N.; Zhang, D.; Liou, J.T.; Sadowski, J.T.; Al-Mahboob, A.; Dadap, J.I.; Herman, I.P.; Sutter, P.; et al. Layer-dependent electronic structure of an atomically heavy two-dimensional dichalcogenide. Phys. Rev. B 2015, 91, 041407(R). [Google Scholar] [CrossRef]
- Jin, W.; Yeh, P.-C.; Zaki, N.; Zhang, D.; Liou, J.T.; Sadowski, J.T.; Barinov, A.; Yablonskikh, M.; Dadap, J.I.; Sutter, P.; Herman, I.P.; Osgood, R.M. Substrate interactions with suspended and supported monolayer MoS2: Angle-resolved photoemission spectroscopy. Phys. Rev. B 2015, 91, 121409(R). [Google Scholar] [CrossRef]
- Kim, H.; Dumcenco, D.; Frégnaux, M.; Benayad, A.; Chen, M.-W.; Kung, Y.-C.; Kis, A.; Renault, O. Free-standing electronic character of monolayerMoS2 in van der Waals epitaxy. Phys. Rev. B 2016, 94, 084101(R). [Google Scholar] [CrossRef]
- Tanabe, I.; Gomez, M.; Coley, W.C.; Le, D.; Echeverria, E.M.; Stecklein, G.; Kandyba, V.; Balijepalli, S.K.; Klee, V.; Nguyen, A.E.; et al. Band structure characterization of WS2 grown by chemical vapor deposition. Appl. Phys. Lett. 2016, 108. [Google Scholar] [CrossRef]
- Yeh, P.C.; Jin, W.; Zaki, N.; Kunstmann, J.; Chenet, D.; Arefe, G.; Sadowski, J.T.; Dadap, J.I.; Sutter, P.; Hone, J.; et al. Direct Measurement of the Tunable Electronic Structure of Bilayer MoS2 by Interlayer Twist. Nano Lett. 2016, 16, 953–959. [Google Scholar] [CrossRef] [PubMed]
- Frégnaux, M.; Kim, H.; Rouchon, D.; Derycke, V.; Bleuse, J.; Voiry, D.; Chhowalla, M.; Renault, O. Chemistry and electronics of single layer MoS2 domains from photoelectron spectromicroscopy using laboratory excitation sources. Surf. Interface Anal. 2016, 48, 465–469. [Google Scholar] [CrossRef]
- Dau, M.T.; Gay, M.; di Felice, D.; Vergnaud, C.; Marty, A.; Beigné, C.; Renaud, G.; Renault, O.; Mallet, P.; le Quang, T.; et al. Beyond van der Waals Interaction: The Case of MoSe2 Epitaxially Grown on Few-Layer Graphene. ACS Nano 2018. [Google Scholar] [CrossRef] [PubMed]
- Ben Aziza, Z.; Pierucci, D.; Henck, H.; Silly, M.G.; David, C.; Yoon, M.; Sirotti, F.; Xiao, K.; Eddrief, M.; Girard, J.-C.; et al. Tunable quasiparticle band gap in few-layer GaSe/graphene van der Waals heterostructures. Phys. Rev. B 2017, 96. [Google Scholar] [CrossRef]
- Ben Aziza, Z.; Henck, H.; Pierucci, D.; Silly, M.G.; Lhuillier, E.; Patriarche, G.; Sirotti, F.; Eddrief, M.; Ouerghi, A. van der Waals Epitaxy of GaSe/Graphene Heterostructure: Electronic and Interfacial Properties. ACS Nano 2016, 10, 9679–9686. [Google Scholar] [CrossRef] [PubMed]
- Aretouli, K.E.; Tsipas, P.; Tsoutsou, D.; Marquez-Velasco, J.; Xenogiannopoulou, E.; Giamini, S.A.; Vassalou, E.; Kelaidis, N.; Dimoulas, A. Two-dimensional semiconductor HfSe2 and MoSe2/HfSe2 van der Waals heterostructures by molecular beam epitaxy. Appl. Phys. Lett. 2015, 106, 143105. [Google Scholar] [CrossRef]
- Xenogiannopoulou, E.; Tsipas, P.; Aretouli, K.E.; Tsoutsou, D.; Giamini, S.A.; Bazioti, C.; Dimitrakopulos, G.P.; Komninou, P.; Brems, S.; Huyghebaert, C.; et al. High-quality, large-area MoSe2 and MoSe2/Bi2Se3 heterostructures on AlN(0001)/Si(111) substrates by molecular beam epitaxy. Nanoscale 2015, 7, 7896–7905. [Google Scholar] [CrossRef] [PubMed]
- Aretouli, K.E.; Tsoutsou, D.; Tsipas, P.; Marquez-Velasco, J.; Giamini, S.A.; Kelaidis, N.; Psycharis, V.; Dimoulas, A. Epitaxial 2D SnSe2/2D WSe2 van der Waals Heterostructures. ACS Appl. Mater. Interfaces 2016, 8, 23222–23229. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.-W.; Kim, H.; Ovchinnikov, D.; Kuc, A.; Heine, T.; Renault, O.; Kis, A. Large-grain MBE-grown GaSe on GaAs with a Mexican hat-like valence band dispersion. NPJ 2D Mater. Appl. 2018, 2, 2. [Google Scholar] [CrossRef]
- Lee, C.H.; Krishnamoorthy, S.; O’Hara, D.J.; Brenner, M.R.; Johnson, J.M.; Jamison, J.S.; Myers, R.C.; Kawakami, R.K.; Hwang, J.; Rajan, S. Molecular beam epitaxy of 2D-layered gallium selenide on GaN substrates. J. Appl. Phys. 2017, 121. [Google Scholar] [CrossRef]
- Henck, H.; Aziza, Z.B.; Zill, O.; Pierucci, D.; Naylor, C.H.; Silly, M.G.; Gogneau, N.; Oehler, F.; Collin, S.; Brault, J.; et al. Interface dipole and band bending in the hybrid p-n heterojunction MoS2/GaN(0001). Phys. Rev. B 2017, 96, 115312. [Google Scholar] [CrossRef]
- Kümmell, T.; Hutten, U.; Heyer, F.; Derr, K.; Neubieser, R.M.; Quitsch, W.; Bacher, G. Carrier transfer across a 2D-3D semiconductor heterointerface: The role of momentum mismatch. Phys. Rev. B 2017, 95, 081304. [Google Scholar] [CrossRef]
- Gupta, P.; Rahman, A.A.; Subramanian, S.; Gupta, S.; Thamizhavel, A.; Orlova, T.; Rouvimov, S.; Vishwanath, S.; Protasenko, V.; Laskar, M.R.; et al. Layered transition metal dichalcogenides: Promising near-lattice-matched substrates for GaN growth. Sci. Rep. 2016, 6, 23708. [Google Scholar] [CrossRef] [PubMed]
- Mayorov, A.S.; Gorbachev, R.V.; Morozov, S.V.; Britnell, L.; Jalil, R.; Ponomarenko, L.A.; Blake, P.; Novoselov, K.S.; Watanabe, K.; Taniguchi, T.; et al. Micrometer-Scale Ballistic Transport in Encapsulated Graphene at Room Temperature. Nano Lett. 2011, 11, 2396–2399. [Google Scholar] [CrossRef] [PubMed]
- Dean, C.R.; Wang, L.; Maher, P.; Forsythe, C.; Ghahari, F.; Gao, Y.; Katoch, J.; Ishigami, M.; Moon, P.; Koshino, M.; et al. Hofstadter’s butterfly and the fractal quantum Hall effect in moiré superlattices. Nature 2013, 497, 598. [Google Scholar] [CrossRef] [PubMed]
- Georgiou, T.; Jalil, R.; Belle, B.D.; Britnell, L.; Gorbachev, R.V.; Morozov, S.V.; Kim, Y.-J.; Gholinia, A.; Haigh, S.J.; Makarovsky, O.; et al. Vertical field-effect transistor based on graphene–WS2 heterostructures for flexible and transparent electronics. Nat. Nanotechnol. 2012, 8, 100. [Google Scholar] [CrossRef] [PubMed]
- Kretinin, A.V.; Cao, Y.; Tu, J.S.; Yu, G.L.; Jalil, R.; Novoselov, K.S.; Haigh, S.J.; Gholinia, A.; Mishchenko, A.; Lozada, M.; et al. Electronic Properties of Graphene Encapsulated with Different Two-Dimensional Atomic Crystals. Nano Lett. 2014, 14, 3270–3276. [Google Scholar] [CrossRef] [PubMed]
- Wang, E.; Chen, G.; Wan, G.; Lu, X.; Chen, C.; Avila, J.; Fedorov, A.V.; Zhang, G.; Asensio, M.C.; Zhang, Y.; et al. Electronic structure of transferred graphene/h-BN van der Waals heterostructures with nonzero stacking angles by nano-ARPES. J. Phys. Condens. Matter 2016, 28, 444002. [Google Scholar] [CrossRef] [PubMed]
- Pierucci, D.; Henck, H.; Naylor, C.H.; Sediri, H.; Lhuillier, E.; Balan, A.; Rault, J.E.; Dappe, Y.J.; Bertran, F.; Fèvre, P.L.; et al. Large area molybdenum disulphide- epitaxial graphene vertical Van der Waals heterostructures. Sci. Rep. 2016, 6, 26656. [Google Scholar] [CrossRef] [PubMed]
- Pierucci, D.; Henck, H.; Avila, J.; Balan, A.; Naylor, C.H.; Patriarche, G.; Dappe, Y.J.; Silly, M.G.; Sirotti, F.; Johnson, A.T.; et al. Band Alignment and Minigaps in Monolayer MoS2-Graphene van der Waals Heterostructures. Nano Lett. 2016, 16, 4054–4061. [Google Scholar] [CrossRef] [PubMed]
- Jin, W.; Yeh, P.-C.; Zaki, N.; Chenet, D.; Arefe, G.; Hao, Y.; Sala, A.; Mentes, T.O.; Dadap, J.I.; Locatelli, A.; et al. Tuning the electronic structure of monolayer graphene/MoS2 van der Waals heterostructures via interlayer twist. Phys. Rev. B 2015, 92. [Google Scholar] [CrossRef]
- Han, S.W.; Cha, G.-B.; Frantzeskakis, E.; Razado-Colambo, I.; Avila, J.; Park, Y.S.; Kim, D.; Hwang, J.; Kang, J.S.; Ryu, S.; et al. Band-gap expansion in the surface-localized electronic structure of MoS2(0002). Phys. Rev. B 2012, 86. [Google Scholar] [CrossRef]
- Jin, C.; Kim, J.; Suh, J.; Shi, Z.; Chen, B.; Fan, X.; Kam, M.; Watanabe, K.; Taniguchi, T.; Tongay, S.; et al. Interlayer electron–phonon coupling in WSe2/hBN heterostructures. Nat. Phys. 2016, 13, 127. [Google Scholar] [CrossRef]
- Lotsch, B.V. Vertical 2D Heterostructures. Annu. Rev. Mater. Res. 2015, 45, 85–109. [Google Scholar] [CrossRef]
- Haigh, S.J.; Gholinia, A.; Jalil, R.; Romani, S.; Britnell, L.; Elias, D.C.; Novoselov, K.S.; Ponomarenko, L.A.; Geim, A.K.; Gorbachev, R. Cross-sectional imaging of individual layers and buried interfaces of graphene-based heterostructures and superlattices. Nat. Mater. 2012, 11, 764. [Google Scholar] [CrossRef] [PubMed]
- Britnell, L.; Ribeiro, R.M.; Eckmann, A.; Jalil, R.; Belle, B.D.; Mishchenko, A.; Kim, Y.J.; Gorbachev, R.V.; Georgiou, T.; Morozov, S.V.; et al. Strong Light-Matter Interactions in Heterostructures of Atomically Thin Films. Science 2013, 340, 1311. [Google Scholar] [CrossRef] [PubMed]
- Splendiani, A.; Sun, L.; Zhang, Y.; Li, T.; Kim, J.; Chim, C.-Y.; Galli, G.; Wang, F. Emerging Photoluminescence in Monolayer MoS2. Nano Lett. 2010, 10, 1271–1275. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.Y.; Shin, J.-H.; Lee, G.-H.; Lee, C.-H. Two-Dimensional Semiconductor Optoelectronics Based on van der Waals Heterostructures. Nanomaterials 2016, 6, 193. [Google Scholar] [CrossRef] [PubMed]
- Fang, H.; Battaglia, C.; Carraro, C.; Nemsak, S.; Ozdol, B.; Kang, J.S.; Bechtel, H.A.; Desai, S.B.; Kronast, F.; Unal, A.A.; et al. Strong interlayer coupling in van der Waals heterostructures built from single-layer chalcogenides. Proc. Natl. Acad. Sci. USA 2014, 111, 6198. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Zhang, Q.; Yap, C.C.R.; Tay, B.K.; Edwin, T.H.T.; Olivier, A.; Baillargeat, D. From Bulk to Monolayer MoS2: Evolution of Raman Scattering. Adv. Funct. Mater. 2012, 22, 1385–1390. [Google Scholar] [CrossRef]
- Sahin, H.; Tongay, S.; Horzum, S.; Fan, W.; Zhou, J.; Li, J.; Wu, J.; Peeters, F.M. Anomalous Raman spectra and thickness-dependent electronic properties of WSe2. Phys. Rev. B 2013, 87. [Google Scholar] [CrossRef]
- Ceballos, F.; Bellus, M.Z.; Chiu, H.-Y.; Zhao, H. Ultrafast Charge Separation and Indirect Exciton Formation in a MoS2–MoSe2 van der Waals Heterostructure. ACS Nano 2014, 8, 12717–12724. [Google Scholar] [CrossRef] [PubMed]
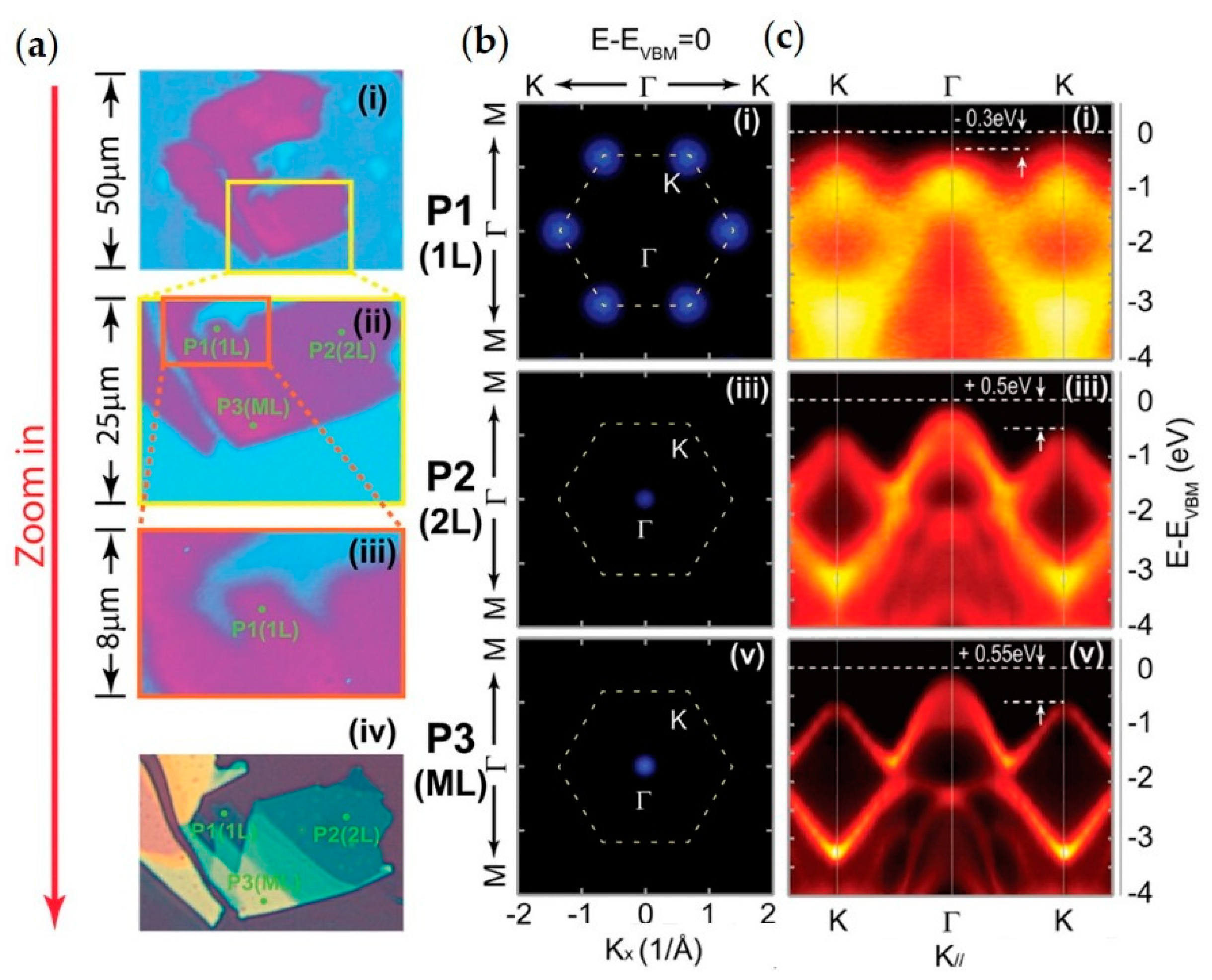
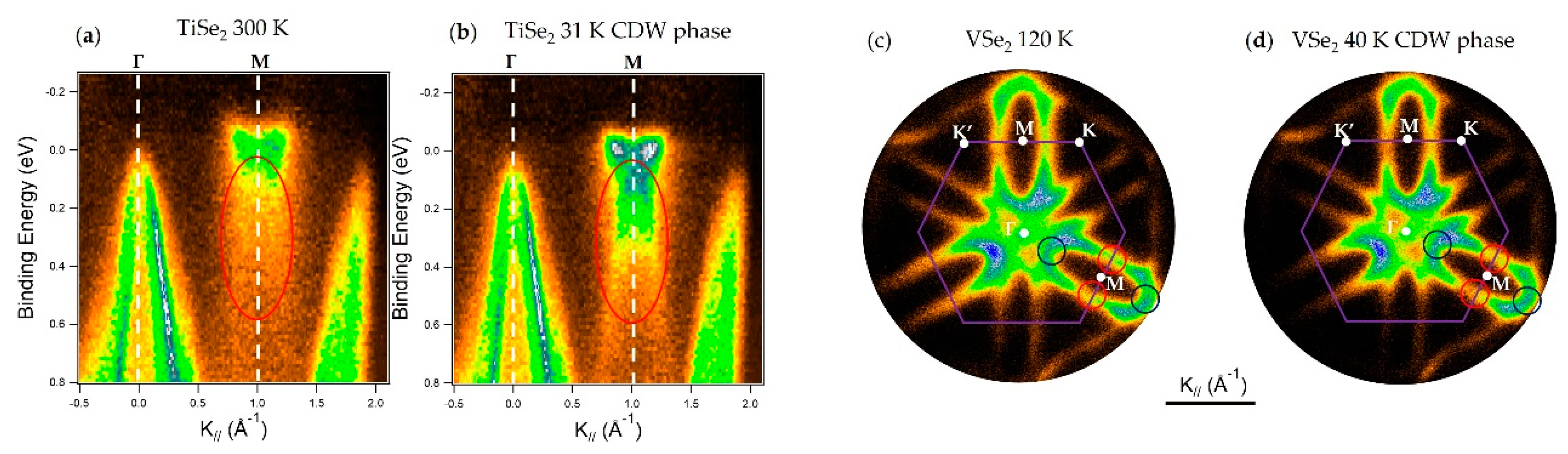
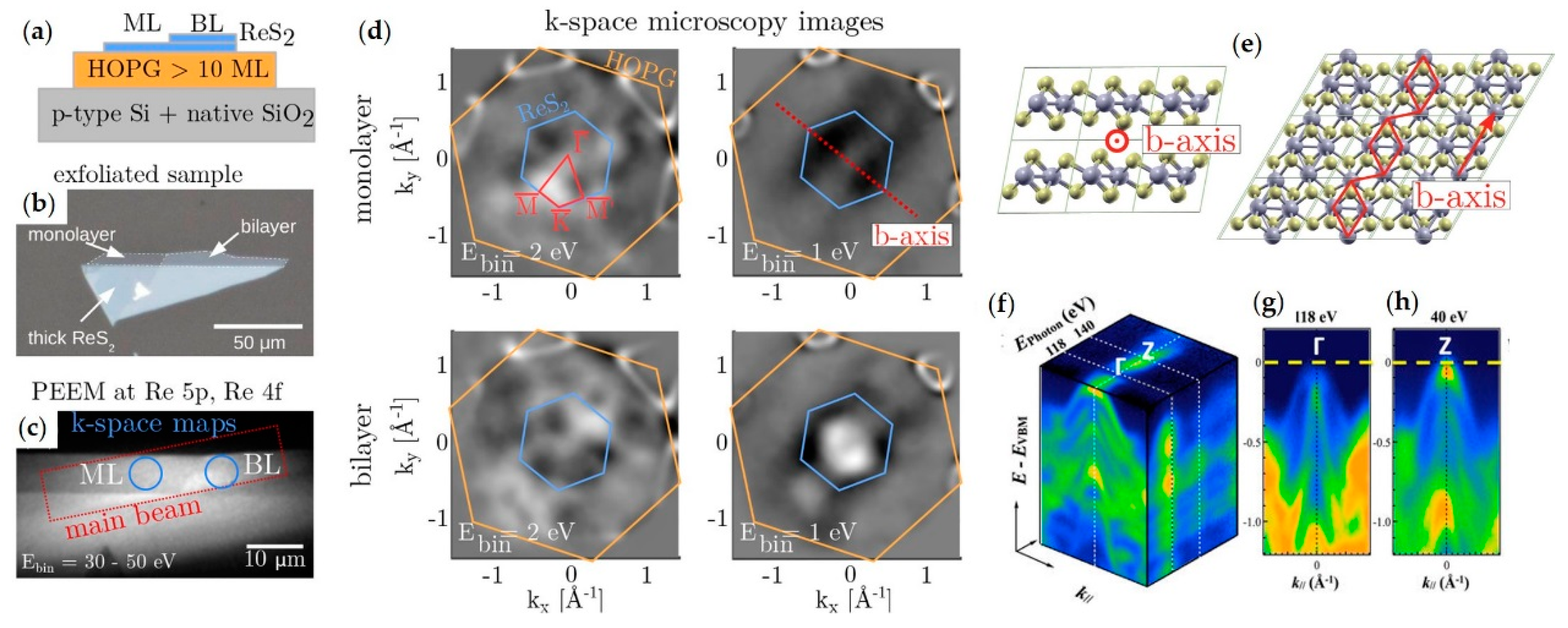
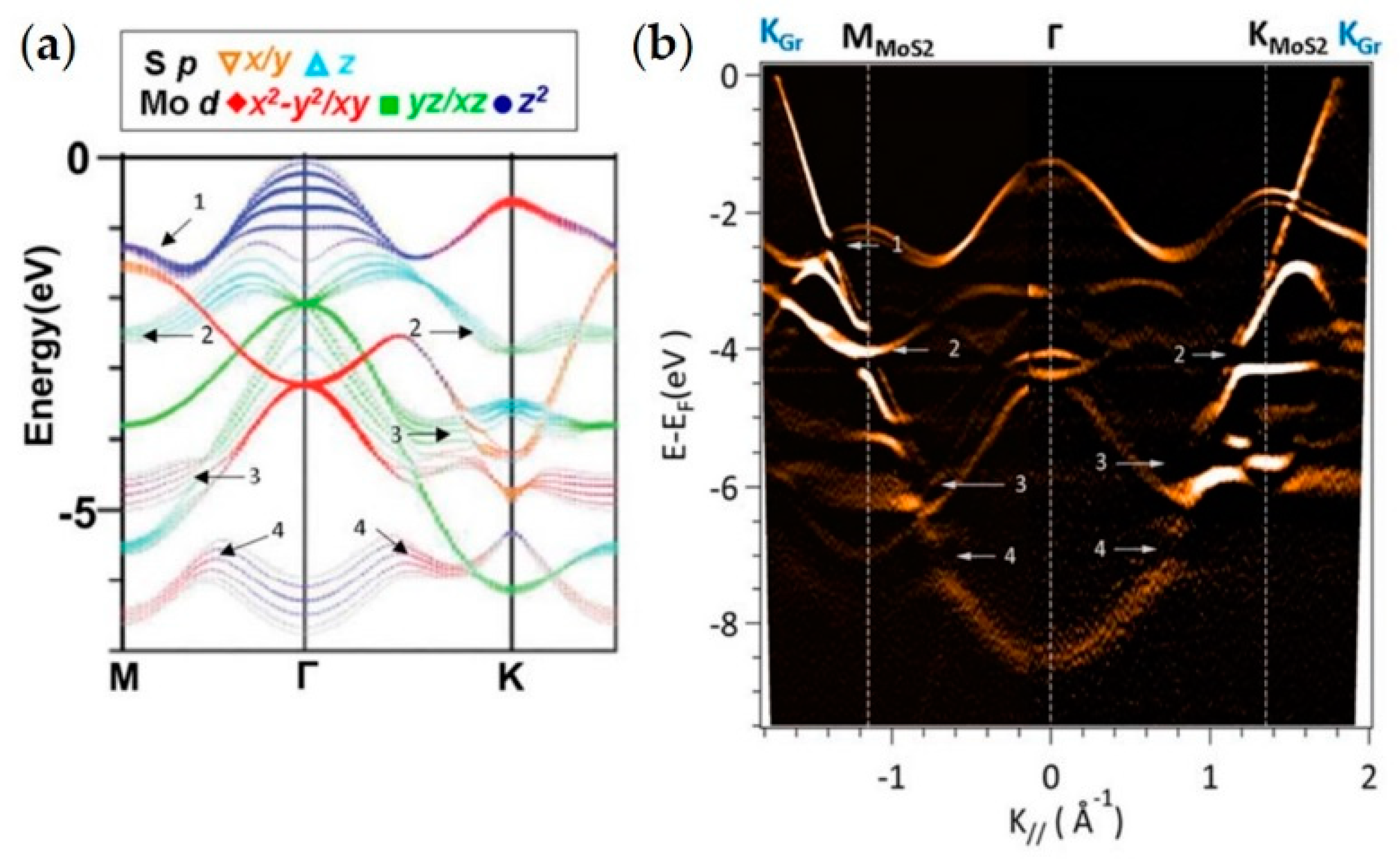
| Type of ARPES | Advantages | Disadvantages | Future Upgrades | |
|---|---|---|---|---|
| Conventional | Easy operation in laboratory and synchrotron facility. Best energy resolution for ARPES. | Requires large samples and several sample rotations. | Electron analyzers with deflectors can scan a sector of k-space without moving the sample. | |
| Spatially-resolved | Synchrotron beamlines | Strong light intensity, possibility to perform ARPES over tens of nanometers, photon versatility, kz sampling. | Requires: precise sample movements, rotations, access to specialized synchrotron beamlines. | Electron analyzers with deflectors can scan a sector of k-space without moving the sample. |
| EF-PEEM | Full-wavevector ARPES with no sample rotation or movement involved. These can be located in stand-alone laboratories with excellent stability. | Limited photon tunability, no kz sampling, lower signal intensity and larger sampling areas with respect to synchrotron nano-ARPES beamlines. | Time-resolved measurements by TOF PEEM, spin-resolved measurements with state-of-the-art detectors. | |
| Spin-resolved | ARPES with spin-resolution. | Intrinsic low signal, limited to large crystal or epitaxial films. | Integration of spin-sensitive detectors in EF-PEEM to perform full-wavevector ARPES and spatially-resolved measurements. | |
| Time-resolved | Studies of: charge carrier dynamics, band gap, empty states, time-dependent phenomena. | Low signal, limited to large crystal or epitaxial films. Complex lasers or time-resolved setups required as excitation sources. Space charge effects. | Advances in TOF PEEM setups and time-resolved light sources to perform spatial- and time-resolved studies. | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cattelan, M.; Fox, N.A. A Perspective on the Application of Spatially Resolved ARPES for 2D Materials. Nanomaterials 2018, 8, 284. https://doi.org/10.3390/nano8050284
Cattelan M, Fox NA. A Perspective on the Application of Spatially Resolved ARPES for 2D Materials. Nanomaterials. 2018; 8(5):284. https://doi.org/10.3390/nano8050284
Chicago/Turabian StyleCattelan, Mattia, and Neil A. Fox. 2018. "A Perspective on the Application of Spatially Resolved ARPES for 2D Materials" Nanomaterials 8, no. 5: 284. https://doi.org/10.3390/nano8050284
APA StyleCattelan, M., & Fox, N. A. (2018). A Perspective on the Application of Spatially Resolved ARPES for 2D Materials. Nanomaterials, 8(5), 284. https://doi.org/10.3390/nano8050284





