Modified Continuum Mechanics Modeling on Size-Dependent Properties of Piezoelectric Nanomaterials: A Review
Abstract
:1. Introduction
2. Novel Modified Continuum Theories for PNs
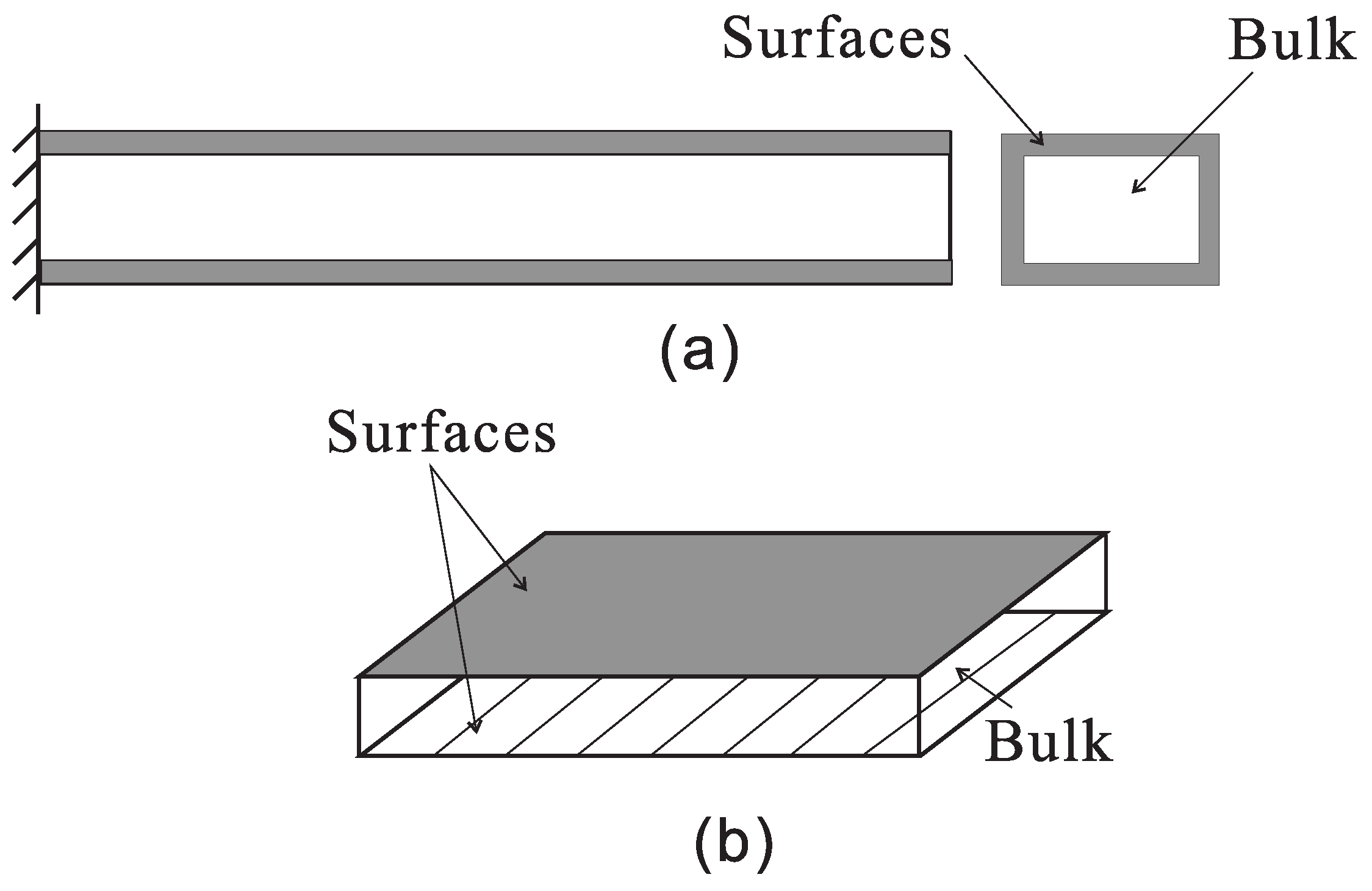
2.1. Surface Piezoelectricity Theory
2.2. Theory of Flexoelectricity
2.3. Non-Local Piezoelectricity Theory
3. Size-Dependent Properties of PNs
3.1. Electromechanical Coupling Behaviors of PNs
3.2. Bending, Vibration and Buckling Behaviors of PNs
3.3. Size-Dependent Dynamic Performance of PNs
4. Modeling of Piezoelectric Nanodevices
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Curie, J.; Curie, P. Development by pressure of polar electricity in hemihedral crystals with inclined faces. Bull. Soc. Min. France 1880, 3, 90. [Google Scholar]
- Heywang, W.; Lubitz, K.; Wersing, W. Piezoelectricity: Evolution and Future of a Technoloy; Springer: Berlin, Germany, 2008. [Google Scholar]
- Tadigadapa, S.; Materi, K. Piezoelectric MEMS sensors: State-of-the-art and perspectives. Meas. Sci. Technol. 2009, 20, 092001. [Google Scholar] [CrossRef]
- Eom, C.-B.; Trolier-McKinstry, S. Thin-film piezoelectric MEMS. MRS Bull. 2012, 37, 1007–1017. [Google Scholar] [CrossRef]
- Wang, Z.L.; Song, J.H. Piezoelectric nanogenerators based on zinc oxide nanowire arrays. Science 2006, 312, 242–246. [Google Scholar] [CrossRef] [PubMed]
- Capsal, J.F.; Dantras, E.; Dandurand, J.; Lacabanne, C. Molecular mobility in piezoelectric hybrid nanocomposites with 0–3 connectivity: Volume fraction influence. J. Non-Cryst. Solids 2011, 357, 3410–3415. [Google Scholar] [CrossRef]
- Chen, X.; Xu, S.; Yao, N.; Shi, Y. 1.6 V Nanogenerator for mechanical energy harvesting using PZT nanofibers. Nano Lett. 2010, 10, 2133–2137. [Google Scholar] [CrossRef] [PubMed]
- Alvine, K.J.; Shutthanandan, V.; Arey, B.W.; Wang, C.; Bennett, W.D.; Pitman, S.G. Pb nanowire formation on Al/lead zirconate titanate surfaces in high-pressure hydrogen. J. Appl. Phys. 2012, 112, 013533. [Google Scholar] [CrossRef]
- Qi, Y.; Jafferis, N.T.; Lyons, K.; Lee, C.M.; Ahmad, H.; McAlpine, M.C. Piezoelectric ribbons printed onto rubber for flexible energy conversion. Nano Lett. 2010, 10, 524–528. [Google Scholar] [CrossRef] [PubMed]
- Spanier, J.E.; Kolpak, A.M.; Urban, J.J.; Grinberg, I.; Ouyang, L.; Yun, W.S.; Rappe, A.M.; Park, H. Ferroelectric phase transition in individual single-crystalline BaTiO3 nanowires. Nano Lett. 2006, 6, 735–739. [Google Scholar] [CrossRef] [PubMed]
- Park, K.I.; Xu, S.; Liu, Y.; Hwang, G.T.; Kang, S.L.; Wang, Z.L.; Lee, K.J. Piezoelectric BaTiO3 thin film nanogenerator on plastic substrates. Nano Lett. 2010, 10, 4939–4943. [Google Scholar] [CrossRef] [PubMed]
- Scott, J.F. Applications of modern ferroelectrics. Science 2007, 315, 954–959. [Google Scholar] [CrossRef] [PubMed]
- Scott, J.F. Ferroelectric Memories; Springer: Berlin, Germany, 2000. [Google Scholar]
- Dodds, J.S.; Meyers, F.N.; Loh, K.J. Piezoelectric characterization of PVDF-TrFE thin films enhanced with ZnO nanoparticles. IEEE Sens. J. 2012, 12, 1889–1890. [Google Scholar] [CrossRef]
- Sun, Y.; Fuge, G.M.; Fox, N.A.; Riley, D.J.; Ashfold, M.N.R. Synthesis of aligned arrays of ultrathin ZnO nanotubes on a Si wafer coated with a thin ZnO film. Adv. Mater. 2005, 17, 2477–2481. [Google Scholar] [CrossRef]
- Wang, X.; Song, J.; Wang, Z.L. Nanowire and nanobelt arrays of zinc oxide from synthesis to properties and to novel devices. J. Mater. Chem. 2007, 17, 711–720. [Google Scholar] [CrossRef]
- Wang, W.Y.; Xu, Y.P.; Zhang, D.F.; Chen, X.L. Synthesis and dielectric properties of cubic GaN nanoparticles. Mater. Res. Bull. 2001, 36, 2155–2162. [Google Scholar] [CrossRef]
- Zhao, S.; Kibria, M.G.; Wang, Q.; Nguyen, H.P.T.; Mi, Z. Growth of large-scale vertically aligned GaN nanowires and their heterostructures with high uniformity on SiOx by catalyst-free molecular beam epitaxy. Nanoscale 2013, 5, 5283–5287. [Google Scholar] [CrossRef] [PubMed]
- Hemmingsson, C.; Pozina, G.; Khromov, S.; Monemar, B. Growth of GaN nanotubes by halide vapor phase epitaxy. Nanotechnology 2011, 22, 085602. [Google Scholar]
- Yu, R.M.; Dong, L.; Pan, C.F.; Niu, S.M.; Liu, H.F.; Liu, W.; Chua, S.J.; Chi, D.Z.; Wang, Z.L. Piezotronic effect on the transport properties of GaN nanobelts for active flexible electronics. Adv. Mater. 2012, 24, 3532–3537. [Google Scholar] [CrossRef] [PubMed]
- Johnson, J.C.; Choi, H.-J.; Knutsen, K.P.; Schaller, R.D.; Yang, P.D.; Saykally, R.J. Single gallium nitride nanowire lasers. Nat. Mater. 2002, 1, 106–110. [Google Scholar] [CrossRef] [PubMed]
- Bai, X.D.; Gao, P.X.; Wang, Z.L.; Wang, E.G. Dual-mode mechanical resonance of individual ZnO nanobelts. Appl. Phys. Lett. 2003, 82, 4806–4808. [Google Scholar] [CrossRef]
- Wang, X.D.; Zhou, J.; Song, J.H.; Liu, J.; Xu, N.S.; Wang, Z.L. Piezoelectric field effect transistor and nanoforce sensor based on a single ZnO nanowire. Nano Lett. 2006, 6, 2768–2772. [Google Scholar] [CrossRef] [PubMed]
- He, J.H.; Hsin, C.L.; Liu, J.; Chen, L.J.; Wang, Z.L. Piezoelectric gated diode of a single ZnO nanowire. Adv. Mater. 2007, 19, 781–784. [Google Scholar]
- Zhou, J.; Gu, Y.; Fei, P.; Mai, W.; Gao, Y.; Yang, R.; Bao, G.; Wang, Z.L. Flexible piezotronic strain sensor. Nano Lett. 2008, 8, 3035–3040. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Wei, Y.; Wang, Z.L. Strain-gated piezotronic logic nanodevices. Adv. Mater. 2010, 22, 4711–4715. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.; Qin, Y.; Xu, C.; Wei, Y.; Yang, R.; Wang, Z.L. Self-powered nanowire devices. Nat. Nanotechnol. 2010, 5, 366–373. [Google Scholar] [CrossRef] [PubMed]
- Boxberg, F.; Søndergaard, N.; Xu, H.Q. Photovoltaics with piezoelectric core-shell nanowires. Nano Lett. 2010, 10, 1108–1112. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.L. The new field of nanopiezotronics. Mater. Today 2007, 10, 20–28. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, C.Y.; Bowen, C. Piezoelectric effects and electromechanical theories at the nanoscale. Nanoscale 2014, 6, 13314. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.; Tran, V.H.; Wang, J.; Fuh, Y.-K.; Lin, L. Direct-write piezoelectric polymeric nanogenerator with high energy conversion efficiency. Nano Lett. 2010, 10, 726–731. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, R.; Peng, B.; Gdoutos, E.E.; Espinosa, H.D. Elasticity size effects in ZnO nanowires-a combined experimental-computational approch. Nano Lett. 2008, 8, 3668–3674. [Google Scholar] [CrossRef] [PubMed]
- Asthana, A.; Momeni, K.; Prasad, A.; Yap, Y.K.; Yassar, R.S. In situ observation of size-scale effects on the mechanical properties of ZnO nanowires. Nanotechnology 2011, 22, 265712. [Google Scholar] [CrossRef] [PubMed]
- Xu, F.; Qin, Q.; Mishra, A.; Gu, Y.; Zhu, Y. Mechanical properties of ZnO nanowires under different loading modes. Nano Res. 2010, 3, 271–280. [Google Scholar] [CrossRef]
- Zhao, M.-H.; Wang, Z.-L.; Mao, S.X. Piezoelectric characterization of individual zinc oxide nanobelt probed by piezoresponse force microscope. Nano Lett. 2004, 4, 587–590. [Google Scholar] [CrossRef]
- Morozovska, A.N.; Svechnikov, S.V.; Eliseev, E.A.; Kalinin, S.V. Extrinsic size effect in piezoresponse force microscopy of thin films. Phys. Rev. B 2007, 76, 054123. [Google Scholar] [CrossRef]
- Minary-Jolandan, M.; Bernal, R.A.; Kuljanishvili, I.; Parpoil, V.; Espinosa, H.D. Individual GaN nanowires exhibit strong piezoelectricity in 3D. Nano Lett. 2012, 12, 970–976. [Google Scholar] [CrossRef] [PubMed]
- Momeni, K.; Asthana, A.; Prasad, A.; Yap, Y.K.; Shahbazian-Yassar, R. Structural inhomogeneity and piezoelectric enhancement in ZnO nanobelts. Appl. Phys. A 2012, 109, 95–100. [Google Scholar] [CrossRef]
- Chen, H.; Shi, D.; Qi, J.; Wang, B. Electronic and mechanical properties of ZnS nanowires with different surface adsorptions. Physica E 2009, 42, 32–37. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Hong, J.W.; Liu, B.; Fang, D.N. Strain effect on ferroelectric behaviors of BaTiO3 nanowires: A molecular dynamics study. Nanotechnology 2010, 21, 015701. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, R.; Espinosa, H.D. Giant piezoelectric size effects in zinc oxide and gallium nitride nanowires. A first principles investigation. Nano Lett. 2011, 11, 786–790. [Google Scholar] [CrossRef] [PubMed]
- Momeni, K.; Odegard, G.M.; Yassar, R.S. Finite size effect on the piezoelectric properties of ZnO nanobelts: A molecular dynamics approach. Acta Mater. 2012, 60, 5117–5124. [Google Scholar] [CrossRef]
- Momeni, K.; Attariani, H. Electromechanical properties of 1D ZnO nanostructures: Nanopiezotronics building blocks, surface and size-scale effects. Phys. Chem. Chem. Phys. 2014, 16, 4522–4527. [Google Scholar] [CrossRef] [PubMed]
- Espinosa, H.D.; Bernal, R.A.; Minary-Jolandan, M. A review of mechanical and electromechanical properties of piezoelectric nanowires. Adv. Mater. 2012, 24, 4656–4675. [Google Scholar] [CrossRef] [PubMed]
- Rödel, J. Effective intrinsic linear properties of laminar piezoelectric composites and simple ferroelectric domain structures. Mech. Mater. 2007, 39, 302–325. [Google Scholar] [CrossRef]
- Shu, Y.C.; Bhattacharya, K. Domain patterns and macroscopic behaviour of ferroelectric materials. Philos. Mag. 2001, 81, 2021–2054. [Google Scholar] [CrossRef]
- Li, J.Y.; Liu, D. On ferroelectric crystals with engineered domain configurations. J. Mech. Phys. Solids 2004, 52, 1719–1742. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal Continuum Field Theories; Springer: New York, NY, USA, 2001. [Google Scholar]
- Streitz, F.H.; Cammarata, R.C.; Sieradzki, K. Surface-stress effects on elastic properties. I. Thin metal films. Phys. Rev. B 1994, 49, 10699–10706. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Murdoch, A.I. A continuum theory of elastic material surfaces. Arch. Ration. Mech. Anal. 1975, 57, 291–323. [Google Scholar] [CrossRef]
- Huang, G.Y.; Yu, S.W. Effect of surface piezoelectricity on the electromechanical behaviour of a piezoelectric ring. Phys. Status Solidi B 2006, 243, R22–R24. [Google Scholar] [CrossRef]
- Yan, Z.; Jiang, L.Y. Surface effects on the electromechanical coupling and bending behaviours of piezoelectric nanowires. J. Phys. D 2011, 44, 075404. [Google Scholar] [CrossRef]
- Yan, Z.; Jiang, L.Y. Surface effects on the electroelastic responses of a thin piezoelectric plate with nanoscale thickness. J. Phys. D 2012, 45, 255401. [Google Scholar] [CrossRef]
- Zhang, C.L.; Chen, W.Q.; Zhang, C. Two-dimensional theory of piezoelectric plates considering surface effect. Eur. J. Mech. A 2013, 41, 50–57. [Google Scholar] [CrossRef]
- Zhang, C.L.; Zhu, J.; Chen, W.Q.; Zhang, C. Two-dimensional theory of piezoelectric shells considering surface effect. Eur. J. Mech. A 2014, 43, 109–117. [Google Scholar] [CrossRef]
- Shen, S.P.; Hu, S.L. A theory of flexoelectricity with surface effect for elastic dielectrics. J. Mech. Phys. Solids 2010, 58, 665–677. [Google Scholar] [CrossRef]
- Chen, T.Y.; Chiu, M.S.; Weng, C.N. Derivation of the generalized Young–Laplace equation of curved interfaces in nanoscaled solids. J. Appl. Phys. 2006, 100, 074308. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Mao, S.; Yeh, Y.W.; Purohit, P.K.; McAlpine, M.C. Nanoscale exoelectricity. Adv. Mater. 2013, 25, 946–974. [Google Scholar] [CrossRef] [PubMed]
- Zubko, P.; Catalan, G.; Tagantsev, A.K. Flexoelectric effect in solids. Annu. Rev. Mater. Res. 2013, 43, 387–421. [Google Scholar] [CrossRef]
- Yudin, P.V.; Tagantsev, A.K. Fundamentals of flexoelectricity in solids. Nanotechnology 2013, 24, 432001. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.N.; Huang, W.B.; Zhang, S.J. Flexoelectric nano-generator: Materials, structures and devices. Nano Energy 2013, 2, 1079–1092. [Google Scholar] [CrossRef]
- Krichen, S.; Sharma, P. Flexoelectricity: A perspective on an unusual electromechanical coupling. J. Appl. Mech. 2016, 83, 030801. [Google Scholar] [CrossRef]
- Catalan, G.; Sinnamon, L.J.; Gregg, J.M. The effect of flexoelectricity on the dielectric properties of inhomogeneously strained ferroelectric thin films. J. Phys. Condens. Matter 2004, 16, 2253–2264. [Google Scholar] [CrossRef]
- Gu, Y.; Li, M.; Morozovska, A.N.; Wang, Y.; Eliseev, E.A.; Gopalan, V.; Chen, L.-Q. Flexoelectricity and ferroelectric domain wall structures: Phase-field modeling and DFT calculations. Phys. Rev. B 2014, 89, 174111. [Google Scholar] [CrossRef]
- Maranganti, R.; Sharma, N.D.; Sharma, P. Electromechanical coupling in nonpiezoelectric materials due to nanoscale non-local size effects: Green’s function solutions and embedded inclusions. Phys. Rev. B 2006, 74, 014110. [Google Scholar] [CrossRef]
- Mindlin, R.D. Polarization gradient in elastic dielectrics. Int. J. Solids Struct. 1968, 4, 637–642. [Google Scholar] [CrossRef]
- Hu, S.L.; Shen, S.P. Electric field gradient theory with surface effect for nano-dielectrics. CMC Comput. Mater. Contin. 2009, 13, 63–87. [Google Scholar]
- Lu, J.; Lv, J.; Liang, X.; Xu, M.; Shen, S.P. Improved approach to measure the direct flexoelectric coefficient of bulk polyvinylidene fluoride. J. Appl. Phys. 2016, 119, 094104. [Google Scholar] [CrossRef]
- Hong, J.W.; Catalan, G.; Scott, J.F.; Artacho, E. The flexoelectricity of barium and strontium titanates from first principles. J. Phys. Condens. Matter 2010, 22, 112201. [Google Scholar] [CrossRef] [PubMed]
- Le Quang, H.; He, Q.C. The number and types of all possible rotational symmetries for flexoelectric tensors. Proc. R. Soc. A 2011, 467, 2369–2386. [Google Scholar] [CrossRef]
- Shu, L.L.; Wei, X.Y.; Pang, T.; Yao, X.; Wang, C.L. Symmetry of flexoelectric coefficients in crystalline medium. J. Appl. Phys. 2011, 110, 104106. [Google Scholar] [CrossRef]
- Yan, Z.; Jiang, L.Y. Flexoelectric effect on the electroelastic responses of bending piezoelectric nanobeams. J. Appl. Phys. 2013, 113, 194102. [Google Scholar] [CrossRef]
- Yan, Z.; Jiang, L.Y. Size-dependent bending and vibration behaviour of piezoelectric nanobeams due to flexoelectricity. J. Phys. D 2013, 46, 355502. [Google Scholar] [CrossRef]
- Zhang, Z.R.; Yan, Z.; Jiang, L.Y. Flexoelectric effect on the electroelastic responses and vibrational behaviors of a piezoelectric nanoplate. J. Appl. Phys. 2014, 116, 014307. [Google Scholar] [CrossRef]
- Yurkov, A.S. Elastic boundary conditions in the presence of the flexoelectric effect. JETP Lett. 2011, 94, 455–458. [Google Scholar] [CrossRef]
- Yan, Z.; Jiang, L.Y. Effect of flexoelectricity on the electroelastic fields of a hollow piezoelectric nanocylinder. Smart Mater. Struct. 2015, 24, 065003. [Google Scholar] [CrossRef]
- Deng, Q.; Liu, L.P.; Sharma, P. Flexoelectricity in soft materials and biological membranes. J. Mech. Phys. Solids 2014, 62, 209–227. [Google Scholar] [CrossRef]
- Altan, B.S.; Aifantis, E.C. On some aspects in the special theory of gradient elasticity. J. Mech. Behav. Mater. 1997, 8, 231–282. [Google Scholar] [CrossRef]
- Eringen, A.C. Linear theory of micropolar elasticity. J. Math. Mech. 1966, 15, 909–923. [Google Scholar]
- Mindlin, R.D.; Tiersten, H.F. Effects of couple-stresses in linear elasticity. Arch. Ration. Mech. Anal. 1962, 11, 415–448. [Google Scholar] [CrossRef]
- Toupin, R.A. Elastic materials with couple-stresses. Arch. Ration. Mech. Anal. 1962, 11, 385–414. [Google Scholar] [CrossRef]
- Yang, F.; Chong, A.C.M.; Lam, D.C.C.; Tong, P. Couple stress based strain gradient theory for elasticity. Int. J. Solids Struct. 2002, 39, 2731–2743. [Google Scholar] [CrossRef]
- Zhou, Z.G.; Wang, B. The scattering of harmonic elastic anti-plane shear waves by a Griffith crack in a piezoelectric material plane by using the non-local theory. Int. J. Eng. Sci. 2002, 40, 303–317. [Google Scholar] [CrossRef]
- Wang, K.F.; Wang, B.L. The electromechanical coupling behavior of piezoelectric nanowires: Surface and small-scale effects. EPL Europhys. Lett. 2012, 97, 66005. [Google Scholar] [CrossRef]
- Liang, X.; Hu, S.L.; Shen, S.P. Effects of surface and flexoelectricity on a piezoelectric nanobeam. Smart Mater. Struct. 2014, 23, 035020. [Google Scholar] [CrossRef]
- Majdoub, M.S.; Sharma, P.; Cagin, T. Enhanced size-dependent piezoelectricity and elasticity in nanostructures due to the flexoelectric effect. Phys. Rev. B 2008, 77, 125424. [Google Scholar] [CrossRef]
- Yan, Z.; Jiang, L.Y. Electromechanical response of a curved piezoelectric nanobeam with the consideration of surface effects. J. Phys. D 2011, 44, 365301. [Google Scholar] [CrossRef]
- Liu, C.C.; Hu, S.L.; Shen, S.P. Effect of flexoelectricity on electrostatic potential in a bent piezoelectric nanowire. Smart Mater. Struct. 2012, 21, 115024. [Google Scholar] [CrossRef]
- Wang, G.F.; Feng, X.Q. Effect of surface stresses on the vibration and buckling of piezoelectric nanowires. EPL Europhys. Lett. 2010, 91, 56007. [Google Scholar] [CrossRef]
- Yan, Z.; Jiang, L.Y. The vibrational and buckling behaviors of piezoelectric nanobeams with surface effects. Nanotechnology 2011, 22, 245703. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.H.; Fang, B.; Zhang, J.H.; Song, J.Z. Surface effects on the wrinkling of piezoelectric films on compliant substrates. J. Appl. Phys. 2011, 110, 114303. [Google Scholar] [CrossRef]
- Yan, Z.; Jiang, L.Y. Vibration and buckling analysis of a piezoelectric nanoplate considering surface effects and in-plane constraints. Proc. R. Soc. A 2012, 468, 3458–3475. [Google Scholar] [CrossRef]
- Yan, Z.; Jiang, L.Y. Surface effects on the vibration and buckling of piezoelectric nanoplates. EPL Europhys. Lett. 2012, 99, 27007. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, C.Y. Vibrating piezoelectric nanofilms as sandwich nanoplates. J. Appl. Phys. 2012, 111, 094303. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, C.; Chen, W. Surface and piezoelectric effects on the buckling of piezoelectric nanofilms due to mechanical loads. Meccanica 2014, 49, 181–189. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, C.Y.; Adhikari, S. Surface effect on the bucklng of piezoelectric nanofilms. J. Phys. D 2012, 45, 285301. [Google Scholar] [CrossRef]
- Xu, X.-J.; Deng, Z.C.; Wang, B. Closed solutions for the electromechanical bending and vibration of thick piezoelectric nanobeams with surface effects. J. Phys. D 2013, 46, 405302. [Google Scholar] [CrossRef]
- Yang, W.J.; Liang, X.; Shen, S.P. Electromechanical responses of piezoelectric nanoplates with flexoelectricity. Acta Mech. 2015, 226, 3097–3110. [Google Scholar] [CrossRef]
- Liang, X.; Yang, W.J.; Hu, S.L.; Shen, S.P. Buckling and vibration of flexoelectric nanofilms subjected to mechanical loads. J. Phys. D 2016, 49, 115307. [Google Scholar] [CrossRef]
- Ke, L.L.; Wang, Y.S. Thermoelectric-mechanical vibration of piezoelectric nanobeams based on the non-local theory. Smart Mater. Struct. 2012, 21, 025018. [Google Scholar] [CrossRef]
- Ke, L.L.; Wang, Y.S.; Wang, Z.D. Nonlinear vibration of the piezoelectric nanobeams based on the non-local theory. Compos. Struct. 2012, 94, 2038–2047. [Google Scholar] [CrossRef]
- Liu, C.; Ke, L.L.; Wang, Y.S.; Yang, J.; Kitipornchai, S. Thermo-electro-mechanical vibration of piezoelectric nanoplates based on the non-local theory. Compos. Struct. 2013, 106, 167–174. [Google Scholar] [CrossRef]
- Zhang, Z.R.; Jiang, L.Y. Size effects on electromechanical coupling fields of a bending piezoelectric nanoplate due to surface effects and flexoelectricity. J. Appl. Phys. 2014, 116, 134308. [Google Scholar] [CrossRef]
- Yan, Z. Size-dependent bending and vibration behaviors of piezoelectric circular nanoplates. Smart Mater. Struct. 2016, 25, 035017. [Google Scholar] [CrossRef]
- Ray, M.C. Exact solutions for flexoelectric response in nanostructures. J. Appl. Mech. 2014, 81, 091002. [Google Scholar] [CrossRef]
- Ray, M.C. Analysis of smart nanobeams integrated with a flexoelectric nano actuator layer. Smart Mater. Struct. 2016, 25, 055011. [Google Scholar] [CrossRef]
- Li, A.Q.; Zhou, S.J.; Zhou, S.S.; Wang, B.L. Size-dependent analysis of a three-layer microbeam including electromechanical coupling. Compos. Struct. 2014, 116, 120–127. [Google Scholar] [CrossRef]
- Hadjesfandiari, A.R. Size-dependent piezoelectricity. Int. J. Solids Struct. 2013, 50, 2781–2791. [Google Scholar] [CrossRef]
- Li, A.Q.; Zhou, S.J.; Qi, L.; Chen, X. A reformulated flexoelectric theory for isotropic dielectrics. J. Phys. D 2015, 48, 465502. [Google Scholar] [CrossRef]
- Mao, S.; Purohit, P.K. Insights into flexoelectric solids from strain-gradient elasticity. J. Appl. Mech. 2014, 81, 081004. [Google Scholar] [CrossRef]
- Yan, Z. Exact solutions for the electromechanical responses of a dielectric nanoring. J. Intell. Mater. Syst. Struct. 2016. [Google Scholar] [CrossRef]
- Wang, J.-S.; Cui, Y.-H.; Feng, X.-Q.; Wang, G.-F.; Qin, Q.-H. Surface effects on the elasticity of nanosprings. EPL Europhys. Lett. 2010, 92, 16002. [Google Scholar] [CrossRef]
- Wang, J.-S.; Ye, H.-M.; Qin, Q.-H.; Xu, J.; Feng, X.-Q. Anisotropic surface effects on the formation of chiral morphologies of nanomaterials. Proc. R. Soc. A 2012, 468, 609–633. [Google Scholar] [CrossRef]
- Wang, J.-S.; Shimada, T.; Wang, G.-F.; Kitamura, T. Effects of chirality and surface stresses on the bending and buckling of chiral nanowires. J. Phys. D 2014, 47, 015302. [Google Scholar] [CrossRef]
- Chen, W.Q. Surface effect on Bleustein–Gulyaev wave in a piezoelectric half-space. Theor. Appl. Mech. Lett. 2011, 1, 041001. [Google Scholar] [CrossRef]
- Zhang, C.L.; Chen, W.Q.; Zhang, C. On propagation of anti-plane shear waves in piezoelectric plates with surface effect. Phys. Lett. A 2012, 376, 3281–3286. [Google Scholar] [CrossRef]
- Zhang, L.L.; Liu, J.X.; Fang, X.Q.; Nie, G.Q. Effects of surface piezoelectricity and non-local scale on wave propagation in piezoelectric nanoplates. Eur. J. Mech. A 2014, 46, 22–29. [Google Scholar] [CrossRef]
- Fang, X.Q.; Yang, Q.; Liu, J.X.; Feng, W.J. Surface/interface effect around a piezoelectric nano-particle in a polymer matrix under compressive waves. Appl. Phys. Lett. 2012, 100, 151602. [Google Scholar] [CrossRef]
- Fang, X.Q.; Liu, J.X.; Huang, M.-J. Effect of interface energy on effective dynamic properties of piezoelectric medium with randomly distributed piezoelectric nano-fibers. J. Appl. Phys. 2012, 112, 094311. [Google Scholar] [CrossRef]
- Zhang, C.L.; Zhang, C.; Chen, W.Q. Modeling of piezoelectric bimorph nano-actuators with surface effects. J. Appl. Mech. 2013, 80, 061015. [Google Scholar] [CrossRef]
- Fan, T.; Yang, L. Surface effect on nano piezoelectric energy harvester based on flexural mode. Polym. Compos. 2016. [Google Scholar] [CrossRef]
- Wang, K.F.; Wang, B.L. Surface effects on the energy-generating performance of piezoelectric circular nanomembrane energy harvesters under pressure loading. EPL Europhys. Lett. 2014, 108, 17001. [Google Scholar] [CrossRef]
- Deng, Q.; Kammoun, M.; Erturk, A.; Sharma, P. Nanoscale flexoelectric energy harvesting. Int. J. Solids Struct. 2014, 51, 3218–3225. [Google Scholar] [CrossRef]
- Wang, K.F.; Wang, B.L. An analytical model for nanoscale unimorph piezoelectric energy harvesters with flexoelectric effect. Compos. Struct. 2016, 153, 253–261. [Google Scholar] [CrossRef]
- Momeni, K.; Odegard, G.M.; Yassar, R.S. Nanocomposite electrical generator based on piezoelectric zinc oxide nanowires. J. Appl. Phys. 2010, 108, 114303. [Google Scholar] [CrossRef]
- Momeni, K.; Mortazavi, S.M.Z. Optimal aspect ratio of zinc oxide nanowires for a nanocomposite electrical generator. J. Comput. Theor. Nanosci. 2012, 9, 1670–1674. [Google Scholar] [CrossRef]
- Momeni, K. A multiscale approach to nanocomposite electrical generators. Nano Energy 2014, 4, 132–139. [Google Scholar] [CrossRef]
| Theories | Size-Dependent Properties | Materials | References |
|---|---|---|---|
| SPT | EMC fields | PZT-5H | [51,52,53,87] |
| SPT | bending | PZT-5H | [52,53,97] |
| SPT | vibration | PZT-5H | [54,55,90,92,93,94,97] |
| SPT | buckling | PZT-5H | [53,90,92,93,95,96] |
| SPT | wrinkling | PZT-5H | [91] |
| SPT | wave propagation | PZT-4 | [115] |
| SPT | wave propagation | PZT-5 | [116] |
| SPT | dynamic characteristics | PZT-4 | [118] |
| SPT | dynamic characteristics | CoFeO/BaTiO | [119] |
| TF | EMC fields | ZnO | [88] |
| TF | EMC fields | BaTiO | [72,74,76] |
| TF | bending | BaTiO | [72,73,74] |
| TF | vibration | BaTiO | [73,74] |
| TF | bending and vibration | PZT-5H | [98] |
| TF | buckling and vibration | Pb(MgNbO) | [99] |
| NPT | vibration | PZT-4 | [100,101,102] |
| SPT and NPT | EMC fields | PZT-5H | [84] |
| SPT and NPT | wave propagation | PZT-5H | [117] |
| SPT and TF | bending | PZT-5H | [85,104] |
| SPT and TF | vibration | PZT-5H | [104] |
| SPT and TF | bending and vibration | BaTiO | [103] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Z.; Jiang, L. Modified Continuum Mechanics Modeling on Size-Dependent Properties of Piezoelectric Nanomaterials: A Review. Nanomaterials 2017, 7, 27. https://doi.org/10.3390/nano7020027
Yan Z, Jiang L. Modified Continuum Mechanics Modeling on Size-Dependent Properties of Piezoelectric Nanomaterials: A Review. Nanomaterials. 2017; 7(2):27. https://doi.org/10.3390/nano7020027
Chicago/Turabian StyleYan, Zhi, and Liying Jiang. 2017. "Modified Continuum Mechanics Modeling on Size-Dependent Properties of Piezoelectric Nanomaterials: A Review" Nanomaterials 7, no. 2: 27. https://doi.org/10.3390/nano7020027
APA StyleYan, Z., & Jiang, L. (2017). Modified Continuum Mechanics Modeling on Size-Dependent Properties of Piezoelectric Nanomaterials: A Review. Nanomaterials, 7(2), 27. https://doi.org/10.3390/nano7020027





