Vibration of Piezoelectric ZnO-SWCNT Nanowires
Abstract
:1. Introduction
2. Methodology
3. Results and Discussions
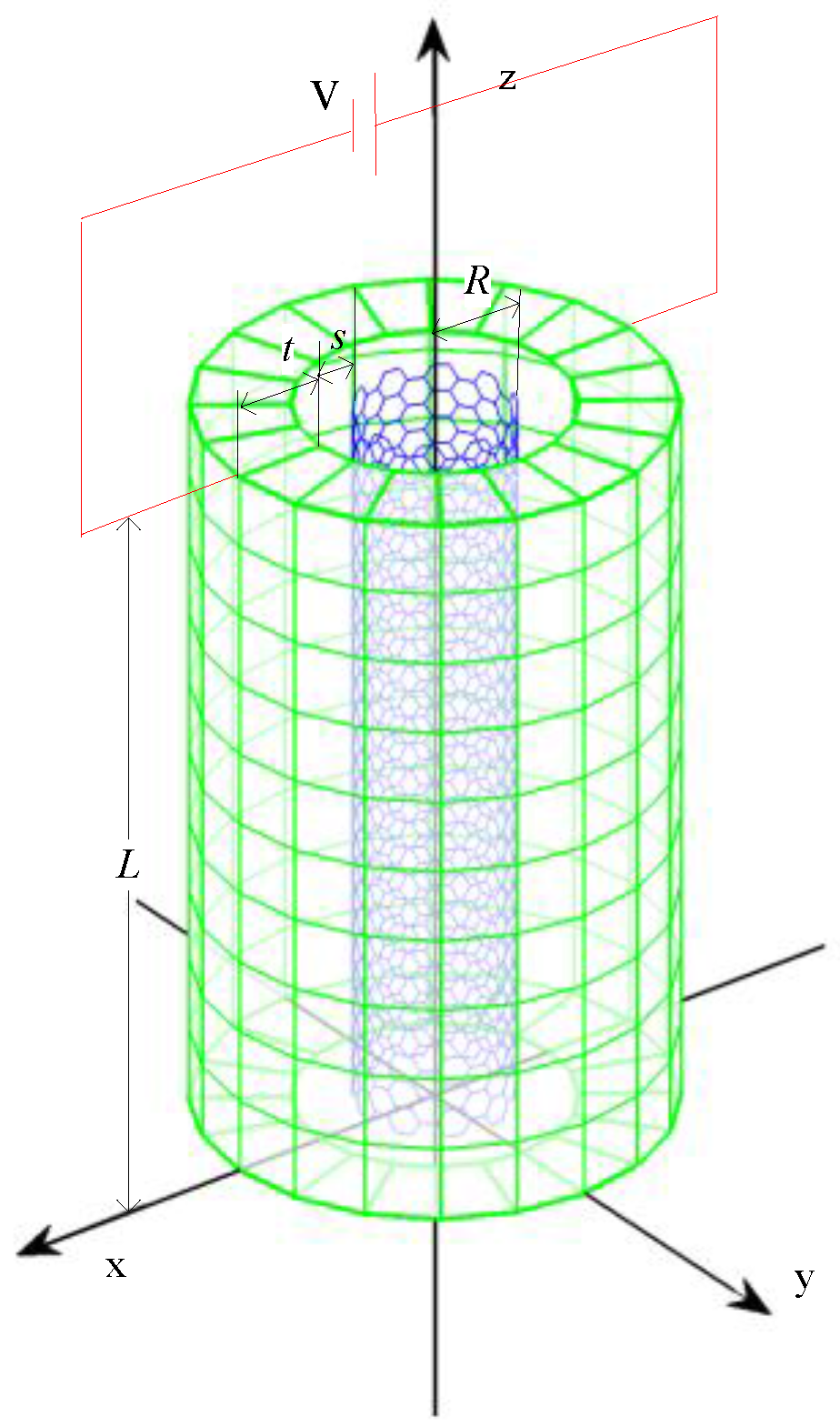
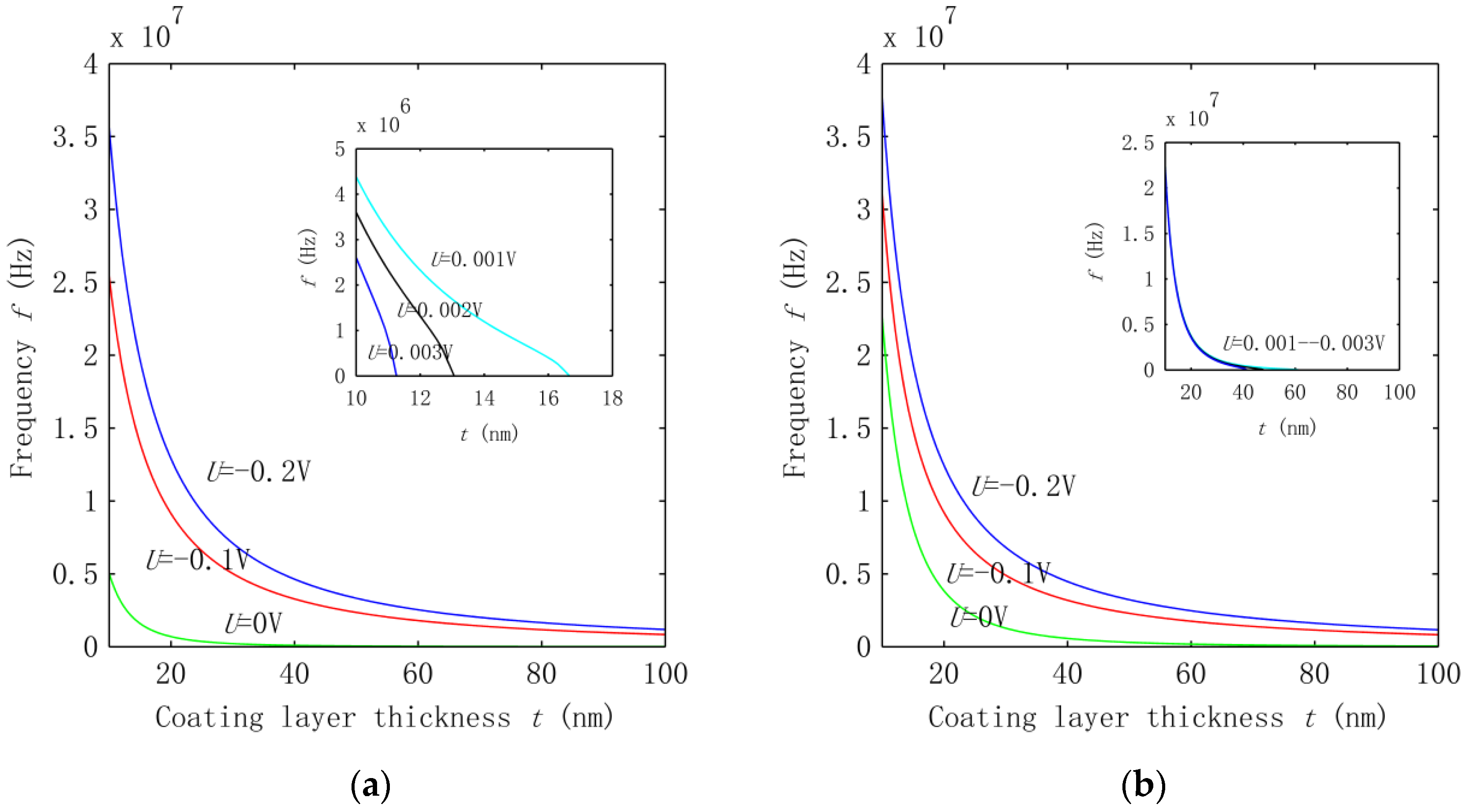
3.1. Influence of the Piezoelectric Effect
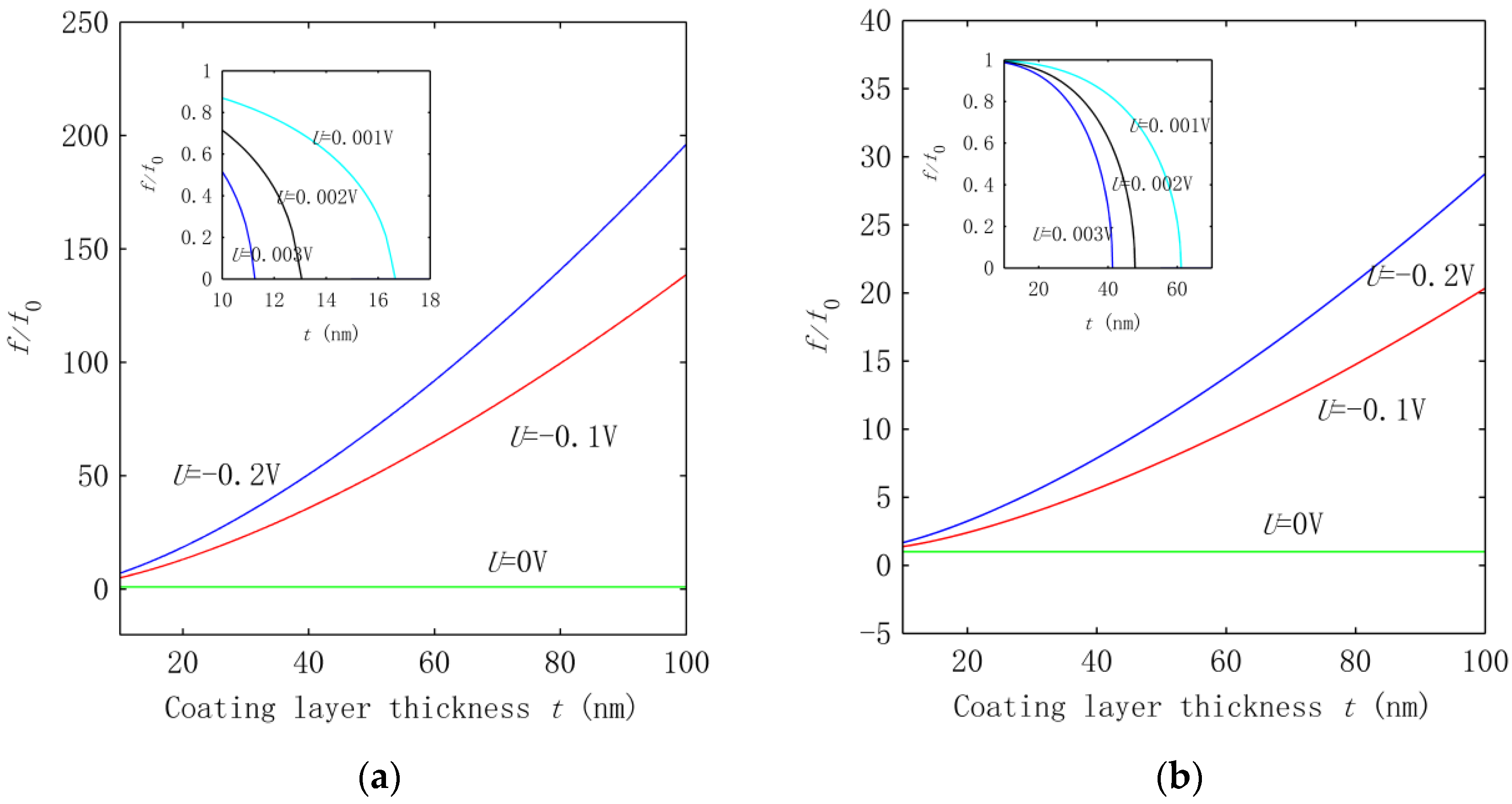
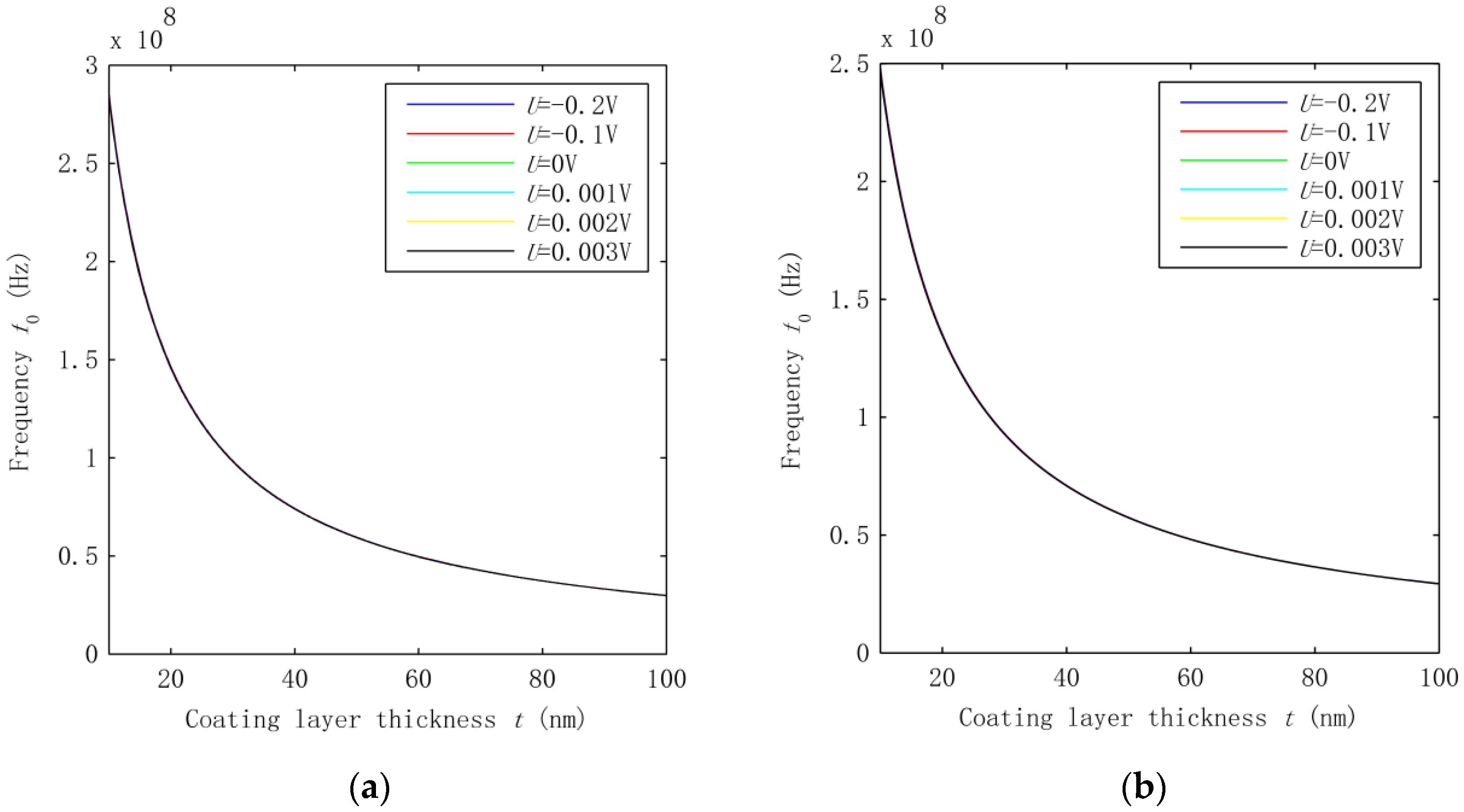
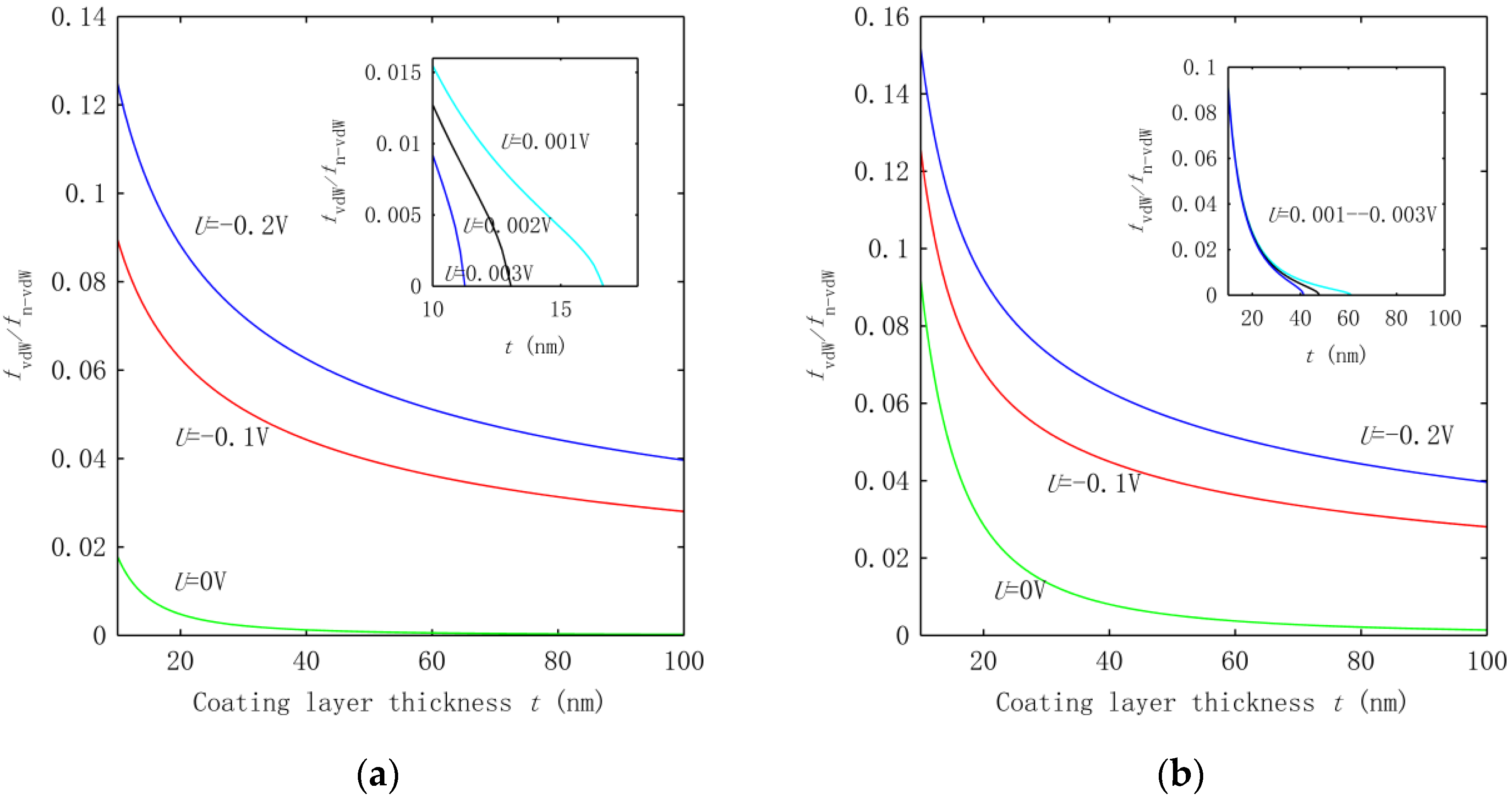
3.2. Effect of Interphase VdW Interaction
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Huang, L.; Lau, S.P.; Yang, H.Y.; Leong, E.S.P.; Yu, S.F. Stable superhydrophobic surface via carbon nanotubes coated with a ZnO thin film. J. Phys. Chem. B 2005, 109, 7746–7748. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Lau, S.P.; Yang, H.Y.; Yu, S.F. Local measurement of secondary electron emission from ZnO-coated carbon nanotubes. Nanotechnology 2006, 17, 1564–1567. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.C.; Lin, B.T.T.; Chu, G.; Tobias, S.; Sahakalkan, S.; Roth, M.L.; Green, H.; Chen, S.Y. Electron transport behavior of individual zinc oxide coated single-walled carbon nanotubes. Nanotechnology 2009, 20, 105703. [Google Scholar] [CrossRef] [PubMed]
- Ma, W.; Tian, D.B. Direct electron transfer and electrocatalysis of hemoglobin in ZnO coated multiwalled carbon nanotubes and Nafion composite matrix. Bioelectrochemistry 2010, 78, 106–112. [Google Scholar] [CrossRef] [PubMed]
- Hu, C.J.; Lin, Y.H.; Tang, C.W.; Tsai, M.Y.; Hsu, W.K.; Kou, H.F. ZnO-Coated Carbon Nanotubes: Flexible Piezoelectric Generators. Adv. Mat. 2011, 23, 2941–2945. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.Y.; Yu, S.W. Effect of surface piezoelectricity on the electromechanical behaviour of a piezoelectric ring. Phys. Status Solidi 2006, 243, R22–R24. [Google Scholar] [CrossRef]
- Yan, Z.; Jiang, L.Y. Surface effects on the electromechanical coupling and bending behaviours of piezoelectric nanowires. J. Phys. D 2011, 44, 075404. [Google Scholar] [CrossRef]
- Yan, Z.; Jiang, L.Y. The vibrational and buckling behaviors of piezoelectric nanobeams with surface effects. Nanotechnology 2011, 22, 245703. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.H.; Fang, B.; Zhang, J.Z.; Song, J.Z. Surface effects on the wrinkling of piezoelectric films on compliant substrates. J. Appl. Phys. 2011, 110, 114303. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, R.; Wang, C.Y. Piezoelectric ZnO-CNT nanotubes under axial strain and electrical voltage. Physica E 2012, 46, 105–112. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, C.Y.; Adhikari, S. Surface effect on the buckling of piezoelectric nanofilms. J. Phys. D 2012, 45, 285301. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, C.Y. Vibrating piezoelectric nanofilms as sandwich nanoplates. J. Appl. Phys. 2012, 111, 094303. [Google Scholar] [CrossRef]
- Jiang, L.Y.; Huang, Y.; Jiang, H.; Ravichandran, G.; Gao, H.; Hwang, K.C.; Liu, B. A cohesive law for carbon nanotube/polymer interfaces based on the van der Waals force. J. Mech. Phys. Solids 2006, 54, 2436–2452. [Google Scholar] [CrossRef]
- Tan, H.; Jiang, L.Y.; Huang, Y.; Liu, B.; Hwang, K.C. The effect of van der Waals-based interface cohesive law on carbon nanotube-reinforced composite materials. Comps. Sci. Technol. 2007, 67, 2941–2946. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Zhao, J.H.; Jia, Y.; Mabrouki, T.; Gong, Y.D.; Wei, N.; Rabczuk, T. An analytical solution on interface debonding for large diameter carbon nanotube-reinforced composite with functionally graded variation interphase. Compos. Struc. 2013, 104, 261–269. [Google Scholar] [CrossRef]
- Zhao, J.H.; Jiang, J.W.; Jia, Y.; Guo, W.L.; Rabczuk, T. A theoretical analysis of cohesive energy between carbon nanotubes, graphene and substrates. Carbon 2013, 57, 108–119. [Google Scholar] [CrossRef]
- Zhao, J.H.; Lu, L.X.; Zhang, Z.L.; Guo, W.L.; Rabczuk, T. Continuum modeling of the cohesive energy for the interfaces between films, spheres, coats and substrates. Comp. Mater. Sci. 2015, 96, 432–438. [Google Scholar] [CrossRef]
- Aran, R.; Rinaldi, A.; Notargiacomo, A.; Bini, F.; Marinozzi, F.; Pea, M.; Lovat, G.; Celozzi, S. Effect of the Scaling of the Mechanical Properties on the Performances of ZnO Piezo-Semiconductive Nanowires. In AIP Conference Proceedings, Proceedings of the Nanoforum 2013, Rome, Italy, 18–20 September 13; American Institute of Physics Inc.: College Park, MD, USA, 2014. [Google Scholar]
- Fang, J.H. Multiscale Analysis for Deformation and Failure of Material; John Wiley & Sons Ltd.: West Sussex, UK, 2010. [Google Scholar]
- Wang, C.Y.; Ru, C.Q.; Mioduchowski, A. Axisymmetric and beamlike vibrations of multiwall carbon nanotubes. Phys. Rev. B 2005, 72, 075414. [Google Scholar] [CrossRef]
- Wang, C.Y.; Ru, C.Q.; Mioduchowski, A. Free vibration of multiwall carbon nanotubes. J. Appl. Phys. B 2005, 97, 114323. [Google Scholar] [CrossRef]
- Wang, C.Y.; Adhikari, S. ZnO-CNT composite nanotubes as nanoresonators. Phys. Lett. A 2011, 375, 2171–2175. [Google Scholar] [CrossRef]
- Batra, R.C.; Gupta, S.S. Wall thickness and radial breathing modes of single-walled carbon nanotubes. J. Appl. Mech. 2008, 75, 061010. [Google Scholar] [CrossRef]
- Wang, C.Y.; Zhang, L.C. A critical assessment of the elastic properties and effective wall thickness of single-walled carbon nanotubes. Nanotechnology 2008, 19, 075705. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.Y.; Zhang, L.C. An elastic shell model for characterizing single-walled carbon nanotubes. Nanotechnology 2008, 19, 195704. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Y.; Wang, C.; Feng, Y. Vibration of Piezoelectric ZnO-SWCNT Nanowires. Nanomaterials 2016, 6, 242. https://doi.org/10.3390/nano6120242
Xiao Y, Wang C, Feng Y. Vibration of Piezoelectric ZnO-SWCNT Nanowires. Nanomaterials. 2016; 6(12):242. https://doi.org/10.3390/nano6120242
Chicago/Turabian StyleXiao, Yao, Chengyuan Wang, and Yuantian Feng. 2016. "Vibration of Piezoelectric ZnO-SWCNT Nanowires" Nanomaterials 6, no. 12: 242. https://doi.org/10.3390/nano6120242
APA StyleXiao, Y., Wang, C., & Feng, Y. (2016). Vibration of Piezoelectric ZnO-SWCNT Nanowires. Nanomaterials, 6(12), 242. https://doi.org/10.3390/nano6120242





