Strain Engineering of Anisotropic Electronic, Transport, and Photoelectric Properties in Monolayer Sn₂Se₂P₄

Abstract

In this study, we demonstrate that the Sn₂Se₂P₄ monolayer exhibits intrinsic anisotropic electronic characteristics with the strain-synergistic modulation of carrier transport and optoelectronic properties, as revealed by various levels of density functional theory calculations combined with the non-equilibrium Green’s function method. The calculations reveal that a-axis uniaxial compression of the Sn₂Se₂P₄ monolayer induces an indirect-to-direct bandgap transition (from 1.73 eV to 0.97 eV, as calculated by HSE06), reduces the hole effective mass by ≥70%, and amplifies current density by 684%. Conversely, a-axis uniaxial expansion (+8%) boosts ballistic transport (a/b-axis current ratio > 10⁵), rivaling black phosphorus. Notably, a striking negative differential conductance arises with the maximum I_peak/I_valley in the order of 10⁵ under the 2% uniaxial compression along the b-axis of the Sn₂Se₂P₄ monolayer. Visible-range anisotropic absorption coefficients (~10⁵ cm⁻¹) are achieved, where −4% a-axis strain elevates the photocurrent density (6.27 μA mm⁻² at 2.45 eV) and external quantum efficiency (39.2%) beyond many 2D materials benchmarks. Non-monotonic strain-dependent photocurrent density peaks at 2.00 eV correlate with hole effective mass reduction patterns, confirming the carrier mobility of the Sn₂Se₂P₄ monolayer as the governing parameter for photogenerated charge separation. These results establish Sn₂Se₂P₄ as a multifunctional material enabling strain-tailored anisotropy for logic transistors, negative differential resistors, and photovoltaic devices, while guiding future investigations on environmental stabilization and heterostructure integration toward practical applications.

1. Introduction

The rapid development of integrated circuits has driven the continuous demand for performance enhancement in electronic devices, positioning two-dimensional (2D) semiconductors as promising candidates for applications in field-effect transistors (FETs) and photoelectric conversion systems [1,2,3,4,5,6,7,8]. However, critical limitations persist in existing 2D materials: transition metal dichalcogenides (TMDs) like MoS₂ and ReS₂ suffer from restricted carrier mobility [9,10,11,12], while high-mobility phosphorenes (e.g., black phosphorus and violet phosphorus) exhibit poor environmental stability due to oxidation susceptibility [13,14,15]. Furthermore, the narrow band gap of materials such as silicene and germanene increases heat loss and reduces energy conversion efficiency [16,17]. To address these challenges, it is essential not only to explore novel 2D materials through density functional theory (DFT) computational simulations but also to develop property-modification strategies like strain engineering, doping, and van der Waals heterostructure construction [18,19].

As a particularly effective approach, strain engineering enables the precise modulation of electronic structures in 2D materials owing to their exceptional mechanical flexibility. Appropriate mechanical strain enables the precise modulation of bandgap magnitude, bandgap type, and band curvature in two-dimensional materials. This strain engineering strategy allows the bandgap range to be tuned to 0.77–1.19 eV for optimal channel material performance in electronic devices or 1.1–1.6 eV for photovoltaic applications [20,21,22]. Hence, the controlled manipulation of band structures holds promise for enhancing electronic transport and optoelectronic characteristics in functional devices. This capability has been successfully demonstrated in graphene, hexagonal boron nitride (hBN), TMDs, and MXenes, opening new avenues for designing high-performance nanodevices [23,24,25,26,27].

Recent attention has been focused on a novel family of ternary 2D materials with puckered honeycomb structures—triphosphides and triarsenides (general formula AX₃, where A = P/As and X = group II/XIII/XIV/XV elements) [28,29,30,31]. Two-dimensional triarsenides (CaAs₃, GeAs₃) demonstrate exceptional carrier mobility exceeding ~3 × 10⁴ cm² V⁻¹ s⁻¹ [28,32], while their triphosphide counterparts (GeP₃, SnP₃) are renowned for their high optical absorption coefficients (~10⁵ cm⁻¹) across the visible-to-infrared spectrum [30,33]. To expand this material family beyond conventional stoichiometries, recent theoretical studies have proposed structural derivatives through unit cell doubling and selective chalcogen substitution, leading to the prediction of Ge₂S₂P₄ and Sn₂S₂P₄ monolayers with exceptional photocatalytic water-splitting capabilities [34,35].

Particularly noteworthy is the high-performance two-dimensional monolayer (ML) Sn₂Se₂P₄ predicted by Trung et al., exhibiting phonon-dispersion-validated dynamic stability and ultra-high anisotropic mobility properties [36]. An ab initio molecular dynamics (AIMD) simulation was employed to heat the Sn₂Se₂P₄ monolayer at 500 K for 10 ps, showing sufficient thermal stability. As determined by the Perdew–Burke–Ernzerhof (PBE) calculations, the Sn₂Se₂P₄ monolayer exhibits an indirect bandgap of 1.04 eV, which decreases and transitions to a direct bandgap under biaxial compressive strain. Remarkably, this material demonstrates an outstanding carrier transport performance, with electron and hole mobilities reaching 5.4 × 10³ cm² V⁻¹ s⁻¹ and an extraordinary 7.4 × 10⁴ cm² V⁻¹ s⁻¹, respectively. These superior properties position Sn₂Se₂P₄ as a promising candidate for next-generation electronic and optoelectronic devices. While existing studies have primarily investigated the effects of biaxial strain on this material, the comprehensive modulation of electrical transport and optoelectronic properties in Sn₂Se₂P₄ through uniaxial strain—a more flexible and controllable tuning strategy—remain systematically underexplored. Notably, whether uniaxial strain can effectively modulate the bandgap of Sn₂Se₂P₄ into the optimal range for optoelectronic devices while preserving or even enhancing its exceptional carrier mobility remains an open question. Motivated by the pivotal role of strain engineering in optimizing the performance of two-dimensional (2D) materials, we systematically investigate the electronic structure, carrier transport properties, and optoelectronics characteristics of Sn₂Se₂P₄ monolayers under uniaxial strain, aiming to establish a strain-dependent framework for multifunctional device design.

In this work, we systematically investigate the strain-tunable anisotropic properties of orthorhombic Sn₂Se₂P₄ monolayers through first-principles calculations. Our density functional theory (DFT) analysis reveals the following: (1) direction-dependent bandgap engineering from indirect to direct transitions under uniaxial compression along the a-axis; (2) strain-modulated effective mass reductions (holes under a-axis compression) correlated with enhanced transport properties; (3) non-equilibrium Green’s function (NEGF) calculations demonstrating anisotropic current–voltage characteristics with current ratios exceeding 10⁵ and strain-enhanced negative differential conductance (NDC) effects; and (4) optoelectronic property optimization under specific strain conditions, achieving an external quantum efficiency (39.2%) and photocurrent density (6.27 μA mm⁻²) surpassing conventional photovoltaic materials. These findings establish Sn₂Se₂P₄ as a versatile platform for developing strain-engineered nanoelectronic and optoelectronic devices.

2. Calculational Methods

2.1. Details of Structural Optimization and Electronic Structure

The geometric optimization and electronic properties of the Sn₂Se₂P₄ monolayer were calculated using density functional theory (DFT) implemented in the QuantumATK software (ver. S-2021.06) [37,38]. The Perdew–Burke–Ernzerhof (PBE) formulation of the generalized gradient approximation (GGA) was employed in conjunction with the linear combination of atomic orbitals (LCAO) method [39]. The PseuDodojo pseudopotential was adopted to replace the atomic all-electron potential [40], while the medium-precision numerical basis was used for the wave function expansion. A real-space density mesh cutoff of 105 Hartree was applied, and the first Brillouin zone of Sn₂Se₂P₄ was sampled with a 4 × 3 × 1 k-point grid. Structural optimization convergence was achieved when the maximum force on each atom decreased below 0.001 eV Å⁻¹. A vacuum spacing of 25 Å was implemented along the non-periodic direction to eliminate interlayer interactions. To enhance the accuracy of bandgap results, the Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional was subsequently employed [41].

2.2. The Calculational Method for Carrier Transport Properties

We employed the NEGF method based on DFT to calculate the carrier transport properties [42,43]. In DFT calculations, again, the PBE functional with the LCAO method and PseuDodojo pseudopotentials were utilized for calculating the carrier transport. For current–voltage (I−V) characteristic calculations, Brillouin zone sampling was implemented with k-grid configurations of 1 × 3 × 132 and 4 × 1 × 76 along the a-axis and b-axis directions, respectively. The I−V characteristics of the two-probe system were subsequently derived through Landauer–Büttiker formalism [44]:

$$I\left(V_{\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}}\right)={\displaystyle \frac{2e}{h}}\int T\left(E,{\epsilon }_{\mathrm{L}},{\epsilon }_{\mathrm{R}}\right)\times \left[f_{\mathrm{R}}\left(E,{\epsilon }_{\mathrm{R}}\right)-f_{\mathrm{L}}\left(E,{\epsilon }_{\mathrm{L}}\right)\right]dE$$

(1)

where $V_{\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}}$ represents the bias voltage added to both sides of the electrodes and is defined as $e{V}_{\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}}={\epsilon }_{\mathrm{R}}-{\epsilon }_{\mathrm{L}}$. The Fermi energy levels of the left and right electrodes are denoted as ${\epsilon }_{\mathrm{L}}$ and ${\epsilon }_{\mathrm{R}}$, respectively. E represents the electrons. T is the carrier transport coefficient, and the Fermi Dirac distribution of the left and right electrodes are denoted as $f_{\mathrm{L}}(E,{\epsilon }_{\mathrm{L}})$ and $f_{\mathrm{R}}(E,{\epsilon }_{\mathrm{R}})$, respectively.

2.3. Calculational Method for Photocurrent

The photocurrent density (J_ph) was calculated through the integration of NEGF methodology within the first-order perturbation theory framework, based on the first-born approximation [45,46]. The perturbation induced by electron–photon interactions was defined through the Hamiltonian, expressed as:

$$\widehat{H}={\widehat{H}}_0+{\displaystyle \frac{e}{m_0}}A·\widehat{p}$$

(2)

where ${\widehat{H}}_0$ is the Hamiltonian of the two-probe device, e denotes the electron charge, $m_0$ represents the free electron mass, $\widehat{p}$ is the momentum operator, and A is defined as the electromagnetic vector potential. The transmission coefficients can be obtained using [47]:

$$T_{\mathsf{\alpha }}\left(E\right)=\mathrm{T}\mathrm{r}\left\{\mathrm{i}{\Gamma }_{\mathsf{\alpha }}\left[\left(1-f_{\mathsf{\alpha }}\right)G_{\mathrm{p}\mathrm{h}}^{<}+f_{\mathsf{\alpha }}{G}_{\mathrm{p}\mathrm{h}}^{>}\right]\right\}$$

(3)

Tr denotes the trace operator. $G_{\mathrm{p}\mathrm{h}}^{<}$ and $G_{\mathrm{p}\mathrm{h}}^{>}$ are the lesser and greater Keldysh Green’s functions approximate to the first order, while ${\Gamma }_{\mathsf{\alpha }}$ and $f_{\mathsf{\alpha }}$ are the line width function and Fermi distribution for the $\mathsf{\alpha }$ (left or right) electrode. J_ph is formulated as [48,49]:

$$J_{\mathrm{p}\mathrm{h}}={\displaystyle \frac{e}{S\hslash }}\int {\displaystyle \frac{dE}{2\pi }}\sum _{\mathsf{\alpha }}{T}_{\mathsf{\alpha }}\left(E\right)$$

(4)

Furthermore, the functional, basis, pseudopotentials, and k-point grids employed in the photocurrent calculations remained identical to those adopted in carrier transport simulations.

3. Results and Discussion

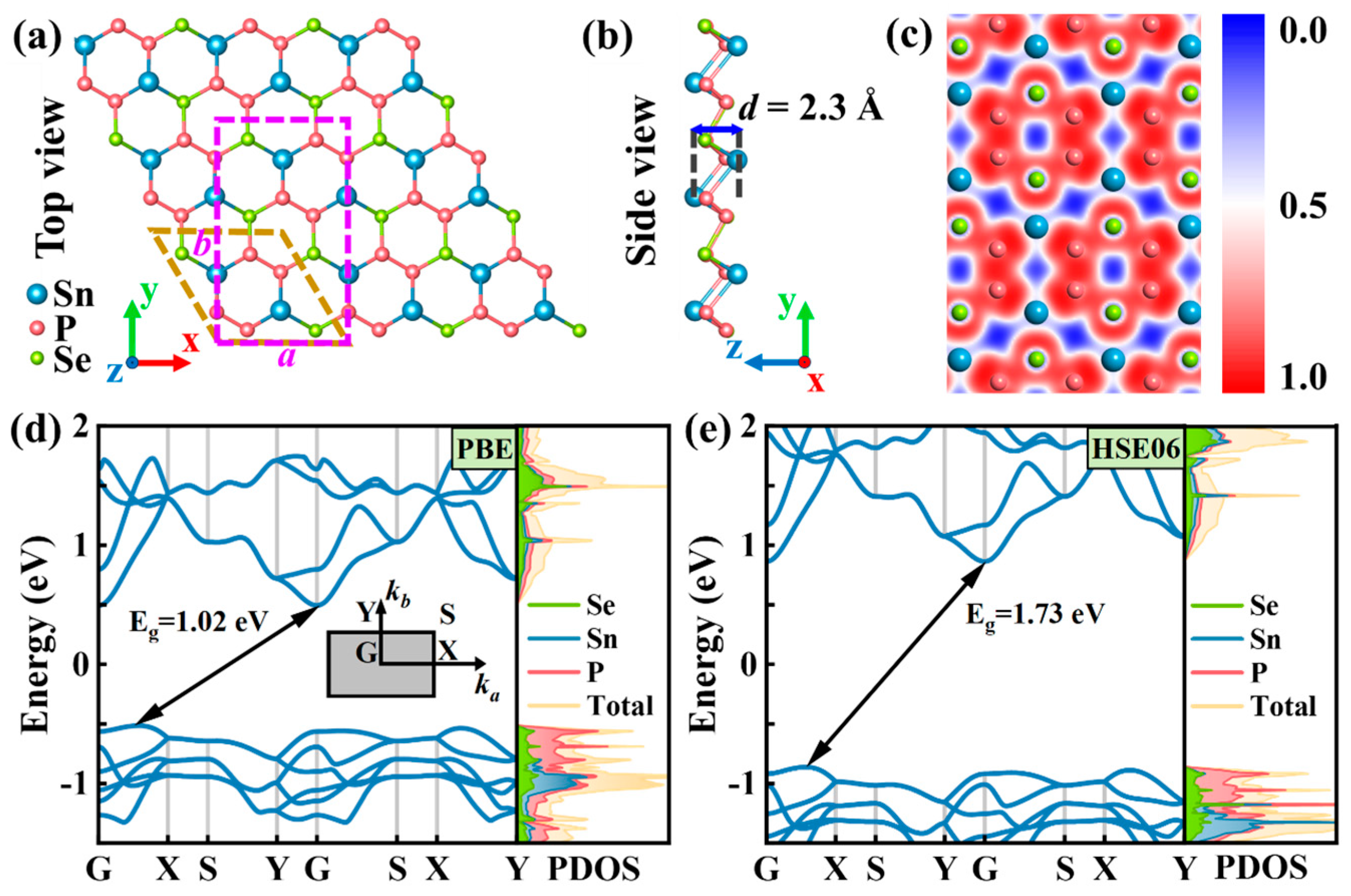
3.1. Structural and Electronic Properties of Sn₂Se₂P₄

The Sn₂Se₂P₄ monolayer was constructed by substituting two P atoms in the SnP₃ hexagonal unit cell with Se atoms [33]. Subsequent geometric optimization using the Vienna ab initio simulation package (VASP) refined the atomic coordinates with an energy convergence threshold of 1 × 10⁻⁶ eV. Figure 1a,b present the top and side views of the optimized 2D Sn₂Se₂P₄ monolayer, respectively. To facilitate carrier mobility calculations, the hexagonal primitive cell was transformed into an orthogonal unit cell, demarcated by bronze and purple dashed lines. The optimized monolayer exhibited a thickness of d = 2.30 Å and lattice constants of a = 7.17 Å and b = 12.42 Å, aligning closely with the theoretical predictions by Trung et al. Prior computational evaluations established its thermal, dynamic, and mechanical stability [36]. The electron localization function (ELF) analysis elucidated the bonding characteristics through the spatial mapping of the electron pair distribution. As depicted in Figure 1c, the electrons are localized around the P and Se atoms, thereby revealing that Se–P and P–P bonds exhibit typical covalent features, while Sn–P and Sn–Se bonds demonstrate ionic character.

The electronic band structure of the Sn₂Se₂P₄ monolayer calculated using the PBE functional exhibited indirect bandgap semiconductor characteristics with a computed bandgap of 1.02 eV (Figure 1d). To address the well-known bandgap underestimation inherent in the PBE method, we employed the HSE06 hybrid functional, resulting in a significant increase in the bandgap to 1.73 eV (Figure 1e), which aligned with previously reported data [36]. Spin–orbit coupling (SOC) effects were investigated through PBE + SOC and HSE06 + SOC band structure calculations (Figure S1), revealing a neglectable difference in the band gap values. Projected density of states (PDOS) analysis (Figure 1d,e) demonstrated that the conduction band minimum (CBM) arose from the hybridized contributions of Se, Sn, and P atomic orbitals, while the valence band maximum (VBM) was predominantly governed by P orbital states.

To systematically investigate the strain-dependent modulation of electronic structures, uniaxial strains ranging from −8% to +8% were applied along the a- and b-axis of the Sn₂Se₂P₄ monolayer (Figure 2a). HSE06-calculated band evolution under uniaxial strains (Figure 2b,c) revealed that the indirect bandgap characteristic persisted under b-axis strain, whereas compressive a-axis strain induced CBM-VBM degeneracy at the G-point of the Brillouin zone, triggering an indirect-to-direct bandgap transition. Concurrently, the bandgap decreased monotonically from 1.73 eV to 0.97 eV with increasing compressive strain. The strain-dependent shifts in band edge positions and HSE06-calculated band gaps along both axes are illustrated in Figure 2d,e. The redox potentials given by the Nernst equation (ESI†) for photocatalytic water splitting at pH = 0 (purple dashed) and pH = 7 (green dashed) are annotated [50], with E_CBM lying below the reduction potential and E_VBM above the oxidation potential, satisfying photocatalytic water splitting requirements. Notably, structures with b-axis strains of −4% to +8% optimally meet the pH = 0 criteria, while those between −4% and −8% align with pH = 7 conditions (see ESI†), demonstrating strain engineering’s precision in tailoring photocatalytic performance.

Figure 2f further reveals the strain-dependent modulation of carrier effective masses. The electron effective mass exhibits weak strain dependence along both the a-axis (0.25–0.36 $m_{\mathrm{e}}^{\mathrm{*}}$) and b-axis (0.46–0.71 $m_{\mathrm{e}}^{\mathrm{*}}$). In contrast, the hole effective masses show prominent anisotropic responses: along the a-axis, the hole effective mass abruptly increases to 1.98 $m_{\mathrm{e}}^{\mathrm{*}}$ under +2% tensile strain but sharply decreases to 0.14 $m_{\mathrm{e}}^{\mathrm{*}}$ at −2% compressive strain. Conversely, b-axis hole effective masses remain within 1.23–2.51 $m_{\mathrm{e}}^{\mathrm{*}}$ across all strain conditions. Notably, the significant reduction in hole effective mass (<1 $m_{\mathrm{e}}^{\mathrm{*}}$) within the a-axis compressive strain range of −2% to −8% predicts an order-of-magnitude enhancement in hole mobility, providing a theoretical foundation for optimizing carrier transport properties via strain engineering.

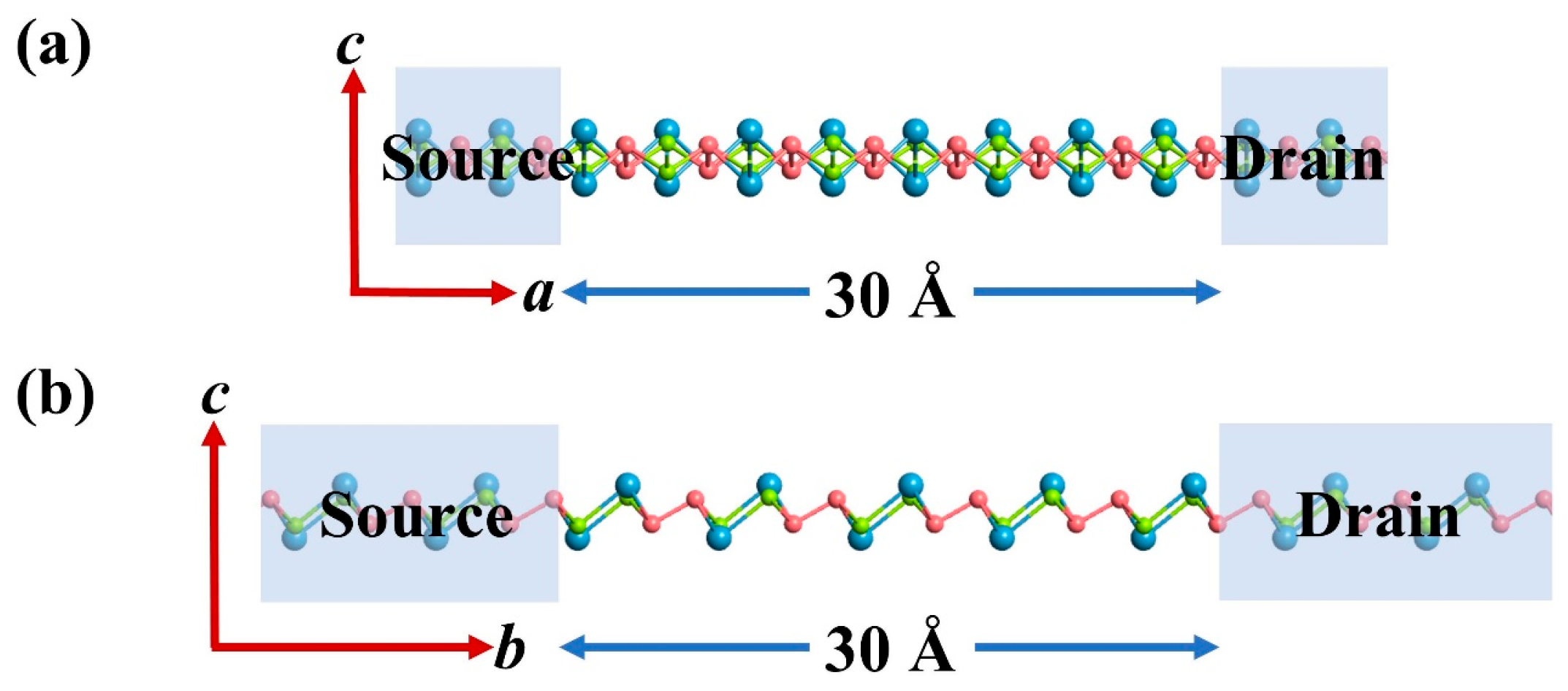
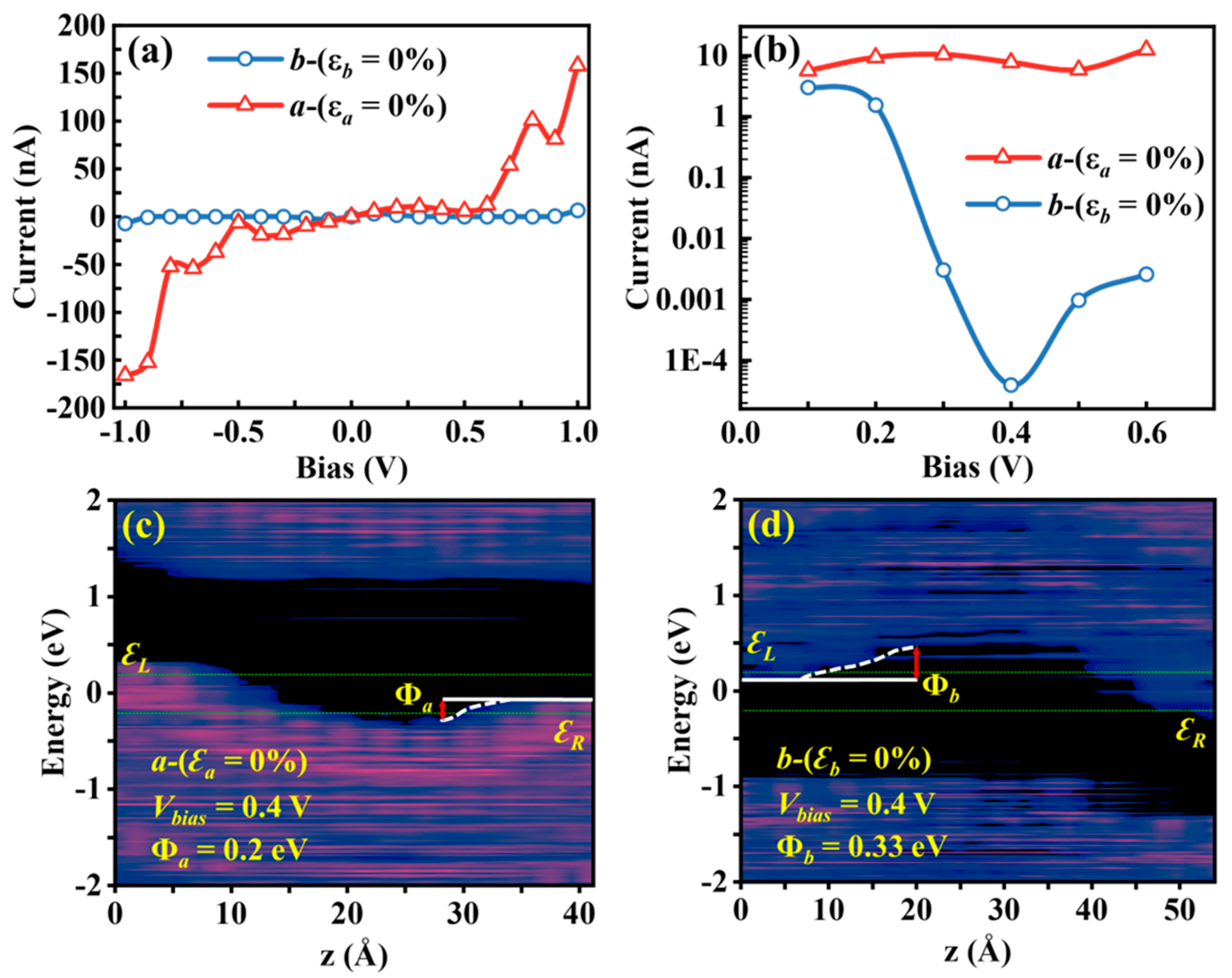
3.2. Anisotropic I–V Characteristics

The pronounced anisotropic carrier mobility in the Sn₂Se₂P₄ monolayer—with a-axis hole mobility (${\mu }_h^a$ = 7.4 × 10⁴ cm² V⁻¹·s⁻¹, ~300 times higher than electron mobility) and b-axis electron mobility (${\mu }_e^b$ = 5.4 × 10³ cm² V⁻¹·s⁻¹, ~62 times greater than hole mobility)—motivated our design of the two-probe configurations to reveal the intrinsic transport behavior (Figure 3a,b). To eliminate metal–semiconductor contact barriers, homogeneous heavily doped electrodes were implemented. The hole transport channel along the a-axis was engineered by elevating the electrode’s VBM 0.15 eV above the Fermi level, achieving a hole density of 10¹⁴ cm⁻². Conversely, the electron transport channel along the b-axis was configured by lowering the CBM 0.15 eV below the Fermi level, corresponding to an electron density of 10¹⁴ cm⁻².

The unstrained-state (ε = 0%) transport properties of Sn₂Se₂P₄ monolayer exhibited prominent directional dependence (Figure 4a). In the |V| ≤ 1.0 V bias range, the a-axis hole transport demonstrated a linear current–voltage response, achieving I_a = 1.57 × 10² nA at V = 1.0 V. In contrast, the b-axis electron transport showed abnormal negative differential conductance (NDC) near a 0.4 V bias (Figure 4b), where the current abruptly dropped to 4.0 × 10⁻⁵ nA, creating a current ratio of 10⁵ versus the a-axis transport. This phenomenon arose from the b-direction effective barrier height elevation (Φ_b = 0.33 eV, 0.12 eV higher than the a-direction effective barrier height Φ_a) that impeded electron transport, according to the projected local density of states (PLDOS) plots (Figure 4c,d). Consequently, focusing on this distinctive −0.6 V to 0.6 V bias window, we explored strain-modulated I−V characteristics under uniaxial strain engineering.

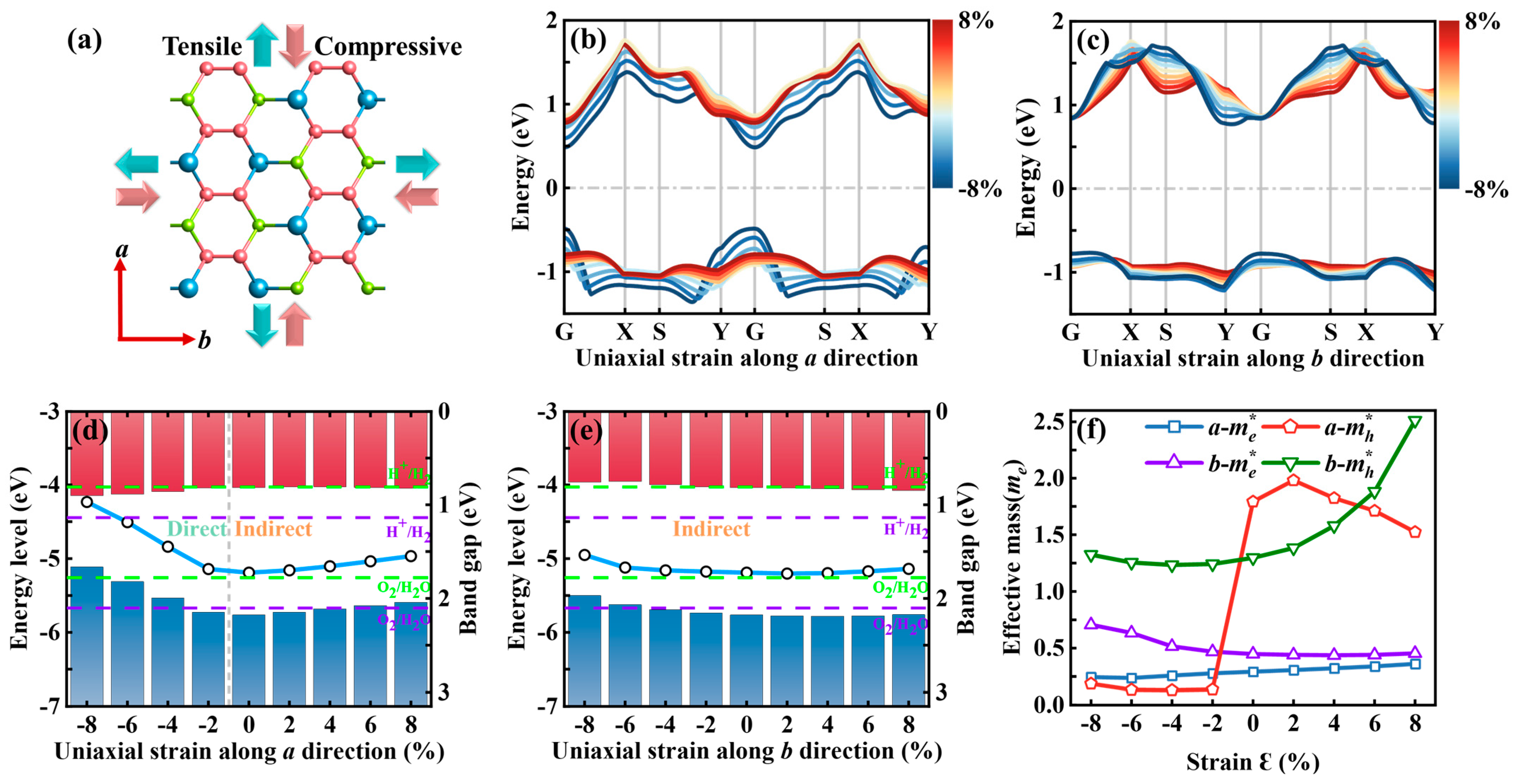
3.3. Uniaxial Strain-Modulated I–V Characteristics

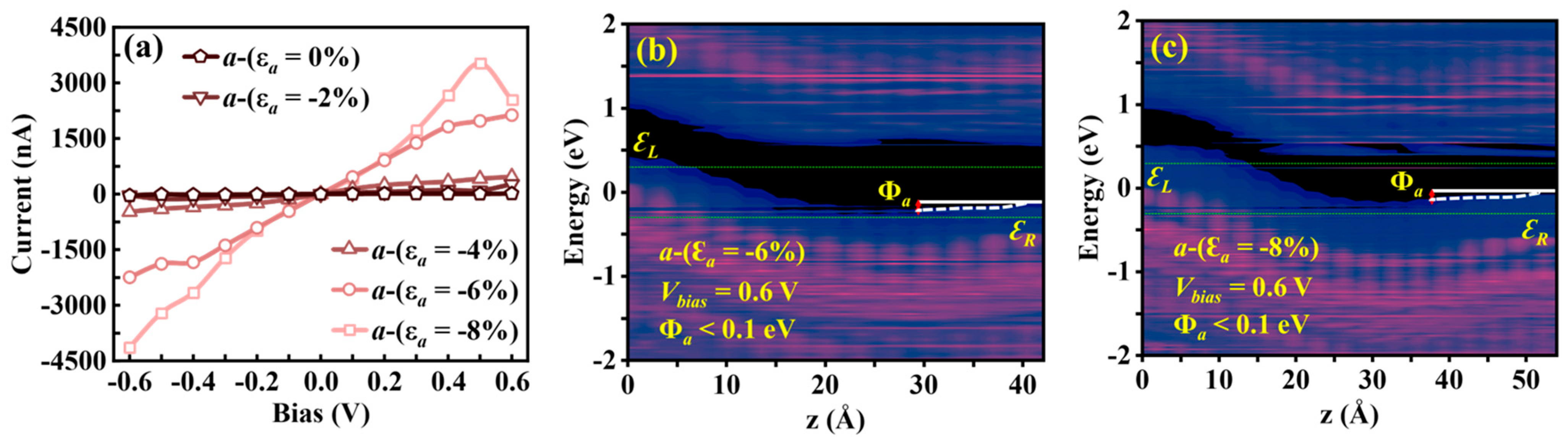
3.3.1. a-Axis Strain-Modulated I–V Characteristics

By applying uniaxial a-axis strain (−8% ≤ ε_a ≤ +8%) to the Sn₂Se₂P₄ monolayer, we observed a strong correlation between the magnitude of a-axis strain (tensile/compressive) and the anisotropic carrier transport properties (Figure 5 and Figure 6). Under a-axis tensile strain (+2% ≤ ε_a ≤ +8%), the current in the low-bias regime (|V| < 0.4 V) decreased by 90% compared to the unstrained structure, while a strain-enhanced effect emerged at 0.4 V < |V| < 0.6 V: the current I_a increased by 421% as ε_a rose from +2% to +8% (Figure 5a). According to Figure 5c–e, PLDOS analysis revealed that tensile strain reduced the effective barrier height of the a-axis transport channel to Φ_a = 0.12 eV at ε_a = +8%, marking a 20% reduction from the unstrained value (Φ_a = 0.15 eV). Notably, strain simultaneously enhanced transport anisotropy, achieving an a/b-axis current ratio of 10⁵ at V = 0.6 V for ε_a = +8% (Figure 5b). This ratio matched the switching performance of black phosphorus (10⁵), fulfilling the ON/OFF ratio requirements for field-effect transistors (FETs) [51]. The phenomenon aligned with an 80% reduction in the a-axis effective barrier height (Φ_a = 0.12 eV versus Φ_b = 0.62 eV) at V = 0.6 V under ε_a = +8% (Figure 5f).

In contrast, compressive a-axis strain (ε_a = −6% and −8%) significantly enhanced the carrier transport efficiency of the Sn₂Se₂P₄ monolayer (Figure 6a). At ε_a = −8%, the current density I_a reached 3.53 × 10³ nA, representing a two-order-of-magnitude enhancement over the unstrained structure. First-principles calculations revealed that this nonlinear response originated from strain-induced band reconstruction: compressive strain triggered a transition from an indirect to a direct bandgap (E_g decreased from 1.73 eV to 0.97 eV), accompanied by a 0.43 eV downward shift in the CBM and a 0.38 eV upward shift in the VBM toward the Fermi level (Figure 2b). PLDOS calculations further confirmed that, compared to the unstrained structure (Figure 5c), compressive strains of ε_a = −6% and −8% reduced the a-axis effective barrier height to Φ_a < 0.1 eV (Figure 6b,c), thereby markedly facilitating hole tunneling transport.

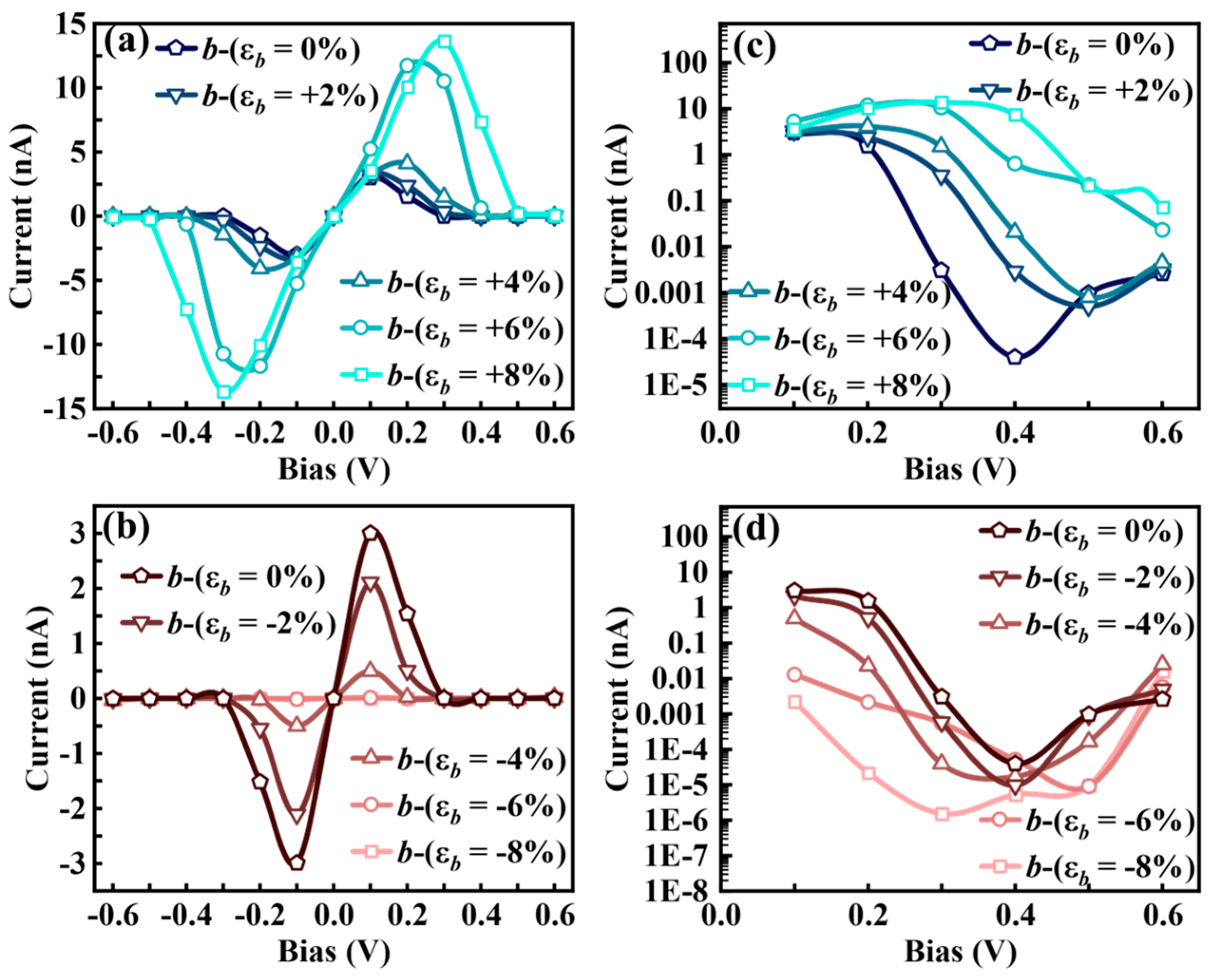
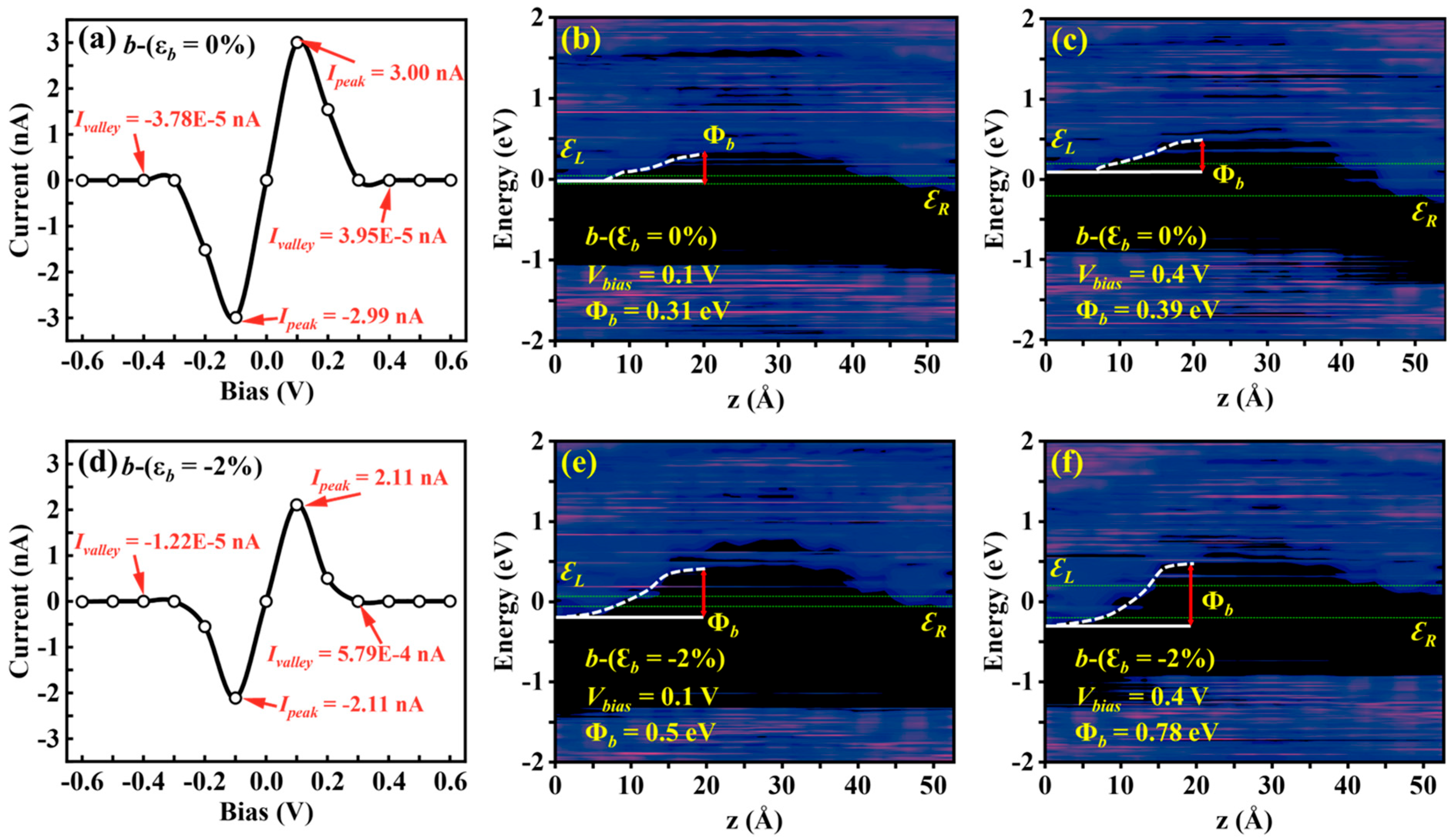
3.3.2. b-Axis Strain-Modulated I–V Characteristics and NDC Effects

The transport properties of the Sn₂Se₂P₄ monolayer under b-axis strain exhibit unique NDC modulation in 0.1–0.4 V (−0.4 to −0.1 V) bias regimes. Under b-axis strain (ε_b = 0% and −2%), the transport current initially rises within 0–0.4 V bias, abruptly decreases, and subsequently recovers beyond 0.4 V (Figure 7a,c). The calculated logarithmic-scale I−V characteristics (Figure 7b,d) reveal the pronounced NDC behavior in both the unstrained structure and ε_b = −2% strained case within 0.1–0.4 V, achieving a peak-to-valley current ratio (I_peak/I_valley) in the order of 10⁵ (Figure 8a,d). This ratio surpasses the reported NDC effects in graphene (50–200) [52], phosphorene (25) [53], phosphorene/ReS₂ heterostructures (4.2–6.9) [15], and MoS₂/WSe₂ heterostructures (10³) [54]. PLDOS analysis demonstrates that the effective barrier height Φ_b at V = 0.4 V (Figure 8c,f) is significantly higher than at V = 0.1 V (Figure 8b,e) for both cases, leading to suppressed carrier transport. This disparity in carrier transport capacity between the peak and valley states directly induces the pronounced NDC effect.

3.4. Photocurrent Transport Properties

To investigate the optoelectronic performance of the Sn₂Se₂P₄ monolayer in practical device environments, we construct optical nanodevices along the a- and b-axes, leveraging its intrinsic anisotropy. As shown in Figure 9a,b, the device features an intrinsic Sn₂Se₂P₄ scattering region (length set as 50 Å) for linearly polarized light irradiation, connected to heavily doped p-type (source) and n-type (drain) Sn₂Se₂P₄ semi-infinite electrodes. While the PBE functional inherently underestimates band gaps, high-concentration doping strategies align the effective band gaps with theoretical predictions, ensuring computational reliability. Building on our prior discovery that a-axis compressive strain (−8% ≤ ε_a ≤ −2%) induces indirect-to-direct bandgap transitions, we further investigate its modulation effects on optoelectronic performance.

As shown in Figure 10a, the optical absorption coefficient of the Sn₂Se₂P₄ monolayer exhibits pronounced anisotropy across the visible spectrum (1.61–3.11 eV). The unstrained structure (ε_a = 0%) achieves an a-axis absorption coefficient of ~10⁵ cm⁻¹, comparable to that of the same family of ternary 2D monolayers, including Sn₂Te₂P(As)₄ (10⁴–10⁵ cm⁻¹) [55], Ge₂S₂P(As)₄ (about 10⁵ cm⁻¹) [34], SnGeS₂As₄ (10⁵–10⁶ cm⁻¹) [56], and Sn₂S₂P₄ (about 10⁵ cm⁻¹) [35]. Under a-axis compressive strain (−8% ≤ ε_a ≤ −2%), absorption is further enhanced, accompanied by distinct spectral separation between the a-axis and b-axis absorption profiles, indicating strain-induced anisotropy enhancement. This phenomenon aligns with strain-modulated carrier transport properties, confirming the synergistic control of optoelectronic and transport properties.

Photocurrent density (J_ph), as a critical metric for optoelectronic device performance, quantifies the photogenerated current per unit area under illumination, reflecting the material’s light absorption and conversion efficiency. By computing the J_ph, we demonstrate that strain engineering enhances the photovoltaic conversion efficiency of the Sn₂Se₂P₄ monolayer. At ε_a = −4%, the a-axis device achieves a J_ph peak of 6.27 μA mm⁻² at 2.45 eV (Figure 10b), representing a 684% enhancement over the unstrained state (0.80 μA mm⁻²) and surpassing the InSe (0.018 μA mm⁻²) and NaCuTe (1.68 μA mm⁻²) counterparts [57,58]. In contrast, the b-axis device under the same strain conditions only yields 2.51 μA mm⁻² (Figure 10c), highlighting the a-axis as the preferred photoelectric channel. Notably, the J_ph peak around 2.00 eV initially rises sharply from 0.80 μA mm⁻² (ε_a = 0%) to 5.59 μA mm⁻² (ε_a = −2%), then declines to 0.89 μA mm⁻² (ε_a = −8%). This trend aligns with strain-dependent hole effective mass variations (Figure 2f), suggesting carrier transport limitations under extreme strains. Overall, the ε_a = −2% and ε_a = −4% strains significantly enhance J_ph while preserving the anisotropy of photocurrent density.

Furthermore, photoresponsivity (R_ph) and external quantum efficiency (EQE) also serve as critical metrics for evaluating optoelectronic device performance. Their expressions are defined as follows [59]:

$$R_{\mathrm{p}\mathrm{h}}={\displaystyle \frac{J_{\mathrm{p}\mathrm{h}}}{I_{\omega }E}}$$

(5)

$$\mathrm{E}\mathrm{Q}\mathrm{E}=R_{\mathrm{p}\mathrm{h}}{\displaystyle \frac{hc}{e\lambda }}$$

(6)

where E is the photon energy, I_ω represents the photon flux, h denotes Planck’s constant, c is the speed of light, e is the electron charge, and λ represents wavelength.

We investigate the R_ph and EQE of the a-axis and b-axis devices in the Sn₂Se₂P₄ monolayer, applying the same methodology as used for J_ph (Figures S2 and S3). Given the deterministic influence of photocurrent density on R_ph and EQE, their strain-dependent trends under a-axis compressive strain align with the photocurrent density behavior. Specifically, an optimization threshold exists within the strain modulation window: R_ph and EQE peak at ε_a = −2% and ε_a = −4%, with performance gains diminishing outside this range. Thus, our analysis focuses on devices under ε_a = −2% and ε_a = −4%.

As shown in Figure S2a, the calculated R_ph reaches 0.16 A/W at 2.45 eV (ε_a = −4%) and 0.17 A/W at 2.00 eV (ε_a = −2%), surpassing the reported values for MoS₂ (0.016 A/W) and graphene (5 × 10⁻⁴ A/W) [60]. Similarly, Figure S3a shows EQE values of 39.2% at 2.45 eV (ε_a = −4%) and 34.9% at 2.00 eV (ε_a = −2%), exceeding those of SnS (22.01%) [61], NaCuTe (34.3%) [58], NaCuSe (8%) [58], and KAgSe (17.9%) [62]. Consistent with the anisotropy of photocurrent density, the R_ph and EQE retain pronounced anisotropy (Figure 10e,f), with significant enhancements over the unstrained counterpart.

In this part, we demonstrate that the Sn₂Se₂P₄ monolayer under moderate a-axis compressive strains (ε_a = −2% and ε_a = −4%) simultaneously achieves enhanced light absorption, tunable optoelectronic properties, and optimized carrier transport. Its integrated performance surpasses benchmark 2D optoelectronic materials (e.g., MoS₂, SnS) and establishes a novel material platform for designing spectrally selective and directionally sensitive integrated optoelectronic devices.

4. Conclusions

This study systematically unveils the anisotropic electronic, transport, and optoelectronic properties of Sn₂Se₂P₄ monolayers under strain engineering through DFT and NEGF methodologies. The pristine Sn₂Se₂P₄ monolayer exhibits an indirect bandgap of 1.73 eV (HSE06). Under −8% a-axis compressive strain, the bandgap monotonically decreases to 0.97 eV with concurrent indirect-to-direct transition and drastic hole effective mass reduction ($m_{\mathrm{h}}^{\mathrm{*}}$: 1.79→0.13 $m_{\mathrm{e}}^{\mathrm{*}}$), thereby surmounting the intrinsic mobility limitations caused by the high effective mass in conventional TMDs. Notably, ballistic transport simulations (30 Å channel length) of the Sn₂Se₂P₄ monolayer reveal an a/b-axis current ratio reaching ~10⁵ at 0.4 V under ±1 V bias, comparable to black phosphorus, with sustained performance under 6–8% a-axis tensile strain. b-axis compression (0–2%) induces pronounced NDC effects (I_peak/I_valley ≈ 10⁵). a-axis strain engineering for the Sn₂Se₂P₄ monolayer induces strong anisotropy in optoelectronic responses, including optical absorption coefficients (>10⁵ cm⁻¹), photocurrent density (J_ph), responsivity (R_ph), and external quantum efficiency (EQE). At −4% a-axis strain under 2.45 eV photon energy, J_ph peak reaches 6.27 μA mm⁻² (684% enhancement versus unstrained state) with an EQE of 39.2%, significantly surpassing benchmark materials like NaCuTe (1.68 μA mm⁻², 39.4%). Most compellingly, the non-monotonic J_ph peak evolution at 2.00 eV under a-axis compression (−8%→0%) correlates strongly with strain-dependent $m_{\mathrm{h}}^{\mathrm{*}}$ variations, demonstrating carrier mobility as the dominant factor in photocarrier extraction for Sn₂Se₂P₄ monolayers. These findings demonstrate that the Sn₂Se₂P₄ monolayer achieves the synergistic modulation of electronic–optoelectronic properties through uniaxial strain engineering, with its tailorable anisotropy establishing an ideal platform for developing multifunctional nano-devices in the post-Moore era. Future investigations should prioritize environmental stability enhancement and 2D heterostructure integration to expedite experimental validation and device implementation.