Analytical Capacitance Model for Carbon Nanotube Field-Effect Transistors Including Interface-Trap Effects
Abstract
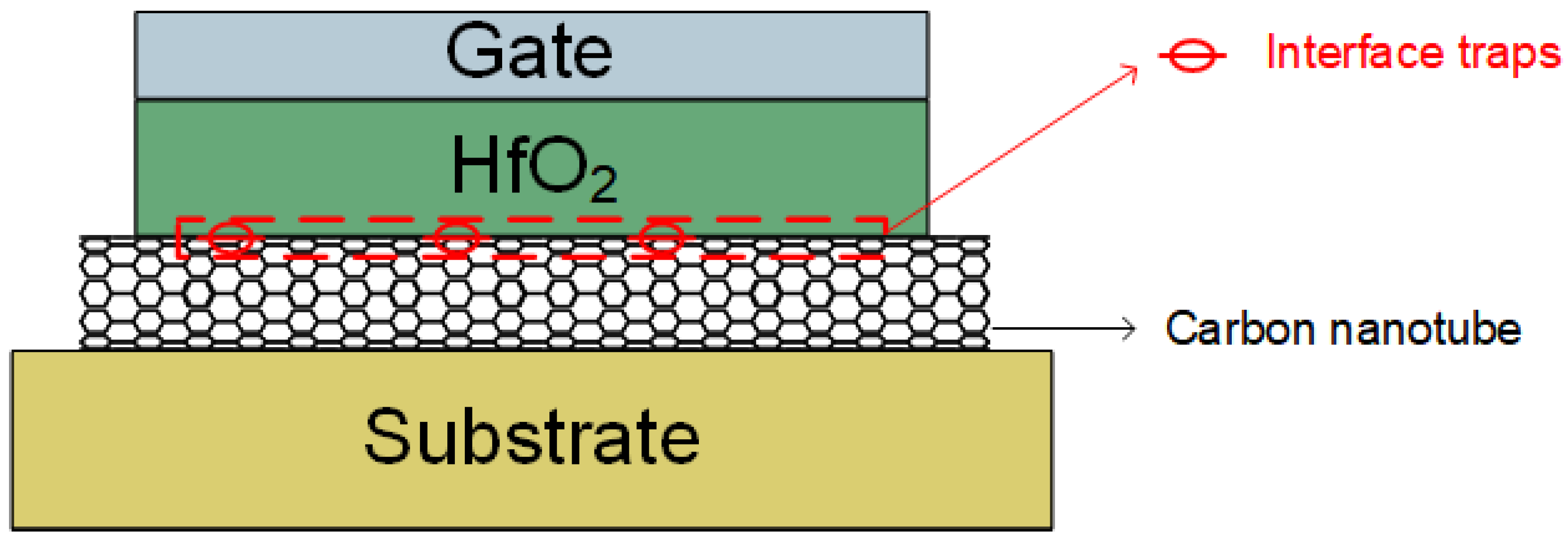
1. Introduction
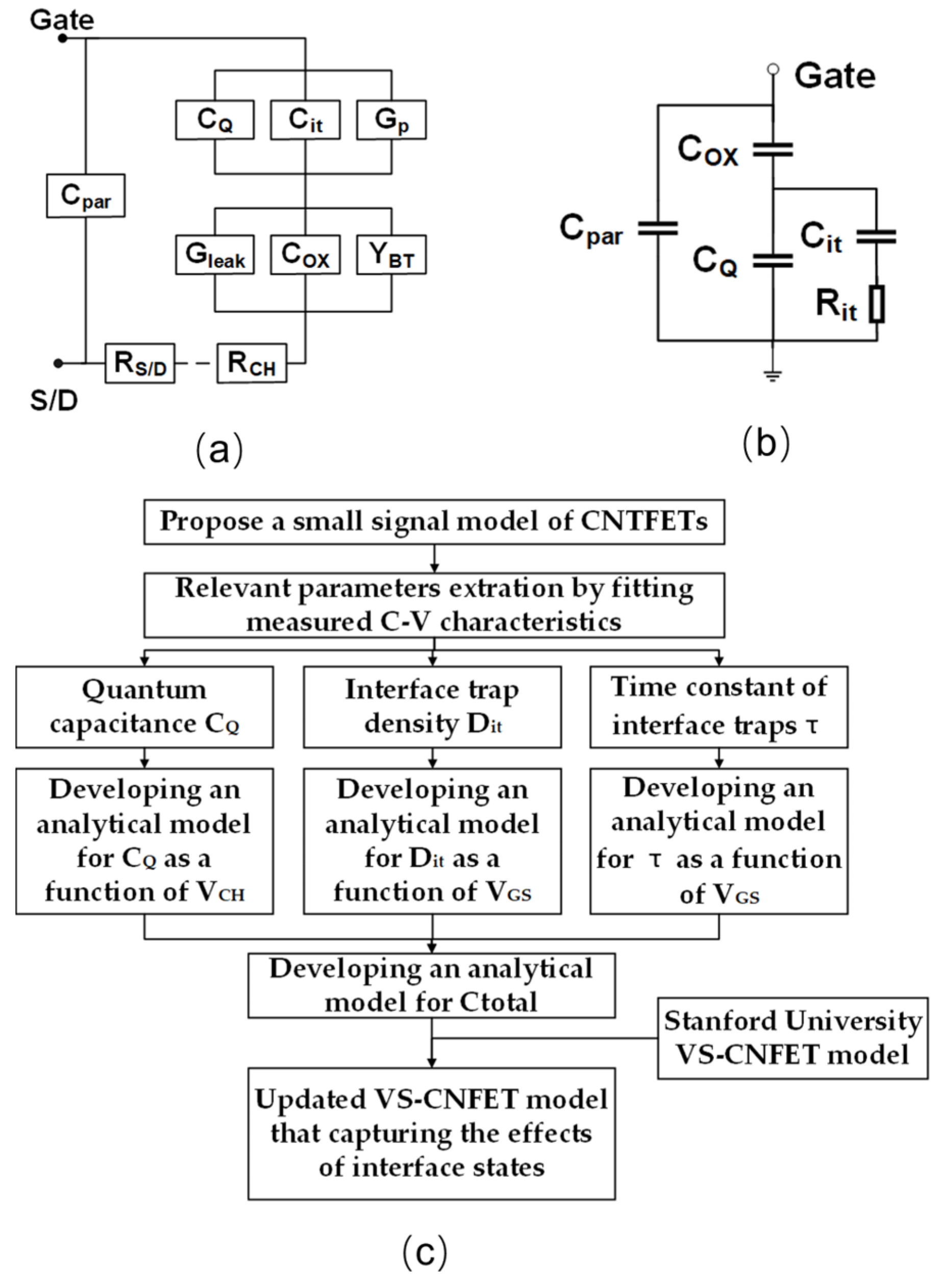
2. Theoretical Concept
3. Results and Discussion
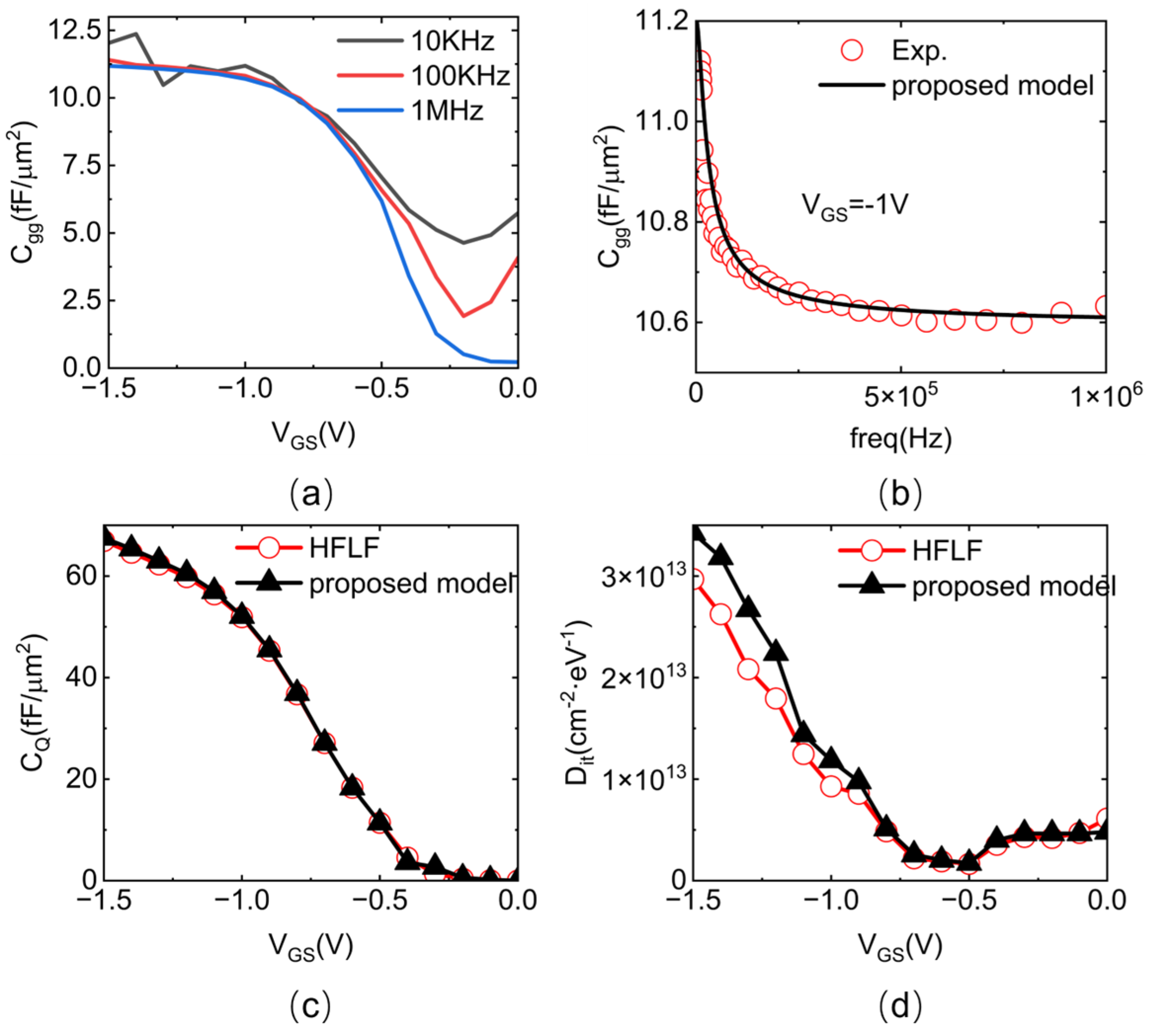
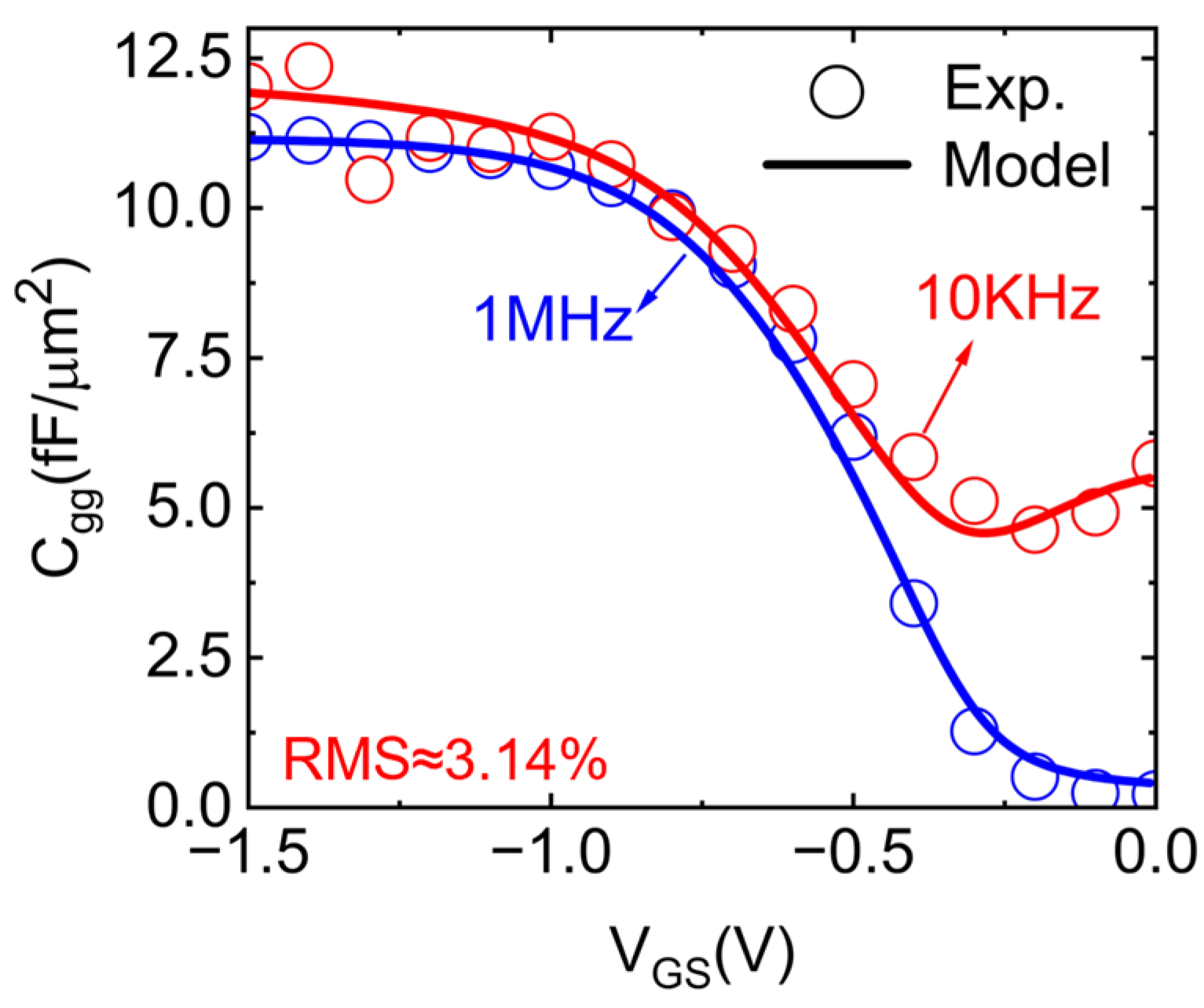
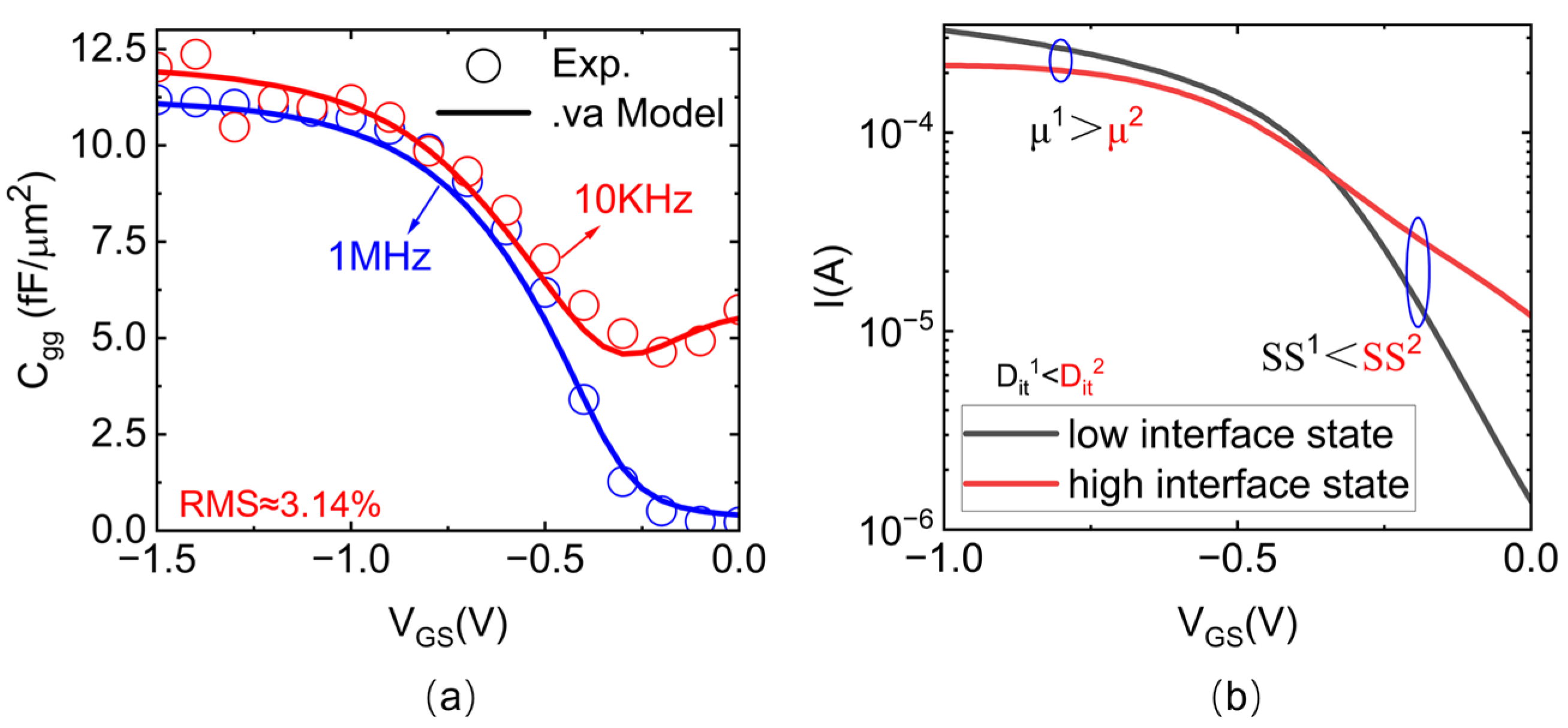
3.1. Parameter Extraction
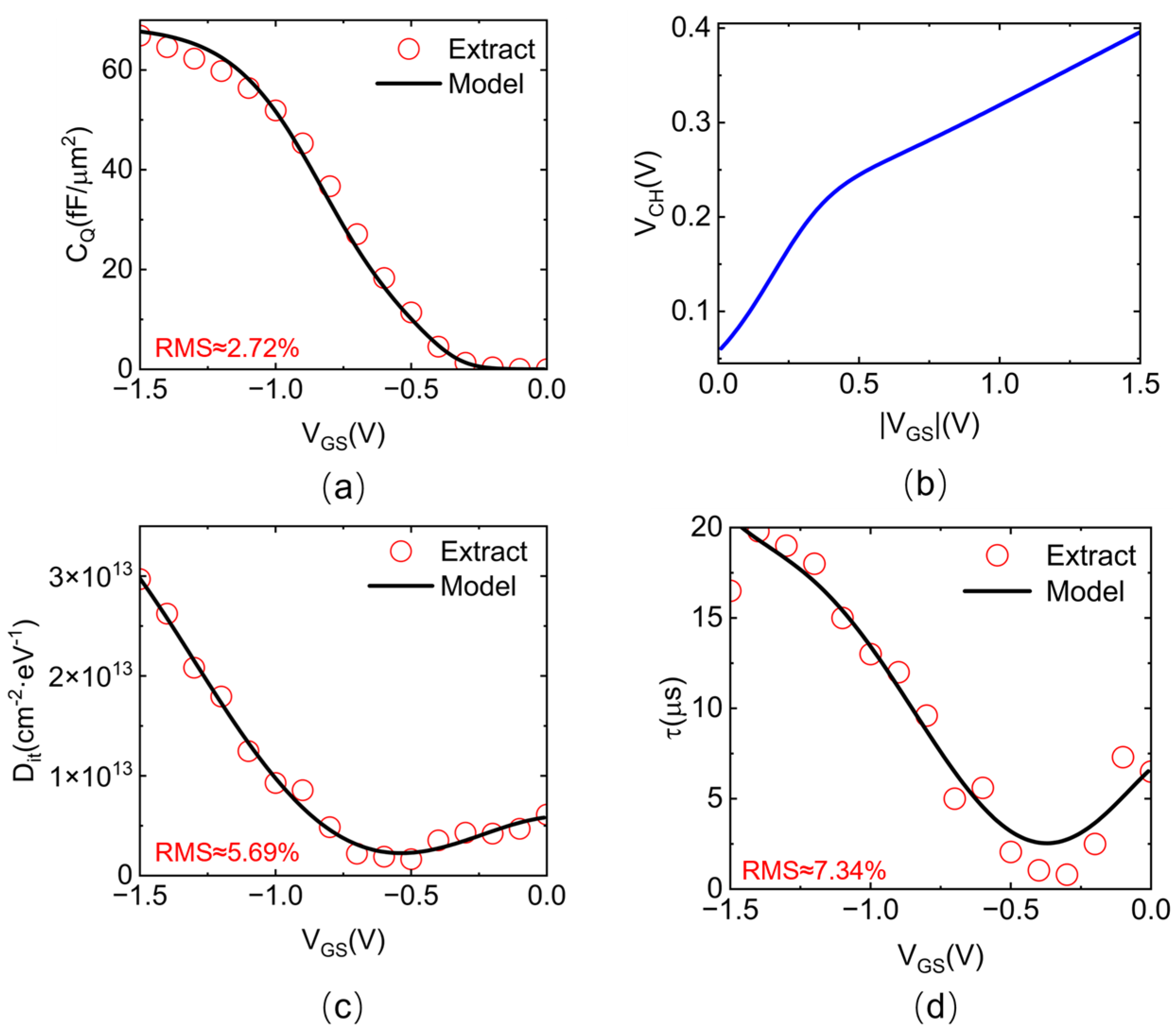
3.2. Analytical Model Development
3.3. VSCNFET Model Enhancement
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tans, S.J.; Verschueren, A.R.; Dekker, C. Room-temperature transistor based on a single carbon nanotube. Nature 1998, 393, 49–52. [Google Scholar] [CrossRef]
- Javey, A.; Guo, J. Ballistic carbon nanotube field-effect transistors. Nature 2003, 424, 654–657. [Google Scholar] [CrossRef] [PubMed]
- Heinze, S.; Tersoff, J. Carbon Nanotubes as Schottky Barrier Transistors. Phys. Rev. Lett. 2002, 89, 106801. [Google Scholar] [CrossRef]
- Zhong, D.; Zhang, Z. Gigahertz integrated circuits based on carbon nanotube films. Nat. Electron. 2018, 1, 40–45. [Google Scholar] [CrossRef]
- Deng, J.; Wong, H.-S.P. Modeling and Analysis of Planar-Gate Electrostatic Capacitance of 1-D FET With Multiple Cylindrical Conducting Channels. IEEE Trans. Electron. Devices 2007, 54, 2377–2385. [Google Scholar] [CrossRef]
- Zhao, C.; Zhong, D. Exploring the Performance Limit of Carbon Nanotube Network Film Field-Effect Transistors for Digital Integrated Circuit Applications. Adv. Funct. Mater. 2019, 29, 1808574. [Google Scholar] [CrossRef]
- Si, J.; Xu, L. Advances in High-Performance Carbon-Nanotube Thin-Film Electronics. Adv. Funct. Mater. 2019, 5, 1900122. [Google Scholar] [CrossRef]
- Long, G.; Jin, W. Carbon nanotube-based flexible high-speed circuits with sub-nanosecond stage delays. Nat. Commun. 2022, 13, 6734. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, P. Highly Uniform Carbon Nanotube Field-Effect Transistors and Medium Scale Integrated Circuits. Nano Lett. 2016, 16, 5120–5128. [Google Scholar] [CrossRef]
- Xia, P.; Feng, X. Impact and Origin of Interface States in MOS Capacitor with Monolayer MoS2 and HfO2 High-k Dielectric. Sci. Rep. 2017, 7, 40669. [Google Scholar] [CrossRef]
- Illarionov, Y.Y.; Konbloch, T. Insulators for 2D nanoelectronics: The gap to bridge. Nat. Commun. 2020, 11, 3385. [Google Scholar] [CrossRef] [PubMed]
- Park, R.S.; Shulaker, M.M. Hysteresis in Carbon Nanotube Transistors: Measurement and Analysis of Trap Density, Energy Level, and Spatial Distribution. ACS Nano 2016, 10, 4599–4608. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Chien, J.-C. Extremely Bendable, High-Performance Integrated Circuits Using Semiconducting Carbon Nanotube Networks for Digital, Analog, and Radio-Frequency Applications. Nano Lett. 2012, 12, 1527–1533. [Google Scholar] [CrossRef] [PubMed]
- Yoon, J.; Choi, B. Evaluation of interface trap densities and quantum capacitance in carbon nanotube network thin-film transistors. Nanotechnology 2016, 27, 295704. [Google Scholar] [CrossRef]
- Cai, L.; Zhang, S. Capacitance-Voltage Characteristics of Thin-film Transistors Fabricated with Solution-Processed Semiconducting Carbon Nanotube Networks. Nanoscale Res. Lett. 2015, 10, 291. [Google Scholar] [CrossRef]
- Xu, L.; Gao, N.; Zhang, Z.; Peng, L.M. Lowering interface state density in carbon nanotube thin film transistors through using stacked Y2O3/HfO2 gate dielectric. Appl. Phys. Lett. 2018, 113, 083105. [Google Scholar] [CrossRef]
- Leong, C.H.; Chun, M.W. Compact device modelling of interface trap charges with quantum capacitance in MoS2-based field-effect transistors. Semicond. Sci. Technol. 2020, 35, 045023. [Google Scholar] [CrossRef]
- Stemmer, S.; Chobpattana, V. Frequency dispersion in III-V metal-oxide-semiconductor capacitors. Appl. Phys. Lett. 2012, 100, 233510. [Google Scholar] [CrossRef]
- Deng, J.; Wong, H.-S.P. A Compact SPICE Model for Carbon-Nanotube Field-Effect Transistors Including Nonidealities and Its Application—Part I: Model of the Intrinsic Channel Region. IEEE Trans. Electron. Devices 2007, 54, 3186–3194. [Google Scholar] [CrossRef]
- Deng, J.; Wong, H.-S.P. A Compact SPICE Model for Carbon-Nanotube Field-Effect Transistors Including Nonidealities and Its Application—Part II: Full Device Model and Circuit Performance Benchmarking. IEEE Trans. Electron. Devices 2007, 54, 3195–3205. [Google Scholar] [CrossRef]
- Claus, M.; Haferlach, M. Critical review of CNTFET compact models. TechConnect Briefs 2012, 2, 770–775. [Google Scholar]
- Bejenari, I.; Schröter, M. Analytical drain current model for non-ballistic Schottky-Barrier CNTFETs. In Proceedings of the 2017 47th European Solid-State Device Research Conference (ESSDERC), Leuven, Belgium, 11–14 September 2017; pp. 90–93. [Google Scholar]
- Fregonese, S.; Cazin d’Honincthun, H. Computationally Efficient Physics-Based Compact CNTFET Model for Circuit Design. IEEE Trans. Electron. Devices 2008, 55, 1317–1327. [Google Scholar] [CrossRef]
- Maneux, C.; Fregonese, S. Multiscale simulation of carbon nanotube transistors. Solid-State Electron. 2013, 89, 26–67. [Google Scholar] [CrossRef]
- Annamalai, M.; Schröter, M. A Physics-Based Compact Model for the Static Drain Current in Heterojunction Barrier CNTFETs—Part I: Barrier-Related Current. IEEE Trans. Electron. Devices 2024, 71, 23–29. [Google Scholar] [CrossRef]
- Annamalai, M.; Schröter, M. A Physics-Based Compact Model for the Static Drain Current in Heterojunction Barrier CNTFETs—Part II: Scattering, High-Field Effects, and Model Verification. IEEE Trans. Electron. Devices 2024, 71, 30–36. [Google Scholar] [CrossRef]
- Lee, C.-S.; Pop, E. A Compact Virtual-Source Model for Carbon Nanotube FETs in the Sub-10-nm Regime—Part I: Intrinsic Elements. IEEE Trans. Electron. Devices 2015, 62, 3061–3069. [Google Scholar] [CrossRef]
- Lee, C.-S.; Pop, E. A Compact Virtual-Source Model for Carbon Nanotube FETs in the Sub-10-nm Regime—II: Extrinsic Elements, Performance Assessment, and Design Optimization. IEEE Trans. Electron. Devices 2015, 62, 3070–3078. [Google Scholar] [CrossRef]
- Lundstrom, M.S.; Antoniadis, D.A. Compact Models and the Physics of Nanoscale FETs. IEEE Trans. Electron. Devices 2014, 61, 225–233. [Google Scholar] [CrossRef]
- Gaur, A.; Agarwal, T. A MOS capacitor model for ultra-thin 2D semiconductors: The impact of interface defects and channel resistance. 2D Mater. 2020, 7, 035018. [Google Scholar] [CrossRef]
- Ilani, S.; Donev, L.A.K. Measurement of the quantum capacitance of interacting electrons in carbon nanotubes. Nat. Phys. 2006, 2, 687–691. [Google Scholar] [CrossRef]
- Xiao, H.; Liu, Y. Interface and Border Traps in the Gate Stack of Carbon Nanotube Film Transistors with an Yttria Dielectric. ACS Appl. Electron. Mater. 2023, 5, 3908–3916. [Google Scholar] [CrossRef]
- Liu, Y.; Ding, S. Interface States in Gate Stack of Carbon Nanotube Array Transistors. ACS Nano 2024, 18, 19086–19098. [Google Scholar] [CrossRef] [PubMed]
- Xiu, F.; Meyer, N. Quantum Capacitance in Topological Insulators. Sci. Rep. 2012, 2, 669. [Google Scholar] [CrossRef] [PubMed]
- Fang, N.; Nagashio, K. Band tail interface states and quantum capacitance in a monolayer molybdenum disulfide field-effect-transistor. J. Phys. D Appl. Phys. 2018, 51, 065110. [Google Scholar] [CrossRef]
- Castagné, R.; Vapaille, A. Description of the SiO2/Si interface properties by means of very low frequency MOS capacitance measurements. Surf. Sci. 1971, 28, 157–193. [Google Scholar] [CrossRef]
- Nicollian, E.H.; Goetzberger, A. The si-sio, interface—Electrical properties as determined by the metal-insulator-silicon conductance technique. Bell Syst. Tech. J. 1967, 46, 1033–1055. [Google Scholar] [CrossRef]
- Bennett, R.K.A.; Pop, E. How Do Quantum Effects Influence the Capacitance and Carrier Density of Monolayer MoS2 Transistors. Nano Lett. 2023, 23, 1666–1672. [Google Scholar] [CrossRef]
- Annamalai, M.; Schröter, M. Compact Formulation for the Bias Dependent Quasi-Static Mobile Charge in Schottky-Barrier CNTFETs. IEEE Trans. Nanotechnol. 2021, 20, 754–760. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, B.; Zhan, R.; Teng, Z.; Xue, Y.; Hu, X.; Jiang, J.; Zhang, P. Analytical Capacitance Model for Carbon Nanotube Field-Effect Transistors Including Interface-Trap Effects. Nanomaterials 2025, 15, 604. https://doi.org/10.3390/nano15080604
Zhou B, Zhan R, Teng Z, Xue Y, Hu X, Jiang J, Zhang P. Analytical Capacitance Model for Carbon Nanotube Field-Effect Transistors Including Interface-Trap Effects. Nanomaterials. 2025; 15(8):604. https://doi.org/10.3390/nano15080604
Chicago/Turabian StyleZhou, Bin, Rui Zhan, Zilin Teng, Yiheng Xue, Xiaoyan Hu, Jianhua Jiang, and Panpan Zhang. 2025. "Analytical Capacitance Model for Carbon Nanotube Field-Effect Transistors Including Interface-Trap Effects" Nanomaterials 15, no. 8: 604. https://doi.org/10.3390/nano15080604
APA StyleZhou, B., Zhan, R., Teng, Z., Xue, Y., Hu, X., Jiang, J., & Zhang, P. (2025). Analytical Capacitance Model for Carbon Nanotube Field-Effect Transistors Including Interface-Trap Effects. Nanomaterials, 15(8), 604. https://doi.org/10.3390/nano15080604




