First-Principles Calculations, Machine Learning and Monte Carlo Simulations of the Magnetic Coercivity of FexCo1−x Bulks and Nanoclusters
Abstract
1. Introduction
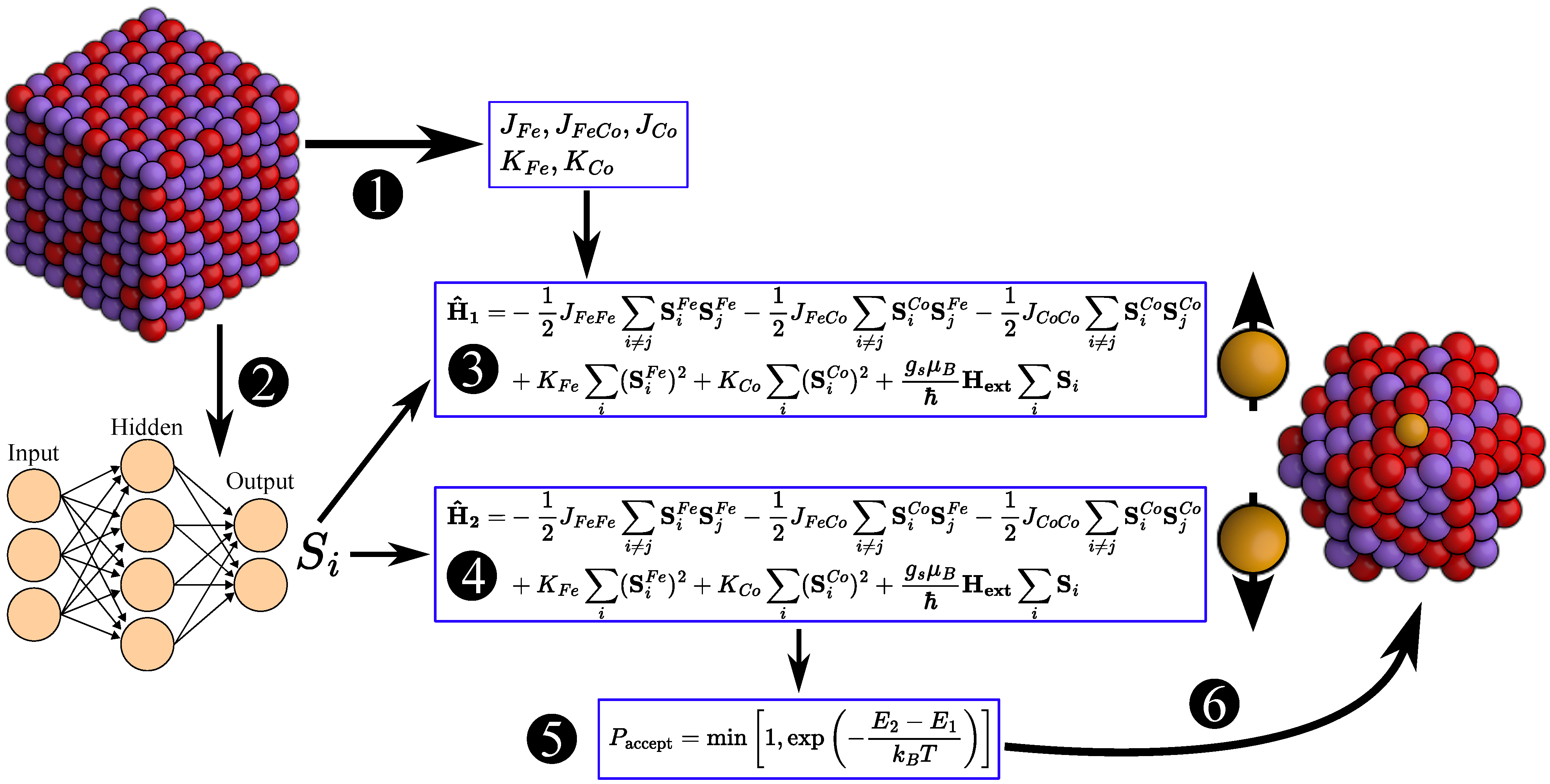
2. Computational Methods
3. Results
3.1. Density-Functional Theory Calculations
| Functional (U Value) | Lattice Parameter (Å) | Magnetic Moment per Fe () |
|---|---|---|
| PBE | 2.768 | 2.125 |
| PBE + U (1 eV) | 2.783 | 2.401 |
| PBE + U (2 eV) | 2.798 | 2.604 |
| PBE + U (3 eV) | 2.805 | 2.651 |
| PBE + U (4 eV) | 2.815 | 2.712 |
| PBE + U (5 eV) | 2.827 | 2.800 |
| Expt. [35] | 2.866 | 2.217 |
| Functional (U Value) | Lattice Parameter (Å) | Lattice Parameter c (Å) | Magnetic Moment per Co () |
|---|---|---|---|
| PBE | 2.408 | 3.906 | 1.532 |
| PBE + U (1 eV) | 2.408 | 3.911 | 1.584 |
| PBE + U (2 eV) | 2.407 | 3.915 | 1.631 |
| PBE + U (3 eV) | 2.405 | 3.922 | 1.668 |
| PBE + U (4 eV) | 2.395 | 3.998 | 1.773 |
| PBE + U (5 eV) | 2.420 | 3.876 | 1.721 |
| Expt. [36] | 2.507 | 4.069 | 1.58 |
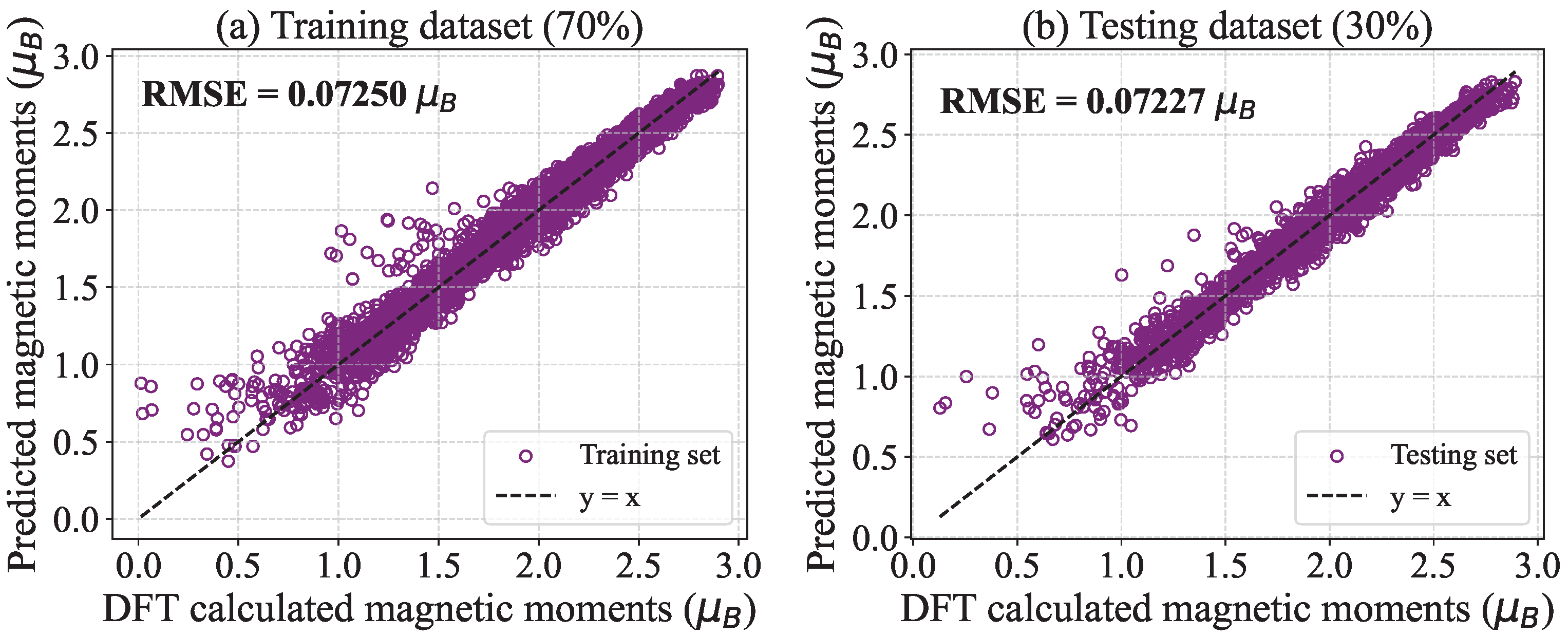
3.2. Exchange Coupling , Anisotropy , and Spin Vector
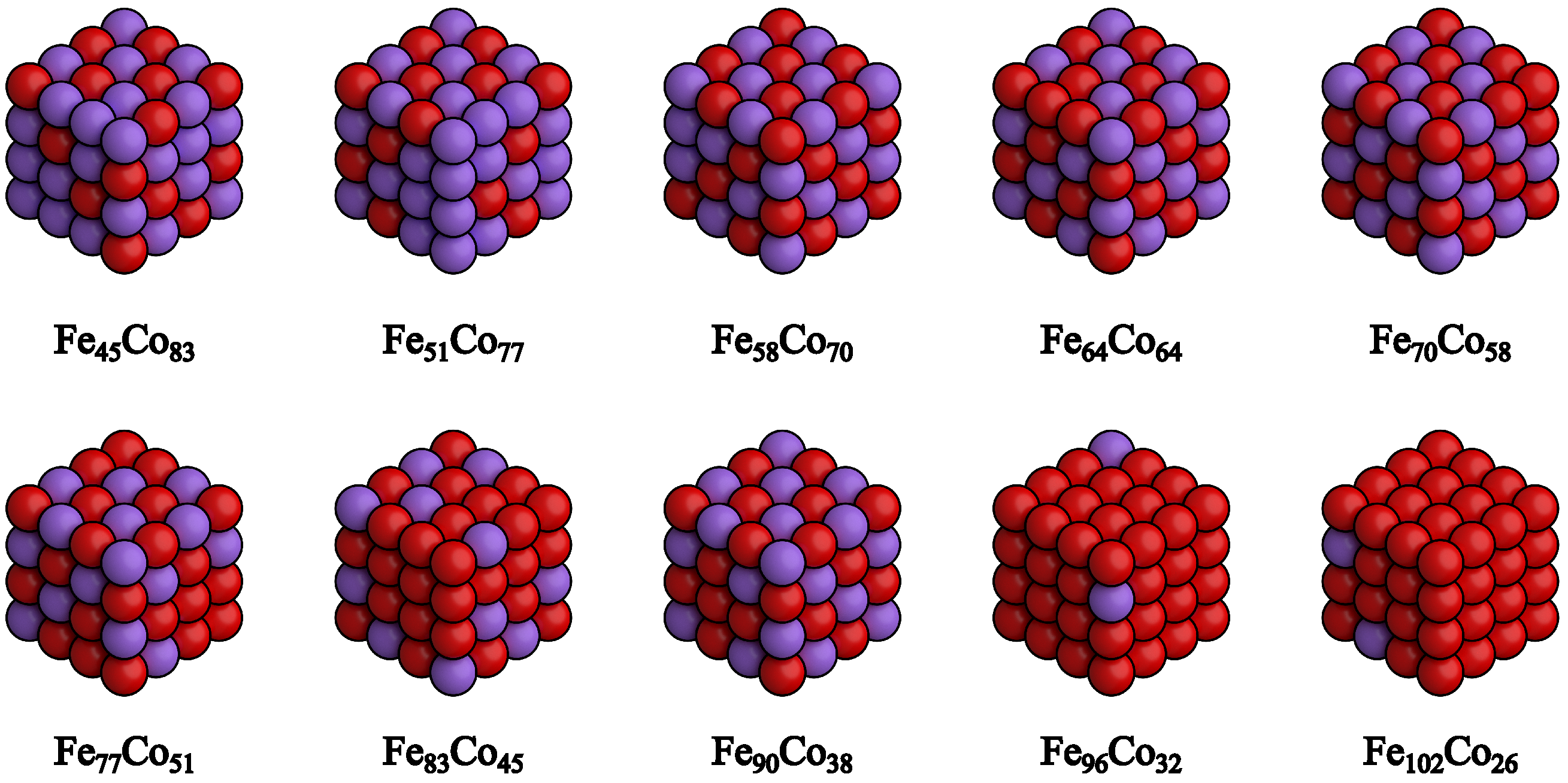
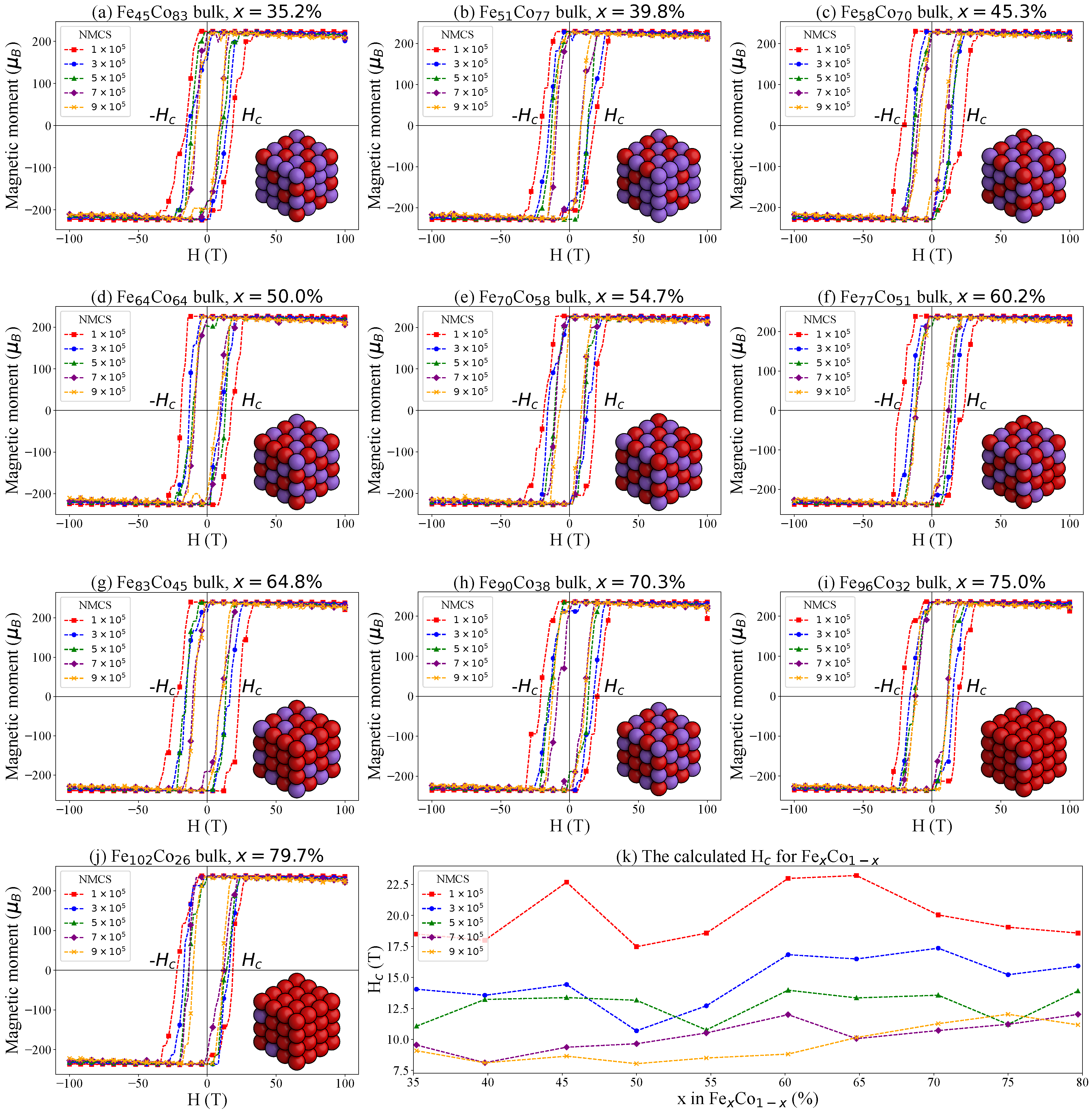
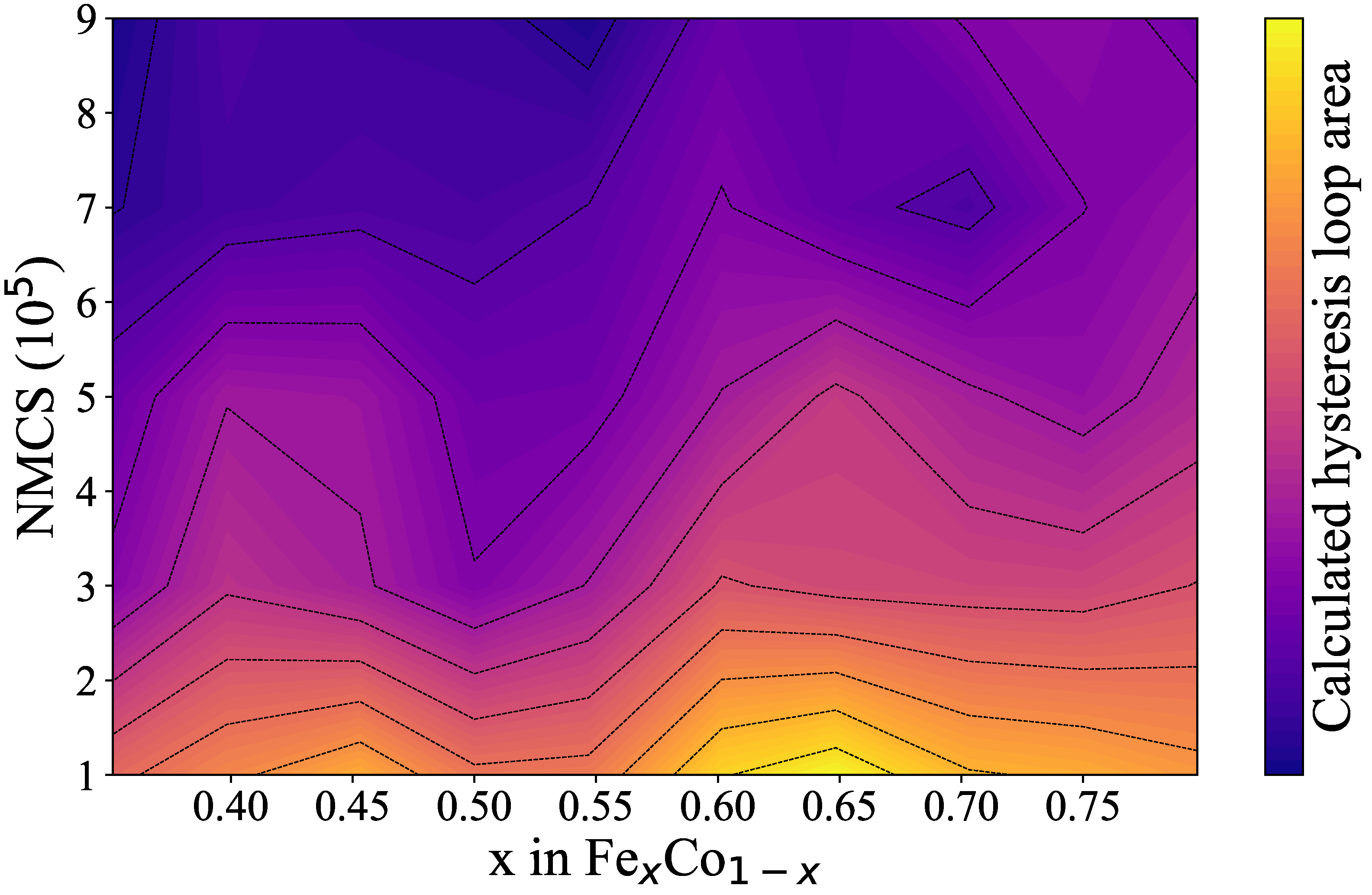
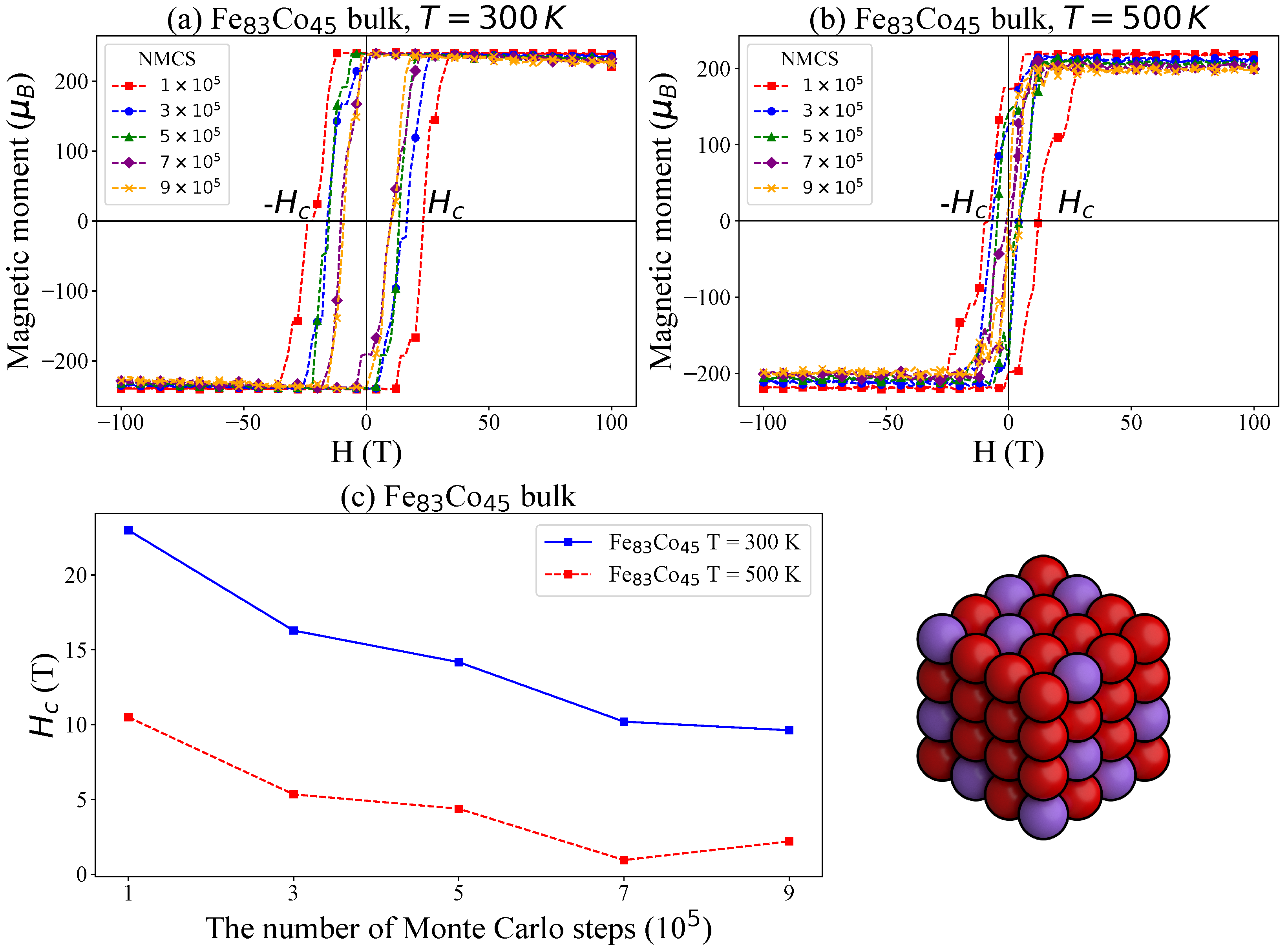
3.3. Monte Carlo Simulations of the FexCo1−x Bulks
3.4. Monte Carlo Simulations of the Fe58Co32 Nanocluster
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DFT | Density-Functional Theory |
| ML | Machine Learning |
| MC | Monte Carlo |
| HPC | High-Performance Computing |
| GGA | Generalized Gradient Approximation |
| BCC | Body-Centered Cubic |
| HCP | Hexagonal Close-Packed |
| SOC | Spin-Orbit Coupling |
| VSM | Vibrating Sampling Magnetometer |
| MD | Molecular Dynamics |
| MEAM | Modified Embedded Atom Method |
| PBCs | Periodic Boundary Conditions |
| SSF | Single Spin Flip |
| CSF | Cluster Spin Flip |
| RMSE | Root-Mean-Square Error |
| NMCS | Number of the Monte Carlo Steps |
References
- Sundar, R.S.; Deevi, S.C. Soft Magnetic FeCo Alloys: Alloy Development, Processing, and Properties. Int. Mater. Rev. 2005, 50, 157–192. [Google Scholar] [CrossRef]
- Sourmail, T. Near Equiatomic FeCo Alloys: Constitution, Mechanical and Magnetic Properties. Prog. Mater. Sci. 2005, 50, 816–880. [Google Scholar] [CrossRef]
- O’Handley, R.C. Modern Magnetic Materials: Principles and Applications; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Vadillo, V.; Insausti, M.; Gutiérrez, J. FexCo1-x Alloy Nanoparticles: Synthesis, Structure, Magnetic Characterization and Magnetorheological Application. J. Magn. Magn. Mater. 2022, 563, 169975. [Google Scholar] [CrossRef]
- Zhou, B.; Yang, Y.; Qin, Y.; Yang, G.; Wu, M. Fabrication of Equiatomic FeCo Alloy Parts with High Magnetic Properties by Fields Activated Sintering. Manuf. Rev. 2022, 9, 7. [Google Scholar] [CrossRef]
- Burkert, T.; Nordström, L.; Eriksson, O.; Heinonen, O. Giant Magnetic Anisotropy in Tetragonal FeCo Alloys. Phys. Rev. Lett. 2004, 93, 027203. [Google Scholar] [CrossRef]
- Amiri, S.; Shokrollahi, H. The Role of Cobalt Ferrite Magnetic Nanoparticles in Medical Science. Mater. Sci. Eng. C 2013, 33, 1–8. [Google Scholar] [CrossRef]
- Kim, D.H.; Nikles, D.E.; Johnson, D.T.; Brazel, C.S. Heat Generation of Aqueously Dispersed CoFe2O4 Nanoparticles as Heating Agents for Magnetically Activated Drug Delivery and Hyperthermia. J. Magn. Magn. Mater. 2008, 320, 2390–2396. [Google Scholar] [CrossRef]
- Kitchin, J. Modeling Materials Using Density Functional Theory; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Kumar, A.; Singh, P.; Harbola, M.K. Density Functional Theory of Material Design: Fundamentals and Applications—II. Oxf. Open Mater. Sci. 2024, 4, itae002. [Google Scholar] [CrossRef]
- Azouaoui, A.; El Haoua, M.; Salmi, S.; El Grini, A.; Benzakour, N.; Hourmatallah, A.; Bouslykhane, K. Structural, Electronic, and Magnetic Properties of Mn4N Perovskite: Density Functional Theory Calculations and Monte Carlo Study. J. Supercond. Nov. Magn. 2020, 33, 1507–1512. [Google Scholar] [CrossRef]
- Elkoua, I.A.; Masrour, R. DFT and Monte Carlo Study of the Structural, Elastic, Electronic, Magnetic and Magnetocaloric Properties of Ni2MnSi Full-Heusler Alloys. Mater. Sci. Semicond. Process. 2025, 190, 109266. [Google Scholar] [CrossRef]
- Idrissi, S.; Ziti, S.; Labrim, H.; Bahmad, L. Critical Magnetic Behavior of the Rare Earth-Based Alloy GdN: Monte Carlo Simulations and Density Functional Theory Method. J. Mater. Eng. Perform. 2020, 29, 7361–7368. [Google Scholar] [CrossRef]
- Jabar, A.; Masrour, R.; Kadim, G.; Hamedoun, M.; Hourmatallah, A.; Benzakour, N.; Rezzouk, A.; Bouslykhane, K.; Kharbach, J. Intrinsic Ferromagnetism in CoBr2 Nanolayers: A DFT + U and Monte Carlo Study. Commun. Theor. Phys. 2021, 73, 115702. [Google Scholar] [CrossRef]
- Kerrai, H.; Zaim, N.; Kerouad, M.; Zaim, A. Insight into Electronic and Magnetic Properties of Ba2NiOsO6 Double Perovskite: A Monte Carlo Study and a Comparative Investigation between TB-mBJ and GGA+U. Comput. Mater. Sci. 2025, 246, 113404. [Google Scholar] [CrossRef]
- Lamouri, R.; Salmani, E.M.; Dehmani, M.; Ez-Zahraouy, H.; Benyoussef, A. Electronic Properties and Magnetocaloric Effect of GdNi4Si: Ab Initio Calculations, Mean Field Approximation, and Monte Carlo Simulation. J. Supercond. Nov. Magn. 2018, 31, 1819–1825. [Google Scholar] [CrossRef]
- Wierzbowska, M. Exchange Interactions and Tc in Rhenium-Doped Silicon: DFT, DFT + U and Monte Carlo Calculations. J. Phys. Condens. Matter 2012, 24, 126002. [Google Scholar] [CrossRef]
- Li, X.; Yu, H.; Lou, F.; Feng, J.; Whangbo, M.-H.; Xiang, H. Spin Hamiltonians in Magnets: Theories and Computations. Molecules 2021, 26, 803. [Google Scholar] [CrossRef]
- Evans, R.F.L. Atomistic Spin Dynamics. In Handbook of Materials Modeling; Andreoni, W., Yip, S., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 1–23. [Google Scholar]
- Jia, W.; Cao, Z.; Wang, L.; Fu, J.; Chi, X.; Gao, W.; Wang, L.W. The Analysis of a Plane Wave Pseudopotential Density Functional Theory Code on a GPU Machine. Comput. Phys. Commun. 2013, 184, 9–18. [Google Scholar] [CrossRef]
- Jia, W.; Fu, J.; Cao, Z.; Wang, L.; Chi, X.; Gao, W.; Wang, L.W. Fast Plane Wave Density Functional Theory Molecular Dynamics Calculations on Multi-GPU Machines. J. Comput. Phys. 2013, 251, 102–115. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Qin, M.; Schäfer, T.; Andergassen, S.; Corboz, P.; Gull, E. The Hubbard Model: A Computational Perspective. Annu. Rev. Condens. Matter Phys. 2022, 13, 275–302. [Google Scholar] [CrossRef]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-Energy-Loss Spectra and the Structural Stability of Nickel Oxide: An LSDA+U Study. Phys. Rev. B 1998, 57, 1505–1509. [Google Scholar] [CrossRef]
- Skomski, R. Simple Models of Magnetism; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Nehme, Z.; Labaye, Y.; Sayed Hassan, R.; Yaacoub, N.; Greneche, J.M. Modeling of Hysteresis Loops by Monte Carlo Simulation. AIP Adv. 2015, 5, 127124. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Choi, W.M.; Kim, Y.; Seol, D.; Lee, B.J. Modified Embedded-Atom Method Interatomic Potentials for the Co-Cr, Co-Fe, Co-Mn, Cr-Mn and Mn-Ni Binary Systems. Comput. Mater. Sci. 2017, 130, 121–129. [Google Scholar] [CrossRef]
- Swendsen, R.H.; Wang, J.S. Nonuniversal Critical Dynamics in Monte Carlo Simulations. Phys. Rev. Lett. 1987, 58, 86–88. [Google Scholar] [CrossRef]
- Naveas, N.; Pulido, R.; Marini, C.; Hernández-Montelongo, J.; Manso-Silván, M. First-Principles Calculations of Hematite (α-Fe2O3) by Self-Consistent DFT+U+V. iScience 2023, 26, 106033. [Google Scholar] [CrossRef]
- Naveas, N.; Pulido, R.; Marini, C.; Gargiani, P.; Hernandez-Montelongo, J.; Brito, I.; Manso-Silván, M. First-Principles Calculations of Magnetite (Fe3O4) above the Verwey Temperature by Using Self-Consistent DFT+U+V. J. Chem. Theory Comput. 2023, 19, 8610–8623. [Google Scholar] [CrossRef]
- Wang, L.; Maxisch, T.; Ceder, G. Oxidation Energies of Transition Metal Oxides within the GGA+U Framework. Phys. Rev. B 2006, 73, 195107. [Google Scholar] [CrossRef]
- Burzo, E.; Vlaic, P.; Creanga, I. Magnetic Properties of RCo5-based Systems. J. Alloys Compd. 2011, 509, 8289–8294. [Google Scholar] [CrossRef]
- Chen, J.; Selloni, A. Water Adsorption and Oxidation at the Co3O4 (110) Surface. J. Phys. Chem. Lett. 2012, 3, 2808–2814. [Google Scholar] [CrossRef]
- Iglesias, R.; Palacios, S. Ab Initio Studies on the Magnetic Phase Stability of Iron. Acta Materialia 2007, 55, 5123–5127. [Google Scholar] [CrossRef]
- Moruzzi, V.L.; Marcus, P.M.; Schwarz, K.; Mohn, P. Ferromagnetic Phases of Bcc and Fcc Fe, Co, and Ni. Phys. Rev. B 1986, 34, 1784–1791. [Google Scholar] [CrossRef]
- Hsu, J.H.; Chang, C.R. Origin of Enhanced Coercivity in (Fe65Co35)x(Al2O3)1-x Granular Thin Films. J. Magn. Magn. Mater. 1993, 120, 342–344. [Google Scholar] [CrossRef]
- Farabi Khaneghahi, S.; Sharafi, S. Magnetic and Structural Properties of Nanostructured (Fe65Co35)100-xCrx (x = 0, 10) Powders Prepared by Mechanical Alloying Process. Adv. Powder Technol. 2014, 25, 211–218. [Google Scholar] [CrossRef]
- Fu, Y.; Cheng, X.; Yang, Z. Soft Magnetic Properties and Microstructure of Fe65Co35 Thin Films with Different Underlayers. Phys. Status Solidi 2006, 203, 963–969. [Google Scholar] [CrossRef]
- Kernion, S.J.; Keylin, V.; Huth, J.; McHenry, M.E. Secondary Crystallization in (Fe65Co35)79.5+xB13Nb4-xSi2Cu1.5 and (Fe65Co35)83B10Nb4Si2Cu1 Nanocomposite Alloys. J. Appl. Phys. 2012, 111, 07A329. [Google Scholar] [CrossRef]
- Li, H.; Han, Y.; Ren, X.; Tao, Z.; Zhang, K. Anomalous Hall Effect and Transport Properties of Ultra-Thin Fe65Co35 Films. Mater. Tehnol. 2020, 54, 651–653. [Google Scholar] [CrossRef]
- Li, Y.Q.; Yue, M.; Wang, T.; Wu, Q.; Zhang, D.T.; Gao, Y. Investigation of Magnetic Properties of MnBi/Co and MnBi/Fe65Co35 Nanocomposite Permanent Magnets by Micro-Magnetic Simulation. J. Magn. Magn. Mater. 2015, 393, 484–489. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.; Liu, X.; Fu, Y.; Wei, F.; Kamzin, A.S.; Wei, D. Investigation of Microstructure and Soft Magnetic Properties of Fe65Co35 Thin Films Deposited on Different Underlayers. J. Appl. Phys. 2010, 107, 09A325. [Google Scholar] [CrossRef]
- Park, J.; Hong, Y.K.; Lee, J.; Lee, W.; Choi, C.J.; Xu, X.; Lane, A.M. Magnetization and Intrinsic Coercivity for τ-Phase Mn54Al46/α-Phase Fe65Co35 Composite. J. Magn. 2014, 19, 55–58. [Google Scholar] [CrossRef]
- Qian, H.D.; Si, P.Z.; Lim, J.T.; Kim, J.W.; Park, J.; Choi, C.J. Magnetic Properties of Mn54Al46C2.44/Sm2Fe17N3 and Mn54Al46C2.44/Fe65Co35 Composites. J. Korean Phys. Soc. 2018, 73, 1703–1707. [Google Scholar] [CrossRef]
- Wang, Y.; Geng, H.; Wang, J.B.; Nie, S.; Wang, L.S.; Chen, Y.; Peng, D.L. Magnetic Properties of [Fe65Co35–O/SiO2]n Multilayer Thin Films for High-Frequency Application. Appl. Phys. A 2013, 111, 569–574. [Google Scholar] [CrossRef]
- Wang, S.; Ma, J.; Zhang, X.; Li, J. Magnetic Softness and Interparticle Exchange Interactions of (Fe65Co35)1-x(Al2O3)x (x = 0–0.50) Nanogranular Films. Thin Solid Films 2012, 520, 5046–5052. [Google Scholar] [CrossRef]
- Wang, J.B.; Wang, L.S.; Guo, H.Z.; Lei, M.; Zhang, Q.F.; Yue, G.H.; Chen, Y.; Peng, D.L. Structural and Magnetic Properties of Fe65Co35@Ni0.5Zn0.5Fe2O4 Composite Thin Films Prepared by a Novel Nanocomposite Technology. J. Alloys Compd. 2014, 608, 323–328. [Google Scholar] [CrossRef]
- Wang, J.B.; Xiao, W.W.; Ma, D.G.; Wang, L.; Liu, Y.Y.; Tian, X.Z.; Liang, L.J.; Gao, J. Structure, Morphology and Magnetic Performance of (Fe65Co35)x@ (Ni0.5Zn0.5Fe2O4)100–x Nanocomposite Thin Films. Phys. Scr. 2024, 99, 1059b8. [Google Scholar] [CrossRef]
- Hesani, M.; Yazdani, A.; Abedi Ravan, B.; Ghazanfari, M. The Effect of Particle Size on the Characteristics of FeCo Nanoparticles. Solid State Commun. 2010, 150, 594–597. [Google Scholar] [CrossRef]
- Leslie-Pelecky, D.L.; Rieke, R.D. Magnetic Properties of Nanostructured Materials. Chem. Mater. 1996, 8, 1770–1783. [Google Scholar] [CrossRef]

| Magnetic Parameters | Values |
|---|---|
| 0.010837 eV | |
| 0.010061 eV | |
| 0.010338 eV | |
| ≈0 | |
| ≈0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, D.; Zhang, Y.; Li, X.; Xiao, N. First-Principles Calculations, Machine Learning and Monte Carlo Simulations of the Magnetic Coercivity of FexCo1−x Bulks and Nanoclusters. Nanomaterials 2025, 15, 577. https://doi.org/10.3390/nano15080577
Du D, Zhang Y, Li X, Xiao N. First-Principles Calculations, Machine Learning and Monte Carlo Simulations of the Magnetic Coercivity of FexCo1−x Bulks and Nanoclusters. Nanomaterials. 2025; 15(8):577. https://doi.org/10.3390/nano15080577
Chicago/Turabian StyleDu, Dou, Youwei Zhang, Xingwu Li, and Namin Xiao. 2025. "First-Principles Calculations, Machine Learning and Monte Carlo Simulations of the Magnetic Coercivity of FexCo1−x Bulks and Nanoclusters" Nanomaterials 15, no. 8: 577. https://doi.org/10.3390/nano15080577
APA StyleDu, D., Zhang, Y., Li, X., & Xiao, N. (2025). First-Principles Calculations, Machine Learning and Monte Carlo Simulations of the Magnetic Coercivity of FexCo1−x Bulks and Nanoclusters. Nanomaterials, 15(8), 577. https://doi.org/10.3390/nano15080577





