A Modified Model Dielectric Function for Analyzing Optical Spectra of InGaN Nanofilms on Sapphire Substrates
Abstract
1. Introduction
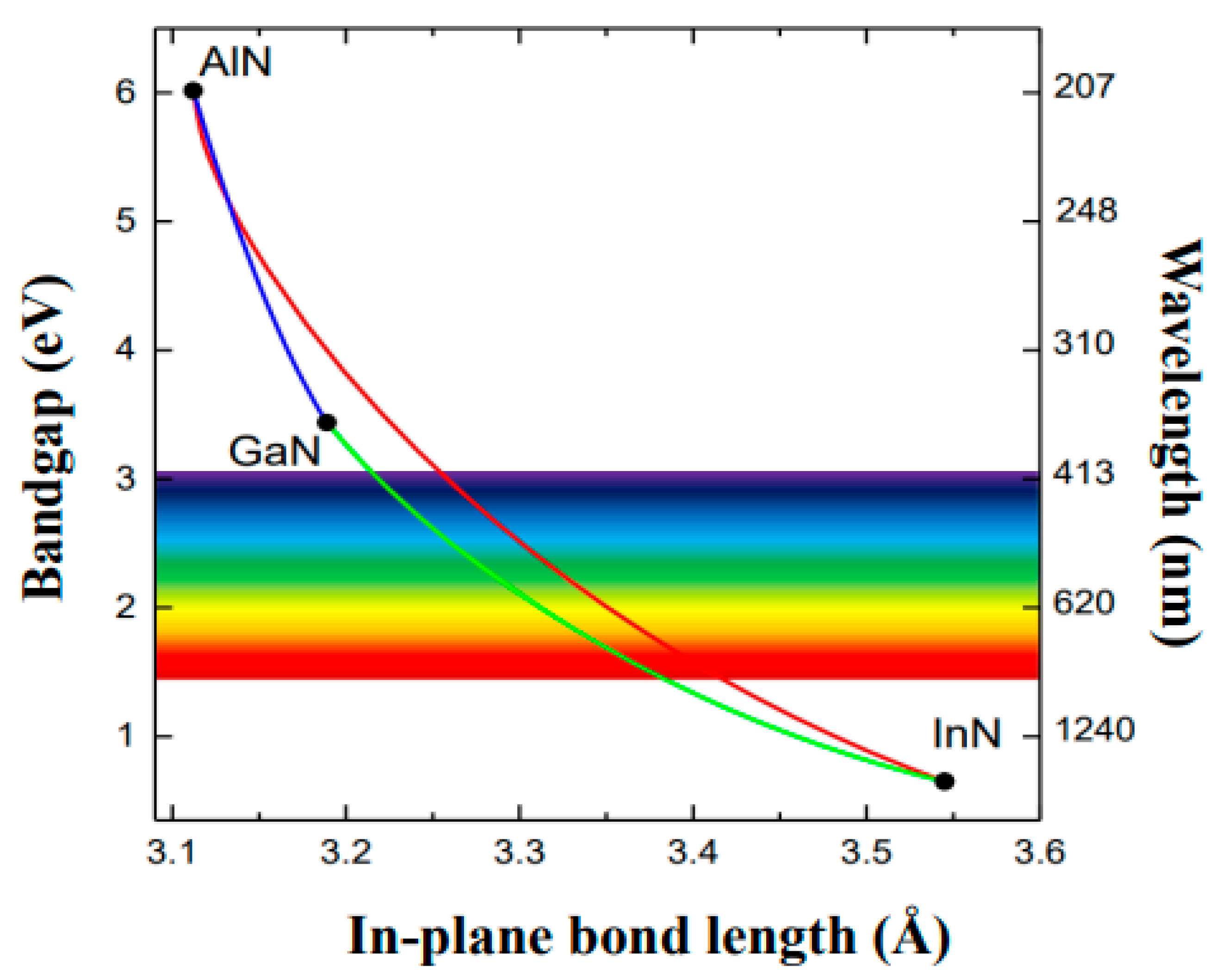
2. Properties of InN, GaN and InGaN
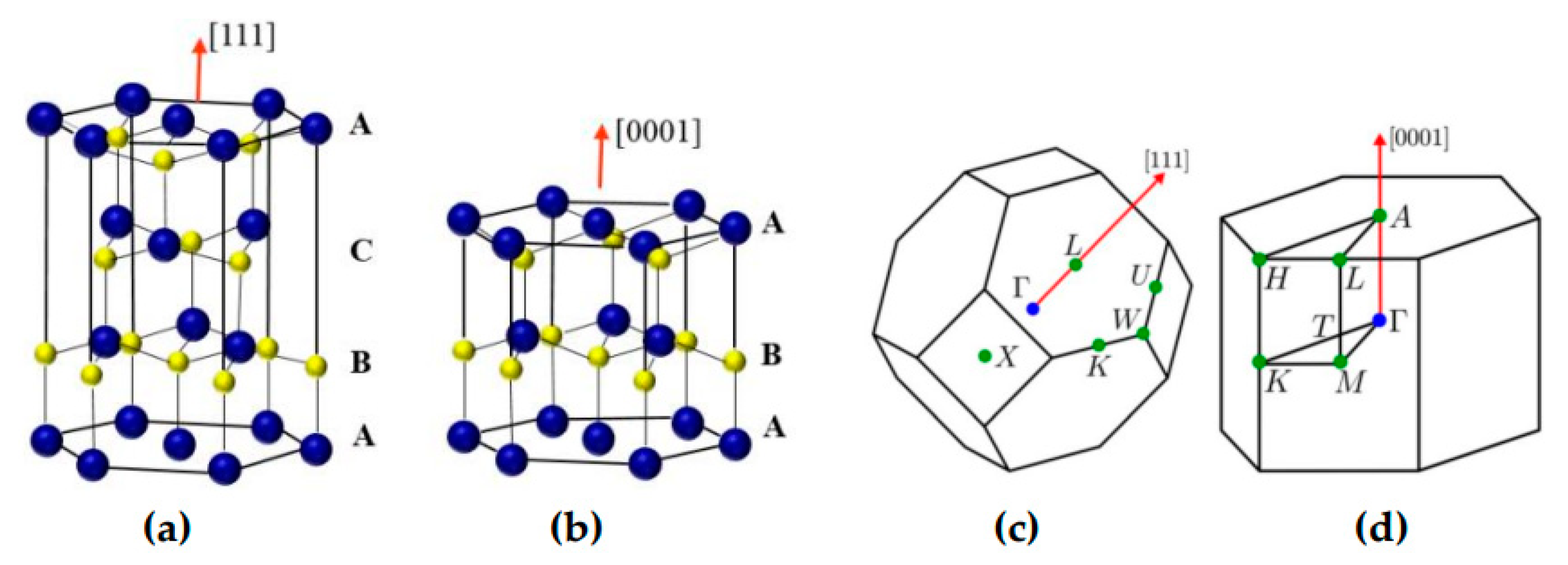
2.1. Crystal Structure
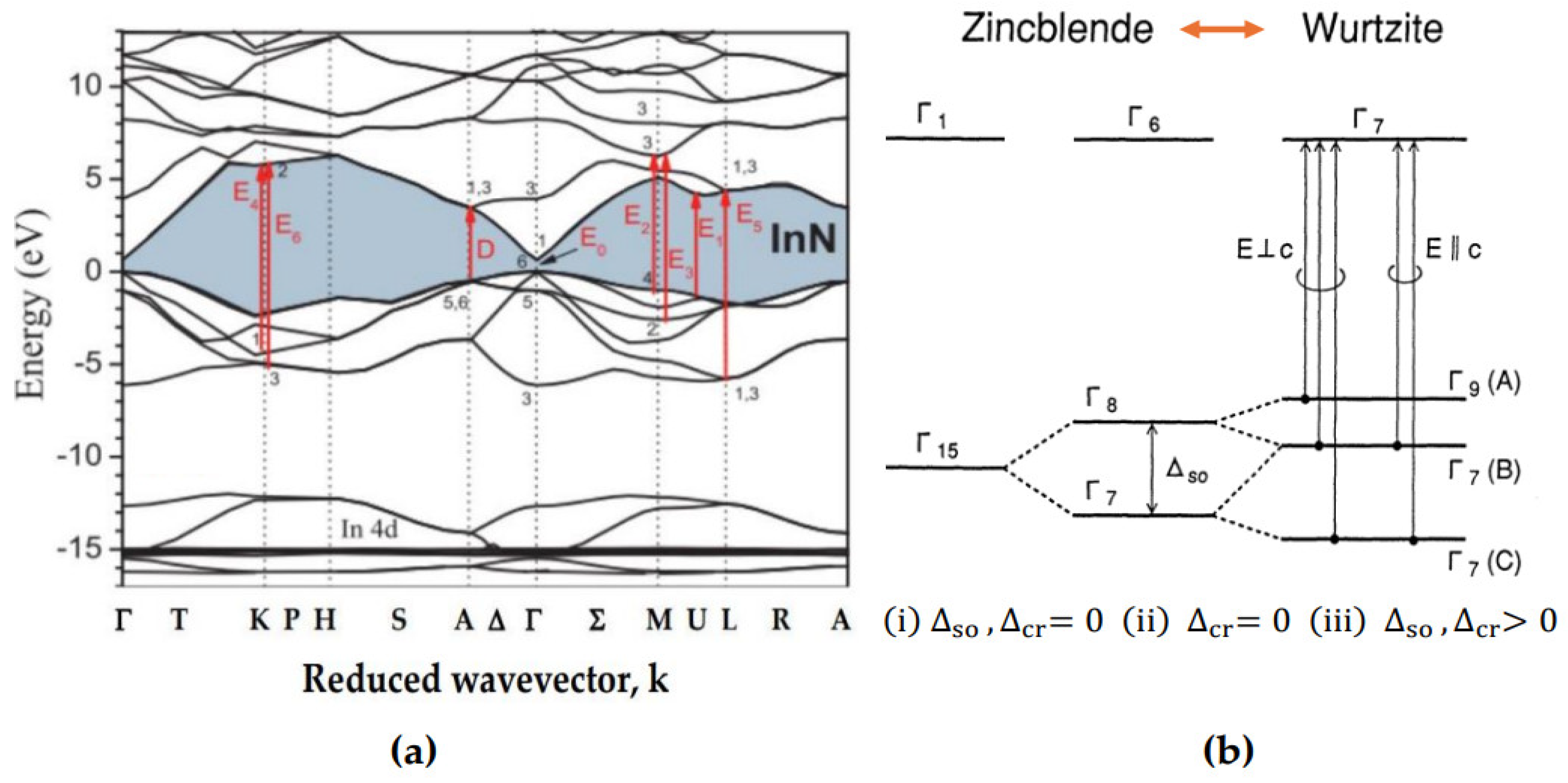
2.2. Band Structure of InN, GaN and Ternary Alloys
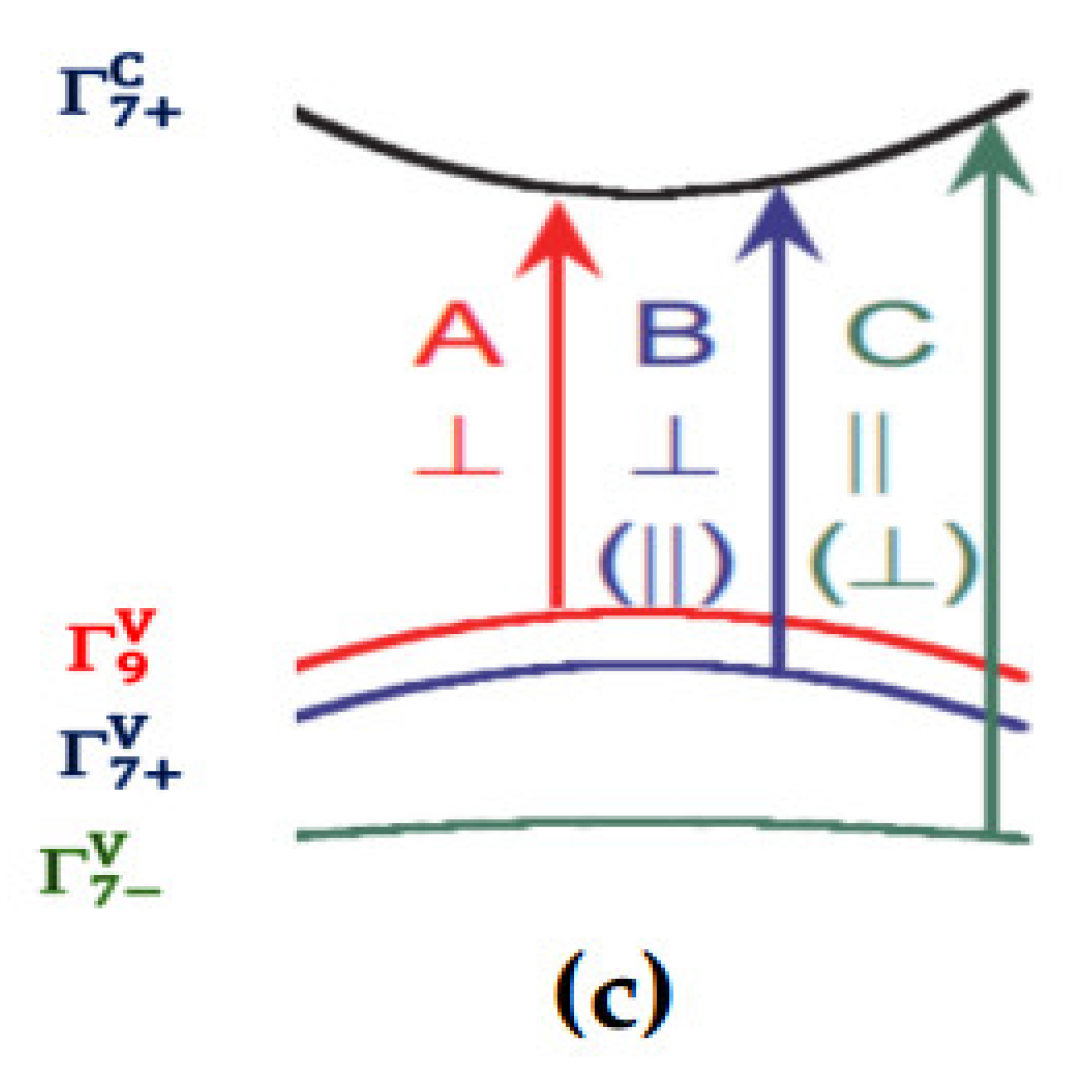
2.2.1. Optical Transitions in InN, GaN and Alloys
2.2.2. Photoluminescence Measurements in Alloys
2.3. Model Dielectric Functions of InN, GaN and
Model Dielectric Function of Sapphire
2.4. Transfer Matrix Method for Multi-Layered Structure
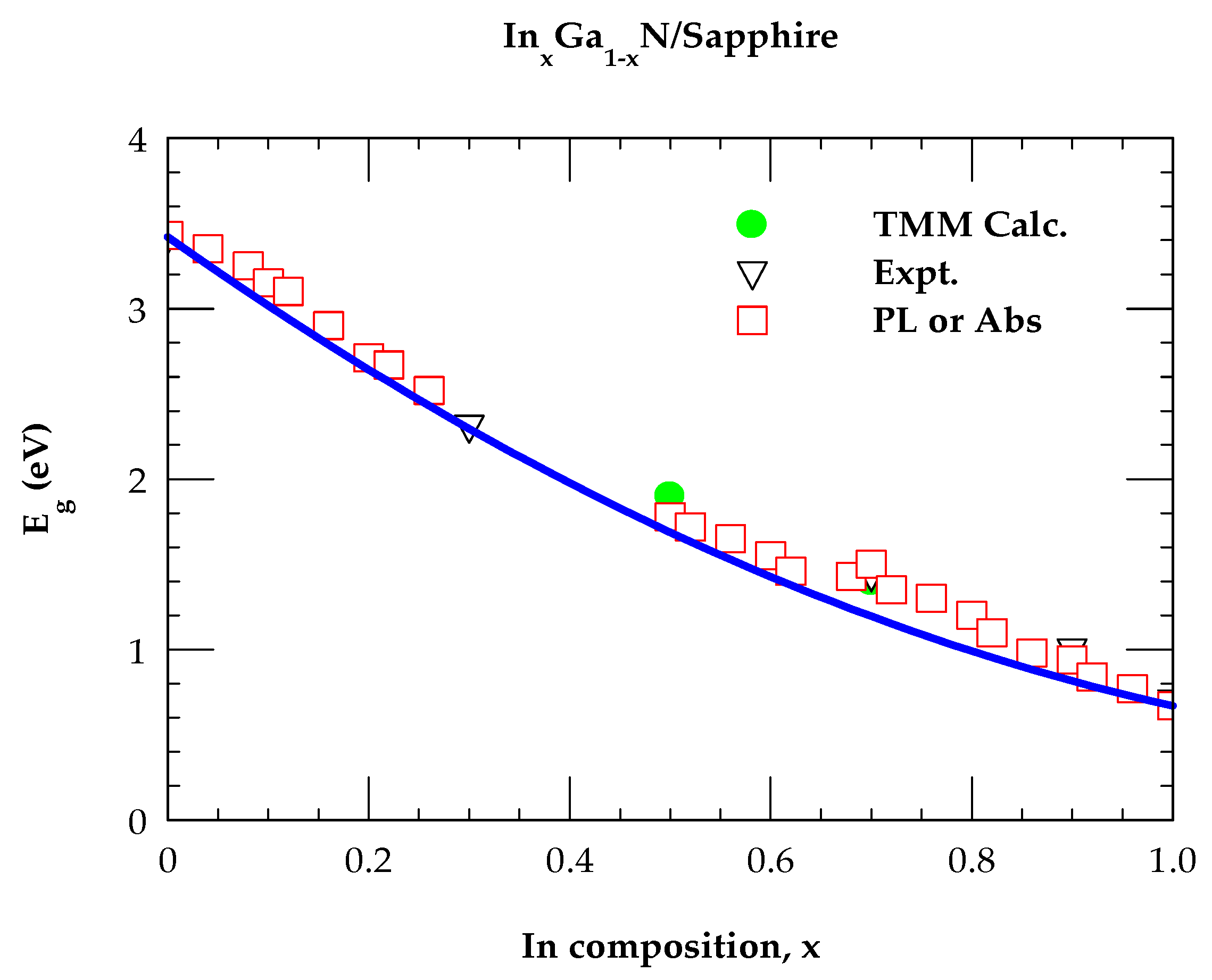
3. Numerical Computations, Results and Discussion
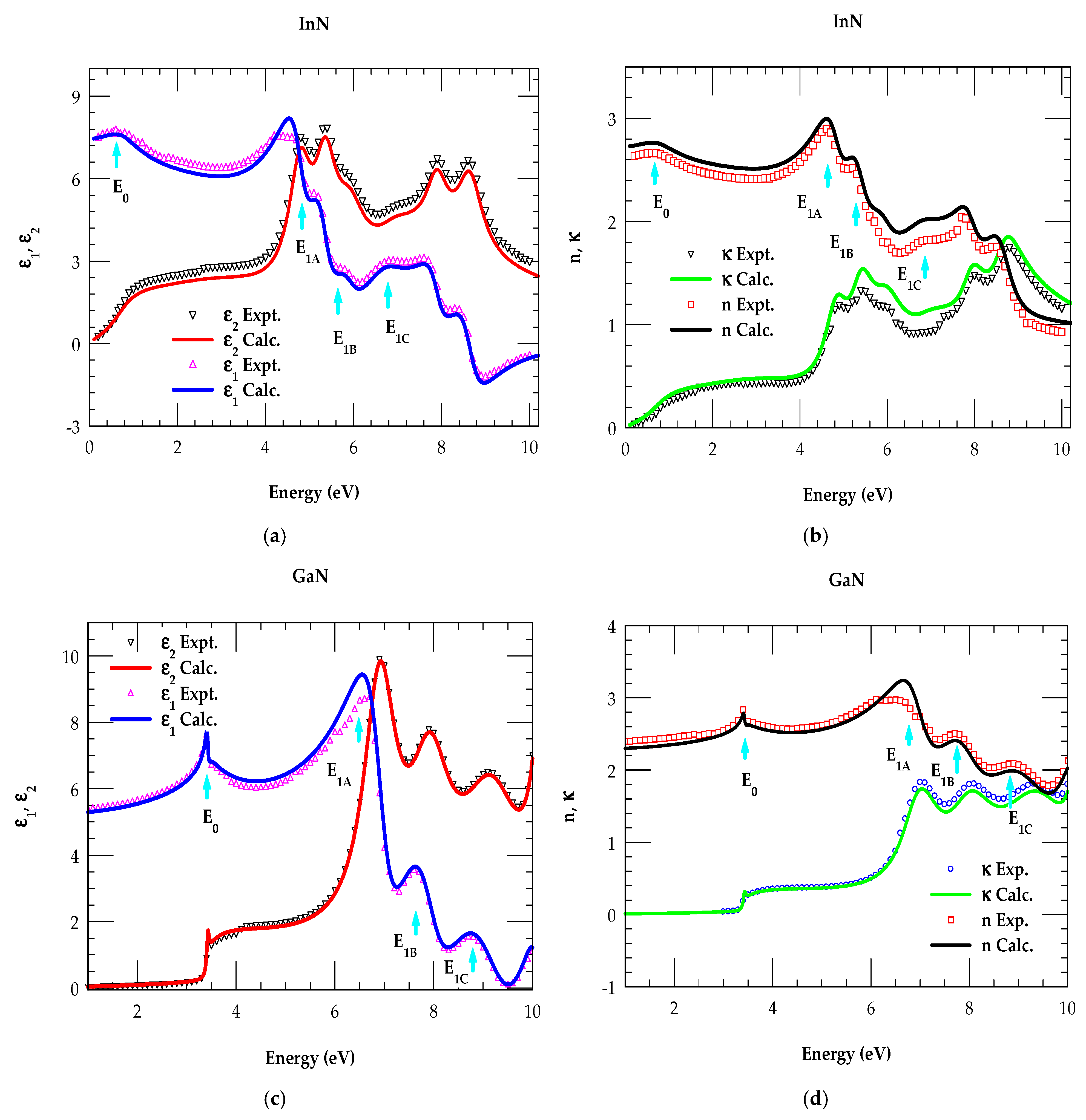
3.1. Modified Dielectric Function Parameters
Dielectric-Related Optical Constants
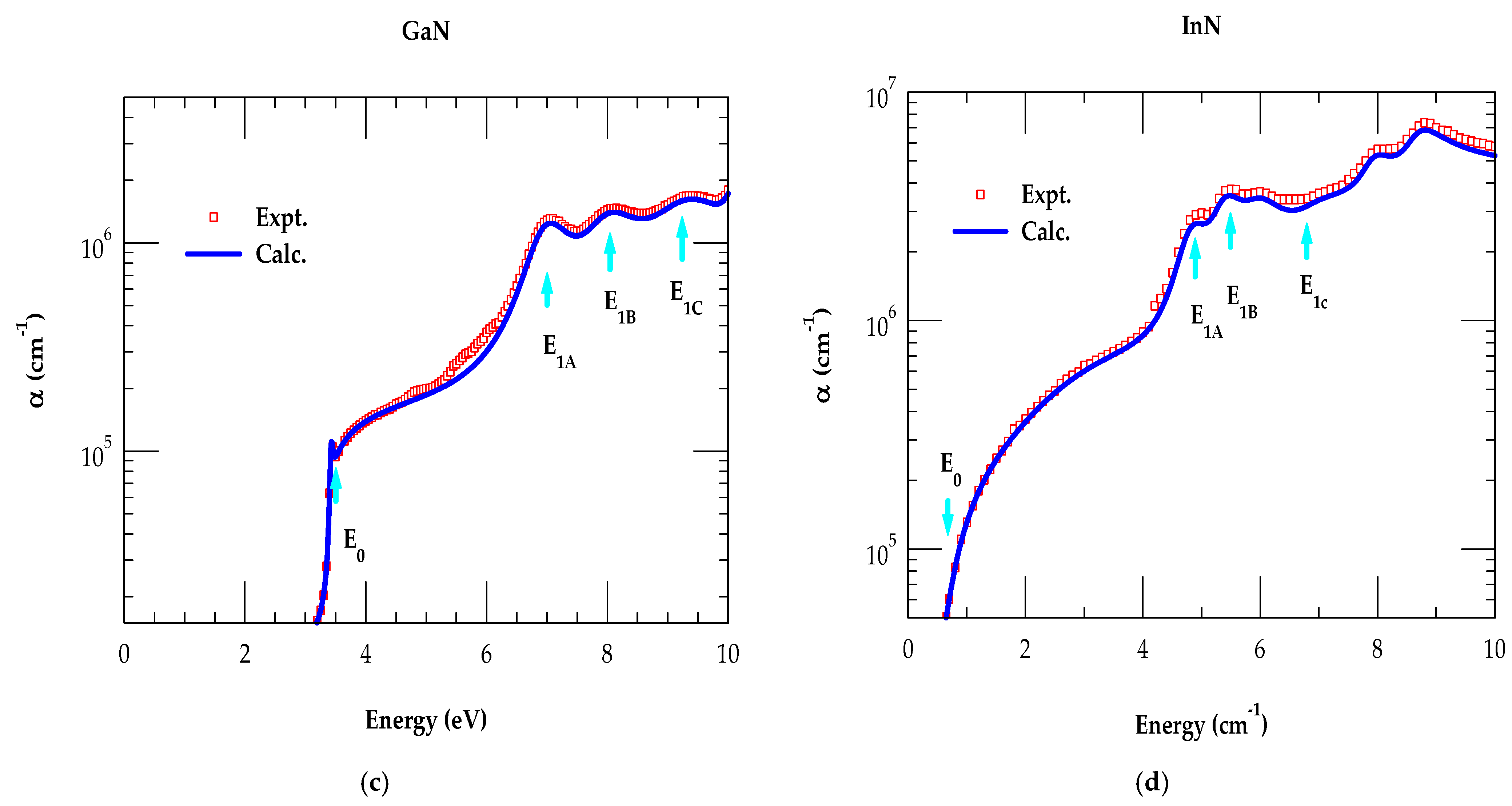
3.2. Optical Constants of Binary Materials
Reflectivity and Absorption Coefficients of Binary Materials
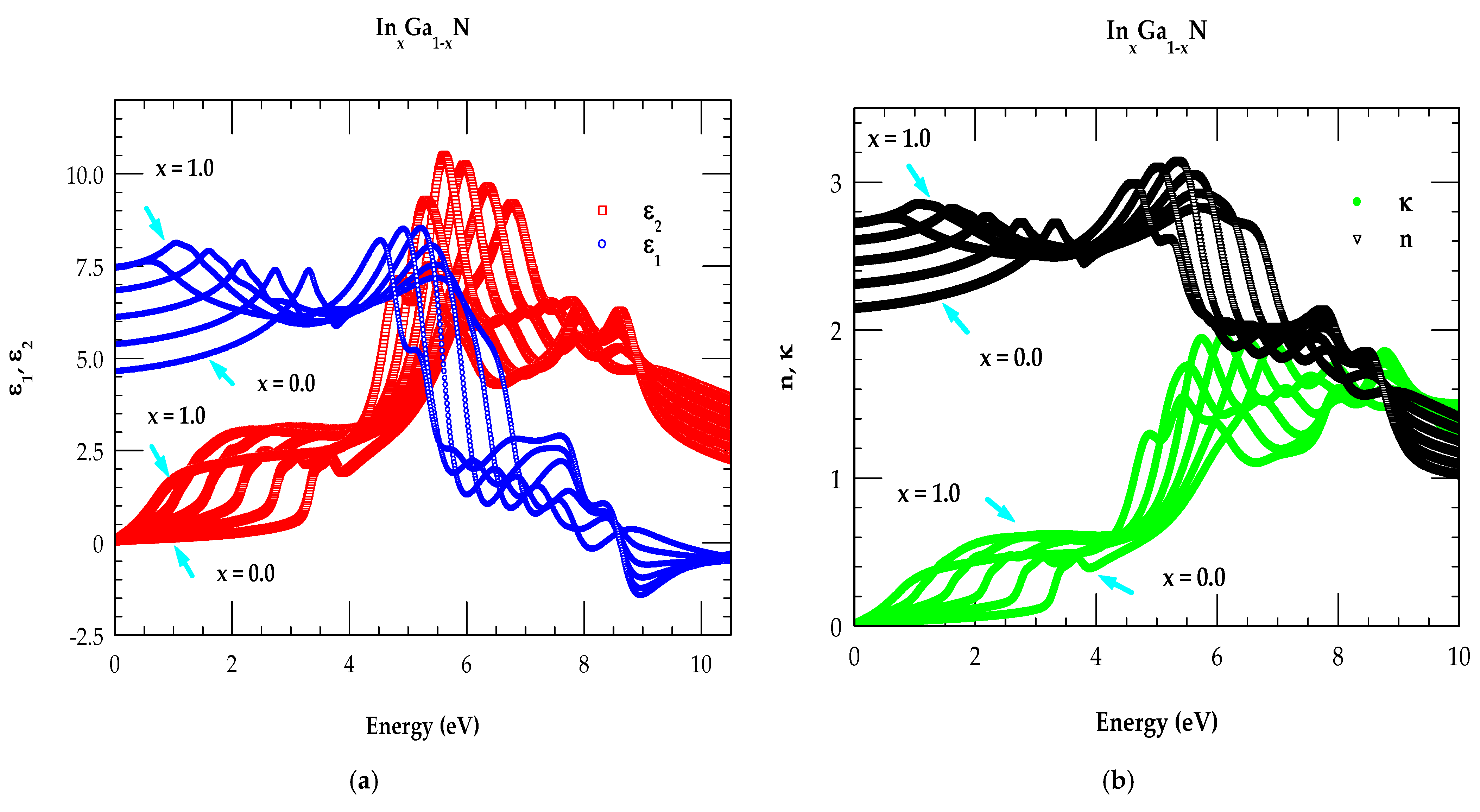
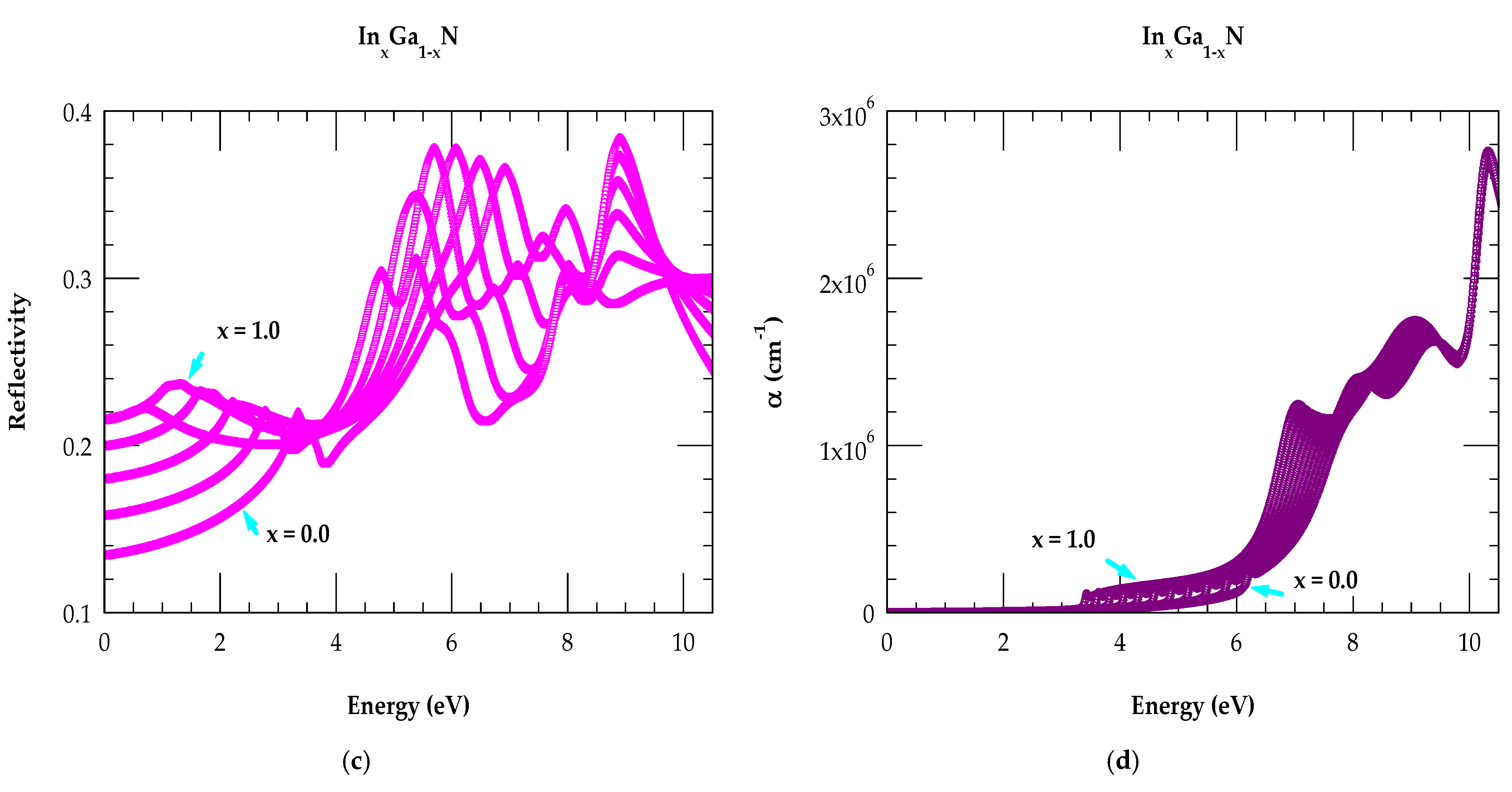
3.3. Optical Constants of InxGa1-xN Ternary Alloys
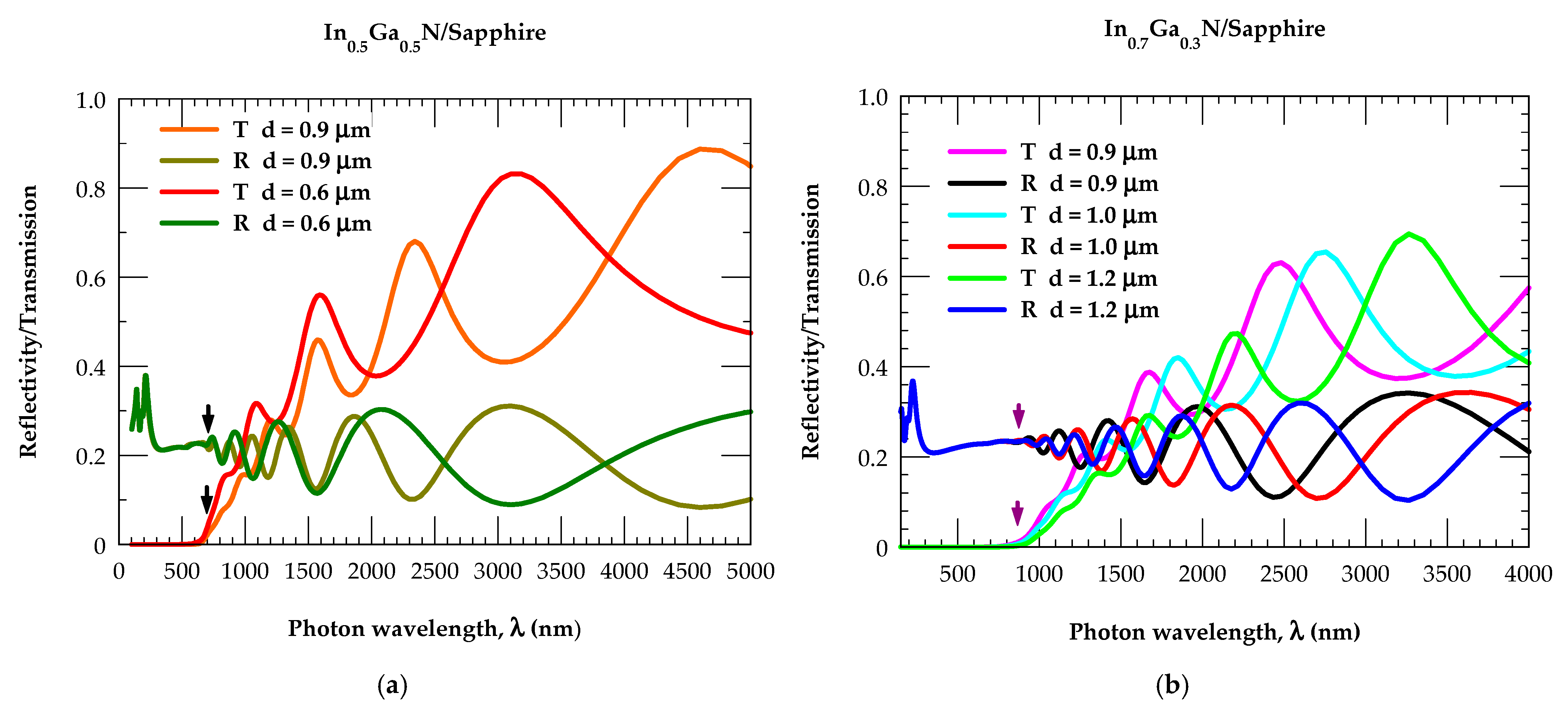
3.4. Thickness- and Composition-Dependent Reflectivity and Transmission Spectra
4. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Mauguin, C. Sur le symbolisme des groupes de repetition ou de symetrie des assemblages cristallins. Z. Kristallogr. 1931, 76, 542. [Google Scholar]
- Schoenflies, A. Theorie der Kristallstruktur; Borntraeger: Berlin, Germany, 1923. [Google Scholar]
- Adachi, S. Properties of Semiconductor Alloys: Group-IV, III–V and II–VI Semiconductors; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Adachi, S. Properties of Crystalline and Amorphous Semiconductors; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1999. [Google Scholar]
- Kawashima, T.; Yoshikawa, H.; Adachi, S.; Fuke, S.; Ohtsuka, K. Optical properties of hexagonal GaN. J. Appl. Phys. 1997, 82, 3528. [Google Scholar]
- Anwar, A.R.; Sajjad, M.T.; Johar, M.A.; Hernández-Gutiérrez, C.A.; Usman, M.; Łepkowski, S.P. Recent Progress in Micro-LED-Based Display Technologies. Laser Photonics Rev. 2022, 16, 2100427. [Google Scholar] [CrossRef]
- Li, J.; Wang, J.; Yi, X.; Liu, Z.; Wei, T.; Yan, J.; Bin, X. III-Nitrides Light Emitting Diodes: Technology and Applications; Springer Series in Materials Science: Berlin/Heidelberg, Germany, 2020; ISBN 978-981-15-7948-6. [Google Scholar] [CrossRef]
- Morkoc, H. Handbook of Nitride Semiconductors and Devices, GaN Based Optical and Electronic Devices; WILEY-VCH: Weinheim, Germany, 2009; Volume 3. [Google Scholar]
- Acharya, A.R.; Gamage, S.; Senevirathna, M.I.; Alevli, M.; Bahadir, K.; Melton, A.G.; Ferguson, I.; Dietz, N.; Thoms, B.D. Thermal stability of InN epilayers grown by high pressure chemical vapor deposition. Appl. Surf. Sci. 2013, 268, 1–5. [Google Scholar] [CrossRef]
- Dreyer, C.E.; Janotti, A.; Van de Walle, C.G.; Vanderbilt, D. Correct Implementation of Polarization Constants in Wurtzite Materials and Impact on III-Nitrides. Phys. Rev. X 2016, 6, 021038. [Google Scholar]
- Bhuiyan, A.G.; Hashimoto, A.; Yamamoto, A. Indium Nitride (InN): A Review on Growth, Characterization, and Properties. J. Appl. Phys. 2003, 94, 2779–2808. [Google Scholar] [CrossRef]
- Talwar, D.N.; Liao, Y.C.; Chen, L.C.; Chen, K.H.; Feng, Z.C. Optical properties of plasma-assisted molecular beam epitaxy grown InN/sapphire. Opt. Mater. 2014, 37, 1–4. [Google Scholar] [CrossRef]
- Talwar, D.N.; Liao, L.C.; Chen, K.H.; Feng, Z.C. Analyzing Structural Optical and Phonon Characteristics of Plasma-Assisted Molecular-Beam Epitaxy-Grown InN/Al2O3 Epifilms. Nanomaterials 2025, 15, 29. [Google Scholar]
- Vurgaftman, I.; Meyer, J.R. Band parameters for nitrogen-containing semiconductors. J. Appl. Phys. 2003, 94, 3675–3696. [Google Scholar]
- Doshi, B.; Brennan, K.F.; Bicknell-Tassius, R.; Grunthaner, F. The effect of strain-induced polarization fields on impact ionization in a multi-quantum-well structure. Appl. Phys. Lett. 1998, 73, 2784–2786. [Google Scholar]
- De Carvalho, L.C.; Schleife, A.; Bechstedt, F. Influence of exchange and correlation on structural and electronic properties of AlN, GaN, and InN polytypes. Phys. Rev. B 2011, 84, 195105. [Google Scholar]
- Bagayoko, D.; Franklin, L. Density-functional theory band gap of wurtzite InN. J. Appl. Phys. 2005, 97, 123708. [Google Scholar]
- Zhang, S.; Zhang, J.; Gao, J.; Wang, X.; Zheng, C.; Zhang, M.; Wu, X.; Xu, L.; Ding, J.; Quan, Z.; et al. Efficient emission of InGaN-based light-emitting diodes: Toward orange and red. Photonics Res. 2020, 8, 1671. [Google Scholar]
- Paszkowicz, W.; Černý, R.; Krukowski, S. Rietveld refinement for indium nitride in the 105–295 K range. Powder Diffr. 2003, 18, 114. [Google Scholar]
- Meyaard, D.S.; Lin, G.B.; Shan, Q.; Cho, J.; Fred Schubert, E.; Shim, H.; Kim, M.H.; Sone, C. Asymmetry of carrier transport leading to efficiency droop in GaInN based light-emitting diodes. Appl. Phys. Lett. 2011, 99, 251115. [Google Scholar]
- Zheng, X.; Guo, W.; Tong, C.; Zeng, P.; Chen, G.; Gao, Y.; Zhu, L.; Chen, Y.; Wang, S.; Lin, Z.; et al. Origin of the inhomogeneous electroluminescence of GaN-based green mini-LEDs unveiled by microscopic hyperspectral imaging. ACS Photonics 2022, 9, 3685. [Google Scholar]
- Kirilenko, P.; Zhuang, Z.; Iida, D.; Velazquez-Rizo, M.; Ohkawa, K. Investigation of a Separated Short-Wavelength Peak in InGaN Red Light-Emitting Diodes. Crystals 2021, 11, 1123. [Google Scholar]
- Li, J.; Li, C.; Xu, M.; Ji, Z.; Shi, K.; Xu, X.; Li, H.; Xu, X. “W-shaped” injection current dependence of electroluminescence line-width in green InGaN/GaN-based LED grown on silicon substrate. Opt. Express 2017, 25, A871. [Google Scholar]
- Wang, Z.; Zhu, S.; Shan, X.; Yuan, Z.; Qian, Z.; Lu, X.; Fu, Y.; Tu, K.; Guan, H.; Cui, X.; et al. Red, green and blue InGaN micro-LEDs for display application: Temperature and current density effects. Opt. Express 2022, 30, 36403. [Google Scholar]
- Lin, C.C.; Wu, Y.R.; Kuo, H.C.; Wong, M.S.; DenBaars, S.P.; Nakamura, S.; Pandey, A.; Mi, Z.; Tian, P.; Ohkawa, K.; et al. The micro-LED roadmap: Status quo and prospects. J. Phys. Photonics 2023, 5, 042502. [Google Scholar]
- Mánuel, J.M.; Morales, F.M.; García, R.; Lim, T.; Kirste, L.; Aidam, R.; Ambacher, O. Improved Structural and Chemical Properties of Nearly Lattice-Matched Ternary and Quaternary Barriers for GaN-Based HEMTs. Cryst. Growth Des. 2011, 11, 2588–2591. [Google Scholar]
- Zhuang, Z.; Iida, D.; Velazquez-Rizo, M.; Ohkawa, K. 630-nmred InGaN micro-light-emitting diodes (<20 μm × 20 μm) exceeding 1 mW/mm2 for full-color micro-displays. Photonics Res. 2021, 9, 1796. [Google Scholar]
- Iida, D.; Ohkawa, K. Recent progress in red light-emitting diodes by III-nitride materials. Semicond. Sci. Technol. 2022, 37, 013001. [Google Scholar]
- Pandey, A.; Xiao, Y.; Reddeppa, M.; Malhotra, Y.; Liu, J.; Min, J.; Wu, Y.; Mi, Z. A red-emitting micrometer scale LED with external quantum efficiency > 8%. Appl. Phys. Lett. 2023, 122, 151103. [Google Scholar]
- Shi, J.; Zhao, P.; Wang, X. Piezoelectric-polarization-enhanced Photovoltaic Performance in Depleted-heterojunction Quantum-Dot Solar Cells. Adv. Mater. 2013, 25, 916–921. [Google Scholar]
- Zheng, X.; Guo, W.; Tong, C.; Zeng, P.; Chen, C.; Gao, Y.; Chen, G.; Ke, Z.; Zheng, Z.; Zhu, L.; et al. Exciton distribution-induced efficiency droop in green microscale light-emitting diodes at cryogenic temperatures. Appl. Phys. Lett. 2022, 121, 201109. [Google Scholar]
- Veal, T.D.; McConville, C.F.; Schaff, W.J. (Eds.) Indium Nitride and Related Alloys; CRC Press/Taylor Francis: Boca Raton, FL, USA, 2010. [Google Scholar]
- Bernardini, F.; Fiorentini, V.; Vanderbilt, D. Spontaneous polarization and piezoelectric constants of III-V nitrides. Phys. Rev. B 1997, 56, R10024–R10027. [Google Scholar]
- Filho, M.A.M.; Farmer, W.; Hsiao, C.-L.; dos Santos, R.B.; Hultman, L.; Birch, J.; Kumar, A.; Gueorguiev, G.K. Density Functional Theory-Fed Phase Field Model for Semiconductor Nanostructures: The Case of Self-Induced Core−Shell InAlN Nanorods. Cryst. Growth Des. 2024, 24, 4717–4727. [Google Scholar]
- Cao, L.; Fan, P.; Vasudev, A.P.; White, J.S.; Yu, Z.; Cai, W.; Schuller, J.A.; Fan, S.; Brongersma, M.L. Semiconductor Nanowire Optical Antenna Solar Absorbers. Nano Lett. 2010, 10, 439–445. [Google Scholar]
- LaPierre, R.R.; Robson, M.; Azizur-Rahman, K.M.; Kuyanov, P. A Review of III-V Nanowire Infrared Photodetectors and Sensors. J. Phys. D Appl. Phys. 2017, 50, 123001. [Google Scholar]
- Hammersley, S.; Watson-Parris, D.; Dawson, P.; Godfrey, M.J.; Badcock, T.J.; Kappers, M.J.; McAleese, C.; Oliver, R.A.; Humphreys, C.J. The consequences of high injected carrier densities on carrier localization and efficiency droop in InGaN/GaN quantum well structures. J. Appl. Phys. 2012, 111, 083512. [Google Scholar]
- Chiu, Y.C.; Bayram, C. Low temperature absolute internal quantum efficiency of InGaN-based light-emitting diodes. Appl. Phys. Lett. 2023, 122, 091101. [Google Scholar]
- Langer, T.; Jonen, H.; Kruse, A.; Bremers, H.; Rossow, U.; Hangleiter, A. Strain-induced defects as nonradiative re-combination centers in green-emitting GaInN/GaN quantum well structures. Appl. Phys. Lett. 2013, 103, 022108. [Google Scholar]
- Abate, Y.; Seidlitz, D.; Fali, A.; Gamage, S.; Babicheva, V.; Yakovlev, V.S.; Stockman, M.I.; Collazo, R.; Alden, D.; Dietz, N. Nanoscopy of Phase Separation in InxGa1−xN Alloys. ACS Appl. Mater. Interfaces 2016, 8, 23160–23166. [Google Scholar] [CrossRef]
- Talwar, D.N.; Becla, P. Microhardness, Young’s and Shear Modulus in Tetrahedrally Bonded Novel II-Oxides and III-Nitrides. Materials 2025, 18, 494. [Google Scholar] [CrossRef]
- Duxbury, N.; Bangert, U.; Dawson, P.; Thrush, E.J.; Van der Stricht, W.; Jacobs, K.; Moerman, I. Indium segregation in InGaN quantum-well structures. Appl. Phys. Lett. 2000, 76, 1600. [Google Scholar]
- Hirako, A.; Kusakabe, K.; Ohkawa, K. Modeling of Reaction Pathways of GaN Growth by Metalorganic Vapor-Phase Epitaxy Using TMGa/NH3/H2 System: A Computational Fluid Dynamics Simulation Study. Jpn. J. Appl. Phys. 2005, 44, 874–879. [Google Scholar]
- Ozturk, M.K.; Corekci, S.; Tamer, M.; Cetin, S.S.; Ozcelik, S.; Ozbay, E. Microstructural Properties of InGaN/GaN Light-Emitting Diode Structures with Different In Content Grown by MOCVD. Appl. Phys. A Mater. Sci. Process. 2014, 114, 1215–1221. [Google Scholar]
- Su, X.; Ye, T.; Wang, S.; Shi, Y.; Fan, L.; Liu, L.; Zhang, G.; Shi, X.; Wei, M.; Zhou, H.; et al. Surface Morphology of GaN Nucleation Layer Grown by MOCVD with Different Carrier Gas. AIP Adv. 2018, 8, 075301. [Google Scholar]
- Rogers, D.J.; Teherani, F.H.; Ougazzaden, A.; Gautier, S.; Divay, L.; Lusson, A.; Durand, O.; Wyczisk, F.; Garry, G.; Monteiro, T.; et al. Use of ZnO Thin Films as Sacrificial Templates for Metal Organic Vapor Phase Epitaxy and Chemical Lift-off of GaN. Appl. Phys. Lett. 2007, 91, 071120. [Google Scholar]
- Wang, J. Optical Properties of In1-xGaxN Epilayers Grown by HPCVD. Master’s Thesis, Georgia State University, Atlanta, GA, USA, 2010. [CrossRef]
- Tchernycheva, M.; Sartel, C.; Cirlin, G.; Travers, L.; Patriarche, G.; Harmand, J.; Dang, L.S.; Renard, J.; Gayral, B.; Nevou, L.; et al. Growth of GaN Free-Standing Nanowires by Plasma-Assisted Molecular Beam Epitaxy: Structural and Optical Characterization. Nanotechnology 2007, 18, 385306. [Google Scholar] [CrossRef]
- Goodman, K.D.; Protasenko, V.V.; Verma, J.; Kosel, T.H.; Xing, H.G.; Jena, D. Green Luminescence of InGaN Nanowires Grown on Silicon Substrates by Molecular Beam Epitaxy. J. Appl. Phys. 2011, 109, 084336. [Google Scholar] [CrossRef]
- Gridchin, V.O.; Kotlyar, K.P.; Reznik, R.R.; Dragunova, A.S.; Kryzhanovskaya, N.V.; Lendyashova, V.V.; Kirilenko, D.A.; Soshnikov, I.P.; Shevchuk, D.S.; Cirlin, G.G. Multi-Colour Light Emission from InGaN Nanowires Monolithically Grown on Si Substrate by MBE. Nanotechnology 2021, 32, 335604. [Google Scholar] [CrossRef]
- Gridchin, V.; Kotlyar, K.; Reznik, R.; Shevchuk, D.; Kirilenko, D.; Bert, N.; Soshnikov, I.; Cirlin, G. Peculiarities of the Structural Properties of InxGa1-xN Polytype Nanostructures Grown by Molecular-Beam Epitaxy. J. Phys. Conf. Ser. 2020, 1482, 012014. [Google Scholar] [CrossRef]
- De, A.; Tangi, M.; Shivaprasad, S. Pre-Nitridation Induced In Incorporation in InxGa1− xN Nanorods on Si (111) Grown by Molecular Beam Epitaxy. J. Appl. Phys. 2015, 118, 025301. [Google Scholar] [CrossRef]
- Valdueza-Felip, S.; Bellet-Amalric, E.; Núñez-Cascajero, A.; Wang, Y.; Chauvat, M.-P.; Ruterana, P.; Pouget, S.; Lorenz, K.; Alves, E.; Monroy, E. High In-Content InGaN Layers Synthesized by Plasma-Assisted Molecular-Beam Epitaxy: Growth Conditions, Strain Relaxation, and In Incorporation Kinetics. J. Appl. Phys. 2014, 116, 233504. [Google Scholar] [CrossRef]
- Grandal, J.; Sánchez-García, M.; Calleja, E.; Luna, E.; Trampert, A. Accommodation Mechanism of InN Nanocolumns Grown on Si (111) Substrates by Molecular Beam Epitaxy. Appl. Phys. Lett. 2007, 91, 021902. [Google Scholar] [CrossRef]
- Fedorov, V.; Bolshakov, A.; Kirilenko, D.; Mozharov, A.; Sitnikova, A.; Sapunov, G.; Dvoretckaia, L.; Shtrom, I.; Cirlin, G.; Mukhin, I. Droplet Epitaxy Mediated Growth of GaN Nanostructures on Si (111) via Plasma-Assisted Molecular Beam Epitaxy. CrystEngComm 2018, 20, 3370–3380. [Google Scholar] [CrossRef]
- Tourbot, G.; Bougerol, C.; Grenier, A.; Den Hertog, M.; Sam-Giao, D.; Cooper, D.; Gilet, P.; Gayral, B.; Daudin, B. Structural and Optical Properties of InGaN/GaN Nanowire Heterostructures Grown by PA-MBE. Nanotechnology 2011, 22, 075601. [Google Scholar] [CrossRef]
- Morassi, M.; Largeau, L.; Oehler, F.; Song, H.-G.; Travers, L.; Julien, F.H.; Harmand, J.-C.; Cho, Y.-H.; Glas, F.; Tchernycheva, M.; et al. Morphology Tailoring and Growth Mechanism of Indium-Rich InGaN/GaN Axial Nanowire Heterostructures by Plasma-Assisted Molecular Beam Epitaxy. Cryst. Growth Des. 2018, 18, 2545–2554. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Nanishi, Y. Indium Droplet Elimination by Radical Beam Irradiation for Reproducible and High-Quality Growth of InN by RF Molecular Beam Epitaxy. Appl. Phys. Express 2009, 2, 5. [Google Scholar]
- Rahman, A.; Hossain, E.; Hussain, S. An Insight Analysis of In0.7Ga0.3N Based pn Homo-Junction Solar Cell using SCAPS-1D Simulation Software. Appl. Sol. Energy 2023, 59, 818–827. [Google Scholar]
- Zhao, C.; Zhang, R.; Liu, B.; Fu, D.; Chen, H.; Li, M.; Xie, Z.; Xiu, X.; Gu, S.; Zheng, Y. The Temperature Dependence of Optical Properties of InGaN Alloys. Sci. China: Phys. Mech. Astron. 2012, 55, 396–399. [Google Scholar]
- Levinshtein, M.E.; Rumyantsev, S.L.; Shur, M.S. Properties of Advanced Semiconductor Materials: GaN, AIN, InN, BN, SiC, SiGe; Wiley: New York, NJ, USA, 2001. [Google Scholar]
- Shimosako, N.; Kinjo, K.; Inose, Y.; Nakaoka, T.; Oto, T.; Kishino, K.; Ema, K. Energy diagram and parameters regarding localized states in InGaN/GaN nanocolumns. J. Appl. Phys. 2021, 130, 143106. [Google Scholar]
- Reshchikov, M.A. Measurement and analysis of photo luminescence in GaN. J. Appl. Phys. 2021, 129, 121101. [Google Scholar]
- Yin, J.; Fathi, E.; Siboni, H.Z.; Xu, C.; Ban, D. Efficiency degradation induced by surface defects-assisted tunneling recombi-nation in GaN/InGaN micro-light-emitting diodes. Appl. Phys. Lett. 2021, 118, 021105. [Google Scholar]
- Stiegler, J.M.; Abate, Y.; Cvitkovic, A.; Romanyuk, Y.E.; Huber, A.J.; Leone, S.R.; Hillenbrand, R. Nanoscale Infrared Absorption Spectroscopy of Individual Nanoparticles Enabled by Scattering-Type Near-Field Microscopy. ACS Nano 2011, 5, 6494–6499. [Google Scholar]
- Knoll, B.; Keilmann, F. Enhanced Dielectric Contrast in Scattering-Type Scanning Near-Field Optical Microscopy. Opt. Commun. 2000, 182, 321–328. [Google Scholar] [CrossRef]
- Ibáñez, J.; Segura, A.; Manjón, F.J.; Artús, L.; Yamaguchi, T.; Nanishi, Y. Electronic structure of wurtzite and rocksalt InN investigated by optical absorption under hydrostatic pressure. Appl. Phys. Lett. 2010, 96, 201903. [Google Scholar] [CrossRef]
- Maurya, T.K.; Kumar, S.; Auluck, S. Ab-initio study of electronic and optical properties of InN in wurtzite and cubic phases. Opt. Commun. 2010, 283, 4655–4661. [Google Scholar]
- Bulutay, C.; Turgut, C.M.; Zakhleniuk, N.A. Carrier-induced refractive index change and optical absorption in wurtzite InN and GaN: Full-band approach. Phys. Rev. B 2010, 81, 155206. [Google Scholar]
- Goldhahn, R.; Winzer, A.T.; Cimalla, V.; Ambacher, O.; Cobet, C.; Richter, W.; Esser, N.; Furthmüller, J.; Bechstedt, F.; Lu, H.; et al. Anisotropy of the dielectric function for wurtzite InN. Superlattices Microstruct. 2004, 36, 591–597. [Google Scholar]
- Goldhahn, R.; Schley, P.; Winzer, A.T.; Gobsch, G.; Cimalla, V.; Ambacher, O.; Rakel, M.; Cobet, C.; Esser, N.; Lu, H.; et al. Detailed analysis of the dielectric function for wurtzite InN and In-rich InAlN alloys. Phys. Stat. Sol. (a) 2006, 203, 42–49. [Google Scholar]
- Buchheim, C.; Goldhahn, R.; Rakel, M.; Cobet, C.; Esser, N.; Rossow, U.; Fuhrmann, D.; Hangleiter, A. Dielectric function and critical points of the band structure for AlGaN alloys. Phys. Stat. Sol. (b) 2005, 242, 2610–2616. [Google Scholar]
- Yu, G.; Wang, G.; Ishikawa, H.; Umeno, M.; Soga, T.; Egawa, T.; Watanabe, J.; Jimbo, T. Optical properties of wurtzite structure GaN on sapphire around fundamental absorption edge (0.78–4.77 eV) by spectroscopic ellipsometry and the optical transmission method. Appl. Phys. Lett. 1997, 70, 3209–3211. [Google Scholar] [CrossRef]
- Guo, Q.; Kato, O.; Fujisawa, M.; Yoshida, A. Optical constants of indium nitride. Solid State Commun. 1992, 83, 721. [Google Scholar]
- Guo, Q.; Ogawa, H.; Yoshida, A. Optical properties of indium nitride in vacuum ultraviolet region. J. Electron Spectrosc. Relat. Phenom. 1996, 79, 9–12. [Google Scholar]
- Lambrecht, W.R.L.; Segall, B.; Rife, J.; Hunter, W.R.; Wickenden, D.K. UV Reflectivity of GaN: Theory and experiment. Phys. Rev. B 1995, 51, 13516. [Google Scholar]
- Logothetidis, S.; Petalas, J.; Cardona, M.; Moustakas, T.D.; Logothetidis, S.; Petalas, J.; Cardona, M.; Moustakas, T.D. The optical properties and electronic transitions of cubi and hexagonal GaN films between 1.5 and 10 eV. Mat. Sci. Eng. 1995, 29, 65. [Google Scholar]
- Bloom, S.; Harbeke, G.; Meier, E.; Ortenburger, I.B. Band Structure and Reflectivity of GaN. Phys. Stat. Solidi B 1974, 66, 161. [Google Scholar]
- Olson, C.G.; Lynch, D.W.; Zehe, A. 10—30-eV optical properties of GaN. Phys. Rev. B 1981, 24, 4629. [Google Scholar] [CrossRef]
- Talwar, D.N. Transfer matrix method for calculating UV–Vis reflectivity/transmission spectra to assess thickness of nanostructured zb CdSe and ZnSe flms grown on GaAs (001). Appl. Phys. A 2023, 129, 44. [Google Scholar] [CrossRef]
- Castiblanco, R.; Vargas, J.; Morales, J.; Torres, J.; Pardo, A. Determination of the Optical Properties of ZnSe Thin Films Using the Transfer Matrix Method. J. Phys. Conf. Ser. 2014, 480, 012025. [Google Scholar] [CrossRef]
- Larramendi, E.M.; Puron, E.; de Melo, O. Thickness measurement and optical properties of very thin ZnxCd(1−x)Te layers. Semicond. Sci. Technol. 2002, 17, 8–12. [Google Scholar]
- Djurišić, A.B.; Li, E.H. Modeling the optical constants of hexagonal GaN, InN, and AlN. J. Appl. Phys. 1999, 85, 2848. [Google Scholar] [CrossRef]
- Cardona, M. Reflectivity of Semiconductors with Wurtzite Structure. Phys. Rev. 1963, 129, 1068. [Google Scholar] [CrossRef]
- Wu, J.; Walukiewicz, W.; Yu, K.M.; Ager, J.W., III; Haller, E.E.; Lu, H.; Schaff, W.J. Small band gap bowing in InxGa1−xN alloys. Appl. Phys. Lett. 2002, 80, 4741–4743. [Google Scholar] [CrossRef]
- Larramendi, E.M.; Gutiérrez, Z.-B.K.; Arens, C.; Woggon, U.; Schikora, D.; Lischka, K. Growth of ZnSe1−xTex epilayers by isothermal closed space sublimation. J. Appl. Phys. 2010, 107, 103510. [Google Scholar] [CrossRef]
- Heavens, O.S. Optical Properties of Thin Films; Dover: New York, NJ, USA, 1965. [Google Scholar]
- Kim, C.C.; Garland, J.W.; Abad, H.; Raccah, P.M. Modeling the optical dielectric function of semiconductors: Extension of the critical-point parabolic-band approximation. Phys. Rev. B 1992, 45, 11749. [Google Scholar]

| Parameter | wz InN | Others (a) | zb InN | Others (a) | wz GaN | Others (a) | zb GaN | Others (a) |
|---|---|---|---|---|---|---|---|---|
| 0.70 | 0.72, 0.69 | 0.56 | 0.54, 0.53 | 3.43 | 3.435 | 3.07 | ||
| 3.549 | 3.49, 3.533 | 5.01 | 5.169, 4.98 | 3.189 | 3.156, 3.242 | 4.49 | 4.461, 4.582 | |
| 5.736 | 5.61, 5.693 | 5.185 | 5.280, 5.145 | |||||
| Thermal stability (°C) | 630 | 800–900 | ||||||
| Saturated velocity (cm/s) | 3.5 × 107 | 2.0 × 107 | ||||||
| Spontan. pol const. C/m2 | 1.026 | 1.312 | ||||||
| K (W·m−1·K−1) | 120 | 80, 142 | 227 | 130, 253 | ||||
| μ (cm2/Vs) | 3000 | 2500–2700 | 1000 | 900–1100 | ||||
| 0.071 | 0.054 | 0.212 | 0.193 | |||||
| 0.067 | 0.190 | |||||||
| 67 | 40, 35.6 | 9.2 | 17, 28.5 | |||||
| 13 | 5 | 18.9 | 10, 15.9 |
| Parameter | GaN | InN | InxGa1−xN |
|---|---|---|---|
| 0.426 | 1.50 | 0.426 + 1.074x | |
| 41.251 | 3.000 | 41.251 − 38.251x | |
| 0.287 | 0.300 | 0.287 + 0.013x | |
| 1.241 | 1.241 | 1.241 + 0.0x | |
| 3.42 | 0.70 | 3.42 − 2.72x | |
| 0.778 | 1.10 | 0.778 + 0.322x | |
| 0.103 | 0.700 | 0.103 + 0.597x | |
| 0.920 | 0.550 | 0.92 − 0.37x | |
| 2.042 | 1.042 | 2.042 − 1.0x | |
| 1.024 | 0.624 | 1.024 − 0.4x | |
| 1.997 | 1.400 | 1.997 − 0.597x | |
| 0.743 | 0.300 | 0.743 − 0.443x | |
| 0.428 | 0.380 | 0.428 − 0.048x | |
| 0.440 | 0.320 | 0.440 − 0.12x | |
| 0.0003 | 0.0003 | 0.0003 + 0.0x | |
| 0.356 | 0.356 | 0.356 + 0.0x | |
| 1.962 | 1.962 | 1.962 + 0.0x | |
| 6.010 | 5.353 | 6.010 − 0.657x | |
| 8.182 | 6.290 | 8.182 − 1.892x | |
| 8.761 | 6.750 | 8.761 − 2.011x | |
| 0.249 | 0.010 | 0.249 − 0.239x | |
| 0.030 | 0.020 | 0.030 − 0.01x | |
| 3.900 | 3.900 | 3.900 + 0.0x | |
| 0.000 | 29.00 | 0.000 + 29.00x | |
| 5.200 | 5.200 | 5.200 + 0.0x | |
| 7.900 | 7.900 | 7.900 + 0.0x | |
| 0.000 | 10.00 | 0.00 + 10.00x | |
| 0.600 | 0.600 | 0.600 + 0.0x | |
| 8.650 | 8.650 | 8.650 + 0.0x | |
| 0.000 | 17.00 | 0.00 + 17.00x | |
| 0.700 | 0.700 | 0.700 + 0.0x |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Talwar, D.N.; Lin, H.-H.; Haraldsen, J.T. A Modified Model Dielectric Function for Analyzing Optical Spectra of InGaN Nanofilms on Sapphire Substrates. Nanomaterials 2025, 15, 485. https://doi.org/10.3390/nano15070485
Talwar DN, Lin H-H, Haraldsen JT. A Modified Model Dielectric Function for Analyzing Optical Spectra of InGaN Nanofilms on Sapphire Substrates. Nanomaterials. 2025; 15(7):485. https://doi.org/10.3390/nano15070485
Chicago/Turabian StyleTalwar, Devki N., Hao-Hsiung Lin, and Jason T. Haraldsen. 2025. "A Modified Model Dielectric Function for Analyzing Optical Spectra of InGaN Nanofilms on Sapphire Substrates" Nanomaterials 15, no. 7: 485. https://doi.org/10.3390/nano15070485
APA StyleTalwar, D. N., Lin, H.-H., & Haraldsen, J. T. (2025). A Modified Model Dielectric Function for Analyzing Optical Spectra of InGaN Nanofilms on Sapphire Substrates. Nanomaterials, 15(7), 485. https://doi.org/10.3390/nano15070485







