Feature of Nonlinear Electromagnetic Properties and Local Atomic Structure of Metals in Two Systems of Nanocomposites Cox(MgF2)100−x and (CoFeZr)x(MgF2)100−x
Abstract
1. Introduction
2. Objects and Methods of Research
3. Structural-Phase Transformations and Nonlinear Electromagnetic Properties of Variable-Composition Nanocomposites Cox(MgF2)100−x and (CoFeZr)x(MgF2)100−x
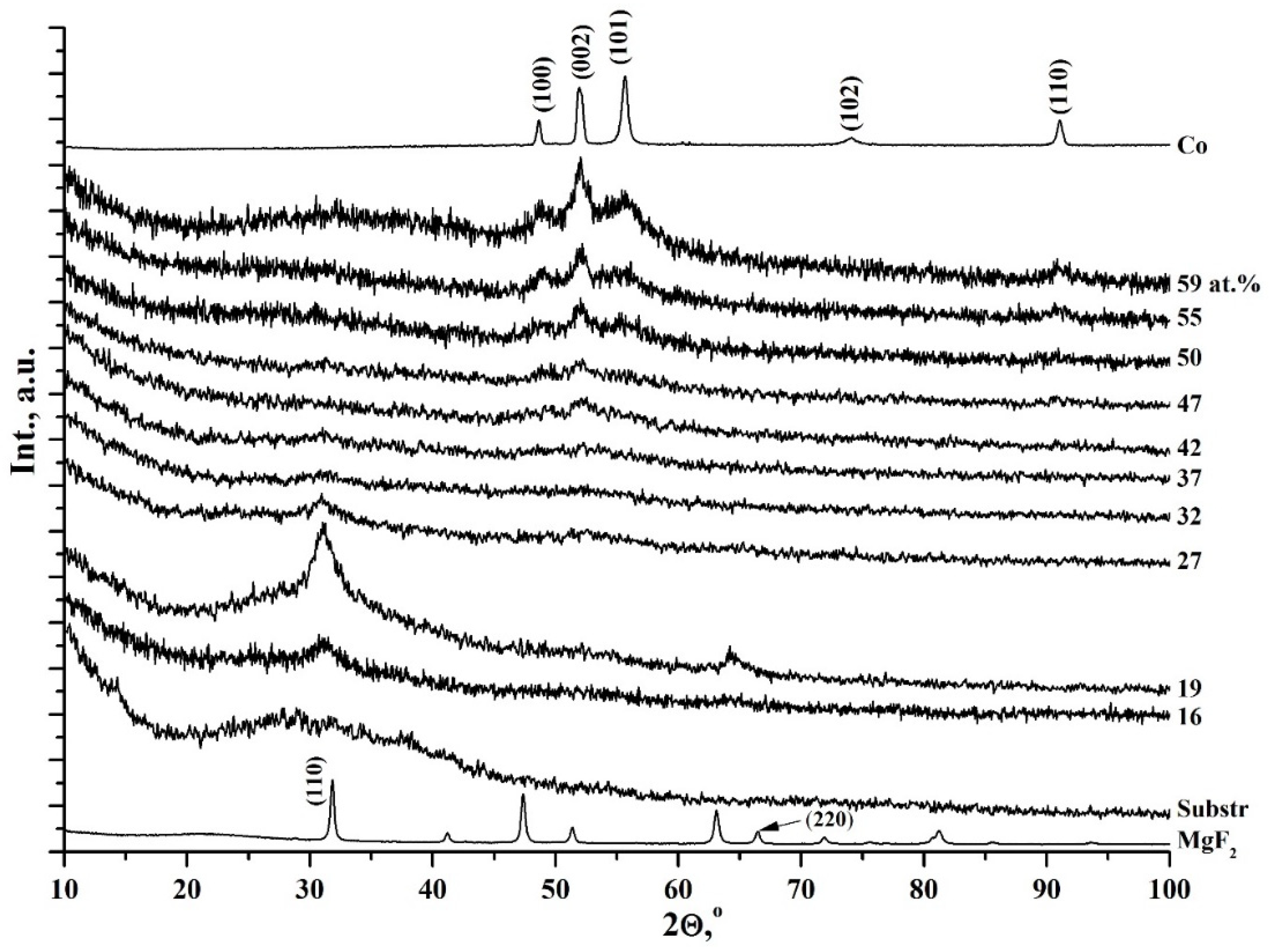
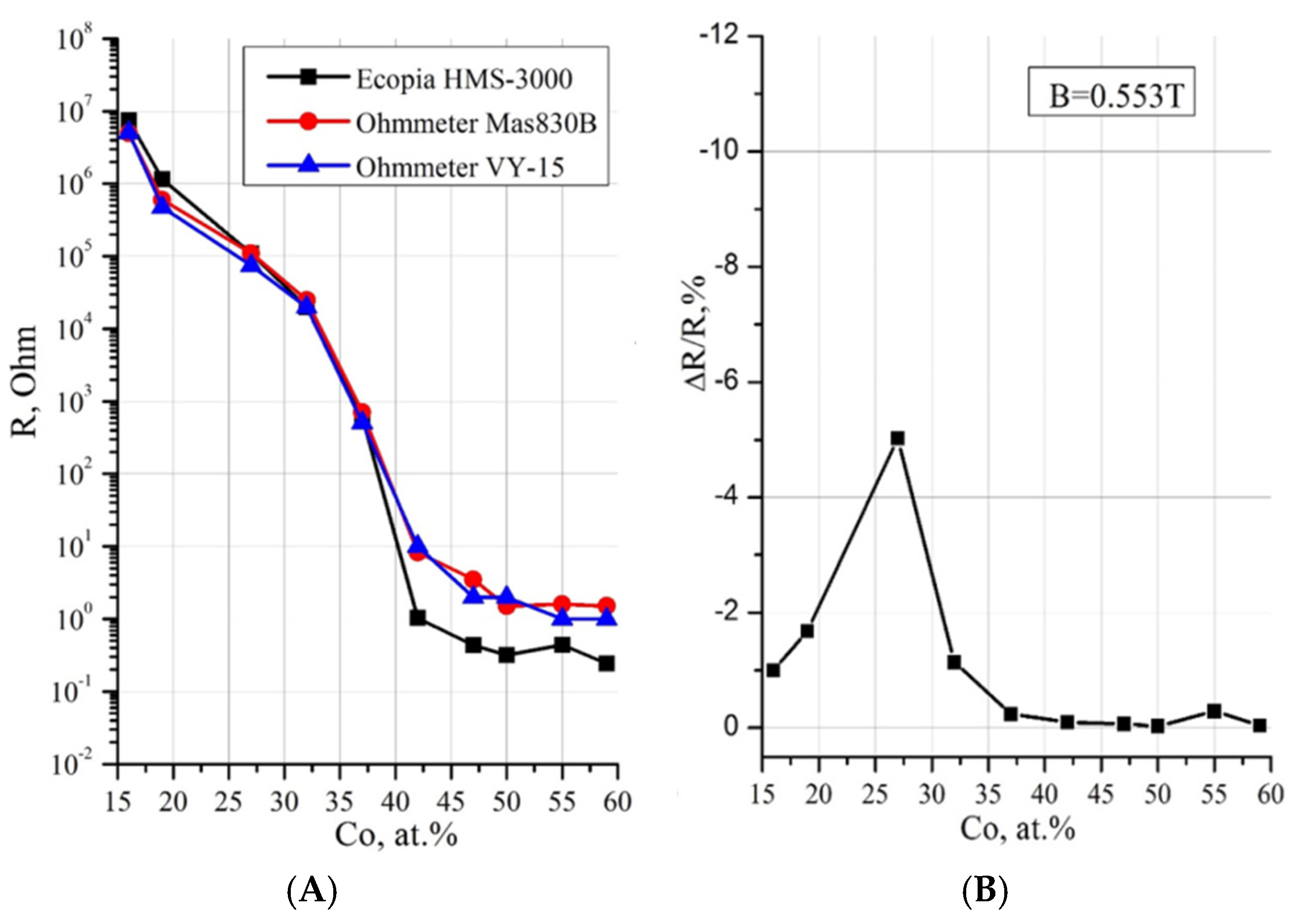
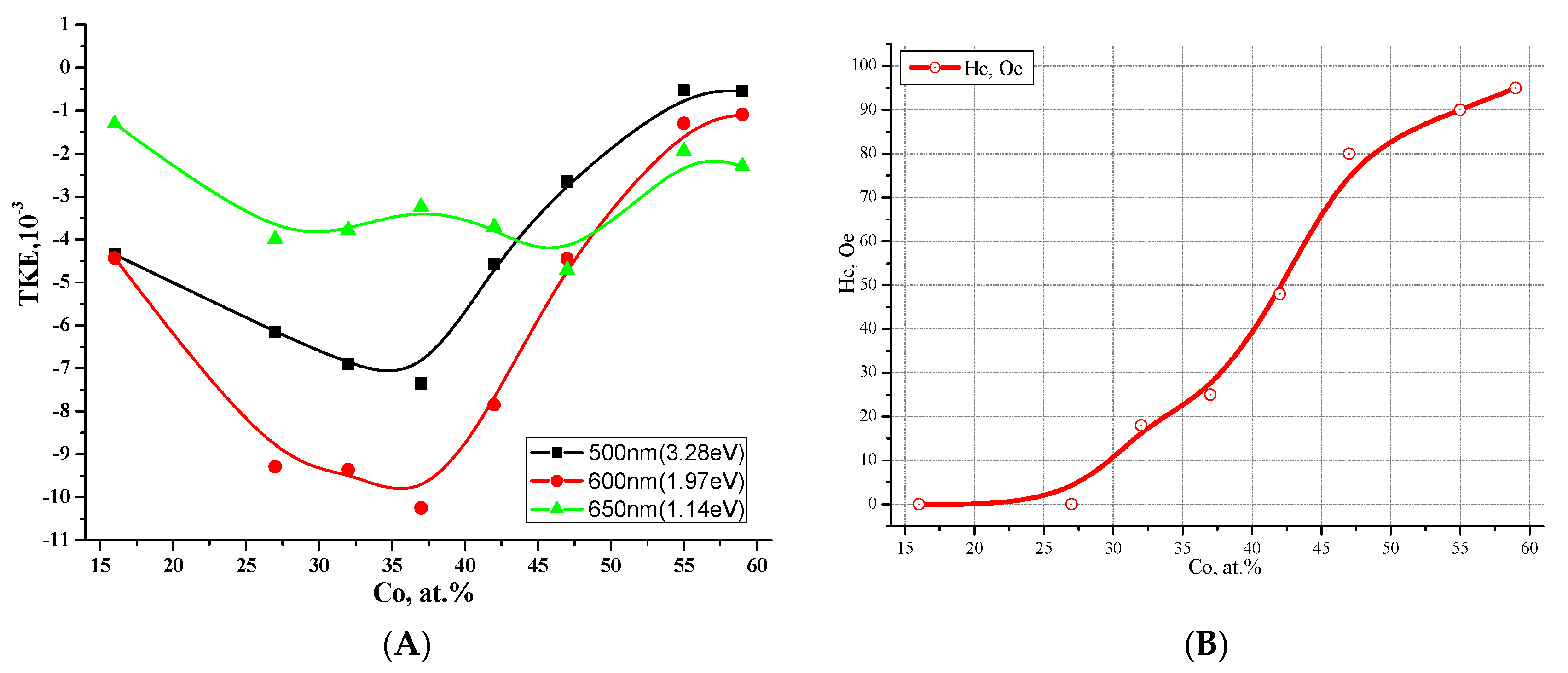
3.1. Metal–Dielectric Nanocomposites Cox(MgF2)100−x
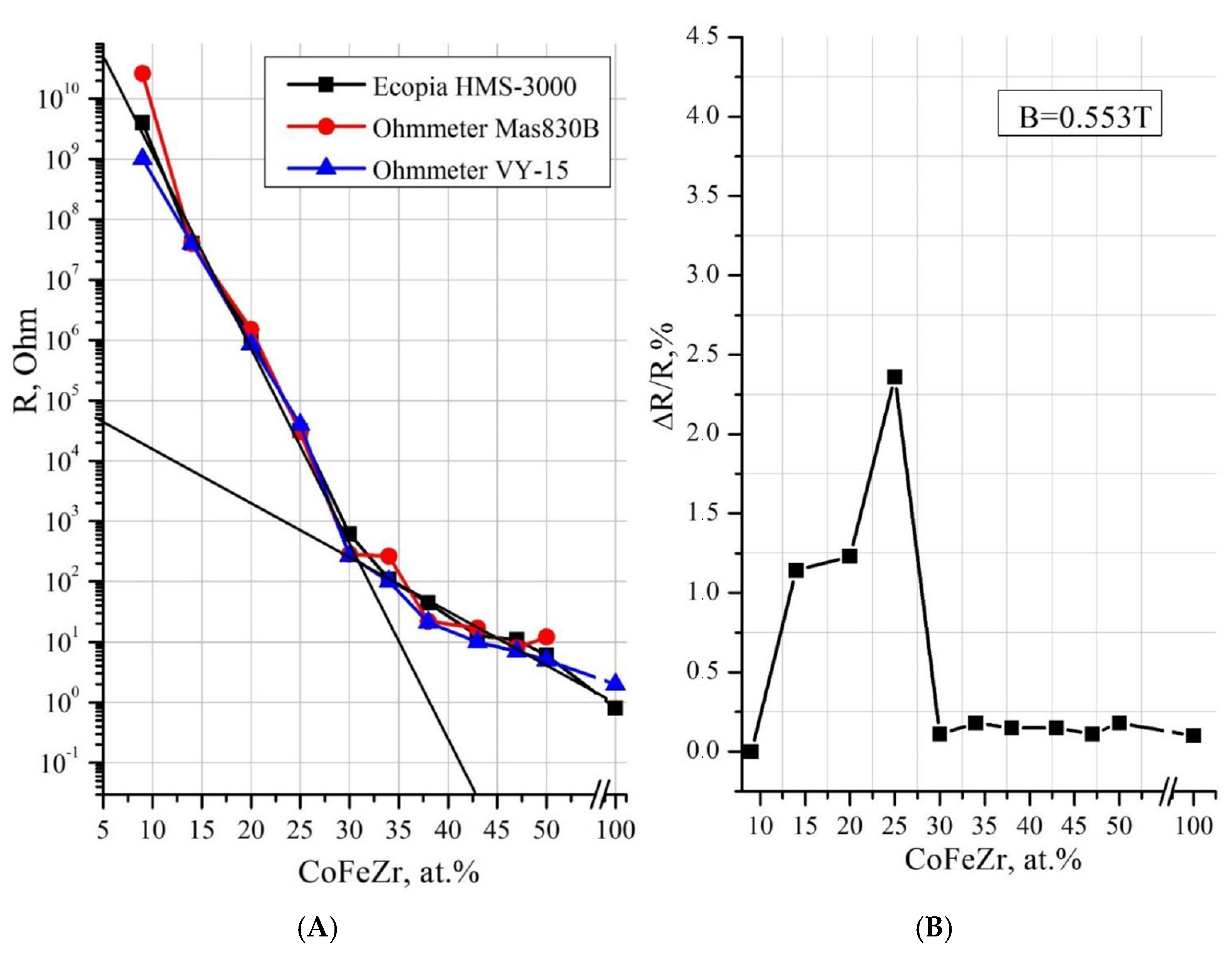
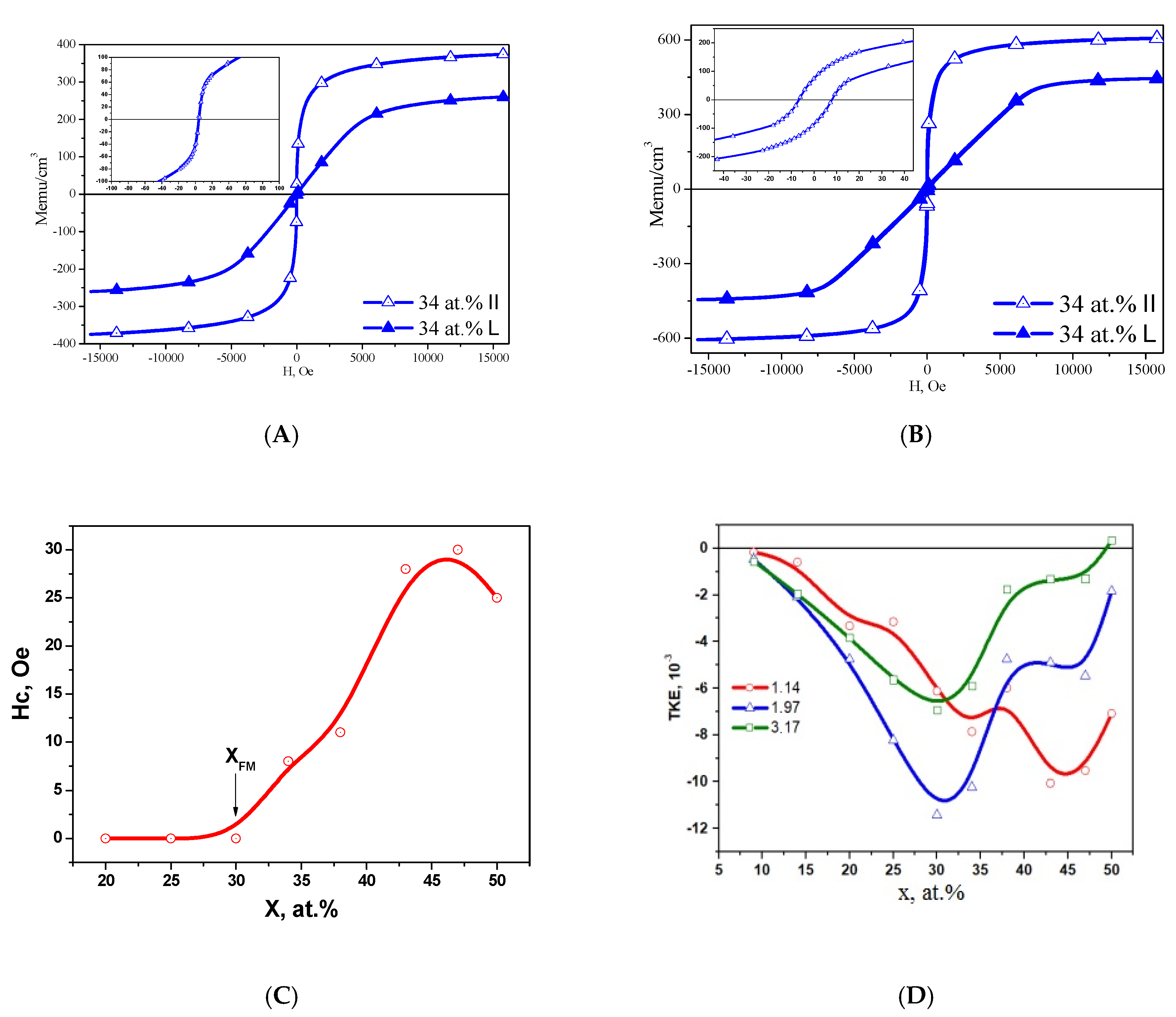
3.2. Alloy–Dielectric Nanocomposites (CoFeZr)x(MgF2)100−x
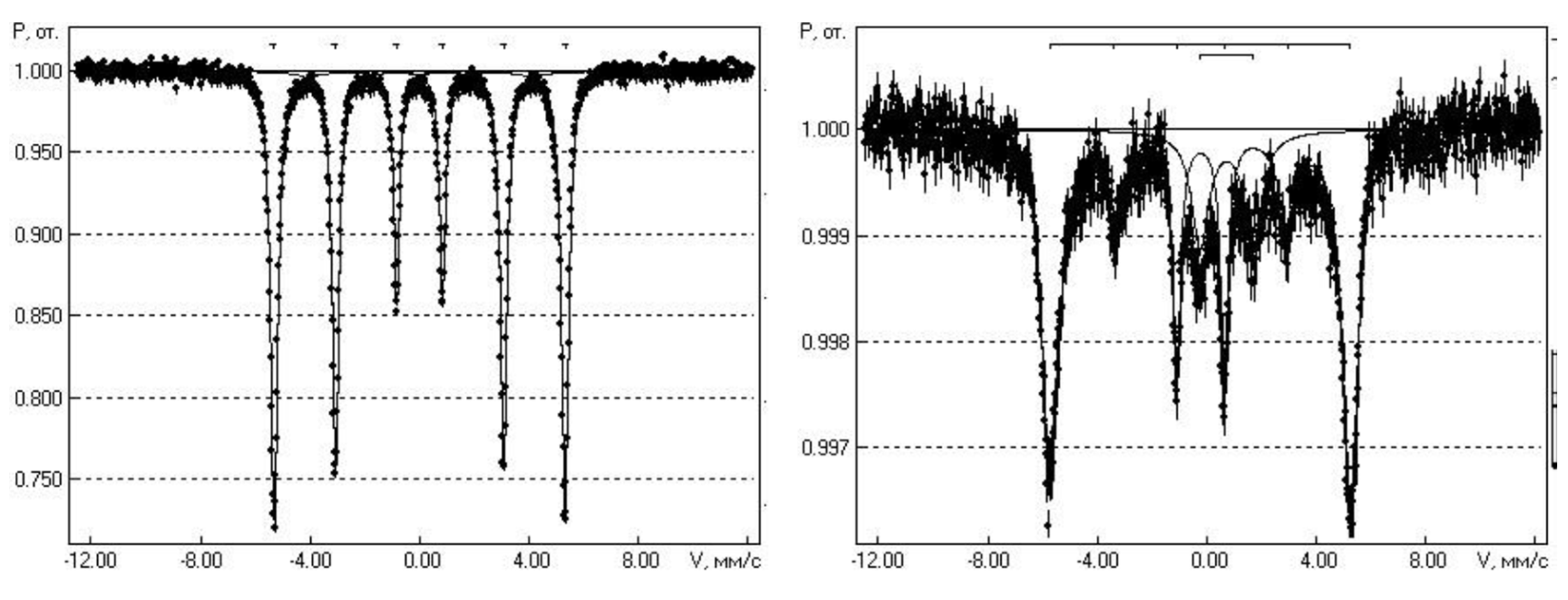
4. XANES Spectra of the K-Edges of Co and Fe in Nanocomposites Cox(MgF2)100−x and (CoFeZr)x(MgF2)100−x
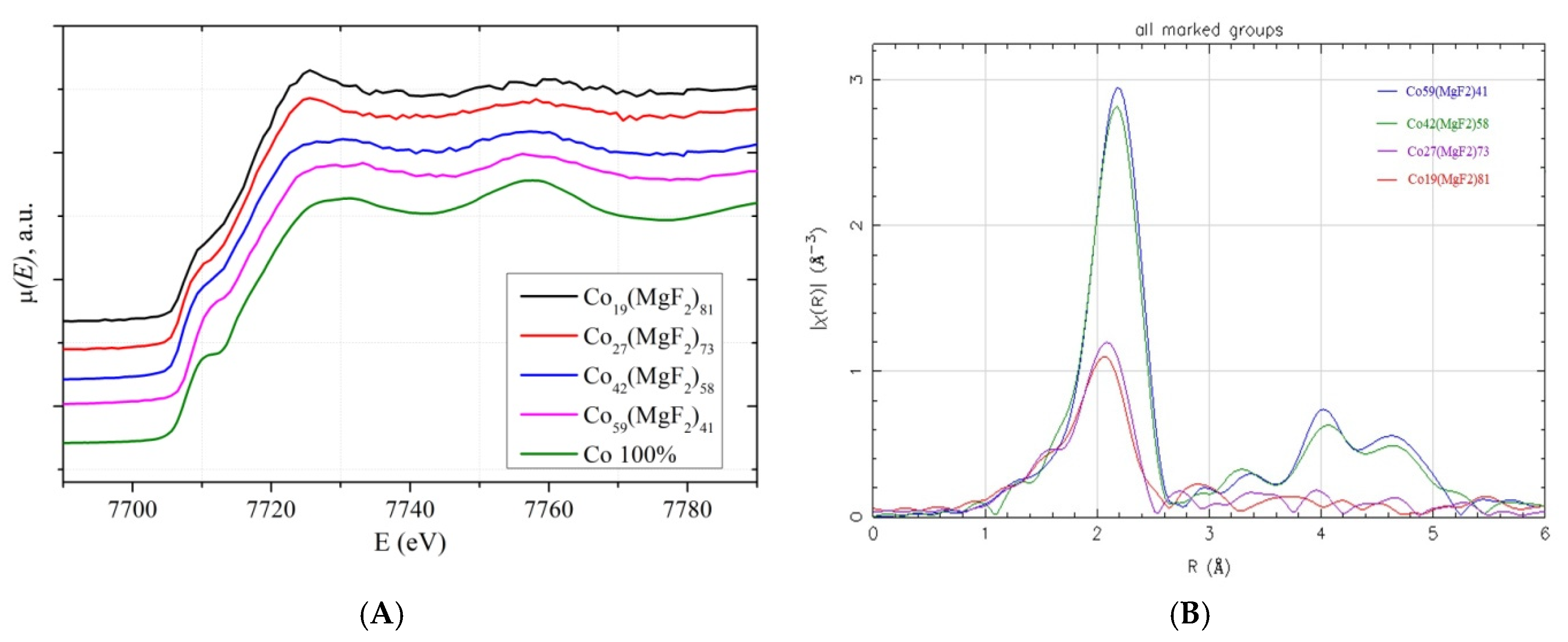
4.1. XANES Spectra of Co K-Edges in Cox(MgF2)100−x Nanocomposites
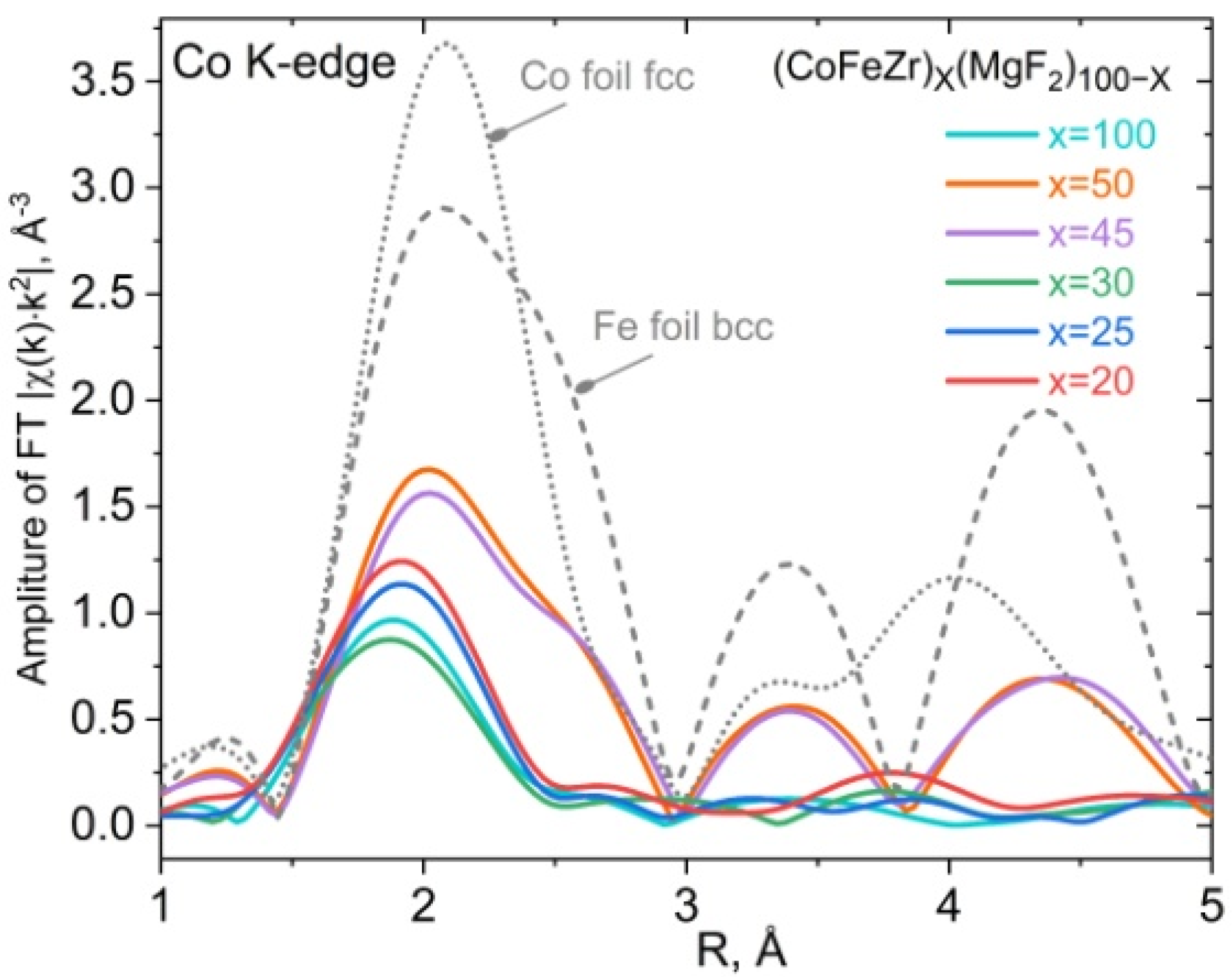
4.2. XANES Spectra of Co and Fe K-Edges in Nanocomposites (CoFeZr)x(MgF2)100−x
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abeles, B.; Sheng, P.; Coutts, M.D.; Arie, Y. Structural and electrical properties of granular metal films. Adv. Phys. 1975, 24, 407–461. [Google Scholar] [CrossRef]
- Abeles, B. Applied Solid State Science: Advances in Materials and Device Research; Wolfe, R., Ed.; Academic Press: New York, NY, USA, 1976. [Google Scholar]
- Gerber, A. Magnetoresistance of granular ferromagnets. Phys. Rev. B 1997, 55, 6446. [Google Scholar] [CrossRef]
- Erkowitz, J.; Mitchell, J.R.; Carey, M.J.; Young, A.P.; Zhang, S.; Spada, F.E.; Parker, F.T.; Hutten, A.; Thomast, G. Giant Magnetoresistance in Heterogeneous Cu-Co Alloys. Phys. Rev. Lett. 1992, 68, 3745. [Google Scholar] [CrossRef]
- Baibich, M.N.; Broto, J.M.; Fert Van Dau, F.N.; Petroff, F.; Etienne, P.; Creuzet, G.; Friederich, A.; Chazelas, J. Giant magnetoresistance of (001)Fe/(001)Cr magnetic superlattices. Phys. Rev. Lett. 1988, 61, 2472–2475. [Google Scholar] [CrossRef] [PubMed]
- Xiao, J.Q.; Jiang, J.S.; Chien, C.L. Giant Magnetoresistance in Nonmultilayer Magnetic Systems. Phys. Rev. Lett. 1992, 68, 3749. [Google Scholar] [CrossRef] [PubMed]
- Miyazaki, T.; Tezuka, N. Giant magnetic tunneling effect in Fe/Al2O3/Fe junction. J. Magn. Magn. Mater. 1995, 139, L231–L234. [Google Scholar] [CrossRef]
- Moodera, J.S.; Kinder, L.R.; Wong, T.M.; Meservey, R. Large Magnetoresistance at Room Temperature in Ferromagnetic Thin Film Tunnel Junctions. Phys. Rev. Lett. 1995, 74, 3273. [Google Scholar] [CrossRef]
- Levy, P.M. Giant Magnetoresistance in Magnetic Layered and Granular Materials. Solid State Phys.-Adv. Res. Appl. 1994, 47, 367–462. [Google Scholar] [CrossRef]
- Stogney, O.V.; Kalinin, Y.E.; Sitnikov, A.V. Resistive and magnetoresistive properties of granulated amorphous composites CoFeB–SiOn. Phys. Met. Met. Sci. 2001, 91, 24–31. [Google Scholar]
- Gridnev, S.A.; Kalinin, Y.E.; Sitnikov, A.V.; Stognei, O.V. Nonlinear Phenomena in Nano—And Microheterogeneous Systems; BINOM Knowledge Laboratory: Moscow, Russia, 2012; p. 352. [Google Scholar]
- Pakhomov, A.B.; Yan, X. Resistivity and Hall resistivity in percolating (NiFe)–SiO2 films. Sol. State Commun. 1996, 99, 139–142. [Google Scholar] [CrossRef]
- Arozon, B.A. Anomalous Hall effect in granular Fe/SiO2 films in the tunnel conductivity mode. Lett. JETP 1999, 90, 87. [Google Scholar]
- Cid, B.; de Araújo, C.B.; Reyna, A.S. Nonlinear spectroscopy of metal-dielectric nanocomposites. In Modern Luminescence from Fundamental Concepts to Materials and Applications. Volume 1: Concepts of Luminescence; Woodhead Publishing Series in Electronic and Optical Materials: London, UK, 2023; pp. 111–151. [Google Scholar] [CrossRef]
- Sharma, N.; Destouches, N.; Florian, C.; Serna, R. Tailoring metal-dielectric nanocomposite materials with ultrashort laser pulses for dichroic color control. Nanoscale 2019, 11, 18779. [Google Scholar] [CrossRef] [PubMed]
- Sheng, P.; Klafter, J. Hopping Conductivity in Granular Disordered Systems. Phys. Rev. B 1983, 27, 2583–2586. [Google Scholar] [CrossRef]
- Honda, S. Tunneling giant magnetoresistence in heterogeneous Fe—SiО2 granular. Phys. Rev. B 1997, 56, 14566–14573. [Google Scholar] [CrossRef]
- Slonczewski, J.C. Conductance and exchange coupling of two ferromagnets separated by tunneling barrier. Phys. Rev. B 1989, 39, 6995–7002. [Google Scholar] [CrossRef] [PubMed]
- Mott, N.; Davis, E. Electronic Processes in Non-Crystalline Substances; Mir: Moscow, Russia, 1982; p. 368. [Google Scholar]
- Hughes, R.C. Electronic and ionic charge carriers in irradiated single crystal and fused quartz. Rad. Eff. 1975, 26–25, 235. [Google Scholar] [CrossRef]
- Mott, N.F. Electronic Properties of Vitreous Silicon Dioxide, Physics of SiO2 and Its Interfaces; Pergamon Press: Oxford, UK, 1978; pp. 1–13. [Google Scholar]
- Tikadzumi, S. Physics of Ferromagnetism and Magnetic Properties of Substances; Mir: Moskow, Russia, 1983; p. 456. [Google Scholar]
- Chien, C.L. Granular magnetic solids. J. Appl. Phys. 1991, 69, 5267–5272. [Google Scholar] [CrossRef]
- Sumiyama, K.; Suzuki, K.; Makhlouf, S.A.; Wakoh, K.; Kamiyama, T.; Yamamuro, S.; Konno, T.J.; Xu, Y.F.; Sakurai, M.; Hihara, T. Structural evolution and magnetic properties of nano-granular metallic alloys. J. Non-Cryst. Solids 1995, 192–193, 539–545. [Google Scholar] [CrossRef]
- Laurent, K.C. Magnetic properties of granular Co–polimer films. J. Appl. Phys. 1989, 65, 2017–2020. [Google Scholar] [CrossRef]
- Frydman, A.; Kirk, T.L.; Diyes, R.C. Superparamagnetism in discontinuous Ni films. Solid State Commun. 2000, 114, 481–486. [Google Scholar] [CrossRef]
- Mitani, S.; Fujimori, H.; Ohnuma, S. Spin-dependent tunneling phenomena in insulating granular systems. J. Magn. Magn. Mater. 1997, 165, 141–148. [Google Scholar] [CrossRef]
- Inoue, J.; Maekawa, S. Theory of tunneling magnetoresistance in granular magnetic films. Phys. Rev. B 1996, 53, 11927–11929. [Google Scholar] [CrossRef]
- Sankar, S.; Berkowitz, A.E.; Smith, D.J. Spin–dependent transport of Co–SiO2 granular films approaching percolation. Phys. Rev. B 2000, 62, 14273–14278. [Google Scholar] [CrossRef]
- Kalinin, Y.E.; Sitnikov, A.V.; Stognei, O.V.; Zolotukhin, I.V.; Neretin, P.V. Electrical properties and giant magnetoresistance of the CoFeB–SiO2 amorphous granular composites. Mater. Sci. Eng. 2001; 304–306, 941–945. [Google Scholar]
- Buravtseva, V.E.; Ganshina, E.A.; Gushchin, V.S.; Pkhongkhirun, S.; Syr’ev, N.E.; Kalinin, Y.E.; Sitnikov, A.V.; Stognej, O.V. Giant magnetoresistance and magnetooptical properties of granular metal-dielectric nanocomposites. Izv. RAN. Ser. Phys. 2003, 67, 918–920. [Google Scholar]
- Gan’shina, E.A.; Granovsky, A.; Shevyakov, D.; Sitnikov, A.; Lahderanta, E.; Rylkov, V. Magneto-Optical Spectroscopy of (CoFeB)x-(Al-O)100-x Nanocomposites: Evidence of Superferromagnetism. JEEE Magn. Lett. 2020, 11, 1–4. [Google Scholar] [CrossRef]
- Kobayashi, N.; Ohnuma, S.; Masumoto, T.; Fujimori, H. (Fe-Co)-(Mg-fluoride) insulating nanogranular system with enhanced tunnel-type giant magnetoresistance. J. Appl. Phys. 2001, 90, 4159–4162. [Google Scholar] [CrossRef]
- Yao, D.; Ge, S.; Zhang, B.; Zuo, H.; Zhou, X. Fabrication and magnetism of Fe65 Co35 -MgF 2 granular films for high frequency application. J. Appl. Phys. 2008, 103, 113901. [Google Scholar] [CrossRef]
- Tregubova, T.; Stognei, O.; Kirpan, V. Moscow International Symposium on Magnetism. EPJ Web Conf. 2018, 185, 01014. [Google Scholar] [CrossRef]
- Tregubova, T.; Stogney, O.; Tregubov, I.M.; Kirpan, V.V. Electrical and magnetoresistive properties of oxygen-free composites Cox(MgF2)100−x. Vestn. Voronezh State Tech. Univ. 2017, 13, 122–127. [Google Scholar]
- Zvezdin, A.K.; Kotov, V.A. Modern Magnetooptics and Magnetooptical Materials; CRC Press: Boca Raton, FL, USA, 1997; 404p. [Google Scholar] [CrossRef]
- Penfold, C.; Collins, R.T.; Tufaile, A.P.B.; Souche, Y. Transverse magneto-optical Kerr effect: The phase change of reflected light. J. Magn. Magn. Mater. 2002, 242–245, 964–966. [Google Scholar] [CrossRef]
- Zimmermann, P.; Peredkov, S.; Abdala, P.M.; DeBeer, S.; Tromp, M.; Müller, C.; van Bokhoven, J.A. Modern X-ray spectroscopy: XAS and XES in the laboratory. Coord. Chem. Rev. 2020, 423, 213466. [Google Scholar] [CrossRef]
- Ravel, B.; Newville, M. Athena, Artemis, Hephaestus: Data analysis for X-ray absorption spectroscopy using IFEFFIT. J. Synchrotron Radiat. 2005, 12, 537–541. [Google Scholar] [CrossRef] [PubMed]
- Domashevskaya, E.P.; Ivkov, S.A.; Sitnikov, A.V.; Stogney, O.V.; Kozakov, A.T.; Nikolsky, A.V. Влияние относительного содержания металлической компоненты в диэлектрической матрице на образование и размеры нанокристаллов кобальта в пленочных композитах Cox(MgF2)100−x. Solid State Phys. 2019, 61, 211–219. [Google Scholar] [CrossRef]
- Ivkov, S.A.; Barkov, K.A.; Domashevskaya, E.P.; Ganshina, E.A.; Goloshchapov, D.L.; Ryabtsev, S.V.; Sitnikov, A.V.; Seredin, P.V. Nonlinear Transport and Magnetic/Magneto-Optical Properties of Coх(MgF2)100−x Nanostructures. Appl. Sci. 2023, 13, 2992. [Google Scholar] [CrossRef]
- Sun, Y.; Sullivan, C.R.; Li, W.; Kopp, D.; Johnson, F.; Taylor, S.T. Soft Magnetic Properties of Obliquely Deposited Co–Zr–O Films. IEEE Trans. Magn. 2007, 43, 4060. [Google Scholar] [CrossRef]
- Domashevskaya, E.P.; Ivkov, S.A.; Sitnikov, A.V.; Stogney, O.V.; Kozakov, A.T.; Nikolsky, A.V.; Barkov, K.A.; Builov, N.S. The features of CoFeZr alloy nanocrystals formation in film composites of (CoFeZr)x(MgF2)100−x. J. Alloys Compd. 2021, 870, 159398. [Google Scholar] [CrossRef]
- Domashevskaya, E.P.; Ivkov, S.A.; Seredin, P.V.; Goloshchapov, D.L.; Barkov, K.A.; Ryabtsev, S.V.; Segal, Y.G.; Sitnikov, A.V.; Ganshina, E.A. Nonlinear Electromagnetic Properties of Thinfilm Nanocomposites (CoFeZr)x(MgF2)100−x. Magnetochemistry 2023, 6, 160. [Google Scholar] [CrossRef]
- Spivak, L.V.; Sosunov, A.V.; Shchepina, N.E. Phase transformations during heating of Co−C nanocomposite. Tech. Phys. Lett. 2022, 48, 66. [Google Scholar] [CrossRef]
- Spivak, L.V.; Shchepina, N.E. Features of polymorphic transformation during heating and cooling of cobalt. J. Tech. Phys. 2022, 92, 569–574. [Google Scholar] [CrossRef]
- Тhomas, M.E.; Stefan, K.A.; Thomas, M.C.; Kim, T. Infrared properties of polycrystalline magnesium fluoride. Infrared Phys. Technol. 1998, 39, 213–222. [Google Scholar] [CrossRef]
- X-Ray NIST Photoelectron Spectroscopy Database. Available online: https://srdata.nist.gov (accessed on 20 February 2025).
- Jaccarino, V.; Walker, L.R. Discontinuous occurrence of localized moments. Phys. Rev. Lett. 1965, 15, 258–259. [Google Scholar] [CrossRef]
- Grössinger, R.; Hilscher, G.; Wiesinger, G. Temperature and concentration dependence of magnetization, magnetocrystalline anisotropy and hyperfine parameters in Zr(Fe1−xAlx)2. J. Magn. Magn. Mater. 1981, 23, 47–58. [Google Scholar] [CrossRef]
- El-Hilo, M.; O’Grady, K.; Chantrell, R.W. Chantrell, The ordering temperature in fine particle systems. J. Magn. Magn. Mater. 1992, 117, 21–28. [Google Scholar] [CrossRef]
- Norman, D. X-ray absorption spectroscopy (EXAFS and XANES) at surfaces. J. Phys. C Solid State Phys. 1986, 19, 3273–3311. [Google Scholar] [CrossRef]
- Bunker, G. Introduction to XAFS: A Practical Guide to Absorption Fine Structure Spectroscopy; Cambridge University Press: New York, NY, USA, 2010; 106p. [Google Scholar]
- Guan, D.; Xu, H.; Zhang, Q.; Huang, Y.C.; Shi, C.; Chang, Y.C.; Xu, X.; Tang, J.; Gu, Y.; Pao, C.W.; et al. Identifying a Universal Activity Descriptor and a Unifying Mechanism Concept on Perovskite Oxides for Green Hydrogen Production. Adv. Mater. 2023, 35, 2305074. [Google Scholar] [CrossRef]
- Guan, D.; Zhang, K.; Hu, Z.; Wu, X.; Chen, J.L.; Pao, C.W.; Guo, Y.; Zhou, W.; Shao, Z. Combined Corner-Sharing and Edge-Sharing Networks. Adv. Mater. 2021, 33, 2103392. [Google Scholar] [CrossRef]
- Zubavichus, Y.V.; Slovokhotov, Y.L. X-ray synchrotron radiation in physicochemical studies. Adv. Chem. 2001, 70, 429–463. [Google Scholar] [CrossRef]
- Fetisov, G.V. Synchrotron Radiation: Methods for Studying the Structure of Matter; Fizmatlit: Moscow, Russia, 2007; 672p. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Domashevskaya, E.P.; Ivkov, S.A.; Ganshina, E.A.; Guda, L.V.; Vlasenko, V.G.; Sitnikov, A.V. Feature of Nonlinear Electromagnetic Properties and Local Atomic Structure of Metals in Two Systems of Nanocomposites Cox(MgF2)100−x and (CoFeZr)x(MgF2)100−x. Nanomaterials 2025, 15, 463. https://doi.org/10.3390/nano15060463
Domashevskaya EP, Ivkov SA, Ganshina EA, Guda LV, Vlasenko VG, Sitnikov AV. Feature of Nonlinear Electromagnetic Properties and Local Atomic Structure of Metals in Two Systems of Nanocomposites Cox(MgF2)100−x and (CoFeZr)x(MgF2)100−x. Nanomaterials. 2025; 15(6):463. https://doi.org/10.3390/nano15060463
Chicago/Turabian StyleDomashevskaya, Evelina Pavlovna, Sergey Alexandrovich Ivkov, Elena Alexandrovna Ganshina, Lyubov Vladimirovna Guda, Valeriy Grigoryevich Vlasenko, and Alexander Victorovich Sitnikov. 2025. "Feature of Nonlinear Electromagnetic Properties and Local Atomic Structure of Metals in Two Systems of Nanocomposites Cox(MgF2)100−x and (CoFeZr)x(MgF2)100−x" Nanomaterials 15, no. 6: 463. https://doi.org/10.3390/nano15060463
APA StyleDomashevskaya, E. P., Ivkov, S. A., Ganshina, E. A., Guda, L. V., Vlasenko, V. G., & Sitnikov, A. V. (2025). Feature of Nonlinear Electromagnetic Properties and Local Atomic Structure of Metals in Two Systems of Nanocomposites Cox(MgF2)100−x and (CoFeZr)x(MgF2)100−x. Nanomaterials, 15(6), 463. https://doi.org/10.3390/nano15060463







