Investigating Simulated Cellular Interactions on Nanostructured Surfaces with Antibacterial Properties: Insights from Force Curve Simulations
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Sample Fabrication
2.3. Characterization of HTE Surfaces by Water Contact Angle (WCA)
2.4. X-Ray Photoelectron Spectroscopy (XPS)
2.5. Scanning Electron Microscopy (SEM) Analysis
2.6. Atomic Force Microscopy (AFM) Measurements
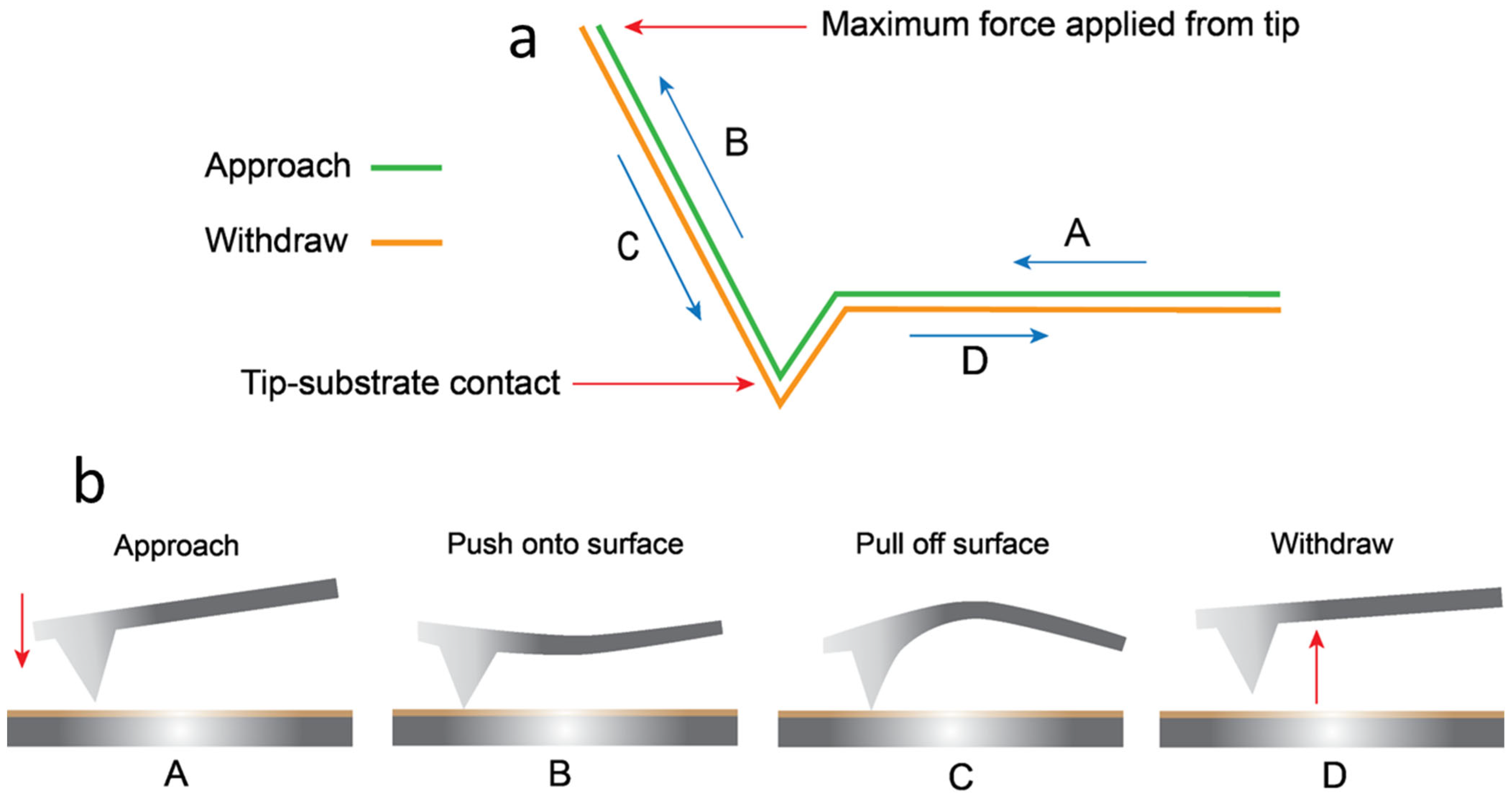
2.7. Force Curves
2.8. Statistical Analysis
3. Results and Discussion
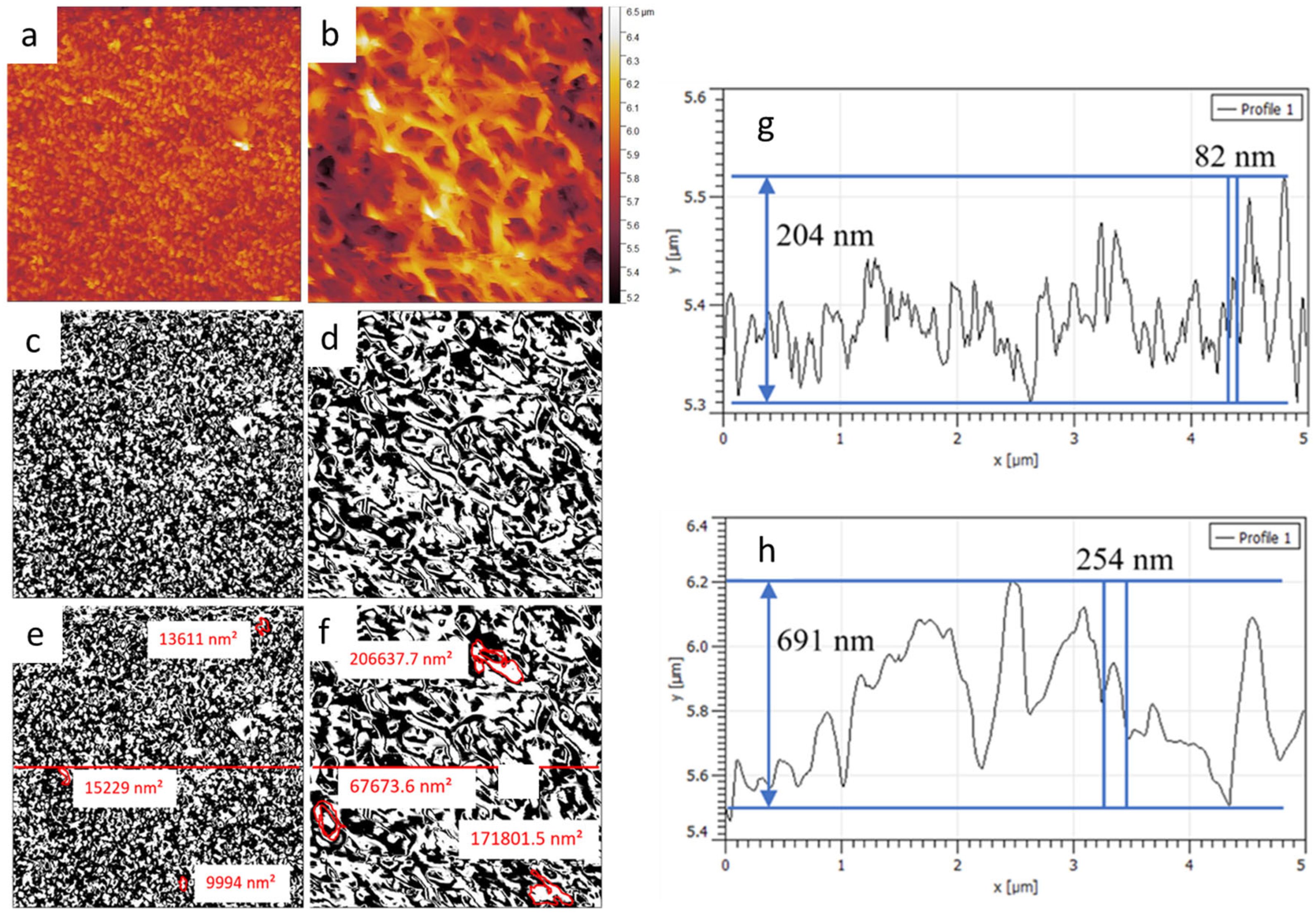
3.1. SEM
3.2. Surface Characterization
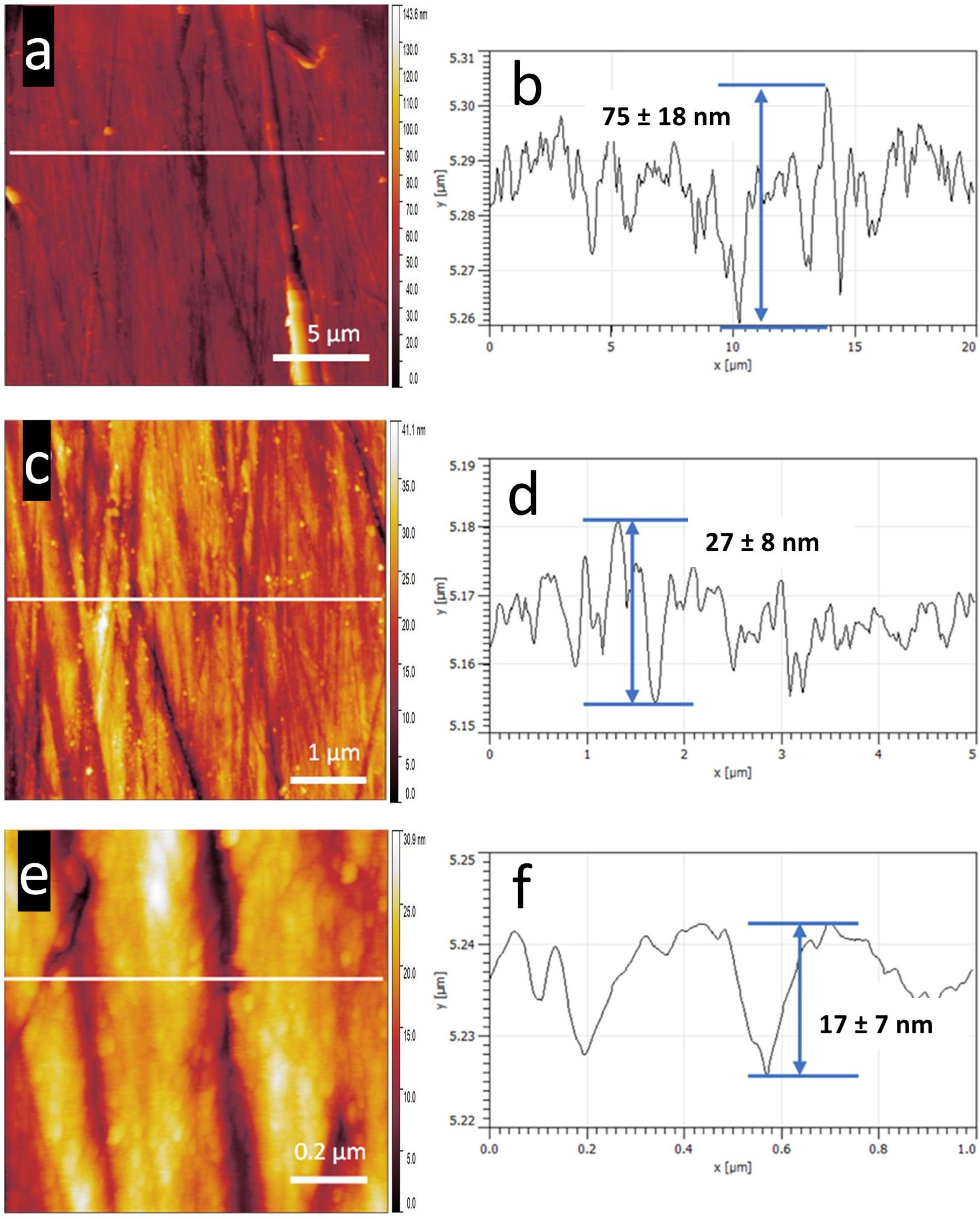
3.3. Roughness Analysis
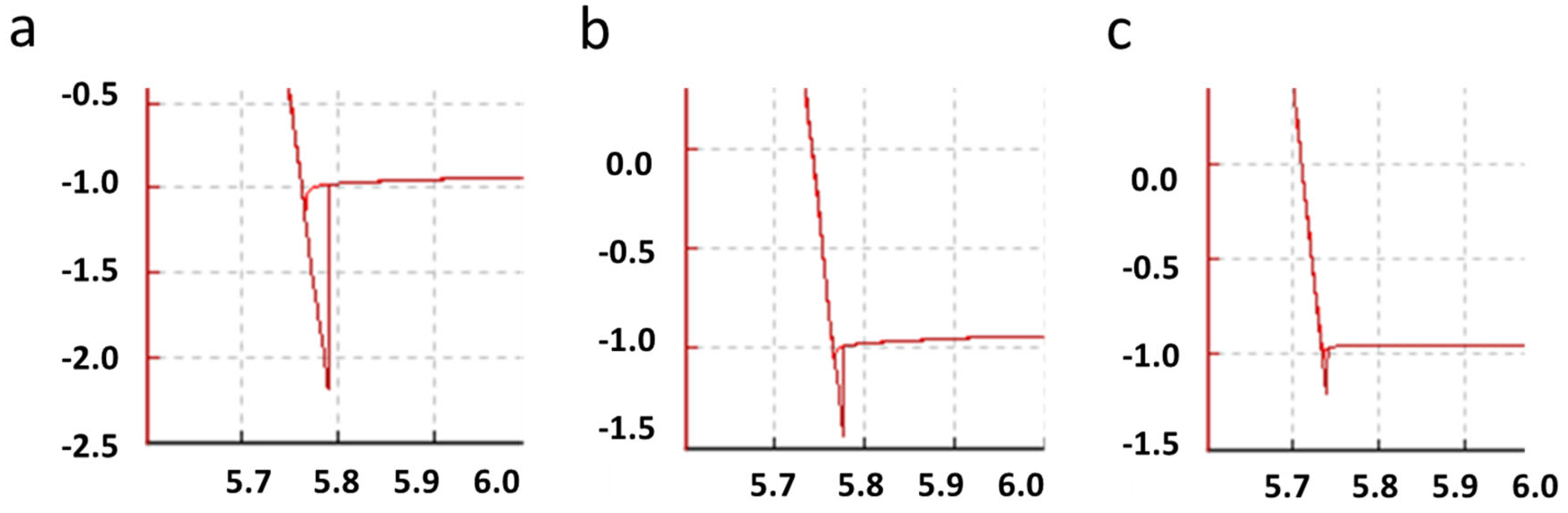
3.4. Adhesion Force
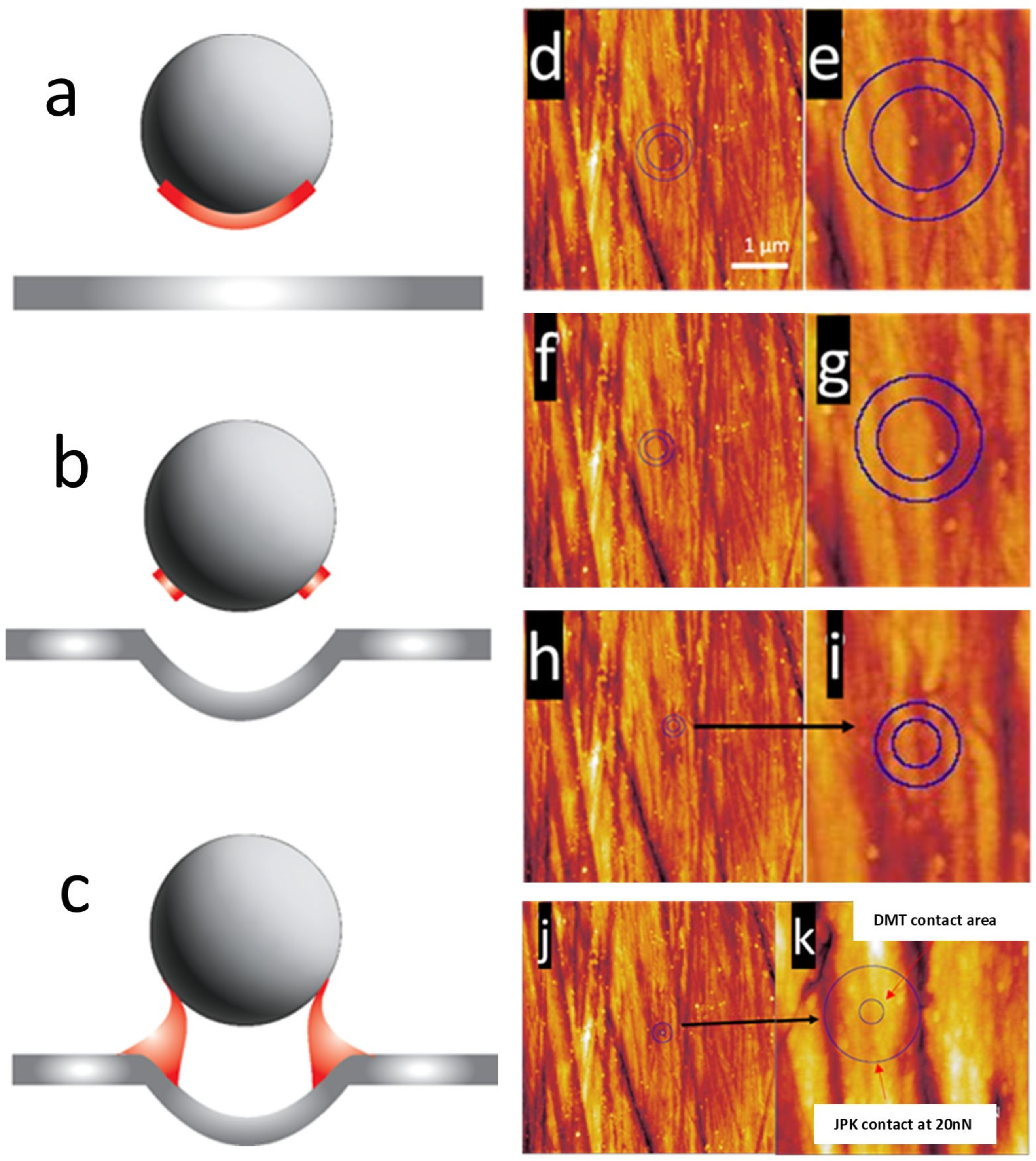
3.5. Tip Contact Area
3.6. Comparison of KOH NS to NaOH NS
3.7. Stiffness Analysis
3.8. Surface Energy Analysis
3.9. Short- and Long-Range Forces on NS

4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rasouli, M.R.; Restrepo, C.; Maltenfort, M.G.; Purtill, J.J.; Parvizi, J. Risk factors for surgical site infection following total joint arthroplasty. J. Bone Jt. Surg. Am. 2014, 96, e158. [Google Scholar] [CrossRef] [PubMed]
- Lenguerrand, E.; Whitehouse, M.R.; Beswick, A.D.; Kunutsor, S.K.; Foguet, P.; Porter, M.; Blom, A.W. Risk factors associated with revision for prosthetic joint infection following knee replacement: An observational cohort study from England and Wales. Lancet Infect. Dis. 2019, 19, 589–600. [Google Scholar] [CrossRef] [PubMed]
- Bright, R.; Hayles, A.; Wood, J.; Palms, D.; Barker, D.; Vasilev, K. Interplay between Immune and Bacterial Cells on a Biomimetic Nanostructured Surface: A “Race for the Surface” Study. ACS Appl. Bio Mater. 2023, 6, 3472–3483. [Google Scholar] [CrossRef] [PubMed]
- Valderrama, J.O. The legacy of Johannes Diderik van der Waals, a hundred years after his Nobel Prize for physics. J. Supercrit. Fluids 2010, 55, 415–420. [Google Scholar] [CrossRef]
- Israelachvili, J.N. (Ed.) Van der Waals Forces. In Intermolecular and Surface Forces; Academic Press: San Diego, CA, USA, 2011; pp. 107–132. [Google Scholar] [CrossRef]
- Chen, Y.; Busscher, H.J.; van der Mei, H.C.; Norde, W. Statistical Analysis of Long- and Short-Range Forces Involved in Bacterial Adhesion to Substratum Surfaces as Measured Using Atomic Force Microscopy. Appl. Environ. Microbiol. 2011, 77, 5065–5070. [Google Scholar] [CrossRef]
- Chen, Y.; Harapanahalli, A.K.; Busscher, H.J.; Norde, W.; van der Mei, H.C. Nanoscale cell wall deformation impacts long-range bacterial adhesion forces on surfaces. Appl. Environ. Microbiol. 2014, 80, 637–643. [Google Scholar] [CrossRef]
- Elbourne, A.; Chapman, J.; Gelmi, A.; Cozzolino, D.; Crawford, R.J.; Truong, V.K. Bacterial-nanostructure interactions: The role of cell elasticity and adhesion forces. J. Colloid Interface Sci. 2019, 546, 192–210. [Google Scholar] [CrossRef]
- Leite, F.L.; Herrmann, P.S.P. Application of atomic force spectroscopy (AFS) to studies of adhesion phenomena: A review. J. Adhes. Sci. Technol. 2005, 19, 365–405. [Google Scholar] [CrossRef]
- Seo, Y.; Jhe, W. Atomic force microscopy and spectroscopy. Rep. Prog. Phys. 2008, 71, 016101. [Google Scholar] [CrossRef]
- Cappella, B.; Baschieri, P.; Frediani, C.; Miccoli, P.; Ascoli, C. Force-distance curves by AFM. IEEE Eng. Med. Biol. Mag. 1997, 16, 58–65. [Google Scholar] [CrossRef]
- Dzyaloshinskii, I.E.; Lifshitz, E.M.; Pitaevskii, L.P.; Priestley, M.G. The general theory of van der Waals forces. In Perspectives in Theoretical Physics; Pitaevski, L.P., Ed.; Pergamon: Amsterdam, The Netherlands, 1992; pp. 443–492. [Google Scholar] [CrossRef]
- Saint Jean, M.; Hudlet, S.; Guthmann, C.; Berger, J. Van der Waals and capacitive forces in atomic force microscopies. J. Appl. Phys. 1999, 86, 5245–5248. [Google Scholar] [CrossRef]
- Cappella, B.; Dietler, G. Force-distance curves by atomic force microscopy. Surf. Sci. Rep. 1999, 34, 1–3, 5–104. [Google Scholar] [CrossRef]
- Lauritsen, J.V.; Foster, A.S.; Olesen, G.H.; Christensen, M.C.; Kuhnle, A.; Helveg, S.; Rostrup-Nielsen, J.R.; Clausen, B.S.; Reichling, M.; Besenbacher, F. Chemical identification of point defects and adsorbates on a metal oxide surface by atomic force microscopy. Nanotechnology 2006, 17, 3436–3441. [Google Scholar] [CrossRef] [PubMed]
- Parsons, D.F.; Walsh, R.B.; Craig, V.S. Surface forces: Surface roughness in theory and experiment. J. Chem. Phys. 2014, 140, 164701. [Google Scholar] [CrossRef]
- Gulati, K.; Adachi, T. Profiling to Probing: Atomic force microscopy to characterize nano-engineered implants. Acta Biomater. 2023, 170, 15–38. [Google Scholar] [CrossRef]
- Wood, J.; Hayles, A.; Bright, R.; Palms, D.; Vasilev, K.; Hasan, J. Nanomechanical tribological characterisation of nanostructured titanium alloy surfaces using AFM: A friction vs velocity study. Colloids Surf. B Biointerfaces 2022, 217, 112600. [Google Scholar] [CrossRef]
- Bright, R.; Fernandes, D.; Wood, J.; Palms, D.; Burzava, A.; Ninan, N.; Brown, T.; Barker, D.; Vasilev, K. Long-term antibacterial properties of a nanostructured titanium alloy surface: An in vitro study. Mater. Today Bio 2022, 13, 100176. [Google Scholar] [CrossRef]
- Bright, R.; Hayles, A.; Fernandes, D.; Visalakshan, R.M.; Ninan, N.; Palms, D.; Burzava, A.; Barker, D.; Brown, T.; Vasilev, K. In Vitro Bactericidal Efficacy of Nanostructured Ti6Al4V Surfaces is Bacterial Load Dependent. ACS Appl. Mater. Interfaces 2021, 13, 38007–38017. [Google Scholar] [CrossRef]
- Maugis, D. Adhesion of Spheres—The Jkr-Dmt Transition Using a Dugdale Model. J. Colloid Interface Sci. 1992, 150, 243–269. [Google Scholar] [CrossRef]
- Brown, I.W.M.; Bowden, M.E.; Kernmitt, T.; MacKenzie, K.J.D. Structural and thermal characterisation of nanostructured alumina templates. Curr. Appl. Phys. 2006, 6, 557–561. [Google Scholar] [CrossRef]
- Weber, J.; Singhal, R.; Zekri, S.; Kumar, A. One-dimensional nanostructures: Fabrication, characterisation and applications. Int. Mater. Rev. 2008, 53, 235–255. [Google Scholar] [CrossRef]
- Levin, P.A.; Angert, E.R. Small but Mighty: Cell Size and Bacteria. Cold Spring Harb. Perspect. Biol. 2015, 7, a019216. [Google Scholar] [CrossRef] [PubMed]
- Van De Merwe, W.P.; Czégé, J.; Milham, M.E.; Bronk, B.V. Rapid optically based measurements of diameter and length for spherical or rod-shaped bacteria in vivo. Appl. Opt. 2004, 43, 5295–5302. [Google Scholar] [CrossRef] [PubMed]
- Lendeckel, U.; Venz, S.; Wolke, C. Macrophages: Shapes and functions. ChemTexts 2022, 8, 12. [Google Scholar] [CrossRef]
- Jones, R.; Pollock, H.M.; Cleaver, J.A.S.; Hodges, C.S. Adhesion forces between glass and silicon surfaces in air studied by AFM: Effects of relative humidity, particle size, roughness, and surface treatment. Langmuir 2002, 18, 8045–8055. [Google Scholar] [CrossRef]
- Wei, Z.; Zhao, Y.P. Growth of liquid bridge in AFM. J. Phys. D-Appl. Phys. 2007, 40, 4368–4375. [Google Scholar] [CrossRef]
- Green, N.H.; Allen, S.; Davies, M.C.; Roberts, C.J.; Tendler, S.J.B.; Williams, P.M. Force sensing and mapping by atomic force microscopy. TrAC-Trends Anal. Chem. 2002, 21, 64–73. [Google Scholar] [CrossRef]
- Garcia, R. Nanomechanical mapping of soft materials with the atomic force microscope: Methods, theory and applications. Chem. Soc. Rev. 2020, 49, 5850–5884. [Google Scholar] [CrossRef]
- Flater, E.E.; Zacharakis-Jutz, G.E.; Dumba, B.G.; White, I.A.; Clifford, C.A. Towards easy and reliable AFM tip shape determination using blind tip reconstruction. Ultramicroscopy 2014, 146, 130–143. [Google Scholar] [CrossRef]
- Bright, R.; Hayles, A.; Wood, J.; Ninan, N.; Palms, D.; Visalakshan, R.M.; Burzava, A.; Brown, T.; Barker, D.; Vasilev, K. Bio-Inspired Nanostructured Ti-6Al-4V Alloy: The Role of Two Alkaline Etchants and the Hydrothermal Processing Duration on Antibacterial Activity. Nanomaterials 2022, 12, 1140. [Google Scholar] [CrossRef]
- Butt, H.J.; Cappella, B.; Kappl, M. Force measurements with the atomic force microscope: Technique, interpretation and applications. Surf. Sci. Rep. 2005, 59, 1–152. [Google Scholar] [CrossRef]
- Brunner, R.; Etsion, I.; Talke, F.E. A simple atomic force microscopy calibration method for direct measurement of surface energy on nanostructured surfaces covered with molecularly thin liquid films. Rev. Sci. Instrum. 2009, 80, 055109. [Google Scholar] [CrossRef] [PubMed]
- Ponsonnet, L.; Reybier, K.; Jaffrezic, N.; Comte, V.; Lagneau, C.; Lissac, M.; Martelet, C. Relationship between surface properties (roughness, wettability) of titanium and titanium alloys and cell behaviour. Mater. Sci. Eng. C-Biomim. Supramol. Syst. 2003, 23, 551–560. [Google Scholar] [CrossRef]
- Nečas, D.; Klapetek, P. Gwyddion: An open-source software for SPM data analysis. Open Phys. 2012, 10, 181–188. [Google Scholar] [CrossRef]
- Israelachvili, J.N.; Tabor, D. Van der Waals Forces: Theory and Experiment. In Progress in Surface and Membrane Science; Danielli, J.F., Rosenberg, M.D., Cadenhead, D.A., Eds.; Elsevier: Amsterdam, The Netherlands, 1973; Volume 7, pp. 1–55. [Google Scholar]
- Traini, D.; Young, P.M.; Rogueda, P.; Price, R. The use of AFM and surface energy measurements to investigate drug-canister material interactions in a model pressurized metered dose inhaler formulation. Aerosol Sci. Technol. 2006, 40, 227–236. [Google Scholar] [CrossRef]
- Lin, D.C.; Dimitriadis, E.K.; Horkay, F. Elasticity of rubber-like materials measured by AFM nanoindentation. Express Polym. Lett. 2007, 1, 576–584. [Google Scholar] [CrossRef]
- Johnson, K.L.; Kendall, K.; Roberts, A.D.; Tabor, D. Surface energy and the contact of elastic solids. Proc. R. Soc. London A Math. Phys. Sci. 1997, 324, 301–313. [Google Scholar] [CrossRef]
- Derjaguin, B.V.; Muller, V.M.; Toporov, Y.P. Effect of contact deformations on the adhesion of particles. J. Colloid Interface Sci. 1975, 53, 314–326. [Google Scholar] [CrossRef]
- Xu, D.; Liechti, K.M.; Ravi-Chandar, K. On the modified Tabor parameter for the JKR-DMT transition in the presence of a liquid meniscus. J. Colloid Interface Sci. 2007, 315, 772–785. [Google Scholar] [CrossRef]
- Israelachvili, J.N. (Ed.) Unifying Concepts in Intermolecular and Interparticle Forces. In Intermolecular and Surface Forces; Academic Press: San Diego, CA, USA, 2011; pp. 191–204. [Google Scholar] [CrossRef]
- Hopcroft, M.A.; Nix, W.D.; Kenny, T.W. What is the Young’s Modulus of Silicon? J. Microelectromech. Syst. 2010, 19, 229–238. [Google Scholar] [CrossRef]
- Niinomi, M.; Liu, Y.; Nakai, M.; Liu, H.; Li, H. Biomedical titanium alloys with Young’s moduli close to that of cortical bone. Regen. Biomater. 2016, 3, 173–185. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Wang, S.Y.; Xiang, X.; Tao, W.Q. Mechanism of surface nanostructure changing wettability: A molecular dynamics simulation. Comput. Mater. Sci. 2020, 171, 109223. [Google Scholar] [CrossRef]
- Packham, D.E. Work of adhesion: Contact angles and contact mechanics. Int. J. Adhes. Adhes. 1996, 16, 121–128. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, N.; Xu, J. Fabrication and application of superhydrophilic surfaces: A review. J. Adhes. Sci. Technol. 2014, 28, 769–790. [Google Scholar] [CrossRef]
- Chen, Y.; Norde, W.; van der Mei, H.C.; Busscher, H.J. Bacterial cell surface deformation under external loading. mBio 2012, 3, e00378-12. [Google Scholar] [CrossRef]
- Israelachvili, J.N. (Ed.) Adhesion and Wetting Phenomena. In Intermolecular and Surface Forces; Academic Press: San Diego, CA, USA, 2011; pp. 415–467. [Google Scholar] [CrossRef]
- Chandra, D.; Yang, S. Stability of high-aspect-ratio micropillar arrays against adhesive and capillary forces. Acc. Chem. Res. 2010, 43, 1080–1091. [Google Scholar] [CrossRef]
- Jones, R.; Hodges, C.S. Applications of atomic force microscopy to granular materials: Inter-particle forces in air. In Granular Materials; Antony, S.J., Hoyle, W., Ding, Y., Eds.; The Royal Society of Chemistry: London, UK, 2007; pp. 229–254. [Google Scholar] [CrossRef]
- Rasband, W.S. ImageJ; U.S. National Institutes of Health: Bethesda, MD, USA, 2015. Available online: http://imagej.nih.gov/ij (accessed on 24 February 2025).
- Dorrer, C.; Rühe, J. Wetting of silicon nanograss:: From superhydrophilic to superhydrophobic surfaces. Adv. Mater. 2008, 20, 159–163. [Google Scholar] [CrossRef]
- Lin, N.; Berton, P.; Moraes, C.; Rogers, R.D.; Tufenkji, N. Nanodarts, nanoblades, and nanospikes: Mechano-bactericidal nanostructures and where to find them. Adv. Colloid Interface Sci. 2018, 252, 55–68. [Google Scholar] [CrossRef]
- Lee, K.Y.; Case, E.D. Effects of adhesion on the effective Young’s modulus in glass slide/glue laminates. J. Mater. Sci. 1996, 31, 2253–2264. [Google Scholar] [CrossRef]
- Guo, S.; Meng, Q.; Zhao, X.; Wei, Q.; Xu, H. Design and fabrication of a metastable beta-type titanium alloy with ultralow elastic modulus and high strength. Sci. Rep. 2015, 5, 14688. [Google Scholar] [CrossRef]
- Dai, G.; Gu, H.; Zhang, J.; Jiang, J.; Sun, J.; Sun, Z. Modifying Microstructure and Improving Mechanical Properties of New Ti-Al-V Titanium Alloys via Fe Addition. Materials 2024, 17, 5161. [Google Scholar] [CrossRef] [PubMed]
- Magazzù, A.; Marcuello, C. Investigation of Soft Matter Nanomechanics by Atomic Force Microscopy and Optical Tweezers: A Comprehensive Review. Nanomaterials 2023, 13, 963. [Google Scholar] [CrossRef] [PubMed]
- Wood, J.; Bright, R.; Palms, D.; Barker, D.; Vasilev, K. Damage Behavior with Atomic Force Microscopy on Anti-Bacterial Nanostructure Arrays. Nanomaterials 2024, 14, 253. [Google Scholar] [CrossRef]
- Shivakoti, I.; Bhowmik, A.; Santhosh, A.J. Unlocking the potential of titanium and its alloys: A mini-review on innovative surface modification techniques. AIP Adv. 2024, 14, 100705. [Google Scholar] [CrossRef]
- Wang, J.; Pan, Z.; Wang, Y.; Wang, L.; Su, L.; Cuiuri, D.; Zhao, Y.-h.; Li, H. Evolution of crystallographic orientation, precipitation, phase transformation and mechanical properties realized by enhancing deposition current for dual-wire arc additive manufactured Ni-rich NiTi alloy. Addit. Manuf. 2020, 34, 101240. [Google Scholar] [CrossRef]
- Anna, S.L.; McKinley, G.H. Elasto-capillary thinning and breakup of model elastic liquids. J. Rheol. 2001, 45, 115–138. [Google Scholar] [CrossRef]
- Vagharchakian, L.; Restagno, F.; Leger, L. Capillary bridge formation and breakage: A test to characterize antiadhesive surfaces. J. Phys. Chem. B 2009, 113, 3769–3775. [Google Scholar] [CrossRef]
- Tsibouklis, J.; Stone, M.; Thorpe, A.A.; Graham, P.; Peters, V.; Heerlien, R.; Smith, J.R.; Green, K.L.; Nevell, T.G. Preventing bacterial adhesion onto surfaces: The low-surface-energy approach. Biomaterials 1999, 20, 1229–1235. [Google Scholar] [CrossRef]
- Hölscher, H.; Ebeling, D.; Schwarz, U.D. Friction at Atomic-Scale Surface Steps: Experiment and Theory. Phys. Rev. Lett. 2008, 101, 246105. [Google Scholar] [CrossRef]
- Hotchkiss, K.M.; Reddy, G.B.; Hyzy, S.L.; Schwartz, Z.; Boyan, B.D.; Olivares-Navarrete, R. Titanium surface characteristics, including topography and wettability, alter macrophage activation. Acta Biomater. 2016, 31, 425–434. [Google Scholar] [CrossRef]
- Zhao, G.; Schwartz, Z.; Wieland, M.; Rupp, F.; Geis-Gerstorfer, J.; Cochran, D.L.; Boyan, B.D. High surface energy enhances cell response to titanium substrate microstructure. J. Biomed. Mater. Res. A 2005, 74, 49–58. [Google Scholar] [CrossRef] [PubMed]
- Lim, J.Y.; Shaughnessy, M.C.; Zhou, Z.Y.; Noh, H.; Vogler, E.A.; Donahue, H.J. Surface energy effects on osteoblast spatial growth and mineralization. Biomaterials 2008, 29, 1776–1784. [Google Scholar] [CrossRef] [PubMed]
- Feng, B.; Weng, J.; Yang, B.C.; Qu, S.X.; Zhang, X.D. Characterization of surface oxide films on titanium and adhesion of osteoblast. Biomaterials 2003, 24, 4663–4670. [Google Scholar] [CrossRef]
- Leite, F.L.; Bueno, C.C.; Da Róz, A.L.; Ziemath, E.C.; Oliveira, O.N. Theoretical Models for Surface Forces and Adhesion and Their Measurement Using Atomic Force Microscopy. Int. J. Mol. Sci. 2012, 13, 12773–12856. [Google Scholar] [CrossRef]
- Boinovich, L.B. Long-range surface forces and their role in the progress of nanotechnology. Uspekhi Khimii 2007, 76, 510–528. [Google Scholar] [CrossRef]
- Thormann, E. Surface forces between rough and topographically structured interfaces. Curr. Opin. Colloid Interface Sci. 2017, 27, 18–24. [Google Scholar] [CrossRef]
- Muraoka, M.; Arnold, W. A method of evaluating local elasticity and adhesion energy from the nonlinear response of AFM cantilever vibrations. JSME Int. J. Ser. A-Solid Mech. Mater. Eng. 2001, 44, 396–405. [Google Scholar] [CrossRef]
- Tabor, D.; Winterton, R.H.S. Surface Forces: Direct Measurement of Normal and Retarded van der Waals Forces. Nature 1968, 219, 1120–1121. [Google Scholar] [CrossRef]
- Butt, H.J. Measuring electrostatic, van der Waals, and hydration forces in electrolyte solutions with an atomic force microscope. Biophys. J. 1991, 60, 1438–1444. [Google Scholar] [CrossRef]
- Guggisberg, M.; Bammerlin, M.; Loppacher, C.; Pfeiffer, O.; Abdurixit, A.; Barwich, V.; Bennewitz, R.; Baratoff, A.; Meyer, E.; Güntherodt, H.J. Separation of interactions by noncontact force microscopy. Phys. Rev. B 2000, 61, 11151–11155. [Google Scholar] [CrossRef]
- Hudlet, S.; Saint Jean, M.; Guthmann, C.; Berger, J. Evaluation of the capacitive force between an atomic force microscopy tip and a metallic surface. Eur. Phys. J. B 1998, 2, 5–10. [Google Scholar] [CrossRef]
- Law, B.M.; Rieutord, F. Electrostatic forces in atomic force microscopy. Phys. Rev. B 2002, 66, 035402. [Google Scholar] [CrossRef]
- Khachatourian, A.; Chan, H.K.; Stace, A.J.; Bichoutskaia, E. Electrostatic force between a charged sphere and a planar surface: A general solution for dielectric materials. J. Chem. Phys. 2014, 140, 074107. [Google Scholar] [CrossRef]
- Sugimoto, Y.; Pou, P.; Abe, M.; Jelinek, P.; Perez, R.; Morita, S.; Custance, O. Chemical identification of individual surface atoms by atomic force microscopy. Nature 2007, 446, 64–67. [Google Scholar] [CrossRef]





| Surface | JKR (N/m) | DMT (N/m) |
|---|---|---|
| Silicon | 4.0 ± 0.6 | 5.3 ± 0.7 |
| AR-Ti | 185.3 ± 122.6 | 247.1 ± 163.5 |
| KOH NS | 13.4 ± 8.8 | 17.2 ± 11.8 |
| NaOH NS | 4.4 ± 3.5 | 5.9 ± 4.7 |
| Samples | Surface Energy (pN/nm) | Snap-to-Contact Force (nN) | Snap-to-Contact Distance (nm) | Snap-off-Contact Force (nN) | Snap-off-Contact Distance (nm) |
|---|---|---|---|---|---|
| Si control | 6.7–35 | 10–180 | 2–28 | 37–270 | 10–30 |
| Glass control | 850–1350 | 150–290 | 5–11 | 6700–10,600 | 149–245 |
| AR-Ti (control) | 6.9–130 | 86–190 | 9–15 | 550–830 | 17–20 |
| Ti6Al4V KOH | 4–24 | 1–20 | 208 | 22–96 | 15–22 |
| Ti6Al4V NaOH | 3.4–17 | - | - | 20–136 | 6–36 |
| Tip Velocity (µm/s) | NaOH 100 nN | NaOH 50 nN | KOH 100 nN | KOH 50 nN |
|---|---|---|---|---|
| 2 | 27.3 ± 1.6 | 28.6 ± 1.6 | 24.1 ± 5.7 | 17.6 ± 2.1 |
| 1.5 | 30.7 ± 3.7 | 28.8 ± 1.4 | 23.5 ± 4.5 | 17.2 ± 1.6 |
| 1 | 31.3 ± 2.4 | 28.6 ± 1.6 | 25.2 ± 4.0 | 17.7 ± 2.1 |
| 0.5 | 30.0 ± 3.2 | 28.6 ± 1.6 | 27.4 ± 4.1 | 17.4 ± 2.8 |
| 0.25 | 30.9 ± 3.9 | 28.8 ± 1.0 | 31.6 ± 4.5 | 18.1 ± 2.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wood, J.; Palms, D.; Luu, Q.T.; Vasilev, K.; Bright, R. Investigating Simulated Cellular Interactions on Nanostructured Surfaces with Antibacterial Properties: Insights from Force Curve Simulations. Nanomaterials 2025, 15, 462. https://doi.org/10.3390/nano15060462
Wood J, Palms D, Luu QT, Vasilev K, Bright R. Investigating Simulated Cellular Interactions on Nanostructured Surfaces with Antibacterial Properties: Insights from Force Curve Simulations. Nanomaterials. 2025; 15(6):462. https://doi.org/10.3390/nano15060462
Chicago/Turabian StyleWood, Jonathan, Dennis Palms, Quan Trong Luu, Krasimir Vasilev, and Richard Bright. 2025. "Investigating Simulated Cellular Interactions on Nanostructured Surfaces with Antibacterial Properties: Insights from Force Curve Simulations" Nanomaterials 15, no. 6: 462. https://doi.org/10.3390/nano15060462
APA StyleWood, J., Palms, D., Luu, Q. T., Vasilev, K., & Bright, R. (2025). Investigating Simulated Cellular Interactions on Nanostructured Surfaces with Antibacterial Properties: Insights from Force Curve Simulations. Nanomaterials, 15(6), 462. https://doi.org/10.3390/nano15060462








