Deterministic Fabrication of Fluorescent Nanostructures Featuring Distinct Optical Transitions
Abstract
1. Introduction
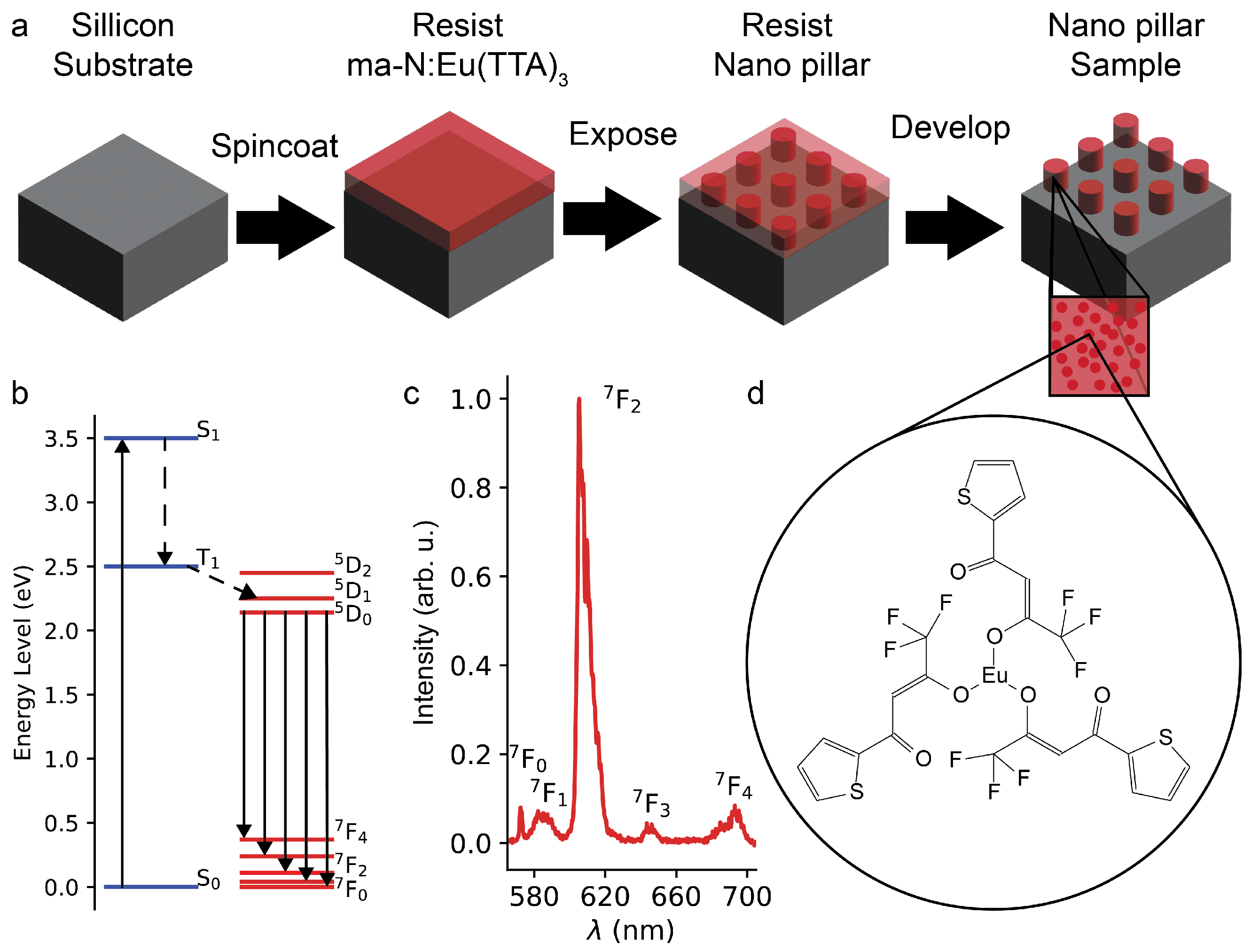
2. Materials and Methods
3. Results
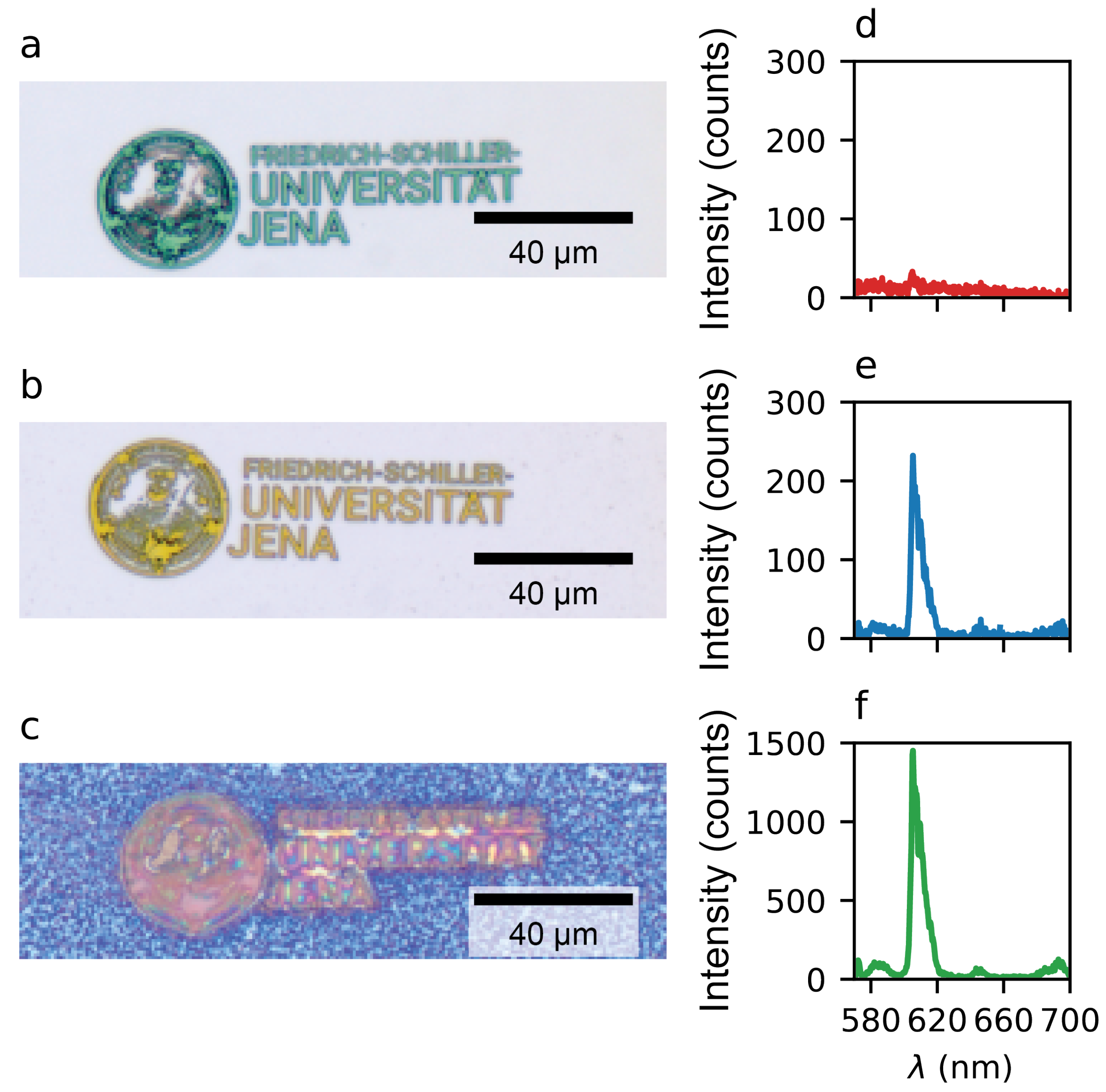
3.1. Fluorescence of Exposed Doped Resist
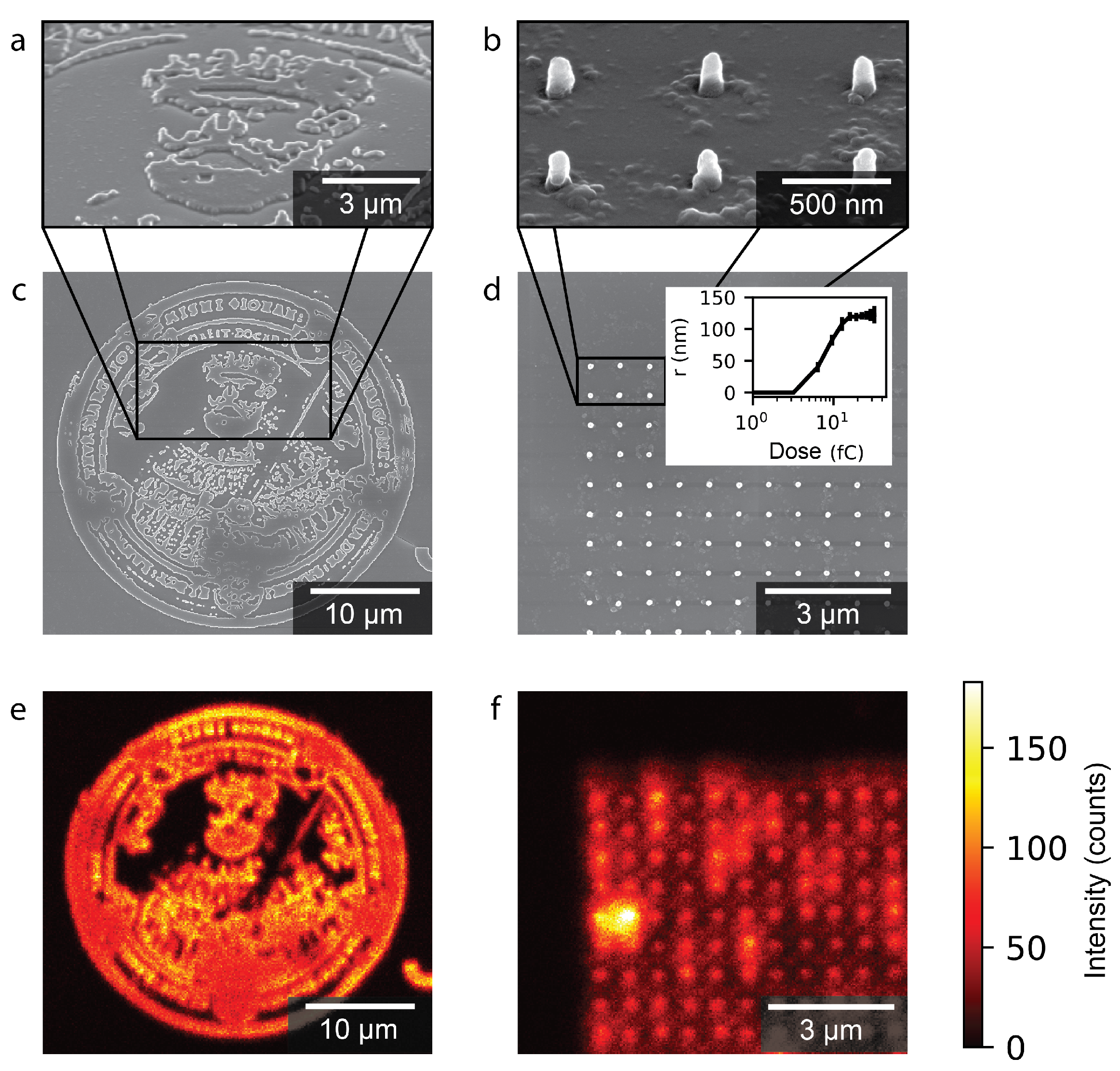
3.2. Deterministic Fabrication of Fluorescent Nanostructures
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Eu(TTA)3 | Europium(III) thenoyltrifluoroacetonate |
| ED | Electric dipole |
| MD | Magnetic dipole |
| LDOS | Local density of optical states |
| EBL | Electron-beam lithography |
| SEM | Scanning Electron Microscope |
| wavelength |
Appendix A. Concentration in Resist
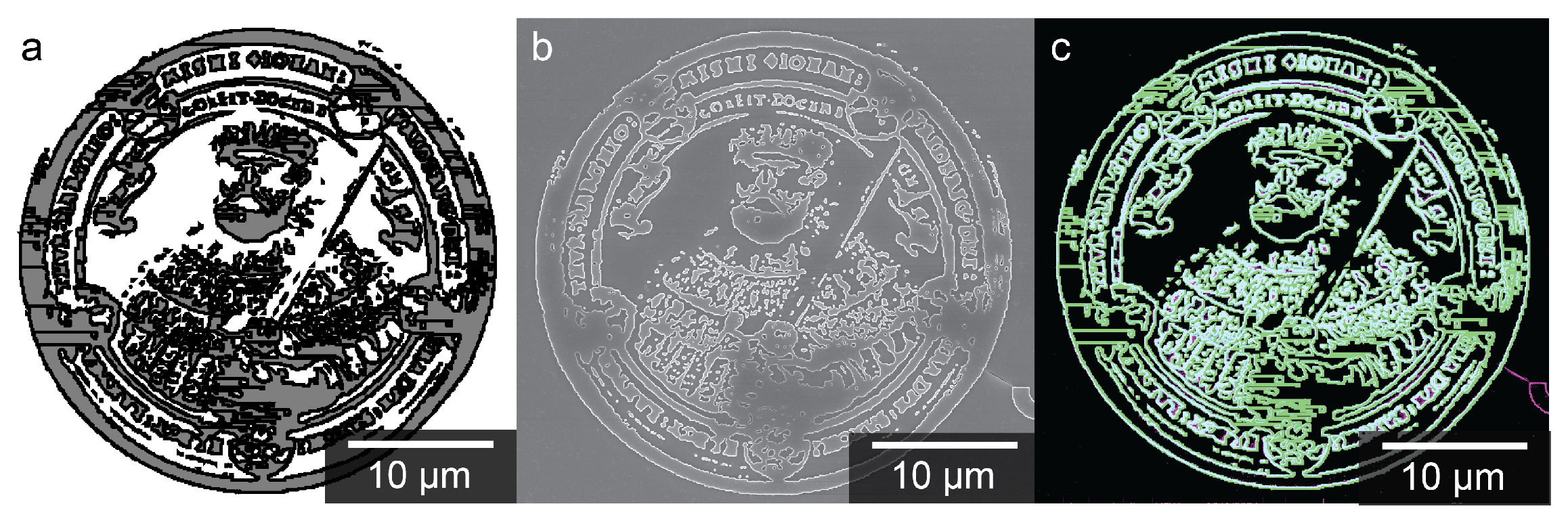
Appendix B. Layout Compared to SEM
References
- Allen, L.; Eberly, J.H. Optical Resonance and Two-Level Atoms; Courier Corporation: North Chelmsford, MA, USA, 1987; Volume 28. [Google Scholar]
- Purcell, E.M.; Torrey, H.C.; Pound, R.V. Resonance absorption by nuclear magnetic moments in a solid. Phys. Rev. 1946, 69, 37. [Google Scholar] [CrossRef]
- Saliba, L.F.; de Sousa Filho, P.C.; de Castro, G.R.; Serra, O.A.; Martines, M.A.U. Luminescent properties of Eu (ttfa) 3 complexes incorporated into MSU-4 mesoporous silica matrices. Biointerface Res. Appl. Chem. 2016, 6, 1872–1878. [Google Scholar]
- Baranov, D.G.; Savelev, R.S.; Li, S.V.; Krasnok, A.E.; Alù, A. Modifying magnetic dipole spontaneous emission with nanophotonic structures. Laser Photonics Rev. 2017, 11, 1600268. [Google Scholar] [CrossRef]
- Ofelt, G.S. Intensities of Crystal Spectra of Rare-Earth Ions. J. Chem. Phys. 1962, 37, 511–520. [Google Scholar] [CrossRef]
- Judd, B.R. Optical Absorption Intensities of Rare-Earth Ions. Phys. Rev. 1962, 127, 750–761. [Google Scholar] [CrossRef]
- Carnall, W.; Fields, P.; Rajnak, K. Spectral intensities of the trivalent lanthanides and actinides in solution. II. Pm3+, Sm3+, Eu3+, Gd3+, Tb3+, Dy3+, and Ho3+. J. Chem. Phys. 1968, 49, 4412–4423. [Google Scholar] [CrossRef]
- Noginova, N.; Zhu, G.; Mavy, M.; Noginov, M.A. Magnetic dipole based systems for probing optical magnetism. J. Appl. Phys. 2008, 103, 07E901. [Google Scholar] [CrossRef]
- Blasse, G.; Bril, A.; Nieuwpoort, W. On the Eu3+ fluorescence in mixed metal oxides. J. Phys. Chem. Solids 1966, 27, 1587–1592. [Google Scholar] [CrossRef]
- Karaveli, S.; Zia, R. Spectral Tuning by Selective Enhancement of Electric and Magnetic Dipole Emission. Phys. Rev. Lett. 2011, 106, 193004. [Google Scholar] [CrossRef] [PubMed]
- Rolly, B.; Bebey, B.; Bidault, S.; Stout, B.; Bonod, N. Promoting magnetic dipolar transition in trivalent lanthanide ions with lossless Mie resonances. Phys. Rev. B 2012, 85, 245432. [Google Scholar] [CrossRef]
- Ni, X.; Naik, G.V.; Kildishev, A.V.; Barnakov, Y.; Boltasseva, A.; Shalaev, V.M. Effect of metallic and hyperbolic metamaterial surfaces on electric and magnetic dipole emission transitions. Appl. Phys. B 2011, 103, 553–558. [Google Scholar] [CrossRef]
- Hussain, R.; Keene, D.; Noginova, N.; Durach, M. Spontaneous emission of electric and magnetic dipoles in the vicinity of thin and thick metal. Opt. Express 2014, 22, 7744–7755. [Google Scholar] [CrossRef] [PubMed]
- Hussain, R.; Kruk, S.S.; Bonner, C.E.; Noginov, M.A.; Staude, I.; Kivshar, Y.S.; Noginova, N.; Neshev, D.N. Enhancing Eu3+ magnetic dipole emission by resonant plasmonic nanostructures. Opt. Lett. 2015, 40, 1659–1662. [Google Scholar] [CrossRef] [PubMed]
- Aigouy, L.; Cazé, A.; Gredin, P.; Mortier, M.; Carminati, R. Mapping and Quantifying Electric and Magnetic Dipole Luminescence at the Nanoscale. Phys. Rev. Lett. 2014, 113, 076101. [Google Scholar] [CrossRef]
- Choi, B.; Iwanaga, M.; Sugimoto, Y.; Sakoda, K.; Miyazaki, H.T. Selective Plasmonic Enhancement of Electric- and Magnetic-Dipole Radiations of Er Ions. Nano Lett. 2016, 16, 5191–5196. [Google Scholar] [CrossRef]
- Murai, S.; Saito, M.; Sakamoto, H.; Yamamoto, M.; Kamakura, R.; Nakanishi, T.; Fujita, K.; Verschuuren, M.A.; Hasegawa, Y.; Tanaka, K. Directional outcoupling of photoluminescence from Eu(III)-complex thin films by plasmonic array. APL Photonics 2017, 2, 026104. [Google Scholar] [CrossRef]
- Wiecha, P.R.; Majorel, C.; Girard, C.; Arbouet, A.; Masenelli, B.; Boisron, O.; Lecestre, A.; Larrieu, G.; Paillard, V.; Cuche, A. Enhancement of electric and magnetic dipole transition of rare-earth-doped thin films tailored by high-index dielectric nanostructures. Appl. Opt. 2019, 58, 1682–1690. [Google Scholar] [CrossRef]
- Vaskin, A.; Mashhadi, S.; Steinert, M.; Chong, K.E.; Keene, D.; Nanz, S.; Abass, A.; Rusak, E.; Choi, D.Y.; Fernandez-Corbaton, I.; et al. Manipulation of Magnetic Dipole Emission from Eu3+ with Mie-Resonant Dielectric Metasurfaces. Nano Lett. 2019, 19, 1015–1022. [Google Scholar] [CrossRef]
- Sanz-Paz, M.; Ernandes, C.; Esparza, J.U.; Burr, G.W.; van Hulst, N.F.; Maitre, A.; Aigouy, L.; Gacoin, T.; Bonod, N.; Garcia-Parajo, M.F.; et al. Enhancing Magnetic Light Emission with All-Dielectric Optical Nanoantennas. Nano Lett. 2018, 18, 3481–3487. [Google Scholar] [CrossRef]
- Reynier, B.; Charron, E.; Markovic, O.; Yang, X.; Gallas, B.; Ferrier, A.; Bidault, S.; Mivelle, M. Full control of electric and magnetic light–matter interactions through a nanomirror on a near-field tip. Optica 2023, 10, 841–845. [Google Scholar] [CrossRef]
- Bashiri, A.; Vaskin, A.; Tanaka, K.; Steinert, M.; Pertsch, T.; Staude, I. Color Routing of the Emission from Magnetic and Electric Dipole Transitions of Eu3+ by Broken-Symmetry TiO2 Metasurfaces. ACS Nano 2024, 18, 506–514. [Google Scholar] [CrossRef]
- Montagnac, M.; Brûlé, Y.; Cuche, A.; Poumirol, J.M.; Weber, S.J.; Müller, J.; Larrieu, G.; Larrey, V.; Fournel, F.; Boisron, O.; et al. Control of light emission of quantum emitters coupled to silicon nanoantenna using cylindrical vector beams. Light Sci. Appl. 2023, 12, 239. [Google Scholar] [CrossRef] [PubMed]
- Mie, G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Ann. Der Phys. 1908, 330, 377–445. [Google Scholar] [CrossRef]
- Kuznetsov, A.I.; Miroshnichenko, A.E.; Fu, Y.H.; Zhang, J.; Luk’yanchuk, B. Magnetic light. Sci. Rep. 2012, 2, 492. [Google Scholar] [CrossRef]
- Evlyukhin, A.B.; Novikov, S.M.; Zywietz, U.; Eriksen, R.L.; Reinhardt, C.; Bozhevolnyi, S.I.; Chichkov, B.N. Demonstration of Magnetic Dipole Resonances of Dielectric Nanospheres in the Visible Region. Nano Lett. 2012, 12, 3749–3755. [Google Scholar] [CrossRef]
- Gómez-Medina, R. Electric and magnetic dipolar response of germanium nanospheres: Interference effects, scattering anisotropy, and optical forces. J. Nanophotonics 2011, 5, 053512. [Google Scholar] [CrossRef]
- Staude, I.; Miroshnichenko, A.E.; Decker, M.; Fofang, N.T.; Liu, S.; Gonzales, E.; Dominguez, J.; Luk, T.S.; Neshev, D.N.; Brener, I.; et al. Tailoring directional scattering through magnetic and electric resonances in subwavelength silicon nanodisks. ACS Nano 2013, 7, 7824–7832. [Google Scholar] [CrossRef]
- Koshelev, K.; Bogdanov, A.; Kivshar, Y. Meta-optics and bound states in the continuum. Sci. Bull. 2019, 64, 836–842. [Google Scholar] [CrossRef] [PubMed]
- Bakker, R.M.; Permyakov, D.; Yu, Y.F.; Markovich, D.; Paniagua-Domínguez, R.; Gonzaga, L.; Samusev, A.; Kivshar, Y.; Luk’yanchuk, B.; Kuznetsov, A.I. Magnetic and Electric Hotspots with Silicon Nanodimers. Nano Lett. 2015, 15, 2137–2142. [Google Scholar] [CrossRef]
- Barreda, A.; Hell, S.; Weissflog, M.; Minovich, A.; Pertsch, T.; Staude, I. Metal, dielectric and hybrid nanoantennas for enhancing the emission of single quantum dots: A comparative study. J. Quant. Spectrosc. Radiat. Transf. 2021, 276, 107900. [Google Scholar] [CrossRef]
- Sugimoto, H.; Fujii, M. Magnetic Purcell Enhancement by Magnetic Quadrupole Resonance of Dielectric Nanosphere Antenna. ACS Photonics 2021, 8, 1794–1800. [Google Scholar] [CrossRef]
- Vaskin, A.; Kolkowski, R.; Koenderink, A.F.; Staude, I. Light-emitting metasurfaces. Nanophotonics 2019, 8, 1151–1198. [Google Scholar] [CrossRef]
- Krasnok, A.E.; Simovski, C.R.; Belov, P.A.; Kivshar, Y.S. Superdirective dielectric nanoantennas. Nanoscale 2014, 6, 7354–7361. [Google Scholar] [CrossRef]
- Liu, S.; Srinivasan, K.; Liu, J. Nanoscale Positioning Approaches for Integrating Single Solid-State Quantum Emitters with Photonic Nanostructures. Laser Photonics Rev. 2021, 15, 2100223. [Google Scholar] [CrossRef]
- Curto, A.G.; Volpe, G.; Taminiau, T.H.; Kreuzer, M.P.; Quidant, R.; van Hulst, N.F. Unidirectional Emission of a Quantum Dot Coupled to a Nanoantenna. Science 2010, 329, 930–933. [Google Scholar] [CrossRef]
- Staude, I.; Sreenivasan, V.K.A.; Shishkin, I.; Samusev, K.; Decker, M.; Neshev, D.N.; Zvyagin, A.V.; Kivshar, Y.S. Selective placement of quantum dots on nanoscale areas of metal-free substrates. Phys. Status Solidi (RRL)-Rapid Res. Lett. 2014, 8, 710–713. [Google Scholar] [CrossRef]
- Dawood, F.; Wang, J.; Schulze, P.A.; Sheehan, C.J.; Buck, M.R.; Dennis, A.M.; Majumder, S.; Krishnamurthy, S.; Ticknor, M.; Staude, I.; et al. The Role of Liquid Ink Transport in the Direct Placement of Quantum Dot Emitters onto Sub-Micrometer Antennas by Dip-Pen Nanolithography. Small 2018, 14, 1801503. [Google Scholar] [CrossRef]
- Pang, L.; Shen, Y.; Tetz, K.; Fainman, Y. PMMA quantum dots composites fabricated via use of pre-polymerization. Opt. Express 2005, 13, 44–49. [Google Scholar] [CrossRef] [PubMed]
- Werschler, F.; Lindner, B.; Hinz, C.; Conradt, F.; Gumbsheimer, P.; Behovits, Y.; Negele, C.; de Roo, T.; Tzang, O.; Mecking, S.; et al. Efficient Emission Enhancement of Single CdSe/CdS/PMMA Quantum Dots through Controlled Near-Field Coupling to Plasmonic Bullseye Resonators. Nano Lett. 2018, 18, 5396–5400. [Google Scholar] [CrossRef]
- Badolato, A.; Hennessy, K.; Atatüre, M.; Dreiser, J.; Hu, E.; Petroff, P.M.; Imamolu, A. Deterministic Coupling of Single Quantum Dots to Single Nanocavity Modes. Science 2005, 308, 1158–1161. [Google Scholar] [CrossRef]
- Barrios, C.A.; Carrasco, S.; Canalejas-Tejero, V.; López-Romero, D.; Navarro-Villoslada, F.; Moreno-Bondi, M.C.; Fierro, J.L.G.; Capel-Sánchez, M.C. Fabrication of luminescent nanostructures by electron-beam direct writing of PMMA resist. Mater. Lett. 2012, 88, 93–96. [Google Scholar] [CrossRef]
- Lee, H.M.; Kim, Y.N.; Kim, B.H.; Kim, S.O.; Cho, S.O. Fabrication of Luminescent Nanoarchitectures by Electron Irradiation of Polystyrene. Adv. Mater. 2008, 20, 2094–2098. [Google Scholar] [CrossRef]
- Decker, M.; Ruther, M.; Kriegler, C.E.; Zhou, J.; Soukoulis, C.M.; Linden, S.; Wegener, M. Strong optical activity from twisted-cross photonic metamaterials. Opt. Lett. 2009, 34, 2501–2503. [Google Scholar] [CrossRef]
- Tseng, A.; Chen, K.; Chen, C.; Ma, K. Electron beam lithography in nanoscale fabrication: Recent development. IEEE Trans. Electron. Packag. Manuf. 2003, 26, 141–149. [Google Scholar] [CrossRef]
- Chen, Y. Nanofabrication by electron beam lithography and its applications: A review. Microelectron. Eng. 2015, 135, 57–72. [Google Scholar] [CrossRef]
- Taminiau, T.H.; Karaveli, S.; van Hulst, N.F.; Zia, R. Quantifying the magnetic nature of light emission. Nat. Commun. 2012, 3, 979. [Google Scholar] [CrossRef]
- Chu, T.Y. Syntheses, Characterization and Application of Lanthanide Complexes Containing Polymers. Ph.D. Thesis, Polytechnic University, Hung Hom, Kowloon, Hong Kong, 1999. [Google Scholar]
- Wiglusz, R.; Bednarkiewicz, A.; Strek, W. Synthesis and optical properties of Eu3+ ion doped nanocrystalline hydroxya patites embedded in PMMA matrix. J. Rare Earths 2011, 29, 1111–1116. [Google Scholar] [CrossRef]
- Binnemans, K. Interpretation of europium (III) spectra. Coord. Chem. Rev. 2015, 295, 1–45. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rikers, M.; Bashiri, A.; Barreda, Á.; Steinert, M.; Choi, D.-Y.; Pertsch, T.; Staude, I. Deterministic Fabrication of Fluorescent Nanostructures Featuring Distinct Optical Transitions. Nanomaterials 2025, 15, 219. https://doi.org/10.3390/nano15030219
Rikers M, Bashiri A, Barreda Á, Steinert M, Choi D-Y, Pertsch T, Staude I. Deterministic Fabrication of Fluorescent Nanostructures Featuring Distinct Optical Transitions. Nanomaterials. 2025; 15(3):219. https://doi.org/10.3390/nano15030219
Chicago/Turabian StyleRikers, Marijn, Ayesheh Bashiri, Ángela Barreda, Michael Steinert, Duk-Yong Choi, Thomas Pertsch, and Isabelle Staude. 2025. "Deterministic Fabrication of Fluorescent Nanostructures Featuring Distinct Optical Transitions" Nanomaterials 15, no. 3: 219. https://doi.org/10.3390/nano15030219
APA StyleRikers, M., Bashiri, A., Barreda, Á., Steinert, M., Choi, D.-Y., Pertsch, T., & Staude, I. (2025). Deterministic Fabrication of Fluorescent Nanostructures Featuring Distinct Optical Transitions. Nanomaterials, 15(3), 219. https://doi.org/10.3390/nano15030219






