Machine Learning for Thermal Transport Prediction in Nanoporous Materials: Progress, Challenges, and Opportunities
Abstract
1. Introduction
2. Theoretical Background
2.1. Nanoporous Materials
2.2. Thermal Transport in Nanoporous Materials
2.3. Structure–Property Relationships
2.4. Challenges in Traditional Computational Approaches
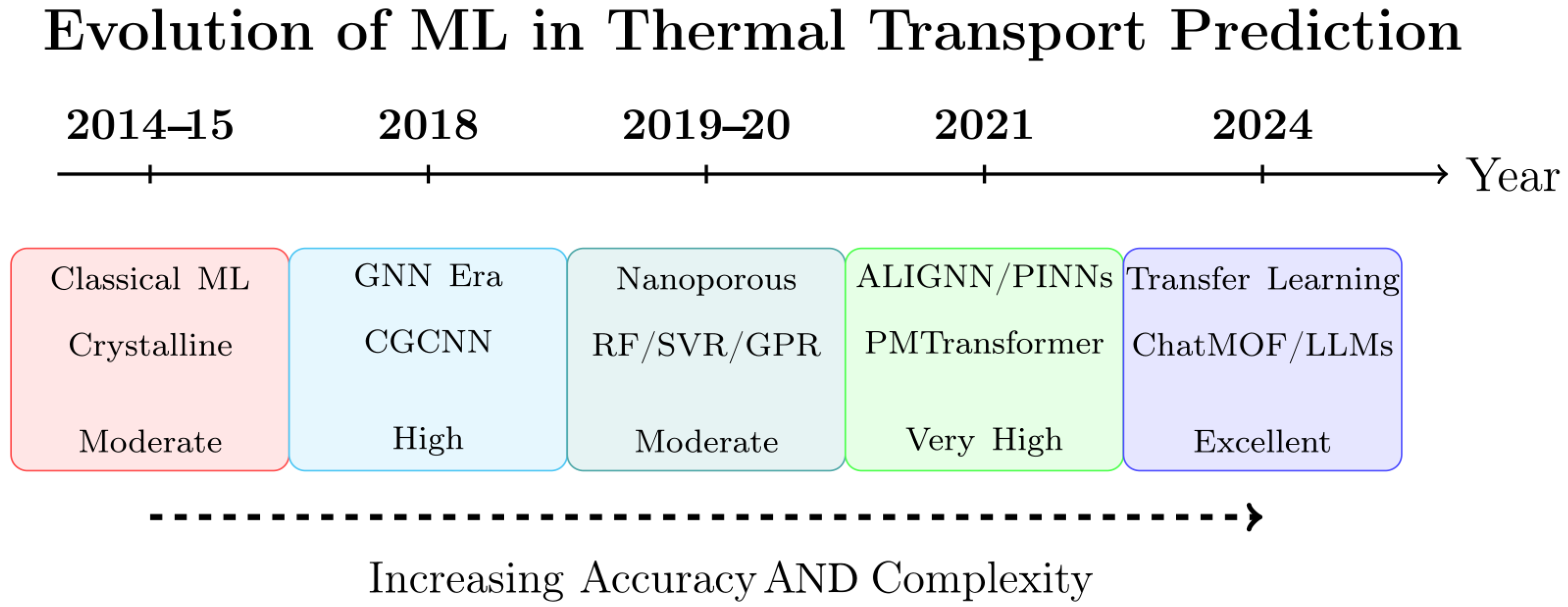
3. Evolution of Artificial Intelligence Approaches in Nanoporous Materials
3.1. Early Machine Learning Models
3.2. Deep Learning Revolution
3.2.1. Convolutional Neural Networks
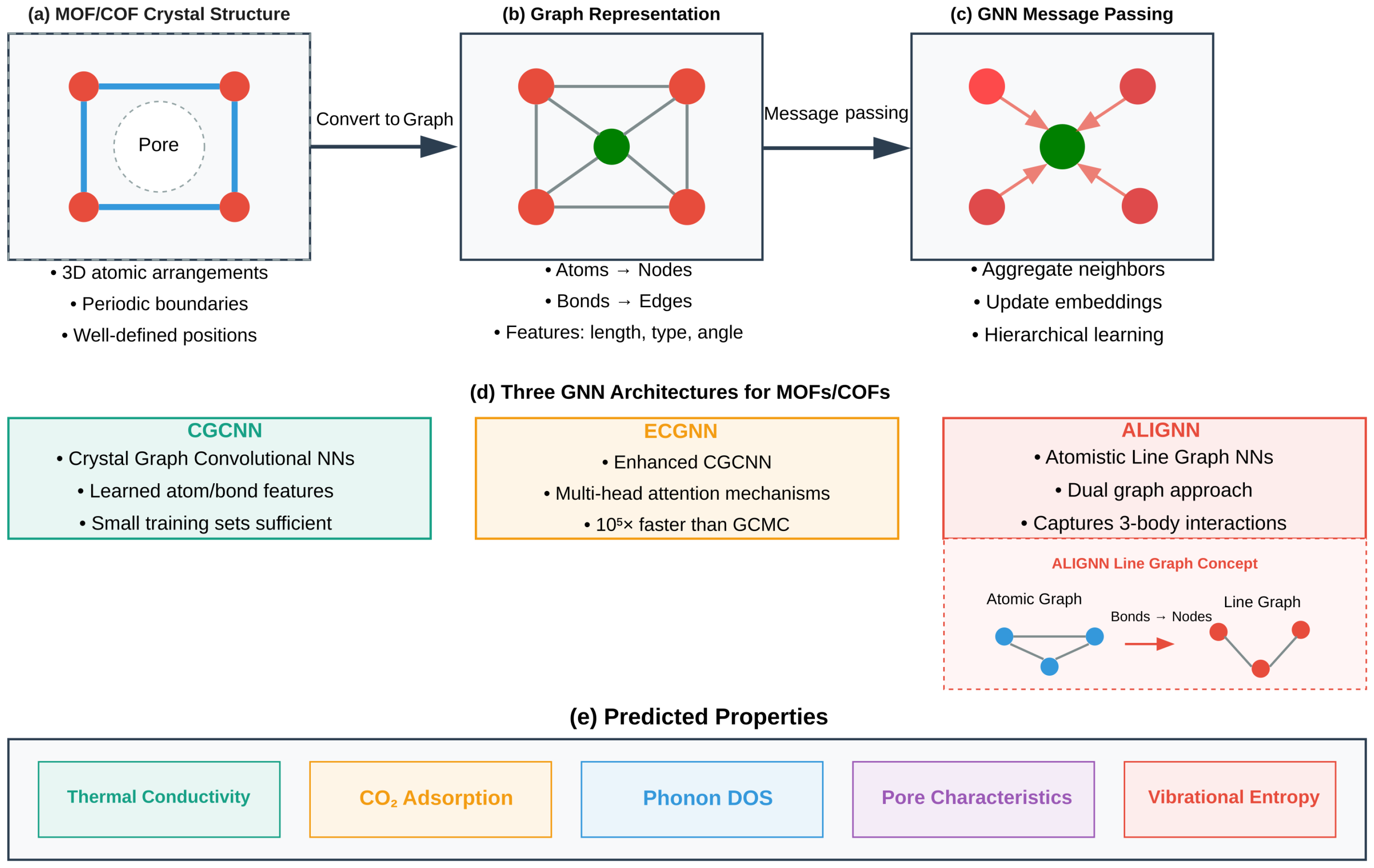
3.2.2. Graph Neural Networks
3.2.3. Generative Models
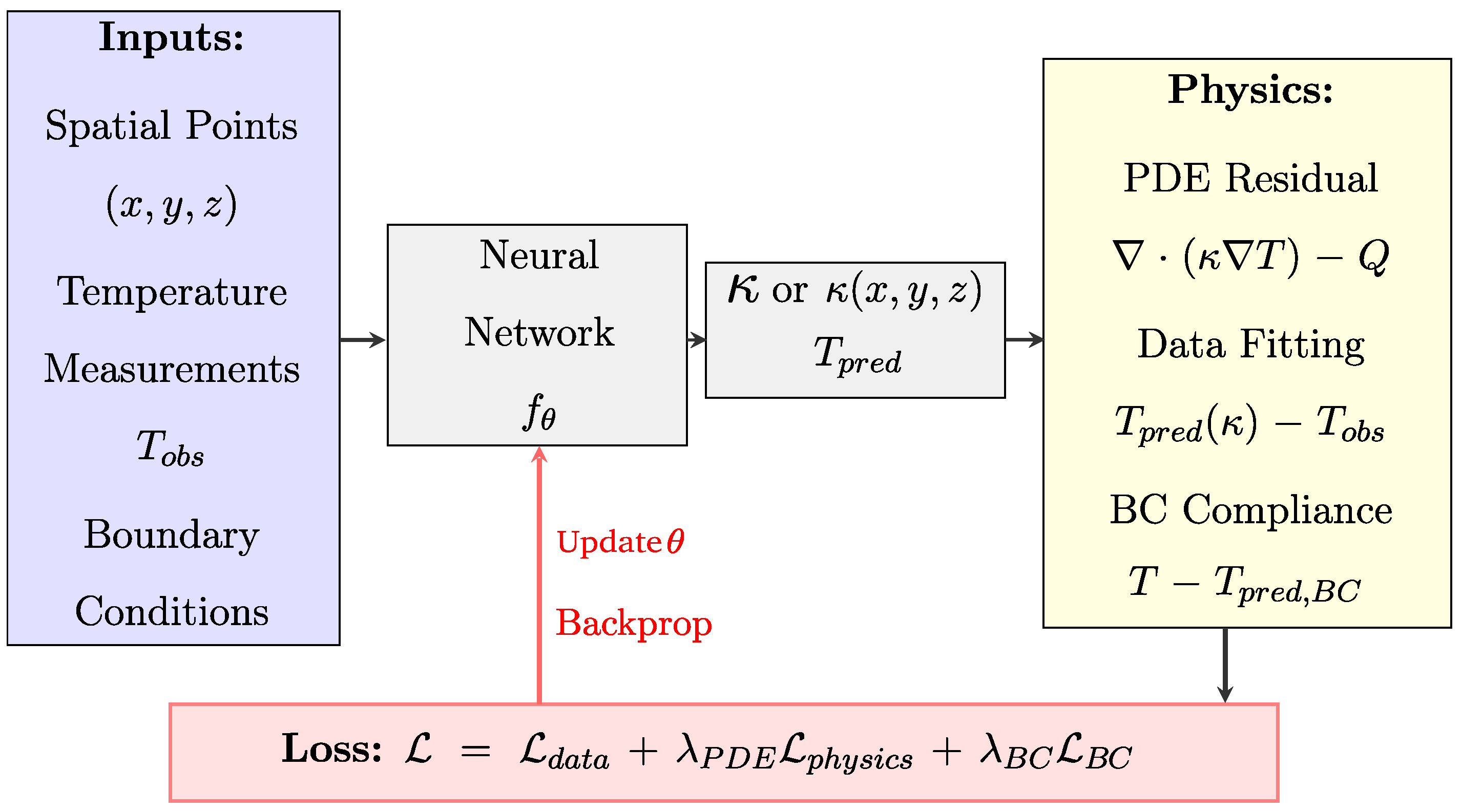
3.2.4. Physics-Informed Neural Networks
4. Transparency in Artificial Intelligence
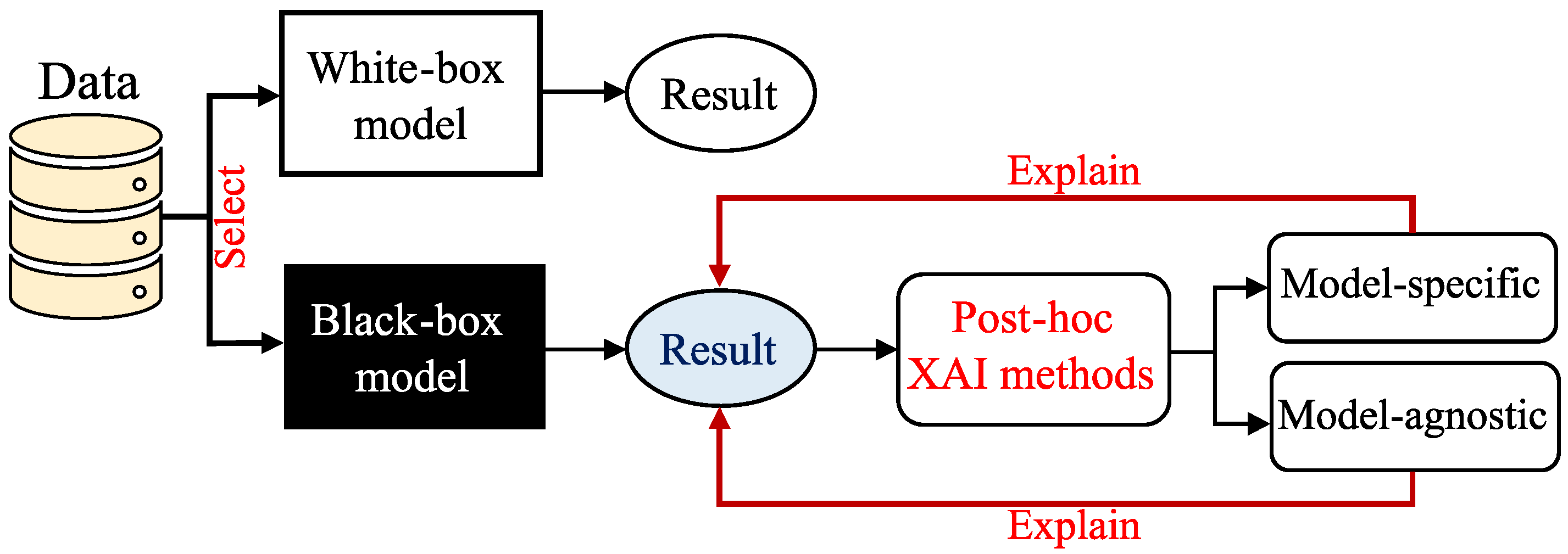
4.1. Explainable AI
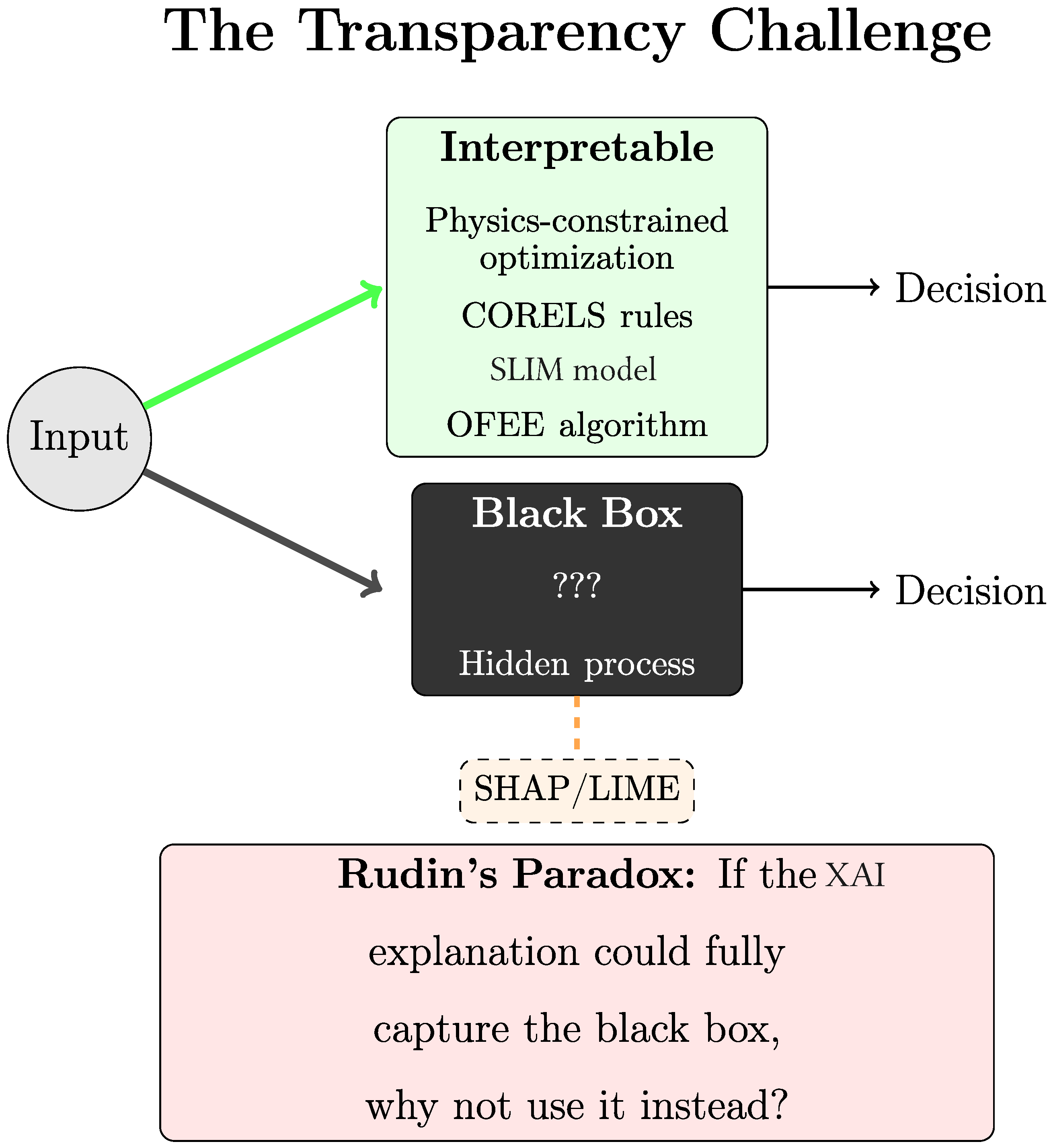
4.2. Interpretable AI
4.3. Ethical and Societal Considerations
4.4. Applications of Explainable/Interpretable AI in Nanoporous Materials
5. Limitations
6. Emerging Opportunities and Future Directions
6.1. Transfer Learning and Domain Adaptation
6.2. Multimodal Learning
6.3. Other Approaches
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| ALIGNN | Atomistic Line Graph Neural Network |
| CAM | Class Activation Mapping |
| CGCNN | Crystal Graph Convolutional Neural Network |
| CGAN | Conditional GAN |
| CNNs | Convolutional Neural Networks |
| COFs | Covalent Organic Frameworks |
| CSD | Cambridge Structural Database |
| DFT | Density Functional Theory |
| DNNs | Deep Neural Networks |
| ECGNN | Enhanced Crystal Graph Convolutional Neural Network |
| GANs | Generative Adversarial Networks |
| GCMC | Grand Canonical Monte Carlo |
| GNNs | Graph Neural Networks |
| Grad-CAM | Gradient-Weighted Class Activation Mapping |
| LIME | Local Interpretable Model-Agnostic Explanations |
| MD | Molecular Dynamics |
| ML | Machine Learning |
| MOFs | Metal–Organic Frameworks |
| NNs | Neural Networks |
| PDP | Partial Dependence Plots |
| PINNs | Physics-Informed Neural Networks |
| SHAP | Shapley Additive exPlanations |
| TL | Transfer Learning |
| VAEs | Variational Autoencoders |
| XAI | eXplainable Artificial Intelligence |
| SLIM | Supersparse Linear Integer Model |
References
- Fu, Z.; Corker, J.; Papathanasiou, T.; Wang, Y.; Zhou, Y.; Madyan, O.A.; Liao, F.; Fan, M. Critical review on the thermal conductivity modelling of silica aerogel composites. J. Build. Eng. 2022, 57, 104814. [Google Scholar] [CrossRef]
- An, L.; Di Luigi, M.; Petit, D.; Hu, Y.; Chen, Y.; Armstrong, J.N.; Li, Y.C.; Ren, S. Nanoengineering Porous Silica for Thermal Management. ACS Appl. Nano Mater. 2022, 5, 2655–2663. [Google Scholar] [CrossRef]
- Babaei, H.; McGaughey, A.J.H.; Wilmer, C.E. Effect of pore size and shape on the thermal conductivity of metal-organic frameworks. Chem. Sci. 2017, 8, 583–589. [Google Scholar] [CrossRef]
- Islamov, M.; Babaei, H.; Anderson, R.; Sezginel, K.B.; Long, J.R.; McGaughey, A.J.; Gomez-Gualdron, D.A.; Wilmer, C.E. High-throughput screening of hypothetical metal-organic frameworks for thermal conductivity. npj Comput. Mater. 2023, 9, 11. [Google Scholar] [CrossRef]
- Ziman, J. Electrons and Phonons: The Theory of Transport Phenomena in Solids; Oxford University Press: Oxford, UK, 2001. [Google Scholar] [CrossRef]
- Baroni, S.; de Gironcoli, S.; Dal Corso, A.; Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 2001, 73, 515–562. [Google Scholar] [CrossRef]
- Jain, A. Machine learning in materials research: Developments over the last decade and challenges for the future. Curr. Opin. Solid State Mater. Sci. 2024, 33, 101189. [Google Scholar] [CrossRef]
- Tafreshi, O.A.; Saadatnia, Z.; Ghaffari-Mosanenzadeh, S.; Okhovatian, S.; Park, C.B.; Naguib, H.E. Machine learning-based model for predicting the material properties of nanostructured aerogels. SPE Polym. 2023, 4, 24–37. [Google Scholar] [CrossRef]
- Xie, T.; Grossman, J.C. Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties. Phys. Rev. Lett. 2018, 120, 145301. [Google Scholar] [CrossRef] [PubMed]
- Raissi, M.; Perdikaris, P.; Karniadakis, G. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Choudhary, K.; DeCost, B. Atomistic line graph neural network for improved materials property predictions. npj Comput. Mater. 2021, 7, 185. [Google Scholar] [CrossRef]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The Graph Neural Network Model. IEEE Trans. Neural Netw. 2009, 20, 61–80. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. arXiv 2017, arXiv:1609.02907. [Google Scholar]
- Li, J.R.; Kuppler, R.J.; Zhou, H.C. Selective gas adsorption and separation in metal–organic frameworks. Chem. Soc. Rev. 2009, 38, 1477–1504. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.C.; Long, J.R.; Yaghi, O.M. Introduction to Metal—Organic Frameworks. Chem. Rev. 2012, 112, 673–674. [Google Scholar] [CrossRef] [PubMed]
- Moghadam, P.Z.; Rogge, S.M.; Li, A.; Chow, C.M.; Wieme, J.; Moharrami, N.; Aragones-Anglada, M.; Conduit, G.; Gomez-Gualdron, D.A.; Van Speybroeck, V.; et al. Structure-Mechanical Stability Relations of Metal-Organic Frameworks via Machine Learning. Matter 2019, 1, 219–234. [Google Scholar] [CrossRef]
- Diercks, C.S.; Yaghi, O.M. The atom, the molecule, and the covalent organic framework. Science 2017, 355, eaal1585. [Google Scholar] [CrossRef]
- Smit, B. Molecular Simulations of Zeolites: Adsorption, Diffusion, and Shape Selectivity. Chem. Rev. 2008, 108, 4125–4184. [Google Scholar] [CrossRef] [PubMed]
- McGaughey, A.J.H.; Kaviany, M. Quantitative validation of the Boltzmann transport equation phonon thermal conductivity model under the single-mode relaxation time approximation. Phys. Rev. B 2004, 69, 094303. [Google Scholar] [CrossRef]
- Prasher, R. Thermal conductivity of composites of aligned nanoscale and microscale wires and pores. J. Appl. Phys. 2006, 100, 034307. [Google Scholar] [CrossRef]
- Huang, B.; Ni, Z.; Millward, A.; McGaughey, A.; Uher, C.; Kaviany, M.; Yaghi, O. Thermal conductivity of a metal-organic framework (MOF-5): Part II. Measurement. Int. J. Heat Mass Transf. 2007, 50, 405–411. [Google Scholar] [CrossRef]
- McGaughey, A.J.H.; Jain, A. Nanostructure thermal conductivity prediction by Monte Carlo sampling of phonon free paths. Appl. Phys. Lett. 2012, 100, 061911. [Google Scholar] [CrossRef]
- Hopkins, P.E.; Reinke, C.M.; Su, M.F.; Olsson, R.H.I.; Shaner, E.A.; Leseman, Z.C.; Serrano, J.R.; Phinney, L.M.; El-Kady, I. Reduction in the Thermal Conductivity of Single Crystalline Silicon by Phononic Crystal Patterning. Nano Lett. 2011, 11, 107–112. [Google Scholar] [CrossRef] [PubMed]
- Jiang, P.; Lindsay, L.; Koh, Y.K. Role of low-energy phonons with mean-free-paths > 0.8 μm in heat conduction in silicon. J. Appl. Phys. 2016, 119, 245705. [Google Scholar] [CrossRef]
- Marconnet, A.M.; Asheghi, M.; Goodson, K.E. From the Casimir Limit to Phononic Crystals: 20 Years of Phonon Transport Studies Using Silicon-on-Insulator Technology. J. Heat Transf. 2013, 135, 061601. [Google Scholar] [CrossRef]
- Yenigun, O.; Barisik, M. Effect of nano-film thickness on thermal resistance at water/silicon interface. Int. J. Heat Mass Transf. 2019, 134, 634–640. [Google Scholar] [CrossRef]
- Chen, G. Non-Fourier phonon heat conduction at the microscale and nanoscale. Nat. Rev. Phys. 2021, 3, 555–569. [Google Scholar] [CrossRef]
- Alaie, S.; Goettler, D.F.; Su, M.; Leseman, Z.C.; Reinke, C.M.; El-Kady, I. Thermal transport in phononic crystals and the observation of coherent phonon scattering at room temperature. Nat. Commun. 2015, 6, 7228. [Google Scholar] [CrossRef]
- Lee, J.; Lee, W.; Wehmeyer, G.; Dhuey, S.; Olynick, D.L.; Cabrini, S.; Dames, C.; Urban, J.J.; Yang, P. Investigation of phonon coherence and backscattering using silicon nanomeshes. Nat. Commun. 2017, 8, 14054. [Google Scholar] [CrossRef]
- Tan, F.; Han, S.; Peng, D.; Wang, H.; Yang, J.; Zhao, P.; Ye, X.; Dong, X.; Zheng, Y.; Zheng, N.; et al. Nanoporous and Highly Thermal Conductive Thin Film of Single-Crystal Covalent Organic Frameworks Ribbons. J. Am. Chem. Soc. 2021, 143, 3927–3933. [Google Scholar] [CrossRef] [PubMed]
- Cheng, R.; Wei, W.; Zhang, J.; Li, S. Understanding the Heat Transfer Performance of Zeolitic Imidazolate Frameworks upon Gas Adsorption by Molecular Dynamics Simulations. J. Phys. Chem. B 2023, 127, 9390–9398. [Google Scholar] [CrossRef] [PubMed]
- Sabet, S.; Barisik, M.; Mobedi, M.; Beskok, A. An extended Kozeny-Carman-Klinkenberg model for gas permeability in micro/nano-porous media. Phys. Fluids 2019, 31, 112001. [Google Scholar] [CrossRef]
- Wieme, J.; Vandenbrande, S.; Lamaire, A.; Kapil, V.; Vanduyfhuys, L.; Van Speybroeck, V. Thermal Engineering of Metal–Organic Frameworks for Adsorption Applications: A Molecular Simulation Perspective. Acs Appl. Mater. Interfaces 2019, 11, 38697–38707. [Google Scholar] [CrossRef] [PubMed]
- Sen, T.; Barisik, M. Internal surface electric charge characterization of mesoporous silica. Sci. Rep. 2019, 9, 137. [Google Scholar] [CrossRef]
- Babaei, H.; DeCoster, M.E.; Jeong, M.; Hassan, Z.M.; Islamoglu, T.; Baumgart, H.; McGaughey, A.J.; Redel, E.; Farha, O.K.; Hopkins, P.E.; et al. Observation of reduced thermal conductivity in a metal-organic framework due to the presence of adsorbates. Nat. Commun. 2020, 11, 4010. [Google Scholar] [CrossRef] [PubMed]
- Schnell, S.K.; Vlugt, T.J. Thermal conductivity in zeolites studied by non-equilibrium molecular dynamics simulations. Int. J. Thermophys. 2013, 34, 1197–1213. [Google Scholar] [CrossRef]
- Huang, C.; Zhao, X.; Regner, K.; Yang, R. Thermal conductivity model for nanoporous thin films. Phys. E-Low-Dimens. Syst. Nanostructures 2018, 97, 277–281. [Google Scholar] [CrossRef]
- Ferreira de Souza, N.; Picard, C.; Franco, L.F.M.; Coasne, B. Thermal Conductivity of a Fluid-Filled Nanoporous Material: Underlying Molecular Mechanisms and the Rattle Effect. J. Phys. Chem. B 2024, 128, 2516–2527. [Google Scholar] [CrossRef] [PubMed]
- Hollingsworth, S.A.; Dror, R.O. Molecular dynamics simulation for all. Neuron 2018, 99, 1129–1143. [Google Scholar] [CrossRef]
- Eyert, V.; Wormald, J.; Curtin, W.A.; Wimmer, E. Machine-learned interatomic potentials: Recent developments and prospective applications. J. Mater. Res. 2023, 38, 5079–5094. [Google Scholar] [CrossRef]
- Dubbeldam, D.; Walton, K.S.; Vlugt, T.J.H.; Calero, S. Design, Parameterization, and Implementation of Atomic Force Fields for Adsorption in Nanoporous Materials. Adv. Theory Simul. 2019, 2, 1900135. [Google Scholar] [CrossRef]
- Petretto, G.; Dwaraknath, S.; PC Miranda, H.; Winston, D.; Giantomassi, M.; Van Setten, M.J.; Gonze, X.; Persson, K.A.; Hautier, G.; Rignanese, G.M. High-throughput density-functional perturbation theory phonons for inorganic materials. Sci. Data 2018, 5, 180065. [Google Scholar] [CrossRef]
- Hasnip, P.J.; Refson, K.; Probert, M.I.J.; Yates, J.R.; Clark, S.J.; Pickard, C.J. Density functional theory in the solid state. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372, 20130270. [Google Scholar] [CrossRef]
- Guo, Z.; Han, Z.; Feng, D.; Lin, G.; Ruan, X. Sampling-accelerated prediction of phonon scattering rates for converged thermal conductivity and radiative properties. npj Comput. Mater. 2024, 10, 31. [Google Scholar] [CrossRef]
- Yang, X.; Tiwari, J.; Feng, T. Reduced anharmonic phonon scattering cross-section slows the decrease of thermal conductivity with temperature. Mater. Today Phys. 2022, 24, 100689. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013; Volume 112. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning (Information Science and Statistics); Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: Berlin/Heidelberg, Germany, 2013; Volume 26. [Google Scholar]
- Seko, A.; Togo, A.; Hayashi, H.; Tsuda, K.; Chaput, L.; Tanaka, I. Prediction of Low-Thermal-Conductivity Compounds with First-Principles Anharmonic Lattice-Dynamics Calculations and Bayesian Optimization. Phys. Rev. Lett. 2015, 115, 205901. [Google Scholar] [CrossRef]
- Carrete, J.; Li, W.; Mingo, N.; Wang, S.; Curtarolo, S. Finding Unprecedentedly Low-Thermal-Conductivity Half-Heusler Semiconductors via High-Throughput Materials Modeling. Phys. Rev. X 2014, 4, 011019. [Google Scholar] [CrossRef]
- Wei, H.; Bao, H.; Ruan, X. Machine learning prediction of thermal transport in porous media with physics-based descriptors. Int. J. Heat Mass Transf. 2020, 160, 120176. [Google Scholar] [CrossRef]
- Merillas, B.; Vareda, J.A.P.; Martín-de León, J.; Rodríguez-Pérez, M.A.; Durães, L. Thermal Conductivity of Nanoporous Materials: Where Is the Limit? Polymers 2022, 14, 2556. [Google Scholar] [CrossRef]
- Malfait, W.J.; Ebert, H.P.; Brunner, S.; Wernery, J.; Galmarini, S.; Zhao, S.; Reichenauer, G. The poor reliability of thermal conductivity data in the aerogel literature: A call to action! J.-Sol-Gel Sci. Technol. 2024, 109, 569–579. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Seko, A.; Hayashi, H.; Nakayama, K.; Takahashi, A.; Tanaka, I. Representation of compounds for machine-learning prediction of physical properties. Phys. Rev. B 2017, 95, 144110. [Google Scholar] [CrossRef]
- Jablonka, K.M.; Ongari, D.; Moosavi, S.M.; Smit, B. Big-Data Science in Porous Materials: Materials Genomics and Machine Learning. Chem. Rev. 2020, 120, 8066–8129. [Google Scholar] [CrossRef] [PubMed]
- Minakshi, M.; Sharma, A.; Sohel, F.; Pivrikas, A.; Shinde, P.A.; Ariga, K.; Shrestha, L.K. Machine Learning—Guided Design of Biomass-Based Porous Carbon for Aqueous Symmetric Supercapacitors. ChemPlusChem 2025, 90, e202500342. [Google Scholar] [CrossRef]
- Merchant, A.; Batzner, S.; Schoenholz, S.S.; Aykol, M.; Cheon, G.; Cubuk, E.D. Scaling deep learning for materials discovery. Nature 2023, 624, 80–85. [Google Scholar] [CrossRef] [PubMed]
- Vu, T.S.; Ha, M.Q.; Nguyen, D.N.; Nguyen, V.C.; Abe, Y.; Tran, T.; Tran, H.; Kino, H.; Miyake, T.; Tsuda, K.; et al. Towards understanding structure–property relations in materials with interpretable deep learning. npj Comput. Mater. 2023, 9, 215. [Google Scholar] [CrossRef]
- Shargh, A.K.; Abdolrahim, N. An interpretable deep learning approach for designing nanoporous silicon nitride membranes with tunable mechanical properties. npj Comput. Mater. 2023, 9, 82. [Google Scholar] [CrossRef] [PubMed]
- Huang, Q.; Hong, D.; Niu, B.; Long, D.; Zhang, Y. An interpretable deep learning strategy for effective thermal conductivity prediction of porous materials. Int. J. Heat Mass Transf. 2024, 221, 125064. [Google Scholar] [CrossRef]
- Xie, E.; Wang, X.; Siepmann, J.I.; Chen, H.; Snurr, R.Q. Generative AI for design of nanoporous materials: Review and future prospects. Digit. Discov. 2025, 4, 2336–2363. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Graczyk, K.M.; Matyka, M. Predicting porosity, permeability, and tortuosity of porous media from images by deep learning. Sci. Rep. 2020, 10, 21488. [Google Scholar] [CrossRef]
- Liu, C.; Guo, R.; Su, Y. A deep learning based prediction model for effective elastic properties of porous materials. Sci. Rep. 2025, 15, 6707. [Google Scholar] [CrossRef] [PubMed]
- Du, C.; Zou, G.; A, Z.; Lu, B.; Feng, B.; Huo, J.; Xiao, Y.; Jiang, Y.; Liu, L. Highly accurate and efficient prediction of effective thermal conductivity of sintered silver based on deep learning method. Int. J. Heat Mass Transf. 2023, 201, 123654. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Kamrava, S.; Tahmasebi, P.; Sahimi, M. Linking Morphology of Porous Media to Their Macroscopic Permeability by Deep Learning. Transp. Porous Media 2020, 131. [Google Scholar] [CrossRef]
- Santos, J.E.; Xu, D.; Jo, H.; Landry, C.J.; Prodanović, M.; Pyrcz, M.J. PoreFlow-Net: A 3D convolutional neural network to predict fluid flow through porous media. Adv. Water Resour. 2020, 138, 103539. [Google Scholar] [CrossRef]
- Prifling, B.; Röding, M.; Townsend, P.; Neumann, M.; Schmidt, V. Large-Scale Statistical Learning for Mass Transport Prediction in Porous Materials Using 90,000 Artificially Generated Microstructures. Front. Mater. 2021, 8, 786502. [Google Scholar] [CrossRef]
- Vishnyakov, A. Machine Learning in Computational Design and Optimization of Disordered Nanoporous Materials. Materials 2025, 18, 534. [Google Scholar] [CrossRef]
- Cong, G.; Gupta, A.; Neumann, R.; de Bayser, M.; Steiner, M.; Ó Conchúir, B. Prediction of CO2 Adsorption in Nano-Pores with Graph Neural Networks. arXiv 2022, arXiv:2209.07567. [Google Scholar]
- Fung, V.; Zhang, J.; Juarez, E.; Sumpter, B.G. Benchmarking graph neural networks for materials chemistry. npj Comput. Mater. 2021, 7, 84. [Google Scholar] [CrossRef]
- Shi, X.; Zhou, L.; Huang, Y.; Wu, Y.; Hong, Z. A review on the applications of graph neural networks in materials science at the atomic scale. Mater. Genome Eng. Adv. 2024, 2, e50. [Google Scholar] [CrossRef]
- Deng, D.; Lei, Z.; Hong, X.; Zhang, R.; Zhou, F. Describe Molecules by a Heterogeneous Graph Neural Network with Transformer-like Attention for Supervised Property Predictions. ACS Omega 2022, 7, 3713–3721. [Google Scholar] [CrossRef] [PubMed]
- Xu, F.; Yang, Z.; Wang, L.; Meng, D.; Long, J. MESPool: Molecular Edge Shrinkage Pooling for hierarchical molecular representation learning and property prediction. Briefings Bioinform. 2023, 25, bbad423. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Wang, Z.; Li, H. Application of an Improved Graph Neural Network for Drug Property Prediction. IEEE Access 2024, 12, 46812–46820. [Google Scholar] [CrossRef]
- Hu, J.; Zuo, Y.; Hao, Y.; Shu, G.; Wang, Y.; Feng, M.; Li, X.; Wang, X.; Sun, J.; Ding, X.; et al. Prediction of lattice thermal conductivity with two-stage interpretable machine learning. Chin. Phys. B 2023, 32, 046301. [Google Scholar] [CrossRef]
- Choudhary, K.; Yildirim, T.; Siderius, D.W.; Kusne, A.G.; McDannald, A.; Ortiz-Montalvo, D.L. Graph neural network predictions of metal organic framework CO2 adsorption properties. Comput. Mater. Sci. 2022, 210, 111388. [Google Scholar] [CrossRef]
- Gurunathan, R.; Choudhary, K.; Tavazza, F. Rapid prediction of phonon structure and properties using the atomistic line graph neural network (ALIGNN). Phys. Rev. Mater. 2023, 7, 023803. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; Volume 27. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Yao, Z.; Sánchez-Lengeling, B.; Bobbitt, N.S.; Bucior, B.J.; Kumar, S.G.H.; Collins, S.P.; Burns, T.; Woo, T.K.; Farha, O.K.; Snurr, R.Q.; et al. Inverse design of nanoporous crystalline reticular materials with deep generative models. Nat. Mach. Intell. 2021, 3, 76–86. [Google Scholar] [CrossRef]
- Du, C.; Zou, G.; Huo, J.; Feng, B.; A, Z.; Liu, L. Generative AI-enabled microstructure design of porous thermal interface materials with desired effective thermal conductivity. J. Mater. Sci. 2023, 58, 16160–16171. [Google Scholar] [CrossRef]
- Lagaris, I.; Likas, A.; Fotiadis, D. Artificial neural networks for solving ordinary and partial differential equations. IEEE Trans. Neural Netw. 1998, 9, 987–1000. [Google Scholar] [CrossRef] [PubMed]
- Farea, A.; Yli-Harja, O.; Emmert-Streib, F. Understanding Physics-Informed Neural Networks: Techniques, Applications, Trends, and Challenges. AI 2024, 5, 1534–1557. [Google Scholar] [CrossRef]
- Ngo, S.I.; Lim, Y.I. Solution and Parameter Identification of a Fixed-Bed Reactor Model for Catalytic CO2 Methanation Using Physics-Informed Neural Networks. Catalysts 2021, 11, 1304. [Google Scholar] [CrossRef]
- Liu, B.; Wang, Y.; Rabczuk, T.; Olofsson, T.; Lu, W. Multi-scale modeling in thermal conductivity of Polyurethane incorporated with Phase Change Materials using Physics-Informed Neural Networks. Renew. Energy 2024, 220, 119565. [Google Scholar] [CrossRef]
- Faroughi, S.A.; Soltanmohammadi, R.; Datta, P.; Mahjour, S.K.; Faroughi, S. Physics-Informed Neural Networks with Periodic Activation Functions for Solute Transport in Heterogeneous Porous Media. Mathematics 2024, 12, 63. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Marrero, C.O.; Perdikaris, P.; Tartakovsky, G.D.; Barajas-Solano, D. Physics-Informed Deep Neural Networks for Learning Parameters and Constitutive Relationships in Subsurface Flow Problems. Water Resour. Res. 2020, 56, e2019WR026731. [Google Scholar] [CrossRef]
- Yang, G.; Xu, R.; Tian, Y.; Guo, S.; Wu, J.; Chu, X. Data-driven methods for flow and transport in porous media: A review. Int. J. Heat Mass Transf. 2024, 235, 126149. [Google Scholar] [CrossRef]
- Yan, X.; Lin, J.; Wang, S.; Zhang, Z.; Liu, P.; Sun, S.; Yao, J.; Zhang, K. Physics-informed neural network simulation of two-phase flow in heterogeneous and fractured porous media. Adv. Water Resour. 2024, 189, 104731. [Google Scholar] [CrossRef]
- Molnar, C. Interpretable Machine Learning, 2nd ed.; Shroff Publishers: Navi Mumbai, India, 2022. [Google Scholar]
- Cybenko, G.V. Approximation by superpositions of a sigmoidal function. Math. Control. Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Gunning, D.; Aha, D. DARPA’s explainable artificial intelligence (XAI) program. AI Mag. 2019, 40, 44–58. [Google Scholar]
- Adadi, A.; Berrada, M. Peeking Inside the Black-Box: A Survey on Explainable Artificial Intelligence (XAI). IEEE Access 2018, 6, 52138–52160. [Google Scholar] [CrossRef]
- Clement, T.; Kemmerzell, N.; Abdelaal, M.; Amberg, M. XAIR: A Systematic Metareview of Explainable AI (XAI) Aligned to the Software Development Process. Mach. Learn. Knowl. Extr. 2023, 5, 78–108. [Google Scholar] [CrossRef]
- Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning Deep Features for Discriminative Localization. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2921–2929. [Google Scholar] [CrossRef]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization. Int. J. Comput. Vision 2020, 128, 336–359. [Google Scholar] [CrossRef]
- Shwartz-Ziv, R.; Armon, A. Tabular data: Deep learning is not all you need. Inf. Fusion 2022, 81, 84–90. [Google Scholar] [CrossRef]
- Di Martino, F.; Delmastro, F. Explainable AI for clinical and remote health applications: A survey on tabular and time series data. Artif. Intell. Rev. 2022, 56, 5261–5315. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. In Advances in Neural Information Processing Systems; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should I Trust You?”: Explaining the Predictions of Any Classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 13–17 August 2016; KDD ’16. pp. 1135–1144. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. Anchors: High-Precision Model-Agnostic Explanations. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar] [CrossRef]
- Wachter, S.; Mittelstadt, B.; Russell, C. Counterfactual explanations without opening the black box: Automated decisions and the GDPR. Harv. J. Law Technol. 2017, 31, 841. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Rudin, C. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 2019, 1, 206–215. [Google Scholar] [CrossRef] [PubMed]
- Angelino, E.; Larus-Stone, N.; Alabi, D.; Seltzer, M.; Rudin, C. Learning certifiably optimal rule lists for categorical data. J. Mach. Learn. Res. 2017, 18, 8753–8830. [Google Scholar]
- Ustun, B.; Rudin, C. Supersparse linear integer models for optimized medical scoring systems. Mach. Learn. 2016, 102, 349–391. [Google Scholar] [CrossRef]
- Lazebnik, T.; Bunimovich-Mendrazitsky, S.; Rosenfeld, A. An algorithm to optimize explainability using feature ensembles. Appl. Intell. 2024, 54, 2248–2260. [Google Scholar] [CrossRef]
- Petersen, B.K.; Landajuela, M.; Mundhenk, T.N.; Santiago, C.P.; Kim, S.K.; Kim, J.T. Deep symbolic regression: Recovering mathematical expressions from data via risk-seeking policy gradients. In Proceedings of the International Conference on Learning Representations, Vienna, Austria, 4 May 2021. [Google Scholar]
- Dey, K.; Barisik, M.; Liang, Y. Machine learning-guided reparameterization of the TIP4P water model for accurate thermal and electrical property predictions. J. Mol. Liq. 2025, 437, 128568. [Google Scholar] [CrossRef]
- Karpatne, A.; Atluri, G.; Faghmous, J.H.; Steinbach, M.; Banerjee, A.; Ganguly, A.; Shekhar, S.; Samatova, N.; Kumar, V. Theory-Guided Data Science: A New Paradigm for Scientific Discovery from Data. IEEE Trans. Knowl. Data Eng. 2017, 29, 2318–2331. [Google Scholar] [CrossRef]
- Strubell, E.; Ganesh, A.; McCallum, A. Energy and Policy Considerations for Modern Deep Learning Research. Proc. Aaai Conf. Artif. Intell. 2020, 34, 13693–13696. [Google Scholar] [CrossRef]
- Barua, N.K.; Hall, E.; Cheng, Y.; Oliynyk, A.O.; Kleinke, H. Interpretable Machine Learning Model on Thermal Conductivity Using Publicly Available Datasets and Our Internal Lab Dataset. Chem. Mater. 2024, 36, 7089–7100. [Google Scholar] [CrossRef]
- Peng, X.; Pan, R.; Li, X.; Zhong, W.; Qian, F. Molecular descriptor-assisted interpretable machine learning: A scheme for guiding the synthesis of zeolites with target structures. Chem. Eng. Sci. 2025, 308, 121378. [Google Scholar] [CrossRef]
- Liu, B.; Lu, W.; Olofsson, T.; Zhuang, X.; Rabczuk, T. Stochastic interpretable machine learning based multiscale modeling in thermal conductivity of Polymeric graphene-enhanced composites. Compos. Struct. 2024, 327, 117601. [Google Scholar] [CrossRef]
- Huang, X.; Ma, S.; Zhao, C.; Wang, H.; Ju, S. Exploring high thermal conductivity polymers via interpretable machine learning with physical descriptors. npj Comput. Mater. 2023, 9, 191. [Google Scholar] [CrossRef]
- Loftis, C.; Yuan, K.; Zhao, Y.; Hu, M.; Hu, J. Lattice Thermal Conductivity Prediction Using Symbolic Regression and Machine Learning. J. Phys. Chem. A 2021, 125, 435–450. [Google Scholar] [CrossRef] [PubMed]
- Xu, P.; Ji, X.; Li, M.; Lu, W. Small data machine learning in materials science. npj Comput. Mater. 2023, 9, 42. [Google Scholar] [CrossRef]
- Ojih, J.; Shen, C.; Rodriguez, A.; Zhang, H.; Choudhary, K.; Hu, M. High-throughput computational discovery of 3218 ultralow thermal conductivity and dynamically stable materials by dual machine learning models. J. Mater. Chem. A 2023, 11, 24169–24183. [Google Scholar] [CrossRef]
- Luo, Y.; Li, M.; Yuan, H.; Liu, H.; Fang, Y. Predicting lattice thermal conductivity via machine learning: A mini review. npj Comput. Mater. 2023, 9, 4. [Google Scholar] [CrossRef]
- Chen, A.; Zhang, X.; Zhou, Z. Machine learning: Accelerating materials development for energy storage and conversion. InfoMat 2020, 2, 553–576. [Google Scholar] [CrossRef]
- Ying, P.; Liang, T.; Xu, K.; Zhang, J.; Xu, J.; Zhong, Z.; Fan, Z. Sub-Micrometer Phonon Mean Free Paths in Metal–Organic Frameworks Revealed by Machine Learning Molecular Dynamics Simulations. ACS Appl. Mater. Interfaces 2023, 15, 36412–36422. [Google Scholar] [CrossRef] [PubMed]
- Qian, X.; Yang, R. Machine learning for predicting thermal transport properties of solids. Mater. Sci. Eng. R Rep. 2021, 146, 100642. [Google Scholar] [CrossRef]
- Li, W.; Carrete, J.; Katcho, N.A.; Mingo, N. ShengBTE: A solver of the Boltzmann transport equation for phonons. Comput. Phys. Commun. 2014, 185, 1747–1758. [Google Scholar] [CrossRef]
- Park, H.; Kang, Y.; Kim, J. Enhancing Structure–Property Relationships in Porous Materials through Transfer Learning and Cross-Material Few-Shot Learning. Acs Appl. Mater. Interfaces 2023, 15, 56375–56385. [Google Scholar] [CrossRef] [PubMed]
- Elmorsy, M.; El-Dakhakhni, W.; Zhao, B. Enhancing Effective Thermal Conductivity Predictions in Digital Porous Media Using Transfer Learning. Interpore J. 2025, 2, IPJ250825-7. [Google Scholar] [CrossRef]
- Pai, S.S.; Banthiya, A. Transfer-learning-based Surrogate Model for Thermal Conductivity of Nanofluids. arXiv 2022, arXiv:2201.00435. [Google Scholar]
- Chang, R.; Wang, Y.X.; Ertekin, E. Towards overcoming data scarcity in materials science: Unifying models and datasets with a mixture of experts framework. npj Comput. Mater. 2022, 8, 242. [Google Scholar] [CrossRef]
- Gupta, V.; Choudhary, K.; Tavazza, F.; Campbell, C.; Liao, W.k.; Choudhary, A.; Agrawal, A. Cross-property deep transfer learning framework for enhanced predictive analytics on small materials data. Nat. Commun. 2021, 12, 6595. [Google Scholar] [CrossRef]
- Meng, Y.; Jiang, J.; Wu, J.; Wang, D. Transformer-based deep learning models for predicting permeability of porous media. Adv. Water Resour. 2023, 179, 104520. [Google Scholar] [CrossRef]
- Gong, S.; Wang, S.; Zhu, T.; Shao-Horn, Y.; Grossman, J.C. Multimodal machine learning for materials science: Composition-structure bimodal learning for experimentally measured properties. arXiv 2023, arXiv:2309.04478. [Google Scholar]
- OpenAI. GPT-4 Technical Report. arXiv 2024, arXiv:2303.08774. [Google Scholar]
- Kang, Y.; Kim, J. ChatMOF: An artificial intelligence system for predicting and generating metal-organic frameworks using large language models. Nat. Commun. 2024, 15, 4705. [Google Scholar] [CrossRef]
- MacLeod, B.P.; Parlane, F.G.L.; Morrissey, T.D.; Häse, F.; Roch, L.M.; Dettelbach, K.E.; Moreira, R.; Yunker, L.P.E.; Rooney, M.B.; Deeth, J.R.; et al. Self-driving laboratory for accelerated discovery of thin-film materials. Sci. Adv. 2020, 6, eaaz8867. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Sahu, A.K.; Talwalkar, A.; Smith, V. Federated Learning: Challenges, Methods, and Future Directions. IEEE Signal Process. Mag. 2020, 37, 50–60. [Google Scholar] [CrossRef]
- Sharma, A.; Sanvito, S. Quantum-Accurate Machine Learning Potentials for Metal-Organic Frameworks using Temperature Driven Active Learning. arXiv 2024, arXiv:2405.06465. [Google Scholar]
- Ito, K.; Yokoi, T.; Hyodo, K.; Mori, H. Machine learning interatomic potential with DFT accuracy for general grain boundaries in α-Fe. npj Comput. Mater. 2024, 10, 255. [Google Scholar] [CrossRef]
- Mortazavi, B.; Podryabinkin, E.V.; Roche, S.; Rabczuk, T.; Zhuang, X.; Shapeev, A.V. Machine-learning interatomic potentials enable first-principles multiscale modeling of lattice thermal conductivity in graphene/borophene heterostructures. Mater. Horiz. 2020, 7, 2359–2367. [Google Scholar] [CrossRef]
- Juneja, R.; Singh, A.K. Guided patchwork kriging to develop highly transferable thermal conductivity prediction models. J. Phys. Mater. 2020, 3, 024006. [Google Scholar] [CrossRef]

| Method | Training Time | Inference Time | Accuracy | Scalability | Interpretability | Data Requirements |
|---|---|---|---|---|---|---|
| MD Simulations | N/A | High | Low–High | Low | High | Low |
| DFT+Phonons | N/A | Very High | Medium–High | Very Low | Very High | Low |
| Classical ML | Low | Very Low | Medium | Medium | Medium | Medium |
| DNNs | High | Very Low | High | Medium–High | Low | High |
| GNNs [12,13] | High | Very Low | High | High | Medium | Medium–High |
| PINNs [10] | Very High | Medium | High | Medium | High | Medium |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghasemi, A.; Barisik, M. Machine Learning for Thermal Transport Prediction in Nanoporous Materials: Progress, Challenges, and Opportunities. Nanomaterials 2025, 15, 1660. https://doi.org/10.3390/nano15211660
Ghasemi A, Barisik M. Machine Learning for Thermal Transport Prediction in Nanoporous Materials: Progress, Challenges, and Opportunities. Nanomaterials. 2025; 15(21):1660. https://doi.org/10.3390/nano15211660
Chicago/Turabian StyleGhasemi, Amirehsan, and Murat Barisik. 2025. "Machine Learning for Thermal Transport Prediction in Nanoporous Materials: Progress, Challenges, and Opportunities" Nanomaterials 15, no. 21: 1660. https://doi.org/10.3390/nano15211660
APA StyleGhasemi, A., & Barisik, M. (2025). Machine Learning for Thermal Transport Prediction in Nanoporous Materials: Progress, Challenges, and Opportunities. Nanomaterials, 15(21), 1660. https://doi.org/10.3390/nano15211660






