First-Principles Study on the Photocatalytic Performance of K(Ta0.5Nb0.5)O3 Doped with Metals (Cd, Sn, Hf)
Abstract
1. Introduction
2. Materials and Methods
3. Structural Characterization and Bond Length Analysis
4. Electronic Structure
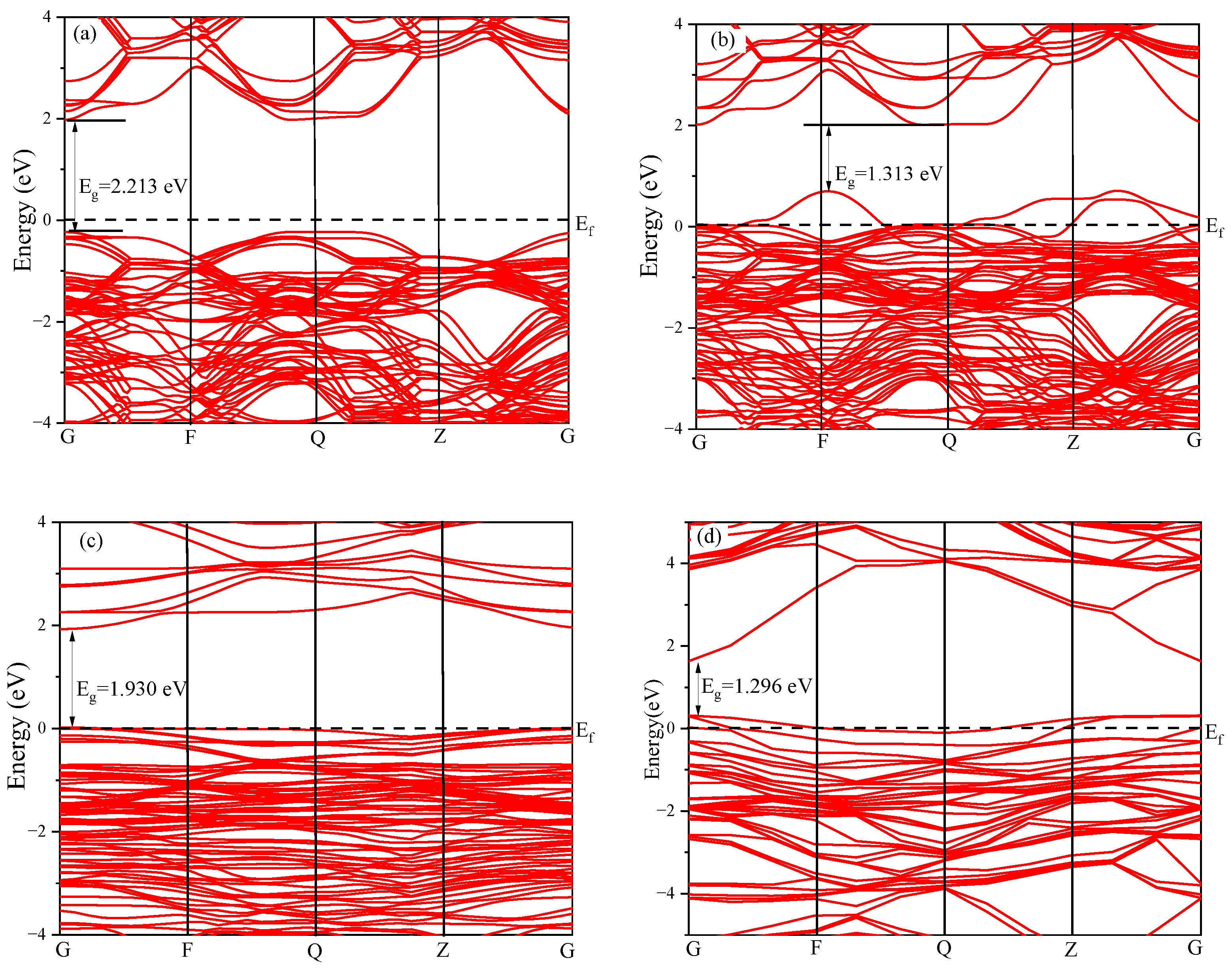
4.1. Band Structure Analysis
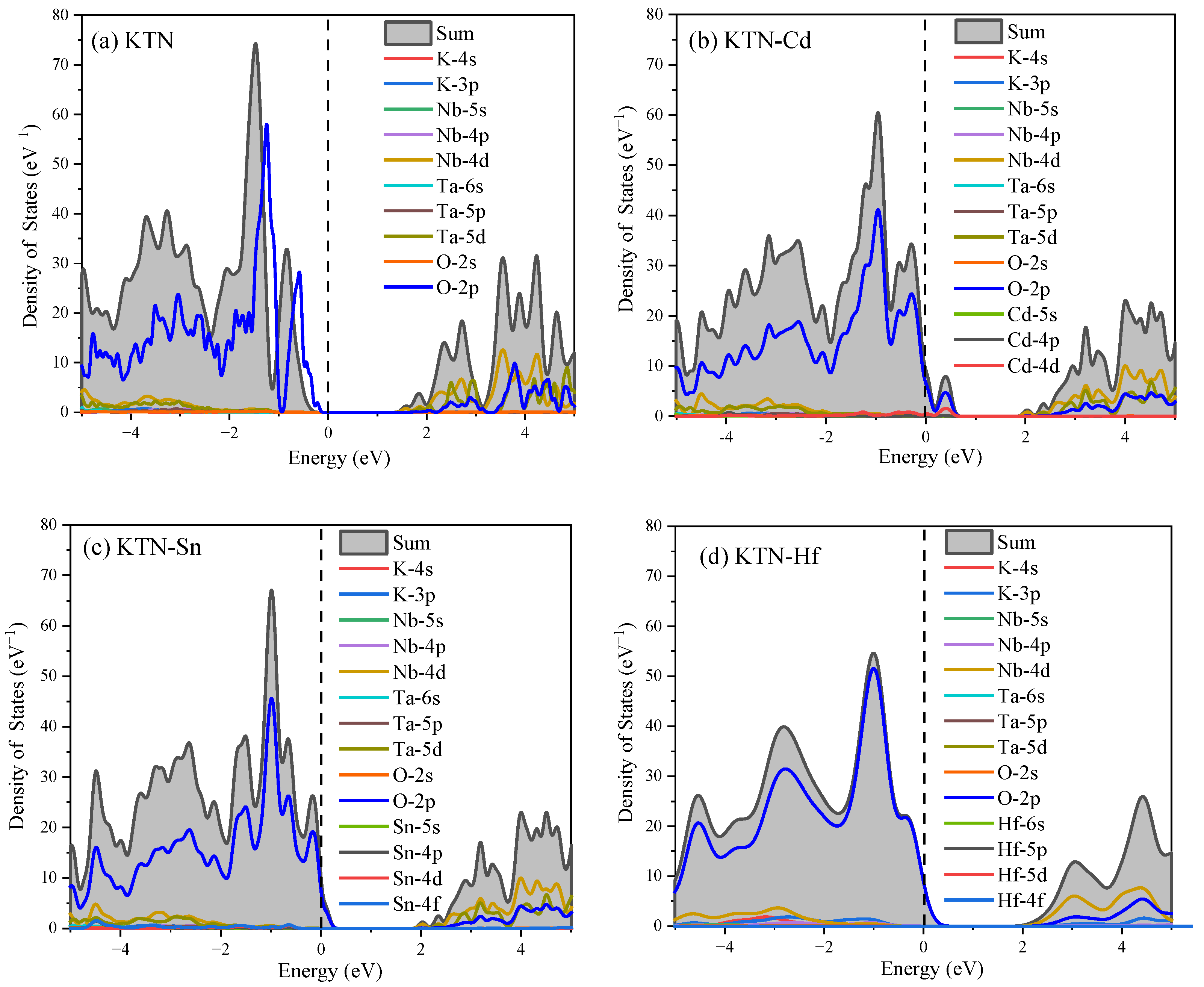
4.2. State Density Analysis
5. Optical Properties
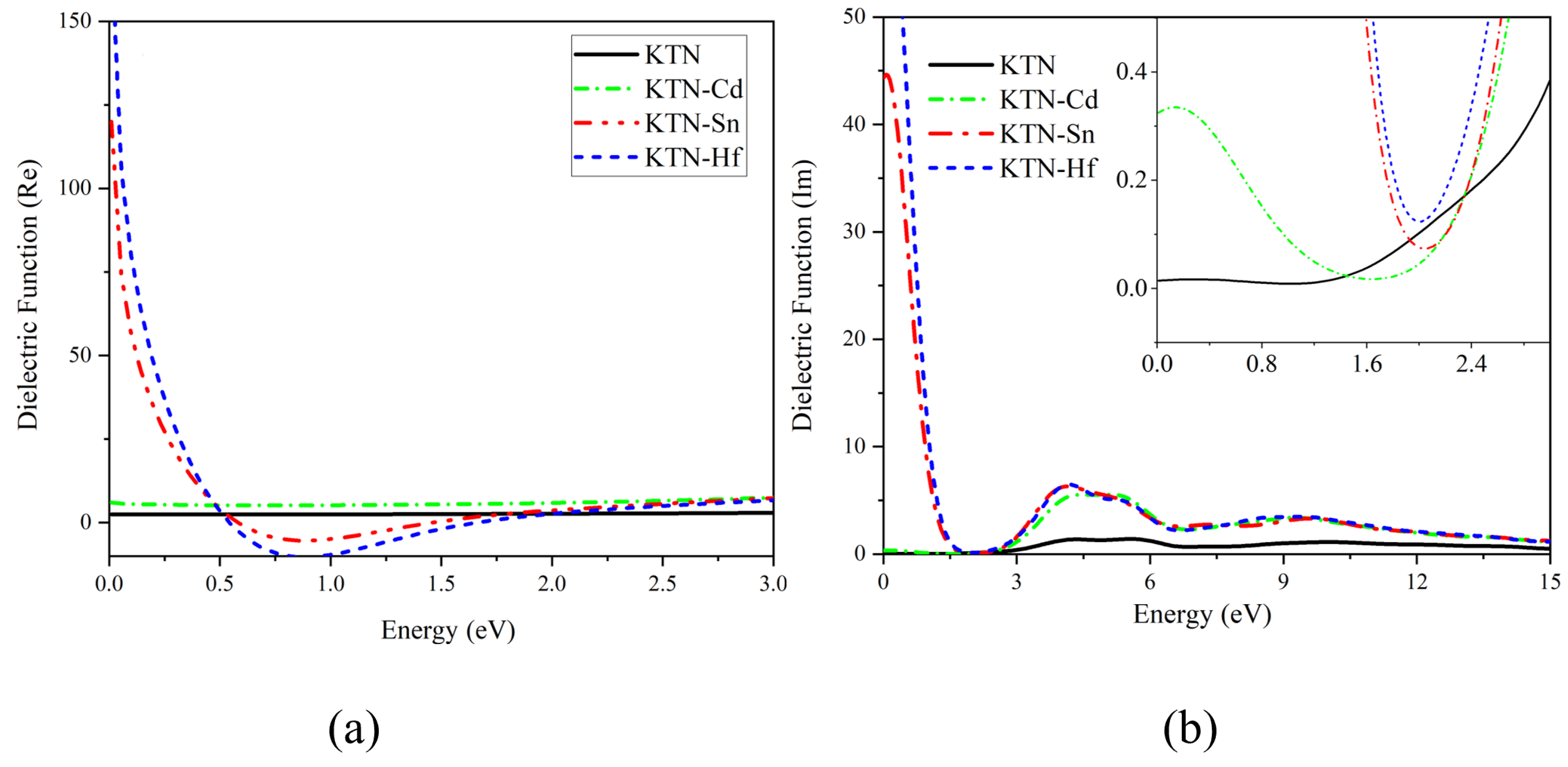
5.1. Dielectric Function
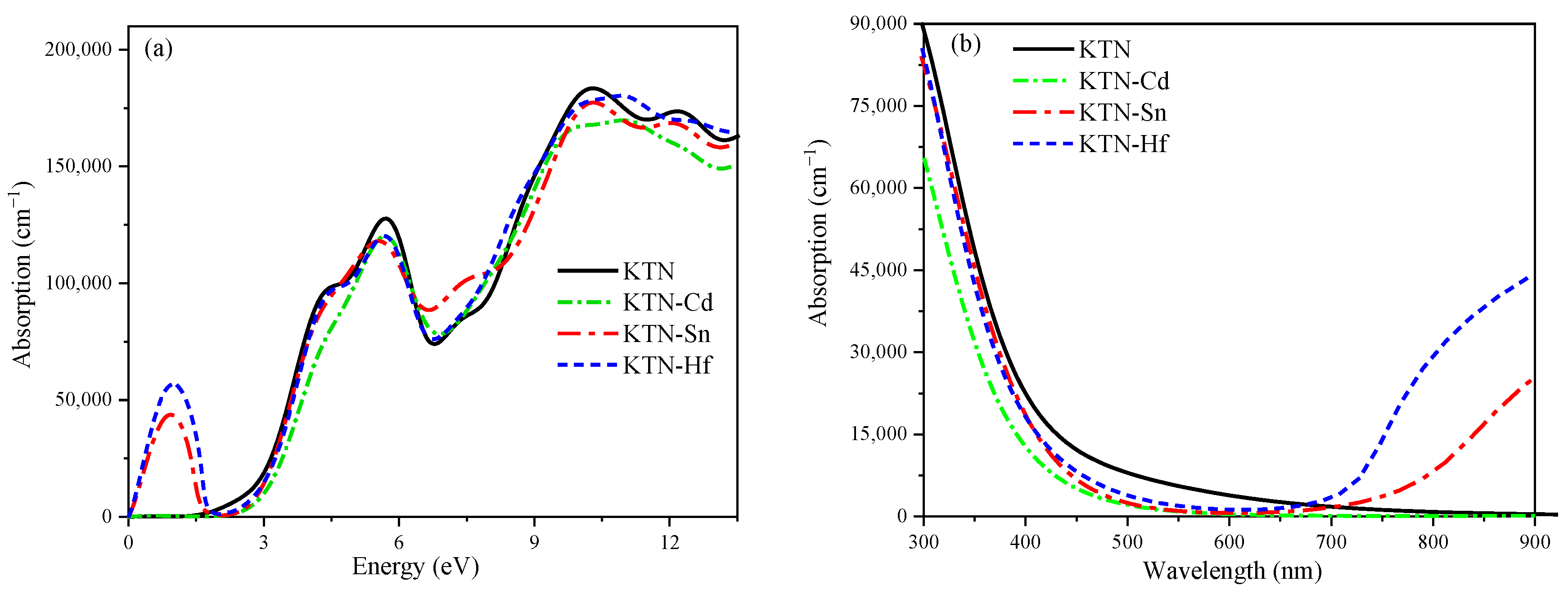
5.2. Absorption Spectrum
6. Effective Mass
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fujishima, A.; Honda, K. Electrochemical Photolysis at a Semiconductor Electrode. Nature 1972, 238, 37–38. [Google Scholar] [CrossRef]
- Bibi, S.; Shah, S.S.; Muhammad, F.; Samar, A.; Shabnam, S. Cu-doped mesoporous TiO2 photocatalyst for efficient degradation of organic dye via visible light photocatalysis. Chemosphere 2023, 339, 139583. [Google Scholar] [CrossRef] [PubMed]
- Piątkowska, A.; Janus, M.; Szymański, K.; Sylwia, M. C-, N-and S-doped TiO2 photocatalysts: A review. Catalysts 2021, 11, 144. [Google Scholar] [CrossRef]
- Hadjltaief, H.B.; Galvez, M.E.; Ben Zina, M.; Da Costa, P. TiO2/clay as a heterogeneous catalyst in photocatalytic/photochemical oxidation of anionic reactive blue 19. Arab. J. Chem. 2019, 12, 1454–1462. [Google Scholar] [CrossRef]
- Grosso, D.; Boissière, C.; Smarsly, B.; Brezesinski, T.; Pinna, N.; Albouy, P.A.; Amenitsch, H.; Antonietti, M.; Sanchez, C. Periodically ordered nanoscale islands and mesoporous films composed of nanocrystalline multimetallic oxides. Nat. Mater. 2004, 3, 787–792. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Wang, Y.; Ma, J.; Li, S.; Pan, H.; Nan, C.-W.; Lin, Y.-H. Controllable electrical, magnetoelectric and optical properties of BiFeO3 via domain engineering. Prog. Mater. Sci. 2022, 127, 100943. [Google Scholar] [CrossRef]
- Huang, X.; Wang, Y.; Xing, B.; Jin, X.; Liu, M.; Ruan, J.; Wen, X.; Tan, P.; Tian, H. Impact of defect concentration on piezoelectricity in Mn/Fe-doped KTN crystals. Appl. Phys. Lett. 2024, 19, 124. [Google Scholar] [CrossRef]
- Kalinin, S.V.; Kim, Y.; Fong, D.D.; Morozovska, A.N. Surface-screening mechanisms in ferroelectric thin films and their effect on polarization dynamics and domain structures. Rep. Prog. Phys. 2018, 81, 036502. [Google Scholar] [CrossRef]
- Hussain, F.; Khesro, A.; Muhammad, R.; Wang, D. Effect of Ta-doping on functional properties of K0.51Na0.49NbO3. Mater. Res. Express 2019, 6, 106309. [Google Scholar] [CrossRef]
- Feizpour, M.; Bafrooei, H.B.; Hayati, R.; Ebadzadeh, T. Microwave-assisted synthesis and sintering of potassium sodium niobate lead-free piezoelectric ceramics. Ceram. Int. 2014, 40, 871–877. [Google Scholar] [CrossRef]
- Li, C.; Wang, X.; Wu, Y.; Liang, F.; Wang, F.; Zhao, X.; Zhang, H. Three-dimensional nonlinear photonic crystal in naturally grown potassium–tantalate–niobate perovskite ferroelectrics. Light Sci. Appl. 2020, 9, 8. [Google Scholar] [CrossRef]
- Luan, Y.H.; Li, T.W.; Wang, X.P.; Hao, J.X.; Zhao, H.Y.; Fu, Q.M.; Tao, H.; Gao, D.; Ma, Z.B. Diamond grown on KTN substrate and its photocatalytic performance. Diam. Abras. Tool Eng. 2024, 44, 9–14. [Google Scholar]
- Huan, Y.; Shen, H.; Zhu, Y.; Li, M.; Li, H.; Wang, Z.; Wei, T. Enhanced ferro-photocatalytic performance for ANbO3 (A = Na, K) nanoparticles. Math. Biosci. Eng. 2019, 16, 4122–4134. [Google Scholar]
- Keyu, Z.; Duanming, Z.; Zhicheng, Z.; Fengxia, Y.; Han, X. Synthesis and optical properties of tetragonal KTa0.6Nb0.4O3 nanoparticles. Appl. Surf. Sci. 2009, 256, 1317–1321. [Google Scholar] [CrossRef]
- Yang, Y. First-principles study on the mechanism of Hf and Ti doping promoting hydrogen release in ZrCoH3. Phys. B 2024, 695, 416591. [Google Scholar] [CrossRef]
- Cui, Z.Y.; Xie, Z.S.; Wang, Y.J.; Yuan, G.L.; Liu, J.M. Research progress and prospects of photocatalytic devices with perovskite ferroelectric semiconductors. Acta Phys. Sin. 2020, 69, 127706. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, J.; Yang, L.; Cao, Z.; Yuan, C.; Zhou, C.; Wang, H.; Rao, G. Controlling light-induced dielectric response of Sr/Ni-modified (K0.5Na0.5)NbO3 ceramics by narrow band gap method. Mater. Sci. Semicond. Process. 2022, 143, 106521. [Google Scholar] [CrossRef]
- Xu, Y.; Li, G.; Jing, Y.; Zhang, H.; Wang, X.; Lu, Y.; Lan, Z. n-type absorber by Cd2+ doping achieves high-performance carbon-based CsPbIBr2 perovskite solar cells. J. Colloid Interface Sci. 2022, 608, 40–47. [Google Scholar] [CrossRef]
- Saini, N.; Jindal, R.; Tripathi, A. Influence of B-site cation in lattice dynamics of bilayered Ruddlesden–Popper Sr3B2O7 (B = Zr, Mo, Sn, Hf) compounds. J. Raman Spectrosc. 2023, 54, 847–856. [Google Scholar] [CrossRef]
- Gelkop, Y.; Di Mei, F.; Frishman, S.; Garcia, Y.; Falsi, L.; Perepelitsa, G.; Conti, C.; DelRe, E.; Agranat, A.J. Hyperbolic optics and superlensing in room-temperature KTN from self-induced k-space topological transitions. Nat. Commun. 2021, 12, 7241. [Google Scholar] [CrossRef]
- Joung, M.; Xu, H.; Seo, I. Piezoelectric nanogenerators synthesized using KNbO3 nanowires with various crystal structures. J. Mater. Chem. A 2014, 2, 18547–18553. [Google Scholar] [CrossRef]
- Wang, V.; Xu, N.; Liu, J.-C.; Tang, G.; Geng, W.-T. VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code. Comput. Phys. Commun. 2021, 267, 108033. [Google Scholar] [CrossRef]
- Peng, H.; Perdew, J.P. Rehabilitation of the Perdew-Burke-Ernzerhof generalized gradient approximation for layered materials. Phys. Rev. B 2017, 95, 2469–9950. [Google Scholar] [CrossRef]
- Dunja, G.; Anton, K. DFT Study of Azole Corrosion Inhibitors on Cu2O Model of Oxidized Copper Surfaces: I. Molecule–Surface and Cl–Surface Bonding. Metals 2018, 8, 310. [Google Scholar]
- Sanick, H.D.; Cocchi, C. Electronic Structure of Cesium-based Photocathode Materials from Density Functional Theory: Performance of PBE, SCAN, and HSE06 functionals. Electron. Struct. 2021, 12, 04596. [Google Scholar]
- Sheng, C.; Theogene, B.; Mina, G. First-principles study on the electronic properties of perovskites MASn a Pb(1-a)XbY(3-b) (X, Y=Cl, Br, I). Results Phys. 2019, 14, 102408. [Google Scholar]
- Chandrasekhar, K.D.; Wu, H.C.; Huang, C.L.; Yang, H.D. Effects of Jahn–Teller distortion on the skyrmion stability of (Cu1-xNix)2OSeO3. J. Mater. Chem. C 2016, 4, 5270–5274. [Google Scholar] [CrossRef]
- Zhang, Q.; Ping, Y.; An, W.; Sun, W.; Zhong, J. Effect of the magnetization parameter on electron acceleration during relativistic magnetic reconnection in ultra-intense laser-produced plasma. Chin. Phys. B 2022, 31, 604–610. [Google Scholar] [CrossRef]
- Elouafi, A.; Moubah, R.; Tizliouine, A.; Derkaoui, S.; Omari, L.H.; Lassri, H. Effects of Ru doping and of oxygen vacancies on the optical properties in α-Fe2O3 powders. Appl. Phys. A 2020, 126, 228. [Google Scholar] [CrossRef]
- Liu, Y.; Zeng, J.; Zhu, Z.; Dong, X.; Deng, W. A physics-based compact model for MoS2 field-effect transistors considering the band-tail effect and contact resistance. Jpn. J. Appl. Phys. 2020, 59, 104004. [Google Scholar] [CrossRef]
- Jiwei, Z.; Cheung, M.H.; Xu, Z.K.; Li, X.; Chen, H.; Colla, E.V.; Wu, T.B. Dielectric and ferroelectric properties of highly oriented (Pb,Nb)(Zr,Sn,Ti)O3 thin films grown by a sol-gel process. Appl. Phys. Lett. 2002, 81, 3621–3623. [Google Scholar] [CrossRef]
- Kin, T.Y.; Choi, J.O.; Anoop, G. (111)-oriented Sn-doped BaTiO3 epitaxial thin films for ultrahigh energy density capacitors. Ceram. Int. 2021, 47, 26856–26862. [Google Scholar]
- Tsymbalov, E.; Shi, Z.; Dao, M.; Suresh, S.; Li, J.; Shapeev, A. Machine learning for deep elastic strain engineering of semiconductor electronic band structure and effective mass. npj Comput. Mater. 2021, 7, 76. [Google Scholar] [CrossRef]
- Wang, S.; Su, L.; Qiu, Y.; Xiao, Y.; Zhao, L.-D. Enhanced thermoelectric performance in Cl-doped BiSbSe3 with optimal carrier concentration and effective mass. J. Mater. Sci. Technol. 2021, 70, 67–72. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, Z.; Feng, T.; Mu, Y.; You, H.; Li, X. Human motion prediction using optimized sliding window polynomial fitting and recursive least squares. J. Chin. Univ. Posts Telecommun. 2021, 28, 76–85. [Google Scholar]
- Masoumi, M.; Jahanshahi, M.; Ahangari, M.G.; Darzi, G.N. Electronic, mechanical and thermal properties of SiO2 nanotube interacting with poly lactic-co-glycolic acid: Density functional theory and molecular dynamics studies. Appl. Surf. Sci. 2021, 546, 148894. [Google Scholar] [CrossRef]
- Hu, F.; Tao, L.; Ye, H.; Li, X.; Chen, X. ZnO/WSe2 vdW heterostructure for photocatalytic water splitting. J. Mater. Chem. C. 2019, 7, 7104–7113. [Google Scholar] [CrossRef]
- Dai, M.Y.; Wen, X.; Xia, R.; Zheng, Y.M.; Wei, L.; Zhang, L.L.; Huang, Y.N. First-principles calculations of the photocatalytic performance of ZnO–MX2 (M = Mo, W; X = S, Se) heterojunctions. RSC Adv. 2025, 15, 23489. [Google Scholar] [CrossRef]
- Peng, Y.T.; Tan, Z.; An, J.; Zhu, J.G.; Zhang, Q.M. The tunable ferroelectricity and piezoelectricity of the KNN piezoceramics by Na concentrations: First-principles calculations—ScienceDirect. J. Eur. Ceram. Soc. 2019, 39, 5252–5259. [Google Scholar] [CrossRef]
- Deng, Y.F.; Wang, J.J.; Zhang, C.X.; Ma, H.; Bai, C.G.; Liu, D.Q.; Wu, F.M.; Yang, B. Structural and Electric Properties of MnO2-Doped KNN-LT Lead-Free Piezoelectric Ceramics. Materials 2020, 10, 705. [Google Scholar]
- Wang, X.; Wang, J.; Yu, Y.; Zhang, H.; Boughton, R.I. Growth of cubic KTa1−xNbxO3 crystal by czochralski method. J. Cryst. Growth 2006, 293, 398–403. [Google Scholar] [CrossRef]
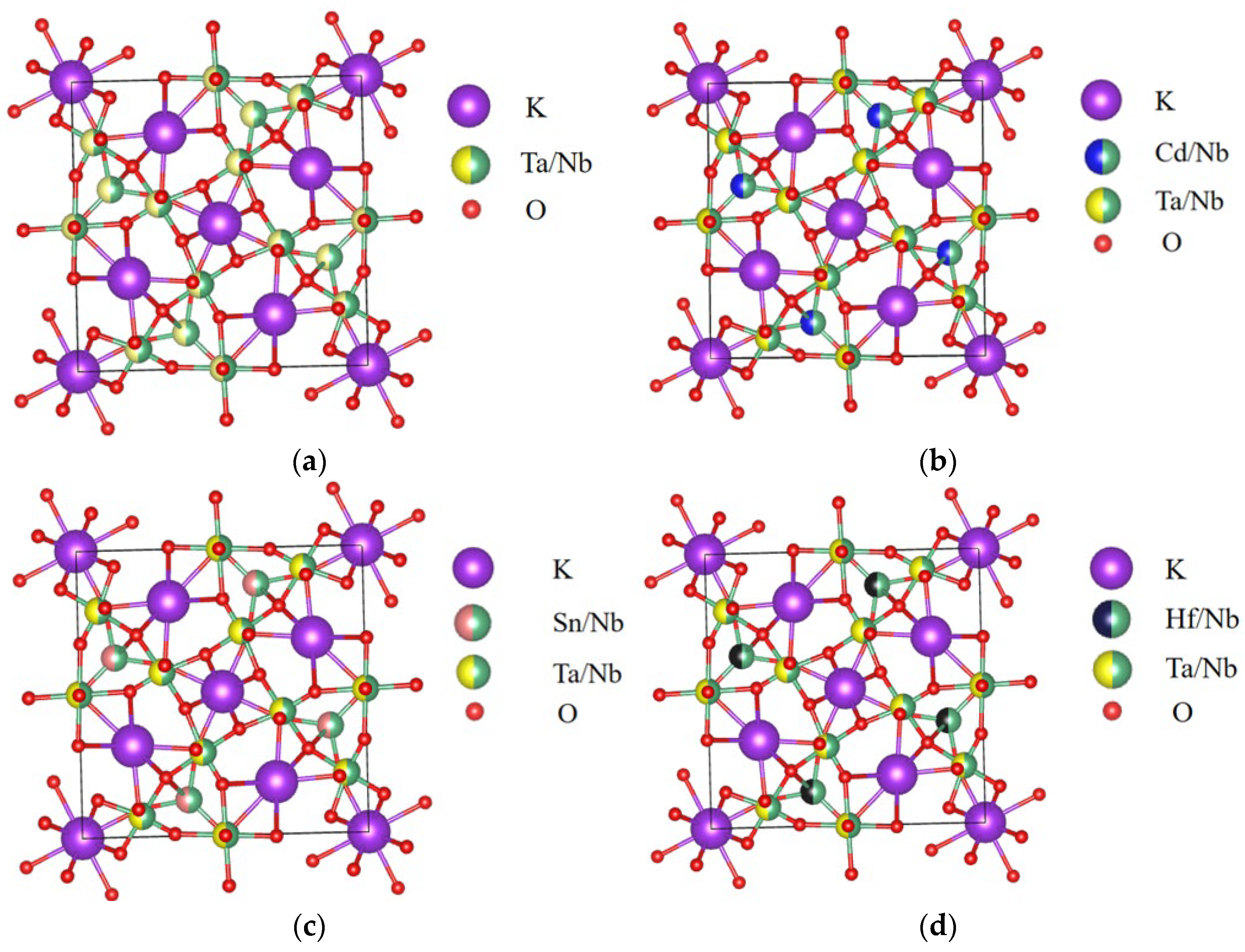
| Parameters | Cd | Sn | Hf |
|---|---|---|---|
| Ionic radius/Å | 0.97 | 0.69 | 0.71 |
| Tolerance factor | 0.892 | 0.935 | 0.931 |
| Octahedral factor | 0.69 | 0.49 | 0.50 |
| System | a/Å | b/Å | c/Å | V/Å3 | Bond Length/Å | Etotal/eV | Ef | Eb |
|---|---|---|---|---|---|---|---|---|
| KTN | 8.0187 | 8.0187 | 8.1753 | 530.0340 | 2.02 (Ta-O) | –14348.5 | –7.9287 | –7.9287 |
| KTN-Cd | 8.0947 | 8.1898 | 8.1925 | 543.1075 | 2.17 (Cd-O) | –18493.1 | –0.0076 | –7.6840 |
| KTN-Sn | 8.0480 | 8.1233 | 8.1422 | 532.3017 | 2.09 (Sn-O) | –11565.3 | –0.1181 | –7.5970 |
| KTN-Hf | 8.0682 | 8.0988 | 8.1822 | 534.6442 | 2.09 (Hf-O) | –18838.8 | –0.0149 | –7.8761 |
| System | KTN | Cd-KTN | Sn-KTN | Hf-KTN |
|---|---|---|---|---|
| m*e/10−31 kg | 0.4584 | 0.0993 | 0.1033 | 0.1003 |
| m*h/10−31 kg | 0.1905 | 18.7428 | 5.9030 | 8.1096 |
| D(m*h/m*e)/10−31 kg | 0.4156 | 188.7492 | 57.1442 | 80.8534 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, C.; Chen, Q.-Y.; Zhou, X.-Y.; Zhao, X.-C.; Lei, B.-C.; Zhang, L.-L.; Zhao, J.; Huang, Y.-N. First-Principles Study on the Photocatalytic Performance of K(Ta0.5Nb0.5)O3 Doped with Metals (Cd, Sn, Hf). Nanomaterials 2025, 15, 1322. https://doi.org/10.3390/nano15171322
Zhao C, Chen Q-Y, Zhou X-Y, Zhao X-C, Lei B-C, Zhang L-L, Zhao J, Huang Y-N. First-Principles Study on the Photocatalytic Performance of K(Ta0.5Nb0.5)O3 Doped with Metals (Cd, Sn, Hf). Nanomaterials. 2025; 15(17):1322. https://doi.org/10.3390/nano15171322
Chicago/Turabian StyleZhao, Can, Qiao-Yue Chen, Xin-Yuan Zhou, Xu-Cai Zhao, Bo-Cheng Lei, Li-Li Zhang, Jing Zhao, and Yi-Neng Huang. 2025. "First-Principles Study on the Photocatalytic Performance of K(Ta0.5Nb0.5)O3 Doped with Metals (Cd, Sn, Hf)" Nanomaterials 15, no. 17: 1322. https://doi.org/10.3390/nano15171322
APA StyleZhao, C., Chen, Q.-Y., Zhou, X.-Y., Zhao, X.-C., Lei, B.-C., Zhang, L.-L., Zhao, J., & Huang, Y.-N. (2025). First-Principles Study on the Photocatalytic Performance of K(Ta0.5Nb0.5)O3 Doped with Metals (Cd, Sn, Hf). Nanomaterials, 15(17), 1322. https://doi.org/10.3390/nano15171322






