First-Principles Study of Topological Nodal Line Semimetal I229-Ge48 via Cluster Assembly
Abstract
1. Introduction
2. Computational Methods
3. Results
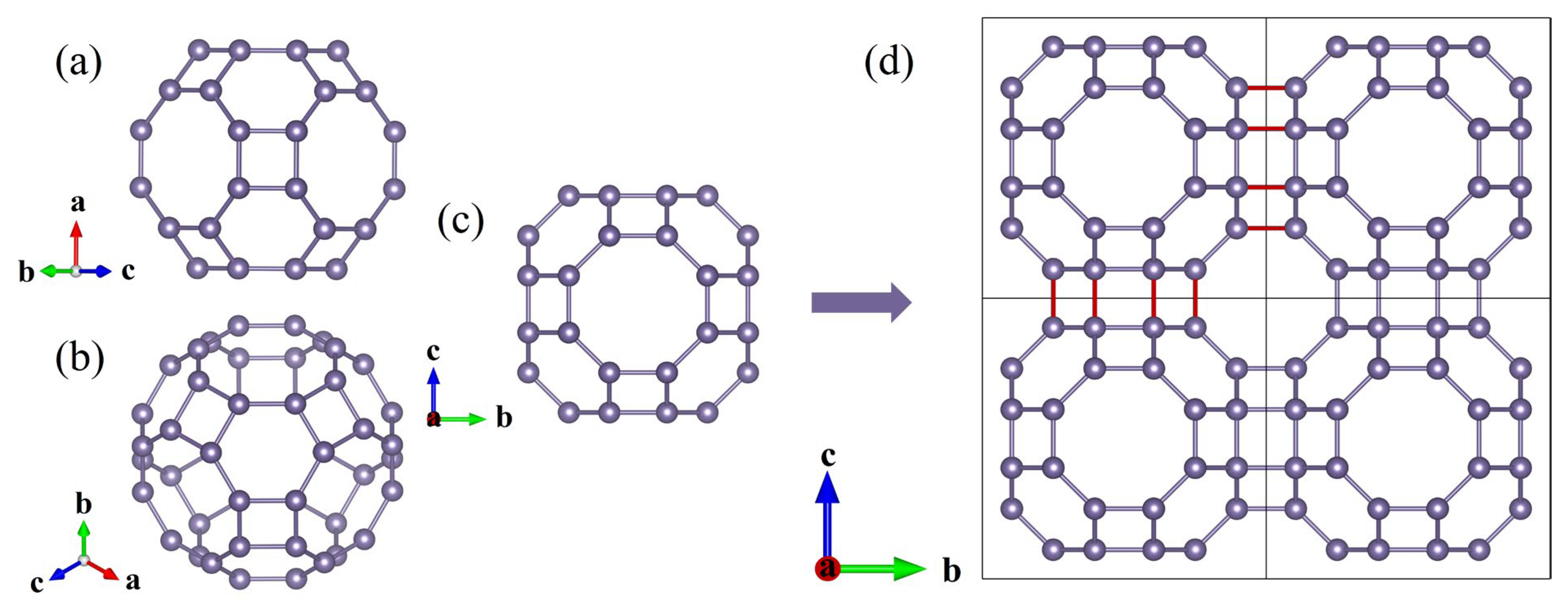
3.1. Geometric Features
3.2. Stabilities
3.3. Mechanical Properties
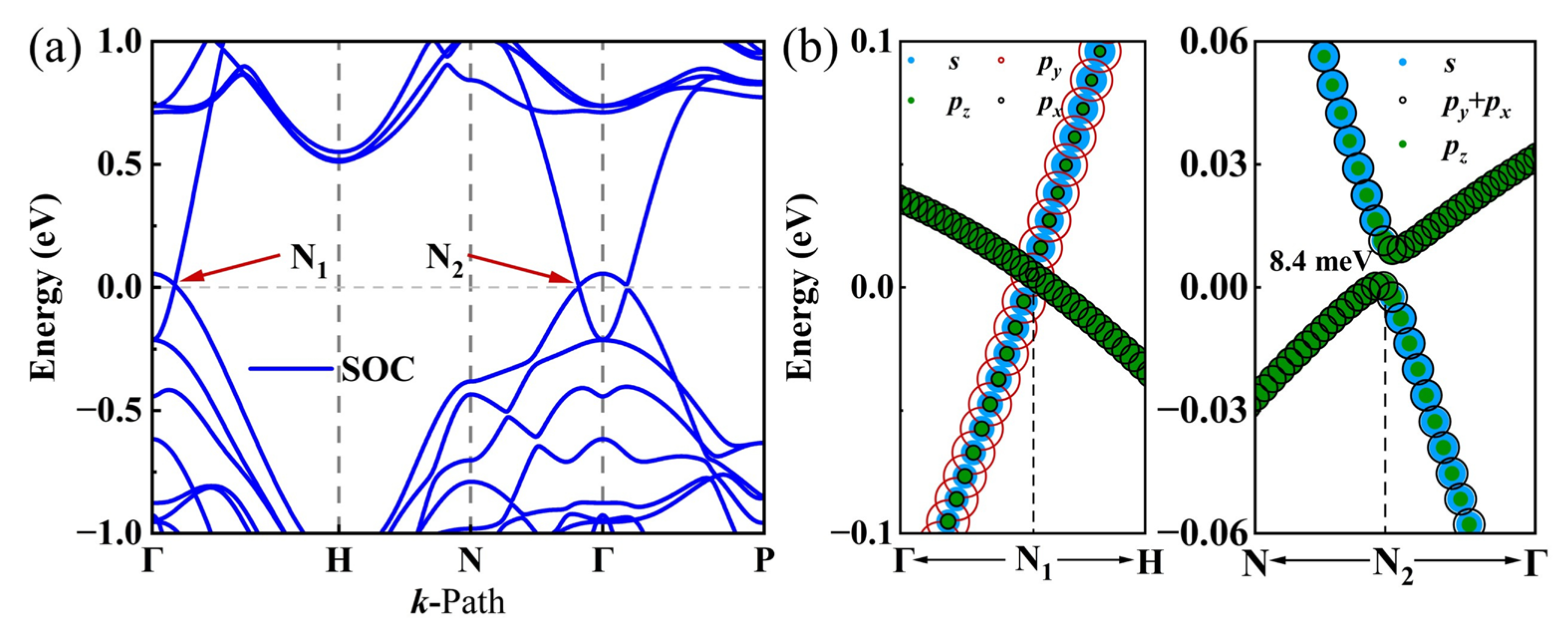
3.4. Topological Electronic Properties
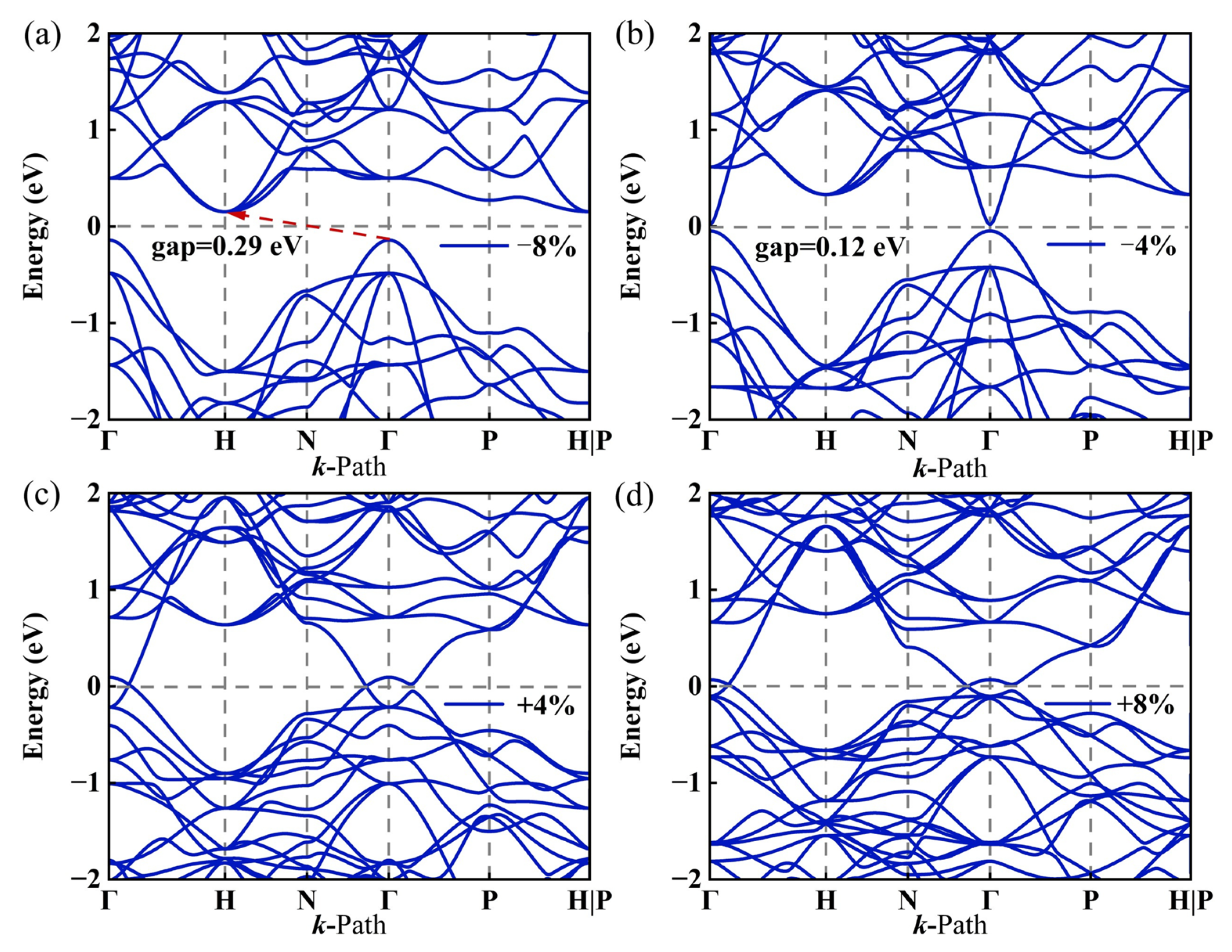
3.5. Strain Control
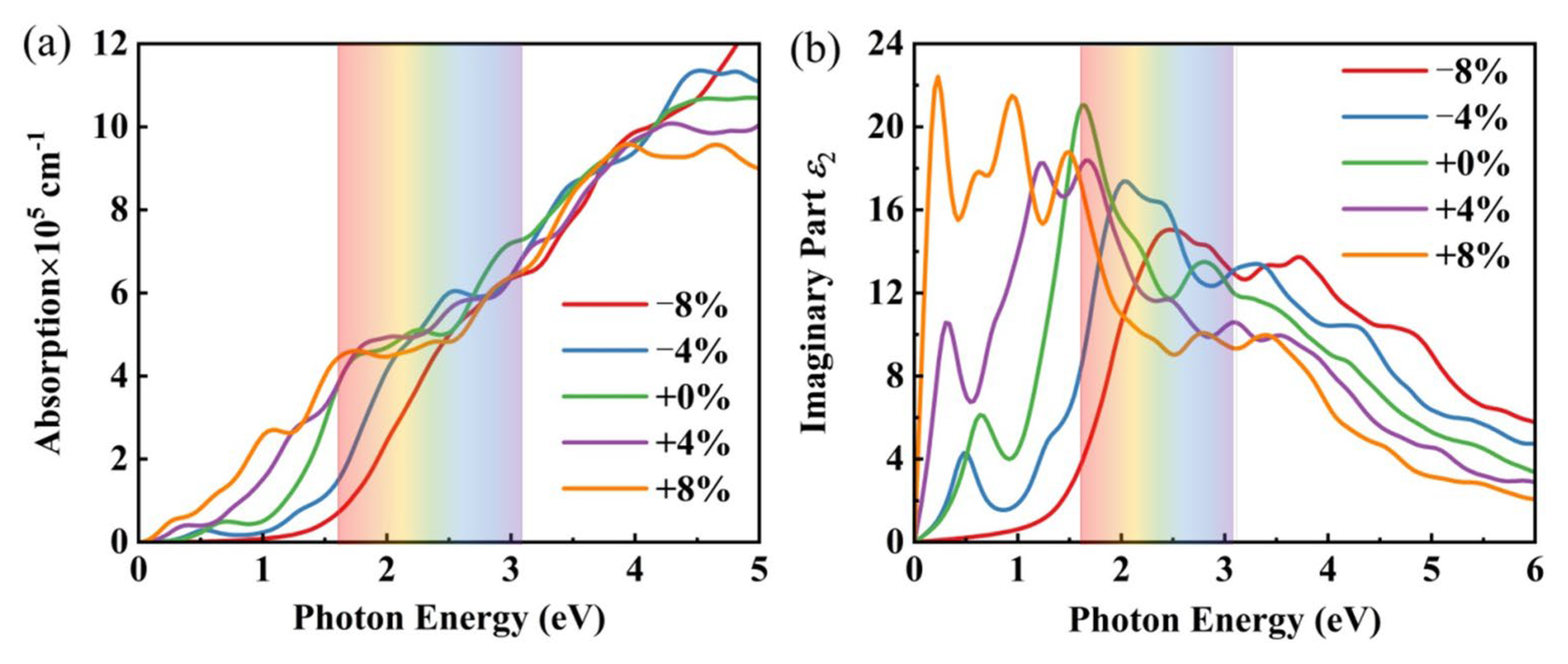
3.6. Optical Properties
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.; Weng, H.; Wu, Q.; Dai, X.; Fang, Z. Three-Dimensional Dirac Semimetal and Quantum Transport in Cd3As2. Phys. Rev. B 2013, 88, 125427. [Google Scholar] [CrossRef]
- Liu, Z.K.; Zhou, B.; Zhang, Y.; Wang, Z.J.; Weng, H.M.; Prabhakaran, D.; Mo, S.-K.; Shen, Z.X.; Fang, Z.; Dai, X.; et al. Discovery of a Three-Dimensional Topological Dirac Semimetal, Na3Bi. Science 2014, 343, 864–867. [Google Scholar] [CrossRef] [PubMed]
- Hosur, P. Friedel Oscillations Due to Fermi Arcs in Weyl Semimetals. Phys. Rev. B 2012, 86, 195102. [Google Scholar] [CrossRef]
- Bian, G.; Chang, T.-R.; Sankar, R.; Xu, S.-Y.; Zheng, H.; Neupert, T.; Chiu, C.-K.; Huang, S.-M.; Chang, G.; Belopolski, I.; et al. Topological Nodal-Line Fermions in Spin-Orbit Metal PbTaSe2. Nat. Commun. 2016, 7, 10556. [Google Scholar] [CrossRef]
- Cheng, Y.; Liu, D.; Liu, X.; Zhang, R.; Cui, X.; Liu, Z.; Song, T. High-Throughput Screening for Ideal 3D Carbon Topological Semimetals via Bottom-up Approach. J. Phys. Chem. C 2024, 128, 13308–13317. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, M.; Wang, J.; Liu, Y.; Liu, G.; Wang, X.; Zhang, G.; Zhang, X. High-Performance Hydrogen Evolution Reaction Catalysts in Two-Dimensional Nodal Line Semimetals. ACS Appl. Mater. Interfaces 2023, 15, 51225–51230. [Google Scholar] [CrossRef]
- Kong, X.; Liu, Z.; Geng, Z.; Zhang, A.; Guo, Z.; Cui, S.; Xia, C.; Tan, S.; Zhou, S.; Wang, Z.; et al. Experimental Demonstration of Topological Catalysis for CO2 Electroreduction. J. Am. Chem. Soc. 2024, 146, 6536–6543. [Google Scholar] [CrossRef]
- Nishihaya, S.; Uchida, M.; Nakazawa, Y.; Kurihara, R.; Akiba, K.; Kriener, M.; Miyake, A.; Taguchi, Y.; Tokunaga, M.; Kawasaki, M. Quantized Surface Transport in Topological Dirac Semimetal Films. Nat. Commun. 2019, 10, 2564. [Google Scholar] [CrossRef]
- Son, D.T.; Spivak, B.Z. Chiral Anomaly and Classical Negative Magnetoresistance of Weyl Metals. Phys. Rev. B 2013, 88, 104412. [Google Scholar] [CrossRef]
- Huang, X.; Zhao, L.; Long, Y.; Wang, P.; Chen, D.; Yang, Z.; Liang, H.; Xue, M.; Weng, H.; Fang, Z.; et al. Observation of the Chiral-Anomaly-Induced Negative Magnetoresistance in 3D Weyl Semimetal TaAs. Phys. Rev. X 2015, 5, 031023. [Google Scholar] [CrossRef]
- Gao, H.; Venderbos, J.W.F.; Kim, Y.; Rappe, A.M. Topological Semimetals from First Principles. Annu. Rev. Mater. Res. 2019, 49, 153–183. [Google Scholar] [CrossRef]
- Cao, W.; Tang, P.; Zhang, S.-C.; Duan, W.; Rubio, A. Stable Dirac Semimetal in the Allotropes of Group-IV Elements. Phys. Rev. B 2016, 93, 241117. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, Y.; Chen, X.-Q.; Franchini, C.; Xu, G.; Weng, H.; Dai, X.; Fang, Z. Dirac Semimetal and Topological Phase Transitions in A3Bi (A = Na, K, Rb). Phys. Rev. B 2012, 85, 195320. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, D.; Teo, H.T.; Wang, Q.; Xue, H.; Zhang, B. Higher-Order Dirac Semimetal in a Photonic Crystal. Phys. Rev. B 2022, 105, L060101. [Google Scholar] [CrossRef]
- Wan, X.; Turner, A.M.; Vishwanath, A.; Savrasov, S.Y. Topological Semimetal and Fermi-Arc Surface States in the Electronic Structure of Pyrochlore Iridates. Phys. Rev. B 2011, 83, 205101. [Google Scholar] [CrossRef]
- Xu, G.; Weng, H.; Wang, Z.; Dai, X.; Fang, Z. Chern Semimetal and the Quantized Anomalous Hall Effect in HgCr2Se4. Phys. Rev. Lett. 2011, 107, 186806. [Google Scholar] [CrossRef] [PubMed]
- Li, X.-P.; Deng, K.; Fu, B.; Li, Y.; Ma, D.-S.; Han, J.; Zhou, J.; Zhou, S.; Yao, Y. Type-III Weyl Semimetals: (TaSe4)2I. Phys. Rev. B 2021, 103, L081402. [Google Scholar] [CrossRef]
- Hořava, P. Stability of Fermi Surfaces and K Theory. Phys. Rev. Lett. 2005, 95, 016405. [Google Scholar] [CrossRef]
- Burkov, A.A.; Hook, M.D.; Balents, L. Topological Nodal Semimetals. Phys. Rev. B 2011, 84, 235126. [Google Scholar] [CrossRef]
- Abramovich, S.; Dutta, D.; Rizza, C.; Santoro, S.; Aquino, M.; Cupolillo, A.; Occhiuzzi, J.; Russa, M.F.L.; Ghosh, B.; Farias, D.; et al. NiSe and CoSe Topological Nodal-Line Semimetals: A Sustainable Platform for Efficient Thermoplasmonics and Solar-Driven Photothermal Membrane Distillation. Small 2022, 18, 2201473. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Vogt, P.; De Padova, P.; Quaresima, C.; Avila, J.; Frantzeskakis, E.; Asensio, M.C.; Resta, A.; Ealet, B.; Le Lay, G. Silicene: Compelling Experimental Evidence for Graphenelike Two-Dimensional Silicon. Phys. Rev. Lett. 2012, 108, 155501. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Lu, S.; Pan, J.; Qin, Z.; Wang, Y.; Wang, Y.; Cao, G.; Du, S.; Gao, H. Buckled Germanene Formation on Pt(111). Adv. Mater. 2014, 26, 4820–4824. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Xie, Y.; Yang, S.A.; Pan, H.; Zhang, F.; Cohen, M.L.; Zhang, S. Nanostructured Carbon Allotropes with Weyl-like Loops and Points. Nano Lett. 2015, 15, 6974–6978. [Google Scholar] [CrossRef] [PubMed]
- Zhong, C.; Chen, Y.; Xie, Y.; Yang, S.A.; Cohen, M.L.; Zhang, S.B. Towards Three-Dimensional Weyl-Surface Semimetals in Graphene Networks. Nanoscale 2016, 8, 7232–7239. [Google Scholar] [CrossRef]
- Zhong, C.; Xie, Y.; Chen, Y.; Zhang, S. Coexistence of Flat Bands and Dirac Bands in a Carbon-Kagome-Lattice Family. Carbon 2016, 99, 65–70. [Google Scholar] [CrossRef]
- Qie, Y.; Liu, J.; Li, X.; Wang, S.; Sun, Q.; Jena, P. Interpenetrating Silicene Networks: A Topological Nodal-Line Semimetal with Potential as an Anode Material for Sodium Ion Batteries. Phys. Rev. Mater. 2018, 2, 084201. [Google Scholar] [CrossRef]
- Kasper, E.; Oehme, M.; Lupaca-Schomber, J. High Ge Content SiGe Alloys: Doping and Contact Formation. ECS Trans. 2008, 16, 893–904. [Google Scholar] [CrossRef]
- Barkalov, O.I.; Tissen, V.G.; McMillan, P.F.; Wilson, M.; Sella, A.; Nefedova, M.V. Pressure-Induced Transformations and Superconductivity of Amorphous Germanium. Phys. Rev. B 2010, 82, 020507. [Google Scholar] [CrossRef]
- Pillarisetty, R. Academic and Industry Research Progress in Germanium Nanodevices. Nature 2011, 479, 324–328. [Google Scholar] [CrossRef]
- Menoni, C.S.; Hu, J.Z.; Spain, I.L. Germanium at High Pressures. Phys. Rev. B 1986, 34, 362–368. [Google Scholar] [CrossRef]
- Tanaka, K. Amorphous Ge under Pressure. Phys. Rev. B 1991, 43, 4302–4307. [Google Scholar] [CrossRef][Green Version]
- Bundy, F.P.; Kasper, J.S. A New Dense Form of Solid Germanium. Science 1963, 139, 340–341. [Google Scholar] [CrossRef]
- Arguilla, M.Q.; Jiang, S.; Chitara, B.; Goldberger, J.E. Synthesis and Stability of Two-Dimensional Ge/Sn Graphane Alloys. Chem. Mater. 2014, 26, 6941–6946. [Google Scholar] [CrossRef]
- Nguyen, M.C.; Zhao, X.; Wang, C.-Z.; Ho, K.-M. Sp3-Hybridized Framework Structure of Group-14 Elements Discovered by Genetic Algorithm. Phys. Rev. B 2014, 89, 184112. [Google Scholar] [CrossRef]
- Lan, H.-S.; Chang, S.T.; Liu, C.W. Semiconductor, Topological Semimetal, Indirect Semimetal, and Topological Dirac Semimetal Phases of Ge1−xSnx Alloys. Phys. Rev. B 2017, 95, 201201. [Google Scholar] [CrossRef]
- Zou, Y.; Wu, N.; Song, T.; Liu, Z.; Cui, X. From Topological Nodal-Line Semimetal to Insulator in ABW-Ge4: A New Member of the Germanium Allotrope. ACS Omega 2023, 8, 27231–27237. [Google Scholar] [CrossRef]
- Zhu, Z.; Li, M.; Li, J. Topological Semimetal to Insulator Quantum Phase Transition in the Zintl Compounds Ba2X (X = Si, Ge). Phys. Rev. B 2016, 94, 155121. [Google Scholar] [CrossRef]
- Bampoulis, P.; Castenmiller, C.; Klaassen, D.J.; van Mil, J.; Liu, Y.; Liu, C.-C.; Yao, Y.; Ezawa, M.; Rudenko, A.N.; Zandvliet, H.J.W. Quantum Spin Hall States and Topological Phase Transition in Germanene. Phys. Rev. Lett. 2023, 130, 196401. [Google Scholar] [CrossRef]
- Basnet, R.; Upreti, D.; McCarthy, T.T.; Ju, Z.; McMinn, A.M.; Sharma, M.M.; Zhang, Y.-H.; Hu, J. Magneto-Transport Study on Sn-Rich Sn1−xGex Thin Films Enabled by CdTe Buffer Layer. J. Vac. Sci. Technol. B 2024, 42, 042210. [Google Scholar] [CrossRef]
- Claridge, S.A.; Castleman, A.W.; Khanna, S.N.; Murray, C.B.; Sen, A.; Weiss, P.S. Cluster-Assembled Materials. ACS Nano 2009, 3, 244–255. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and Simple Analytic Representation of the Electron-Gas Correlation Energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First Principles Phonon Calculations in Materials Science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Martyna, G.J.; Klein, M.L.; Tuckerman, M. Nosé–Hoover Chains: The Canonical Ensemble via Continuous Dynamics. J. Chem. Phys. 1992, 97, 2635–2643. [Google Scholar] [CrossRef]
- Gao, J.; Wu, Q.; Persson, C.; Wang, Z. Irvsp: To Obtain Irreducible Representations of Electronic States in the VASP. Comput. Phys. Commun. 2021, 261, 107760. [Google Scholar] [CrossRef]
- Mostofi, A.A.; Yates, J.R.; Lee, Y.-S.; Souza, I.; Vanderbilt, D.; Marzari, N. Wannier90: A Tool for Obtaining Maximally-Localised Wannier Functions. Comput. Phys. Commun. 2008, 178, 685–699. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, S.; Song, H.-F.; Troyer, M.; Soluyanov, A.A. WannierTools: An Open-Source Software Package for Novel Topological Materials. Comput. Phys. Commun. 2018, 224, 405–416. [Google Scholar] [CrossRef]
- Oku, T.; Nishiwaki, A.; Narita, I.; Gonda, M. Formation and Structure of B24N24 Clusters. Chem. Phys. Lett. 2003, 380, 620–623. [Google Scholar] [CrossRef]
- Lide, D.R. CRC Handbook of Chemistry and Physics, 73rd ed.; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Kim, E.H.; Shin, Y.-H.; Lee, B.-J. A Modified Embedded-Atom Method Interatomic Potential for Germanium. Calphad 2008, 32, 34–42. [Google Scholar] [CrossRef]
- Birch, F. Finite Elastic Strain of Cubic Crystals. Phys. Rev. 1947, 71, 809–824. [Google Scholar] [CrossRef]
- Silvi, B.; Savin, A. Classification of Chemical Bonds Based on Topological Analysis of Electron Localization Functions. Nature 1994, 371, 683–686. [Google Scholar] [CrossRef]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Fan, Q.; Chai, C.; Wei, Q.; Yang, Q.; Zhou, P.; Xing, M.; Yang, Y. Mechanical and Electronic Properties of Si, Ge and Their Alloys in P42/Mnm Structure. Mater. Sci. Semicond. Process. 2016, 43, 187–195. [Google Scholar] [CrossRef]
- Gómez-Abal, R.; Li, X.; Scheffler, M.; Ambrosch-Draxl, C. Influence of the Core-Valence Interaction and of the Pseudopotential Approximation on the Electron Self-Energy in Semiconductors. Phys. Rev. Lett. 2008, 101, 106404. [Google Scholar] [CrossRef]
- Fan, Q.; Sun, Y.; Zhao, Y.; Song, Y.; Yun, S. Group 14 Elements in the Cmcm Phase with a Direct Band Structure for Photoelectric Application. Phys. Scr. 2023, 98, 015701. [Google Scholar] [CrossRef]
- Fan, Q.; Hao, B.; Jiang, L.; Yu, X.; Zhang, W.; Song, Y.; Yun, S. Group 14 Semiconductor Alloys in the P41212 Phase: A Comprehensive Study. Results Phys. 2021, 25, 104254. [Google Scholar] [CrossRef]
- Yuan, Q.; Li, S.; Zhou, L.; He, D. Phase-Pure ST12 Ge Bulks through Secondary Pressure Induced Phase Transition. Solid State Commun. 2022, 348–349, 114742. [Google Scholar] [CrossRef]
- Pugh, S.F. XCII. Relations between the Elastic Moduli and the Plastic Properties of Polycrystalline Pure Metals. Philos. Mag. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Nye, J.F. Physical Properties of Crystals; Oxford University Press: Oxford, UK, 1985. [Google Scholar]
- Ranganathan, S.I.; Ostoja-Starzewski, M. Universal Elastic Anisotropy Index. Phys. Rev. Lett. 2008, 101, 055504. [Google Scholar] [CrossRef]
- Tran, F.; Blaha, P. Accurate Band Gaps of Semiconductors and Insulators with a Semilocal Exchange-Correlation Potential. Phys. Rev. Lett. 2009, 102, 226401. [Google Scholar] [CrossRef]
- Soluyanov, A.A.; Gresch, D.; Wang, Z.; Wu, Q.; Troyer, M.; Dai, X.; Bernevig, B.A. Type-II Weyl Semimetals. Nature 2015, 527, 495–498. [Google Scholar] [CrossRef]
- Sharma, M.M.; Chhetri, S.K.; Acharya, G.; Graf, D.; Upreti, D.; Dahal, S.; Nabi, M.R.U.; Rahman, S.; Sakon, J.; Churchill, H.O.H.; et al. Quantum Oscillation Studies of the Nodal Line Semimetal Ni3In2S2−xSex. Acta Mater. 2025, 289, 120884. [Google Scholar] [CrossRef]
- Meng, J.; Liu, G.; Zhang, W.; Zhao, L.; Liu, H.; Jia, X.; Mu, D.; Liu, S.; Dong, X.; Zhang, J.; et al. Coexistence of Fermi Arcs and Fermi Pockets in a High-Tc Copper Oxide Superconductor. Nature 2009, 462, 335–338. [Google Scholar] [CrossRef]
- Damascelli, A.; Hussain, Z.; Shen, Z.-X. Angle-Resolved Photoemission Studies of the Cuprate Superconductors. Rev. Mod. Phys. 2003, 75, 473–541. [Google Scholar] [CrossRef]
- Sharma, M.M.; Karn, N.K.; Rani, P.; Bhowmik, R.N.; Awana, V.P.S. Bulk Superconductivity and Non-Trivial Band Topology Analysis of Pb2Pd. Supercond. Sci. Technol. 2022, 35, 084010. [Google Scholar] [CrossRef]
- Cui, Y.; Peng, L.; Sun, L.; Qian, Q.; Huang, Y. Two-Dimensional Few-Layer Group-III Metal Monochalcogenides as Effective Photocatalysts for Overall Water Splitting in the Visible Range. J. Mater. Chem. A 2018, 6, 22768–22777. [Google Scholar] [CrossRef]




| Structure | C11 | C12 | C13 | C22 | C23 | C33 | C44 | C55 | C66 | B | G | B/G | Y | ν | Au | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I229-Ge48 | This work | 42 | 26 | 20 | 31 | 14 | 2.21 | 37 | 0.30 | 0.770 | ||||||
| Diamond | This work | 116 | 45 | 61 | 69 | 50 | 1.38 | 121 | 0.21 | 0.313 | ||||||
| Cal. [59] | 121 | 49 | 62 | 73 | 50 | 1.46 | 122 | 0.22 | 0.342 | |||||||
| Exp. [60] | 129 | 48 | 67 | 77 | ||||||||||||
| Ge12 | This work | 83 | 28 | 29 | 91 | 35 | 40 | 48 | 33 | 1.44 | 81 | 0.22 | 0.104 | |||
| Cal. [59] | 88 | 26 | 32 | 100 | 35 | 40 | 50 | 34 | 1.47 | 83 | 0.22 | 0.054 | ||||
| oC24 | This work | 124 | 29 | 23 | 108 | 32 | 110 | 30 | 38 | 41 | 57 | 38 | 1.50 | 93 | 0.23 | 0.119 |
| Cal. [61] | 124 | 32 | 20 | 107 | 30 | 118 | 29 | 38 | 40 | 57 | 39 | 1.46 | 95 | 0.22 | ||
| Ge20 | This work | 112 | 33 | 37 | 98 | 50 | 40 | 60 | 42 | 1.43 | 102 | 0.22 | 0.140 | |||
| Cal. [62] | 112 | 32 | 37 | 96 | 49 | 39 | 59 | 41 | 1.44 | 100 | 0.22 | 0.153 | ||||
| ST12 | This work | 139 | 18 | 24 | 77 | 45 | 36 | 54 | 44 | 1.23 | 104 | 0.18 | 0.358 | |||
| Exp. [63] | 55 | 42 | ||||||||||||||
| hcp | This work | 94 | 39 | 47 | 65 | 26 | 27 | 57 | 23 | 2.53 | 60 | 0.33 | 0.591 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Wang, X.; Wang, N.; Chen, Y.; Wang, S.; Hua, C.; Song, T.; Liu, Z.; Cui, X. First-Principles Study of Topological Nodal Line Semimetal I229-Ge48 via Cluster Assembly. Nanomaterials 2025, 15, 1109. https://doi.org/10.3390/nano15141109
Liu L, Wang X, Wang N, Chen Y, Wang S, Hua C, Song T, Liu Z, Cui X. First-Principles Study of Topological Nodal Line Semimetal I229-Ge48 via Cluster Assembly. Nanomaterials. 2025; 15(14):1109. https://doi.org/10.3390/nano15141109
Chicago/Turabian StyleLiu, Liwei, Xin Wang, Nan Wang, Yaru Chen, Shumin Wang, Caizhi Hua, Tielei Song, Zhifeng Liu, and Xin Cui. 2025. "First-Principles Study of Topological Nodal Line Semimetal I229-Ge48 via Cluster Assembly" Nanomaterials 15, no. 14: 1109. https://doi.org/10.3390/nano15141109
APA StyleLiu, L., Wang, X., Wang, N., Chen, Y., Wang, S., Hua, C., Song, T., Liu, Z., & Cui, X. (2025). First-Principles Study of Topological Nodal Line Semimetal I229-Ge48 via Cluster Assembly. Nanomaterials, 15(14), 1109. https://doi.org/10.3390/nano15141109






