DFT-Based Functionalization of Graphene with Lithium-Modified Groups for Enhanced Hydrogen Detection: Thermodynamic, Electronic, and Spectroscopic Properties
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Graphene Characterization
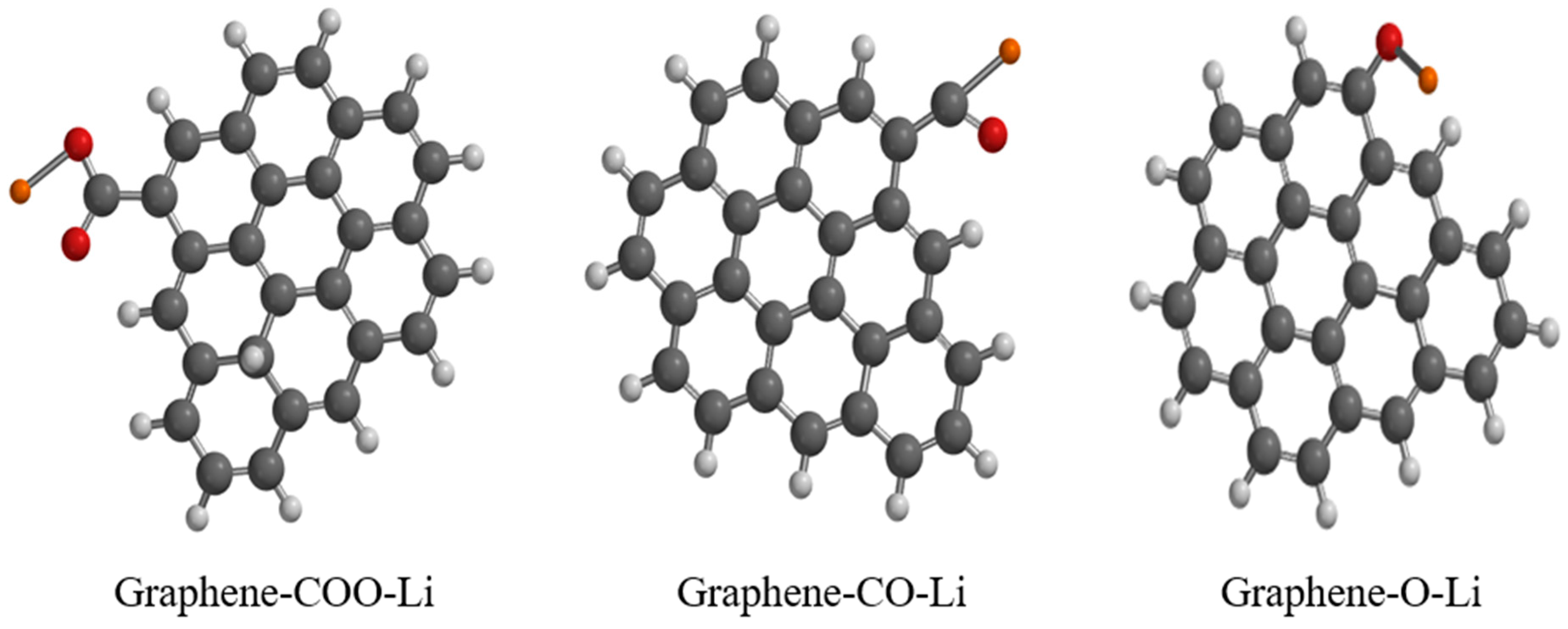
3.2. Functionalized Graphene
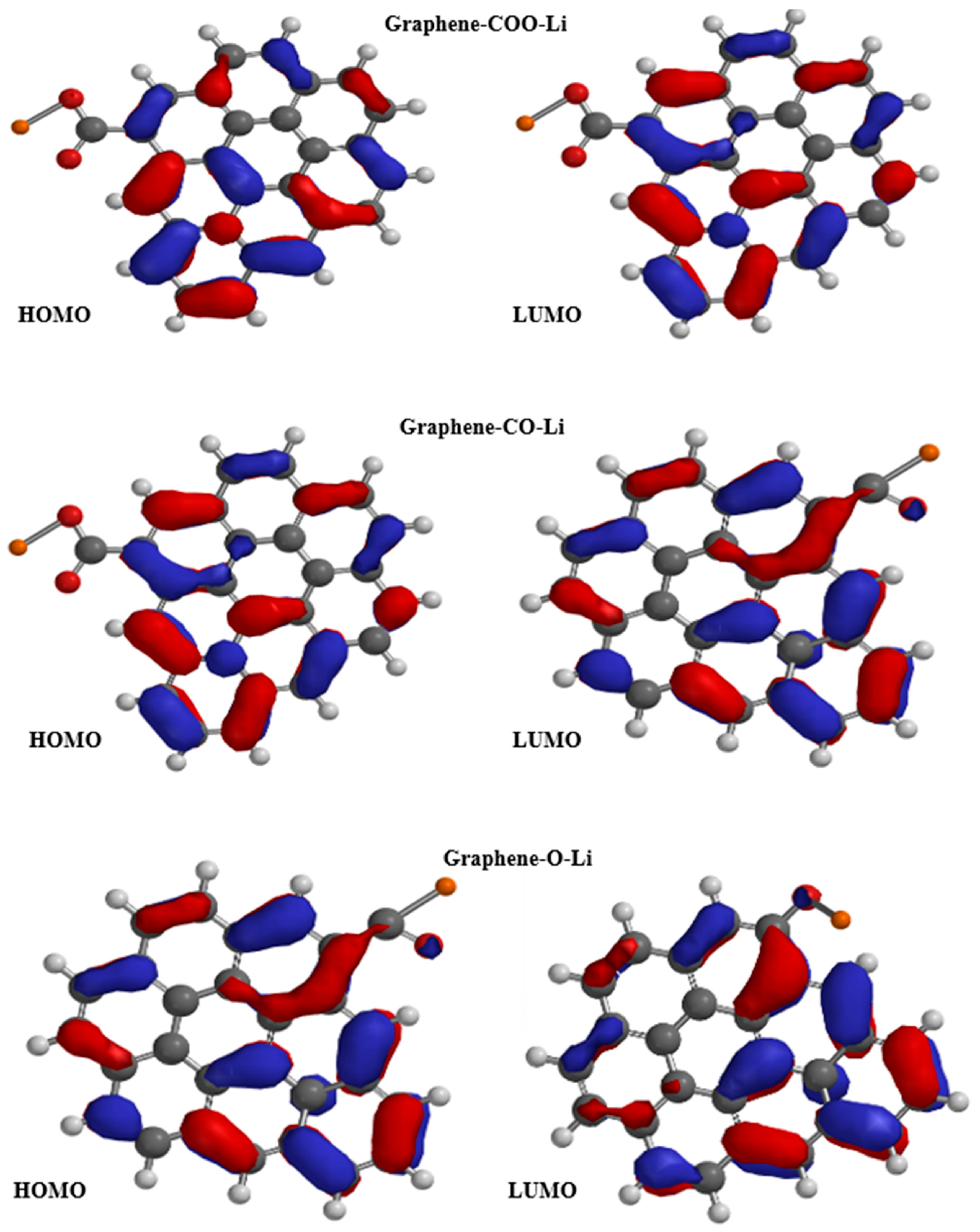
3.3. Frontier Orbitals and Band Gap Modulation in Functionalized Graphene
3.4. Spectroscopic Properties for Functionalized Graphene
3.5. The Behavior of Graphene and Functionalized Graphene in the Presence of Molecular Hydrogen
3.6. Frontier Orbital Behavior of Functionalized Graphene in Hydrogen Atmosphere
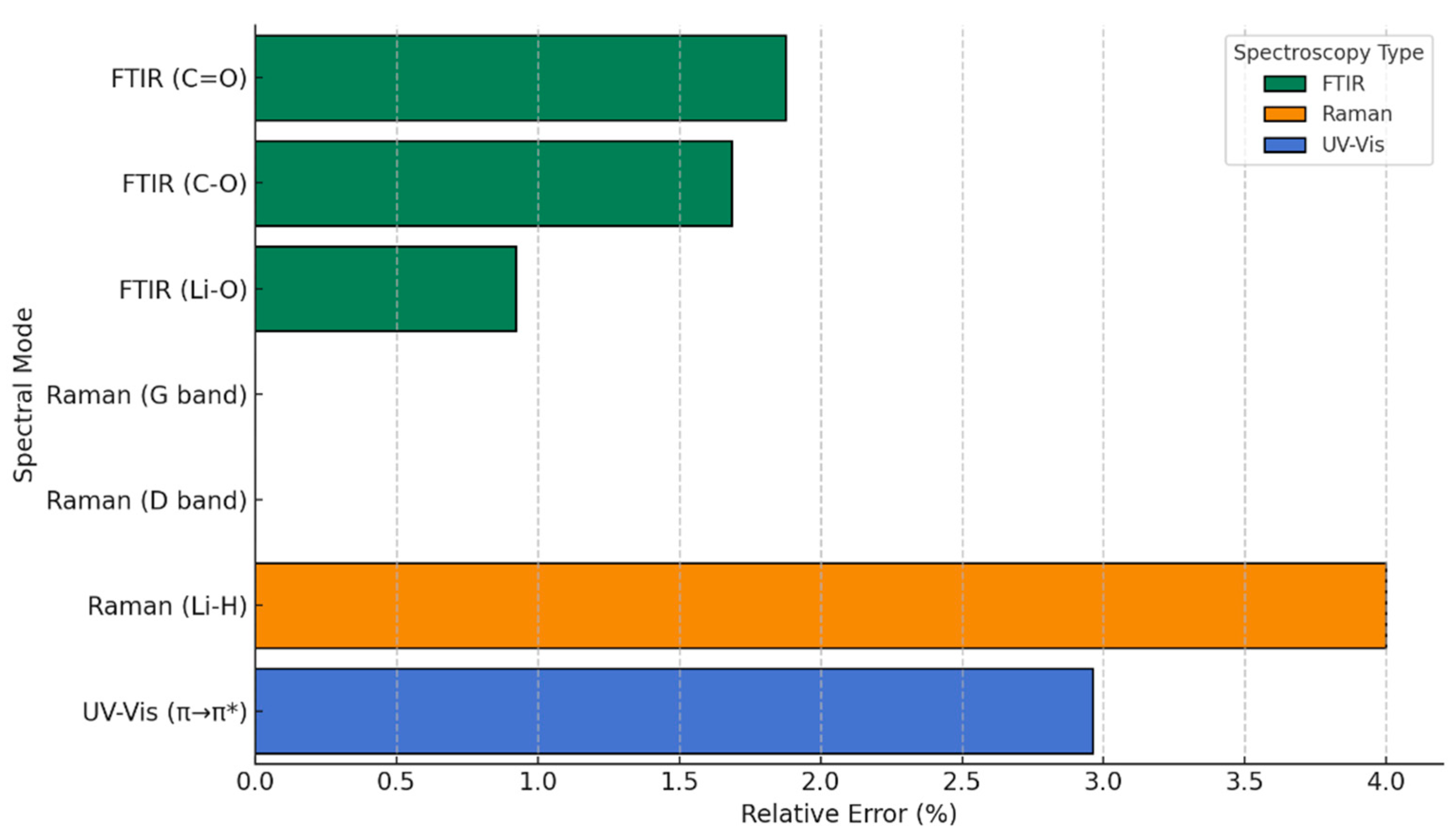
3.7. Spectroscopic Analysis for Graphene-Functionalized Compounds in H2 Atmospheres
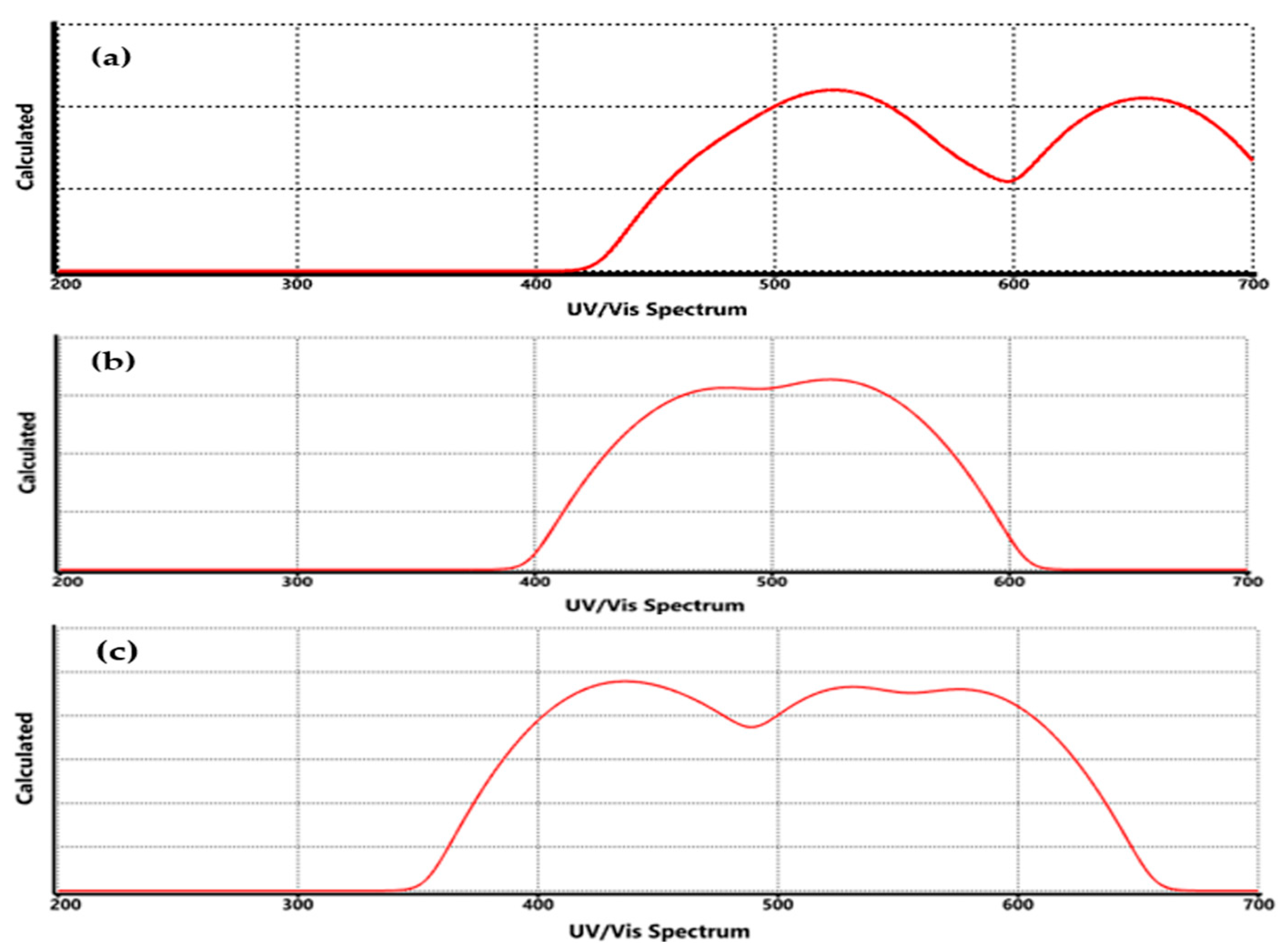
3.8. UV-Vis Spectral Response of Functionalized Graphene to Hydrogen Adsorption
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Joudeh, N.; Linke, D. Nanoparticle classification, physicochemical properties, characterization, and applications: A comprehensive review for biologists. J. Nanobiotechnol. 2022, 20, 262. [Google Scholar] [CrossRef]
- Stergiou, A.; Cantón-Vitoria, R.; Psarrou, M.N.; Economopoulos, P.S.; Tagmatarchis, N. Functionalized graphene and targeted applications—Highlighting the road from chemistry to applications. Prog. Mater. Sci. 2020, 114, 100683. [Google Scholar] [CrossRef]
- Alzate-Carvajal, N.; Luican-Mayer, A. Functionalized graphene surfaces for selective gas sensing. ACS Omega 2020, 5, 21320. [Google Scholar] [CrossRef]
- Urcuyo, R.; González-Flores, D.; Cordero-Solano, K. Perspectives and real applications of graphene at 16 years after its breakthrough. Rev. Colomb. Química 2021, 50, 51–85. [Google Scholar] [CrossRef]
- Singla, M.; Jaggi, N. Theoretical investigations of hydrogen gas sensing and storage capacity of graphene-based materials: A review. Sens. Actuat. A-Phys. 2021, 332, 113118. [Google Scholar] [CrossRef]
- Esteve-Adell, I.; Gil-Agustí, M.; Saenz, L.Z.; Quijano-López, A.; García-Pellicer, M. Grafeno: Obtención, tipos y su aplicación como sensor para detección de gases y sensor de presión. Av. Química 2020, 15, 57–72. [Google Scholar]
- Setianto, S.; Panatarani, C.; Singh, D.; Joni, M. Semi-empirical infrared spectra simulation of pyrene-like molecules insight for simple analysis of functionalization graphene quantum dots. Sci. Rep. 2023, 13, 2282. [Google Scholar] [CrossRef]
- Golovanov, V.V.; Mäki-Jaskari, M.A.; Rantala, T.T. Semi-empirical and Ab initio studies of low-temperature adsorption of oxygen and CO at (110) Face of SnO2. IEEE Sens. J. 2002, 2, 416–421. [Google Scholar] [CrossRef]
- Gómez-Jeria, J.S.; Gonzalez-Tejeda, N.; Soto-Morales, F.A. Comparison of semiempirical and AB initio methods for calculating the electronic structure of C60 and C70 fullerenes. J. Chil. Chem. Soc. 2003, 48, 85–90. [Google Scholar] [CrossRef]
- Liu, Y.; Tu, J.; Wang, C.H.; Luo, J.R.; Ding, L.P.; Wang, P.H.; Zhou, Z.M. Structure characterization of special boundaries in Fe47Mn30Co10Cr10B3 dual-phase high-entropy alloy. J. Alloys Compound. 2021, 858, 157642. [Google Scholar] [CrossRef]
- Tesch, J.; Leicht, P.; Blumenschein, F.; Gragnaniello, L.; Fonin, M.; Marsoner-Steinkasserer, L.E.; Paulus, B.; Voloshina, E.; Dedkov, Y. Structural and electronic properties of graphene nanoflakes on Au(111) and Ag(111). Sci. Rep. 2016, 6, 23439. [Google Scholar] [CrossRef]
- Min, B.J. Determination of the electric dipole moment of a molecule from plane-wave density functional theory calculations. J. Korean Phys. Soc. 2020, 76, 667–669. [Google Scholar] [CrossRef]
- Oselusi, S.O.; Dube, P.; Odugbemi, A.I.; Akinyede, K.A.; Ilori, T.L.; Egieyeh, E.; Sibuyi, N.R.S.; Meyer, M.; Madiehe, A.M.; Wyckoff, G.J.; et al. The role and potential of computer-aided drug discovery strategies in the discovery of novel antimicrobials. Comput. Biol. Med. 2024, 169, 107927. [Google Scholar] [CrossRef]
- Firdaus, R.M.; Desforges, A.; Mohamed, A.R.; Vigolo, B. Progress in adsorption capacity of nanomaterials for carbon dioxide capture: A comparative study. J. Clean. Prod. 2021, 328, 129553. [Google Scholar] [CrossRef]
- Cervantes, F.J.; Ramírez-Montoya, L.A. Immobilized nanomaterials for environmental applications. Molecules 2022, 27, 6659. [Google Scholar] [CrossRef]
- Halim, S.A.; El-Meligy, A.B.; El-Nahas, A.M.; El-Demerdash, S.H. DFT study, and natural bond orbital (NBO) population analysis of 2-(2-Hydroxyphenyl)-1-azaazulene tautomers and their mercapto analouges. Sci. Rep. 2024, 14, 219. [Google Scholar] [CrossRef]
- Idisi, D.O.; Benecha, E.M. Electronic, magnetic, and optical properties of graphene oxide nanosheets doped with Au atoms: A density functional theory study. Eur. Phys. J. Plus. 2022, 137, 820. [Google Scholar] [CrossRef]
- Alves, T.; Mota, W.S.; Barros, C.; Almeida, D.; Komatsu, D.; Zielinska, A.; Cardoso, J.C.; Severino, P.; Souto, E.B.; Chaud, M.V. Review of scientific literature and standard guidelines for the characterization of graphene-based materials. J. Mater. Sci. 2024, 59, 14948–14980. [Google Scholar] [CrossRef]
- Das, A.; Chakraborty, B.; Sood, A.K. Raman spectroscopy of graphene on different substrates and influence of defects. Bull. Mater. Sci. 2008, 31, 579–584. [Google Scholar] [CrossRef]
- Zhu, Y.; Murali, S.; Cai, W.; Li, X.; Suk, J.W.; Potts, J.R.; Ruoff, R.S. Graphene and graphene oxide: Synthesis, properties, and applications. Adv. Mater. 2010, 22, 3906–3924. [Google Scholar] [CrossRef] [PubMed]
- Eda, G.; Fanchini, G.; Chhowalla, M. Large-area ultrathin films of reduced graphene oxide as a transparent and flexible electronic material. Nat. Nanotech. 2008, 3, 270–274. [Google Scholar] [CrossRef]
- Liang, H.F.; Smith, C.T.G.; Mills, C.A.; Silva, S.R.P. The band structure of graphene oxide examined using photoluminescence spectroscopy. J. Mater. Chem. C 2015, 3, 12484–12491. [Google Scholar] [CrossRef]
- Otsuka, H.; Urita, K.; Honma, N.; Honma, N.; Kimuro, T.; Amako, Y.; Kukobat, R.; Bandosz, T.J.; Ukai, J.; Moriguchi, I.; et al. Transient chemical and structural changes in graphene oxide during ripening. Nat. Commun. 2024, 15, 1708. [Google Scholar] [CrossRef]
- Abdolkarimi-Mahabadi, M.; Bayat, A.; Mohammadi, A. Use of UV-Vis spectrophotometry for characterization of carbon nanostructures: A review. Theor. Exp. Chem. 2021, 57, 191–198. [Google Scholar] [CrossRef]
- Ahmad, N.J.; Mohamed, R.; Malek, M.F.; Ikhsan, N.I.; Rusop, M. Ultrasonic-Assisted exfoliation of pristine graphite into few layers of graphene sheets using NH3 as intercalation agent. Mater. Sci. Forum. 2022, 1055, 111–121. [Google Scholar] [CrossRef]
- Syaahiran, M.A.; Mahadi, A.H.; Lim, C.M.; Kooh, M.R.; Chau, Y.C.; Chiang, H.P.; Thotagamuge, R. Theoretical study of CO adsorption interactions with Cr-doped tungsten oxide/graphene composites for gas sensor application. ACS Omega 2021, 7, 528. [Google Scholar] [CrossRef] [PubMed]
- Feng, J.; Dong, H.; Yu, L.; Dong, L. The optical and electronic properties of graphene quantum dots with oxygen-containing groups: A density functional theory study. J. Mater. Chem. C 2017, 5, 5984–5993. [Google Scholar] [CrossRef]
- AlJaber, G.; AlShammari, B.; AlOtaibi, B. From Theory to Experiment: Reviewing the role of graphene in li-ion batteries through density functional theory. Nanomaterials 2025, 15, 992. [Google Scholar] [CrossRef]
- Gómez, E.V.; Ramírez-Guarnizo, N.A.; Perea, J.D.; Sánchez-López, A.; Prías-Barragán, J.J. Exploring molecular and electronic property predictions of reduced graphene oxide nanoflakes via density functional theory. ACS Omega 2022, 7, 3872–3880. [Google Scholar] [CrossRef]
- Kishnani, V.; Yadav, A.; Mondal, K.; Gupta, A. Palladium-Functionalized graphene for hydrogen sensing performance: Theoretical studies. Energies 2021, 14, 5738. [Google Scholar] [CrossRef]
- Hwang, C.; Siegel, D.; Mo, S.K.; Regan, W.; Ismach, A.; Zhang, Y.; Zettl, A.; Lanzara, A. Fermi velocity engineering in graphene by substrate modification. Sci. Rep. 2012, 2, 590. [Google Scholar] [CrossRef]
- Dimakis, N.; Salas, I.; Gonzalez, L.; Vadodaria, O.; Ruiz, K.; Bhatti, M.I. Li and Na Adsorption on graphene and graphene oxide examined by density functional theory, quantum theory of atoms in molecules, and electron localization function. Molecules 2019, 24, 754. [Google Scholar] [CrossRef]
- Singh, R.K.; Nalajala, N.; Kar, T.; Schechter, A. Functionalization of graphene—A critical overview of its improved physical, chemical and electrochemical properties. In Surface Engineering of Graphene. Carbon Nanostructures; Sahoo, S., Tiwari, S., Nayak, G., Eds.; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Huang, Y.; Rong, C.; Zhang, R.; Liu, S. Evaluating frontier orbital energy and HOMO/LUMO gap with descriptors from density functional reactivity theory. J. Mol. Model. 2017, 23, 3. [Google Scholar] [CrossRef]
- Luo, D.; Zhang, X.; Chen, H. Stabilized Li-decoration and enhanced hydrogen storage on reduced graphene oxides. Int. J. Hydrogen Energy 2019, 44, 31192–31203. [Google Scholar] [CrossRef]
- Colson, M.; Alvarez, L.; Soto, S.M.; Joo, S.H.; Li, K.; Lupini, A.; Nawaz, K.; Fomunung, I.; Onyango, M.A.; Danquah, M.K.; et al. A novel sustainable process for multilayer graphene synthesis using CO2 from ambient air. Materials 2022, 15, 5894. [Google Scholar] [CrossRef] [PubMed]
- Thuong, N.T.; Quang, L.D.; Cuong, V.Q.; Ha, C.H.; Lam, N.B.; Kawahara, S. Modification of graphene oxide and its effect on properties of natural rubber/graphene oxide nanocomposites. Beilstein J. Nanotech. 2024, 15, 168–179. [Google Scholar] [CrossRef]
- Gholizadeh, A.; Babaei, A.; Abdolrasouli, M.H. Synthesis and characterization of a large-quantity of functionalized graphene from graphite by a facile bubble-exfoliation method. Nano-Struct. Nano-Objects 2023, 35, 101011. [Google Scholar] [CrossRef]
- Fauziyah, N.A.; Kristanti, D.A.; Kusumaningtyas, P.C.; Wardhani, P.C.; Tola, P.S.; Fadly, T.A. Analysis of carbon functional groups through FTIR patterns in the preparation of reduced graphene oxide (RGO). Rom. J. Appl. Sci. Technol. 2023, 16, 374–376. [Google Scholar] [CrossRef]
- Sacristan, E. El Magnetismo del Grafeno se Puede Controlar con Átomos de Hidrógeno. 2017. Available online: https://www.agenciasinc.es/Entrevistas/El-magnetismo-del-grafeno-se-puede-controlar-con-atomos-de-hidrogeno (accessed on 15 March 2025).
- Ma, Z. Preparation of graphene and its application in lithium batteries. J. Phys. Conf. Ser. 2009, 2009, e012065. [Google Scholar] [CrossRef]
- Chen, W.; Yan, L. Preparation of graphene by a low-temperature thermal reduction at atmosphere pressure. Nanoscale 2010, 2, 559–563. [Google Scholar] [CrossRef]
- Faniyi, O.; Fasakin, O.; Olofinjana, B. The comparative analyses of reduced graphene oxide (RGO) prepared via green, mild and chemical approaches. SN Appl. Sci. 2019, 1, e1181. [Google Scholar] [CrossRef]
- Surekha, G.; Krishnaiah, K.V.; Ravi, N.; Suvarna, R.P. FTIR, Raman and XRD analysis of graphene oxide films prepared by modified Hummers method. J. Phys. Conf. Ser. 2020, 1495, e012012. [Google Scholar] [CrossRef]
- Lai, Q.; Zhu, S.; Luo, X.; Zou, M.; Huang, S. Ultraviolet-visible spectroscopy of graphene oxides. AIP Adv. 2012, 2, 032146. [Google Scholar] [CrossRef]
- Jin, Y.; Zheng, Y.; Podkolzin, S.G.; Lee, W. Band gap of reduced graphene oxide tuned by controlling functional groups. J. Mater. Chem. C 2020, 8, 4885–4894. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, P.; Zhu, X. Li decorated penta-silicene as a high capacity hydrogen storage material: A density functional theory study. Int. J. Hydrogen Energy 2021, 46, 4188–4200. [Google Scholar] [CrossRef]
- Melideo, D.; Desideri, U. The use of hydrogen as alternative fuel for ship propulsion: A case study of full and partial retrofitting of roll-on/roll-off vessels for short distance routes. Int. J. Hydrogen Energy 2024, 50, 1045–1055. [Google Scholar] [CrossRef]
- Riesen, H.; Wiebeler, C.; Schumacher, S. Optical spectroscopy of graphene quantum dots: The case of C132. Phys. Chem. A 2014, 118, 5189–5195. [Google Scholar] [CrossRef]
- Özönder, S.; Ünlü, C.; Güleryüz, C.; Trabzon, L. Doped graphene quantum dots UV–vis absorption spectrum: A high-throughput TDDFT study. CS Omega 2023, 8, 2112–2118. [Google Scholar] [CrossRef]
- Wu, J.B.; Lin, M.L.; Cong, X.; Liu, H.N.; Tan, P.H. Raman spectroscopy of graphene-based materials and its applications in related devices. Chem. Soc. Rev. 2018, 47, 1822–1873. [Google Scholar] [CrossRef]
- Georgakilas, V.; Otyepka, M.; Bourlinos, A.B.; Chandra, V.; Kim, N.; Kemp, K.C.; Hobza, P.; Zboril, R.; Kim, K.S. Functionalization of graphene: Covalent and non-covalent approaches, derivatives and applications. Chem. Rev. 2012, 112, 6156–6214. [Google Scholar] [CrossRef]
- Tene, T.; Guevara, M.; Benalcázar-Palacios, F.; Morocho-Barrionuevo, T.P.; Vacacela-Gomez, C.; Bellucci, S. Optical properties of graphene oxide. Front. Chem. 2023, 11, 1214072. [Google Scholar] [CrossRef]
- Mombeshora, E.T.; Muchuweni, E. Dynamics of reduced graphene oxide: Synthesis and structural models. RSC Adv. 2023, 13, 17633–17655. [Google Scholar] [CrossRef] [PubMed]
- Rangel, E.; Ramírez-Arellano, J.M.; Carrillo, I.; Magana, L.F. Hydrogen adsorption around lithium atoms anchored on graphene vacancies. Int. J. Hydrogen Energy 2011, 36, 13657–13662. [Google Scholar] [CrossRef]
- Prasad, G.; Tamang, S.; Jha, S.; Bhattacharyya, N.K.; Biswas, J. A theoretical insight into graphene-based materials: A DFT study. Results Surf. Interfaces 2025, 18, 100463. [Google Scholar] [CrossRef]
- Spyrou, K.; Gournis, D.; Rudolf, P. Hydrogen storage in graphene-based materials: Efforts towards enhanced hydrogen absorption. ECS J. Solid State Sci. Technol. 2013, 2, M3160. [Google Scholar] [CrossRef]
- Sainio, S.; Niklas, W.; Anja, A.; Titus, C.J.; Nordlund, D.; Kauppinen, E.I.; Leppänen, E.; Palomäki, T.; Koehne, J.E.; Pitkänen, O.; et al. Trends in carbon, oxygen, and nitrogen core in the X-ray absorption spectroscopy of carbon nanomaterials: A guide for the Perplexed. J. Phys. Chem. C 2021, 125, 973–988. [Google Scholar] [CrossRef]
- Zhou, J.; Dong, J. Vibrational property and Raman spectrum of carbon nanoribbon. Appl. Phys. Lett. 2007, 91, 173108. [Google Scholar] [CrossRef]
- Chadha, N.; Sharma, R.; Saini, P. A new insight into the structural modulation of graphene oxide upon chemical reduction probed by Raman spectroscopy and X-ray diffraction. Carbon Lett. 2021, 31, 1125–1131. [Google Scholar] [CrossRef]
- Rimza, T.; Saha, S.; Dhand, C.; Dwivedi, N.; Patel, S.S.; Singh, S.; Kumar, P. Carbon-based sorbents for hydrogen storage: Challenges and sustainability at operating conditions for renewable energy. Chem. Sus. Chem. 2022, 15, e202200281. [Google Scholar] [CrossRef]
- Gao, Y.; Li, Z.; Wang, P.; Li, C.; Yue, Q.; Cui, W.G.; Wang, X.; Yang, Y.; Gao, F.; Zhang, M.; et al. Solid-State Hydrogen Storage origin and design principles of carbon-based light metal single-atom materials. Adv. Funct. Mater. 2024, 34, 2316368. [Google Scholar] [CrossRef]
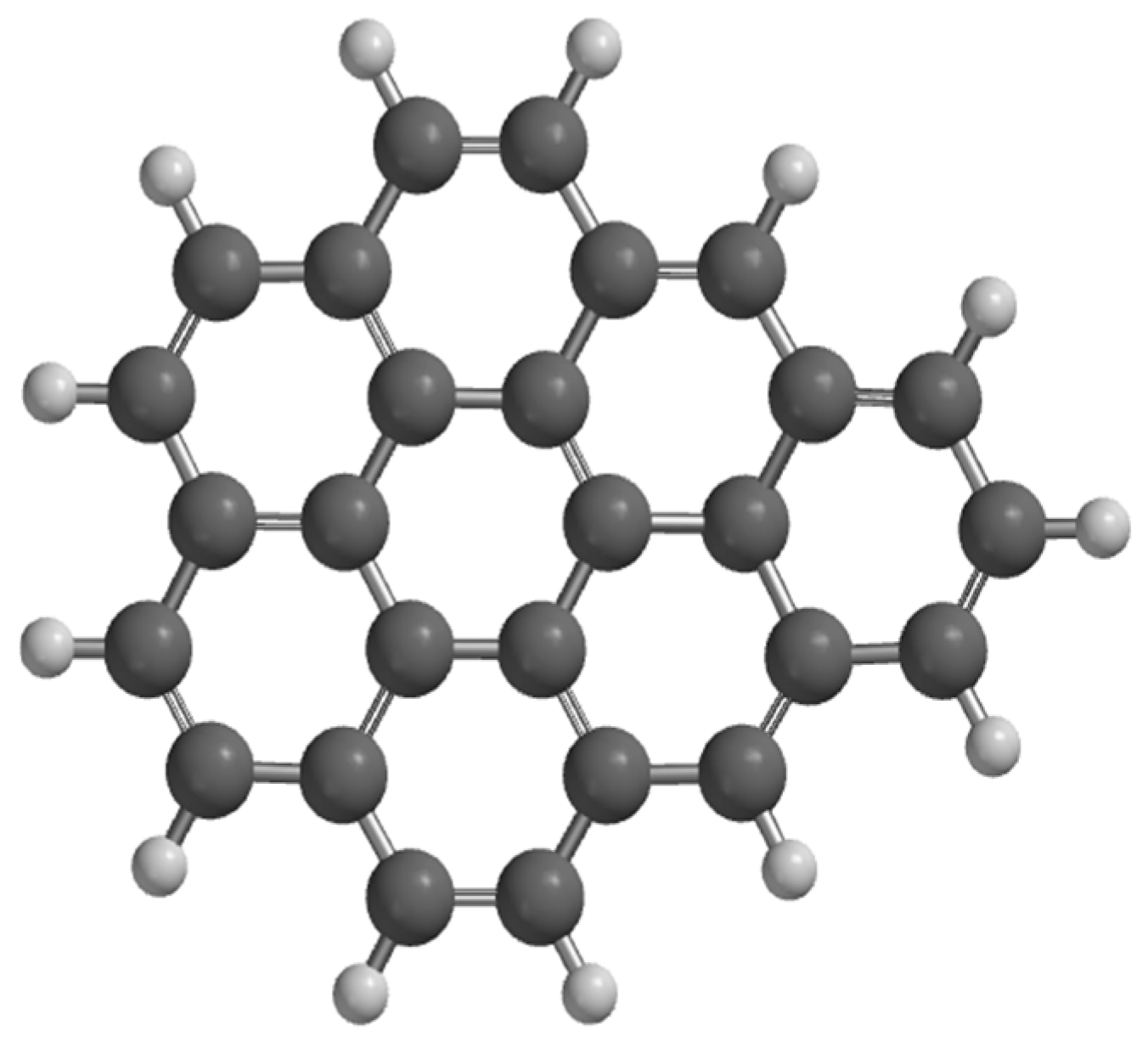
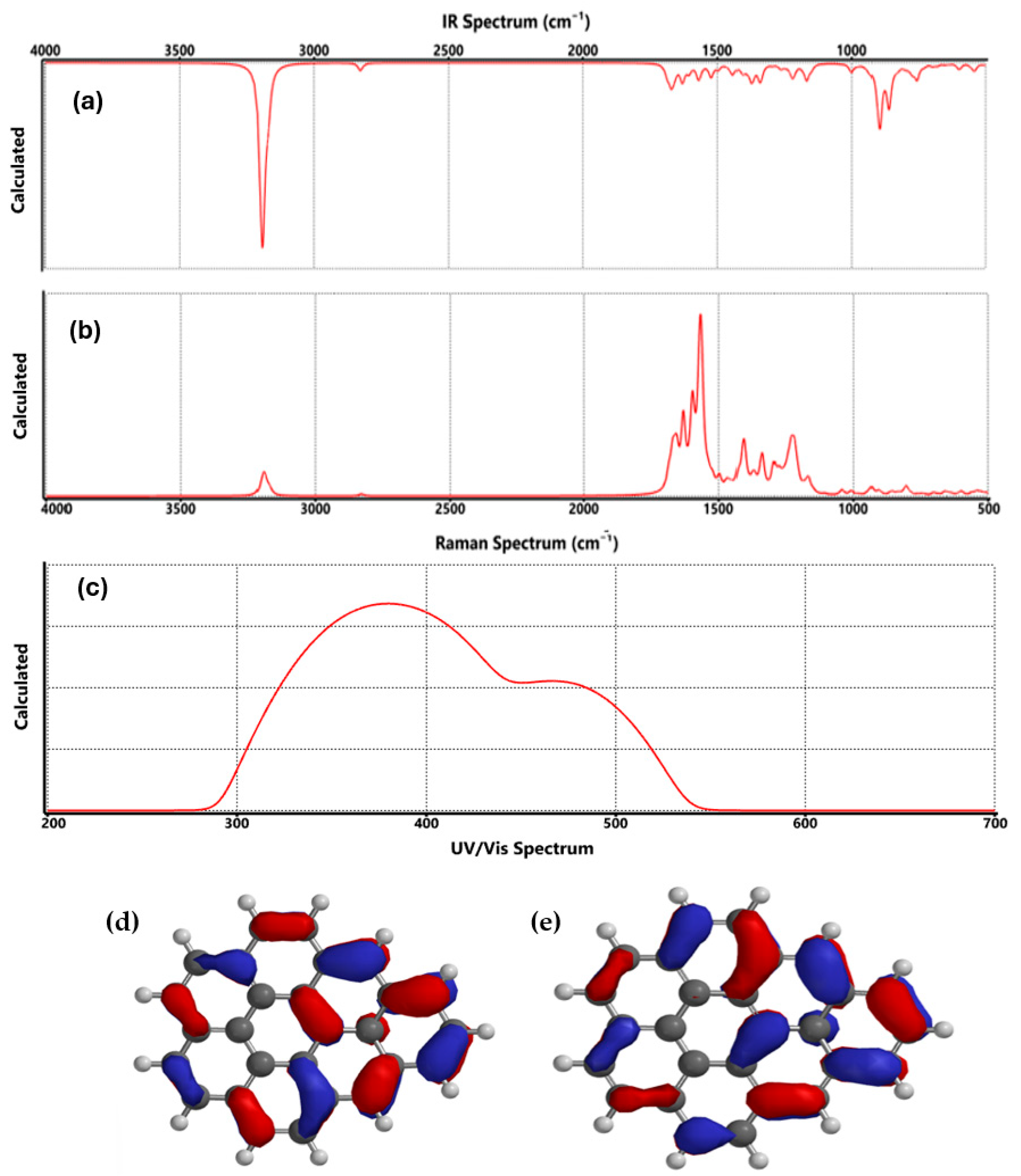
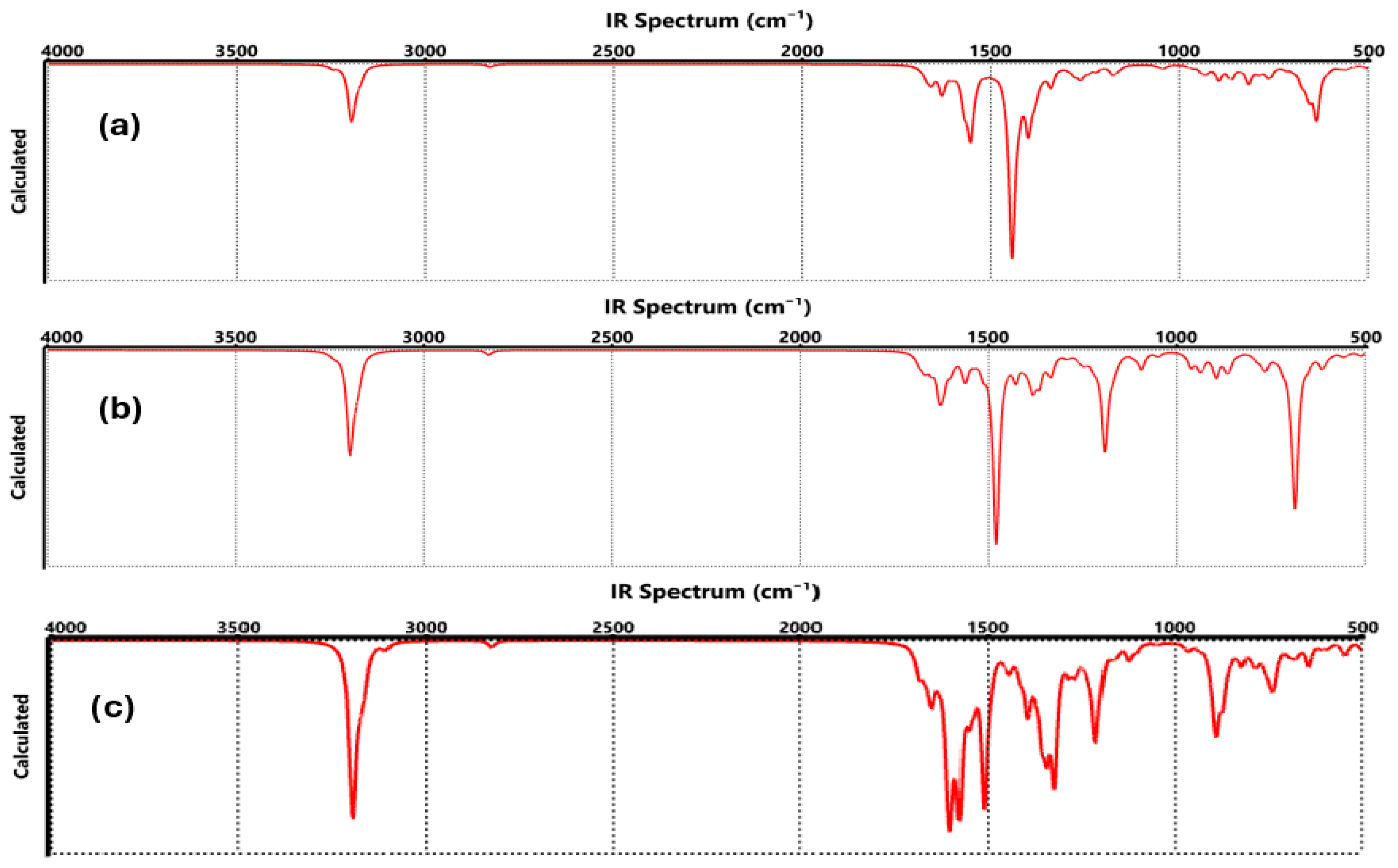
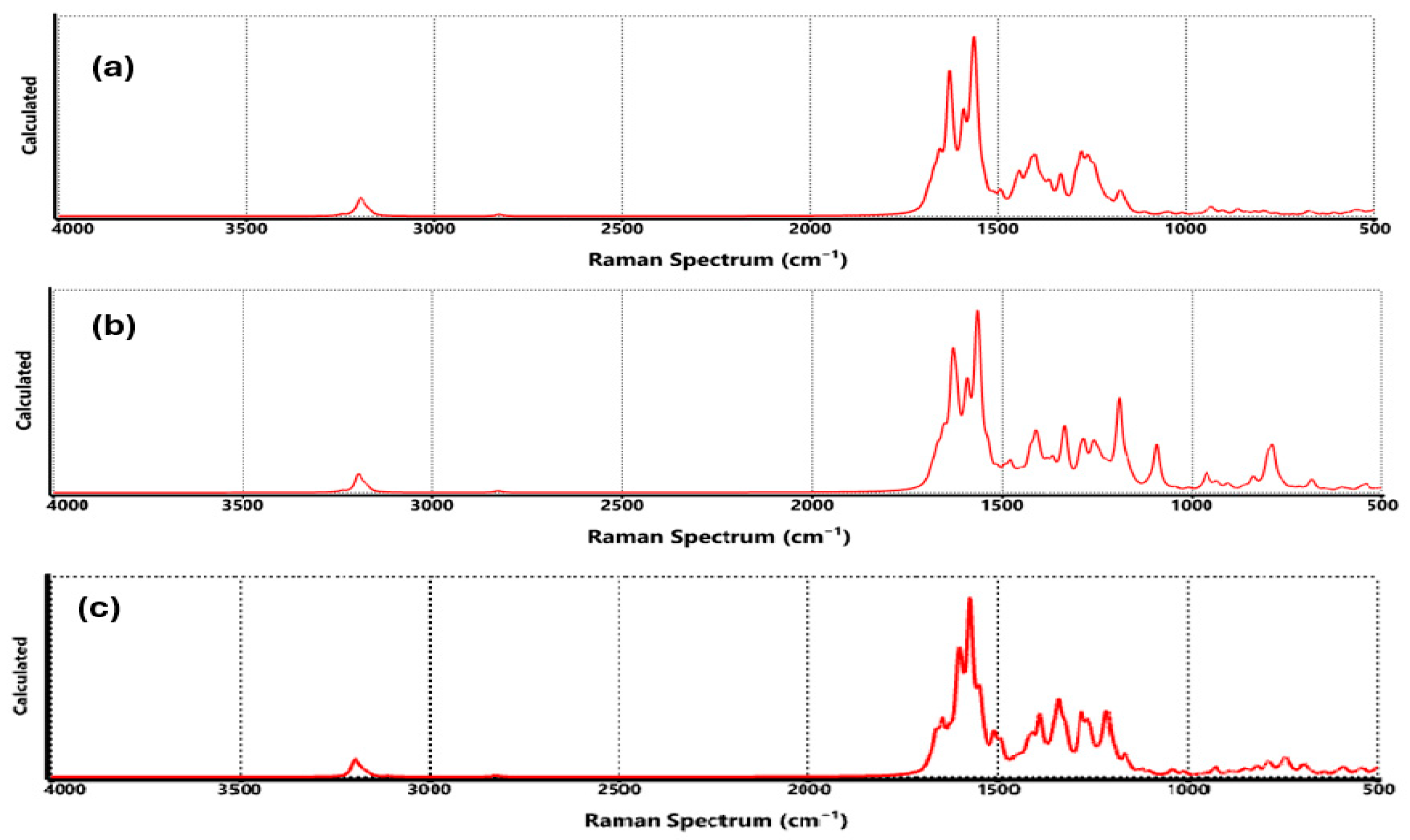
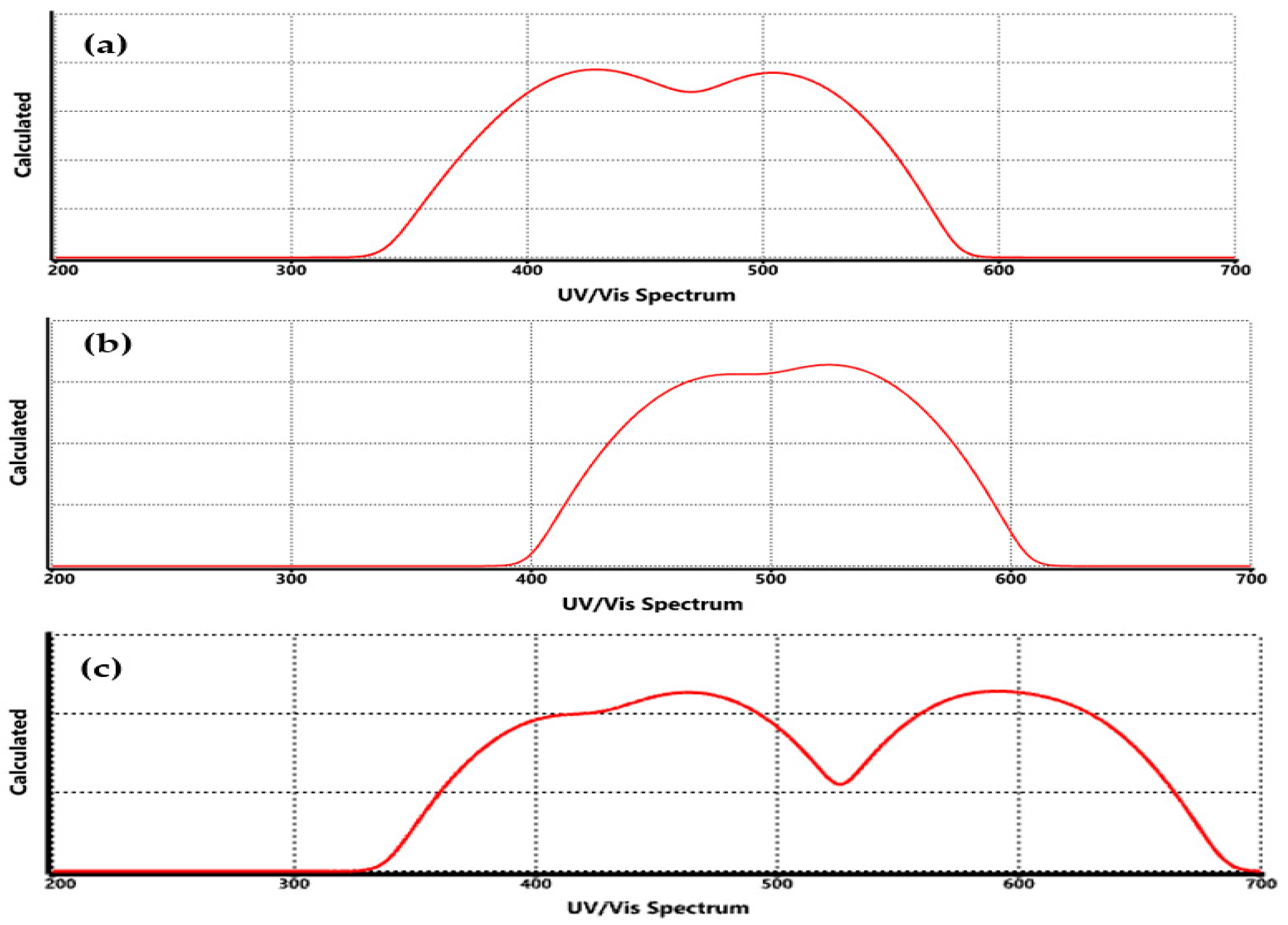
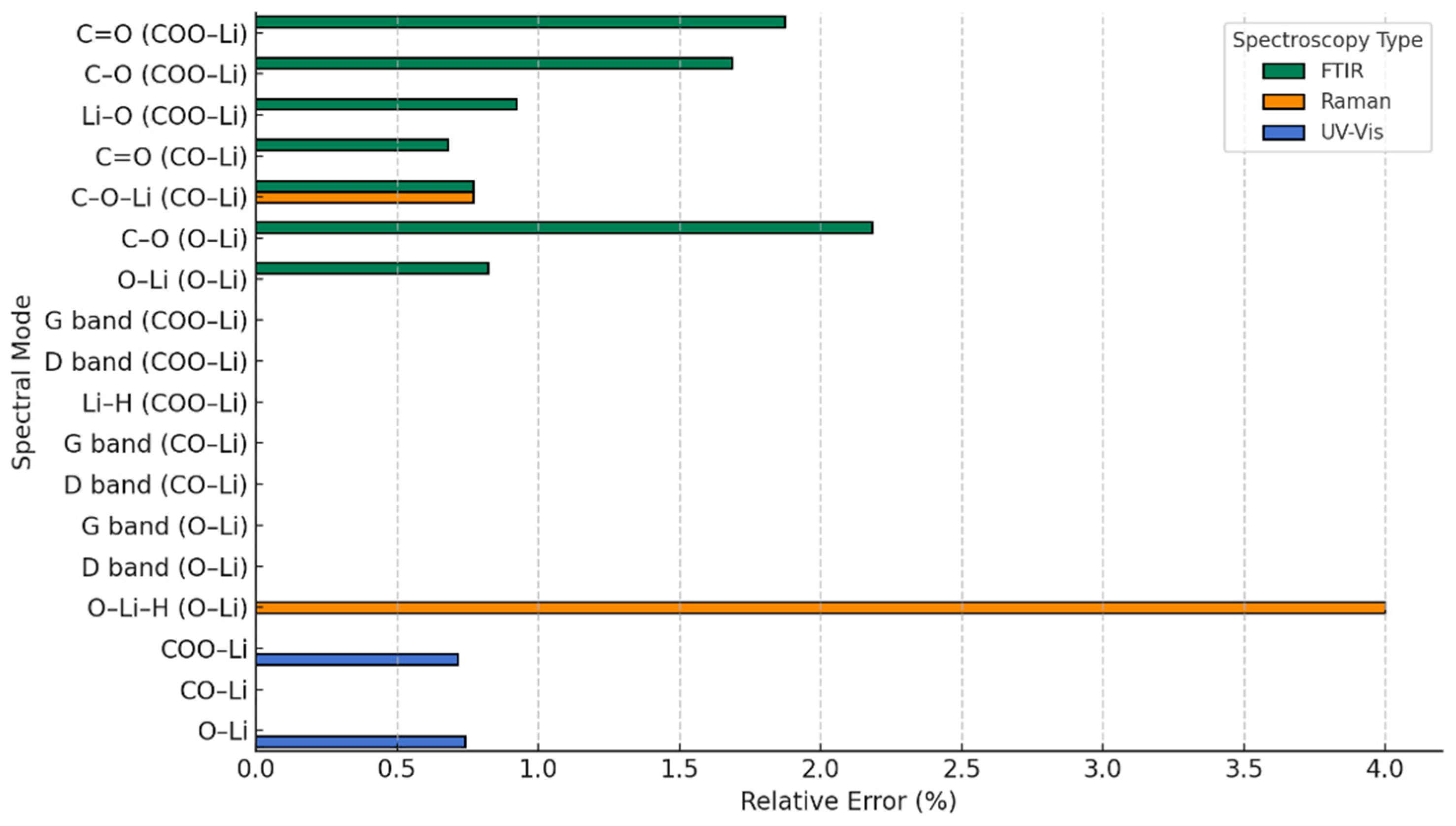
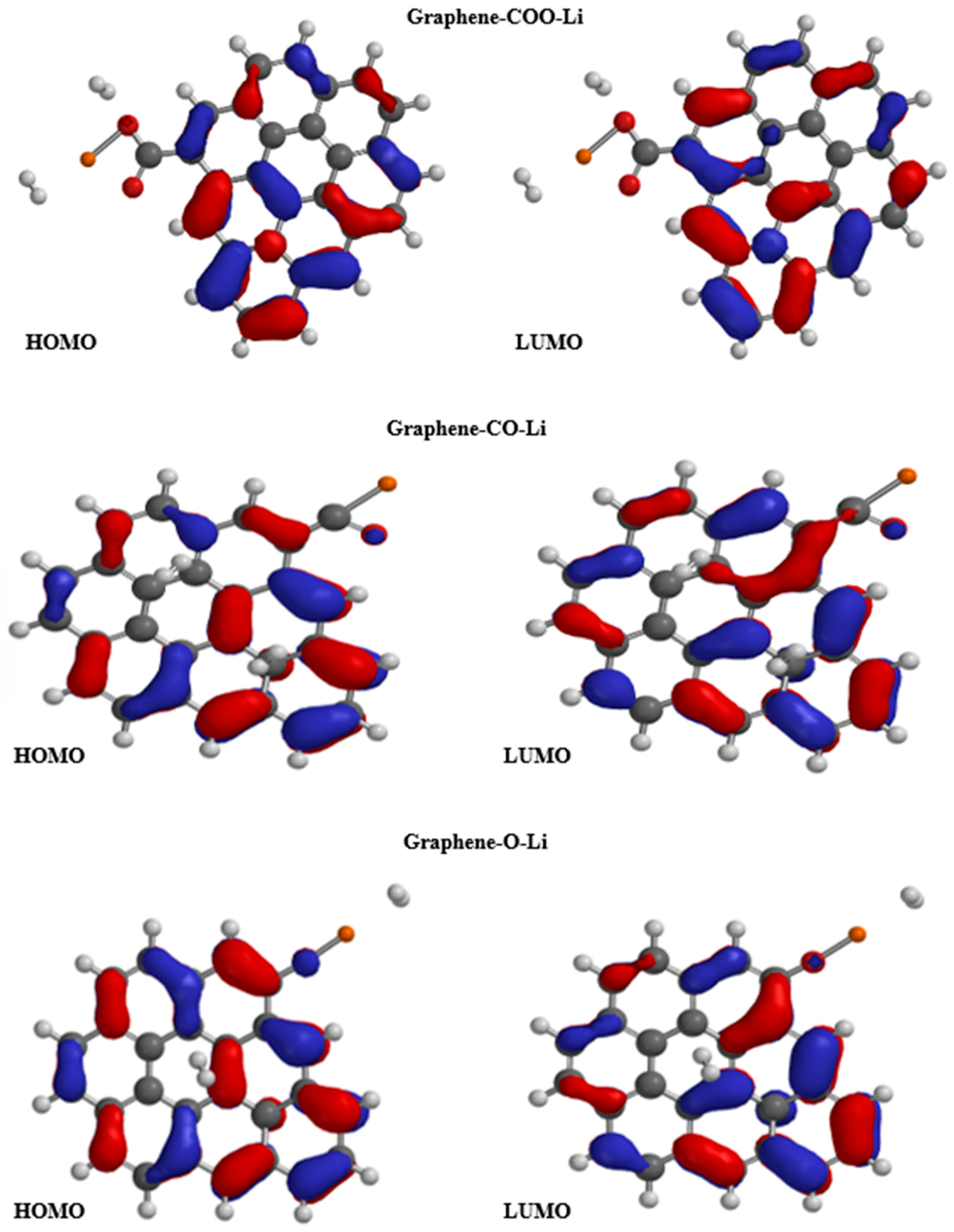
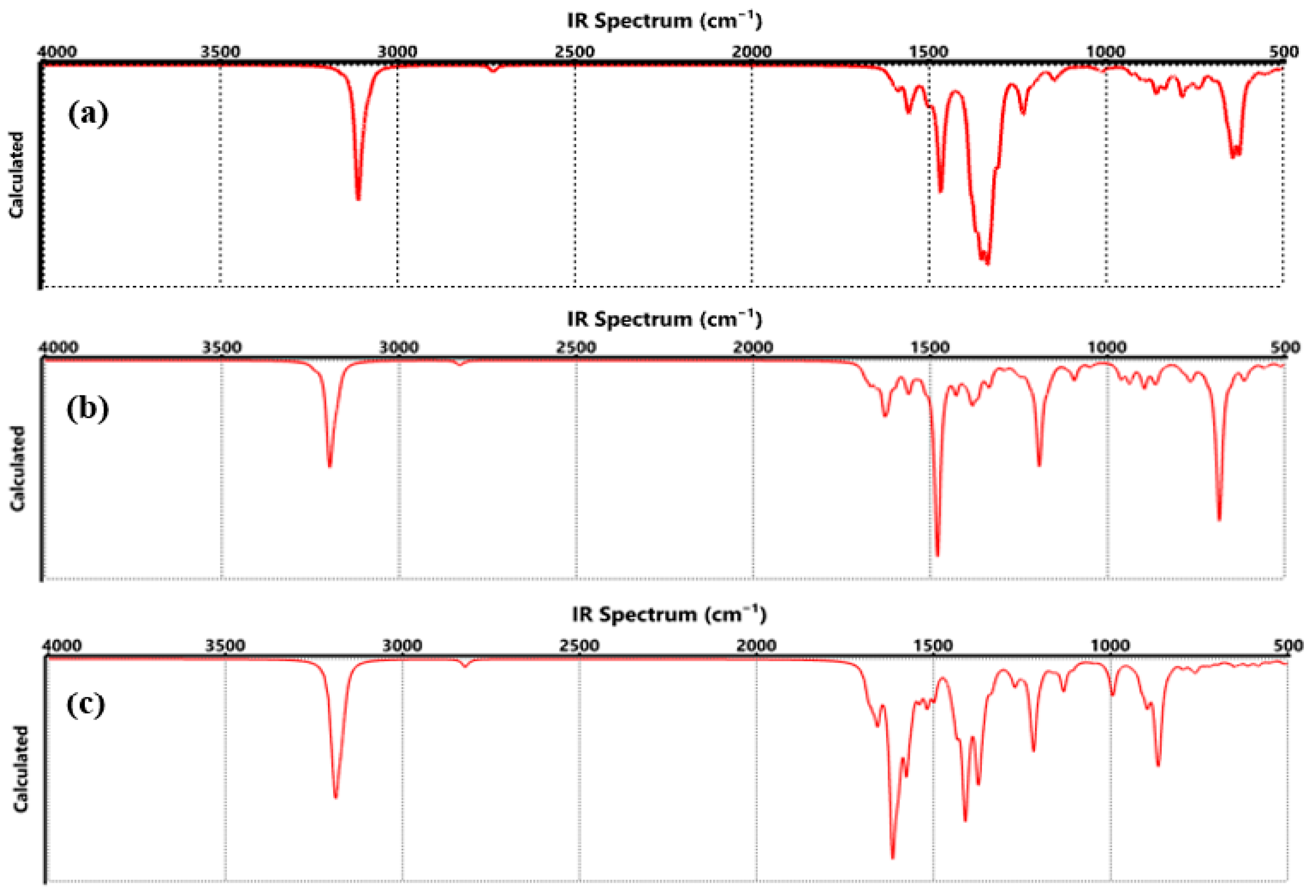
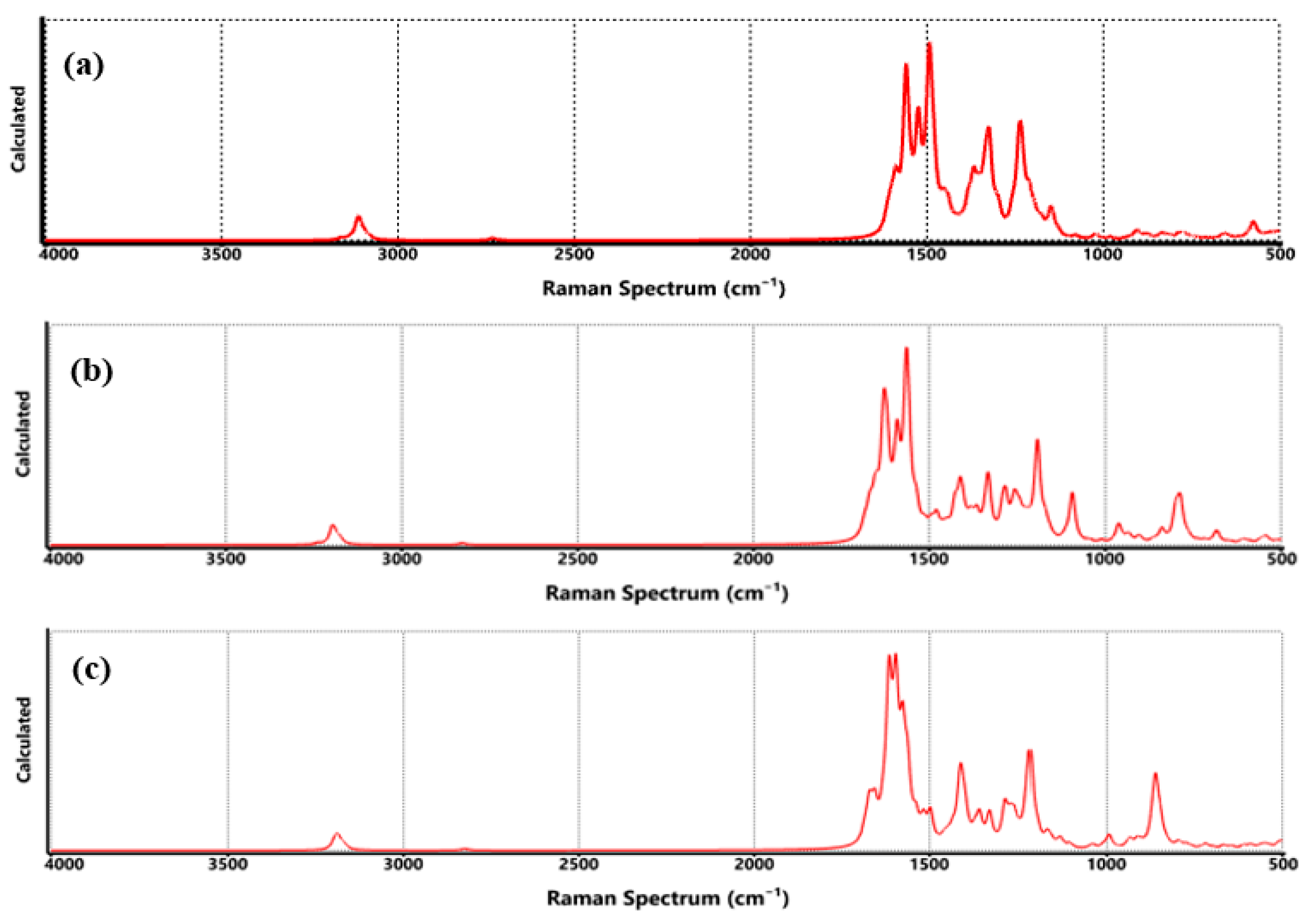
| Technique | Values (This Paper) | Experimental Values | Reference |
|---|---|---|---|
| FTIR |
|
| [25] |
| Raman |
| G band: ~1580 cm−1 (E2g mode)
| [18,19] |
| UV-Vis |
| π→π* transition at ~270 nm
| [20] |
| Property/Sample | Graphene-COO-Li | Graphene-CO-Li | Graphene-O-Li |
|---|---|---|---|
| Δ Gibbs free energy (au) | −1233 | −1157 | −1119 |
| ΔS (J/mol°) | 547 | 537 | 526 |
| Dipole moment (Debye) | 3.66 | 3.47 | 4.83 |
| E LUMO (eV) | −2.49 | −2.49 | −2.61 |
| E HOMO (eV) | −4.01 | −4.02 | −4 |
| Band gap (eV) | 1.52 | 1.53 | 1.39 |
| Area (Å2) | 352 | 346 | 332 |
| Volume (Å3) | 376 | 370 | 356 |
| Technique | System | Theoretical Values (This Study) | Experimental Values (Literature) | Reference |
|---|---|---|---|---|
| FTIR | COO-Li | C=O: 1630, 1554, 1444 cm−1 C-O: 816 cm−1 Li-O: 656–635 cm−1 | C=O: ~1650–1550 cm−1 C–O: ~800–850 cm−1 Li–O: ~650 cm−1 | [27] |
| FTIR | CO-Li | C=O: 1480 cm−1 C-O-Li: 698–611 cm−1 | C=O: ~1450–1500 cm−1 Li-O: ~600–700 cm−1 | [35] |
| FTIR | O-Li | C-O: 1124 cm−1 O-Li: 736 cm−1 | C-O: ~1100–1150 cm−1 Li-O: ~730–750 cm−1 | [47] |
| Raman | COO-Li | G: ~1580 cm−1 D: ~1350 cm−1 Li-H: 500–700 cm−1 | G: ~1580 cm−1 D: ~1350 cm−1 Li-H: ~550–650 cm−1 | [46] |
| Raman | CO-Li | G: ~1580 cm−1 D: ~1350 cm−1 C-O-Li: ~600–700 cm−1 | G: ~1580 cm−1 D: ~1350 cm−1 Li-O: ~620–680 cm−1 | [48] |
| Raman | O-Li | G: ~1580 cm−1 D: ~1350 cm−1 O-Li-H: ~500–700 cm−1 | G: ~1580 cm−1 D: ~1350 cm−1 Li-O-H: ~550–700 cm−1 | [49] |
| UV-Vis | COO-Li | Redshift to 278–285 nm (π→π*) | 275–285 nm (π→π*) in carboxylate systems | [27] |
| UV-Vis | CO-Li | Moderate redshift (~275 nm) | 270–280 nm | [24] |
| UV-Vis | O-Li | Slight redshift (~270–275 nm) | 268–275 nm | [35] |
| Property/Sample | Graphene-COO-Li | Graphene-CO-Li | Graphene-O-Li |
|---|---|---|---|
| Gibbs free energy change (au) | −1269 | −1204 | −1175 |
| Dipole moment (Debye) | 3.74 | 3.48 | 9.68 |
| E LUMO (ev) | −2.83 | −2.48 | −2.10 |
| E HOMO (eV) | −3.30 | −4.02 | −3.59 |
| Band gap (eV) | 0.47 | 1.54 | 1.49 |
| Area (Å2) | 400 | 393 | 380 |
| Volume (Å3) | 401 | 391 | 377 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rangel-Vázquez, N.A.; Bonilla-Petriciolet, A.; Márquez-Brazón, E.A.; Huerta, Y.; Zavala-Arce, R.; Rodríguez-Macías, J.D. DFT-Based Functionalization of Graphene with Lithium-Modified Groups for Enhanced Hydrogen Detection: Thermodynamic, Electronic, and Spectroscopic Properties. Nanomaterials 2025, 15, 1234. https://doi.org/10.3390/nano15161234
Rangel-Vázquez NA, Bonilla-Petriciolet A, Márquez-Brazón EA, Huerta Y, Zavala-Arce R, Rodríguez-Macías JD. DFT-Based Functionalization of Graphene with Lithium-Modified Groups for Enhanced Hydrogen Detection: Thermodynamic, Electronic, and Spectroscopic Properties. Nanomaterials. 2025; 15(16):1234. https://doi.org/10.3390/nano15161234
Chicago/Turabian StyleRangel-Vázquez, Norma A., Adrián Bonilla-Petriciolet, Edgar A. Márquez-Brazón, Yectli Huerta, Rosa Zavala-Arce, and Juan D. Rodríguez-Macías. 2025. "DFT-Based Functionalization of Graphene with Lithium-Modified Groups for Enhanced Hydrogen Detection: Thermodynamic, Electronic, and Spectroscopic Properties" Nanomaterials 15, no. 16: 1234. https://doi.org/10.3390/nano15161234
APA StyleRangel-Vázquez, N. A., Bonilla-Petriciolet, A., Márquez-Brazón, E. A., Huerta, Y., Zavala-Arce, R., & Rodríguez-Macías, J. D. (2025). DFT-Based Functionalization of Graphene with Lithium-Modified Groups for Enhanced Hydrogen Detection: Thermodynamic, Electronic, and Spectroscopic Properties. Nanomaterials, 15(16), 1234. https://doi.org/10.3390/nano15161234









