Structural Stability, Mechanical, and Electronic Properties of Al5TM (TM = Mo, Nb, Os, Re, Ru, Ta, Tc, Ti) Intermetallics
Abstract
1. Introduction
2. Structural and Computational Information
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- King, D.J.M.; Knowles, A.J.; Bowden, D.; Wenman, M.R.; Capp, S.; Gorley, M.; Shimwell, J.; Packer, L.; Gilbert, M.R.; Harte, A. High temperature zirconium alloys for fusion energy. J. Nucl. Mater. 2022, 559, 153431. [Google Scholar] [CrossRef]
- Zhang, W.; Qian, Y.; Sun, R.; Lin, X.; Yao, M.; Qiu, Y.; Yang, J.; Cheng, G.G.; Dong, J.X. Oxidation characteristics of Fe22Cr5Al3Mo-xNb alloys in high temperature steam. Corros. Sci. 2021, 191, 109722. [Google Scholar] [CrossRef]
- Liu, B.; Li, G.; Xiao, X.; Lu, S.; Peng, P. Alloying effect on the mechanical properties of Laves phase NbCr2: A first-principles study. Comput. Mater. Sci. 2023, 218, 111949. [Google Scholar] [CrossRef]
- Pan, Y.; Pu, D. The structural, mechanical, and thermodynamic properties of B2-type TMZr (TM = Ru, Mo, Rh, Os, and Re) compounds from first-principles calculations. Int. J. Quantum Chem. 2019, 119, e26015. [Google Scholar] [CrossRef]
- Liu, Y.; Qu, N.; Zhao, X.; Chen, J.; Zhu, J.; Lai, Z. Stability of FeCrNiTiAl high-entropy alloy at high temperature. Heat Treat. Surf. Eng. 2021, 3, 29–36. [Google Scholar] [CrossRef]
- Bai, Y.; Sun, D.; Li, N.; Kong, F.; Qi, X.; He, X.; Wang, R.; Zheng, Y. High-temperature mechanical properties and thermal shock behavior of ternary-layered MAB phases Fe2AlB2. Int. J. Refract. Met. Hard Mater. 2019, 80, 151–160. [Google Scholar] [CrossRef]
- Ning, W.; Zhai, H.; Xiao, R.; He, D.; Liang, G.; Wu, Y.; Li, W.; Li, X. The corrosion resistance mechanism of Fe-based amorphous coatings synthesised by detonation gun spraying. J. Mater. Eng. Perform. 2020, 29, 3921. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.; Shang, L.; Bai, G.; Li, J.; Xue, F.; Gong, W. Fiber texture-dependent oxidation behaviour of Cr-coated zirconium alloy in high temperature steam. Corros. Sci. 2022, 205, 110449. [Google Scholar] [CrossRef]
- Chen, X.; Liao, D.; Jiang, X.; Zhang, D.; Shi, T. Effect of tungsten doping on the performance of MAO coatings on a Ti6Al4V drill pipe. Surf. Innov. 2020, 8, 279–286. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Y.; Liang, Z.; Bai, P.; Nie, J.; Liu, S.; Chen, B.; Wei, S.; Guan, Q.; Cai, J. Continuous hot corrosion behaviour of an FeCrAlSi coating prepared by laser cladding. Surf. Coat. Technol. 2021, 421, 127424. [Google Scholar] [CrossRef]
- Gussev, M.N.; Field, K.G.; Yamamoto, Y. Design, properties, and weldability of advanced oxidation-resistant FeCrAl alloys. Mater. Des. 2017, 129, 227–238. [Google Scholar] [CrossRef]
- Li, J.; Xu, Y.; Xiao, W.; Ma, C.; Huang, X. Development of Ti–Al–Ta–Nb–(Re) near-α high temperature titanium alloy: Microstructure, thermal stability and mechanical properties. J. Mater. Sci. Technol. 2022, 109, 1–11. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, X.; Wang, F. The electronic, mechanical, anisotropic and thermodynamic properties of ZrAlNi, ZrAlNi2, ZrAl5Ni2 and Zr6Al2Ni ternary intermetallics. Vacuum 2024, 226, 113260. [Google Scholar] [CrossRef]
- Pan, Y.; Wang, P. First-principles investigation of the novel structure, elastic and thermodynamic properties of IrAl3 coating. Mol. Simul. 2019, 45, 1058–1065. [Google Scholar] [CrossRef]
- Duan, Y.; Huang, B.; Sun, Y.; Peng, M.; Zhou, S. Stability, elastic properties and electronic structures of the stable Zr–Al intermetallic compounds: A first-principles investigation. J. Alloys Compd. 2014, 590, 50–60. [Google Scholar] [CrossRef]
- Huang, S.; Dolley, E.; An, K.; Yu, D.; Crawford, C.; Othon, M.A.; Spinelli, I.; Knussman, M.P.; Rebak, R.B. Microstructure and tensile behavior of powder metallurgy FeCrAl accident tolerant fuel cladding. J. Nucl. Mater. 2022, 560, 153524. [Google Scholar] [CrossRef]
- Wang, R.; Zeng, S.; Wang, X.; Ni, J. Machine learning for hierarchical prediction of elastic properties in Fe–Cr–Al system. Comput. Mater. Sci. 2019, 166, 119–123. [Google Scholar] [CrossRef]
- Pan, Y. Exploring the phase stability, mechanical and thermodynamic properties of FeCrAl ternary alloy. J. Mater. Res. Technol. 2023, 26, 8813–8821. [Google Scholar] [CrossRef]
- Guo, S.; Wang, F.; Wang, Y.; Xie, G. Microstructural evolution and properties of Ti/Al clad plate fabricated by vacuum rolling and heat treatment. Mater. Sci. Eng. A 2023, 882, 145445. [Google Scholar] [CrossRef]
- Cao, L.; Zhang, X.; Wang, F. Structural, elastic, anisotropic, electronic, thermal properties and tensile strength of AlTM2Ti (TM = Ni, Fe, Cu, Co, Au) studied by first-principles calculations. Chem. Phys. Lett. 2023, 830, 140796. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, T.; He, Y.; Shang, J.; Wang, K.; Wu, H.; Fan, G. Fabrication and microstructure evolution of novel laminated TiAl composite. Mater. Charact. 2022, 194, 112446. [Google Scholar] [CrossRef]
- Hu, A.; Cai, S. Research on the novel Al–W alloy powder with high volumetric combustion enthalpy. J. Mater. Res. Technol. 2021, 13, 311–320. [Google Scholar] [CrossRef]
- Wang, C.; Liang, S.; Jiang, Y. In-situ fabrication and characteristics of an Al4W/Al12W composite using infiltration method. Vacuum 2019, 160, 95–101. [Google Scholar] [CrossRef]
- Wang, C.; Liang, S.; Cui, J.; Wang, X.; Wei, Y. First-principles study of the mechanical and thermodynamic properties of Al4W, Al5W and Al12W under pressure. Vacuum 2019, 169, 108844. [Google Scholar] [CrossRef]
- Pan, Y. First-principles investigation of the structural, mechanical, and thermodynamic properties of hexagonal and cubic MoAl5 alloy. J. Mater. Eng. Perform. 2021, 30, 8289–8295. [Google Scholar] [CrossRef]
- Wang, M.; Chen, Z.; Xia, C.; Wu, Y.; Chen, D. Theoretical study of elastic and electronic properties of Al5Mo and Al5W intermetallics under pressure. Mater. Chem. Phys. 2017, 197, 145–153. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, X. Theoretical predict the structure, elastic anisotropy and thermodynamic properties of Al5W in Al-rich region. J. Mater. Res. Technol. 2023, 24, 1792–1801. [Google Scholar] [CrossRef]
- Xie, X.; Wei, Q.; Luo, J.; Jia, X.; Zhang, M.; Zhu, X. R32-Al5W: A new stable high-temperature alloy. Results Phys. 2024, 63, 107880. [Google Scholar] [CrossRef]
- Luo, J.; Zhang, M.; Jia, X.; Zhu, X.; Wei, Q. Determination of crystal structure and physical properties of Ru2Al5 intermetallic from first-principles calculations. Chin. Phys. B 2025, 34, 016301. [Google Scholar] [CrossRef]
- Fang, Z.; Hu, Z.; Lv, B.; Sun, B.; Wang, H.; He, P.; Wang, X.; Liang, X.B.; Jin, G. The new Iridium–Hafnium–Aluminum alloy thin films with excellent mechanical properties and oxidation resistance. Appl. Surf. Sci. 2024, 657, 159802. [Google Scholar] [CrossRef]
- Mo, L.; Zhou, X.; Liu, X.; Zhan, M.; Zhao, Y.; Du, J. Microstructure and thermal-physical properties of hypereutectic Al–Ni alloys. J. Mater. Res. Technol. 2023, 24, 6227–6237. [Google Scholar] [CrossRef]
- Hu, X.; Wang, C.; Ma, G.; He, K. Effect of Er on microstructure, electrical conductivity, mechanical properties, and corrosion resistance of an Al–Zr alloy. J. Mater. Eng. Perform. 2025, 34, 6026–6034. [Google Scholar] [CrossRef]
- Yan, H.; Zhang, W.; Chen, L.; Zhang, Y.; Wang, H.; Zhang, M.; Wei, Q. Structural, strength and fracture mechanisms of superconducting transition metal nitrides TM3N5 (TM = W and Mo). Phys. Chem. Chem. Phys. 2025, 27, 6134–6145. [Google Scholar] [CrossRef]
- Yan, H.; Chen, L.; Feng, L.; Chen, Y.; Zhang, M.; Wei, Q. Two dense semiconducting phases of LiInTe2 under high pressure. Vacuum 2024, 225, 113256. [Google Scholar] [CrossRef]
- Wang, X.; Wei, Q.; Luo, J.; Jia, X.; Zhag, M.; Zhu, X.; Wei, B. Pressure-induced phase transitions and electronic structure evolution of Ba4Au. Materials 2025, 18, 3728. [Google Scholar] [CrossRef]
- Wei, Q.; Yang, J.; Jia, X.; Luo, J.; Zhang, M.; Zhu, X. Crystal structures, mechanical properties, and electronic structure analysis of ternary FeCrAl alloys. Phys. Lett. A 2025, 533, 130228. [Google Scholar] [CrossRef]
- Chen, L.; Wei, Q.; Jia, Q.; Zhang, M.; Xu, J.; Jiang, Z. Theoretical exploring superior stiffness and strength of ternary carbosilicides TM0.5Si0.5C (TM = Cr, Mo, W) with excellent stability for extreme conditions. J. Mater. Res. Technol. 2024, 33, 9979–9991. [Google Scholar] [CrossRef]
- Luo, J.; Wei, Q.; Jia, X.; Zhang, M.; Zhu, X. Stability and properties of six new Ru3Al structures: A first-principles study of mechanical, electronic, and superconducting properties. Phys. Lett. A 2024, 525, 129922. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Togo, A. First-principles phonon calculations with phonopy and phono3py. J. Phys. Soc. Jpn. 2023, 92, 012001. [Google Scholar] [CrossRef]
- Mouhat, F.; Coudert, F.-X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 2014, 90, 224104. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Pan, Y. First-principles investigation of the structural stability and mechanical properties of TM3Al2C (TM = Mo, Cr and W) carbides. Mater. Today Commun. 2023, 37, 107178. [Google Scholar] [CrossRef]
- Wei, Q.; Yan, Y.; Jia, X.; Zhang, M. Structural stability, mechanical and electronic properties of TM5Si3B (TM = Zr, Mo, Ta, W) MAB phases. Phys. Lett. A 2024, 519, 129724. [Google Scholar] [CrossRef]
- Pugh, S.F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Philos. Mag. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Tian, M.; Zhang, X.; Wang, F. Structural, mechanical, electronic and thermodynamic properties of YBC, YB2C, YB2C2, Y2B3C2 intermetallics. Mater. Today Commun. 2024, 39, 108696. [Google Scholar] [CrossRef]
- Li, Y.; Duan, Y.; Peng, M.; Zheng, S. Structural, elastic, and thermal properties of TM5Si3C (TM = Ti, Cr, Y) carbides from first-principles calculations. Vacuum 2023, 218, 112616. [Google Scholar] [CrossRef]
- Pu, D.; Pan, Y. New insight into the structural stability, ductility and melting point of Mo5SiB2 under high-pressure environment. Vacuum 2022, 196, 110727. [Google Scholar] [CrossRef]
- Bendjemai, M.; Rached, A.A.; Husain, M.; Bentouaf, A.; Rahman, N.; Tirth, V.; Algahtani, A.; Alghtani, A.H.; Al-Mughanam, T. First-principles calculations to investigate structural, elastic and thermodynamic properties of new M2ScSnC2 (M = V or Nb) quaternary compounds for 312 MAX phases. J. Mater. Res. Technol. 2023, 24, 3211–3221. [Google Scholar] [CrossRef]
- Pu, D.; Pan, Y. First-principles investigation of solution mechanism of C in TM–Si–C matrix as the potential high-temperature ceramics. J. Am. Ceram. Soc. 2022, 105, 2858–2868. [Google Scholar] [CrossRef]
- Anderson, O.L. A simplified method for calculating the Debye temperature from elastic constants. J. Phys. Chem. Solids 1963, 24, 909–917. [Google Scholar] [CrossRef]
- Panda, K.B.; Chandran, K.S.R. Determination of elastic constants of titanium diboride (TiB2) from first principles using FLAPW implementation of the density functional theory. J. Comput. Mater. Sci. 2006, 35, 134–150. [Google Scholar] [CrossRef]
- Li, B.; Qi, H.; Duan, Y.; Peng, M. First-principles calculations: Structural stability, electronic structure, optical properties and thermodynamic properties of AlBN2, Al3BN4 and AlB3N4 nitrides. Mater. Sci. Semicond. Process. 2023, 160, 107400. [Google Scholar] [CrossRef]
- Wu, R.; Liu, D.; Lai, J.; Jiang, D. Prediction of high temperature mechanical and thermodynamic properties of W–Mn alloys based on first principles method. Fusion Eng. Des. 2024, 200, 114218. [Google Scholar] [CrossRef]

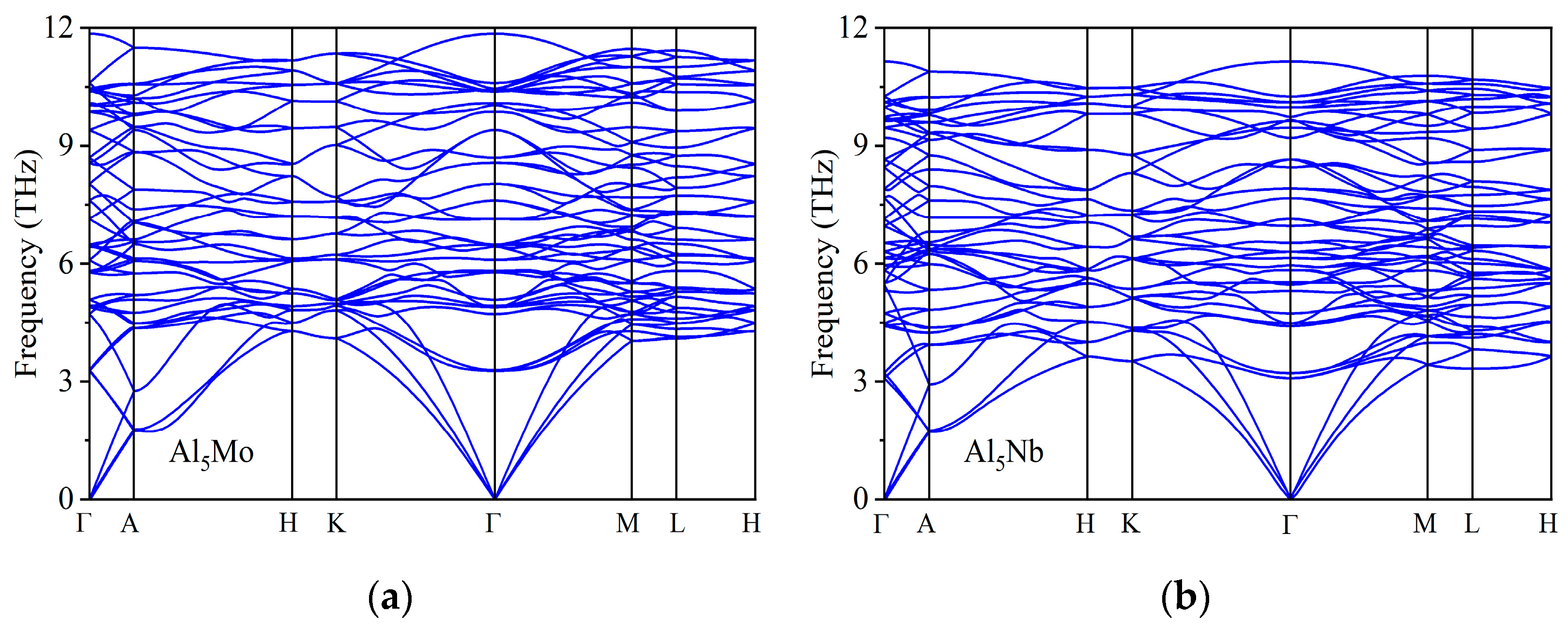
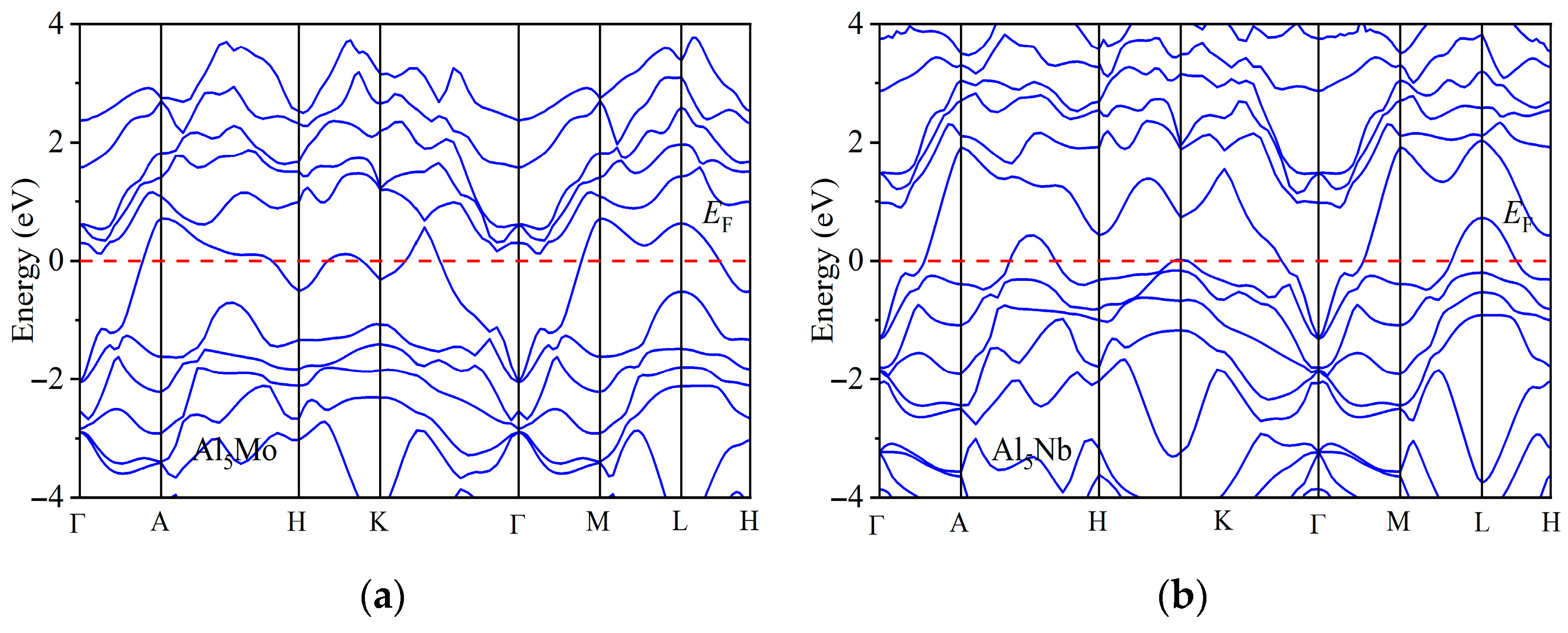
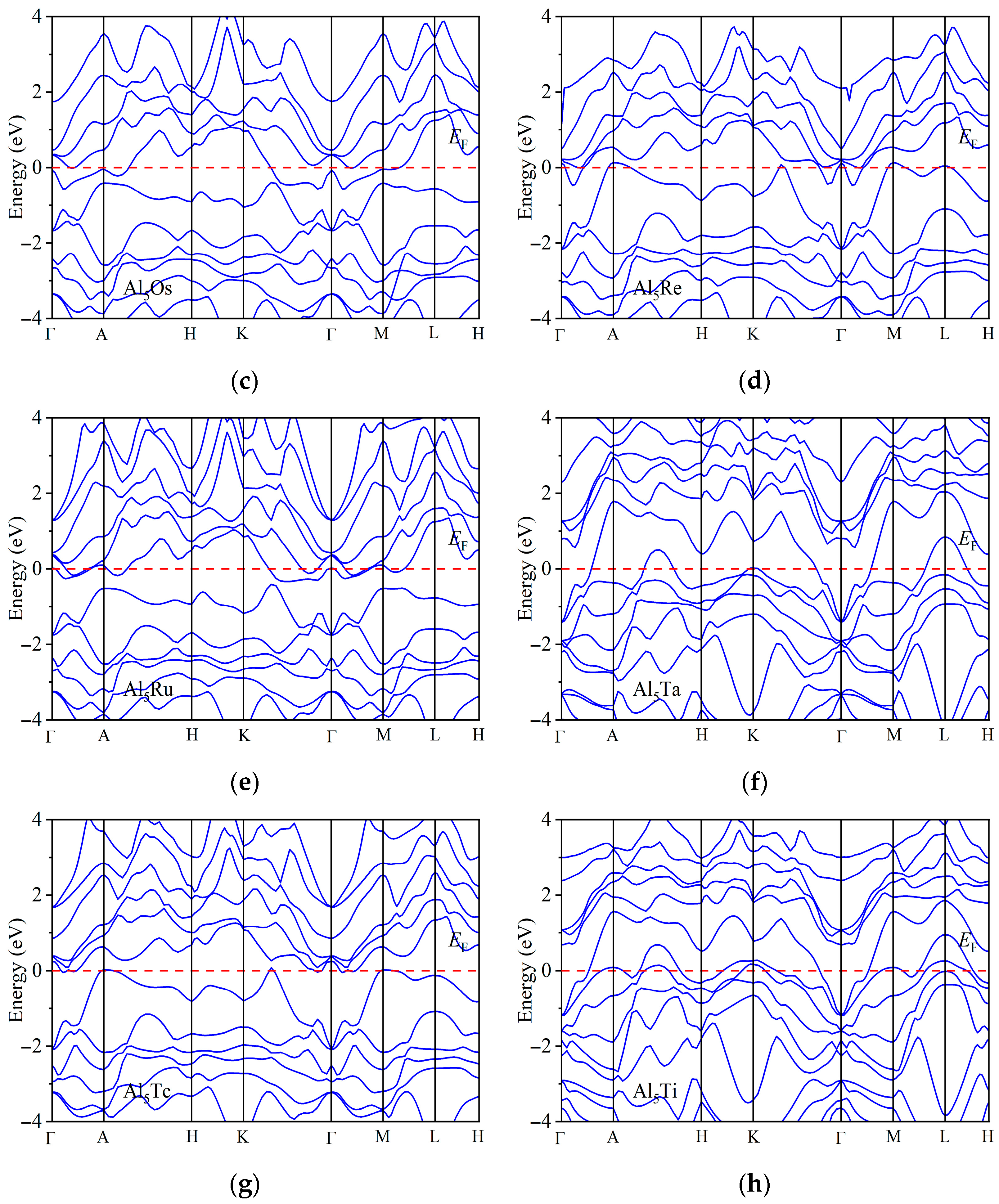
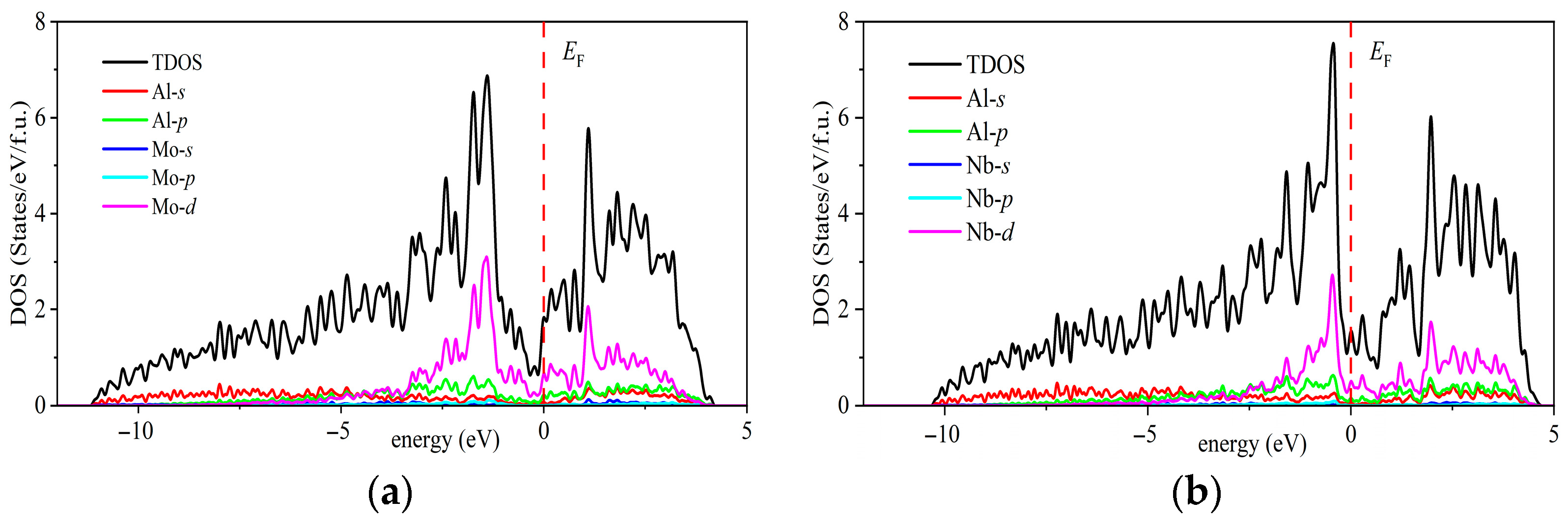
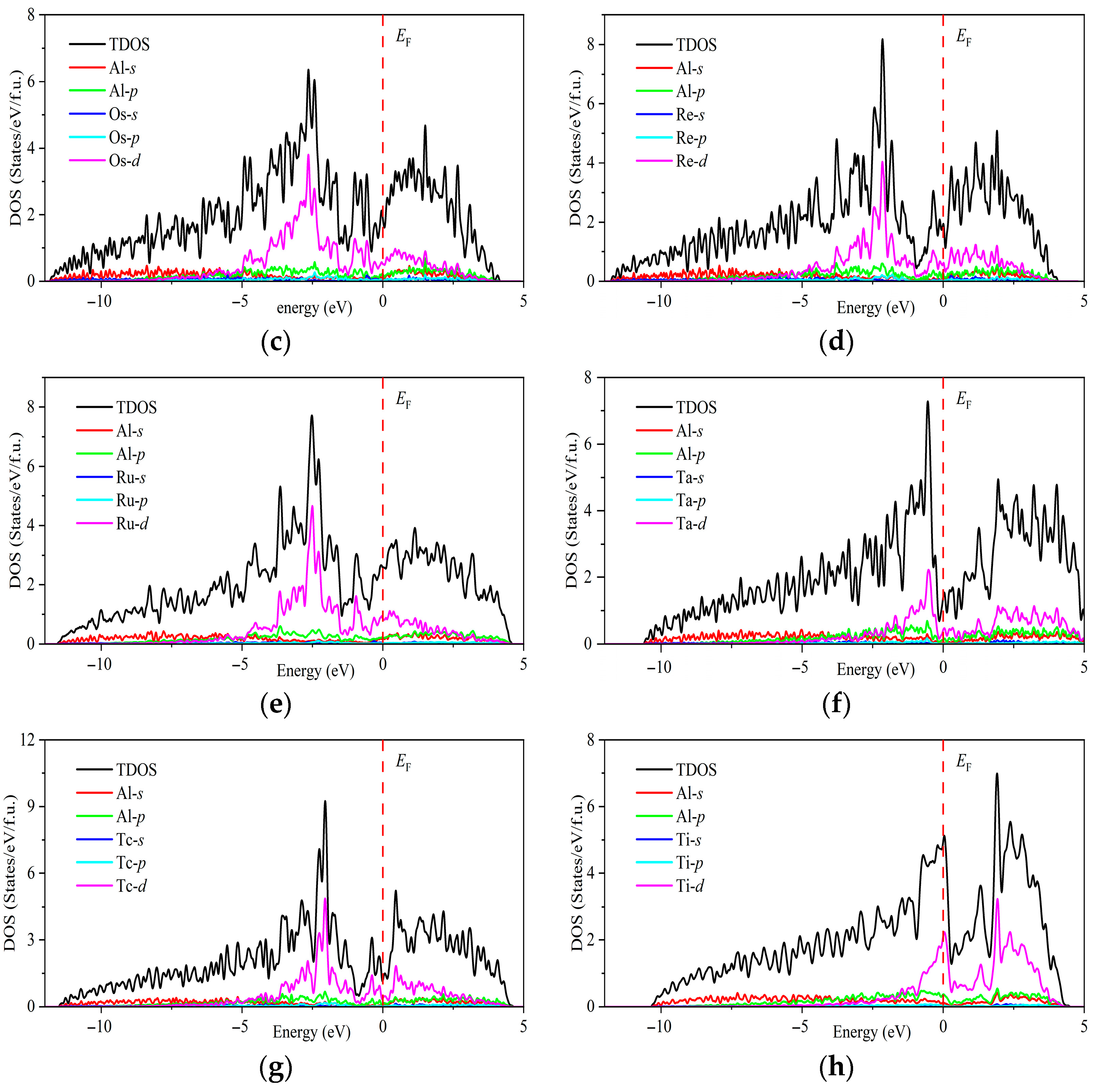
| Space Groups | Al5TM | a | c | ρ | Ef | Ref. |
|---|---|---|---|---|---|---|
| R32 | Al5Mo | 4.95 | 13.16 | 4.125 | −0.295 | this work |
| P63 | Al5Mo | 4.92 | 8.89 | −0.231 | [26] | |
| R32 | Al5Nb | 5.05 | 13.35 | 3.851 | −0.241 | this work |
| R32 | Al5Os | 4.73 | 13.90 | 6.015 | −0.186 | this work |
| R32 | Al5Re | 4.84 | 13.29 | 5.923 | −0.176 | this work |
| R32 | Al5Ru | 4.76 | 13.73 | 4.364 | −0.245 | this work |
| R32 | Al5Ta | 5.04 | 13.35 | 5.353 | −0.183 | this work |
| R32 | Al5Tc | 4.87 | 13.17 | 4.268 | −0.257 | this work |
| R32 | Al5Ti | 5.02 | 13.45 | 3.096 | −0.206 | this work |
| P63 | Al5W | 4.92 | 8.89 | −0.151 | [26] |
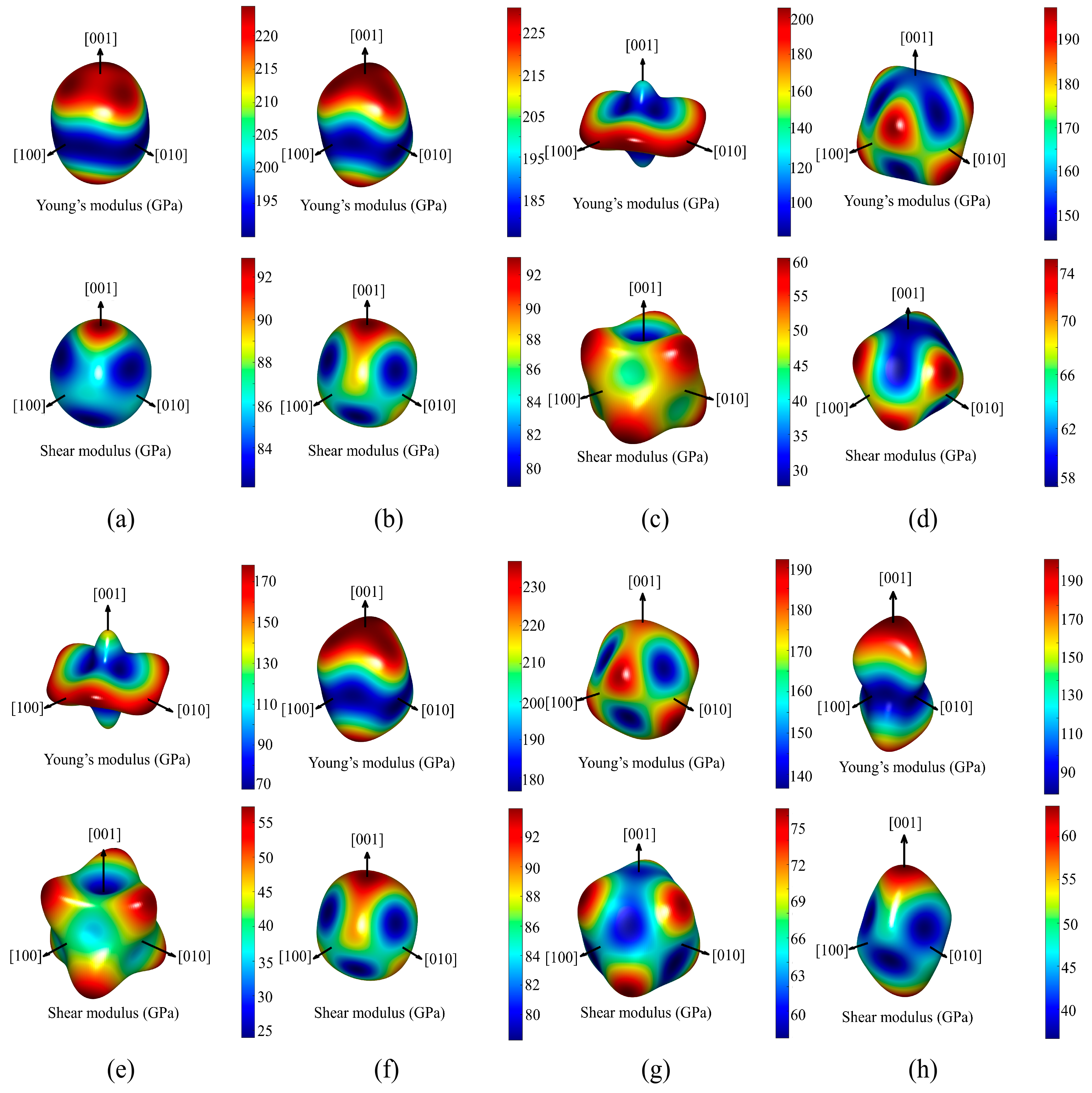
| Al5TM | C11 | C12 | C13 | C14 | C22 | C23 | C33 | C44 | C55 | C66 |
|---|---|---|---|---|---|---|---|---|---|---|
| Al5Mo | 216 | 58 | 64 | −3 | 216 | 64 | 250 | 93 | 93 | 79 |
| Al5Nb | 199 | 48 | 55 | −8 | 199 | 55 | 255 | 94 | 94 | 76 |
| Al5Os | 250 | 78 | 87 | 11 | 250 | 87 | 179 | 29 | 29 | 86 |
| Al5Re | 225 | 68 | 101 | 13 | 225 | 101 | 225 | 61 | 61 | 79 |
| Al5Ru | 215 | 75 | 76 | 12 | 215 | 76 | 181 | 26 | 26 | 70 |
| Al5Ta | 202 | 49 | 58 | −9 | 202 | 58 | 263 | 95 | 95 | 77 |
| Al5Tc | 206 | 66 | 69 | 13 | 206 | 69 | 216 | 63 | 63 | 68 |
| Al5Ti | 124 | 66 | 43 | −10 | 124 | 43 | 224 | 67 | 67 | 29 |
| Al5TM | G | B | E | B/G | v |
|---|---|---|---|---|---|
| Al5Mo | 85.5 | 116.3 | 205.9 | 1.36 | 0.21 |
| Al5Nb | 84.9 | 106.3 | 201.1 | 1.25 | 0.18 |
| Al5Os | 50.1 | 130.3 | 133.3 | 2.60 | 0.33 |
| Al5Re | 65.8 | 134.6 | 169.8 | 2.04 | 0.29 |
| Al5Ru | 44.2 | 118.3 | 117.9 | 2.68 | 0.33 |
| Al5Ta | 85.7 | 109.9 | 204.1 | 1.28 | 0.19 |
| Al5Tc | 65.7 | 113.7 | 165.2 | 1.73 | 0.26 |
| Al5Ti | 48.2 | 84.9 | 121.7 | 1.76 | 0.26 |
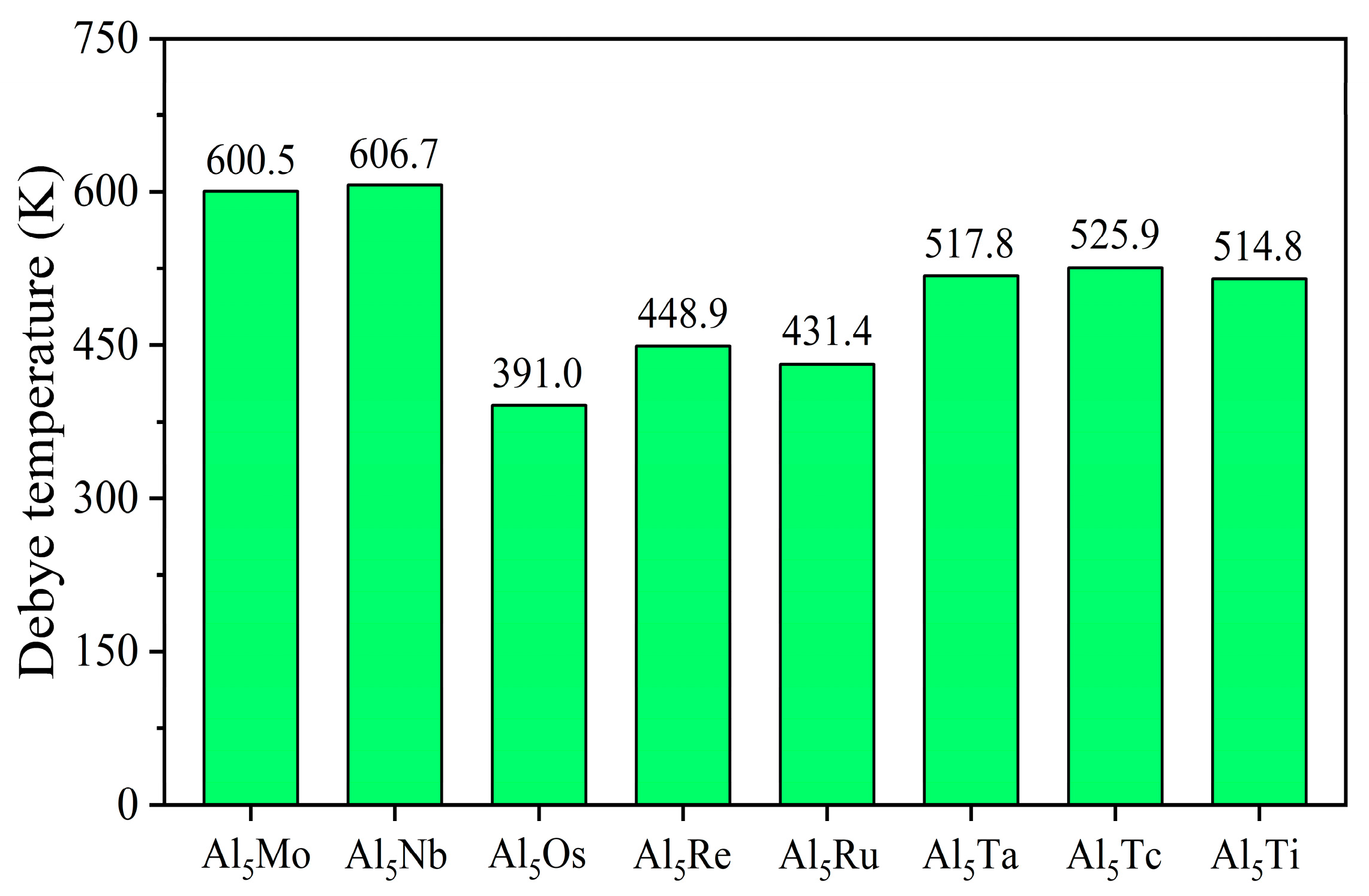
| Al5TM | |||
|---|---|---|---|
| Al5Mo | 7542 | 4590 | 5070 |
| Al5Nb | 7549 | 4696 | 5174 |
| Al5Os | 5724 | 2886 | 3236 |
| Al5Re | 6127 | 3334 | 3719 |
| Al5Ru | 6373 | 3183 | 3571 |
| Al5Ta | 6454 | 3994 | 4405 |
| Al5Tc | 6866 | 3921 | 4359 |
| Al5Ti | 6942 | 3947 | 4388 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Wei, Q.; Luo, J.; Zhang, M.; Wei, B. Structural Stability, Mechanical, and Electronic Properties of Al5TM (TM = Mo, Nb, Os, Re, Ru, Ta, Tc, Ti) Intermetallics. Nanomaterials 2025, 15, 1221. https://doi.org/10.3390/nano15161221
Yang J, Wei Q, Luo J, Zhang M, Wei B. Structural Stability, Mechanical, and Electronic Properties of Al5TM (TM = Mo, Nb, Os, Re, Ru, Ta, Tc, Ti) Intermetallics. Nanomaterials. 2025; 15(16):1221. https://doi.org/10.3390/nano15161221
Chicago/Turabian StyleYang, Jiaxiang, Qun Wei, Jing Luo, Meiguang Zhang, and Bing Wei. 2025. "Structural Stability, Mechanical, and Electronic Properties of Al5TM (TM = Mo, Nb, Os, Re, Ru, Ta, Tc, Ti) Intermetallics" Nanomaterials 15, no. 16: 1221. https://doi.org/10.3390/nano15161221
APA StyleYang, J., Wei, Q., Luo, J., Zhang, M., & Wei, B. (2025). Structural Stability, Mechanical, and Electronic Properties of Al5TM (TM = Mo, Nb, Os, Re, Ru, Ta, Tc, Ti) Intermetallics. Nanomaterials, 15(16), 1221. https://doi.org/10.3390/nano15161221







